1. Introduction
RGB-D sensors are used to identify color and depth simultaneously in real time. With the development of low-cost commercial RGB-D sensors such as Kinect and PrimeSense, computer vision technologies utilizing depth images or color and depth images have been used to develop many vision applications such as object tracking [
1,
2], pose estimation [
3,
4,
5] for human-computer interaction (HCI), 3D modeling [
6,
7,
8] and video surveillance [
9,
10,
11].
The practical use of depth information is recognized as a key technology for many three-dimensional multimedia applications. Over the years, researchers have attempted to develop technologies that generate a high-quality three-dimensional view. Using depth information, high-quality three-dimensional images can be generated in the form of a stereoscopic image, which provides the necessary sense of reality [
12]. Accordingly, extensive multimedia research based on depth information has been conducted, such as depth image-based rendering (DIBR) [
12,
13], free-viewpoint television (FTV) [
14,
15], augmented reality (AR) [
16], virtual reality (VR) [
17] and mixed reality (MR) [
18].
However, depth sensors that rely on infrared laser light with a speckle pattern (e.g., the Kinect sensor) suffer from missing or inaccurate depth information. These problems are caused by the incorrect matching of infrared patterns and a positional difference between the internal infrared sensors. Incorrect pattern matching yields numerous errors, such as optical noise, loss of depth values and flickering. Moreover, the different positions of the depth sensor, which is composed of an infrared projector and camera [
19], mean that the rear regions may be occluded by the front object, making it difficult for depth information to be measured. In particular, there can be much noise around the object shape, as shown in
Figure 1. The result is low-quality depth information, which makes it difficult to utilize the computer vision technologies [
20,
21,
22]. For this reason, enhanced depth information is urgently required for applications.
A number of methods for enhancing the quality of depth information and overcoming the limitations of depth sensors have been proposed. Matyunin et al. [
23] suggested an algorithm that uses color and motion information derived from the image sequences to fill occlusion regions of the depth image and improve the temporal stability. This algorithm can make depth images more stable, rectify errors and smooth the image. The confidence metric for motion vectors, spatial proximity and occlusion is highly dependent on the depth image. Fu et al. [
24] proposed a divisive normalized bilateral filtering method that is a modification of the method proposed in [
25], filling up the depth holes in the spatial domain and reducing the noise in the temporal domain. However, this approach leads to a blurry depth image and has a high computational cost. Joint bilateral-based methods, such as joint bilateral filter [
26], joint bilateral upsampling [
27] and weighted mode filtering [
28], aim to improve the quality of the depth image by utilizing an aligned color and depth image. In these methods, the color image is used as a guide while the edges are preserved. Unfortunately, these methods frequently yield blurring effects and artifacts around boundaries in regions with large holes. Chan et al. [
29] presented a noise-aware filtering method that enhances the quality and resolution of the depth image using an adaptive multi-lateral upsampling filter. However, this approach must be implemented on a GPU for real-time performance, and the parameters in the heuristic model must be set manually. Le et al. [
30] suggested a directional joint bilateral filtering scheme based on [
26]. This method fills the holes and suppresses the noise in the depth image using an adaptive directional filter that is adjusted on the basis of the edge direction of a color image. Although the directional joint bilateral filter performs well if the depth hole regions are located near the object boundaries, it is only applicable to four cases described by the edge directions. Lin et al. [
31] proposed a method based on inpainting [
32] for removing artifacts and padding the occlusions in a depth image. This approach is designed to inpaint the removed regions in a color image by assigning a priority to pixel locations and filling the removed regions based on these priorities. Though this method can eliminate depth noise and temporal variations and smooth inaccurate depth values, the processed depth values are changed from their original values. The computation time remains a problem for real-time applications. Gong et al. [
33] incorporated guidance information from an aligned color image for depth inpainting by extending the inpainting model and the propagation strategy of the fast marching method [
34]. This method reconstructs unknown regions simply but efficiently from the surrounding areas without additional information. However, this approach cannot convey texture information in the holes. Despite all efforts, these methods are time consuming and deliver blurry results, especially when the depth hole area is large.
To extract the object regions, many image segmentation techniques based on color information have been developed [
35,
36,
37,
38,
39]. However, these methods suffer from challenging issues concerning illumination variations, shadows, and complex textures. RGB-D sensors have been employed to solve the problems of color-based image segmentation methods, because depth information is less affected by these issues, even if an image has shadows or complex textures [
10]. One of the first approaches based on the fusion of color and depth information was developed by Gordon et al. [
40], who presented the background model using an approximation of a 4D Gaussian mixture. Using a unimodal approximation, each image pixel is classified as foreground when the background exists in fewer sequences. However, the background model does not provide the correct fit when the background is dynamic and has various values per pixel. Schiller and Koch [
41] proposed an object segmentation method by combining the segmentation of depth measurements with segmentation in the color domain using adaptive background mixture of Gaussian (MoG) models. To determine the depth reliability, the authors concluded that the amplitude information provided by the ToF camera is more effective than the depth variance. Fernandez-Sanchez et al. [
9] generalized the background subtraction algorithm by fusing color and depth information based on a Codebook-based model [
42]. In this method, the depth information is considered as the fourth channel of the codebook, and provides the bias for the foreground based on color information. This approach was extended [
10] by building a late fusion mask technique based on morphological reconstruction to reduce the noise of the disparity estimated by stereo vision. Camplani and Salgado [
43] suggested an efficient combination of classifiers based on a weighted average. One of the classifiers is based on the color features and the other is based on the depth feature, and the support of each classifier in the ensemble is adaptively modified by considering the foreground detected in the previous sequences and the edges of the color and depth images. del Blanco et al. [
11] developed a Bayesian network using a background subtraction method based on [
43] to distinguish foreground and background regions from depth sequence images. This method takes advantage of a spatial estimation model and an algorithm for predicting the changes of foreground depth distribution. However, many of these approaches are designed for video surveillance and require image sequence pairs. Moreover, the segmentation results still contain much noise in the foreground and background.
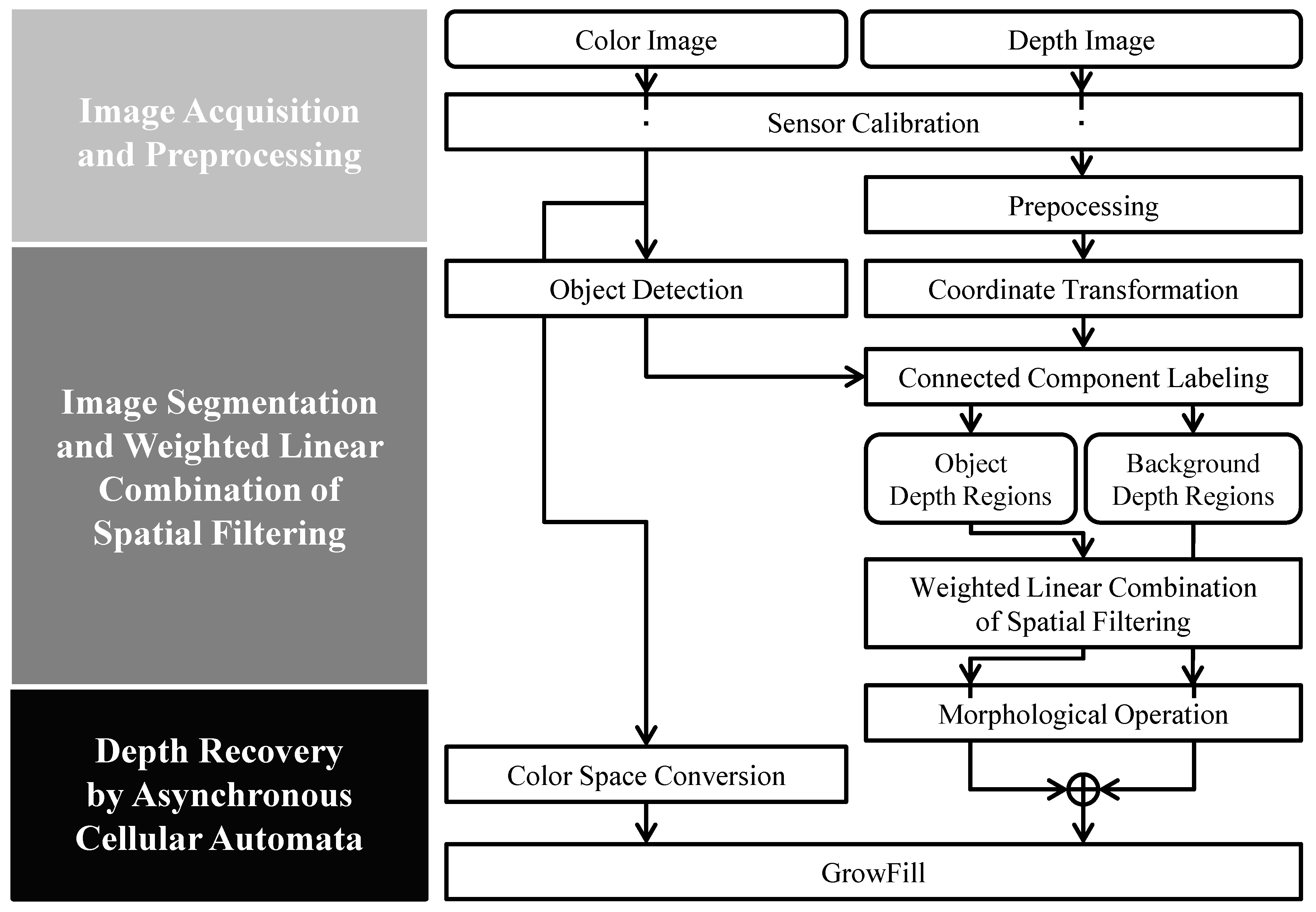
In this paper, we propose a high-performance, low-complexity algorithm based on color and depth information by using asynchronous cellular automata with neighborhood distance maps. Our approach aims to fill the missing depth holes and recover inaccurate object shapes in depth images. The proposed cellular automata-based depth recovery covers whole regions of the inaccurate and noisy depth image. Moreover, a weighted linear combination of spatial filtering algorithms is utilized to fill the inner depth holes in the object. Considering that humans are more sensitive to objects in an image than to its background [
44], we focus on depth holes in the object regions. In general, depth hole filling methods based on color information utilize the color values of pixels that have a valid depth value to fill the neighboring depth holes. These methods fill the depth holes by calculating color-metric distances between the color pixel corresponding to the depth hole and the color pixels having a valid depth value. However, if the depth values of the reference pixels are inaccurate because of inherent depth sensor issues (e.g., misaligned color and depth values around the hand, as depicted in
Figure 1c, top row), there is a high risk of incorrect depth values filling in the hole regions. To minimize this risk, we design a weighted linear combination of spatial filtering algorithms by reflecting the characteristics of the depth holes in the object (e.g., the blue and green markers in
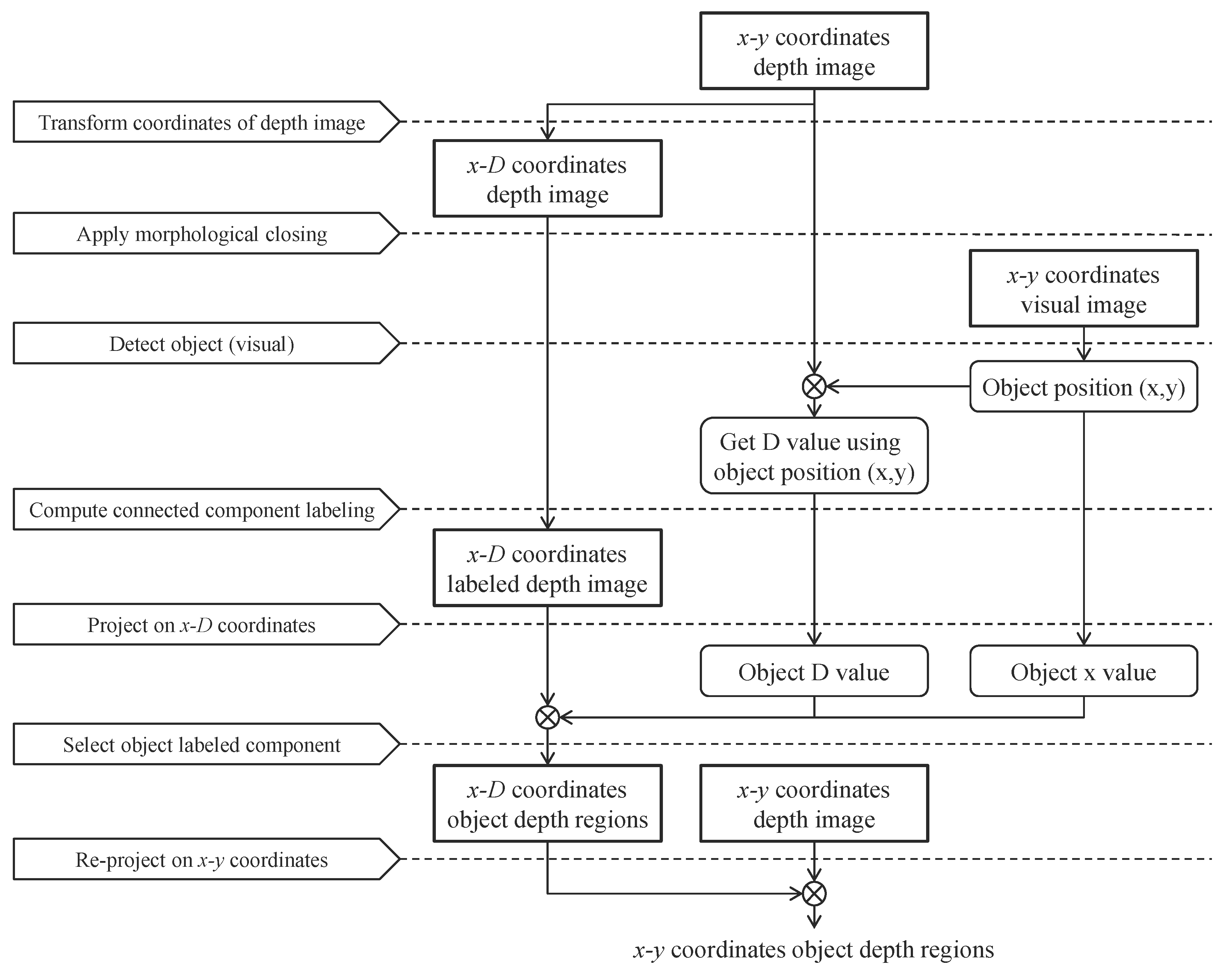
Figure 1). In this algorithm, depth information from the rear regions is used to fill the inner holes. To extract the object depth regions, we introduce an image segmentation algorithm using the connectivity values in the depth domain.
The remainder of this paper is organized as follows.
Section 2 describes the proposed method in detail, including an introduction to image segmentation based on the depth domain, the procedure for filling inner depth holes in an object, and the recovery of a depth image.
Section 3 presents our experimental results, and
Section 4 states the conclusions from this research.
3. Experiments and Discussion
To validate our proposed method, we conducted a series of experiments on real-world Kinect datasets and the Tsukuba Stereo Dataset [
53,
54]. For the real-world datasets, we captured color and depth image pairs using the Kinect and obtained a public Kinect dataset [
9,
43,
55]. The experimental results have been compared with state-of-the-art methods. All experiments were conducted on a desktop computer with Intel i7-3770 3.4 GHz and 16 GB RAM.
The experiments were as follows:
Object segmentation (quantitative and qualitative evaluations).
Inner hole filling (qualitative evaluation).
Depth recovery (quantitative and qualitative evaluations).
ACA, NDMs, and Lab color space on the proposed method (quantitative evaluation).
Enhanced depth images and a practical application of the proposed method.
We evaluated the performance of the object segmentation method with Fernandez’s Kinect dataset [
9] and compared our method with the mixture of Gaussians based on color and depth (MOG4D) [
41], the codebook [
42] based on depth (CB1D) and based on color and depth (CB4D), and the depth-extended codebook (DECB) [
9].
To evaluate the results, the following measures are used:
True positive (TP): the sum of foreground classified as foreground.
True negative (TN): the sum of background classified as background.
False positive (FP): the sum of background misclassified as foreground.
False negative (FN): the sum of foreground misclassified as background.
Precision (P): the proportion of TP and the total classified as foreground, .
Recall (R): the proportion of TP and the ground truth, .
score: the harmonic mean of precision and recall, .
ranges from 0–1, with higher values indicating better performance.
Fernandez’s Kinect dataset [
9] provides image pairs including color, depth, and ground truth images for the foreground. As our proposed method focuses on single object, five different image pairs (Wall #93, Hallway #120, Chair Box #278 and #286, Shelves #197) were selected for the quantitative and qualitative tests. Following the literature, we compare the results reported in [
9], as shown in
Table 1 and
Figure 10. A pre-trained body [
56] and hand [
57] detector were used as the object detector in our algorithm.
Table 1 presents the
scores. Our method outperforms MOG4D, CB1D, and CB4D, and has very similar performance to DECB. From
Figure 10, we can observe that all the compared methods generate much noise on the whole image. The DECB results, which give an average
score that is 0.008 higher than that of our method, also contain much more noise than the image given by our algorithm. In particular, none of the compared methods can extract object regions that have the depth values of the depth image, as shown in
Figure 10e. As the results are used for the following depth recovery algorithms, all the depth regions of the object should be extracted. Otherwise, the actual depth information may be distorted. In addition, when a region with no assigned depth is generated as a segmentation result, the region cannot be estimated in the following algorithms. The purpose of the segmentation at this stage is to extract only the object regions that have actual depth values to fill depth holes or manipulate the object boundary to recover depth values. Therefore, the object segmentation results should be object-oriented and the noise level should be low. Our method is best suited for this purpose.
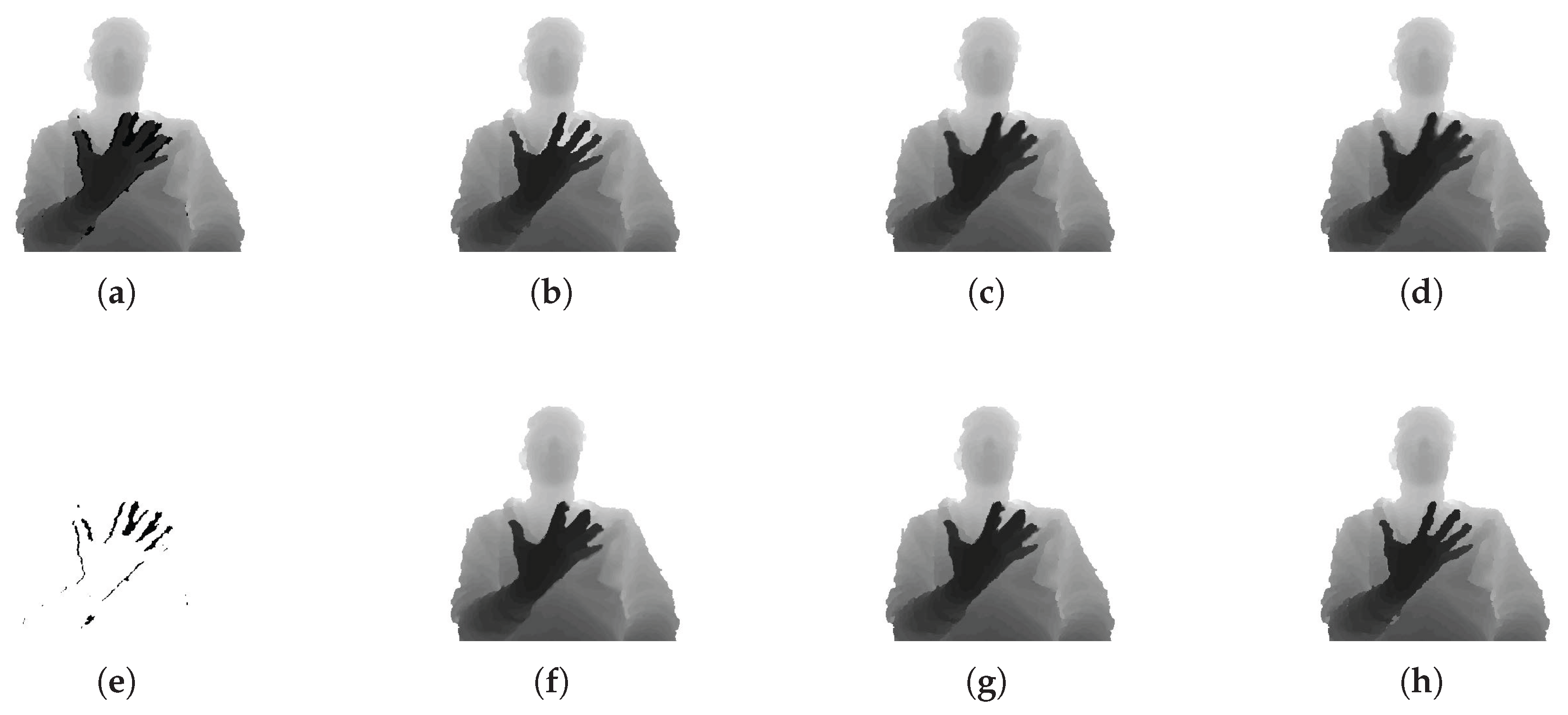
The following describes the performance of the inner hole filling methods, as shown in
Figure 11. To evaluate the performance of inner hole filling, we collected color and depth image pairs acquired by the Kinect sensor in an indoor environment. As in
Figure 11e, inner holes exist in the rear object (body) as a result of the front object (hand) in the segmented regions. The results of inner hole filling by the proposed method are compared to those of five previous methods: flood-fill based on morphological reconstruction [
58], Navier–Stokes-based inpainting [
59], fast marching inpainting [
34], joint bilateral filtering [
26], and guided depth inpainting followed by guided filtering [
33]. We set
,
, and
in Equation (
3) for the proposed method, and set the radius value to 11,
, and
for the methods in [
26,
33,
34,
59], as per the values recommended in [
33].
From the results of the methods in [
26,
33,
34,
59], we can easily observe that the depth values in the inner holes are filled by the depth values of both front and rear objects idirectionally, so that the filled regions are blurred and have incorrect depth values. The methods in [
26,
33] use both the color and depth images. In these methods, the hole regions of the rear object are affected by the front depth values when the inner holes are filled based on color information. This is because the limitations of the depth sensor cause the depth and color regions of the object to be imprecisely matched. In the case of [
34,
59], which use only depth information, the blur effect is inevitable because the information on the boundary is initially unknown. In contrast, the method based on [
58] and the proposed method fill the holes without spreading the depth values of the front object or blurring the output. The difference is that the method based on [
58] fills the holes with the same depth value per hole, which results in a dissimilarity between the filled and actual depth values, whereas the proposed method fills the holes with similar depth values to the actual depth values. The proposed method considers the characteristics of the inner holes and fills them with similar depth values as the rear object without expanding the depth values of the front object. As a result, the proposed method gives the best results among all the methods compared in this experiment.
To evaluate the GrowFill values given by the proposed method, we used the Tsukuba Stereo Dataset. This dataset provides a total of 1800 image pairs including color, ground truth depth (disparity), and occlusion images. The experiments were conducted using both the color images and occluded depth images. The occluded depth images are generated by excluding the occlusion regions from the ground truth depth. In the dataset, all image pairs are based on the right camera, and the color images are illuminated in daylight. We compared our method with the techniques developed by Telea [
34], Lin [
31], and Gong [
33]. The results of Lin’s method [
31] are reported in the corresponding paper. Unless specified otherwise, the neighborhood system of our method was implemented with Moore’s system. The numerical results are evaluated in terms of the peak signal-to-noise ratio (PSNR) [
60] in decibels (dB), the structural similarity (SSIM) [
61] against the ground truth, and the runtime in seconds (s). The runtime is averaged over 10 repeated experiments of our implementation in the C language. Ten different image pairs (frame numbers 1, 214, 291, 347, 459, 481, 509, 525, 715 and 991) were selected [
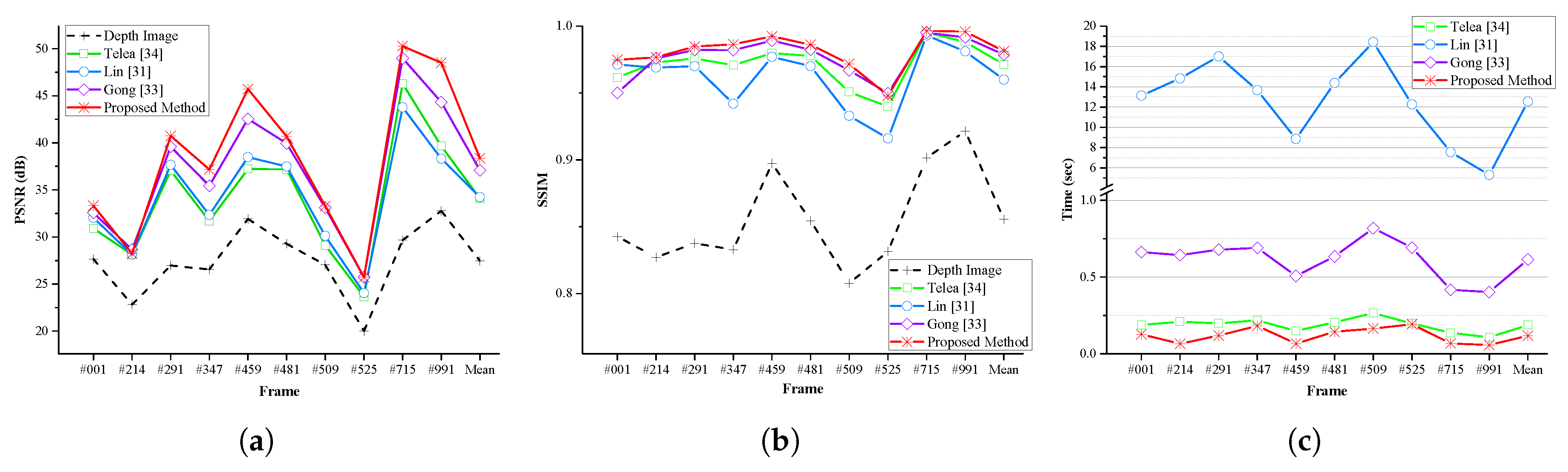
31] and both quantitative and qualitative tests were performed.
Figure 12 presents the visual results of the qualitative evaluation, and
Table 2 and
Figure 13 illustrate the results of the quantitative evaluation. The results obtained from each method show that the proposed method gives better performance than the previous techniques on both the quantitative and qualitative evaluations. The proposed method gives the best performance in all but two cases in the quantitative evaluation results. Frame number 214 (PSNR of Gong’s method [
33] is 0.425 dB higher than that of the proposed method) and frame number 525 (SSIM of Gong’s method [
33] is about 0.002 higher than that of the proposed method). In particular, the proposed method is the fastest among those compared here for all selected datasets. On average, for the selected dataset, the proposed method improves the PSNR by 10.898 dB, whereas the methods of Telea [
34], Lin [
31], and Gong [
33] produce improvements of 6.627 dB, 6.772 dB, and 9.620 dB, respectively. Our method improves the SSIM value by 0.126, compared with enhancements of 0.116, 0.105, and 0.124, respectively, for the other approaches. The average runtime of the proposed method is 0.118 s, faster than that of Telea’s method [
34] (0.187 s) and Gong’s method [
33] (0.615 s), and considerably quicker than Lin’s method [
31] (12.543 s).
Table 3 presents the experimental results using the entire Tsukuba Stereo Dataset. In this experiment, the proposed method was compared with the methods of Telea [
34] and Gong [
33], which represent the fastest and best performing methods among those compared in the previous experiments, respectively. Additionally, we implemented the proposed method with both the Moore and von Neumann neighborhood systems. It is clear that the proposed method outperforms the compared methods. On average, for the entire dataset, the proposed method with the Moore and von Neumann neighborhood systems improves the PSNR by 14.485 dB and 14.067 dB and enhances the SSIM value by 0.116 and 0.115 in 0.138 s and 0.057 s, respectively. The methods of Telea [
34] and Gong [
33] improve the PSNR by 10.691 dB and 13.298 dB and the SSIM value by 0.109 and 0.114 in 0.117 s and 0.544 s, respectively. In particular, the proposed method with Moore’s neighborhood system achieves the best results in terms of PSNR and SSIM, and the proposed method with the von Neumann neighborhood system is the fastest. From these results, we observe that the proposed method performs best among all compared methods, regardless of the neighborhood system used.
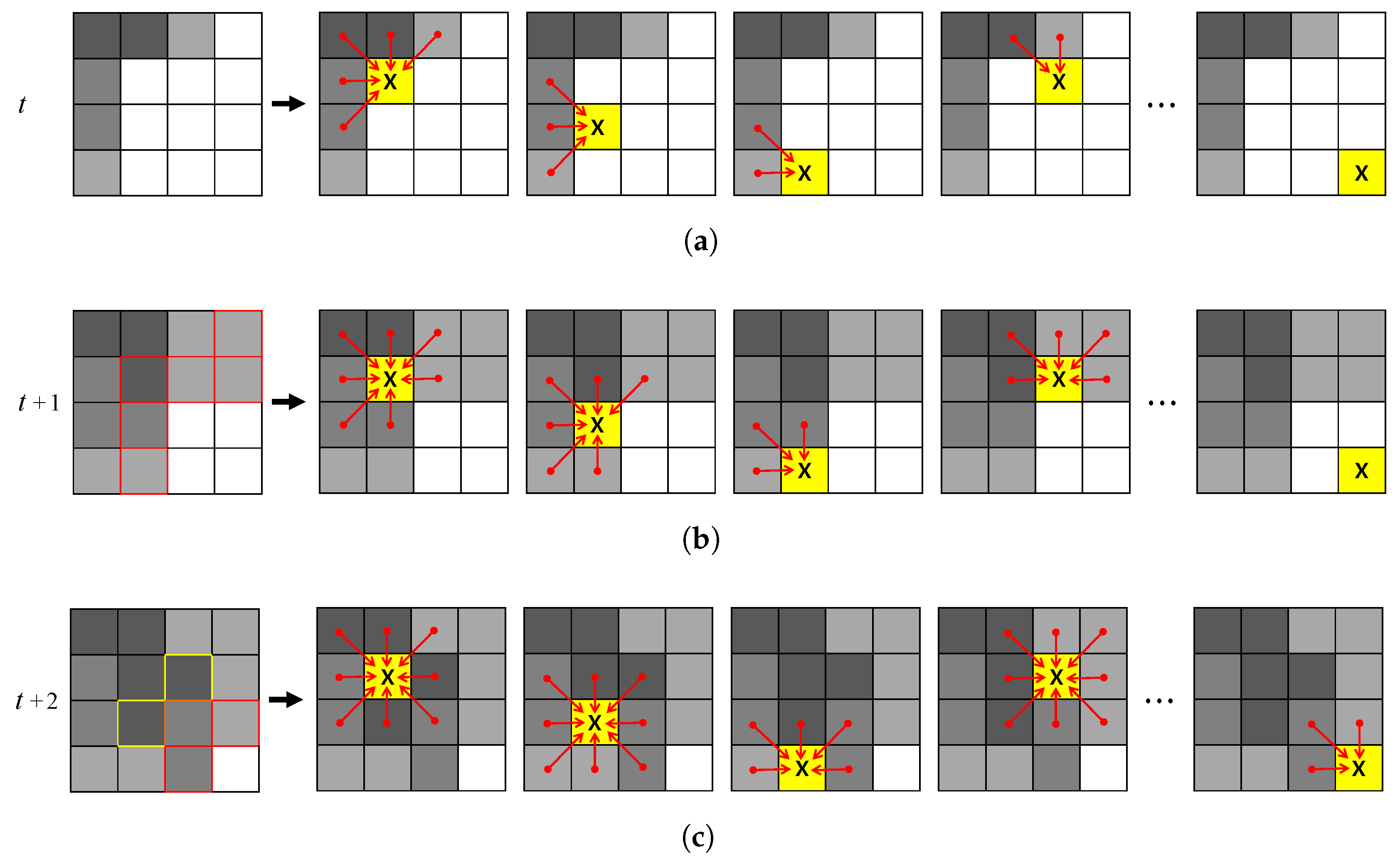
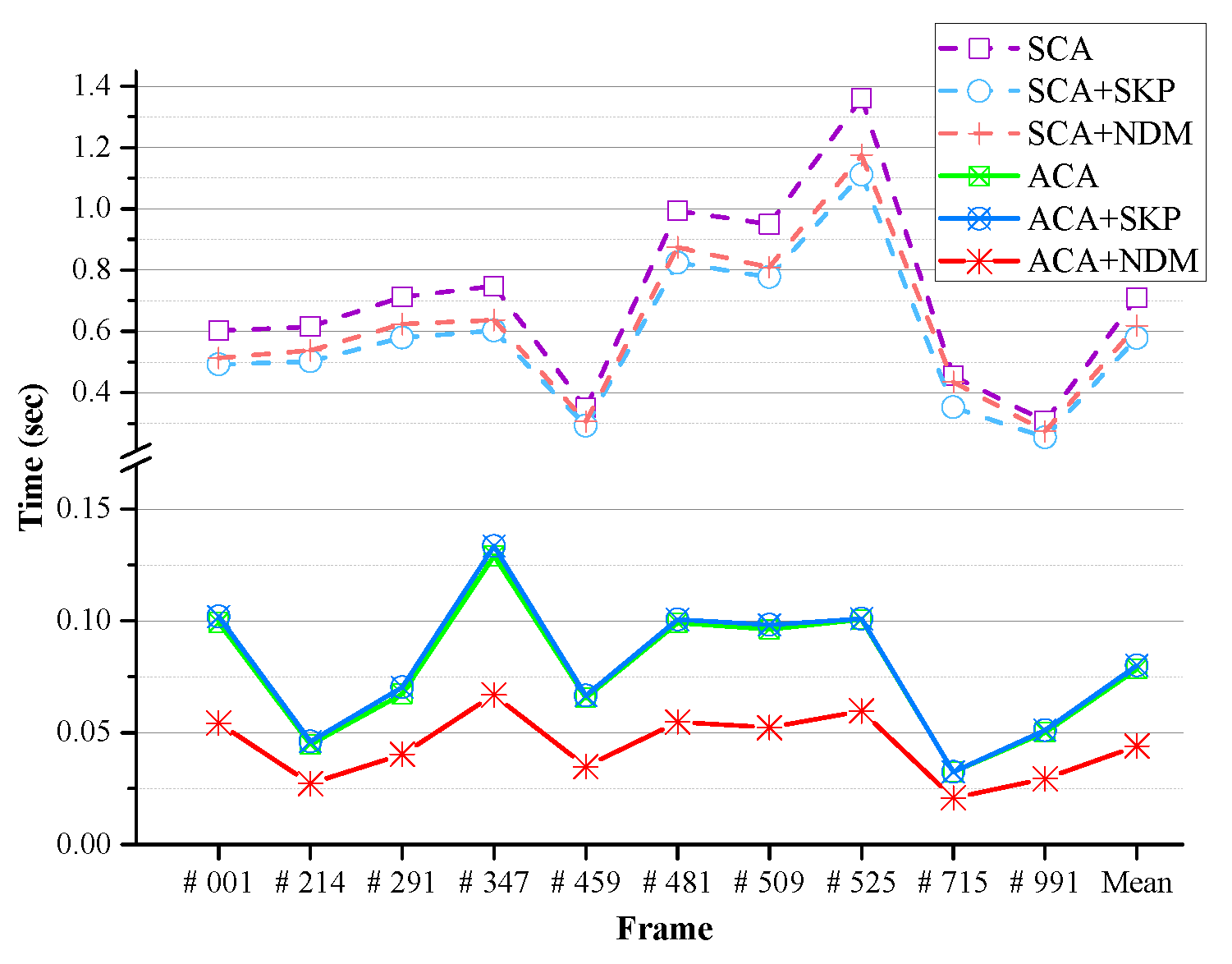
In addition, we compared the performance of the internal algorithms of the proposed method (GrowFill) to verify the effects of the ACA and the NDM.
Table 4 and
Table 5 present the quantitative results for both SCA- and ACA-based methods with Moore’s neighborhood system on the selected Tsukuba Stereo Dataset, respectively. In the experiments, the NDM of our method was compared with the skipping method (SKP) suggested in [
62] to reduce the computational cost. We can see that the PSNR, SSIM, and number of iterations of the algorithms did not deteriorate with the SKP or NDM schemes. However, the runtime is reduced by using the schemes. The pure ACA-based method is about 4.4 times faster than the pure SCA-based method. Nonetheless, the proposed method based on ACA combined with NDM is about 1.3-times faster than the pure ACA-based method, and there is no fall-off in quality. As a result, the proposed method (ACA + NDM) is about six-times faster than the pure SCA-based method. The method based on ACA combined with SKP is slower than the pure ACA-based method, although the method based on SCA combined with SKP is faster than the pure SCA-based method. From these results, we can observe that SKP works faster based on SCA, not on the ACA. In the ACA-based experiments, the method with NDM is about 1.4-times faster than the ACA-based method with SKP.
Figure 14 compares the runtimes of each internal algorithm. In all cases, the ACA-based methods are faster than the SCA-based methods. Further, the proposed method (ACA + NDM) is the fastest. The results in the tables show that the pure ACA-based method requires only one-third of the number of iterations in the SCA-based method under the same experimental conditions. Note that the runtime can only be reduced by reducing the number of iterations. In the
Appendix A, the results obtained with the von Neumann neighborhood system are described in detail.
Table 6 compares the internal algorithms of our method with the Moore and von Neumann neighborhood systems on the entire Tsukuba Stereo Dataset. We can see that the proposed method (ACA + NDM) with the Moore and von Neumann neighborhood system is about 6.5 and 8 times faster than the pure SCA-based method, though the PSNR decreases slightly (by about 0.09 and 0.105 dB, respectively).
The results of the comparison between the RGB and Lab color spaces are presented in
Table 7. The experiments show that the PSNR and SSIM performance is improved, and the number of iterations and runtime are decreased, by transforming from the RGB to Lab color space. Thus, the change of color space is an effective means of improving the performance of the algorithm.
Finally, we conducted experiments on the real-world dataset [
43,
55] and our own dataset to verify the effectiveness of our enhancement method. For the depth normalization, we set
m and
m (near range) for our data and
m and
m (default range) for the dataset in [
43,
55]. The extracted object (
Figure 15c) and background (
Figure 15d) regions were utilized to recover accurate depth information around the object. By taking advantage of the extracted object regions and morphological operations, depth regions around the object were set as the estimable regions in the GrowFill. The yellow marker in
Figure 15e indicates the original depth holes. The red and orange markers in
Figure 15e indicate the expanded depth holes by using the morphological operations on the object and background regions, respectively. The disk-shaped kernels with
for the object and
for the background regions were used in the morphology. The reason for expanding the depth hole is to recover the correct depth information by removing the incorrect depth information in the original depth image as shown in
Figure 16, top row, in which the color regions indicate the corresponding object depth regions and it can be noticed that the background also appears in the object depth regions.
Figure 15f shows the enhanced depth image processed by the proposed method using
Figure 15e as the input image, from which we can easily observe that the quality of the depth image has improved compared with the original depth images (
Figure 15b). In particular, not only are the depth values of the depth images complete but the object boundaries have also been clearly recovered. The enhanced depth images (
Figure 16, bottom row) shows that the object shape is more accurate than the original depth images (
Figure 16, top row). In addition, the results in
Figure 17 were obtained by applying the DIBR technique to generate stereoscopic images with background pixel extrapolation on newly exposed regions after 3D image warping.
Figure 17b shows the visual enhancement given by the proposed method.