Colorization-Based RGB-White Color Interpolation using Color Filter Array with Randomly Sampled Pattern
Abstract
:1. Introduction
2. Preliminaries
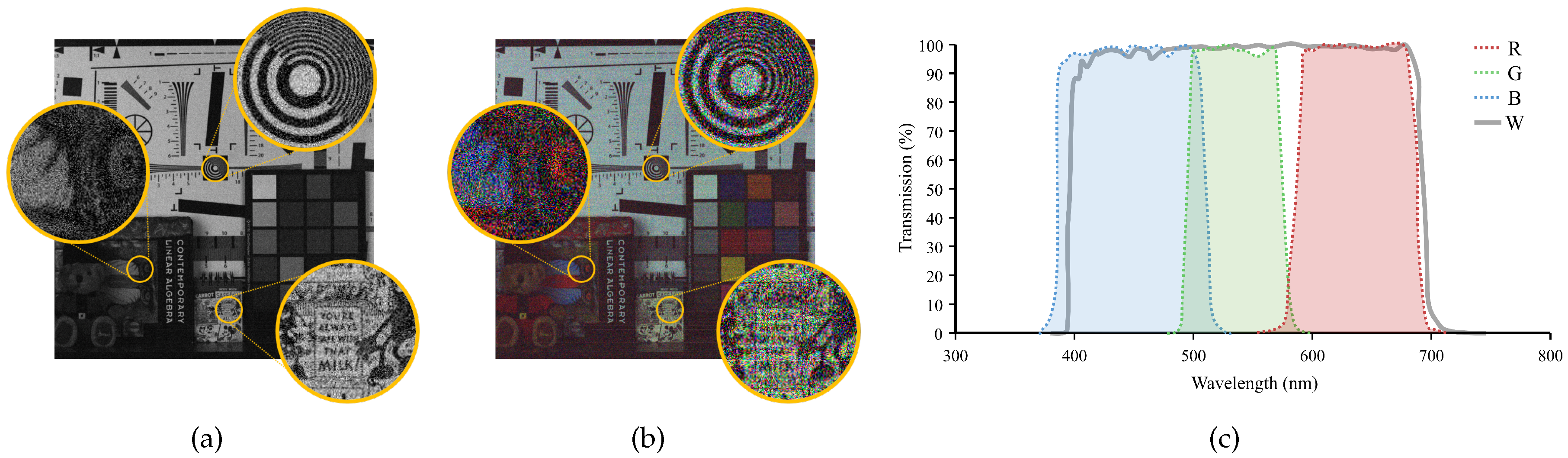
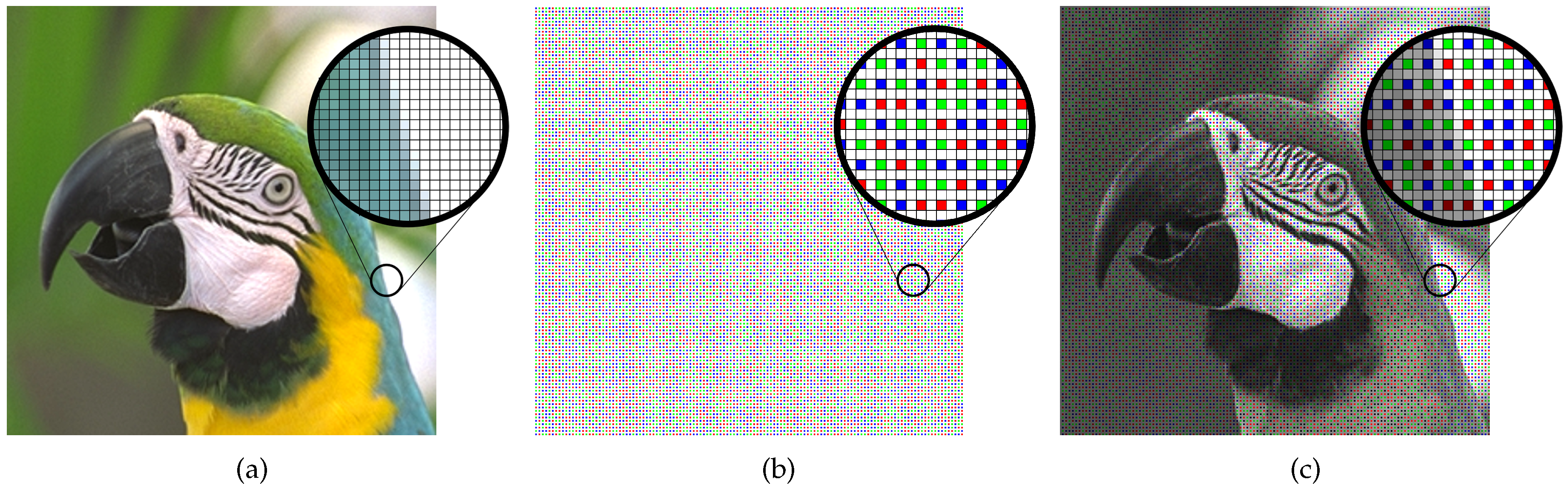
2.1. RGB-White CFA
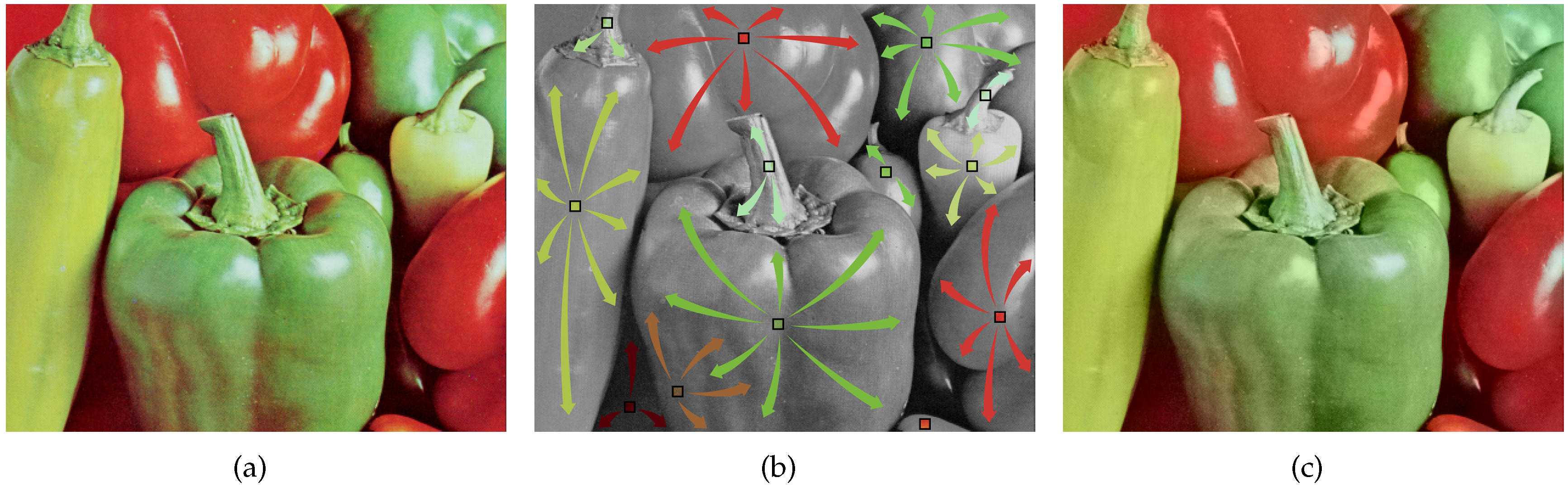
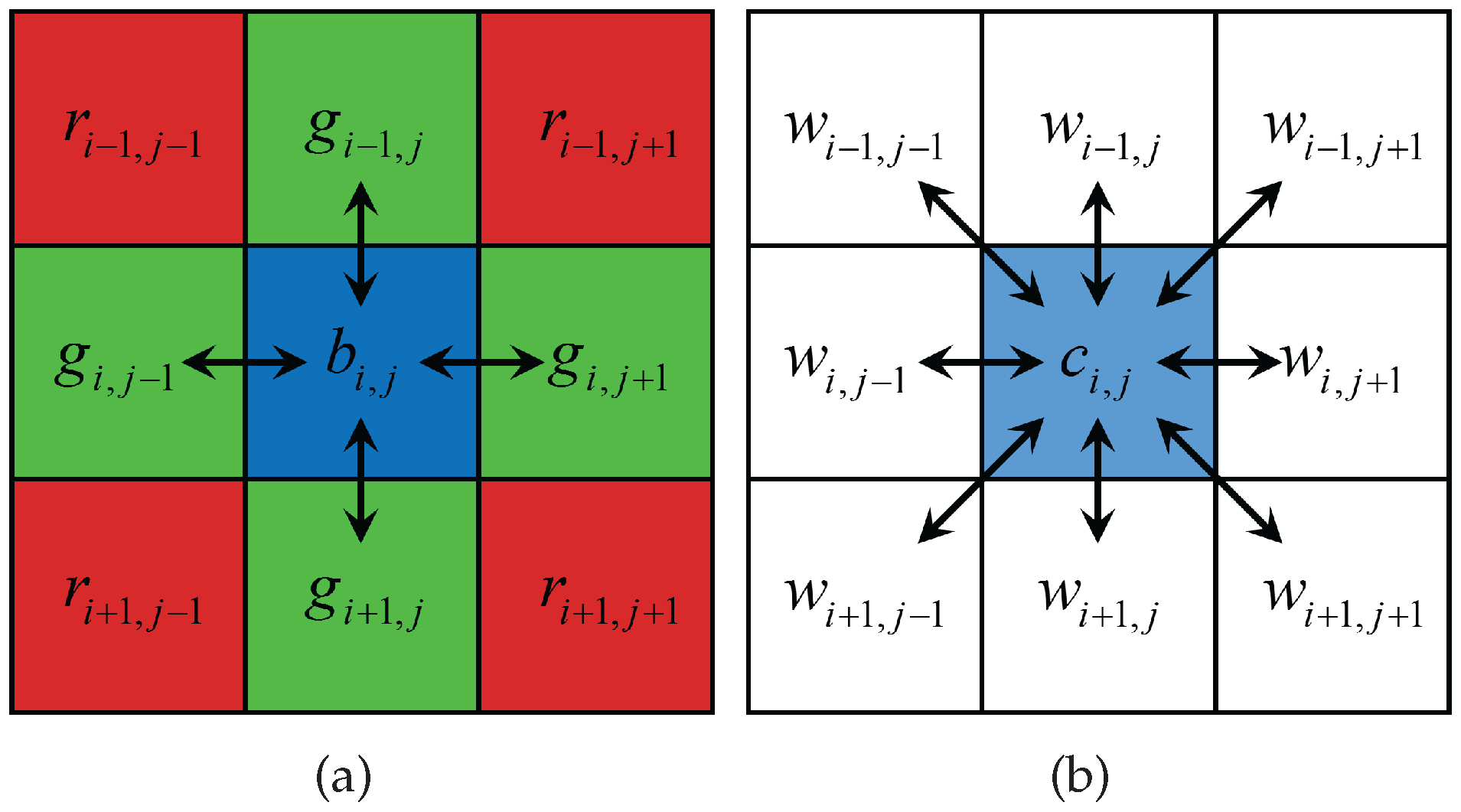
2.2. Levin’s Colorization
3. Proposed Method
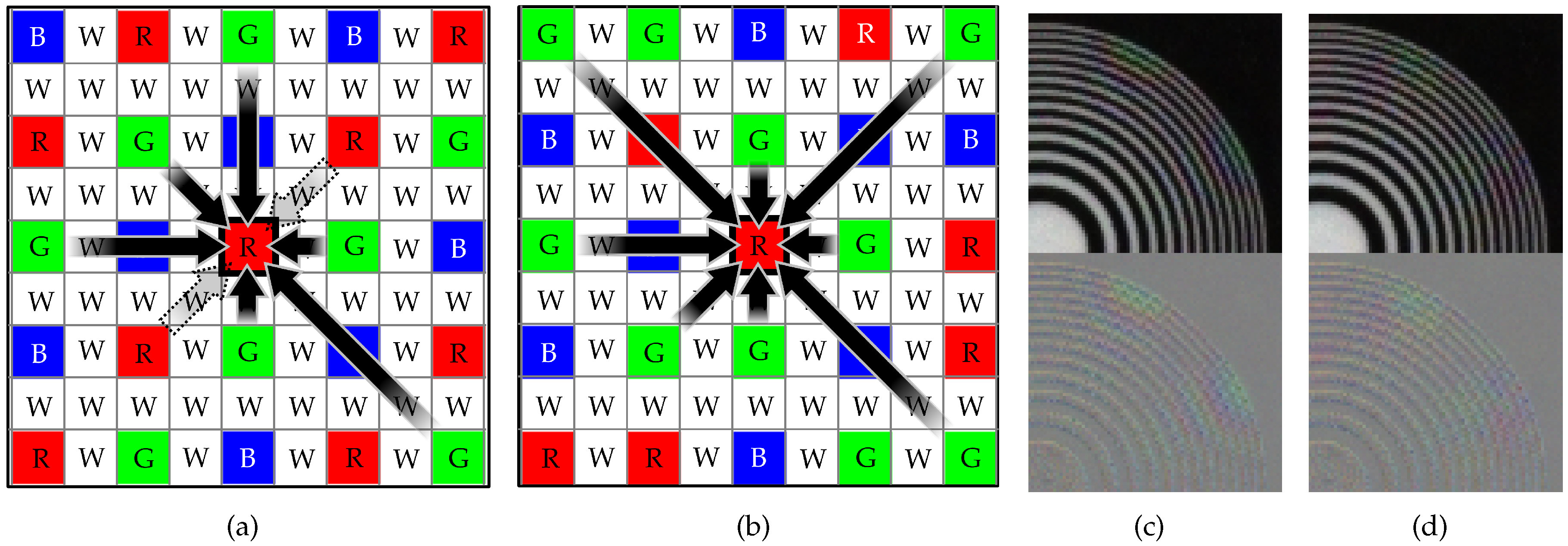
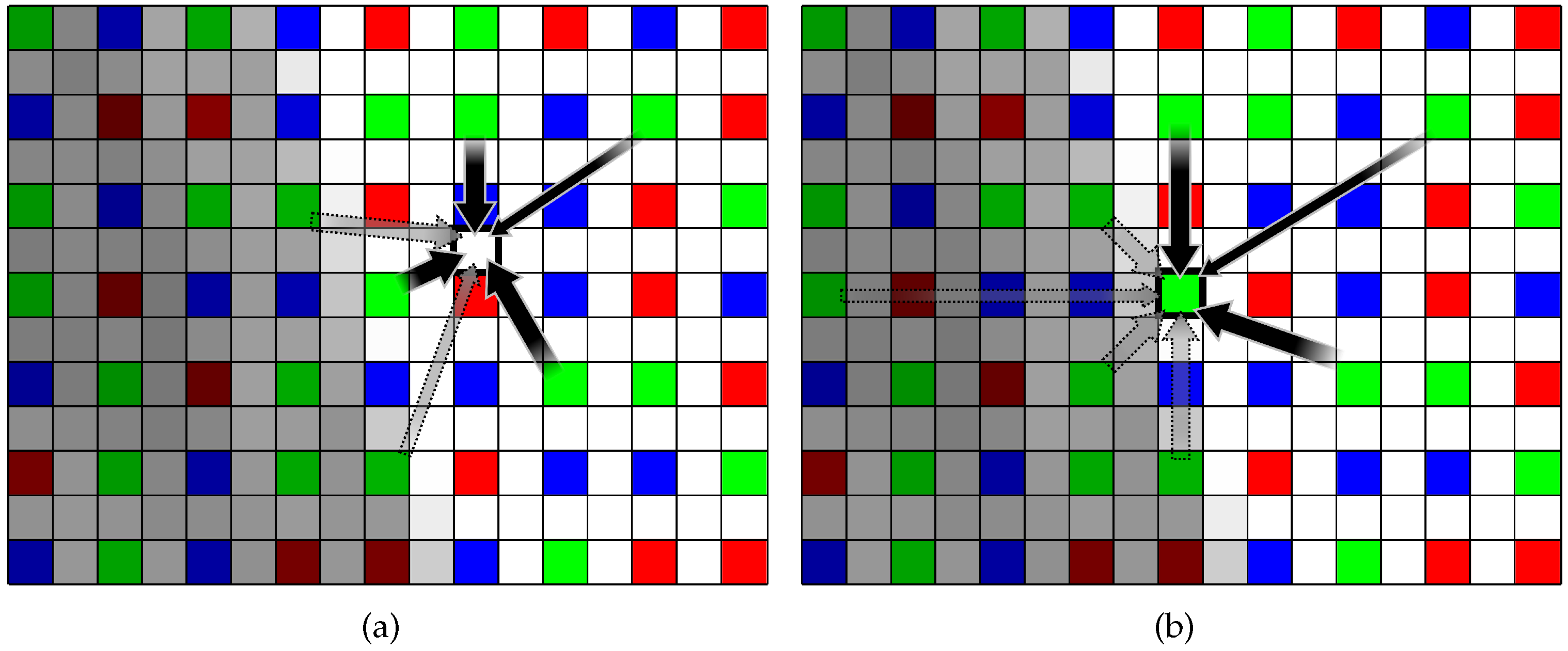
3.1. Proposed Randomly Sampled RGBW CFA Pattern
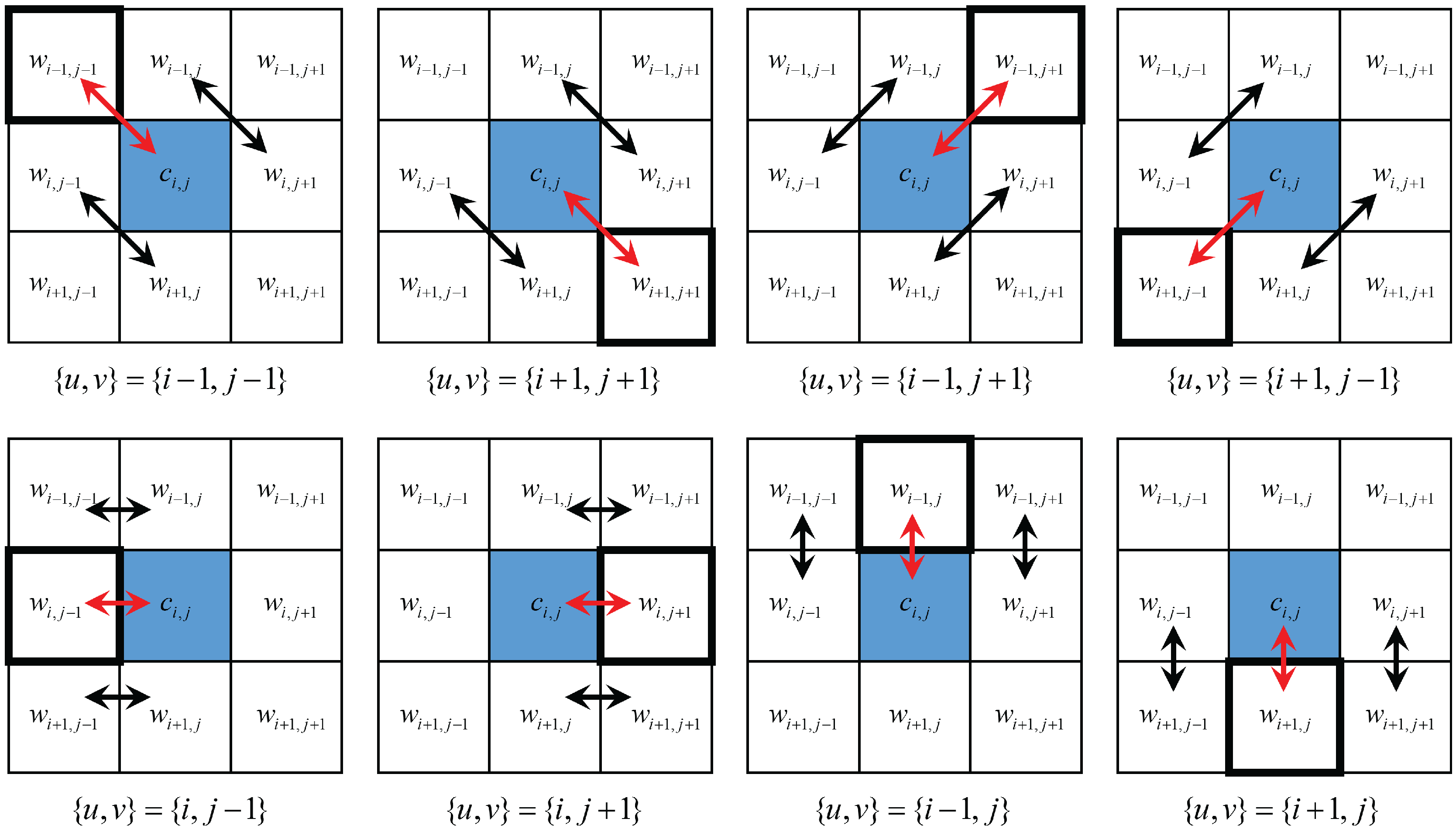
3.2. W Channel Interpolation
3.3. Primary Color Channel Interpolation
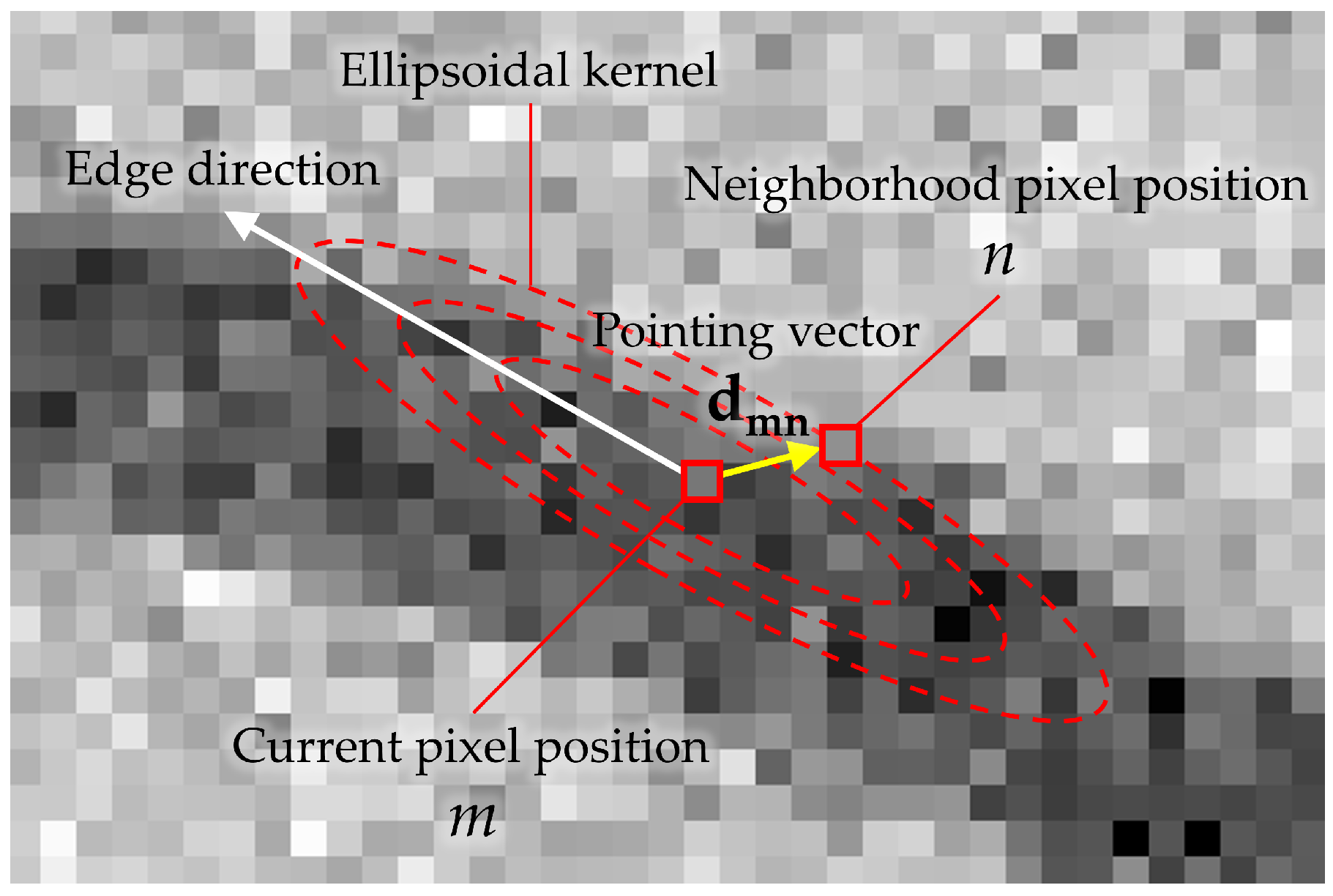
3.4. Post Processing
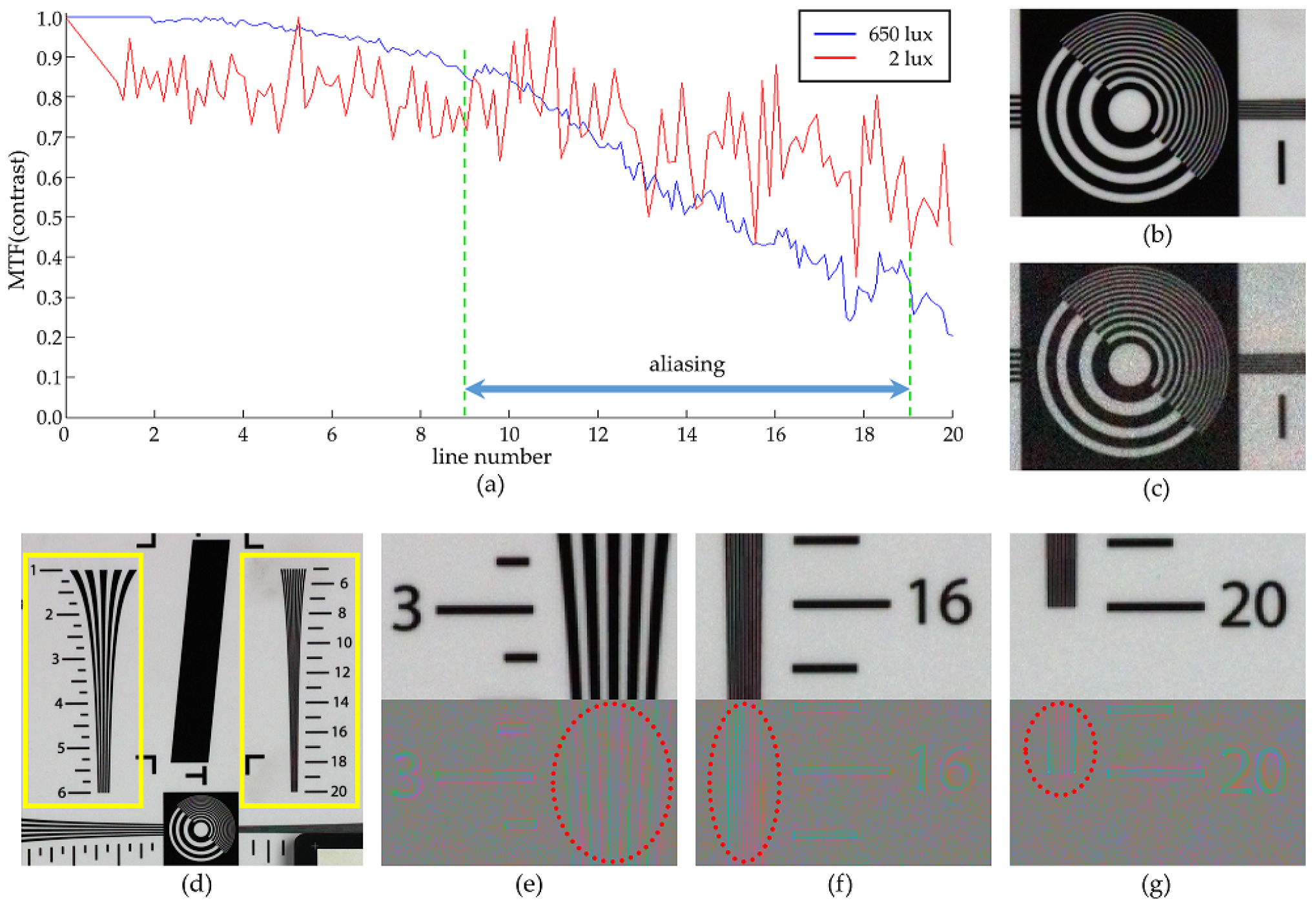
4. Experimental Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bayer, B. Color Imaging Array. U.S. Patent 3,971,065, 20 July 1976. [Google Scholar]
- Kimmel, R. Demosaicing: Image reconstruction from color CCD samples. IEEE Trans. Image Process. 1999, 8, 1221–1228. [Google Scholar] [CrossRef] [PubMed]
- Pei, S.C.; Tam, I.K. Effective color interpolation in CCD color filter arrays using signal correlation. IEEE Trans. Circuits Syst. Video Technol. 2003, 13, 503–513. [Google Scholar]
- Gunturk, B.K.; Altunbasak, Y.; Mersereau, R.M. Color plane interpolation using alternating projections. IEEE Trans. Image Process. 2002, 11, 997–1013. [Google Scholar] [CrossRef] [PubMed]
- Alleysson, D.; Süsstrunk, S.; Hérault, J. Linear demosaicing inspired by the human visual system. IEEE Trans. Image Process. 2005, 14, 439–449. [Google Scholar] [PubMed]
- Gunturk, B.K.; Glotzbach, J.; Altunbasak, Y.; Schafer, R.W.; Mersereau, R.M. Demosaicking: Color filter array interpolation. IEEE Signal Process. Mag. 2005, 22, 44–54. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, X. Color demosaicking via directional linear minimum mean square-error estimation. IEEE Trans. Image Process. 2005, 14, 2167–2178. [Google Scholar] [CrossRef] [PubMed]
- Dubois, E. Frequency-domain methods for demosaicking of Bayer-sampled color images. IEEE Signal Process. Lett. 2005, 12, 847–850. [Google Scholar] [CrossRef]
- Pekkucuksen, I.; Altunbasak, Y. Multiscale Gradients-Based Color Filter Array Interpolation. IEEE Trans. Image Process. 2013, 22, 157–165. [Google Scholar] [CrossRef] [PubMed]
- Menon, D.; Calvagno, G. Color Image Demosaicking: An Overview. Signal Process. Image Commun. 2011, 26, 518–533. [Google Scholar] [CrossRef]
- Kiku, D.; Monno, Y.; Tanaka, M.; Okutomi, M. Beyond Color Difference: Residual Interpolation for Color Image Demosaicking. IEEE Trans. Image Process. 2016, 25, 1288–1300. [Google Scholar] [CrossRef] [PubMed]
- Monno, Y.; Kikuchi, S.; Tanaka, M.; Okutomi, M. A Practical One-Shot Multispectral Imaging System Using a Single Image Sensor. IEEE Trans. Image Process. 2015, 24, 3048–3059. [Google Scholar] [CrossRef] [PubMed]
- Yasuma, F.; Mitsunaga, T.; Iso, D.; Nayar, S.K. Generalized Assorted Pixel Camera: Postcapture Control of Resolution, Dynamic Range, and Spectrum. IEEE Trans. Image Process. 2010, 19, 2241–2253. [Google Scholar] [CrossRef] [PubMed]
- Prasad, D.K. Strategies for Resolving Camera Metamers Using 3+1 Channel. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 954–962. [Google Scholar]
- Schaul, L.; Fredembach, C.; Süsstrunk, S. Color image dehazing using the near-infrared. In Proceedings of the 16th IEEE International Conference on Image Processing (ICIP), Cairo, Egypt, 7–10 November 2009; pp. 1629–1632. [Google Scholar]
- Sadeghipoor, Z.; Lu, Y.M.; Süsstrunk, S. A novel compressive sensing approach to simultaneously acquire color and near-infrared images on a single sensor. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 1646–1650. [Google Scholar]
- Rafinazari, M.; Dubois, E. Demosaicking algorithm for the Fujifilm X-Trans color filter array. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 660–663. [Google Scholar]
- Tian, Q.; Lansel, S.; Farrell, J.E.; Wandell, B.A. Automating the design of image processing pipelines for novel color filter arrays: Local, linear, learned (L3) method. Proc. SPIE 2014, 9023. [Google Scholar] [CrossRef]
- Condat, L. A Generic Variational Approach for Demosaicking from an Arbitrary Color Filter Array. In Proceedings of the 16th IEEE International Conference on Image Processing (ICIP), Cairo, Egypt, 7–10 November 2009; pp. 1605–1608. [Google Scholar]
- Gu, J.; Wolfe, P.J.; Hirakawa, K. Filterbank-based universal demosaicking. In Proceedings of the 17th IEEE International Conference on Image Processing (ICIP), Hong Kong, China, 26–29 September 2010; pp. 1981–1984. [Google Scholar]
- Park, S.W.; Kang, M.G. Generalized color interpolation scheme based on intermediate quincuncial pattern. J. Electron. Imaging 2014, 23, 030501. [Google Scholar] [CrossRef]
- Tachi, M. Image Processing Device, Image Processing Method, and Program Pertaining to Image Correction. U.S. Patent 8,314,863, 20 November 2012. [Google Scholar]
- Yamagami, T.; Sasaki, T.; Suga, A. Image Signal Processing Apparatus Having a Color Filter with Offset Luminance Filter Elements. U.S. Patent 5,323,233, 21 June 1994. [Google Scholar]
- Gindele, E.; Gallagher, A. Sparsely Sampled Image Sensing Device with Color and Luminance Photosites. U.S. Patent 6,476,865, 5 November 2002. [Google Scholar]
- Compton, J.; Hamilton, J. Image Sensor with Improved Light Sensitivity. U.S. Patent 8,139,130, 20 March 2012. [Google Scholar]
- Dougherty, G. Digital Image Processing for Medical Applications; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Bottacchi, S. Noise and Signal Interference in Optical Fiber Transmission Systems: An Optimum Design Approach; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Akiyama, H.; Tanaka, M.; Okutomi, M. Pseudo four-channel image denoising for noisy CFA raw data. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; pp. 4778–4782. [Google Scholar]
- Danielyan, A.; Vehvilainen, M.; Foi, A.; Katkovnik, V.; Egiazarian, K. Cross-color BM3D filtering of noisy raw data. In Proceedings of the 2009 International Workshop on Local and Non-Local Approximation in Image Processing, Tuusula, Finland, 19–21 August 2009; pp. 125–129. [Google Scholar]
- Levin, A.; Lischinski, D.; Weiss, Y. Colorization using optimization. ACM Trans. Graph. 2004, 23, 689–694. [Google Scholar] [CrossRef]
- Takeda, H.; Farsiu, S.; Milanfar, P. Kernel regression for image processing and reconstruction. IEEE Trans. Image Process. 2007, 16, 349–366. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.; Milanfar, P. Multiscale Principal Components Analysis for Image Local Orientation Estimation. In Proceedings of the 36th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 3–6 November 2002; pp. 478–482. [Google Scholar]
- Freedman, D. Statistical Models : Theory and Practice; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- He, K.; Sun, J.; Tang, X. Guided Image Filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1397–1409. [Google Scholar] [CrossRef] [PubMed]
- Buchsbaum, G. A spatial processor model for object colour perception. J. Frankl. Inst. 1980, 310, 1–26. [Google Scholar] [CrossRef]
- Land, E.H.; McCann, J.J. Lightness and Retinex Theory. J. Opt. Soc. Am. 1971, 61, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Land, E. The Retinex Theory of Color Vision. Sci. Am. 1977, 237, 108–129. [Google Scholar] [CrossRef] [PubMed]
- Barnard, K.; Cardei, V.; Funt, B. A comparison of computational color constancy algorithms. I: Methodology and experiments with synthesized data. IEEE Trans. Image Process. 2002, 11, 972–984. [Google Scholar] [CrossRef] [PubMed]
- Barnard, K.; Martin, L.; Coath, A.; Funt, B. A comparison of computational color constancy Algorithms. II. Experiments with image data. IEEE Trans. Image Process. 2002, 11, 985–996. [Google Scholar] [CrossRef] [PubMed]
- Cheng, D.; Prasad, D.K.; Brown, M.S. Illuminant estimation for color constancy: Why spatial-domain methods work and the role of the color distribution. J. Opt. Soc. Am. A 2014, 31, 1049–1058. [Google Scholar] [CrossRef] [PubMed]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image Denoising by Sparse 3-D Transform-Domain Collaborative Filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A Feature Similarity Index for Image Quality Assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef] [PubMed]







| Data | Bayer DLMMSE [7] | Bayer RI [11] | Sony RGBW [22] | Proposed | Akiyama [28] | BM3D-CFA [29] | Proposed + BM3D |
|---|---|---|---|---|---|---|---|
| 1 | 20.6240 | 21.0253 | 22.8337 | 24.0300 | 25.7640 | 26.2185 | 26.5624 |
| 2 | 21.0217 | 21.5777 | 24.1440 | 23.2595 | 28.7567 | 29.0252 | 27.2122 |
| 3 | 20.7928 | 21.5582 | 23.5414 | 23.8333 | 30.6593 | 30.8327 | 29.2358 |
| 4 | 20.7814 | 21.4473 | 23.7901 | 24.1515 | 29.3016 | 29.5208 | 28.4922 |
| 5 | 20.9141 | 21.3347 | 22.7660 | 23.8527 | 25.2292 | 26.0602 | 26.0390 |
| 6 | 20.8267 | 21.2730 | 22.9500 | 24.2042 | 27.0638 | 27.2829 | 27.6730 |
| 7 | 20.7311 | 21.3759 | 23.4218 | 24.3754 | 29.4845 | 29.9281 | 29.4038 |
| 8 | 20.7274 | 20.9955 | 22.7796 | 23.9210 | 25.4553 | 26.1903 | 26.7617 |
| 9 | 20.6406 | 21.3839 | 23.5115 | 24.5921 | 30.5982 | 30.7339 | 30.2494 |
| 10 | 20.6563 | 21.3936 | 23.4530 | 24.5911 | 30.0215 | 30.1505 | 30.2441 |
| 11 | 20.8227 | 21.3718 | 23.2586 | 24.3298 | 27.6005 | 28.0054 | 28.1005 |
| 12 | 20.7841 | 21.4705 | 23.4702 | 24.5056 | 30.5373 | 30.6068 | 30.0079 |
| 13 | 20.6527 | 20.8826 | 21.7919 | 23.4370 | 23.9516 | 24.2884 | 24.9340 |
| 14 | 20.8022 | 21.2953 | 23.0835 | 23.7002 | 26.4241 | 27.0160 | 25.8387 |
| 15 | 21.4102 | 21.8628 | 23.9531 | 24.4306 | 29.1291 | 29.3797 | 28.2387 |
| 16 | 20.6903 | 21.3393 | 23.4063 | 24.5378 | 29.4499 | 29.5209 | 29.0873 |
| 17 | 21.0825 | 21.6626 | 23.8226 | 24.8379 | 29.2484 | 29.5851 | 29.7193 |
| 18 | 20.8700 | 21.4001 | 22.9114 | 23.9673 | 26.0022 | 26.5466 | 26.5046 |
| 19 | 20.6914 | 21.2650 | 23.2757 | 24.3600 | 28.6516 | 29.0308 | 28.7008 |
| 20 | 21.8899 | 22.3182 | 24.1087 | 24.8277 | 26.9488 | 27.8986 | 28.0698 |
| 21 | 20.6429 | 21.2543 | 23.0521 | 24.2204 | 27.4789 | 27.8329 | 28.1341 |
| 22 | 20.6400 | 21.2883 | 23.1219 | 24.1220 | 27.8864 | 28.2483 | 27.8049 |
| 23 | 20.7934 | 21.5650 | 23.3896 | 23.2165 | 31.1036 | 30.8427 | 28.3076 |
| 24 | 20.6561 | 21.1593 | 22.6258 | 23.8926 | 25.9713 | 26.4484 | 26.6763 |
| Avg | 20.8394 | 21.3959 | 23.2693 | 24.1332 | 28.0299 | 28.3831 | 27.9999 |
| Data | Bayer DLMMSE [7] | Bayer RI [11] | Sony RGBW [22] | Proposed | Akiyama [28] | BM3D-CFA [29] | Proposed + BM3D |
|---|---|---|---|---|---|---|---|
| 1 | 23.4743 | 23.7315 | 25.2154 | 26.1998 | 27.1647 | 27.6840 | 28.2742 |
| 2 | 23.7555 | 24.0597 | 26.5783 | 26.0850 | 29.8295 | 30.1677 | 29.1778 |
| 3 | 23.6888 | 24.3995 | 26.5252 | 26.5784 | 31.9909 | 32.3835 | 31.0654 |
| 4 | 23.6173 | 24.1784 | 26.5210 | 26.3983 | 30.3262 | 30.6601 | 30.1931 |
| 5 | 23.6914 | 24.0412 | 24.9118 | 25.8992 | 27.0623 | 27.8761 | 27.7638 |
| 6 | 23.6902 | 24.0157 | 25.5248 | 26.3360 | 28.5588 | 28.8965 | 29.2019 |
| 7 | 23.6396 | 24.2284 | 26.3332 | 26.7672 | 31.2039 | 31.8072 | 31.1182 |
| 8 | 23.4988 | 23.6250 | 25.0019 | 26.0813 | 27.1062 | 27.8035 | 28.3955 |
| 9 | 23.5865 | 24.2659 | 26.5441 | 27.0729 | 32.1003 | 32.3720 | 31.6528 |
| 10 | 23.6309 | 24.2935 | 26.5336 | 27.1205 | 31.4922 | 31.8247 | 31.8130 |
| 11 | 23.6742 | 24.1131 | 25.9178 | 26.5520 | 28.9809 | 29.5593 | 29.5306 |
| 12 | 23.6820 | 24.3276 | 26.4528 | 26.8893 | 31.7944 | 32.1896 | 31.4717 |
| 13 | 23.4140 | 23.4268 | 23.5726 | 25.1309 | 25.5672 | 25.8364 | 26.3775 |
| 14 | 23.5546 | 23.9508 | 25.4867 | 25.7873 | 27.8713 | 28.4915 | 27.3360 |
| 15 | 24.0929 | 24.4846 | 26.5509 | 26.7164 | 30.4343 | 30.7897 | 29.9927 |
| 16 | 23.5826 | 24.1387 | 26.3258 | 27.0410 | 30.6613 | 30.9932 | 31.0541 |
| 17 | 23.8864 | 24.3835 | 26.5670 | 27.2550 | 30.8645 | 31.2523 | 31.3186 |
| 18 | 23.5707 | 24.0102 | 25.1366 | 25.9099 | 27.5905 | 28.0707 | 28.0735 |
| 19 | 23.5820 | 24.0696 | 26.0365 | 26.6651 | 29.8626 | 30.3696 | 30.2485 |
| 20 | 24.6759 | 25.0065 | 26.8145 | 27.1831 | 27.4626 | 28.4592 | 30.0495 |
| 21 | 23.5265 | 24.0586 | 25.6518 | 26.4513 | 28.9960 | 29.4035 | 29.6244 |
| 22 | 23.4976 | 24.0450 | 25.7935 | 26.3496 | 29.1417 | 29.5544 | 29.3926 |
| 23 | 23.6690 | 24.3757 | 26.2651 | 26.2849 | 32.3738 | 32.5457 | 30.7539 |
| 24 | 23.4244 | 23.8393 | 24.8499 | 25.8906 | 27.4968 | 28.0037 | 28.1189 |
| Avg. | 23.6711 | 24.1279 | 25.8796 | 26.4436 | 29.4139 | 29.8748 | 29.6666 |
| Data | Bayer DLMMSE [7] | Bayer RI [11] | Sony RGBW [22] | Proposed | Akiyama [28] | BM3D-CFA [29] | Proposed + BM3D |
|---|---|---|---|---|---|---|---|
| 1 | 0.8672 | 0.8781 | 0.8914 | 0.9244 | 0.9233 | 0.9292 | 0.9524 |
| 2 | 0.7978 | 0.8044 | 0.8313 | 0.8701 | 0.8878 | 0.9156 | 0.9382 |
| 3 | 0.7502 | 0.7671 | 0.7955 | 0.8574 | 0.9330 | 0.9391 | 0.9516 |
| 4 | 0.7961 | 0.8107 | 0.8373 | 0.8856 | 0.9223 | 0.9339 | 0.9519 |
| 5 | 0.9067 | 0.9152 | 0.9190 | 0.9418 | 0.9297 | 0.9337 | 0.9595 |
| 6 | 0.8688 | 0.8789 | 0.8857 | 0.9234 | 0.9189 | 0.9264 | 0.9512 |
| 7 | 0.8290 | 0.8404 | 0.8593 | 0.9052 | 0.9441 | 0.9466 | 0.9631 |
| 8 | 0.8991 | 0.9078 | 0.9171 | 0.9409 | 0.9462 | 0.9500 | 0.9687 |
| 9 | 0.7640 | 0.7807 | 0.8045 | 0.8644 | 0.9425 | 0.9397 | 0.9549 |
| 10 | 0.8024 | 0.8176 | 0.8357 | 0.8900 | 0.9302 | 0.9306 | 0.9530 |
| 11 | 0.8406 | 0.8512 | 0.8678 | 0.9103 | 0.9206 | 0.9310 | 0.9504 |
| 12 | 0.7999 | 0.8140 | 0.8309 | 0.8832 | 0.9124 | 0.9285 | 0.9474 |
| 13 | 0.9100 | 0.9177 | 0.9178 | 0.9431 | 0.9135 | 0.9250 | 0.9499 |
| 14 | 0.8684 | 0.8783 | 0.8913 | 0.9241 | 0.9170 | 0.9252 | 0.9500 |
| 15 | 0.7889 | 0.7998 | 0.8254 | 0.8738 | 0.9293 | 0.9383 | 0.9539 |
| 16 | 0.7934 | 0.8084 | 0.8290 | 0.8830 | 0.9123 | 0.9201 | 0.9419 |
| 17 | 0.8368 | 0.8505 | 0.8689 | 0.9127 | 0.9308 | 0.9338 | 0.9564 |
| 18 | 0.8802 | 0.8890 | 0.8985 | 0.9261 | 0.9028 | 0.9127 | 0.9430 |
| 19 | 0.8295 | 0.8410 | 0.8610 | 0.9051 | 0.9201 | 0.9312 | 0.9512 |
| 20 | 0.7783 | 0.7891 | 0.8195 | 0.8691 | 0.9440 | 0.9472 | 0.9589 |
| 21 | 0.8639 | 0.8735 | 0.8824 | 0.9205 | 0.9241 | 0.9305 | 0.9541 |
| 22 | 0.8263 | 0.8392 | 0.8578 | 0.9011 | 0.9029 | 0.9191 | 0.9424 |
| 23 | 0.7393 | 0.7570 | 0.7808 | 0.8504 | 0.9522 | 0.9432 | 0.9554 |
| 24 | 0.8417 | 0.8533 | 0.8687 | 0.9087 | 0.9234 | 0.9299 | 0.9538 |
| Avg. | 0.8283 | 0.8574 | 0.8401 | 0.9006 | 0.9243 | 0.9317 | 0.9522 |
| Data | Bayer DLMMSE [7] | Bayer RI [11] | Sony RGBW [22] | Proposed | Akiyama [28] | BM3D-CFA [29] | Proposed + BM3D |
|---|---|---|---|---|---|---|---|
| 1 | 0.9154 | 0.9221 | 0.9314 | 0.9497 | 0.9480 | 0.9513 | 0.9668 |
| 2 | 0.8657 | 0.8689 | 0.8924 | 0.9179 | 0.9146 | 0.9378 | 0.9535 |
| 3 | 0.8313 | 0.8436 | 0.8705 | 0.9079 | 0.9483 | 0.9555 | 0.9642 |
| 4 | 0.8650 | 0.8757 | 0.8986 | 0.9275 | 0.9426 | 0.9525 | 0.9653 |
| 5 | 0.9413 | 0.9465 | 0.9478 | 0.9611 | 0.9558 | 0.9579 | 0.9733 |
| 6 | 0.9156 | 0.9215 | 0.9304 | 0.9489 | 0.9468 | 0.9503 | 0.9656 |
| 7 | 0.8878 | 0.8957 | 0.9132 | 0.9386 | 0.9612 | 0.9644 | 0.9738 |
| 8 | 0.9345 | 0.9401 | 0.9465 | 0.9609 | 0.9635 | 0.9668 | 0.9779 |
| 9 | 0.8398 | 0.8522 | 0.8747 | 0.9128 | 0.9599 | 0.9595 | 0.9671 |
| 10 | 0.8715 | 0.8815 | 0.9007 | 0.9313 | 0.9523 | 0.9528 | 0.9681 |
| 11 | 0.8950 | 0.9023 | 0.9161 | 0.9407 | 0.9433 | 0.9505 | 0.9653 |
| 12 | 0.8689 | 0.8785 | 0.8939 | 0.9250 | 0.9345 | 0.9466 | 0.9602 |
| 13 | 0.9428 | 0.9471 | 0.9456 | 0.9596 | 0.9453 | 0.9500 | 0.9661 |
| 14 | 0.9148 | 0.9211 | 0.9307 | 0.9501 | 0.9430 | 0.9477 | 0.9645 |
| 15 | 0.8565 | 0.8641 | 0.8875 | 0.9176 | 0.9480 | 0.9545 | 0.9650 |
| 16 | 0.8634 | 0.8735 | 0.8922 | 0.9257 | 0.9374 | 0.9428 | 0.9591 |
| 17 | 0.8936 | 0.9020 | 0.9186 | 0.9440 | 0.9518 | 0.9529 | 0.9694 |
| 18 | 0.9225 | 0.9285 | 0.9354 | 0.9502 | 0.9397 | 0.9439 | 0.9615 |
| 19 | 0.8888 | 0.8971 | 0.9136 | 0.9386 | 0.9423 | 0.9491 | 0.9648 |
| 20 | 0.8510 | 0.8576 | 0.8882 | 0.9166 | 0.9586 | 0.9627 | 0.9695 |
| 21 | 0.9131 | 0.9194 | 0.9271 | 0.9484 | 0.9489 | 0.9521 | 0.9685 |
| 22 | 0.8875 | 0.8962 | 0.9124 | 0.9353 | 0.9290 | 0.9409 | 0.9579 |
| 23 | 0.8241 | 0.8375 | 0.8606 | 0.9050 | 0.9657 | 0.9611 | 0.9665 |
| 24 | 0.8982 | 0.9059 | 0.9180 | 0.9403 | 0.9473 | 0.9516 | 0.9673 |
| Avg. | 0.8870 | 0.8949 | 0.9102 | 0.9356 | 0.9470 | 0.9523 | 0.9659 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oh, P.; Lee, S.; Kang, M.G. Colorization-Based RGB-White Color Interpolation using Color Filter Array with Randomly Sampled Pattern. Sensors 2017, 17, 1523. https://doi.org/10.3390/s17071523
Oh P, Lee S, Kang MG. Colorization-Based RGB-White Color Interpolation using Color Filter Array with Randomly Sampled Pattern. Sensors. 2017; 17(7):1523. https://doi.org/10.3390/s17071523
Chicago/Turabian StyleOh, Paul, Sukho Lee, and Moon Gi Kang. 2017. "Colorization-Based RGB-White Color Interpolation using Color Filter Array with Randomly Sampled Pattern" Sensors 17, no. 7: 1523. https://doi.org/10.3390/s17071523
APA StyleOh, P., Lee, S., & Kang, M. G. (2017). Colorization-Based RGB-White Color Interpolation using Color Filter Array with Randomly Sampled Pattern. Sensors, 17(7), 1523. https://doi.org/10.3390/s17071523




