Single-Lead Fetal ECG Extraction Based on a Parallel Marginalized Particle Filter
Abstract
:1. Introduction
2. ECG Dynamical Model
3. Proposed Methodology for FECG Extraction
3.1. Modified Abdominal Signal Dynamical Model
3.2. Observation Equation of the Dynamical Model
3.3. Parallel-Marginalized Particle Filter
- Step 1: Initialize the M particles:and set .
- Step 2: Calculate the importance:weight:normalization:
- Step 3: Resample the M particles:
- Step 4: Update the Kalman filter measurement:where the superscript means that there are two cases, i.e., the fetal ECG and the maternal ECG estimates.
- Step 5: Update the particle filter time:where:
- Step 6: Update the Kalman filter time:where:is the process noise covariance matrix, and is the observation noise covariance matrix.
- Step 7:and iterate from step 2.
4. Performance Index of the FECG Extraction
4.1. Performance Index of the Simulated Data
4.2. Performance Index of the Clinical Data
- Step 1: The extracted FECG is divided into N pieces crossing to the R peak, and each piece includes M samples and one QRS complex.
- Step 2: All of the pieces are stored in columns of an M by N matrix , and the vectors are the zero mean and are normalized to the unit length; that is,
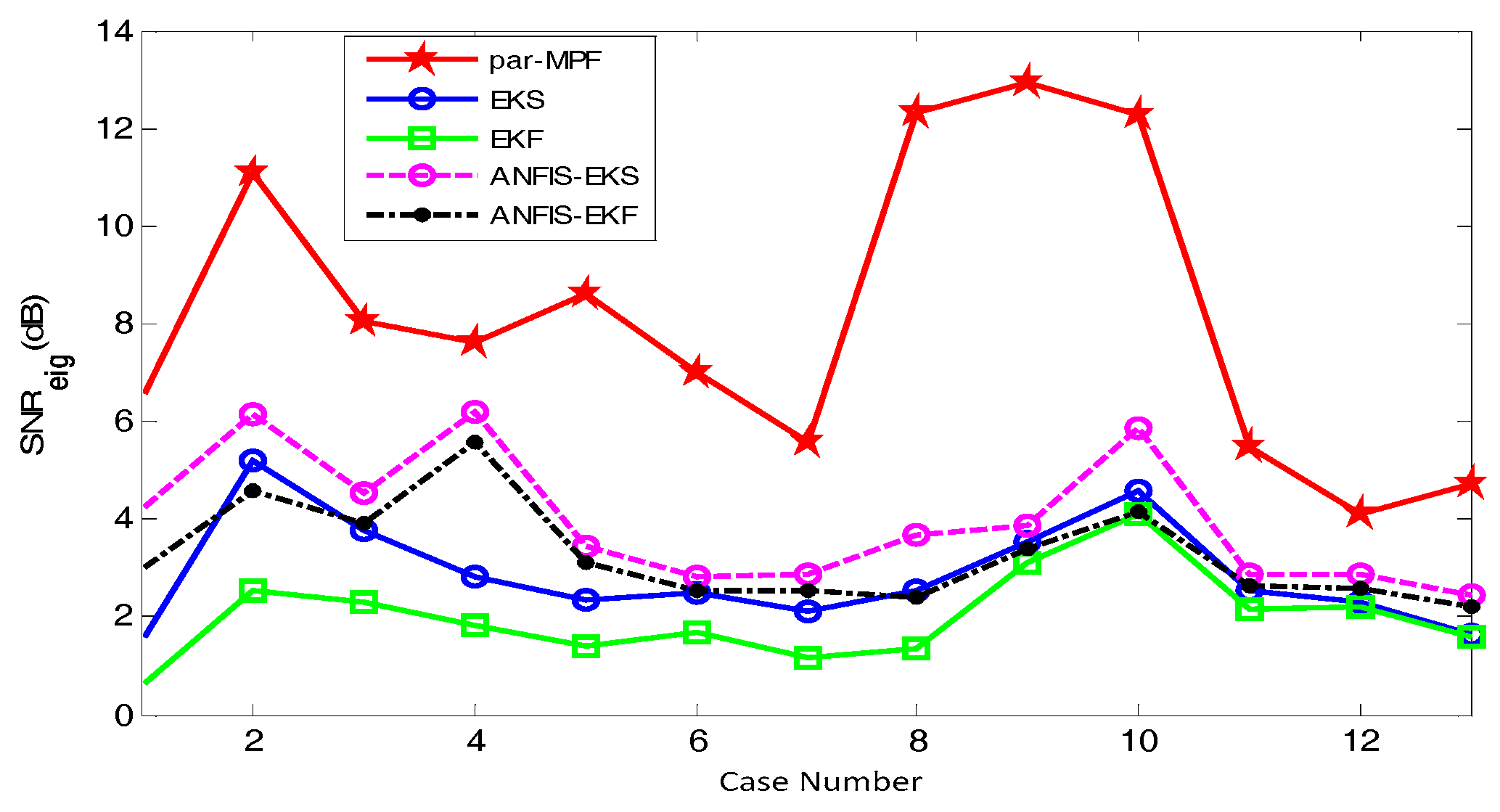
- Step 3: A signal-to-noise ratio based on eigenvalues can be calculated as:where contains the eigenvalues of .
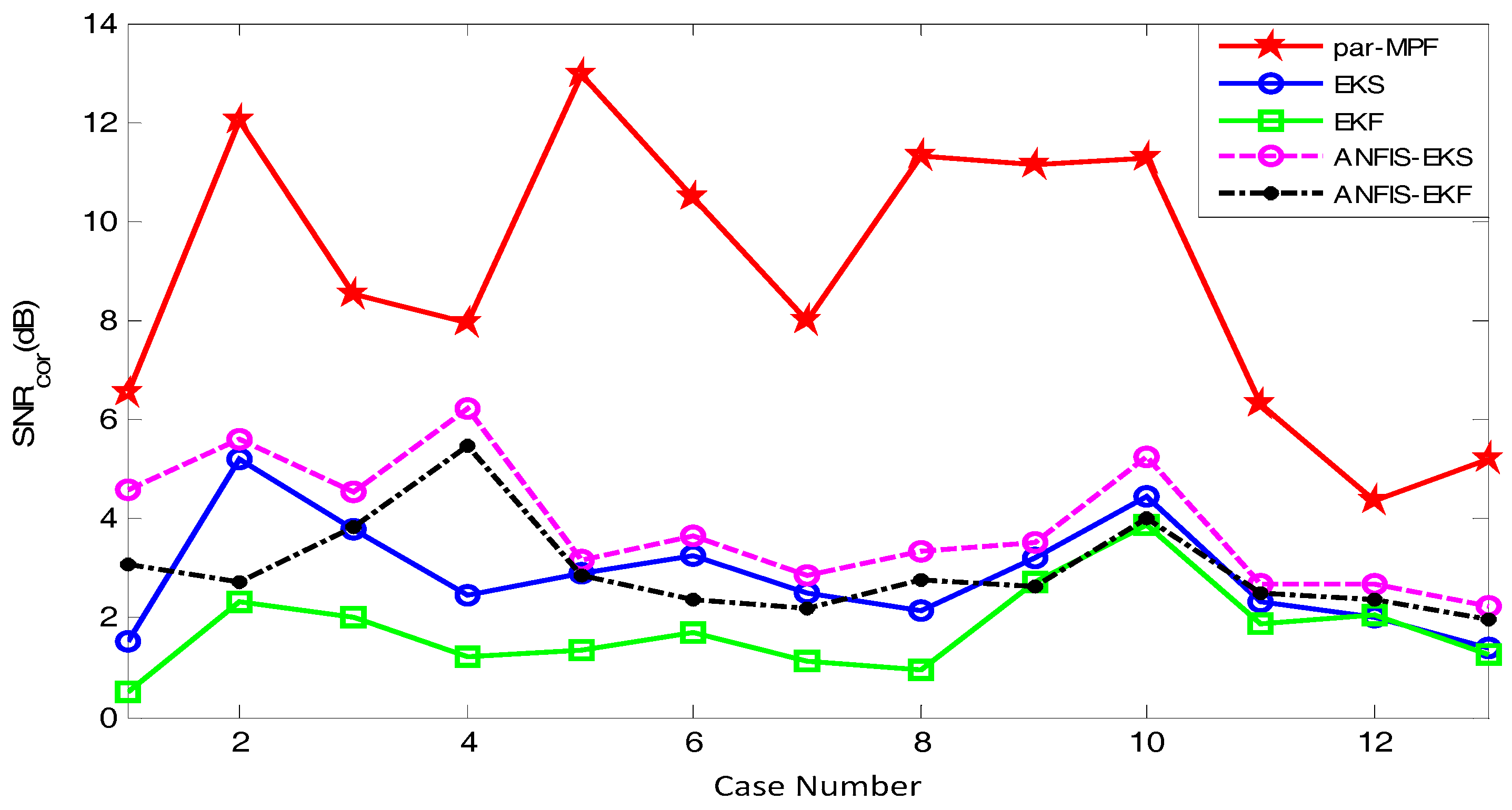
- Step 4: A signal-to-noise ratio based on the cross-correlation coefficients can be calculated aswhereand is the FECG.
5. Results and Analysis
5.1. FECG Extraction on the Simulated Data
5.1.1. Simulated Data without Noise
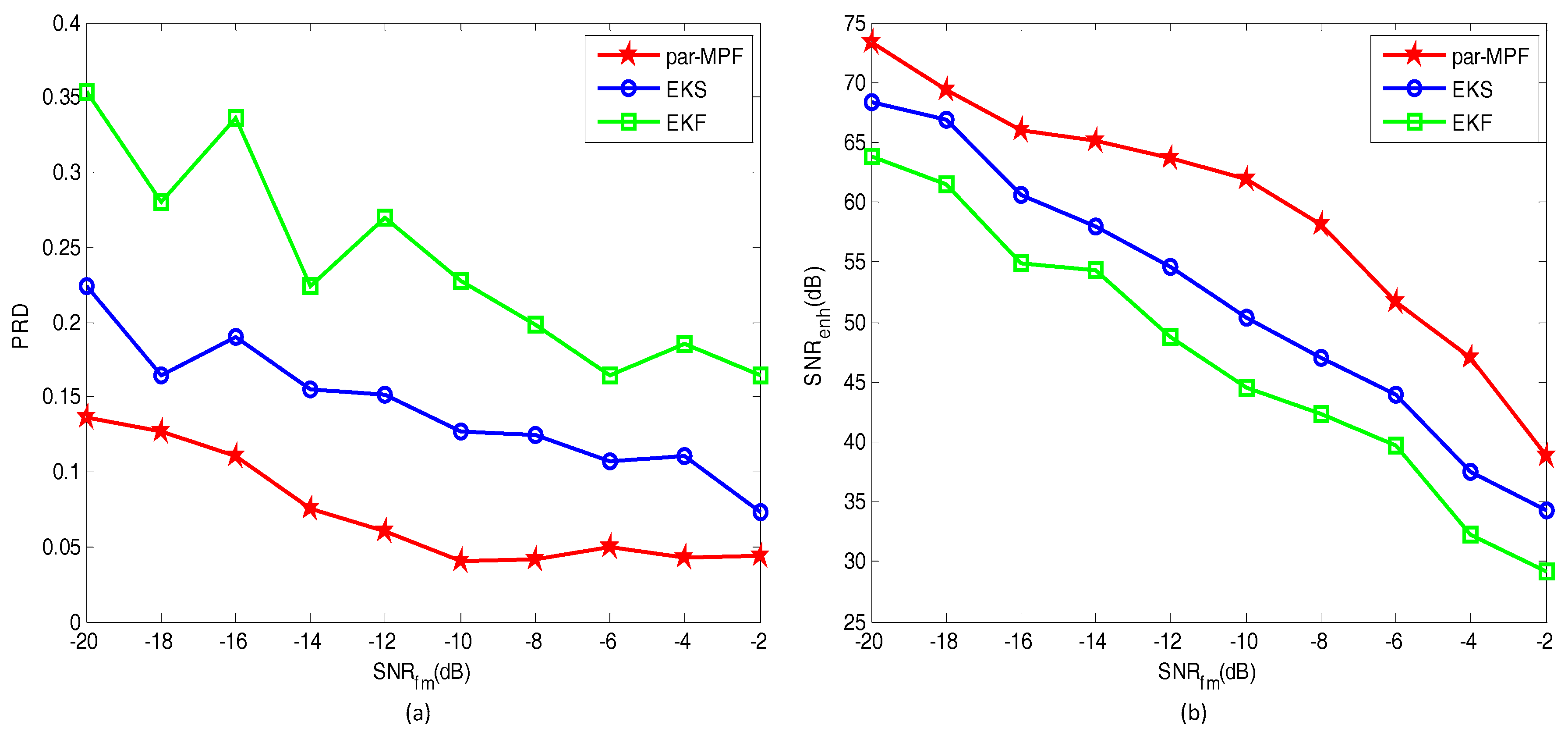
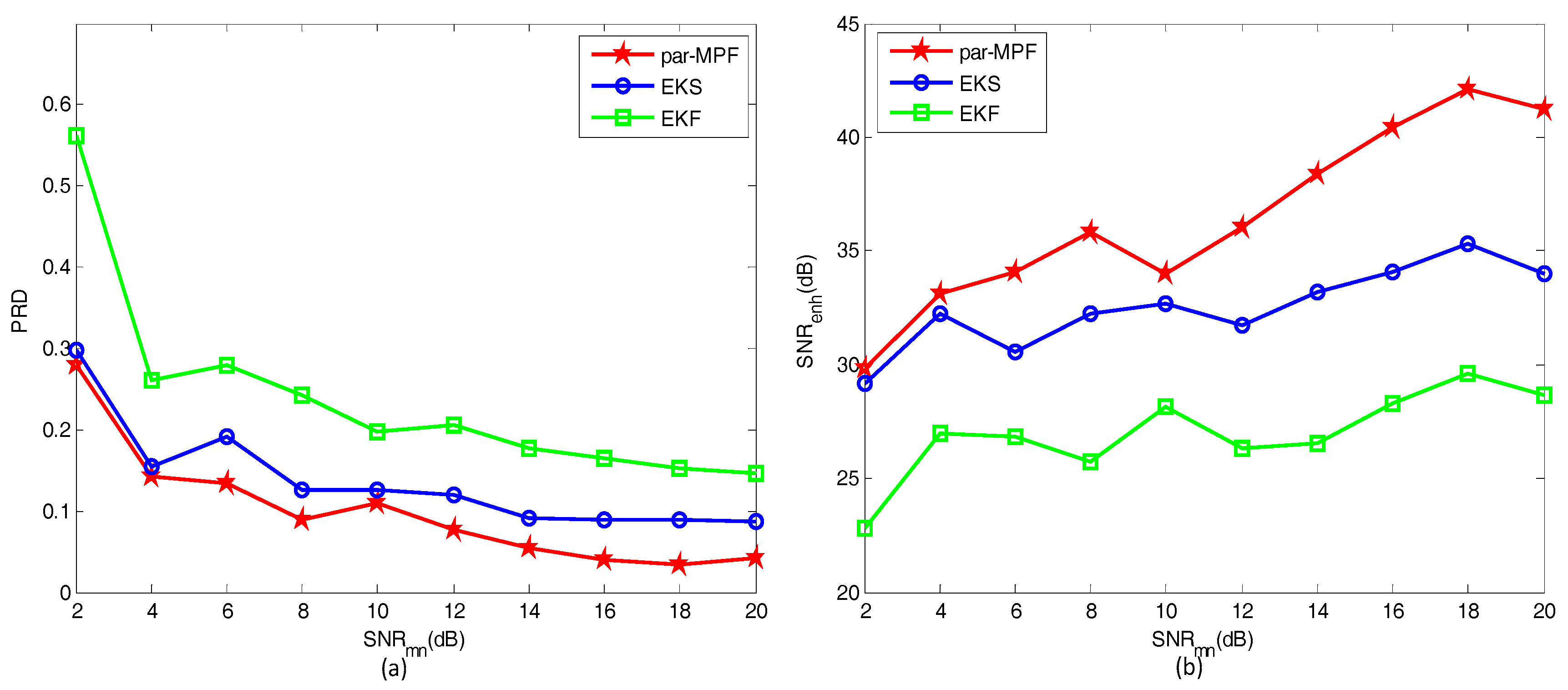
5.1.2. Simulated Data with Noise
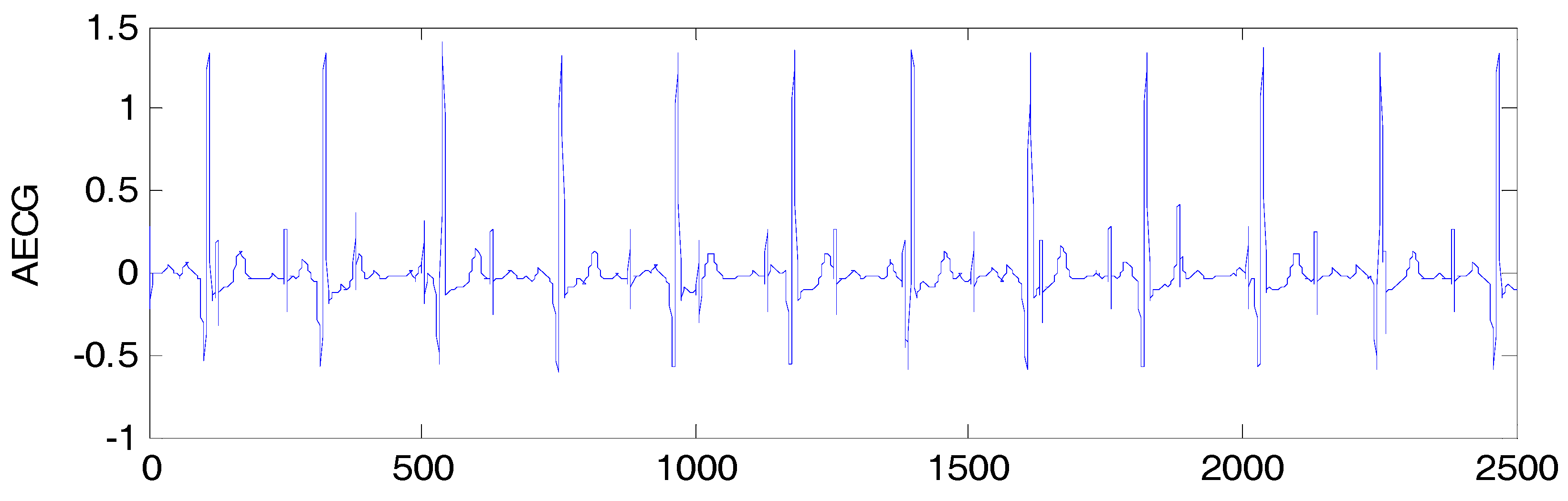
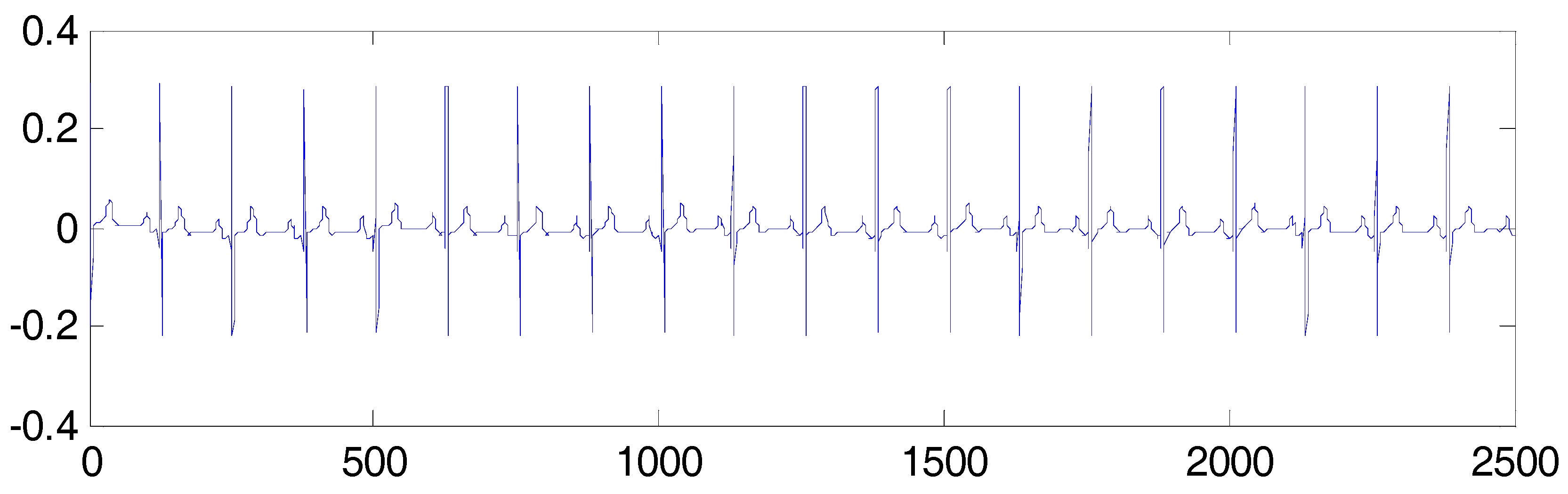
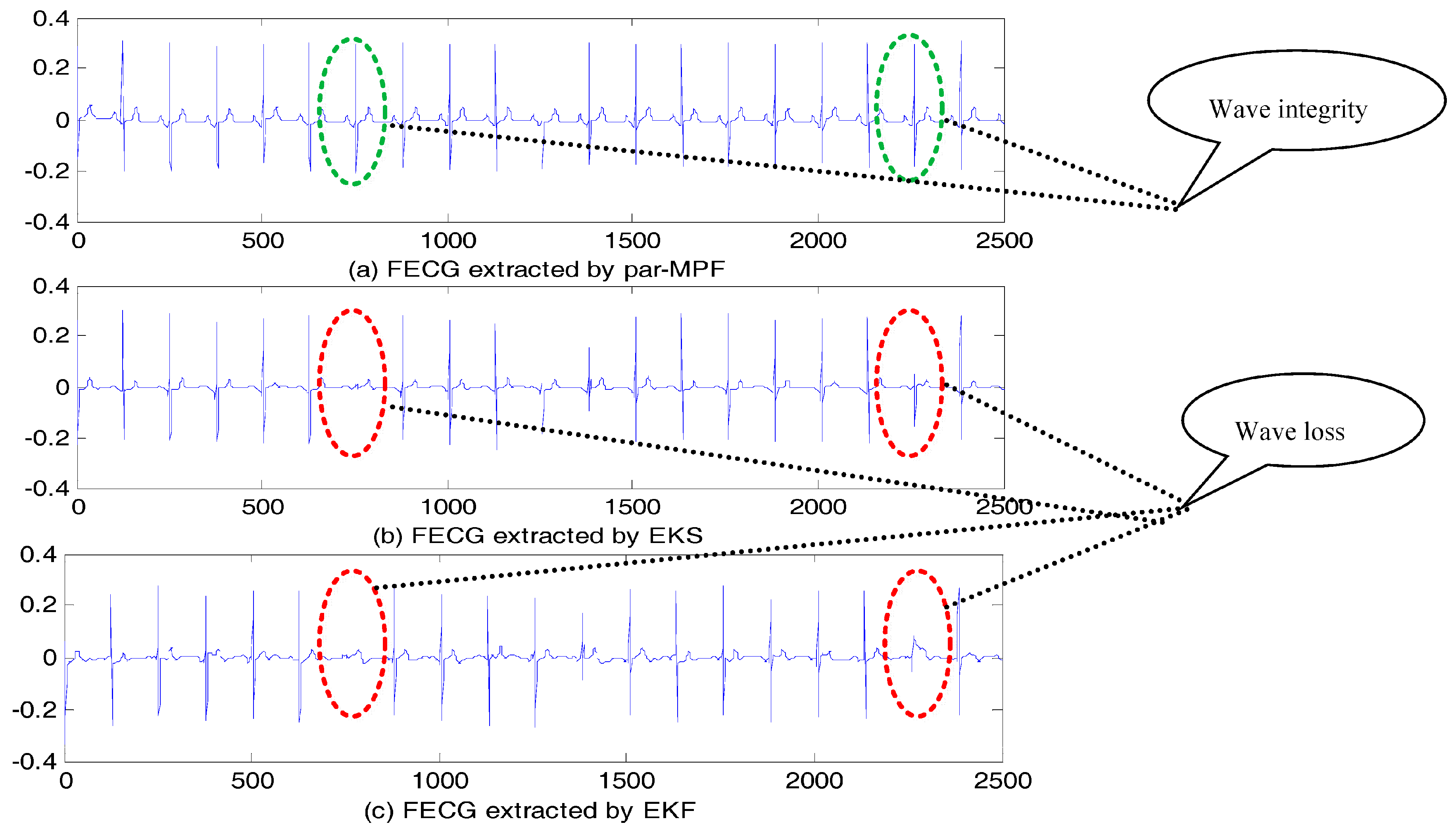
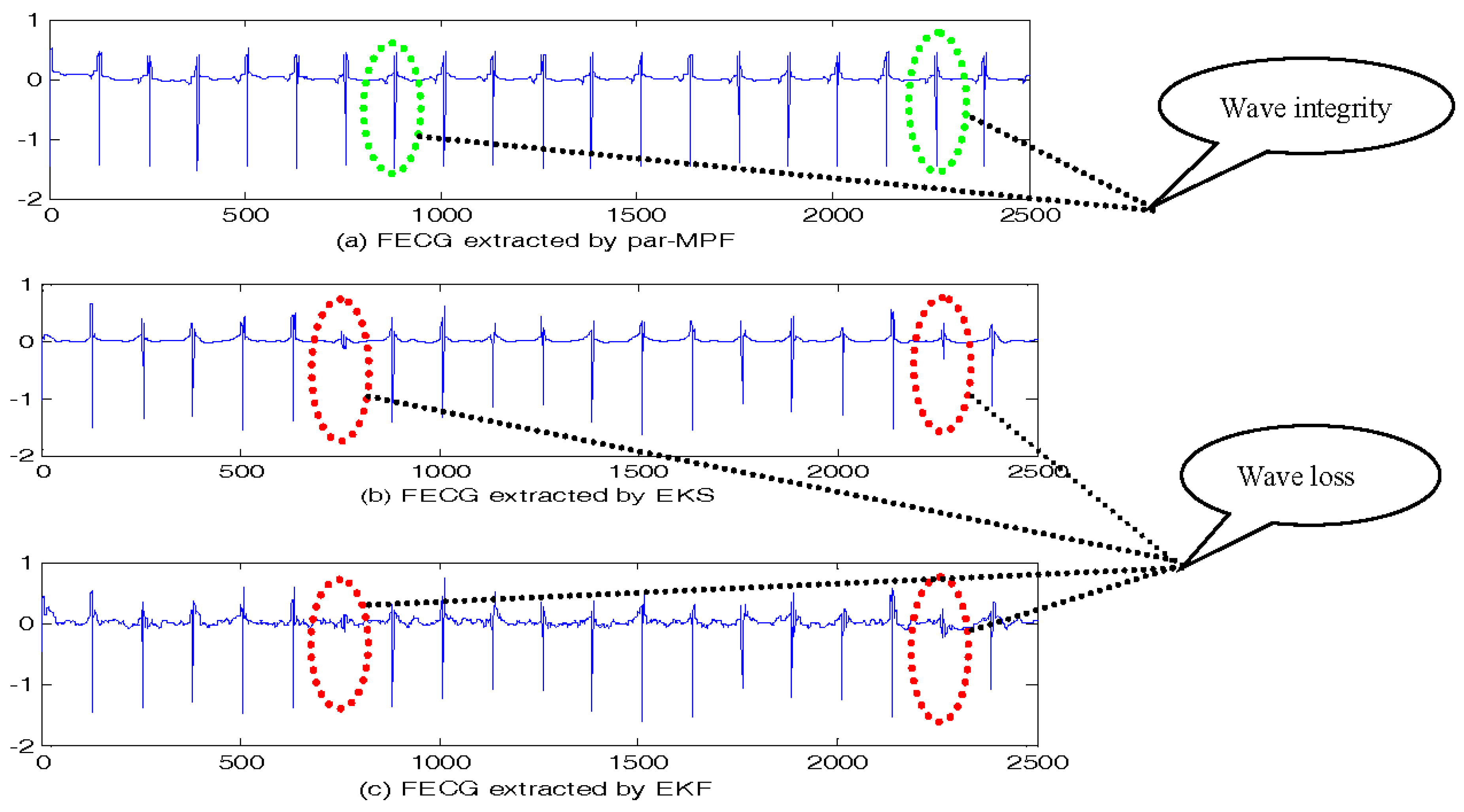
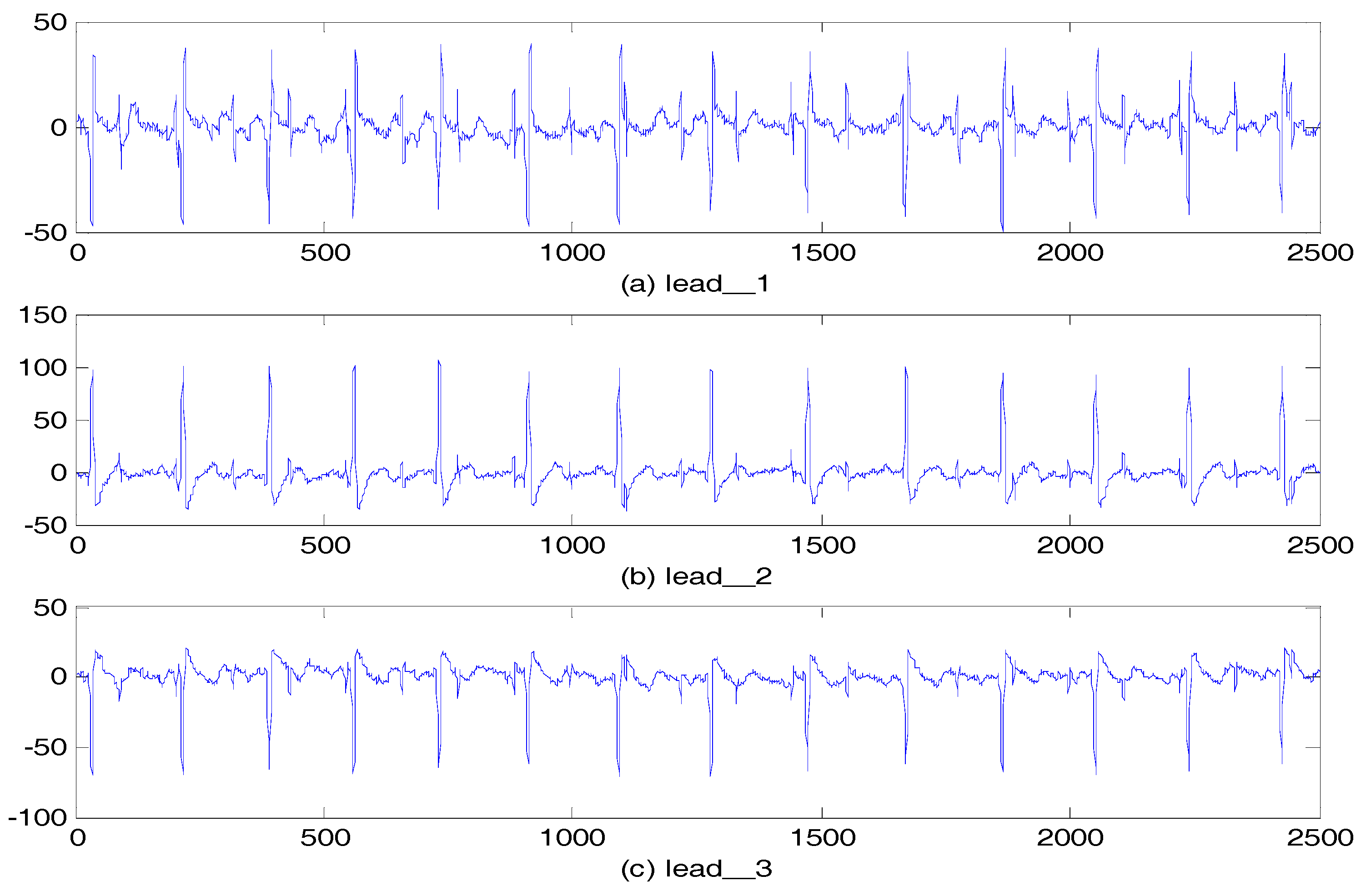
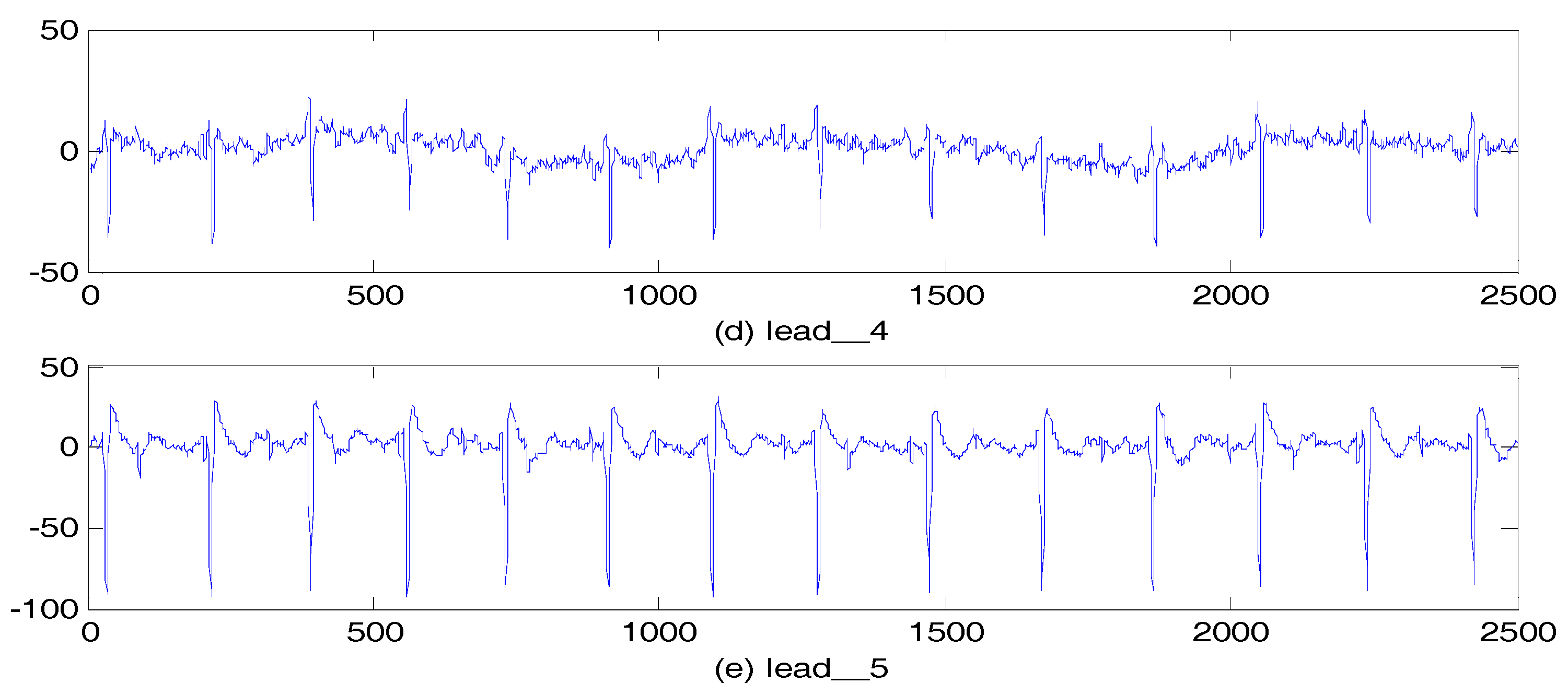
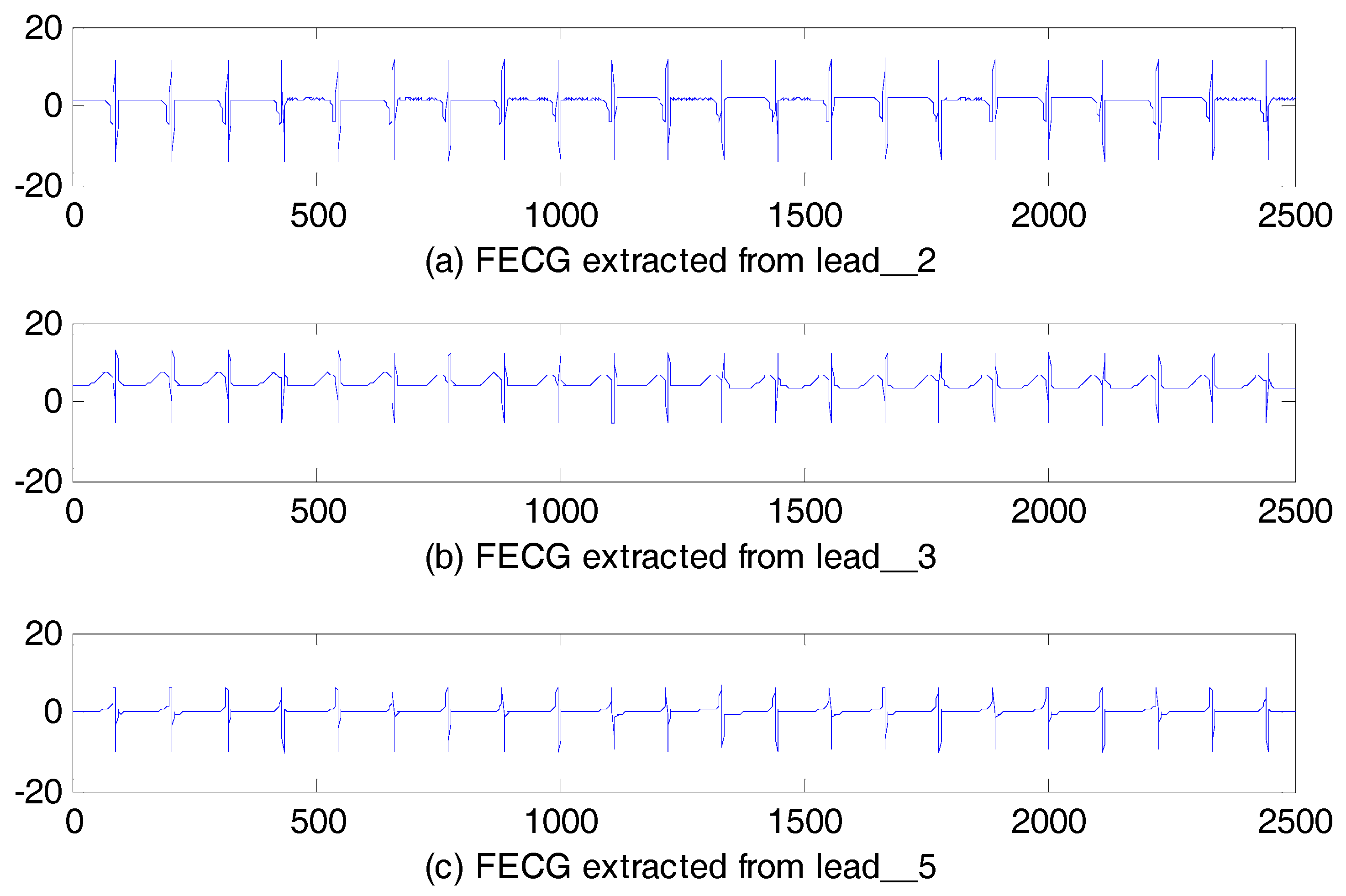
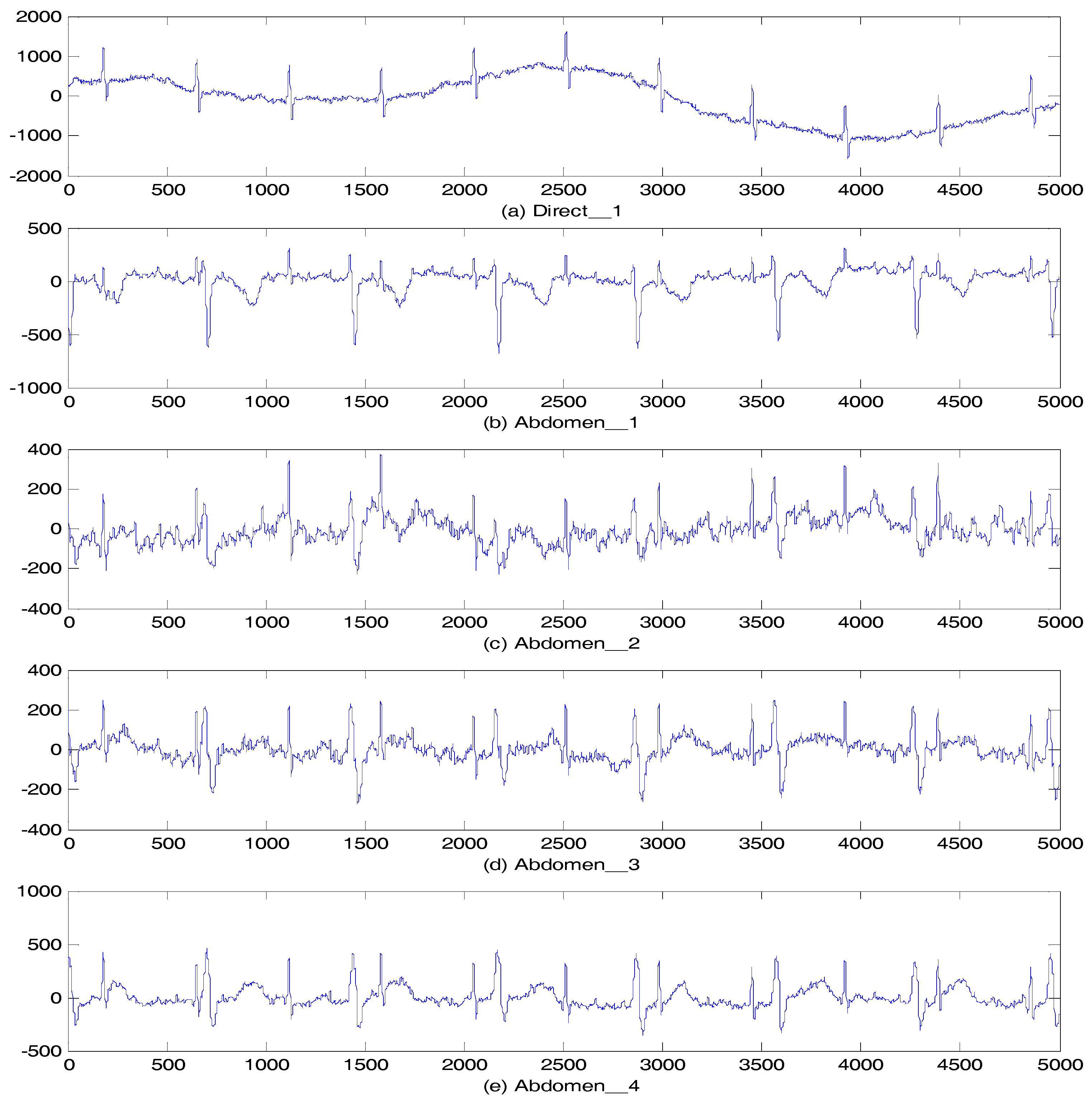
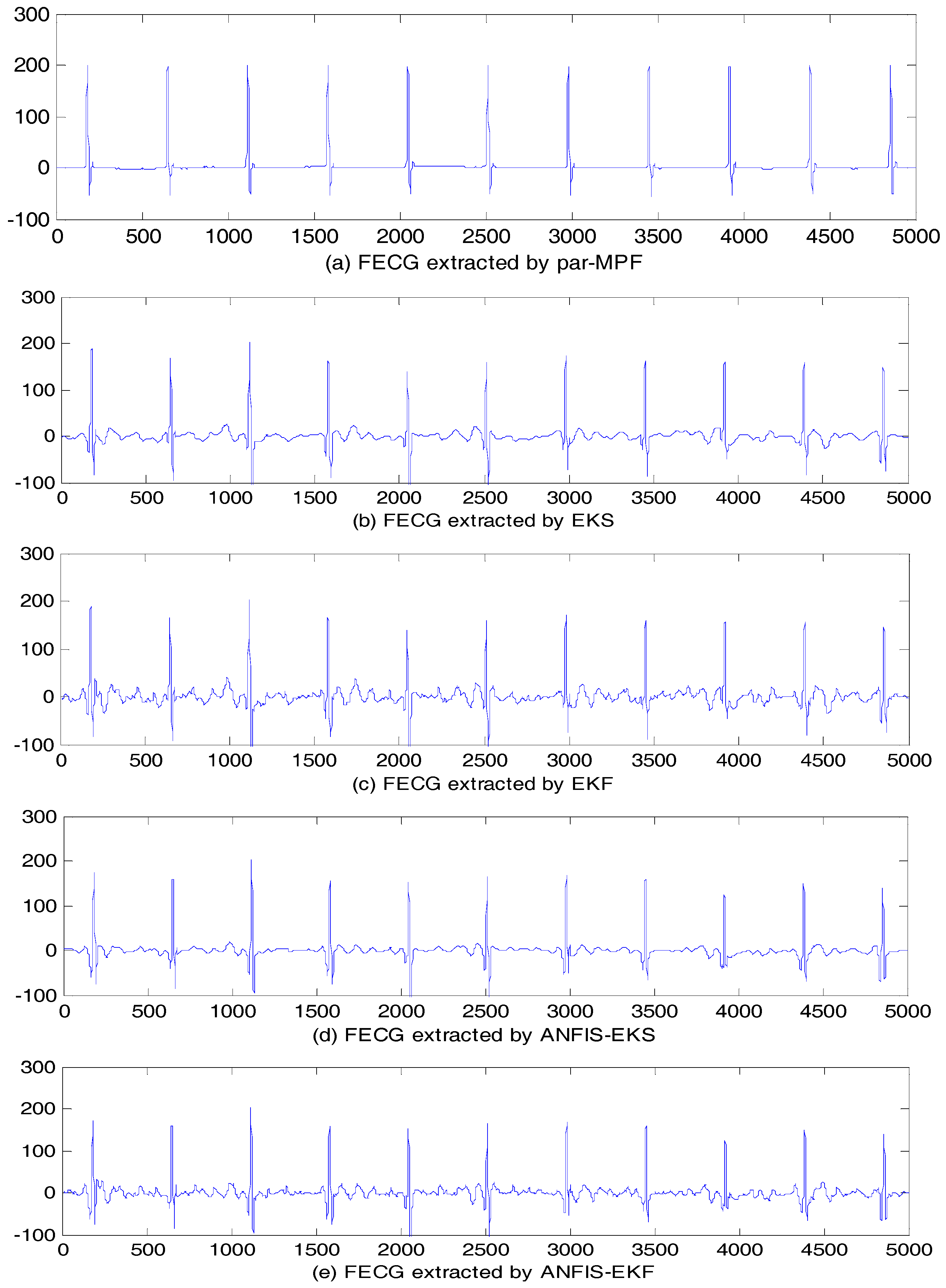
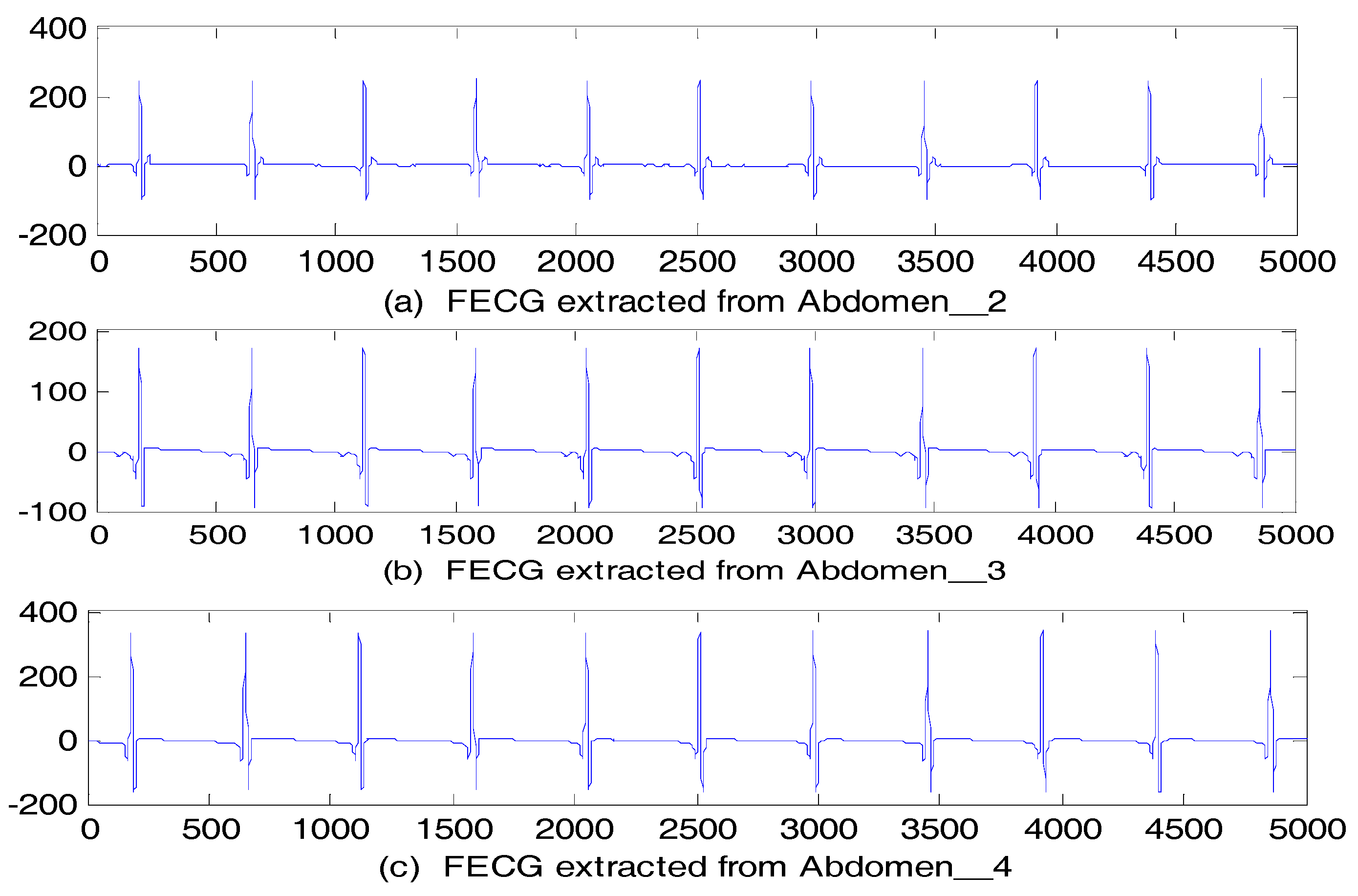
5.2. FECG Extraction on the Different Database.
5.2.1. Database for the Identification of Systems
5.2.2. Abdominal and Direct Fetal ECG Database
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lukosevicius, M.; Marozas, V. Noninvasive fetal QRS detection using an echo state network and dynamic programming. Physiol. Meas. 2014, 35, 1685–1697. [Google Scholar] [CrossRef] [PubMed]
- Ayat, M.; Assaleh, K.; Al-Nashash, H. Extracting fetal ECG from a single maternal abdominal record. In Proceedings of the IEEE 8th GCC Conference and Exhibition (GCCCE), Muscat, Oman, 1–4 February 2015; pp. 1–4. [Google Scholar]
- Puthusserypady, S. Extraction of fetal electrocardiogram using H∞ adaptive algorithms. Med. Biol. Eng. Comput. 2007, 45, 927–937. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Liu, H.X.; Cheng, J.C. Adaptive filtering in phase space for foetal electrocardiogram estimation from an abdominal electrocardiogram signal and a thoracic electrocardiogram signal. IET Signal Process. 2012, 6, 171–177. [Google Scholar]
- Zheng, W.; Wei, X.Y.; Zhong, J.J.; Liu, H.X. Noninvasive fetal ECG estiomation using adaptive comb filter. Comput. Methods Progr. Biomed. 2013, 112, 125–134. [Google Scholar]
- Wu, S.; Shen, Y.; Zhou, Z.; Lin, L.; Zeng, Y.; Gao, X. Research of fetal ECG extraction using wavelet analysis and adaptive filtering. Comput. Biol. Med. 2013, 43, 1622–1627. [Google Scholar] [CrossRef] [PubMed]
- Elmansouri, K.; Latif, R.; Maoulainine, F. Efficient fetal heart rate extraction using undecimated wavelet transform. In Proceedings of the 2nd World Conference on Complex Systems (WCCS), Agadir, Morocco, 10–12 November 2014; pp. 696–701. [Google Scholar]
- Desai, K.D.; Sankhe, M.S. A real-time fetal ECG feature extraction using multiscale discrete wavelet transform. In Proceedings of the 5th International Conference on Biomedical Engineering and Informatics (BMEI), Chongqing, China, 16–18 October 2012; pp. 407–412. [Google Scholar]
- Campolo, M.; Labate, D.; Foresta, F.L.; Morabito, F.C. ECG-derived respiratory signal using Empirical Mode Decomposition. In Proceedings of the IEEE International Workshop on Medical Measurements and Applications, Bari, Italy, 30–31 May 2011; pp. 399–403. [Google Scholar]
- Niknazar, M.; Rivet, B.; Jutten, C. Fetal ECG extraction by extended state kalman filtering based on single-channel recordings. IEEE Trans. Biomed. Eng. 2013, 60, 1345–1352. [Google Scholar] [CrossRef] [PubMed]
- Zeng, X.; Zhou, X.; Li, G.; Liu, Q. Robust adaptive fetal heart rate estimation for single-channel abdominal ECG recording. In Proceedings of the 5th International Conference on Biomedical Engineering and Informatics (BMEI), Chongqing, China, 16–18 October 2012; pp. 587–591. [Google Scholar]
- Panigrahy, D.; Sahu, P.K. Extraction of fetal electrocardiogram (ECG) by extended state Kalman filtering and adaptive neuro-fuzzy inference system (ANFIS) based on single channel abdominal recording. Sadhana 2015, 40, 1091–1104. [Google Scholar] [CrossRef]
- Schon, T.; Gustafsson, F.; Nordlund, P. Marginalized particle filters for mixed linear/nonlinear state-space models. IEEE Trans. Signal Process. 2005, 53, 2279–2289. [Google Scholar] [CrossRef]
- McSharry, P.E.; Clifford, G.D.; Tarassenko, L.; Smith, L.A. A dynamical model for generating synthetic electrocardiogram signals. IEEE Trans. Biomed. Eng. 2003, 50, 289–292. [Google Scholar] [CrossRef] [PubMed]
- Sameni, R.; Shamsollahi, M.B.; Jutten, C.; Clifford, G.D. A nonlinear Bayesian filtering framework for ECG denoising. IEEE Trans. Biomed. Eng. 2007, 54, 2172–2185. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Zeng, X.; Lin, J.; Zhou, X. Genetic particle filtering for denoising of ECG corrupted by muscle artifacts. In Proceedings of the 8th International Conference on Natural Computation, Chongqing, China, 29–31 May 2012; pp. 562–565. [Google Scholar]
- Lin, C.; Bugallo, M.; Mailhes, C.; Tourneret, J.Y. ECG denoising using a dynamical model and a marginalized particle filter. In Proceedings of the Conference Record of the 45th Asilomar Conference on Signals, Systems and Computers (ASILOMAR), Pacific Grove, CA, USA, 6–9 November 2011; pp. 1679–1683. [Google Scholar]
- Jagannath, D.J.; Selvakumar, A.I. Superior foetal electrocardiogram signal elicitation using a novel artificial intelligent Bayesian methodology. Appl. Soft Comput. 2015, 37, 1002–1017. [Google Scholar] [CrossRef]
- Martinez, M.; Calpe, J.; Soria, E.; Guerrero, J.F. Methods to evaluate the performance of fetal electrocardiogram extraction algorithms. In Proceedings of the Computers in Cardiology 2001, Rotterdam, The Netherlands, 23–26 September 2001; pp. 253–256. [Google Scholar]
- Behar, J.; Andreotti, F.; Zaunseder, S.; Li, Q.; Oster, J.; Clifford, G.D. An ECG simulator for generating maternal-foetal activity mixtures on abdominal ECG recordings. Physiol. Meas. 2014, 35, 1537–1550. [Google Scholar] [CrossRef] [PubMed]
- L.LathauwerDaISy: Database for the Identification of Systems. Available online: http://www.esat.kuleuven.ac.be./sista/daisy (accessed on 18 June 2017).
- Jezewski, J.; Matonia, A.; Kupka, T.; Roj, D.; Czabanski, R. Determination of fetal heart rate from abdominal signals: Evaluation of beat-to-beat accuracy in relation to the direct fetal electrocardiogram. Biomed. Tech. 2012, 57, 383–394. [Google Scholar] [CrossRef] [PubMed]
- Abdominal and Direct Foetal ECG Database. Available online: https://www.physionet.org/physiobank/database/adfecgdb (accessed on 18 June 2017).
- Karvounis, E.C.; Tsipouras, M.G.; Fotiadis, D.I. Detection of Fetal Heart Rate through 3-D Phase Space Analysis from Multivariate Abdominal Recordings. IEEE Trans. Biomed. Eng. 2009, 56, 1394–1406. [Google Scholar] [CrossRef] [PubMed]
- Castillo, E.; Morales, D.P.; Botella, G.; Garcia, A.; Parrilla, L.; Palma, A.J. Efficient wavelet-based ECG processing for single-lead FHR extraction. Digit. Signal Process. 2013, 23, 1897–1909. [Google Scholar] [CrossRef]
- Castillo, E.; Morales, D.P.; Garcia, A.; Martinez-Marti, F.; Parrilla, L.; Palma, A.J. Noise Suppression in ECG Signals through Efficient One-Step Wavelet Processing Techniques. J. Appl. Math. 2013, 2013, 4. [Google Scholar] [CrossRef]

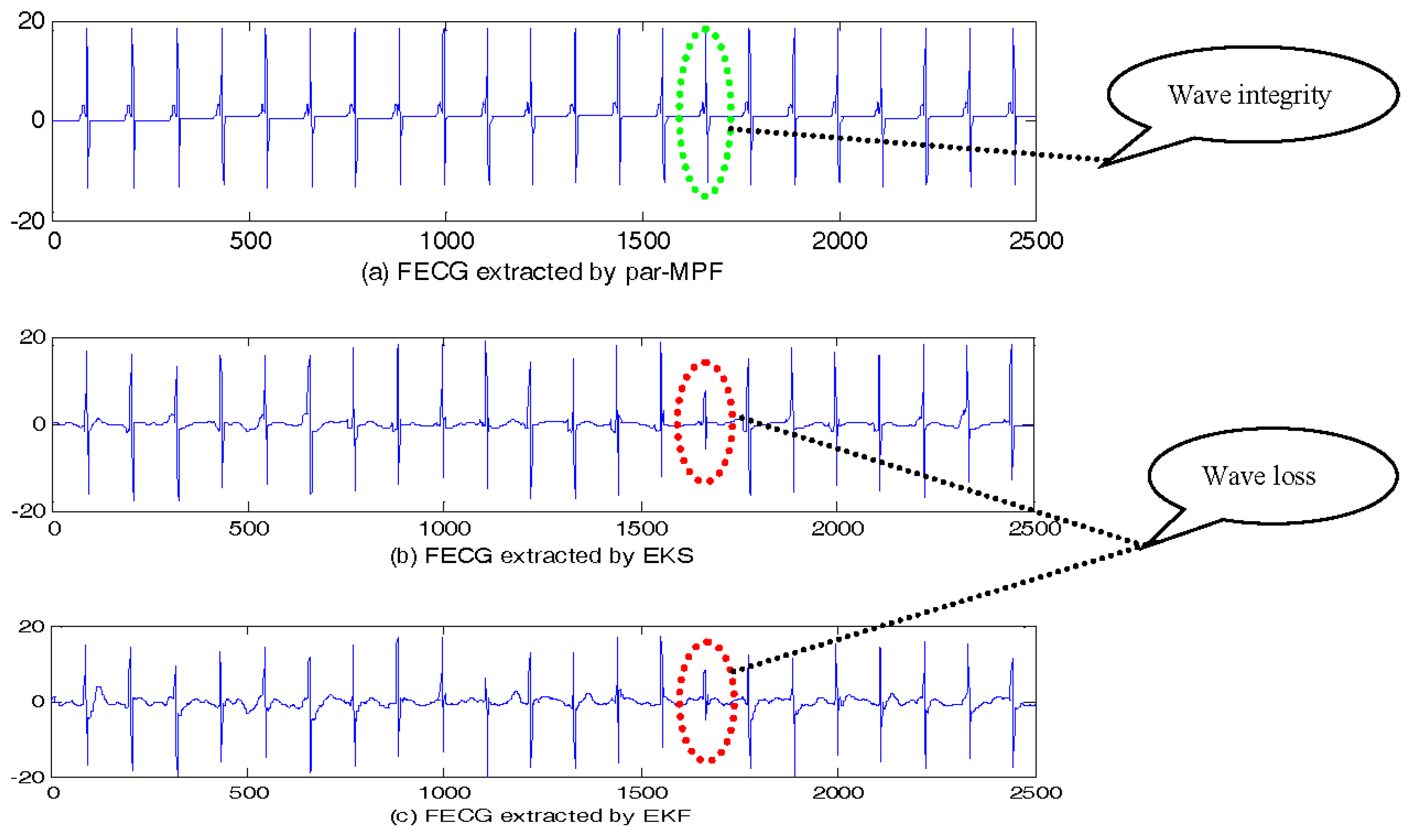
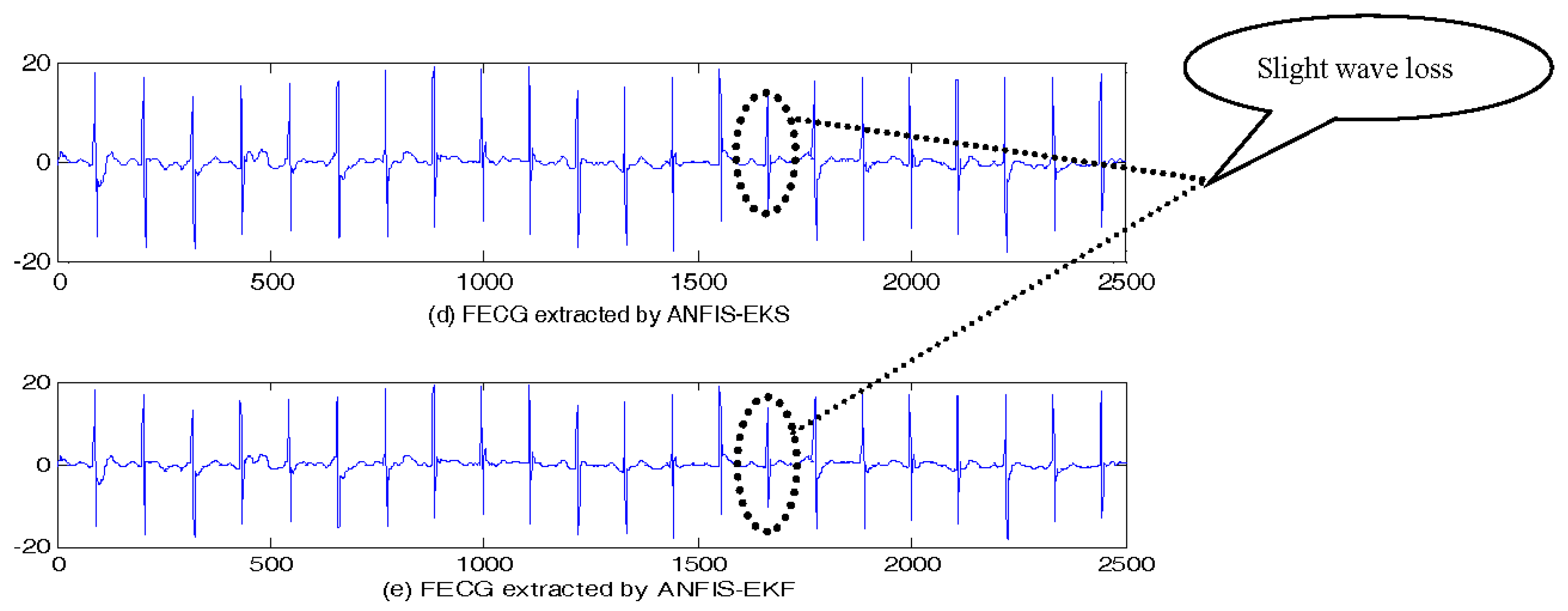
| Filtering Algorithm | Main Idea |
|---|---|
| par-MPF | Marginalized particle filter |
| EKS [10] | Extended Kalman filter + Smooth |
| EKF [11] | Extended Kalman filter |
| ANFIS-EKS [12] | EKS + Adaptive neuro fuzzy inference system |
| ANFIS-EKF [12] | EKF + Adaptive neuro fuzzy inference system |
| Methods | Lead 1 | Lead 2 | Lead 3 | Lead 4 | ||||
|---|---|---|---|---|---|---|---|---|
| par-MPF | 2.0864 | 1.6820 | 2.0849 | 1.7120 | 2.4119 | 2.1926 | 2.1033 | 1.7037 |
| EKS [10] | 1.7497 | 1.5677 | 1.8250 | 1.3714 | 1.3903 | 0.7797 | 1.1414 | 0.9533 |
| EKF [11] | 1.2245 | 1.1506 | 1.2367 | 0.8392 | 1.3590 | 0.7465 | 0.6258 | 0.4130 |
| ANFIS-EKS [12] | 1.8334 | 1.6152 | 1.8709 | 1.4889 | 1.4452 | 1.4917 | 1.1837 | 0.9856 |
| ANFIS-EKF [12] | 1.5097 | 1.3160 | 1.5491 | 1.2557 | 1.3767 | 0.9247 | 0.8465 | 0.6551 |
| Method | Abdomen-1 | Abdomen-2 | Abdomen-3 | Abdomen-4 | ||||
|---|---|---|---|---|---|---|---|---|
| par-MPF | 12.8898 | 14.7332 | 12.1464 | 13.9624 | 11.4695 | 13.2144 | 13.352 | 15.3952 |
| EKS [10] | 3.5025 | 3.6133 | 3.8609 | 4.1144 | 5.0389 | 5.1286 | 6.7488 | 6.9799 |
| EKF [11] | 2.4222 | 2.3902 | 2.236 | 2.2596 | 3.5868 | 3.2583 | 4.2651 | 3.8168 |
| ANFIS-EKS [12] | 4.2285 | 4.5879 | 4.1438 | 4.6256 | 5.5427 | 5.5549 | 7.2039 | 7.2104 |
| ANFIS-EKF [12] | 3.0071 | 3.0873 | 2.5573 | 2.7417 | 3.9021 | 3.8444 | 5.5771 | 5.4508 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Tong, H.; Deng, Y.; Xu, W.; Zhang, Y.; Ye, H. Single-Lead Fetal ECG Extraction Based on a Parallel Marginalized Particle Filter. Sensors 2017, 17, 1456. https://doi.org/10.3390/s17061456
Zhao Z, Tong H, Deng Y, Xu W, Zhang Y, Ye H. Single-Lead Fetal ECG Extraction Based on a Parallel Marginalized Particle Filter. Sensors. 2017; 17(6):1456. https://doi.org/10.3390/s17061456
Chicago/Turabian StyleZhao, Zhidong, Huiling Tong, Yanjun Deng, Wen Xu, Yefei Zhang, and Haihui Ye. 2017. "Single-Lead Fetal ECG Extraction Based on a Parallel Marginalized Particle Filter" Sensors 17, no. 6: 1456. https://doi.org/10.3390/s17061456
APA StyleZhao, Z., Tong, H., Deng, Y., Xu, W., Zhang, Y., & Ye, H. (2017). Single-Lead Fetal ECG Extraction Based on a Parallel Marginalized Particle Filter. Sensors, 17(6), 1456. https://doi.org/10.3390/s17061456





