Acoustic Emission and Echo Signal Compensation Techniques Applied to an Ultrasonic Logging-While-Drilling Caliper
Abstract
:1. Introduction
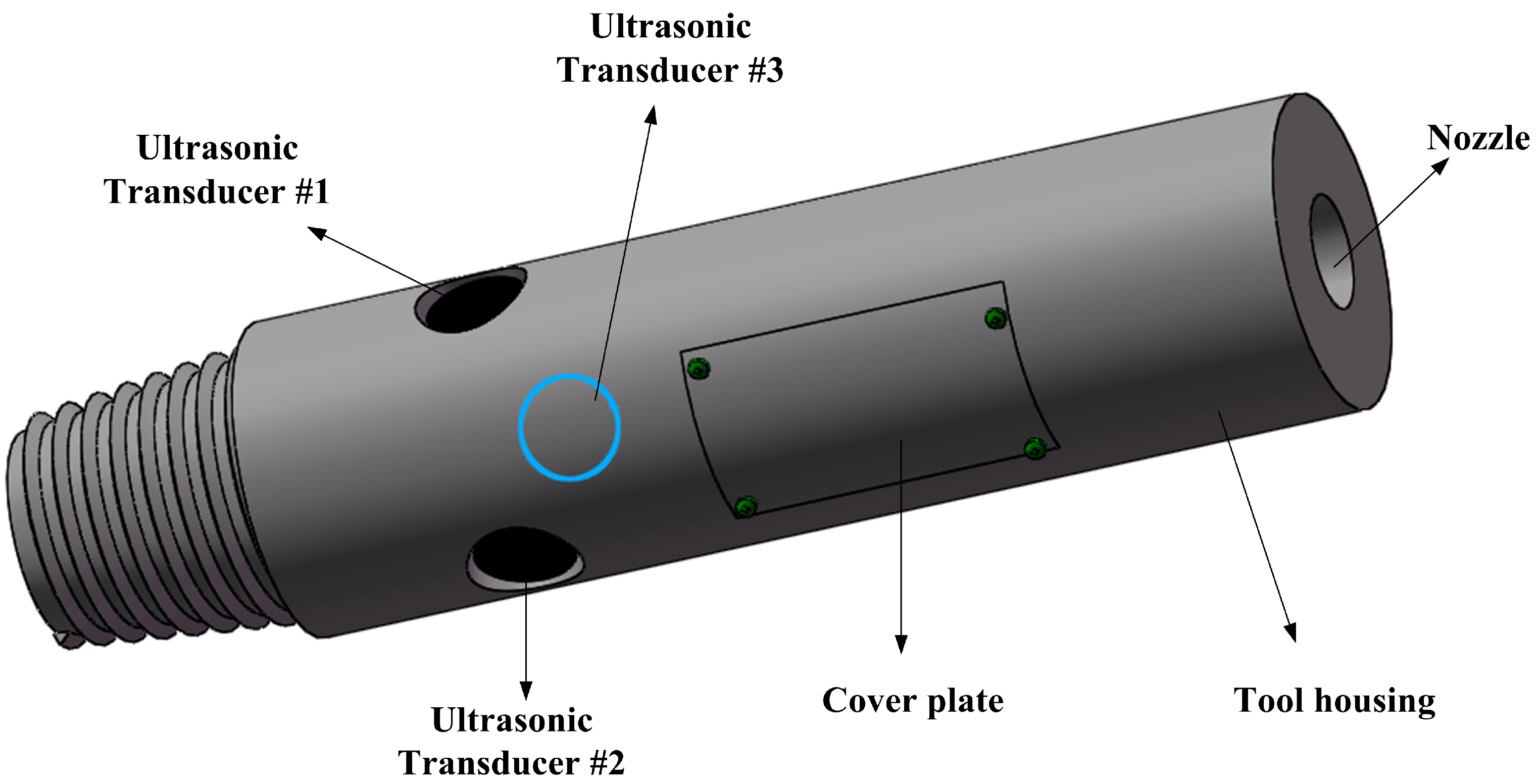
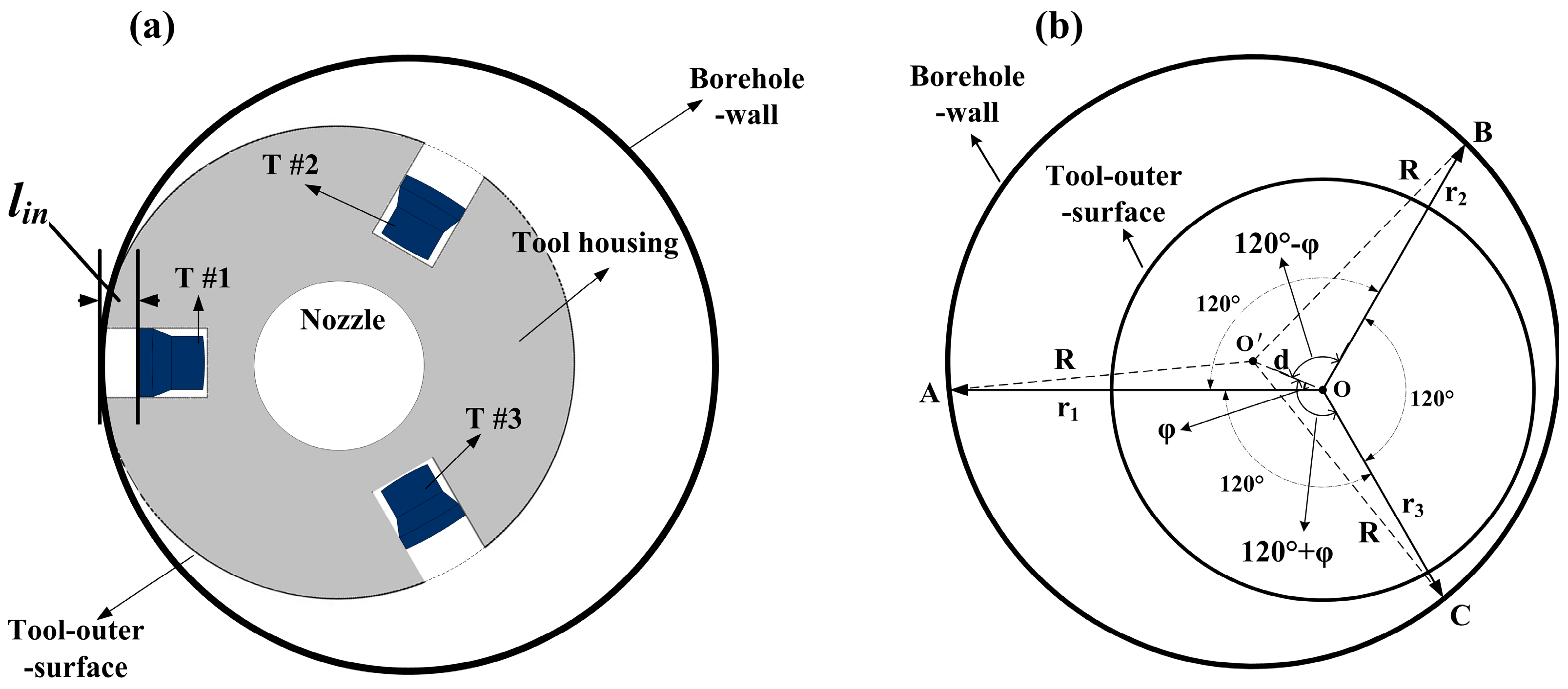
2. Tool Structure and Measurement Principle of Ultrasonic LWD Caliper
3. Acoustic Emission Technique for Reducing Blind Zone
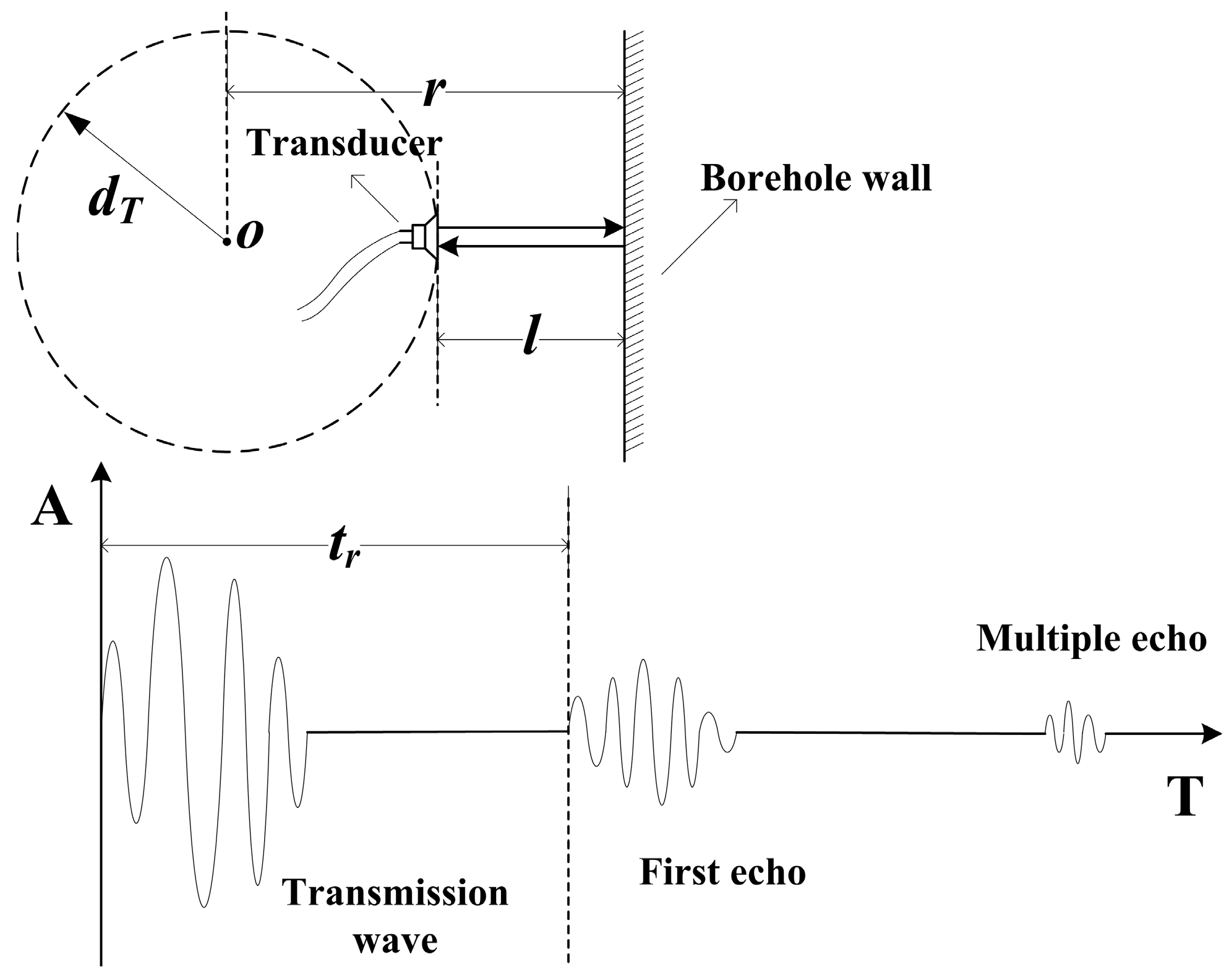
3.1. Generation Mechanism and Theorical Calculation of the Blind Zone in a UDM System
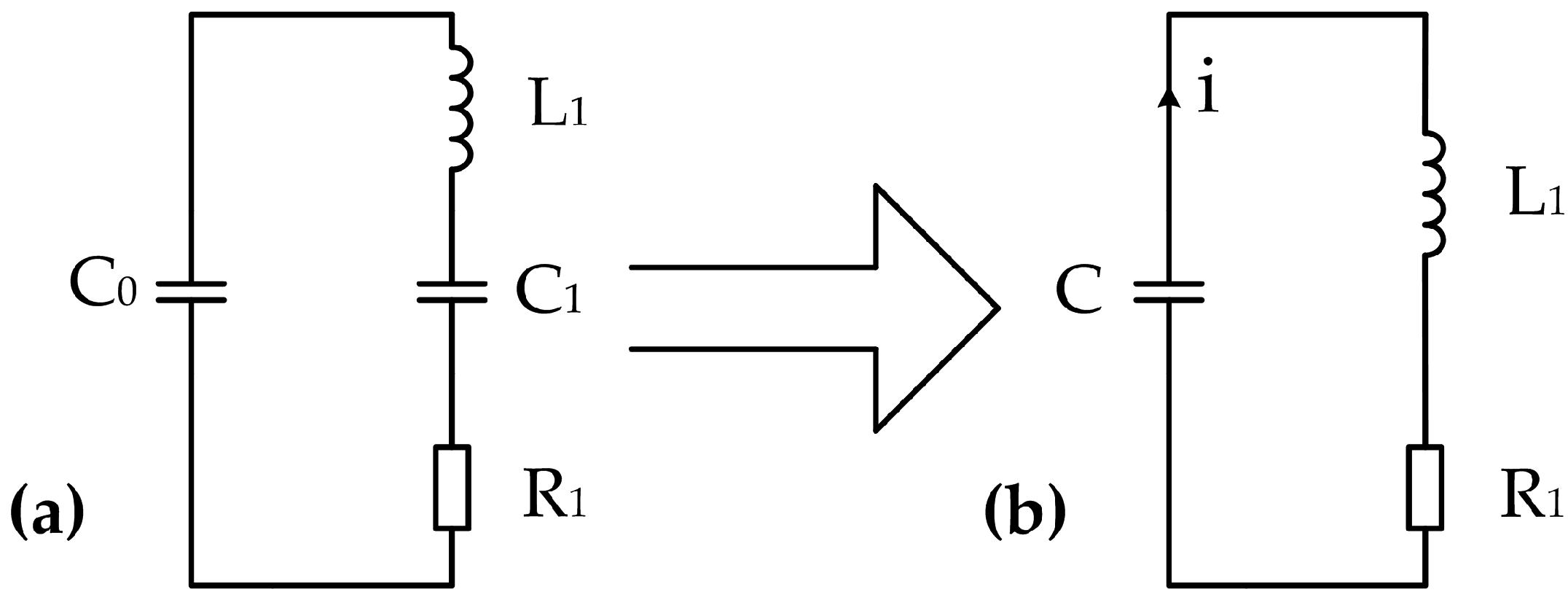
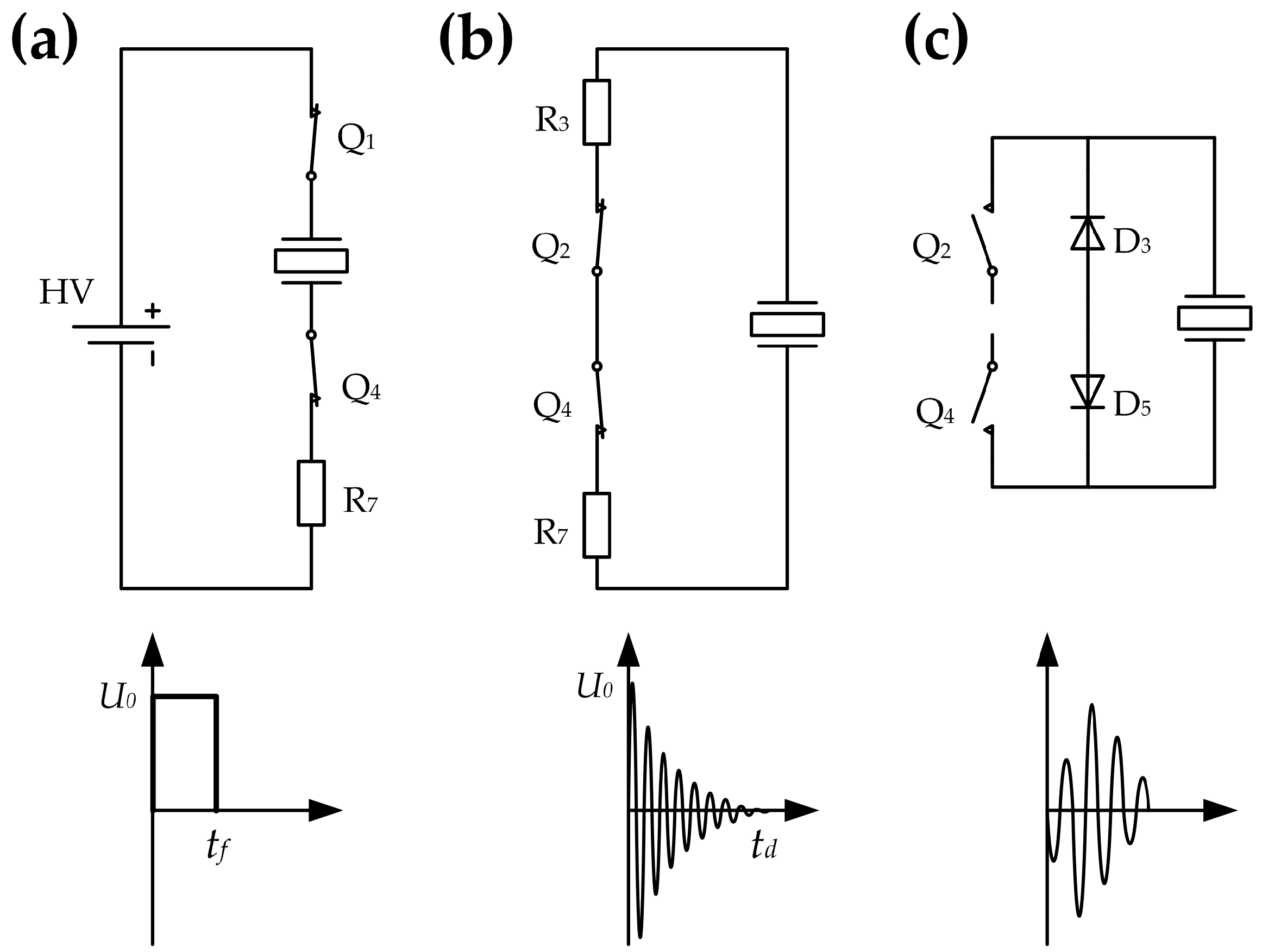
3.2. Circuit Design for Reducing Blind Zone
3.3. Circuit Test
4. Echo Signal Compensation Technique
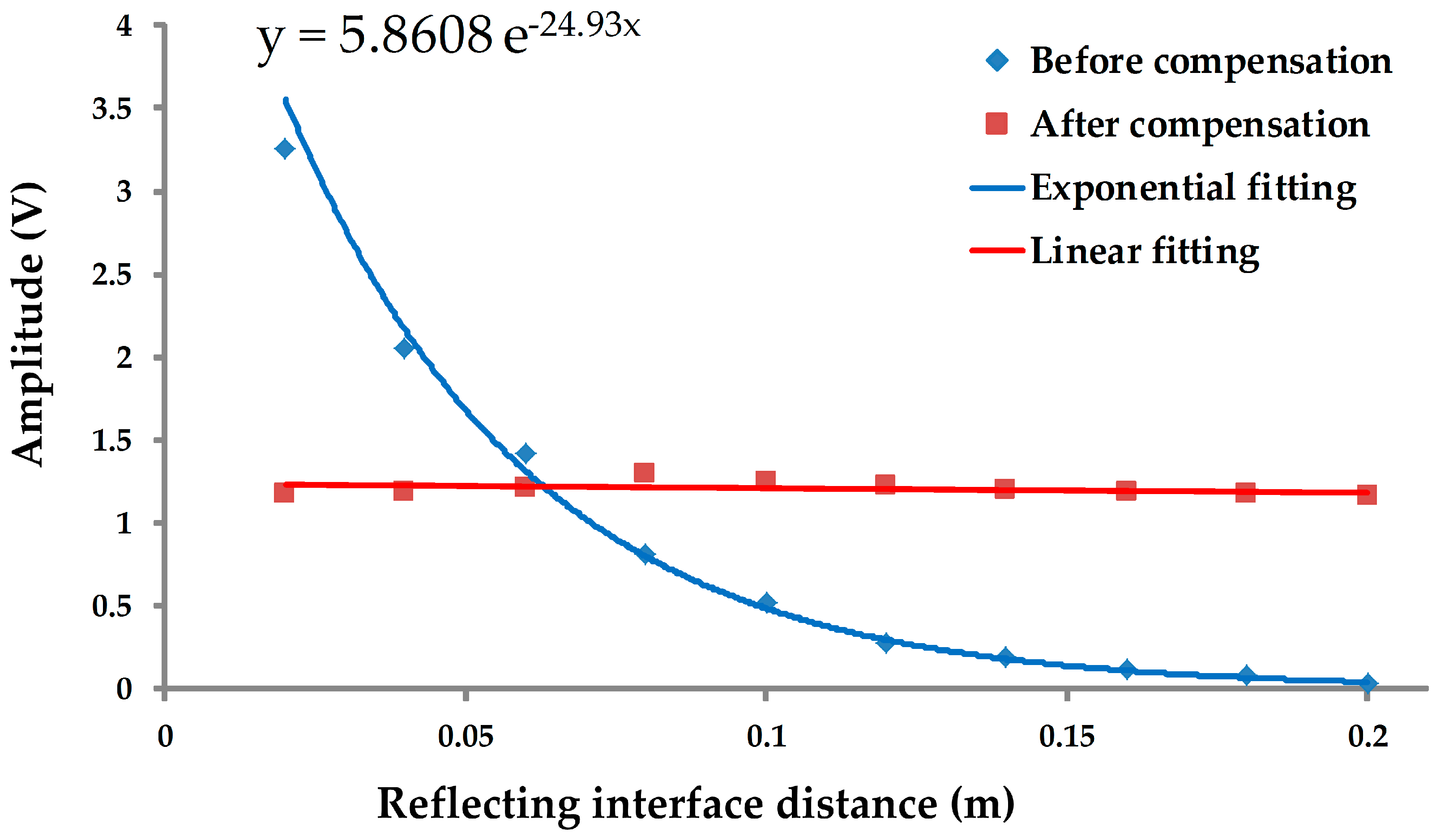
4.1. Principle of Time-Varying Amplification
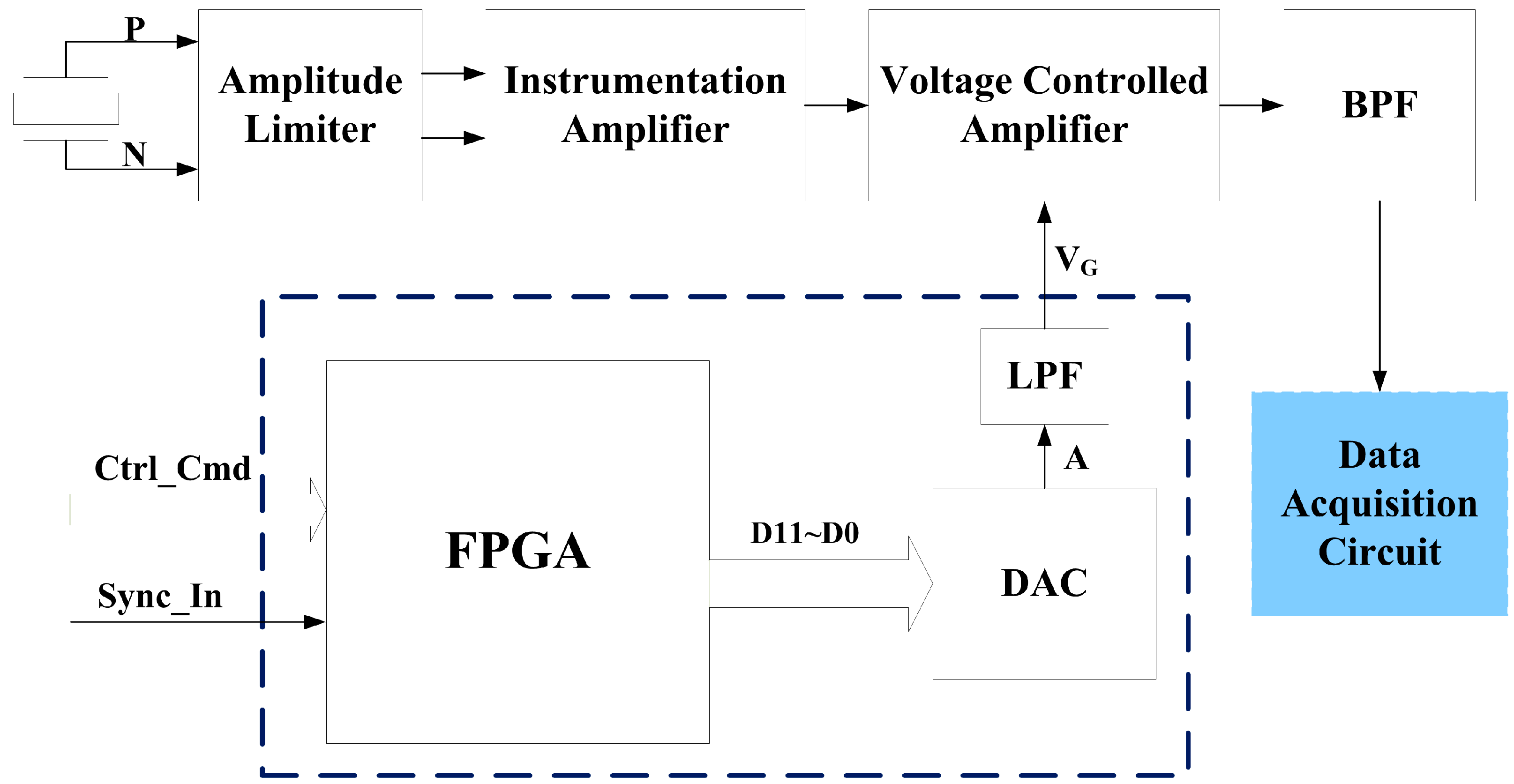
4.2. Circuit Design for Time-Varying Amplification
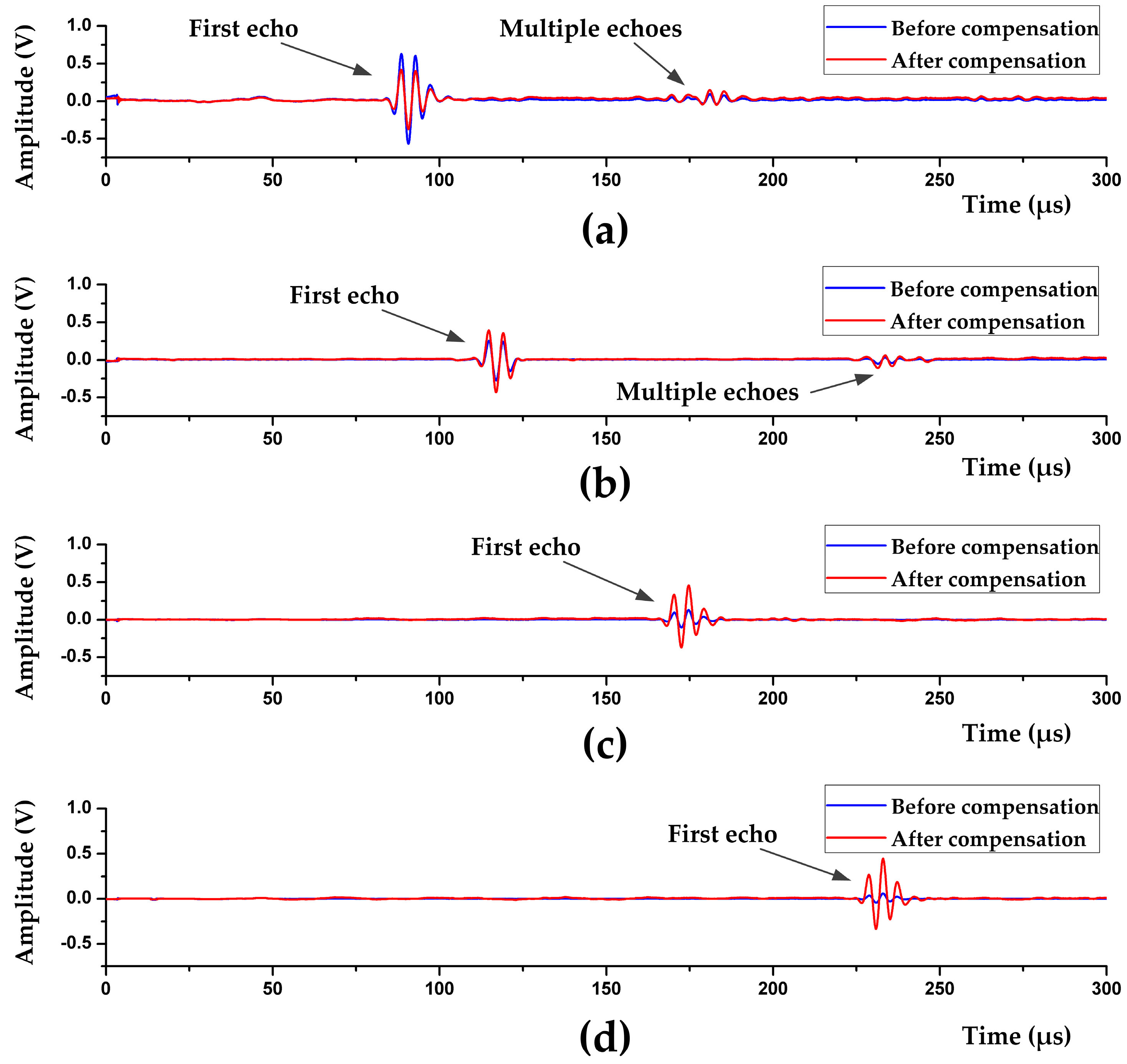
4.3. Circuit Test
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Farag, N.; Bobeth, M.; Pompe, W.; Romanov, A.E.; Speck, J.S. Application of Outcrop Analogues to Optimize LWD Acquisition for More Confident Formation Evaluation in High Angle and Horizontal Wells (Russian). Catal. Today 2008, 138, 193–197. [Google Scholar]
- Bittar, M.; Beste, R.; Li, S.; Wu, H.-H.; Althoff, G. Field Testing of a New LWD Triaxial Sensor for Anisotropy And Dip Measurement In Vertical And Deviated Wells. Physiol. Plant. 2011, 53, 491–496. [Google Scholar]
- Neville, T.J.; Weller, G.; Faivre, O.; Sun, H. A New-Generation LWD Tool With Colocated Sensors Opens New Opportunities for Formation Evaluation. SPE Reserv. Eval. Eng. 2007, 10, 132–139. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Guo, Y. Advances and trends in logging while drilling technology. Well Logging Technol. 2006, 30, 10–15. [Google Scholar]
- Schultz, W.E.; Moake, G.L.; Jackson, C.E. Field Examples of Ultrasonically-Enhanced Density, Neutron-Porosity, and Caliper Logs Obtained While Drilling. SPE Reserv. Eval. Eng. 1996, 1, 252–260. [Google Scholar] [CrossRef]
- Aithoff, G.; Arian, A.; Kavaipatti, A.B.; Varsamis, G. L.; Wieniewski, L.T. Mwd Ultrasonic Caliper Advanced Detection Techniques. Am. J. Respir. Crit. Care Med. 1998, 188, 1052–1057. [Google Scholar]
- Ni, W.; Li, S.; Li, J.; Wei, Z.; Li, S. Design of the Logging While Drilling Caliper Tool Based on Ultrasonic Distance Measurement. Sci. Technol. Rev. 2013, 31, 48–51. [Google Scholar]
- Garcia, J.C.; Montiel-Nelson, J.A.; Nooshabadi, S. A Single-Capacitor Bootstrapped Power-Efficient CMOS Driver. Circuits Syst. II Express Briefs IEEE Trans. 2006, 53, 877–881. [Google Scholar] [CrossRef]
- Design and Application Guide of Bootstrap Circuit for High-Voltage Gate-Drive IC. Available online: https://www.fairchildsemi.com/application-notes/AN/AN-6076.pdf (accessed on 18 December 2014).
- Wang, C.C.; Lee, C.L.; Lin, L.P.; Tseng, Y.-L. Wideband 70 dB CMOS digital variable gain amplifier design for DVB-T receiver’s AGC. In Proceedings of the IEEE International Symposium on Circuits and Systems, Kobe, Japan, 23–26 May 2005; Volume 1, pp. 356–359. [Google Scholar]
- Lin, X.U.; Wang, R.T.; Laboratory, S.A. Compensation for diffusion loss of sound wave in sonar system. J. Meas. Sci. Instrum. 2016, 7, 54–58. [Google Scholar]
- Vasjanov, A.; Barzdenas, V. Design of a time-gain-compensation amplifier for ultrasonic echo signal processing. Proceedings of 2015 Open Conference on Electrical, Electronic and Information Sciences, Vilnius, Lithuania, 21 April 2015. [Google Scholar]
- Lee, D.S.; Ahn, M.J. Ultrasound system and signal processing unit configured for time gain and lateral gain compensation. U.S. Patent 8,016,759, 13 September 2011. [Google Scholar]
- Zhang, M.; Song, R.; Jiang, Y.C.; Feng, Y.S. Investigation on sound distribution and directivity of typical piston transducer. J. PLA Univ. Sci. Technol. 2014, 15, 412–421. [Google Scholar]
- Qin, L.; Gu, C.X.; Wang, L.K.; Zhong, C.; Liu, J.J.; Zhang, B.; Long, D. The Study on Broad Directivity Characteristic of Piston Transducer with Finite Baffle. Appl. Mech. Mater. 2014, 670, 1233–1237. [Google Scholar] [CrossRef]
- Deng, J.; Wang, S.; Han, D. The velocity and attenuation anisotropy of shale at ultrasonic frequency. J. Geophys. Eng. 2009, 6, 269–278. [Google Scholar] [CrossRef]
- Zhang, K.; Ju, X.D.; Lu, J.Q.; Men, B.Y. Design of acoustic logging signal source of imitation based on field programmable gate array. J. Geophys. Eng. 2014, 11, 045008. [Google Scholar] [CrossRef]
- Lu, J.; Ju, X.; Qiao, W.; Men, B.; Wang, R.; Wu, J. Azimuthally acoustic logging tool to evaluate cementing quality. J. Geophys. Eng. 2014, 11, 045006. [Google Scholar] [CrossRef]
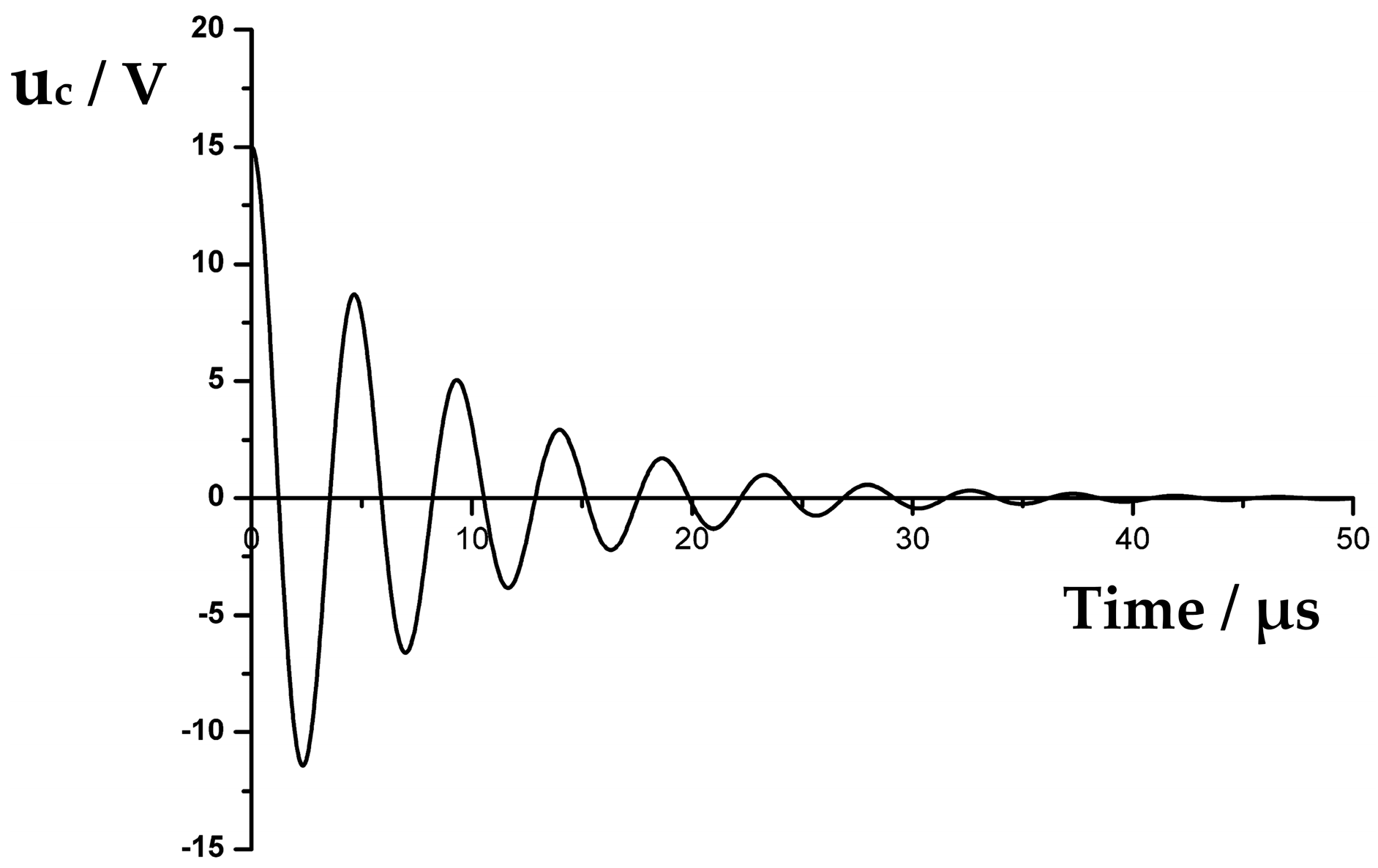
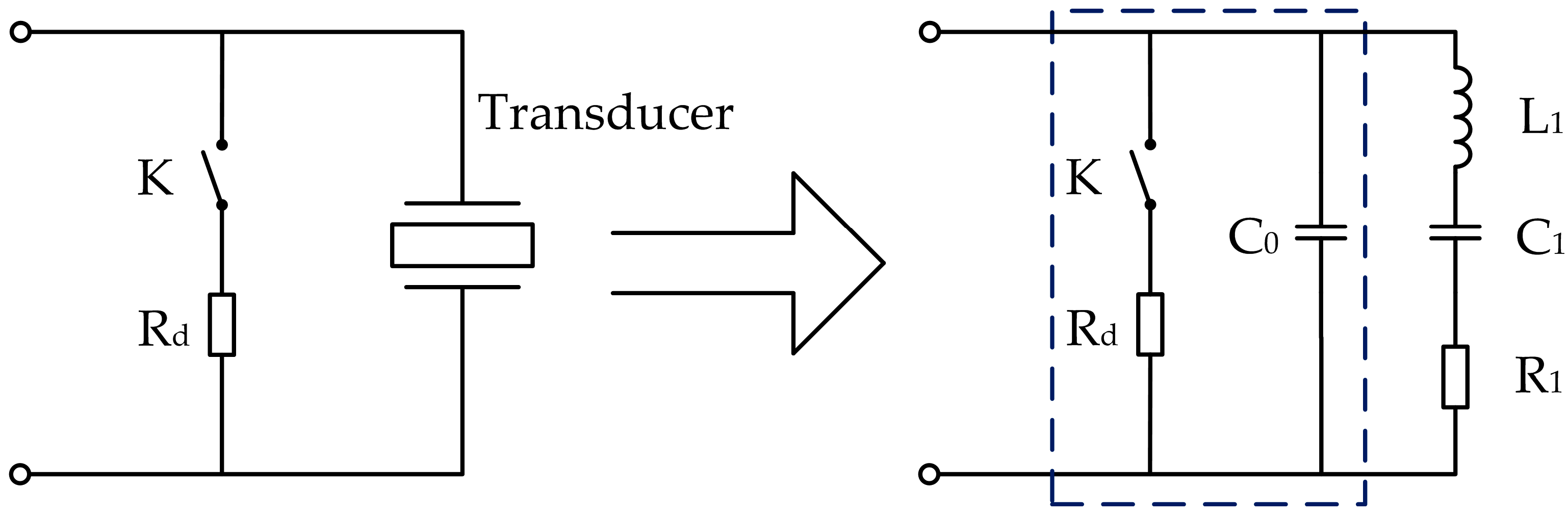
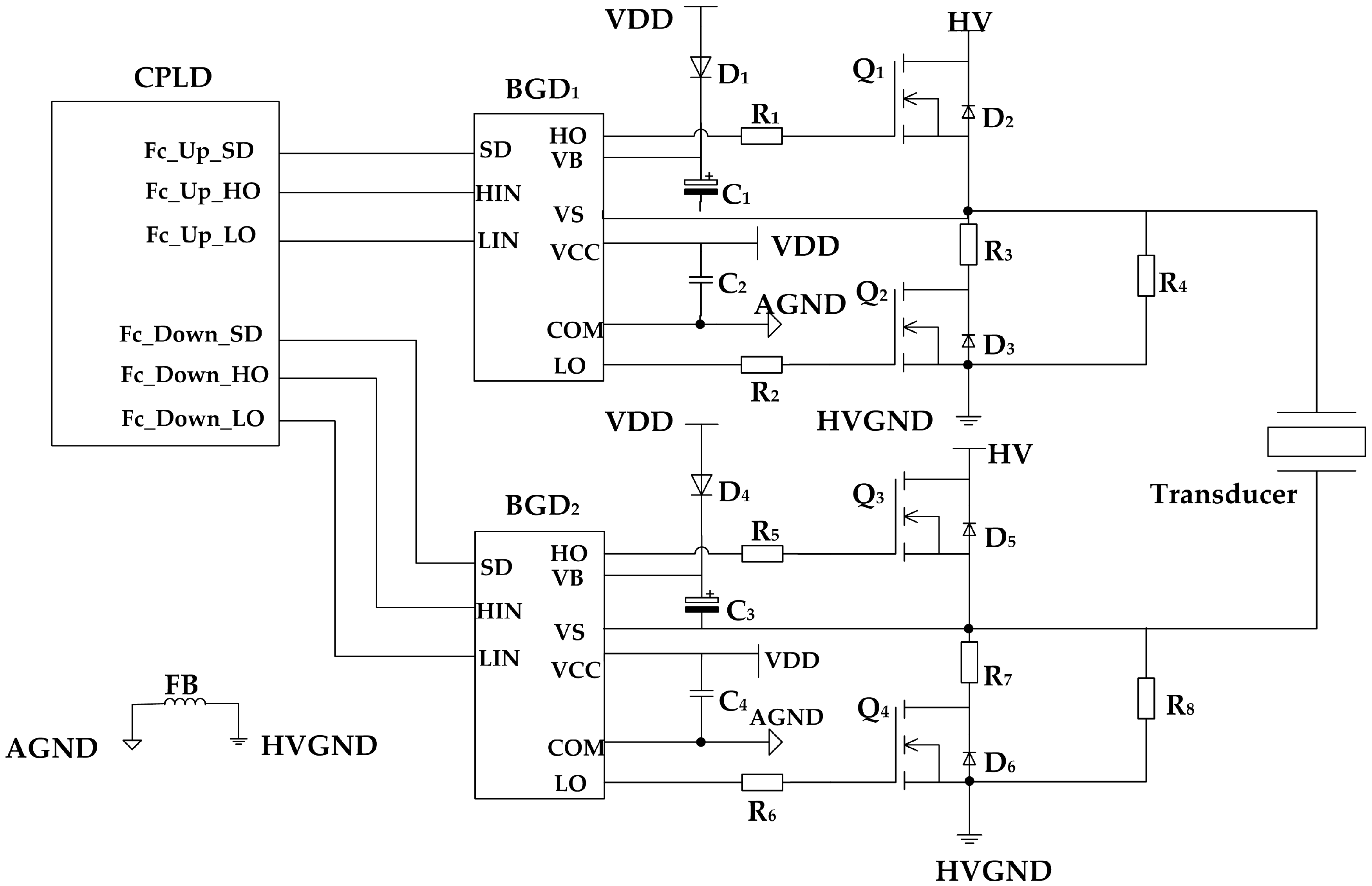
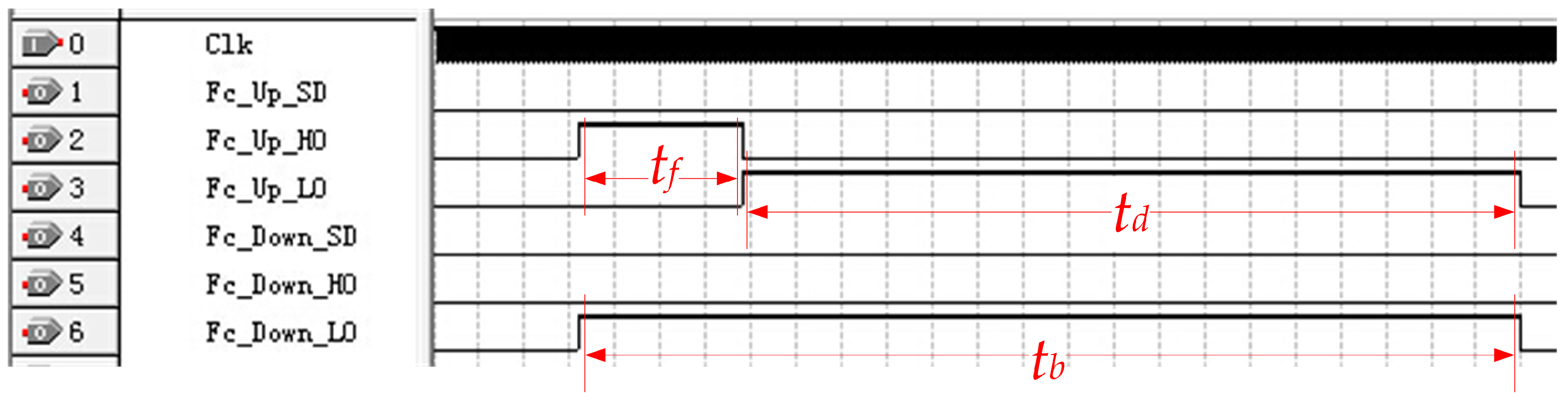

| fs/kHz | Q | Keff | R1/Ω | C0/nF | C1/nF | L1/mH |
|---|---|---|---|---|---|---|
| 221 | 5.25 | 0.47 | 974 | 0.75 | 0.16 | 4.16 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Y.; Ju, X.; Lu, J.; Men, B. Acoustic Emission and Echo Signal Compensation Techniques Applied to an Ultrasonic Logging-While-Drilling Caliper. Sensors 2017, 17, 1351. https://doi.org/10.3390/s17061351
Yao Y, Ju X, Lu J, Men B. Acoustic Emission and Echo Signal Compensation Techniques Applied to an Ultrasonic Logging-While-Drilling Caliper. Sensors. 2017; 17(6):1351. https://doi.org/10.3390/s17061351
Chicago/Turabian StyleYao, Yongchao, Xiaodong Ju, Junqiang Lu, and Baiyong Men. 2017. "Acoustic Emission and Echo Signal Compensation Techniques Applied to an Ultrasonic Logging-While-Drilling Caliper" Sensors 17, no. 6: 1351. https://doi.org/10.3390/s17061351
APA StyleYao, Y., Ju, X., Lu, J., & Men, B. (2017). Acoustic Emission and Echo Signal Compensation Techniques Applied to an Ultrasonic Logging-While-Drilling Caliper. Sensors, 17(6), 1351. https://doi.org/10.3390/s17061351





