A Type-2 Block-Component-Decomposition Based 2D AOA Estimation Algorithm for an Electromagnetic Vector Sensor Array
Abstract
:1. Introduction
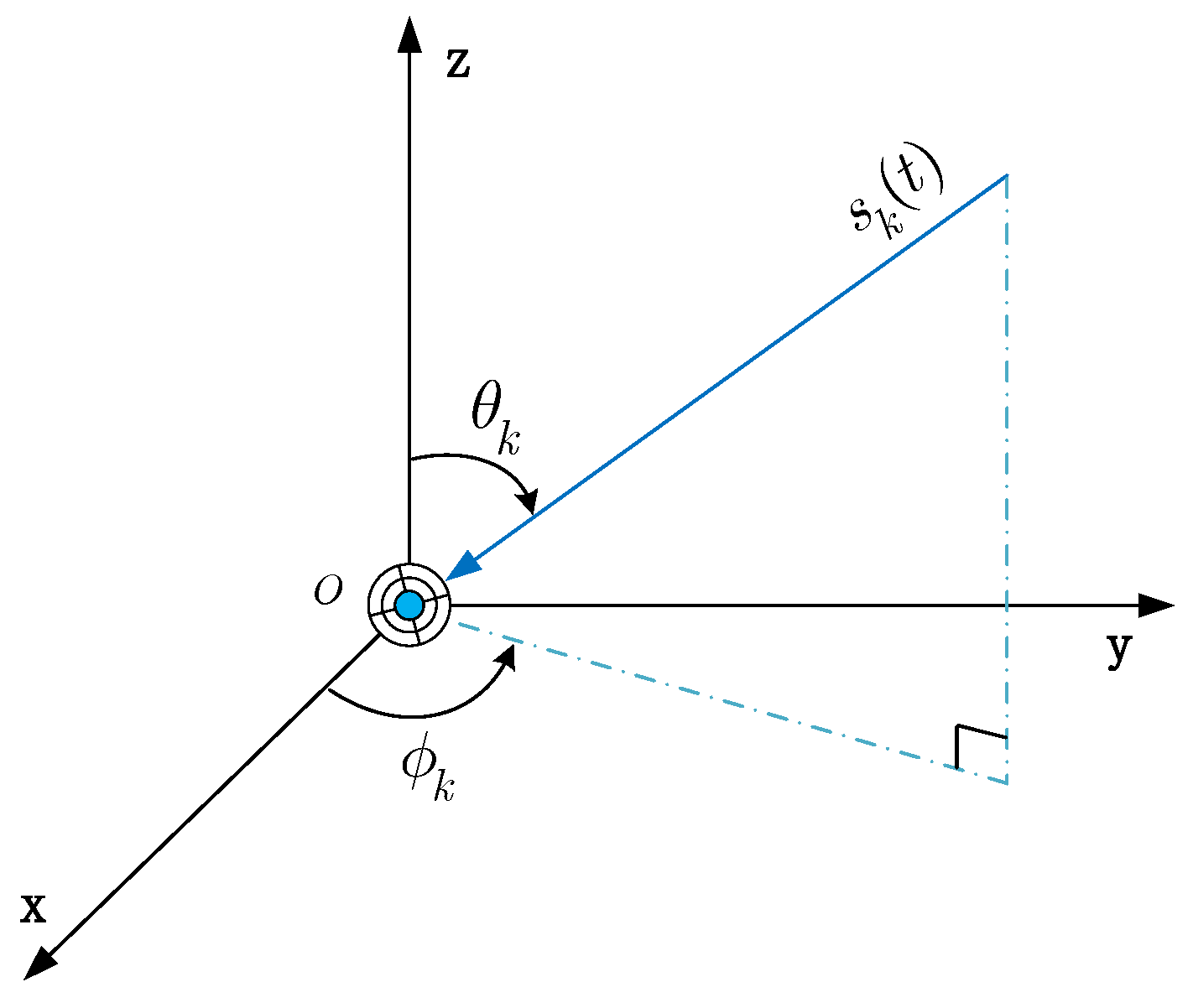
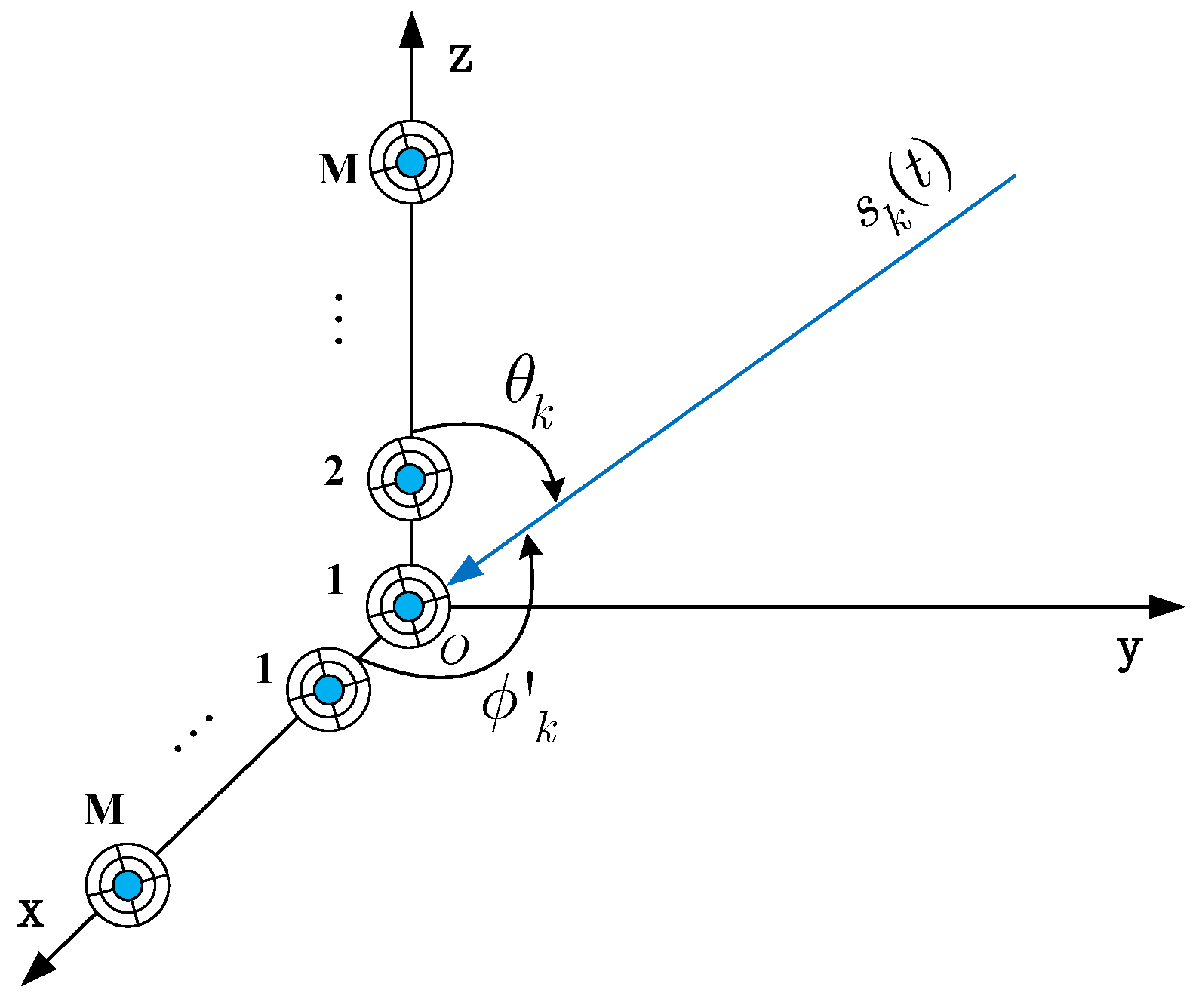
2. Data Model
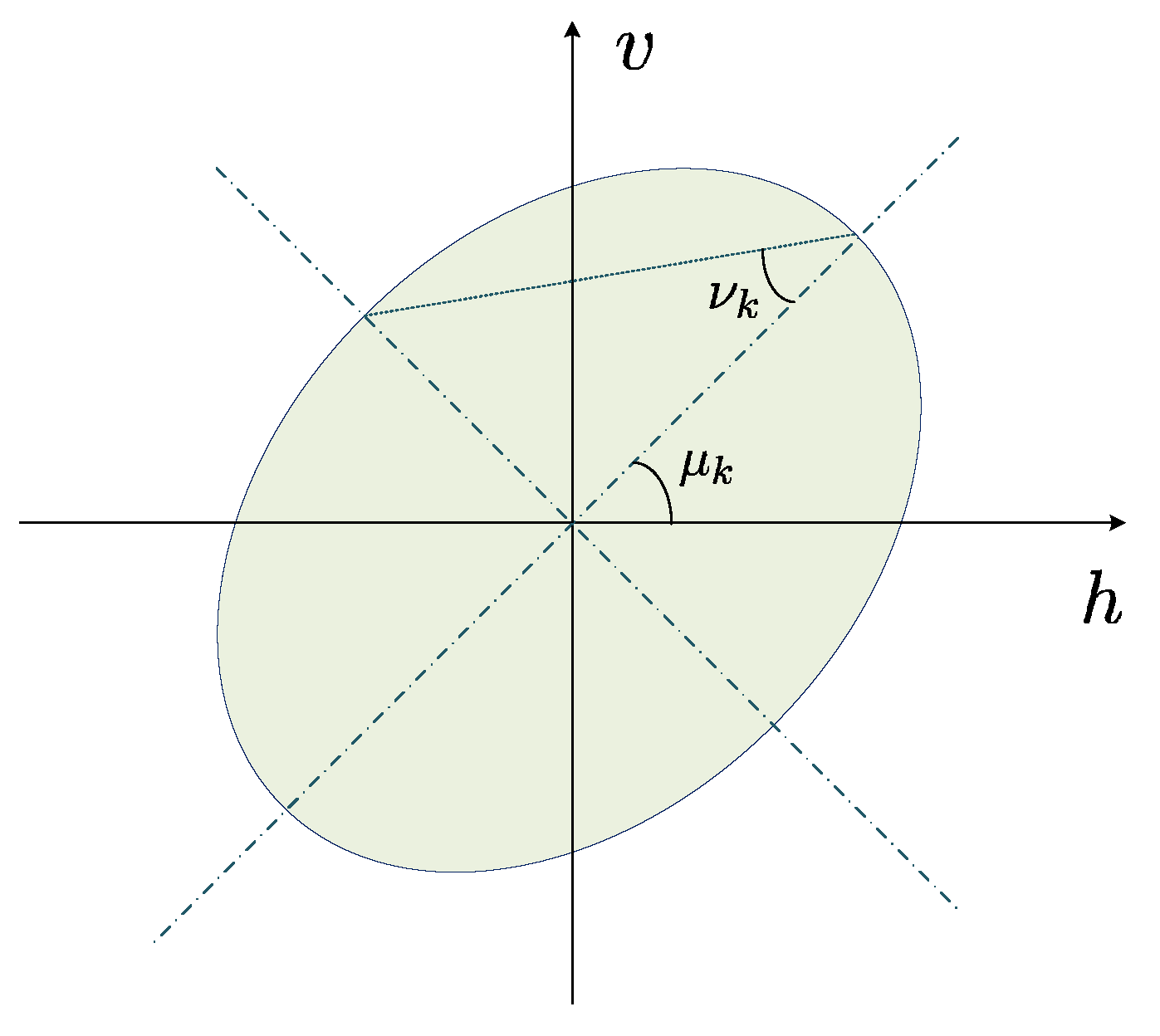
2.1. EMVS Array Signal Model
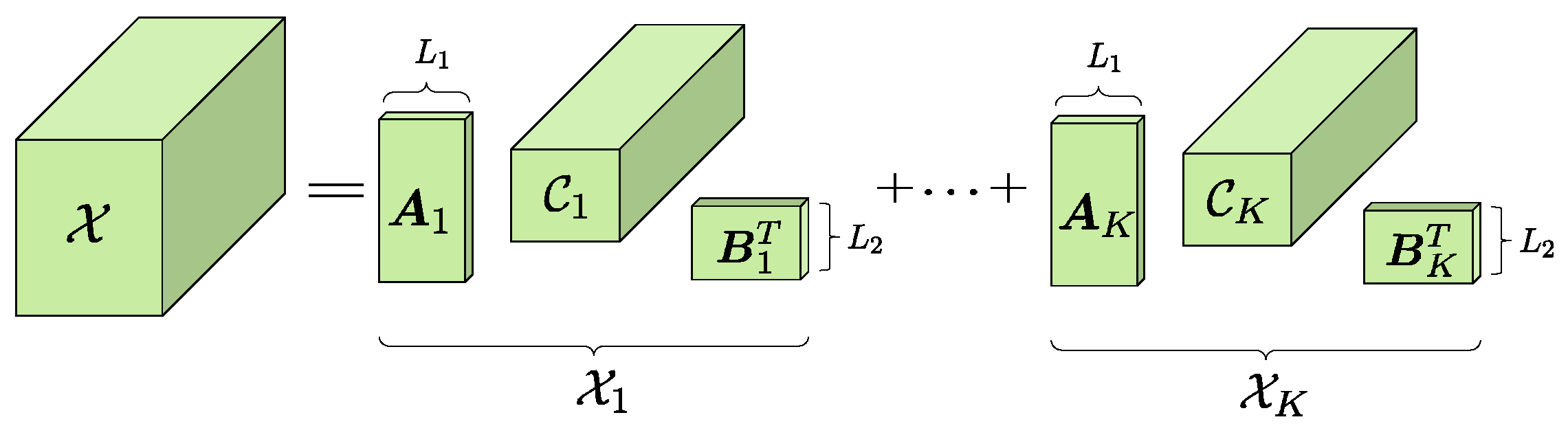
2.2. Block Component Decomposition
3. The Proposed Method
3.1. The BCD Modeling of the EMVS Array
3.1.1. Uniqueness Analysis
3.2. AOA Estimation Algorithm
| Algorithm 1 2D AOA estimation algorithm for the EMVS array based on Type-2 BCD. |
| Input: the received signal ; the number of source signals, K; BCD model parameters, ; the threshold of error, . |
| Output: AOA estimation . |
| 1: Initialization for factor matrices |
| 2: ; |
| 3: ; |
| 4: Presetting for iteration variables |
| 5: ; ; ; . |
| 6: while do |
| 7: ALS for estimating : ; |
| 8: ; |
| 9: ; |
| 10: ALS for estimating : ; |
| 11: Apply QR decomposition: , ; |
| 12: ; |
| 13: ALS for estimating : ; |
| 14: Apply QR decomposition: , ; |
| 15: Calculate the residual: ; |
| 16: end while |
| 17: while do |
| 18: Divide into two parts: ; |
| 19: Apply SVD to each part: ; |
| 20: Obtain the estimates by the subspace approach. |
| 21: ; |
| 22: end while |
4. Numerical Simulations and Discussion
4.1. Implementations of 2D AOA Estimation
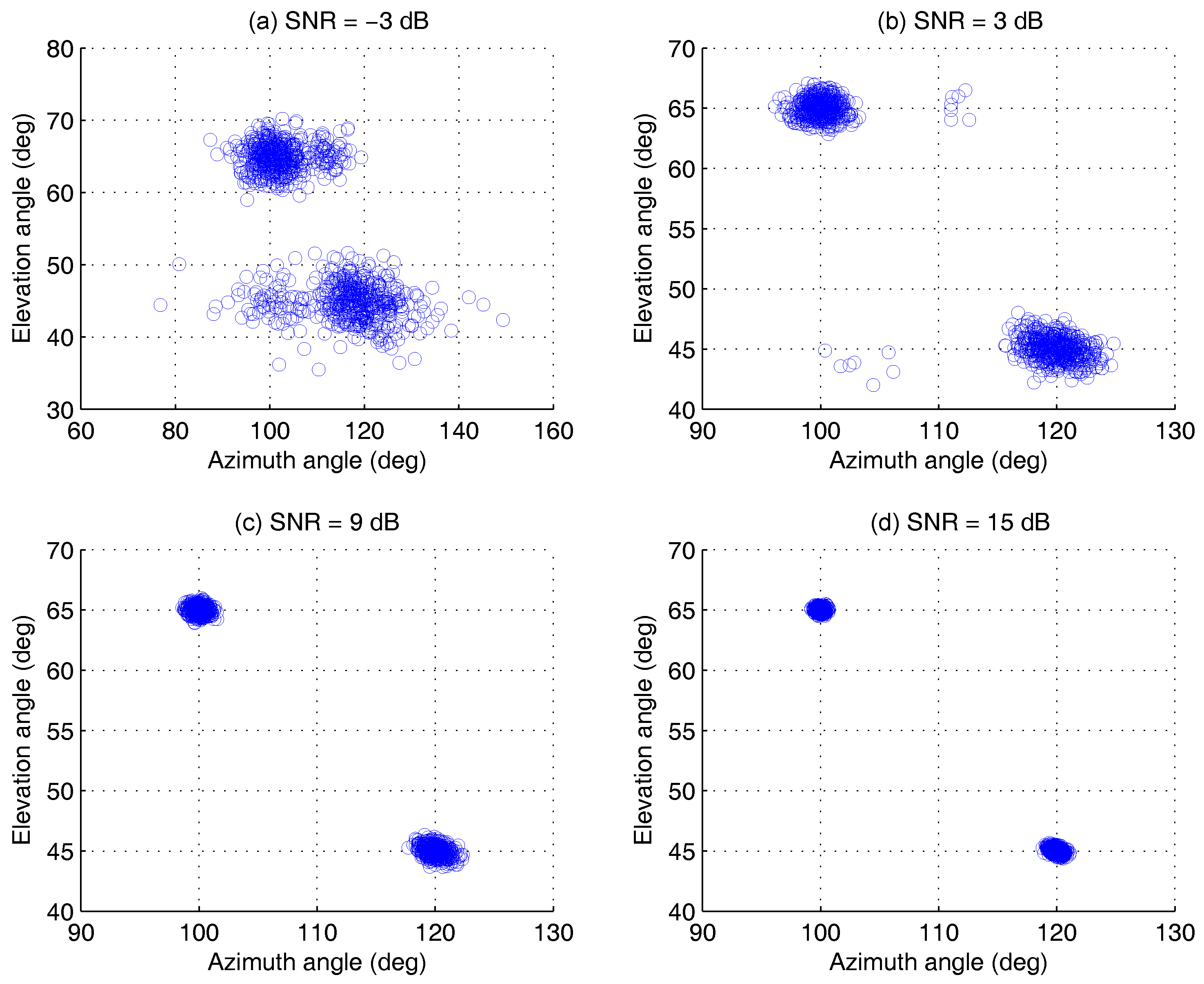
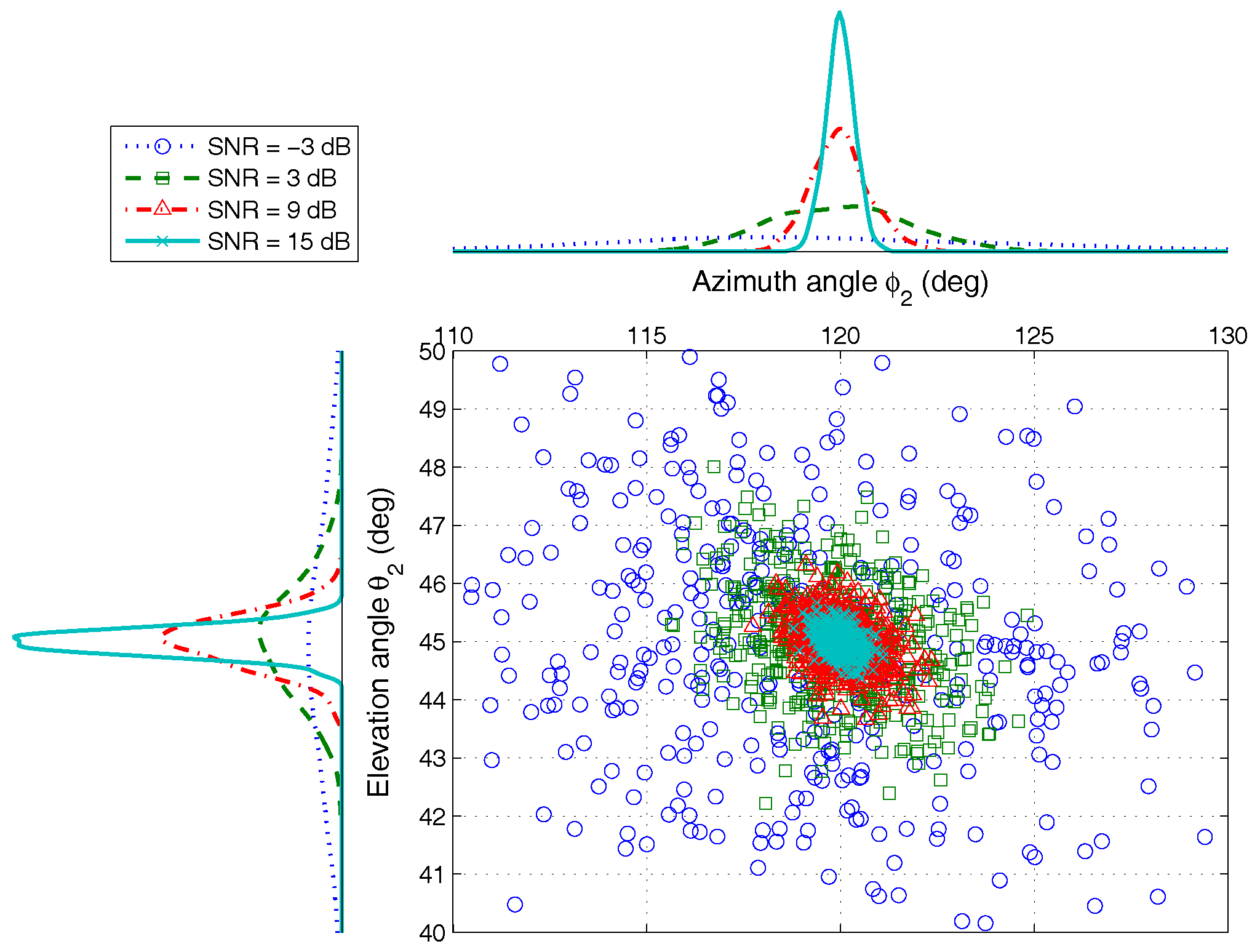
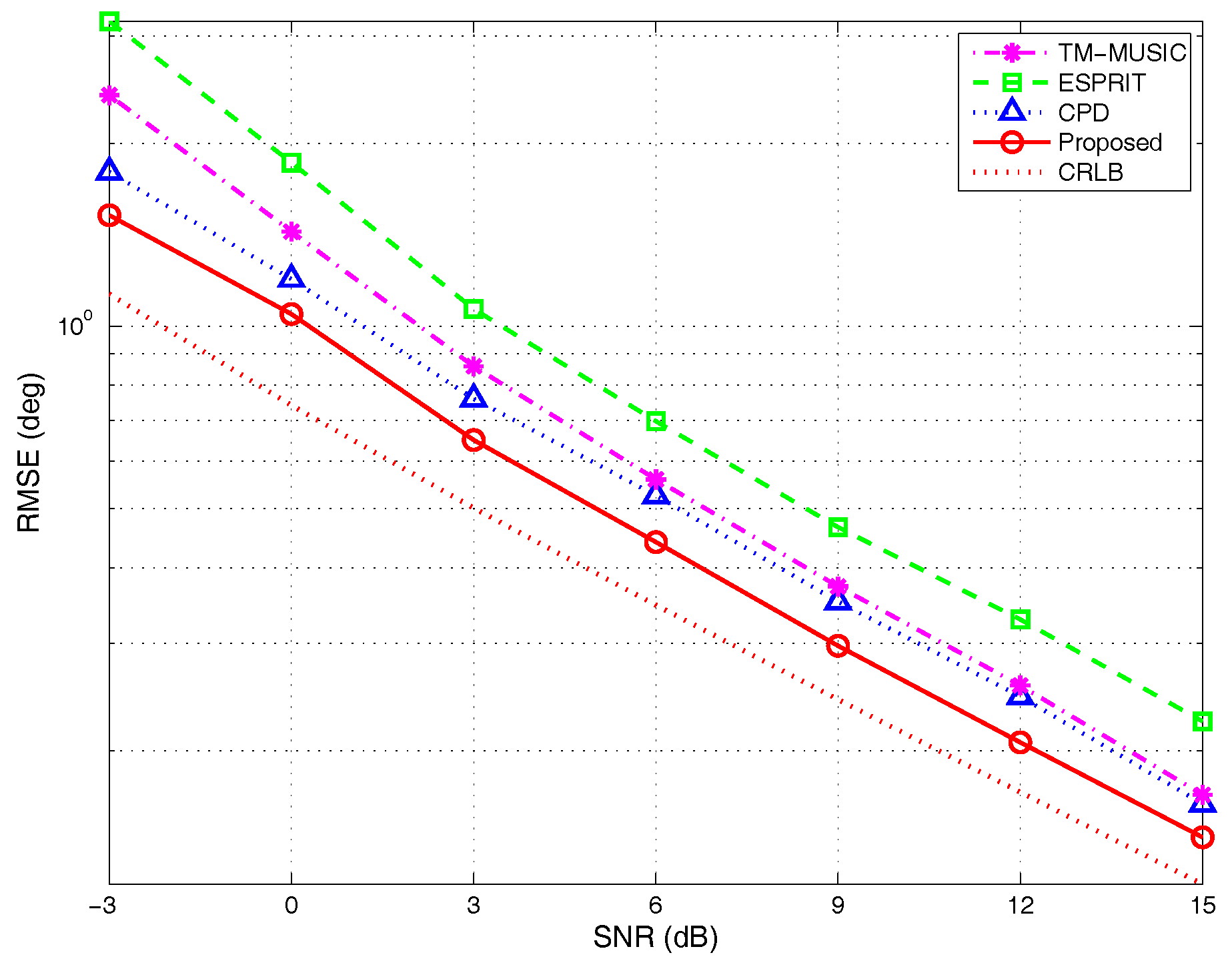
4.1.1. Different SNRs
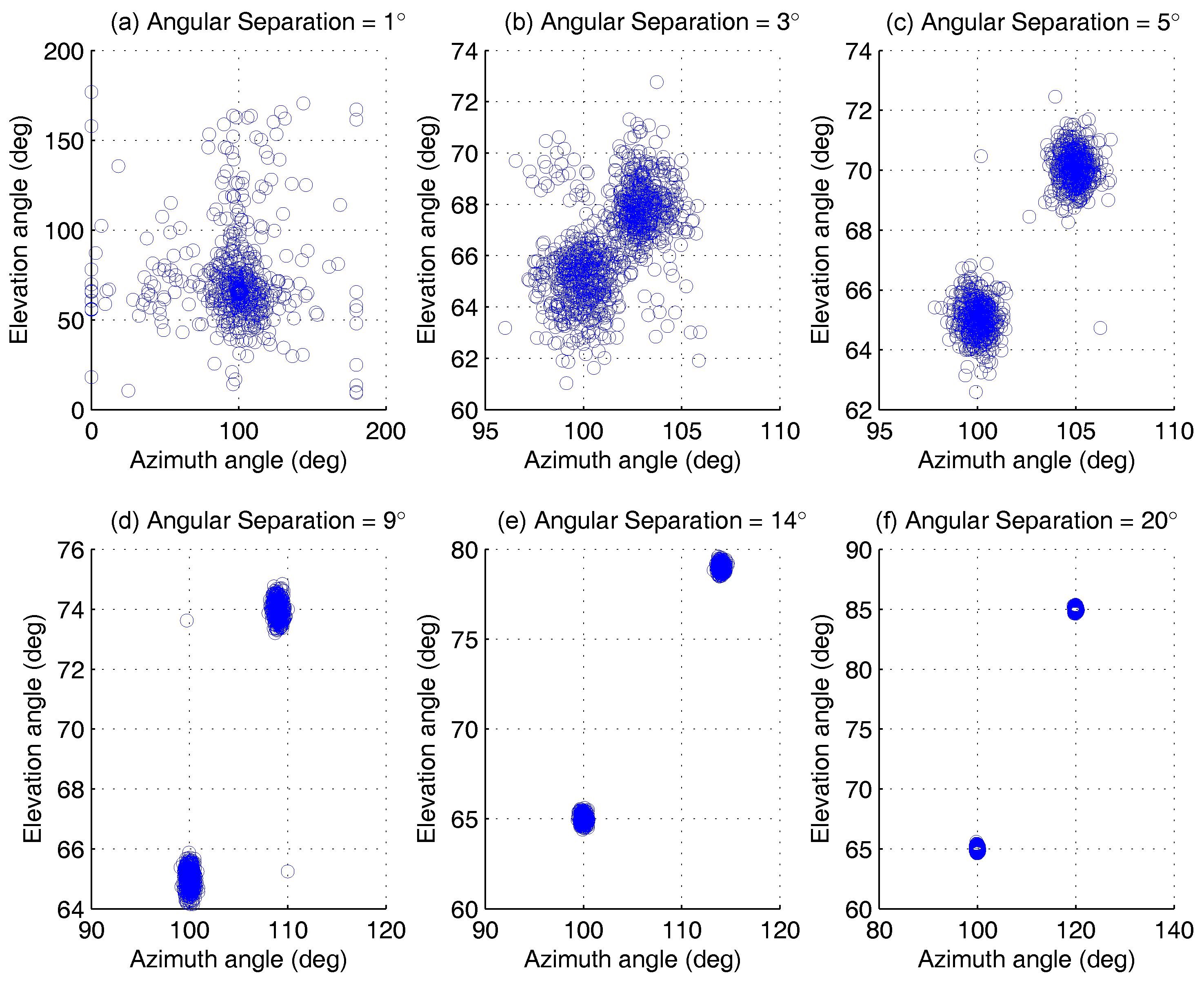
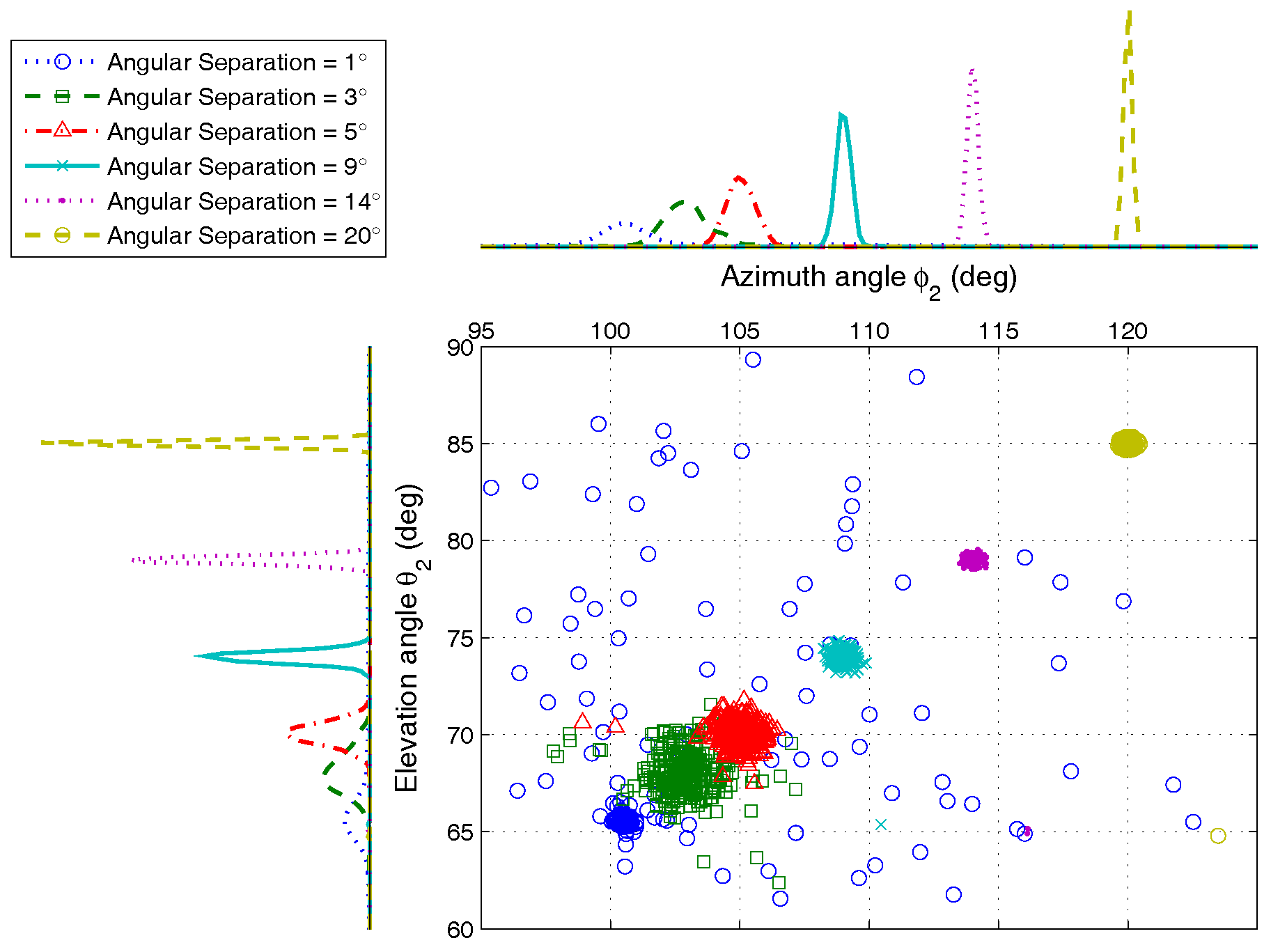
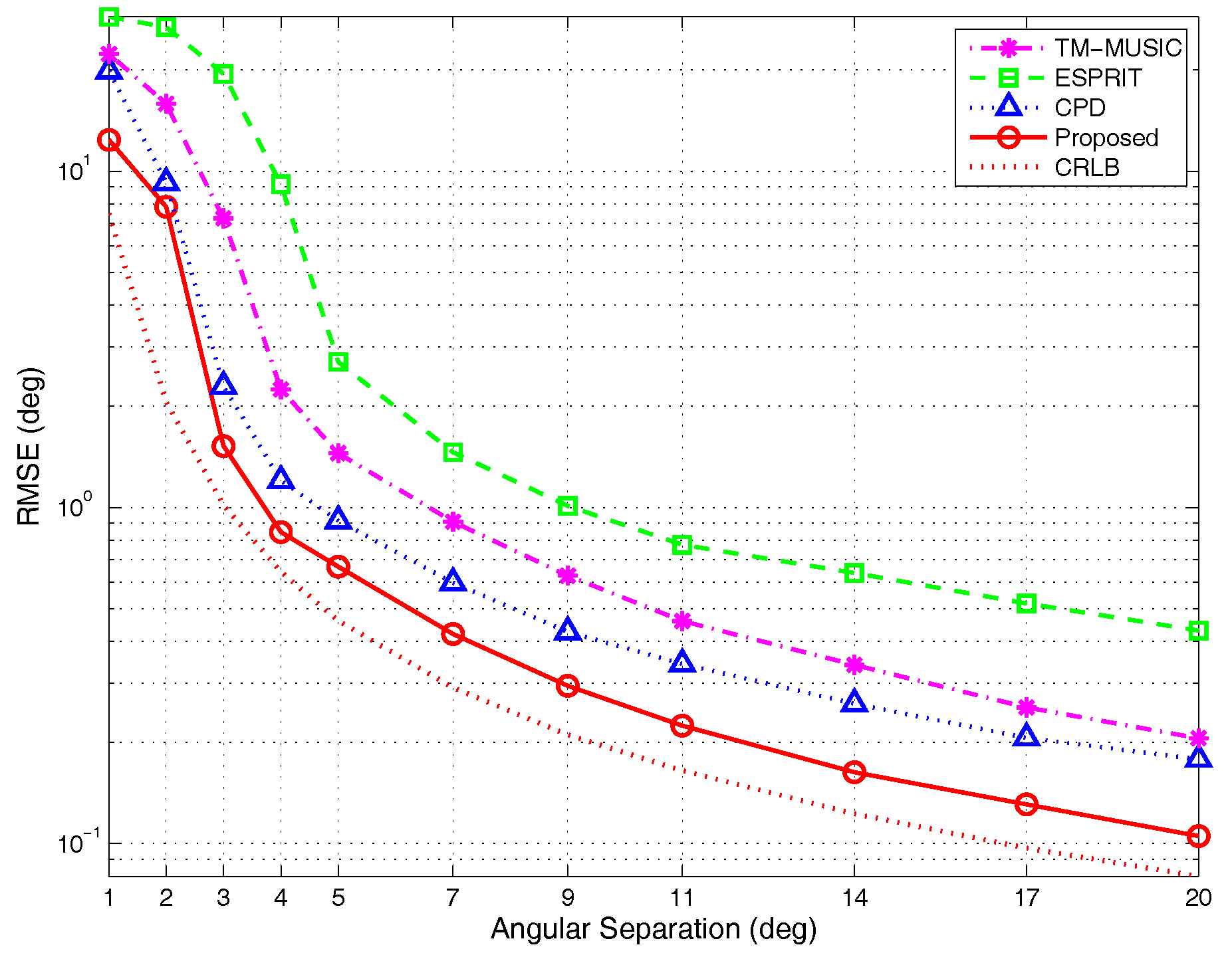
4.1.2. Different Angular Separations
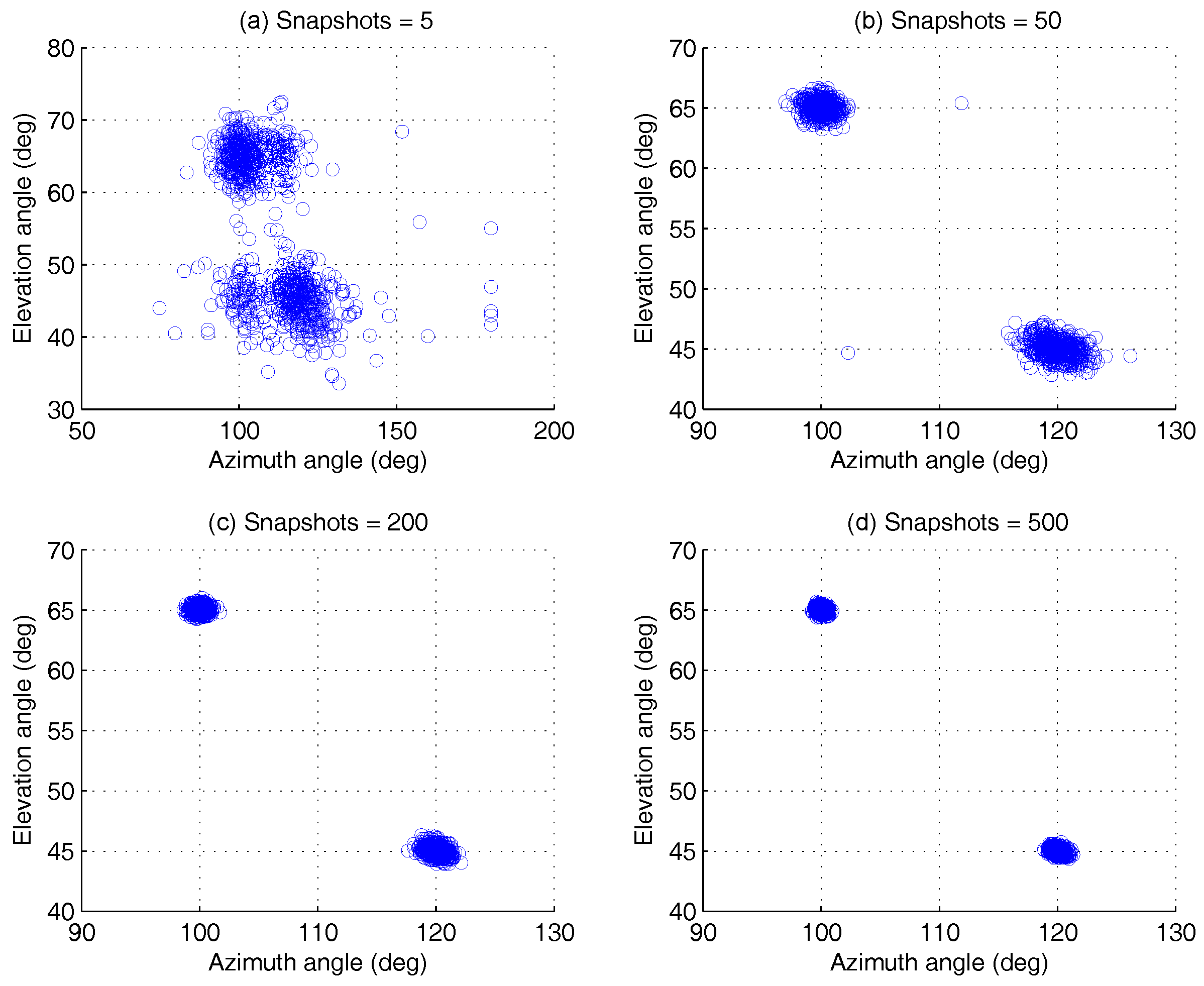
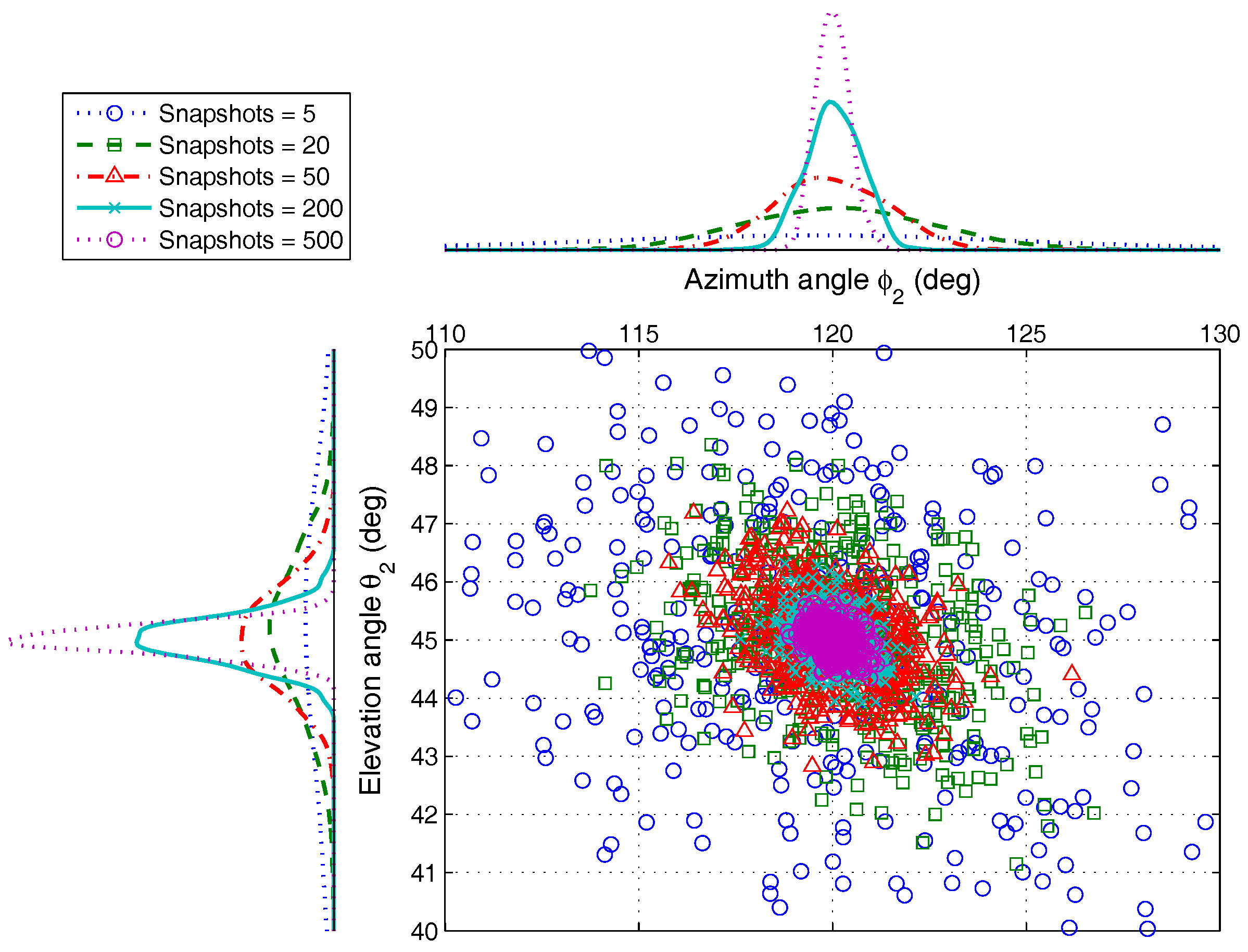
4.1.3. Different Snapshots
4.2. Performance Comparison
4.2.1. RMSE
- (1)
- RMSE versus different SNRs:
- (2)
- RMSE versus different angular separations:
- (3)
- RMSE versus different snapshots:
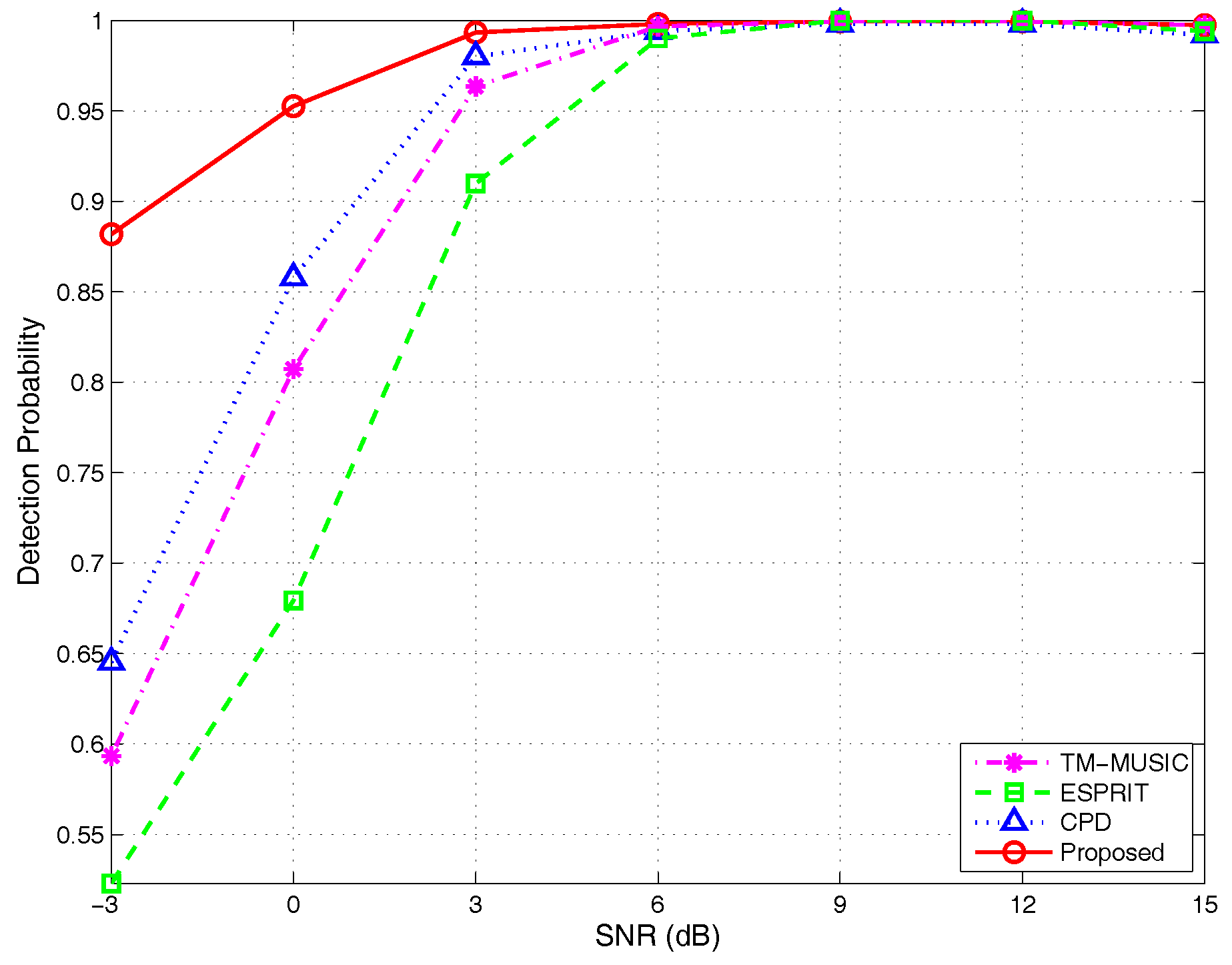
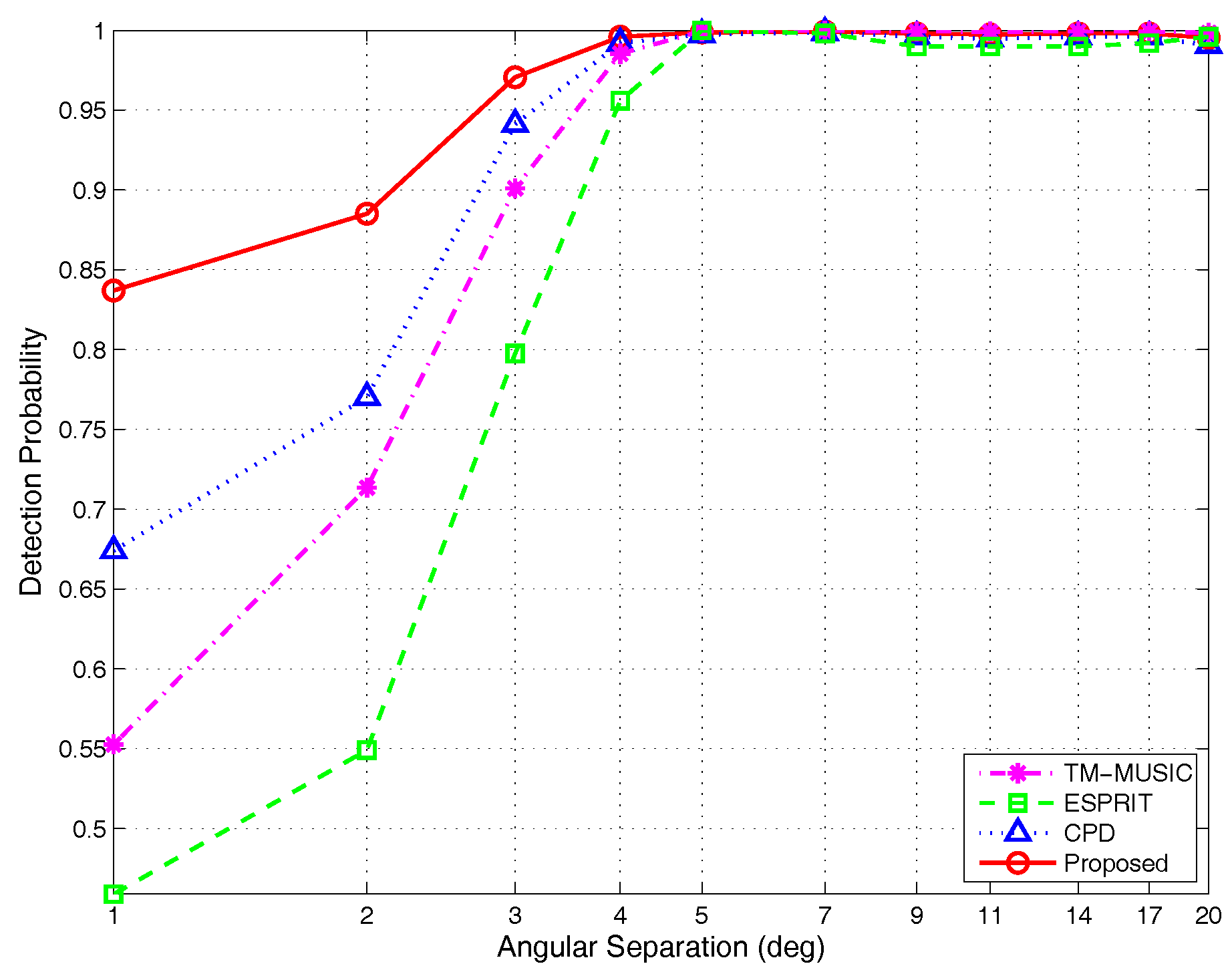
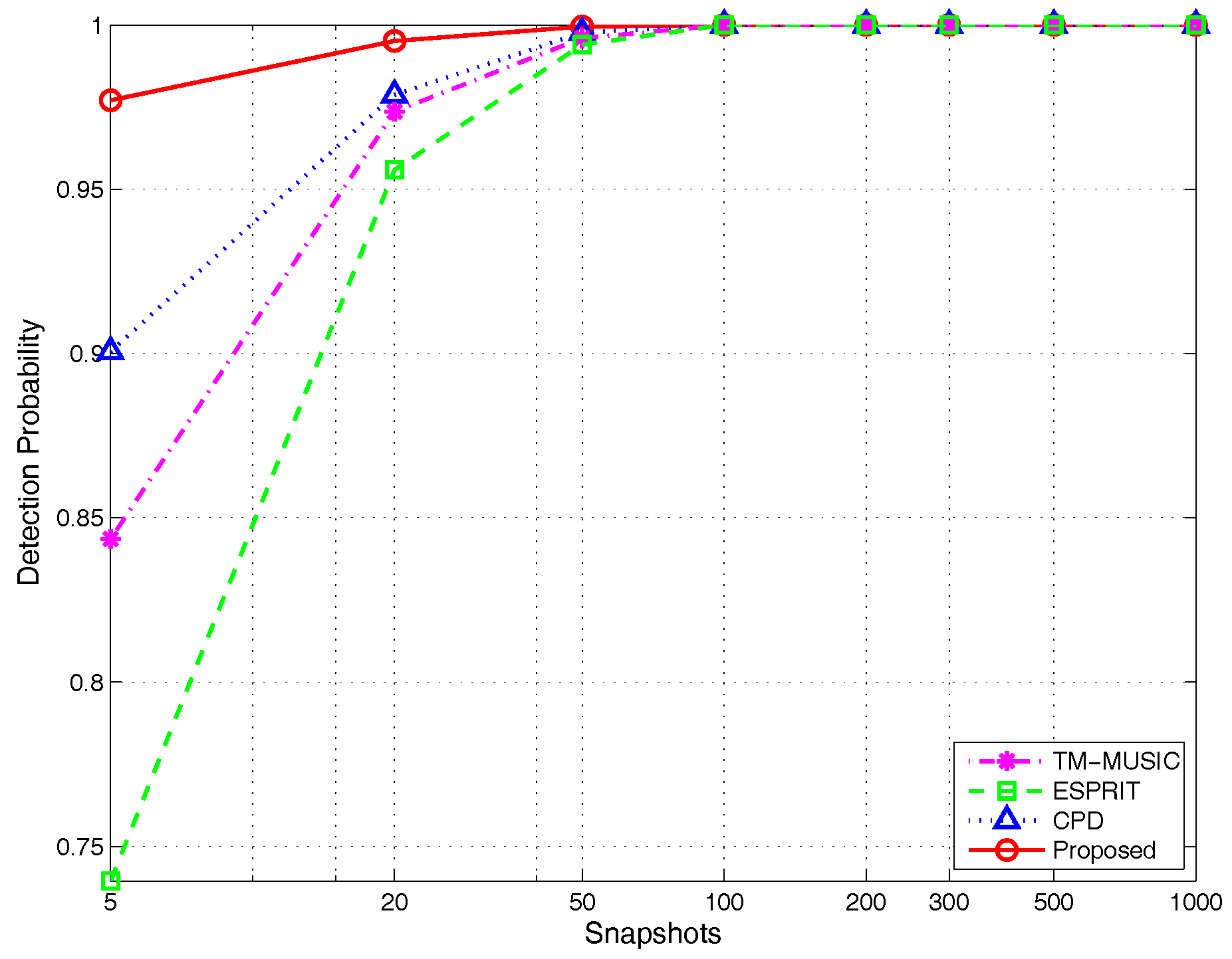
4.2.2. Detection Probability
- (1)
- Detection probability versus different SNRs:
- (2)
- Detection probability versus different angular separations:
- (3)
- Detection probability versus different snapshots:
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Gu, Y.; Leshem, A. Robust adaptive beamforming based on interference covariance matrix reconstruction and steering vector estimation. IEEE Trans. Signal Process. 2012, 60, 3881–3885. [Google Scholar]
- Shi, Z.; Zhou, C.; Gu, Y.; Goodman, N.A.; Qu, F. Source Estimation using Coprime Array: A Sparse Reconstruction Perspective. IEEE Sens. J. 2017, 17, 755–765. [Google Scholar] [CrossRef]
- Boerner, W.M.; Yamaguchi, Y. A state-of-the-art review in radar polarimetry and its applications in remote sensing. IEEE Aerosp. Electr. Syst. Mag. 1990, 5, 3–6. [Google Scholar] [CrossRef]
- Compton, R. The tripole antenna: An adaptive array with full polarization flexibility. IEEE Trans. Antennas Propag. 1981, 29, 944–952. [Google Scholar] [CrossRef]
- Li, J.; Compton, R.T. Two-dimensional angle and polarization estimation using the ESPRIT algorithm. IEEE Trans. Antennas Propag. 1992, 40, 550–555. [Google Scholar] [CrossRef]
- Nehorai, A.; Paldi, E. Vector-sensor array processing for electromagnetic source localization. IEEE Trans. Signal Process. 1994, 42, 376–398. [Google Scholar] [CrossRef]
- Tan, K.C.; Ho, K.C.; Nehorai, A. Linear independence of steering vectors of an electromagnetic vector sensor. IEEE Trans. Signal Process. 1996, 44, 3099–3107. [Google Scholar]
- Wong, K.T.; Zoltowski, M.D. Closed-form direction finding and polarization estimation with arbitrarily spaced electromagnetic vector-sensors at unknown locations. IEEE Trans. Antennas Propag. 2000, 48, 671–681. [Google Scholar] [CrossRef]
- Rahamim, D.; Tabrikian, J.; Shavit, R. Source localization using vector sensor array in a multipath environment. IEEE Trans. Signal Process. 2004, 52, 3096–3103. [Google Scholar] [CrossRef]
- Yuan, X. Estimating the DOA and the Polarization of a Polynomial-Phase Signal Using a Single Polarized Vector-Sensor. IEEE Trans. Signal Process. 2012, 60, 1270–1282. [Google Scholar] [CrossRef]
- Miron, S.; Le Bihan, N.; Mars, J.I. Vector-sensor MUSIC for polarized seismic sources localization. EURASIP J. Adv. Signal Process. 2005, 2005. [Google Scholar] [CrossRef]
- Guo, X.; Miron, S.; Brie, D. Identifiability of the PARAFAC model for polarized source mixture on a vector sensor array. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 30 March–4 April 2008; pp. 2401–2404. [Google Scholar]
- Gong, X.; Liu, Z.; Xu, Y. Quad-quaternion MUSIC for DOA estimation using electromagnetic vector sensors. EURASIP J. Adv. Signal Process. 2008, 2008. [Google Scholar] [CrossRef]
- Guo, X.; Miron, S.; Brie, D. The effect of polarization separation on the performance of Candecomp/Parafac-based vector sensor array processing. Phys. Commun. 2012, 5, 289–295. [Google Scholar] [CrossRef]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Comon, P. Tensors: A Brief Introduction. IEEE Signal Process. Mag. 2014, 31, 44–53. [Google Scholar] [CrossRef]
- Cichocki, A.; Mandic, D.; De Lathauwer, L.; Zhou, G.; Zhao, Q.; Caiafa, C.; Phan, H.A. Tensor decompositions for signal processing applications: From two-way to multiway component analysis. IEEE Signal Process. Mag. 2015, 32, 145–163. [Google Scholar] [CrossRef]
- Carroll, J.D.; Chang, J.J. Analysis of individual differences in multidimensional scaling via an N-way generalization of ’Eckart-Young’ decomposition. Psychometrika 1970, 35, 283–319. [Google Scholar] [CrossRef]
- Harshman, R.A. Foundations of the PARAFAC procedure: Models and conditions for an ’explanatory’ multimodal factor analysis. UCLA Work. Pap. Phon. 1970, 16, 1–84. [Google Scholar]
- Bro, R. PARAFAC. Tutorial and applications. Chemom. Intell. Lab. Syst. 1997, 38, 149–171. [Google Scholar] [CrossRef]
- Nikias, C.L.; Mendel, J.M. Signal processing with higher-order spectra. IEEE Signal Process. Mag. 1993, 10, 10–37. [Google Scholar] [CrossRef]
- Cardoso, J.F.; Souloumiac, A. Blind beamforming for non-Gaussian signals. IEE Proc. F Radar Signal Process. 1993, 140, 362–370. [Google Scholar] [CrossRef]
- Comon, P. Independent component analysis, a new concept? Signal Process. 1994, 36, 287–314. [Google Scholar] [CrossRef]
- Sidiropoulos, N.D.; Bro, R.; Giannakis, G.B. Parallel factor analysis in sensor array processing. IEEE Trans. Signal Process. 2000, 48, 2377–2388. [Google Scholar] [CrossRef]
- Gao, Y.F.; Zou, L.; Wan, Q. A two-dimensional arrival angles estimation for L-shaped array based on tensor decomposition. AEU Int. J. Electron. Commun. 2015, 69, 736–744. [Google Scholar] [CrossRef]
- Gong, X.; Liu, Z.; Xu, Y.; Ahmad, M.I. Direction-of-arrival estimation via twofold mode-projection. Signal Process. 2009, 89, 831–842. [Google Scholar] [CrossRef]
- Guo, X.; Miron, S.; Brie, D.; Zhu, S.; Liao, X. A CANDECOMP/PARAFAC Perspective on Uniqueness of DOA Estimation Using a Vector Sensor Array. IEEE Trans. Signal Process. 2011, 59, 3475–3481. [Google Scholar]
- Han, K.; Nehorai, A. Nested Vector-Sensor Array Processing via Tensor Modeling. IEEE Trans. Signal Process 2014, 62, 2542–2553. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Z.; Xu, Y.; Liu, W. Adaptive tensorial beamformer based on electromagnetic vector-sensor arrays with coherent interferences. Multidimens. Syst. Signal Process. 2015, 26, 803–821. [Google Scholar] [CrossRef]
- Forster, P.; Ginolhac, G.; Boizard, M. Derivation of the theoretical performance of a Tensor MUSIC Algorithm. Signal Process. 2016, 129, 97–105. [Google Scholar] [CrossRef]
- Stegeman, A. Candecomp/Parafac: From Diverging Components to a Decomposition in Block Terms. SIAM J. Matrix Anal. Appl. 2012, 33, 209–215. [Google Scholar] [CrossRef]
- De Lathauwer, L. Decompositions of a higher-order tensor in block terms-Part I: Lemmas for partitioned matrices. SIAM J. Matrix Anal. Appl. 2008, 30, 1022–1032. [Google Scholar] [CrossRef]
- De Lathauwer, L. Decompositions of a higher-order tensor in block terms-Part II: Definitions and uniqueness. SIAM J. Matrix Anal. Appl. 2008, 30, 1033–1066. [Google Scholar] [CrossRef]
- De Lathauwer, L.; Nion, D. Decompositions of a higher-order tensor in block terms-part III: Alternating least squares algorithms. SIAM J. Matrix Anal. Appl. 2008, 30, 1067–1083. [Google Scholar] [CrossRef]
- De Lathauwer, L. Blind Separation of Exponential Polynomials and the Decomposition of a Tensor in Rank-(L_r,L_r,1) Terms. SIAM J. Matrix Anal. Appl. 2011, 32, 1451–1474. [Google Scholar] [CrossRef]
- De Lathauwer, L. Block component analysis, a new concept for blind source separation. In Proceedings of the International Conference on Latent Variable Analysis and Signal Separation, Tel Aviv, Israel, 12–15 March 2012; pp. 1–8. [Google Scholar]
- De Almeida, A.L.; Favier, G.; Mota, J.C.M. PARAFAC-based unified tensor modeling for wireless communication systems with application to blind multiuser equalization. Signal Process. 2007, 87, 337–351. [Google Scholar] [CrossRef]
- Nion, D.; De Lathauwer, L. A block component model-based blind DS-CDMA receiver. IEEE Trans. Signal Process. 2008, 56, 5567–5579. [Google Scholar] [CrossRef]
- Zhao, Q.; Caiafa, C.F.; Mandic, D.P.; Chao, Z.C.; Nagasaka, Y.; Fujii, N.; Zhang, L.; Cichocki, A. Higher order partial least squares (HOPLS): A generalized multilinear regression method. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1660–1673. [Google Scholar] [CrossRef] [PubMed]
- Hunyadi, B.; Camps, D.; Sorber, L.; Van Paesschen, W.; De Vos, M.; Van Huffel, S.; De Lathauwer, L. Block term decomposition for modelling epileptic seizures. EURASIP J. Adv. Signal Process. 2014, 2014. [Google Scholar] [CrossRef]
- Acar, E.; Yener, B. Unsupervised multiway data analysis: A literature survey. IEEE Trans. Knowl. Data Eng. 2009, 21, 6–20. [Google Scholar] [CrossRef]
- Bro, R.; Harshman, R.A.; Sidiropoulos, N.D.; Lundy, M.E. Modeling multi-way data with linearly dependent loadings. J. Chemom. 2009, 23, 324–340. [Google Scholar] [CrossRef]
- Almeida, A.D.; Favier, G.; Mota, J.C. The constrained block-PARAFAC decomposition. In Proceedings of the Three-Way Methods in Chemistry and Psychology, Crete, Greece, 4–9 June 2006. [Google Scholar]
- Sorensen, M.; De Lathauwer, L. Tensor decompositions with Vandermonde factor and applications in signal processing. In Proceedings of the 2012 Conference Record of the Forty Sixth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 4–7 November 2012; pp. 890–894. [Google Scholar]
- Sorber, L.; Van Barel, M.; De Lathauwer, L. Optimization-based algorithms for tensor decompositions: Canonical polyadic decomposition, decomposition in rank-(L_r,L_r,1) terms, and a new generalization. SIAM J. Optim. 2013, 23, 695–720. [Google Scholar] [CrossRef]
- Tichavsky, P.; Phan, A.H.; Cichocki, A. Non-Orthogonal Tensor Diagonalization, a Tool for Block Tensor Decompositions. arXiv, 2014; arXiv:1402.1673. [Google Scholar]
- Gong, X.F.; Lin, Q.H.; Debals, O.; Vervliet, N.; De Lathauwer, L. Coupled Rank-(Lm, Ln,.) Block Term Decomposition by Coupled Block Simultaneous Generalized Schur Decomposition. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 2554–2558. [Google Scholar]
- Swindlehurst, A.; Kailath, T. Azimuth/elevation direction finding using regular array geometries. IEEE Trans. Aerosp. Electron. Syst. 1993, 29, 145–156. [Google Scholar] [CrossRef]
- Zoltowski, M.D.; Haardt, M.; Mathews, C.P. Closed-form 2D angle estimation with rectangular arrays in element space or beamspace via unitary ESPRIT. IEEE Trans. Signal Process. 1996, 44, 316–328. [Google Scholar] [CrossRef]
- Fernandez del Rio, J.; Catedra-Perez, M. The matrix pencil method for two-dimensional direction of arrival estimation employing an L-shaped array. IEEE Trans. Antennas Propag. 1997, 45, 1693–1694. [Google Scholar] [CrossRef]
- Liu, T.H.; Mendel, J.M. Azimuth and elevation direction finding using arbitrary array geometries. IEEE Trans. Signal Process. 1998, 46, 2061–2065. [Google Scholar]
- Tayem, N.; Kwon, H.M. L-shape 2Dimensional arrival angle estimation with propagator method. IEEE Trans. Antennas Propag. 2005, 53, 1622–1630. [Google Scholar] [CrossRef]
- Kikuchi, S.; Tsuji, H.; Sano, A. Pair-matching method for estimating 2D angle of arrival with a cross-correlation matrix. IEEE Antennas Wirel. Propag. Lett. 2006, 5, 35–40. [Google Scholar] [CrossRef]
- Gao, Y.F.; Wan, Q.; Zou, L. A CCM-based Pair-matching Method for Two-dimensional Arrival Angles Estimation. In Proceedings of the 2014 IEEE International Conference on Communication Problem-Solving (ICCP), Beijing, China, 5–7 December 2014; pp. 588–591. [Google Scholar]
- Nion, D.; De Lathauwer, L. An enhanced line search scheme for complex-valued tensor decompositions. Application in DS-CDMA. Signal Process. 2008, 88, 749–755. [Google Scholar] [CrossRef]
- Navasca, C.; De Lathauwer, L.; Kindermann, S. Swamp reducing technique for tensor decomposition. In Proceedings of the 2008 IEEE 16th European Signal Processing Conference, Lausanne, Switzerland, 25–29 August 2008; pp. 1–5. [Google Scholar]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Zoltowski, M.D.; Wong, K.T. ESPRIT-based 2D direction finding with a sparse uniform array of electromagnetic vector sensors. IEEE Trans. Signal Process. 2000, 48, 2195–2204. [Google Scholar] [CrossRef]
- Stoica, P.; Larsson, E.G.; Gershman, A.B. The stochastic CRB for array processing: A textbook derivation. IEEE Signal Process. Lett. 2001, 8, 148–150. [Google Scholar] [CrossRef]
- Miron, S.; Guo, X.; Brie, D. DOA estimation for polarized sources on a vector-sensor array by PARAFAC decomposition of the fourth-order covariance tensor. In Proceedings of the 2008 16th European Signal Processing Conference, Lausanne, Switzerland, 25–29 August 2008; pp. 1–5. [Google Scholar]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.-F.; Gui, G.; Xie, W.; Zou, Y.-B.; Yang, Y.; Wan, Q. A Type-2 Block-Component-Decomposition Based 2D AOA Estimation Algorithm for an Electromagnetic Vector Sensor Array. Sensors 2017, 17, 963. https://doi.org/10.3390/s17050963
Gao Y-F, Gui G, Xie W, Zou Y-B, Yang Y, Wan Q. A Type-2 Block-Component-Decomposition Based 2D AOA Estimation Algorithm for an Electromagnetic Vector Sensor Array. Sensors. 2017; 17(5):963. https://doi.org/10.3390/s17050963
Chicago/Turabian StyleGao, Yu-Fei, Guan Gui, Wei Xie, Yan-Bin Zou, Yue Yang, and Qun Wan. 2017. "A Type-2 Block-Component-Decomposition Based 2D AOA Estimation Algorithm for an Electromagnetic Vector Sensor Array" Sensors 17, no. 5: 963. https://doi.org/10.3390/s17050963
APA StyleGao, Y.-F., Gui, G., Xie, W., Zou, Y.-B., Yang, Y., & Wan, Q. (2017). A Type-2 Block-Component-Decomposition Based 2D AOA Estimation Algorithm for an Electromagnetic Vector Sensor Array. Sensors, 17(5), 963. https://doi.org/10.3390/s17050963






