Property Analysis of the Real-Time Uncalibrated Phase Delay Product Generated by Regional Reference Stations and Its Influence on Precise Point Positioning Ambiguity Resolution
Abstract
:1. Introduction
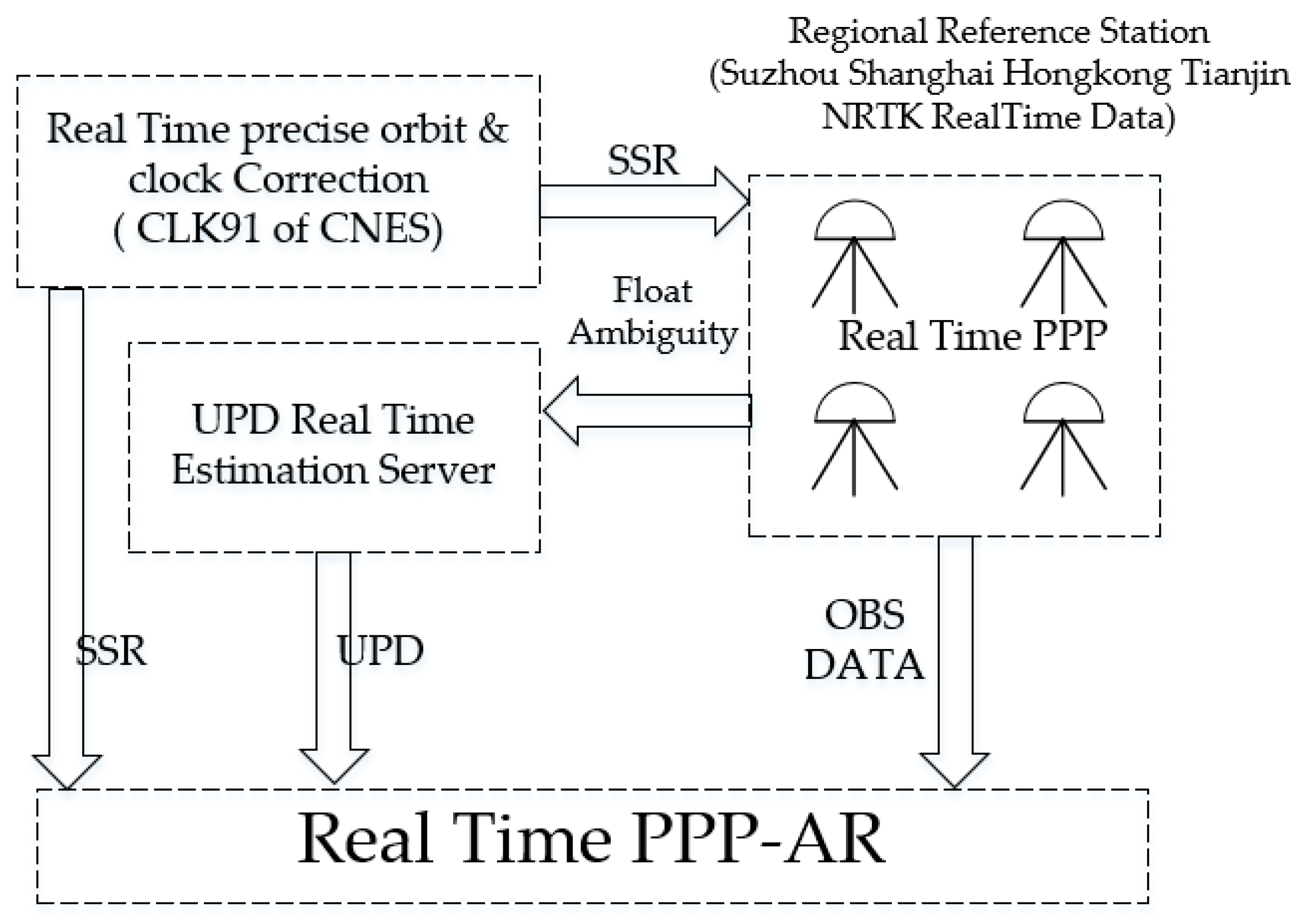
2. RTPPP-AR and RT UPD Estimation
2.1. RTPPP-AR Method
2.2. UPD Real-Time Estimation for Satellite Terminal
3. Experiment Results and Discussion
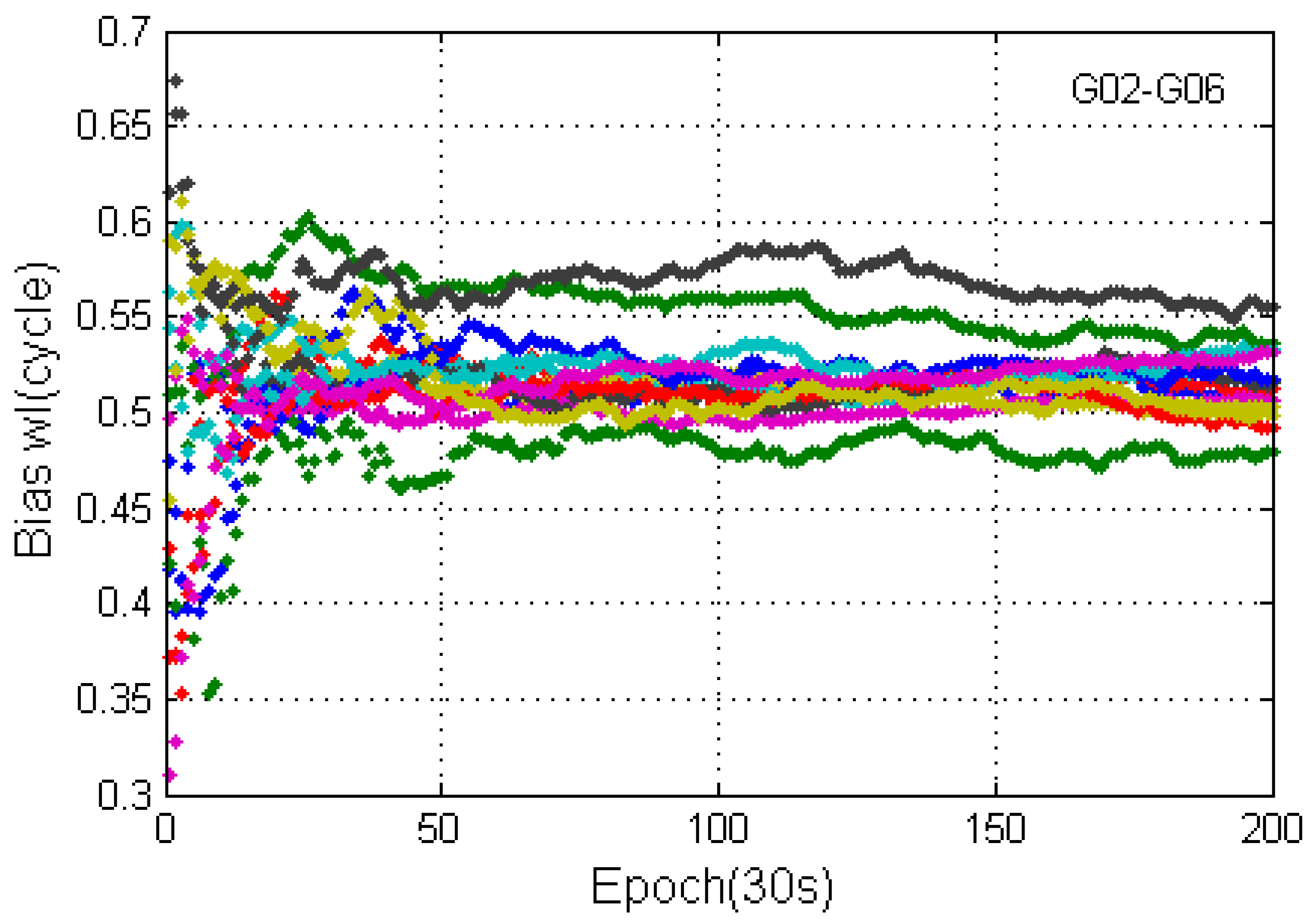
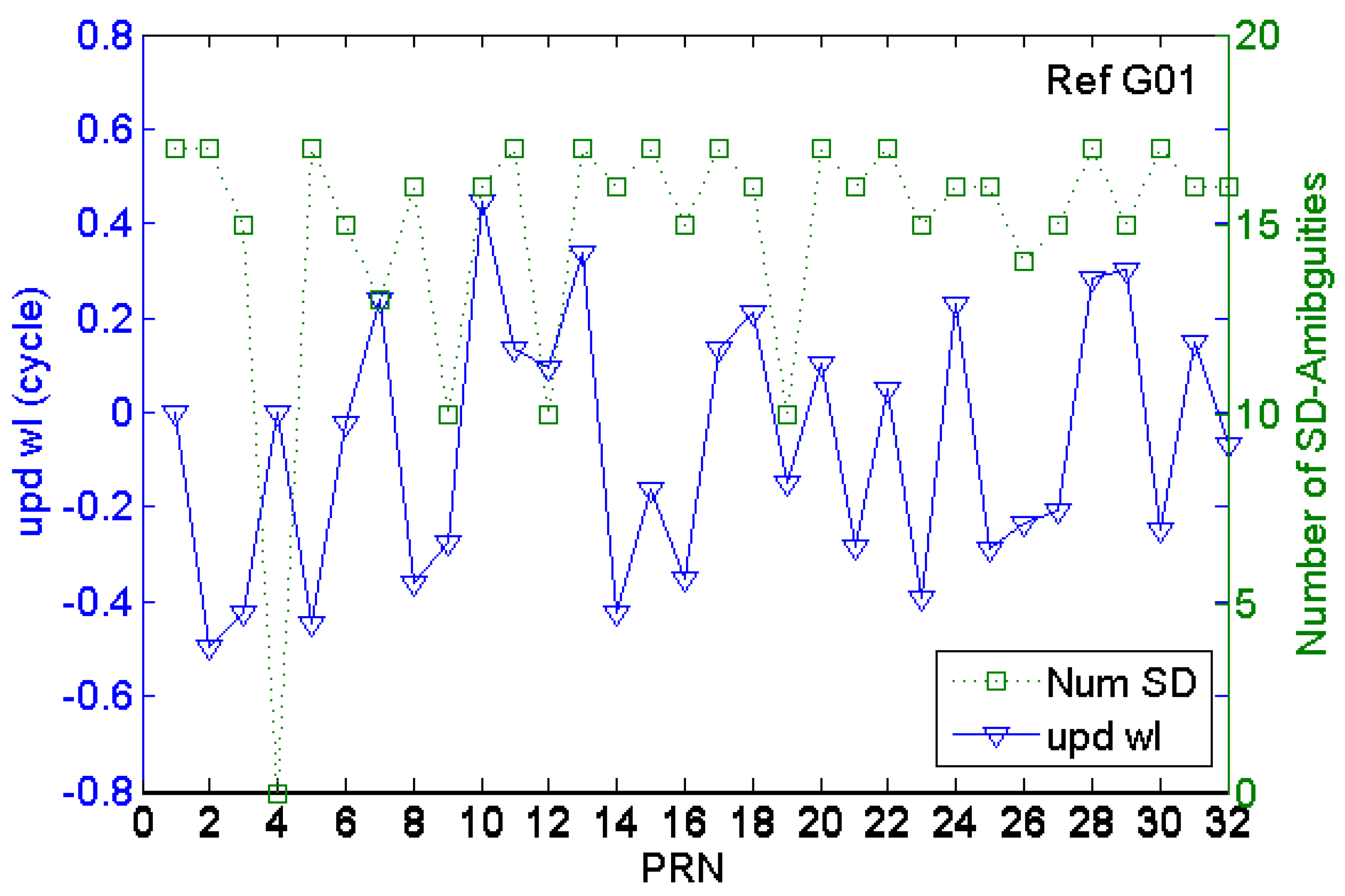
3.1. Real-Time Uncorrected Phase Delay UPD Characteristic of Satellite Terminal
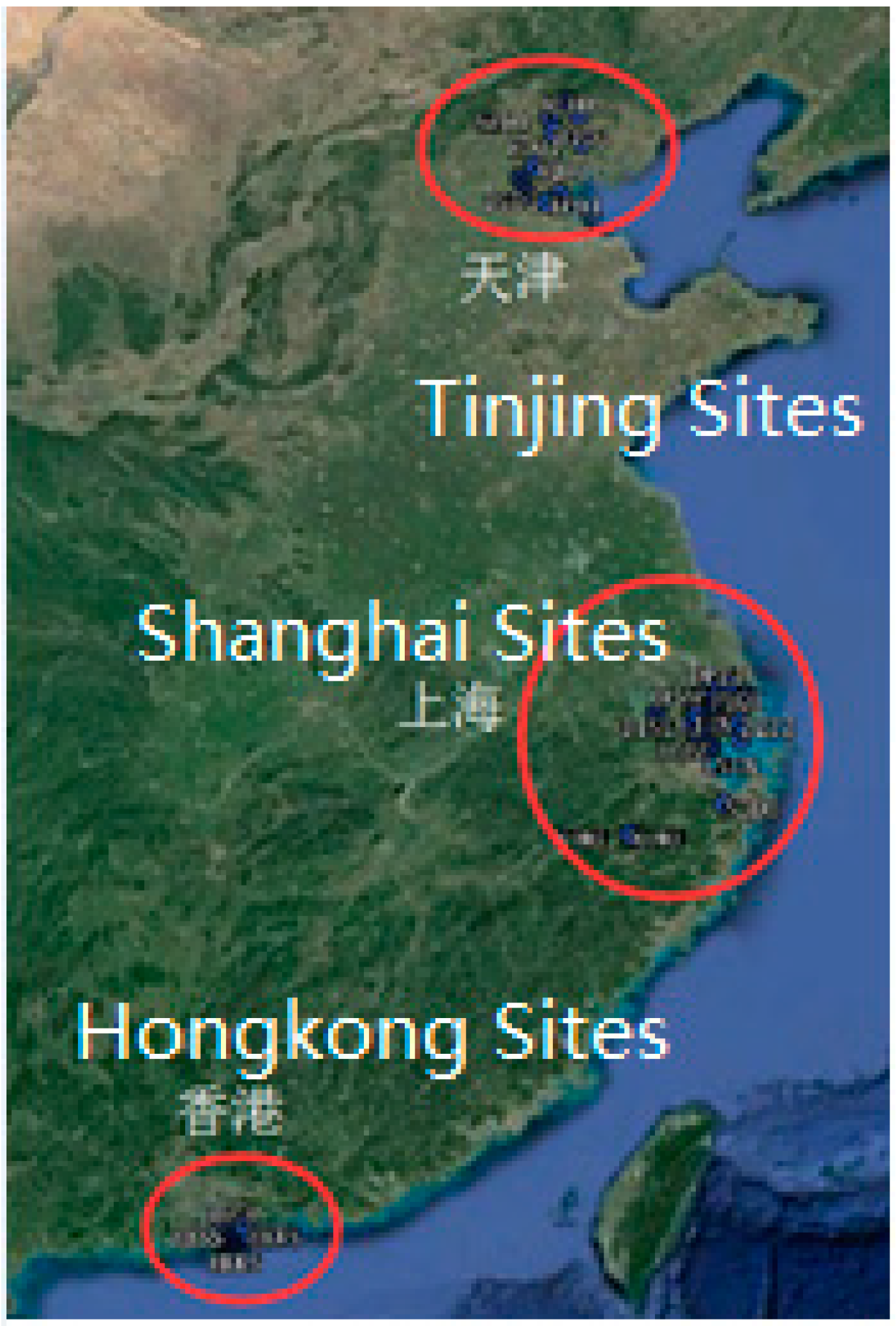
3.2. UPD Estimated by Regional Stations for RTPPP-AR Positioning Experiments
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bisnath, S.; Gao, Y. Current state of precise point positioning and future prospects and limitations. In Proceedings of the IUGG 24th General Assembly, Perugia, Italy, 2–13 July 2007. [Google Scholar]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Abdel-Salam, M. Precise Point Positioning Using Un-Differenced Code and Carrier Phase Observations; UCGE Reports No. 20229; University of Calgary: Calgary, AB, Canada, 2005. [Google Scholar]
- Kouba, J.; Hérous, P. Precise point positioning using IGS orbit and clock products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Wang, J.; Satirapod, C.; Rizos, C. Stochastic assessment of GPS carrier phase measurements for precise static relative positioning. J. Geod. 2002, 76, 95–104. [Google Scholar] [CrossRef]
- Bisnath, S.B.; Langley, R.B. Precise orbit determination of low earth orbiters with GPS point positioning. In Proceedings of the Institute of Navigation National Technical Meeting, Long Beach, CA, USA, 22–24 January 2001; pp. 725–733. [Google Scholar]
- Geng, J.; Meng, X.; Dodson, A.H.; Teferle, F.N. Integer ambiguity resolution in precise point positioning: Method comparison. J. Geod. 2010, 84, 569–581. [Google Scholar] [CrossRef]
- Gao, Y.; Shen, X. A new method for carrier-phase-based precise point positioning. Navigation 2002, 49, 109–116. [Google Scholar] [CrossRef]
- Bertiger, W.; Desai, S.D.; Haines, B.; Harvey, N.; Moore, A.W.; Owen, S.; Weiss, J.P. Single receiver phase ambiguity resolution with GPS data. J. Geod. 2010, 84, 327–337. [Google Scholar] [CrossRef]
- Bock, H.; Jäggi, A.; Dach, R.; Schaer, S. GPS single-frequency orbit determination for low Earth orbiting satellites. Adv. Space Res. 2009, 43, 783–791. [Google Scholar] [CrossRef]
- Beran, T. Single-Frequency, Single-Receiver Spaceborne GPS Orbit Determination. Ph.D. Thesis, Department of Geodesy and Geomatics Engineering, University of New Brunswick, Fredericton, NB, Canada, 2008. [Google Scholar]
- Chen, W.; Hu, C.; Li, Z.; Chen, Y.; Ding, X.; Gao, S.; Ji, S. Kinematic GPS precise point positioning for sea level monitoring with GPS buoy. J. Glob. Position. Syst. 2004, 3, 302–307. [Google Scholar] [CrossRef]
- Banville, S.; Langley, R. Improving real-time kinematic PPP with instantaneous cycle-slip correction. In Proceedings of the ION GNSS 2009, Savannah, GA, USA, 16–19 September 2009. [Google Scholar]
- Li, X.; Ge, M.; Dai, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Accuracy and reliability of multi-GNSS real-time precise positioning: GPS, GLONASS, BeiDou, and Galileo. J. Geod. 2015, 89, 607–635. [Google Scholar] [CrossRef]
- Li, X.; Ge, M.; Lu, C.; Zhang, Y.; Wang, R.; Wickert, J.; Schuh, H. High-rate GPS seismology using real-time precise point positioning with ambiguity resolution. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6165–6180. [Google Scholar]
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Collins, P.; Bisnath, S.; Lahaye, F.; Héroux, P. Undifferenced GPS ambiguity resolution using the decoupled clock model and ambiguity datum fixing. J. Inst. Navig. 2011, 57, 123–135. [Google Scholar] [CrossRef]
- Laurichesse, D.; Mercier, F.; Berthias, J.P.; Broca, P.; Cerri, L. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination. J. Inst. Navig. 2009, 56, 135–149. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X. Improving the estimation of uncalibrated fractional phase offsets for PPP ambiguity resolution. J. Navig. 2012, 65, 513–529. [Google Scholar] [CrossRef]
- Zhang, X.H.; Li, X.X. New method for precise ambiguity integer resolution PPP and experiment. Geomat. Inf. Sci. Wuhan Univ. 2010, 35, 657–660. [Google Scholar]
- Zhang, X.; Li, P.; Li, X.; Feng, Z.; Xiang, Z. An analysis of time-varying property of widelane carier phase ambiguity fractional bias. Acta Geod. Cartogr. Sin. 2013, 42, 798–803, 809. [Google Scholar]
- Li, L.; Cui, Y.; Wang, Y.; Lv, Z. Improvement of narow-lane fractional cycle bias estimation and analysis of its time-varying property. Acta Geod. Cartogr. Sin. 2017, 46, 34–43. [Google Scholar]
- Geng, J.; Teferle, F.N.; Shi, C.; Meng, X.; Dodson, A.H.; Liu, J. Ambiguity resolution in precise point position with hourly data. GPS Solut. 2009, 13, 263–270. [Google Scholar] [CrossRef]
- Gabor, M.J.; Nerem, R.S. GPS carrier phase ambiguity resolution using satellite-satellite single difference. In Proceedings of the ION GNSS 12th International Technical Meeting of the Satellite Division, Nashville, TN, USA, 14–17 September 1999; pp. 1569–1578. [Google Scholar]
- Loyer, S.; Perosanz, F.; Mercier, F.; Capdevilleet, H.; Marty, J. Zero-difference GPS ambiguity resolution at CNES-CLS IGS analysis center. J. Geod. 2012, 86, 991–1003. [Google Scholar] [CrossRef]
- Li, X.; Ge, M.; Zhang, H.; Wickert, J. A method for improving uncalibrated phase delay estimation and ambiguity-fixing in real-time precise point positioning. J. Geod. 2013, 87, 405–416. [Google Scholar] [CrossRef]
- Melbourne, W.G. The case for ranging in GPS-based geodetic systems. In Proceedings of the First International Symposium on Precise Positioning with the Global Positioning System, Rockville, MD, USA, 15–19 April 1985; pp. 373–386. [Google Scholar]
- Wei, M.; Schwarz, K.P. Fast ambiguity resolution using an integer nonlinear programming method. In Proceedings of the ION GNSS, Palm Springs, CA, USA, 12–15 September 1995; pp. 1101–1110. [Google Scholar]
- Li, X.; Zhang, X.; Li, P. Rapid precise orbit determination and positioning based zero-difference integer ambiguity. Chin. J. Geophys. 2012, 55, 833–840. [Google Scholar]
- Li, P.; Zhang, X. Precise point positioning with partial ambiguity fixing. Sensors 2015, 15, 13627–13643. [Google Scholar] [CrossRef] [PubMed]
- Shi, J. Precise point positioning integer ambiguity resolution with decoupled clocks. Geodesy 2012. [Google Scholar] [CrossRef]
- Li, X.X.; Zhang, X.H.; Li, P. PPP for rapid precise positioning and orbit determination with zero-difference integer ambiguity fixing. Chin. J. Geophys. 2012, 55, 833–840. [Google Scholar]
- Teunissen, P.J.G. The least squares ambiguity decorrelation adjustment: A method for fast GPS integer estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Qin, Y.Y.; Zhang, H.Y.; Wang, S.H. Theory of Kalman. Filter and Integrated Navigation; Northwestern Polytechnical University Press: Xi’an, China, 2007. [Google Scholar]
- Geng, J.; Shi, C.; Ge, M.; Dodson, A.H.; Lou, Y.; Zhao, Q.; Liu, J. Improving the estimation of fractional-cycle biases for ambiguity resolution in precise point positioning. J. Geod. 2012, 86, 579–589. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Ge, M. Regional reference network augmented precise point positioning for instantaneous ambiguity resolution. J. Geod. 2011, 85, 151–158. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Odijk, D.; Zhang, B. PPP-RTK: Results of CORS network-based PPP with integer ambiguity resolution. J. Aeronaut. Astronaut. Aviat. Ser. A 2010, 42, 223–230. [Google Scholar]
- Wübbena, G.; Schmitz, M.; Bagge, A. PPP-RTK: Precise Point Positioning Using State-Space Representation in RTK Networks. In Proceedings of the International Technical Meeting of the Satellite Division of the Institute of Navigation, Long Beach, CA, USA, 13–16 September, 2005; pp. 2584–2594. [Google Scholar]
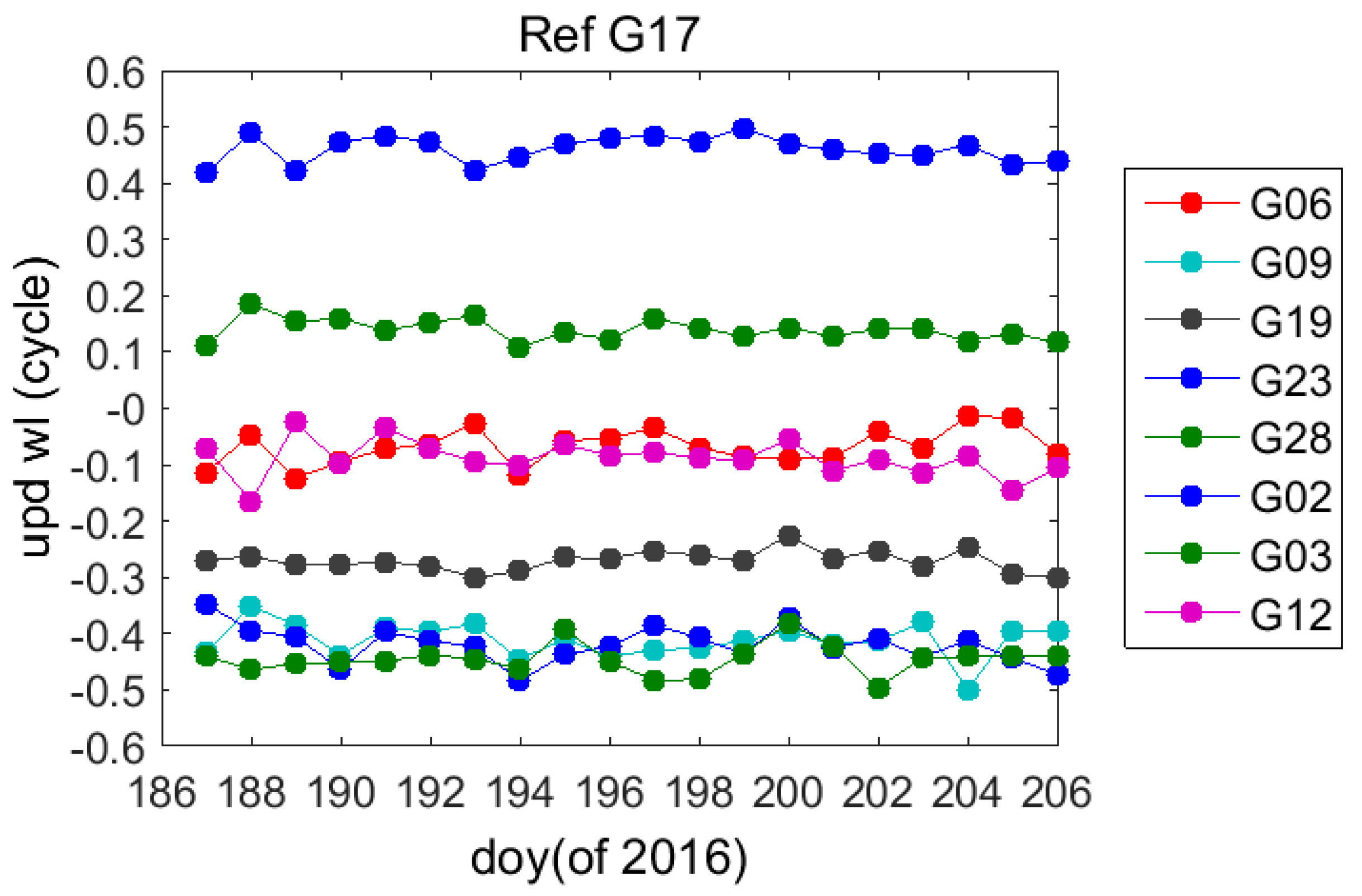
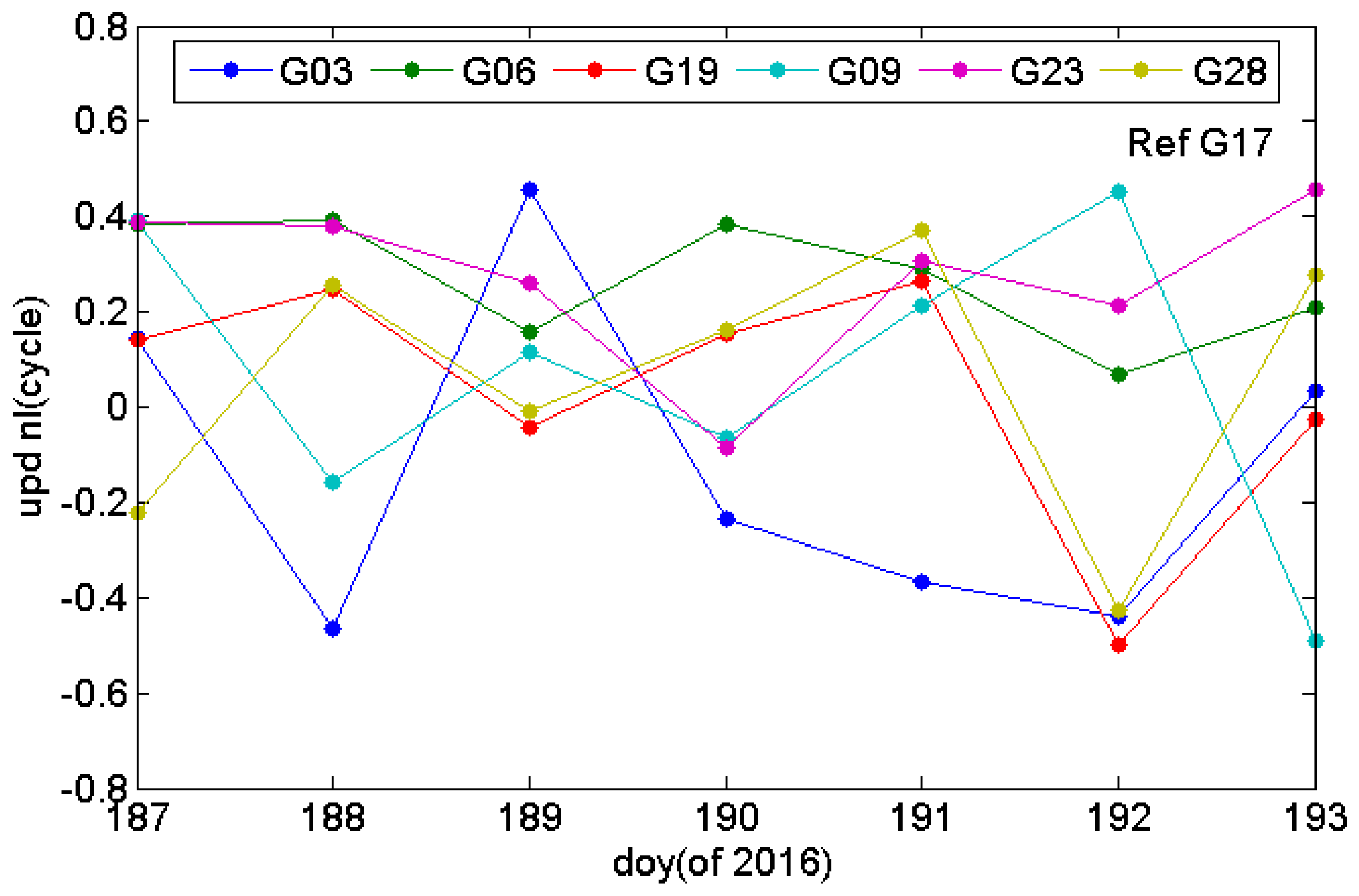

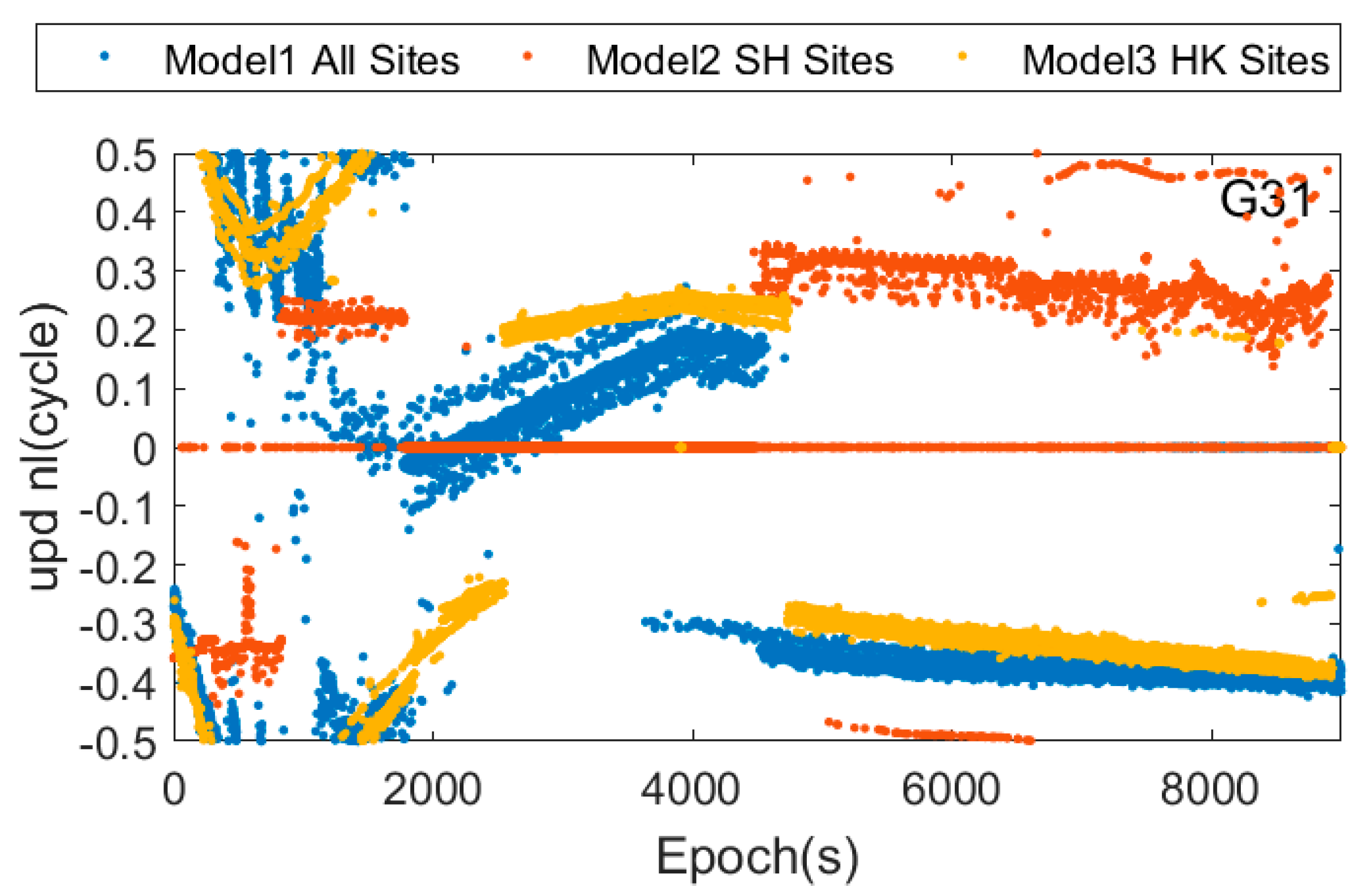
| PRN | G02 | G03 | G06 | G09 | G12 | G19 | G23 | G28 |
|---|---|---|---|---|---|---|---|---|
| STD [cycles] | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.02 | 0.02 | 0.02 |
| STD [m] | 0.026 | 0.026 | 0.026 | 0.026 | 0.026 | 0.017 | 0.017 | 0.017 |
| PRN | G03 | G06 | G09 | G19 | G23 | G28 |
|---|---|---|---|---|---|---|
| STD [cycles] | 0.32 | 0.12 | 0.31 | 0.24 | 0.17 | 0.27 |
| STD [m] | 0.034 | 0.013 | 0.032 | 0.026 | 0.018 | 0.029 |
| Model | Stations for UPD Estimation | Strategy Information |
|---|---|---|
| Model 1: ALL Sites UPD Model | 37 stations in total | All 37 stations were adopted for UPD estimation, and the UPD results were adopted for RTPPP-AR calculation of all stations. |
| Model 2: Shanghai UPD Model | YIWU, XUCH, CJZZ, DING, DPZZ, FUQI, JD01, JSWZ, JZZZ, LJIN, LNGN, XTZZ, ZQZZ (14 stations) | 14 stations in Shanghai regions were adopted for UPD estimation, and the UPD results were adopted for RTPPP-AR calculation of all stations. |
| Model 3: Hong Kong UPD Model | HKKS, HKKT, HKLM, HKMW, HKNP, HKOH, HKPC, HKSC, HKSL, HKSS, HKST, HKTK, HKWS (13 stations) | 13 stations in Hong Kong were adopted for UPD estimation, and the UPD results were adopted for RTPPP-AR calculation of all stations. |
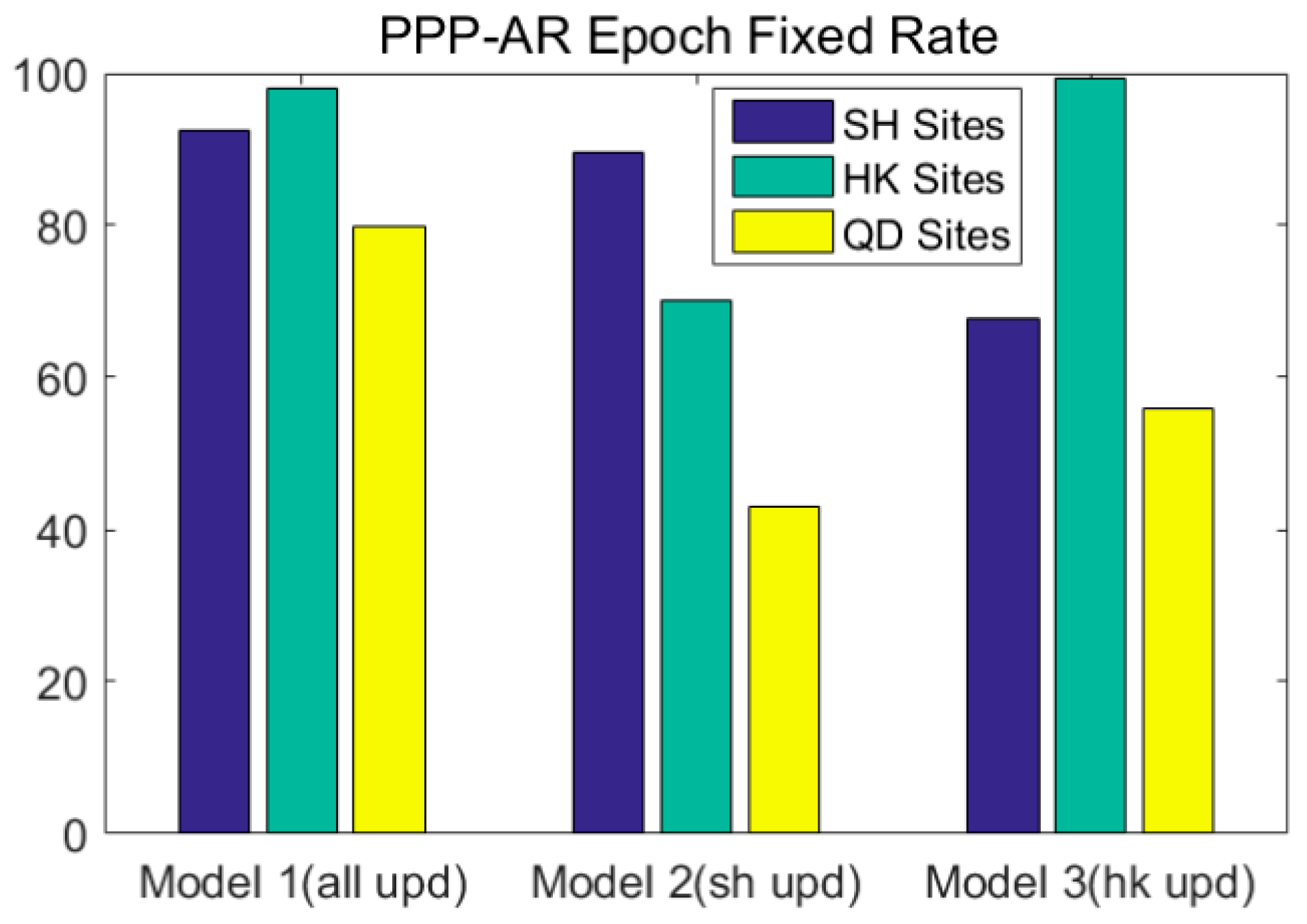
| Station | Model | Station | Model | Station | Model | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |||
| YIWU | 95.6 | 90.3 | 80.9 | HKKS | 92.3 | 69.2 | 98.9 | SZ01 | 85.8 | 52.8 | 52.5 |
| XUCH | 87.8 | 75.8 | 59.1 | HKKT | 98.8 | 74.0 | 99.0 | TG01 | 88.0 | 46.1 | 57.6 |
| CJZZ | 91.3 | 93.3 | 74.2 | HKLM | 99.1 | 83.3 | 99.8 | TGT0 | 80.7 | 57.0 | 56.8 |
| DING | 89.9 | 84.6 | 55.9 | HKMW | 91.0 | 63.3 | 98.8 | TP01 | 86.6 | 68.8 | 56.0 |
| DPZZ | 96.0 | 96.4 | 75.9 | HKNP | 99.2 | 78.0 | 99.2 | WK01 | 73.6 | 46.7 | 47.5 |
| FUQI | 77.1 | 86.2 | 23.3 | HKOH | 98.7 | 64.1 | 99.0 | XLH0 | 86.5 | 62.8 | 51.4 |
| JD01 | 92.8 | 92.3 | 56.9 | HKPC | 99.3 | 70.3 | 99.6 | XQ01 | 61.1 | 39.7 | 35.7 |
| JSWZ | 92.8 | 93.4 | 76.3 | HKSC | 99.3 | 73.7 | 99.8 | XY01 | 83.4 | 65.9 | 76.2 |
| JZZZ | 96.2 | 93.3 | 88.3 | HKSL | 99.2 | 56.8 | 99.8 | YL01 | 81.7 | 69.3 | 57.5 |
| LJIN | 96.8 | 92.8 | 49.0 | HKSS | 99.1 | 65.0 | 99.3 | BD01 | 60.7 | 28.6 | 28.4 |
| XTZZ | 96.3 | 92.7 | 93.7 | HKST | 99.0 | 69.8 | 99.4 | DG01 | 90.4 | 66.5 | 50.6 |
| ZQZZ | 97.0 | 82.6 | 79.2 | HKTK | 98.0 | 72.9 | 99.1 | ||||
| HKWS | 99.4 | 71.5 | 99.4 | ||||||||
| Average | 92.5 | 89.48 | 67.7 | Average | 97.9 | 70.2 | 99.3 | Average | 79.9 | 42.9 | 55.8 |
| Stations in Shanghai, etc. (SH Sites) | Stations in Hong Kong (HK Sites) | Stations in Tianjin (QD Sites) | |||||||||
| Station | Model | Station | Model | Station | Model | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |||
| YIWU | 26 | 1 | 79 | HKKS | 1 | 92 | 1 | SZ01 | 1 | 42 | 37 |
| XUCH | 2 | 14 | 89 | HKKT | 1 | 12 | 2 | TG01 | 3 | 47 | 68 |
| CJZZ | 17 | 15 | 51 | HKLM | 3 | 50 | 2 | TGT0 | 4 | 45 | 7 |
| DING | 2 | 1 | 54 | HKMW | 13 | 84 | 11 | TP01 | 1 | 63 | 5 |
| DPZZ | 1 | 9 | 33 | HKNP | 24 | 83 | 2 | WK01 | 17 | 26 | 24 |
| FUQI | 7 | 5 | 29 | HKOH | 3 | 88 | 8 | XLH0 | 9 | 52 | 24 |
| JD01 | 6 | 23 | 82 | HKPC | 5 | 84 | 3 | XQ01 | 1 | 49 | 3 |
| JSWZ | 2 | 7 | 31 | HKSC | 1 | 15 | 1 | XY01 | 1 | 26 | 10 |
| JZZZ | 2 | 3 | 36 | HKSL | 2 | 75 | 1 | YL01 | 1 | 46 | 11 |
| LJIN | 1 | 8 | 34 | HKSS | 1 | 82 | 1 | BD01 | 2 | 21 | 26 |
| XTZZ | 2 | 5 | 35 | HKST | 12 | 23 | 10 | DG01 | 1 | 50 | 18 |
| ZQZZ | 1 | 4 | 25 | HKTK | 1 | 86 | 1 | ||||
| HKWS | 1 | 6 | 1 | ||||||||
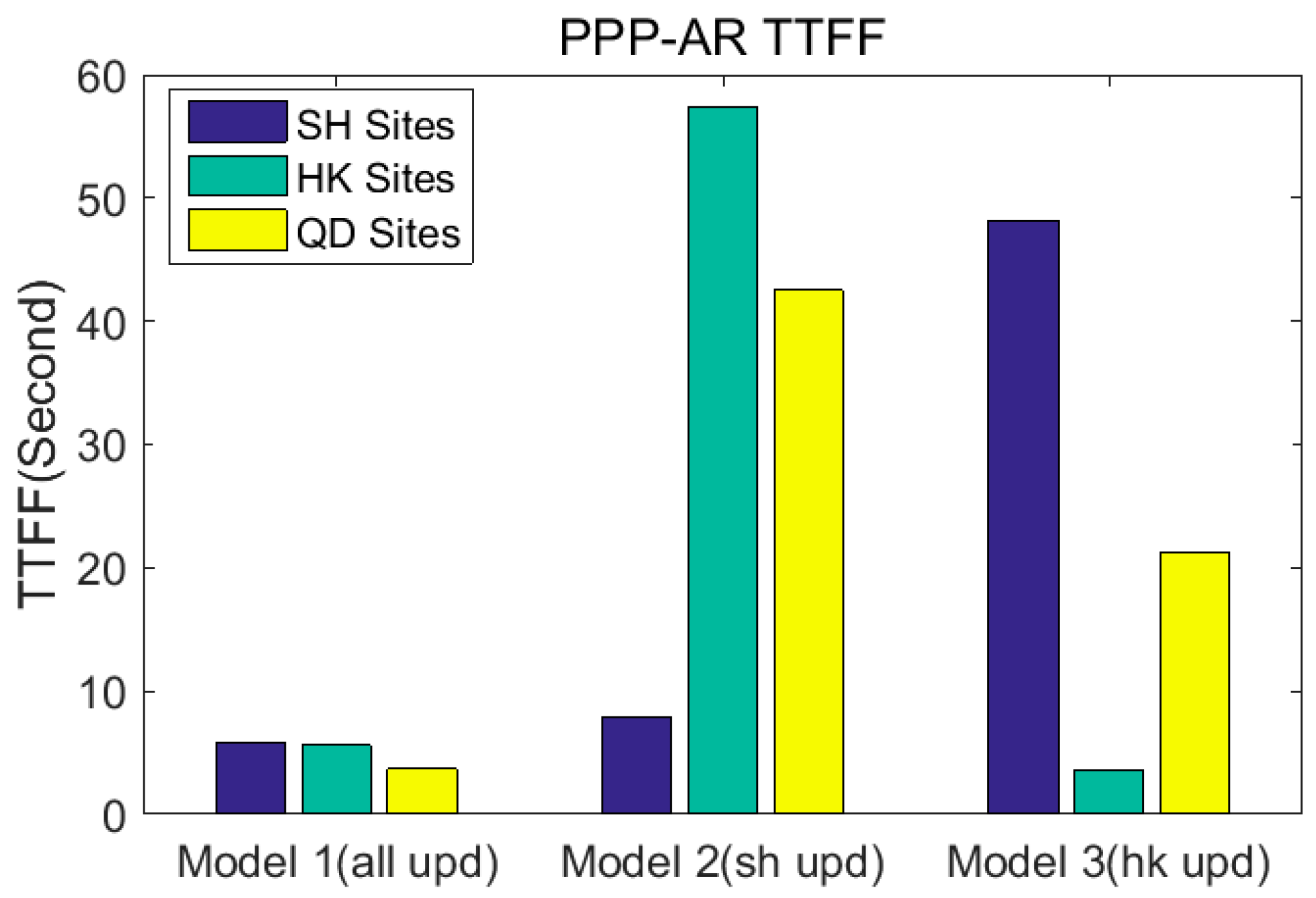
| Average | 5.8 | 7.9 | 48.2 | Average | 5.6 | 57.3 | 3.6 | Average | 3.7 | 42.5 | 21.2 |
| Stations in Shanghai, etc. (SH Sites) | Stations in Hong Kong (HK Sites) | Stations in Tianjin (QD Sites) | |||||||||
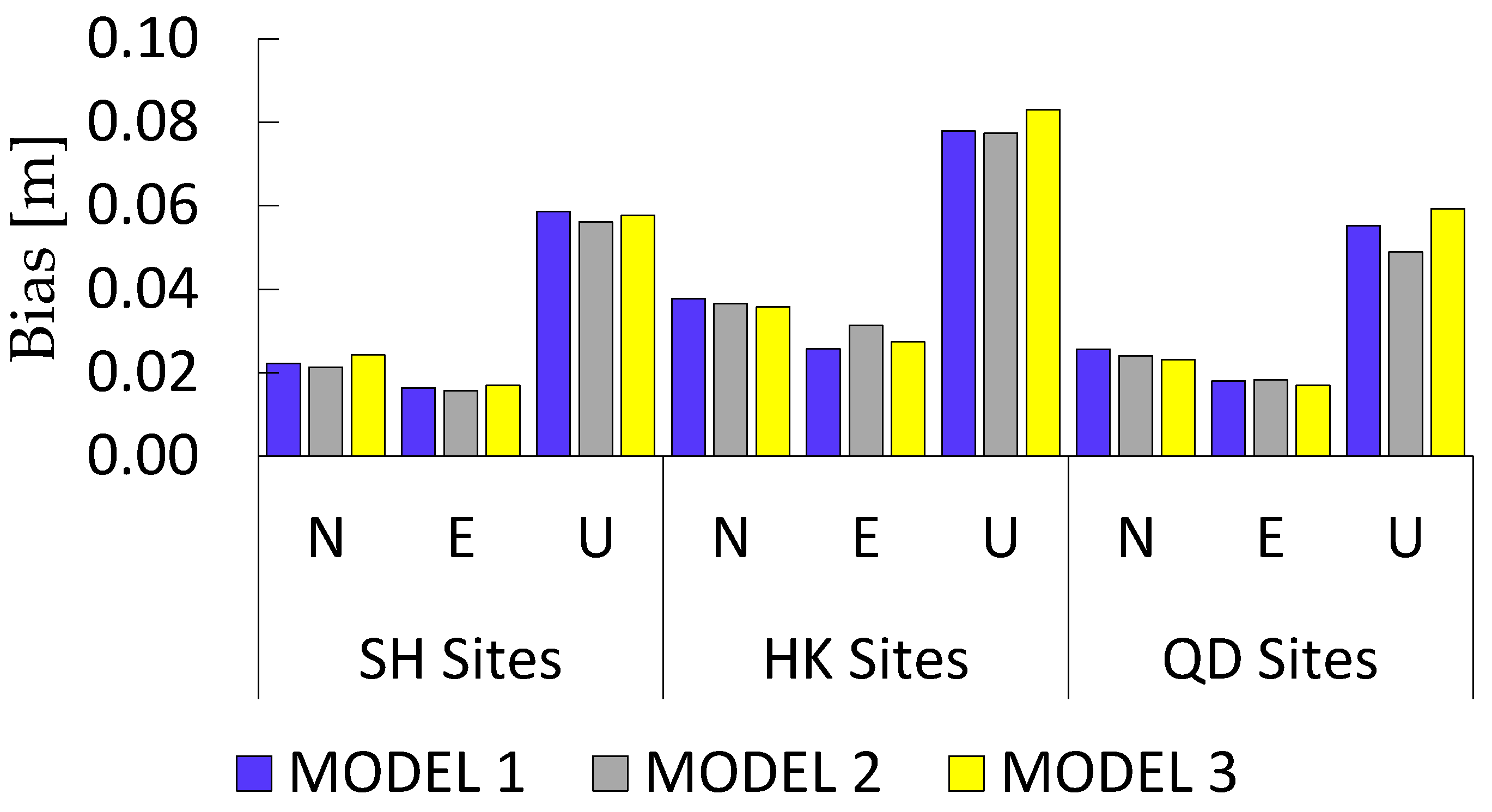
| Regional Station | Bias [m] | MODEL 1 | MODEL 2 | MODEL 3 | Average [m] |
|---|---|---|---|---|---|
| SH Sites | N | 0.022 | 0.021 | 0.024 | 0.022 |
| E | 0.016 | 0.016 | 0.017 | 0.016 | |
| U | 0.059 | 0.056 | 0.058 | 0.058 | |
| HK Sites | N | 0.038 | 0.037 | 0.036 | 0.037 |
| E | 0.026 | 0.031 | 0.027 | 0.028 | |
| U | 0.078 | 0.077 | 0.083 | 0.079 | |
| QD Sites | N | 0.026 | 0.024 | 0.023 | 0.024 |
| E | 0.018 | 0.018 | 0.017 | 0.018 | |
| U | 0.055 | 0.049 | 0.059 | 0.054 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wang, Q.; Jiang, X. Property Analysis of the Real-Time Uncalibrated Phase Delay Product Generated by Regional Reference Stations and Its Influence on Precise Point Positioning Ambiguity Resolution. Sensors 2017, 17, 1162. https://doi.org/10.3390/s17051162
Zhang Y, Wang Q, Jiang X. Property Analysis of the Real-Time Uncalibrated Phase Delay Product Generated by Regional Reference Stations and Its Influence on Precise Point Positioning Ambiguity Resolution. Sensors. 2017; 17(5):1162. https://doi.org/10.3390/s17051162
Chicago/Turabian StyleZhang, Yong, Qing Wang, and Xinyuan Jiang. 2017. "Property Analysis of the Real-Time Uncalibrated Phase Delay Product Generated by Regional Reference Stations and Its Influence on Precise Point Positioning Ambiguity Resolution" Sensors 17, no. 5: 1162. https://doi.org/10.3390/s17051162
APA StyleZhang, Y., Wang, Q., & Jiang, X. (2017). Property Analysis of the Real-Time Uncalibrated Phase Delay Product Generated by Regional Reference Stations and Its Influence on Precise Point Positioning Ambiguity Resolution. Sensors, 17(5), 1162. https://doi.org/10.3390/s17051162





