4.1. Simulation Results
Table 2 presents the results of the two self-calibration attempts based on the calibration algorithm described in
Section 2.3 and
Section 2.4, using the set of all simulated measurements from all three scanner stations. In this instance, the influence of the mechanical misalignments on the scanner measurements is simulated and, therefore, the true values of the calibration parameters are known (
Section 3.2). Parameters
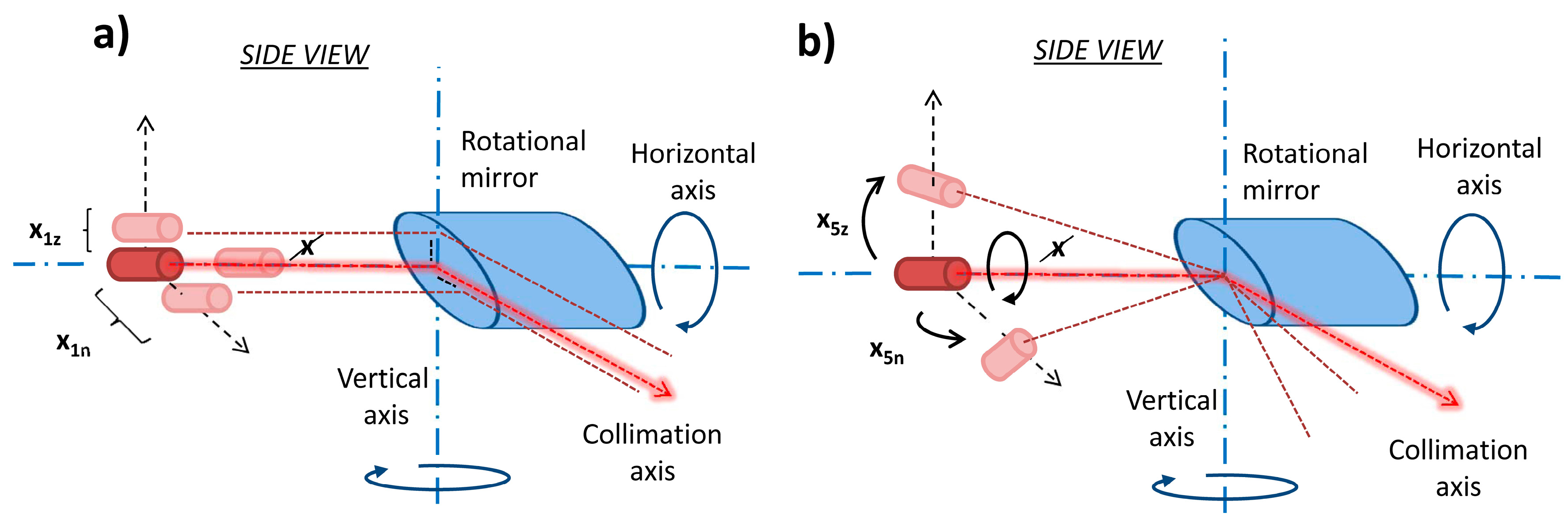
x5z−7 and
x1n+2 combine the influence of two misalignments and, therefore, their values are doubled. The first calibration attempt was conducted without introducing the additional calibration parameter
x1n+2 in the vertical angle equation (Equation (6)). Instead, the parameters
x1n and
x2 are estimated separately as:
. As it can be seen from
Table 2, this leads to a noticeable bias in the estimate of the parameters
x1n and
x5n, which are highly correlated. In the second calibration attempt, the proposed parameter
x1n+2 is introduced, and the estimate of the mentioned parameters is evidently improved. Therefore, only the second attempt is discussed in further detail.
Most of the parameters are estimated with an accuracy and precision of several tenths of arc seconds and several hundredths of millimetres. Two parameters (
x5z−7 and
x5n) are determined with a lower precision of approximately 2.5ʺ, but without bias, while two parameter estimates are somewhat biased (
x1n and
x5z). The bias of the parameter
x1n estimate can be bypassed. Namely, the parameter
x1n+2 contains the combined influence of the parameters
x1n and
x2. Additionally, the parameters
x1n+2 and
x2 are estimated with the higher accuracy and precision than
x1n. Hence, the better estimate of the parameter
x1n can be derived by subtracting the influence of the parameter
x2 from
x1n+2. The corresponding precision can also be estimated using the low of error propagation [
6]. The value and the precision of the parameter
x1n estimated this way are: −0.25 and 0.05 mm. Therefore, the unbiased and more precise estimate is derived. For the evaluation, in one calibration attempt not provided herein, the parameter
x1n was completely removed from the calibration adjustment (from Equation (5)). This led to no noticeable differences in the calibration results. Hence, we kept the parameter for sake of comparison.
When analysing the overall maximum correlations, it is clear that most of the calibration parameters maintained very high correlations towards each other. This is expected because of the similar functional definition of some parameters. However, in this case, it seems that these correlations do not influence the parameter accuracy if the parameters are estimated with the sufficient precision. Therefore, these correlations will not be in the further focus of the work.
Problematic are high correlations with non-calibration parameters (EOPs and OPs), which lead to a bias in the parameter estimates. It is especially visible in the case of the parameter x5z, which is almost perfectly correlated with the translation parameter in the direction of the z axis of the second scanner station. These correlations should be mitigated with a better network design, and this is the part of ongoing investigation in a further study. Finally, most of the calibration parameters sensitive to two-face measurements (Equations (17)–(19)) have low correlations with EOPs and OPs.
The results of both calibration attempts were subjected to the congruency test (Equation (24)). As it can be seen in
Table 3, the adjustment without introducing parameter
x1n+2 clearly failed the statistical test. On the contrary, in the second case, the test statistic was lower than the threshold value, resulting in the test acceptance. This indicates that the network realized in the experiment is sensitive enough to estimate unbiased parameters if the proposed set of calibration parameters is used (Equations (4)–(6)). In other words, the estimated parameters do not significantly differ from their true values and the used network is proved to be valid for further analysis.
4.2. Empirical Results
Table 4 summarizes the results of the self-calibration adjustment using all measurements obtained on the field, from all three stations. In this instance, the true values of the calibration parameters are unknown and only the parameters validated in the previous section are used (Equations (4)–(6)). As it can be seen, the measurement precision and correlations do not noticeably differ from the simulation case. Most of the parameters are estimated with a precision noticeably lower than the measurement noise and would be determined significant by applying usual statistical tests based on the Fisher’s distribution (see [
7]).
Table 5 presents the results of several different calibration attempts using only parameters sensitive to two-face measurements (Equations (17)–(19)). The first attempt (3 × SS) uses all of the measurements from all three scanner stations and it is only a reduced version of the calibration provided in
Table 4. These are the reference results against which the calibration from a single scanner station is compared.
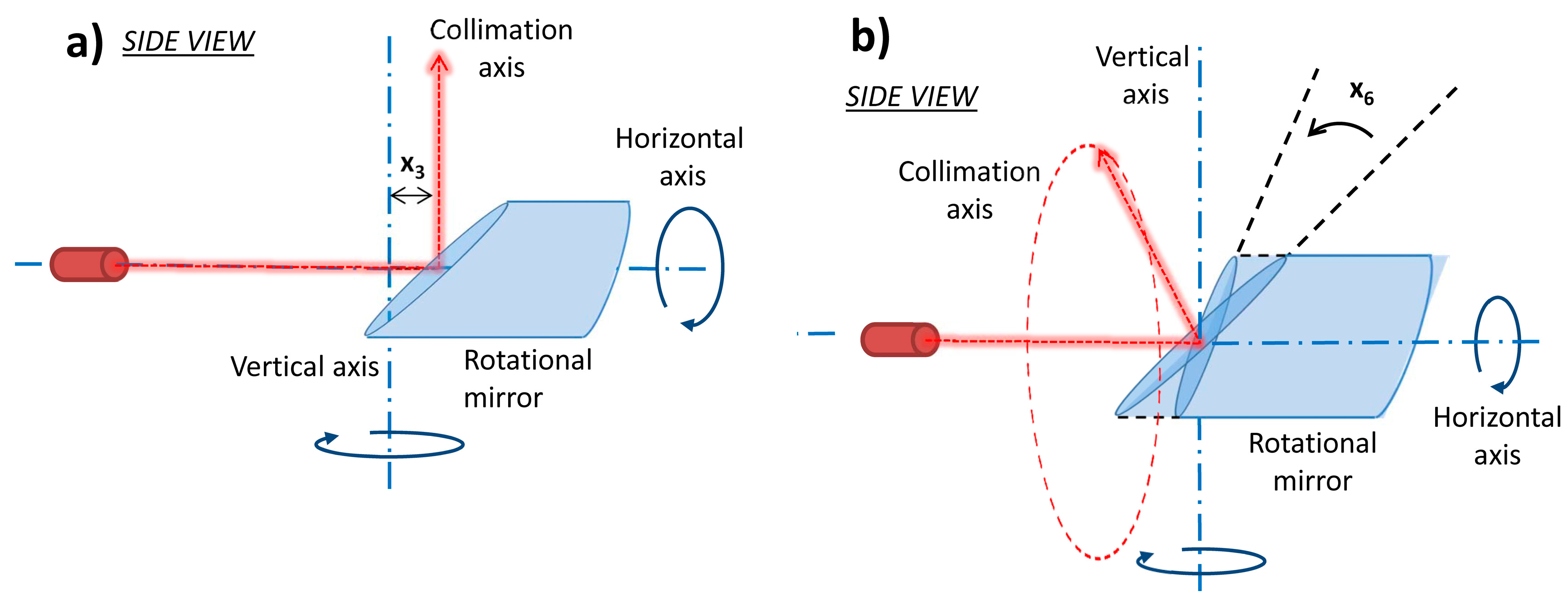
The number of parameters is reduced because the parameters
x10 and
x5z cannot be estimated from a single scanner station without reference information, as explained in
Section 2.3. Additionally, parameter
x1n needs to be estimated a posteriori as explained in the previous section (
Section 4.1). We tried to directly estimate parameters
x10,
x5z and
x1n from a single station in order to test these premises. While the inclusion of the parameters
x10 and
x1n caused that the adjustment could not converge, the parameter
x5z was estimated. However, the estimated value of −97.97° was obviously false and the parameter was perfectly correlated with one point coordinate. Removing the mentioned three parameters leads to the successful calibration.
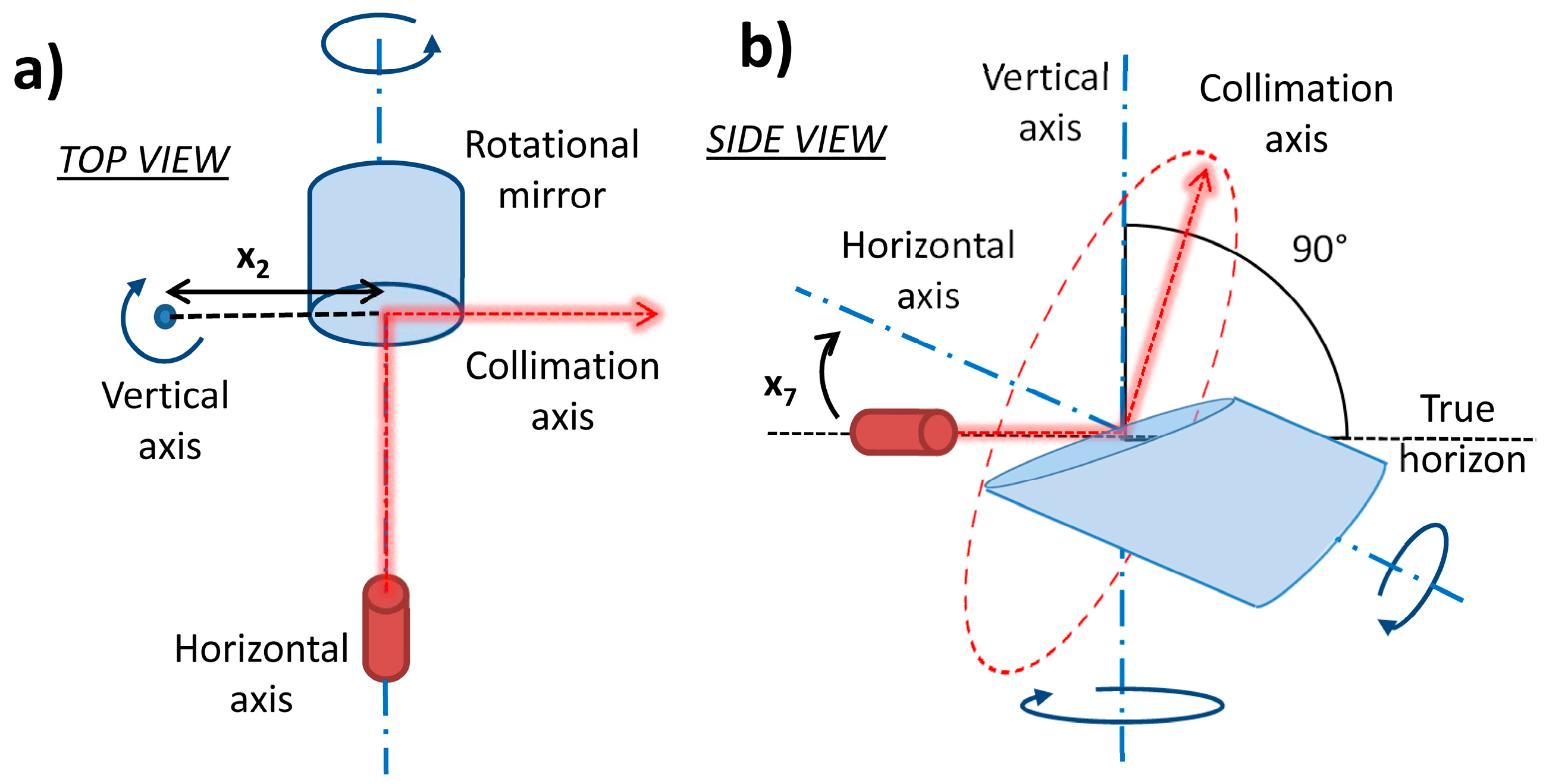
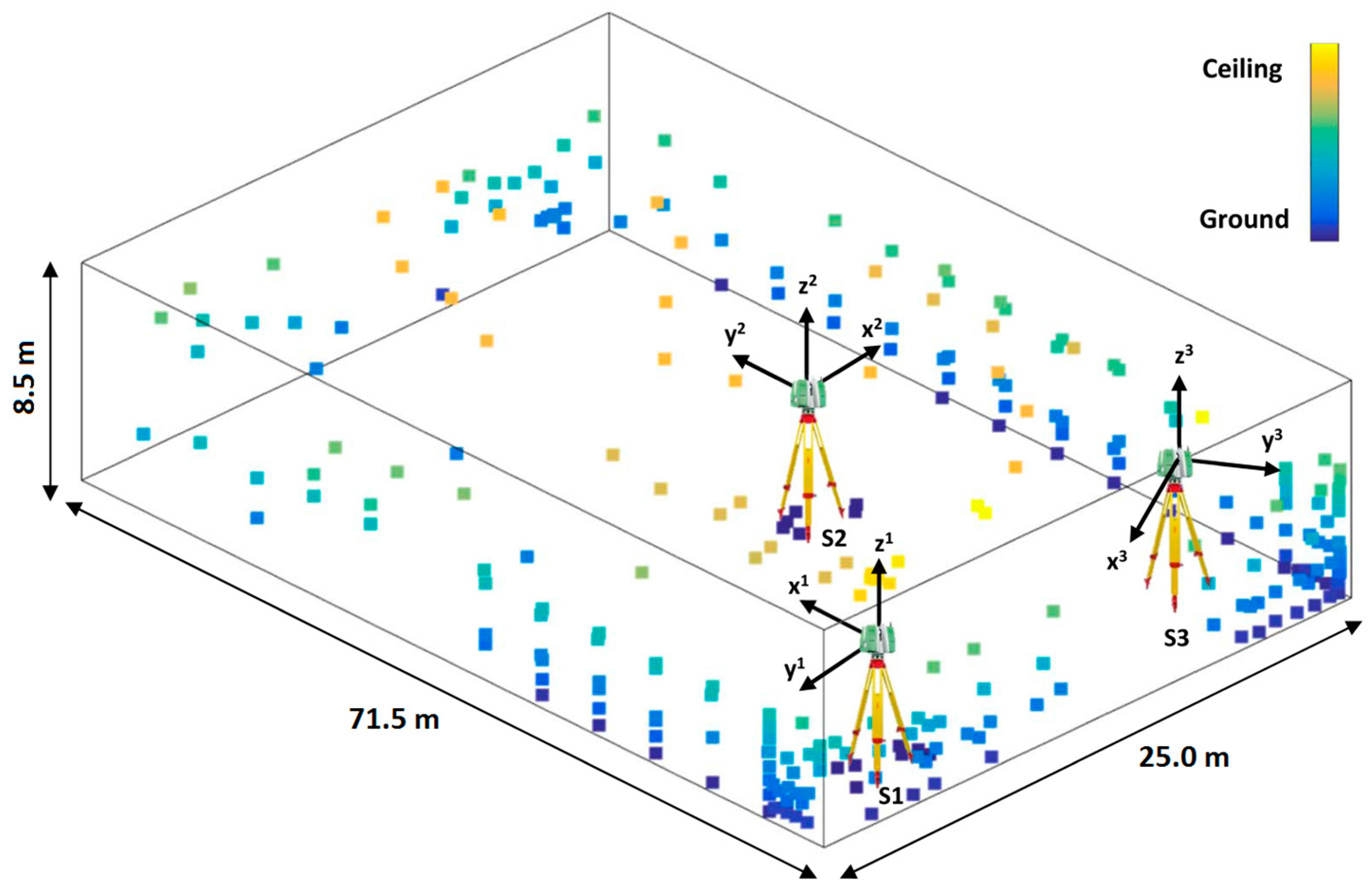
The following calibration attempts are realized using only the data from the first scanner station S1 (
Figure 8). The second station S2 was not used due to the poor network geometry and the poor recoverability of the calibration parameters, while the third station S3 was not used due to the lack of two-face measurements. The self-calibration based on the usual calibration algorithm (
Section 2.3 and
Section 2.4) was conducted with two slightly different realizations. In the first attempt, a separate set of the exterior orientation parameters is used for each scan (1 × SS (2 × EOP)). This is the usual practice in the former works on this topic (e.g., [
33]). However, the implicit formulation of the measurements in two faces (
Section 2.1) justifies using only one set of exterior orientation parameters for both scans from the same scanner station (1 × SS (1 × EOP)). This newly proposed formulation of the adjustment will be proven to be mandatory for the TLS calibration from a single scanner station (
Table 5). The last calibration attempt is realized using the proposed two-face adjustment.
As can be seen, all of the calibration attempts provided quite similar results. This intuitively shows that all of the selected calibration parameters can be estimated from a single scanner station. To justify this hypothesis, the congruency test (Equation (24)) was applied. Estimates of the complete network configuration with all stations (3 × SS) are compared with all three calibration attempts from the single scanner station. The results are presented in the
Table 6.
In the case of the two-face adjustment and the adjustment with the one set of EOP parameters, the test statistics is lower than the threshold value and, therefore, the hypothesis is accepted. This means that estimates of these two approaches do not significantly differ from the full network calibration. However, the first case with the two sets of EOPs failed. The reason lies in the fact that the estimated EOPs have been misplaced and that caused the wrong parameter estimates. This means that the calibration from one scanner station significantly benefits from the inclusion of the implicit two-face measurements and reduction of the number of exterior orientation parameters from 12 to 6.
The reduction of the number of exterior orientation parameters in the case of the full network of several scanner stations was also investigated. The investigation suggested that changing the number of EOPs has no significant impact in this case. The most probable explanation for this is that the EOPs of each scan are very well controlled and precisely estimated in the network adjustment having more than one scanner station. In that case the adjustment does not benefit from this additional constraint—that two consecutive scans from the same scanner station (two-face measurements) share the same position and orientation.
From here, a conclusion can be made: two scans in the first and second cycle (
Section 2.1) sharing the same set of EOPs are mandatory prerequisites for the TLS calibration from a single scanner station, if the scanner position is not well controlled. This control can be achieved by introducing the reference target coordinates retrieved with a more accurate instrument. In that case, the number of exterior orientation parameters used in the adjustment is irrelevant.
Further on, we tested the improvement achieved using the estimated parameters. For this, the field measurements are corrected with two sets of the calibration parameters. The first parameter set is the reference estimate of all calibration parameters from
Table 4, using all scanner stations, while the second set contains the parameters estimated from only one scanner station. For the latter one, the parameters estimated from the two-face adjustment were used (and they equal 1 × SS (1 × EOP)). These corrected measurements were used for the simultaneous registration of all scans, based on the algorithm described in
Section 2.3 and
Section 2.4, but without estimating the calibration parameters again.
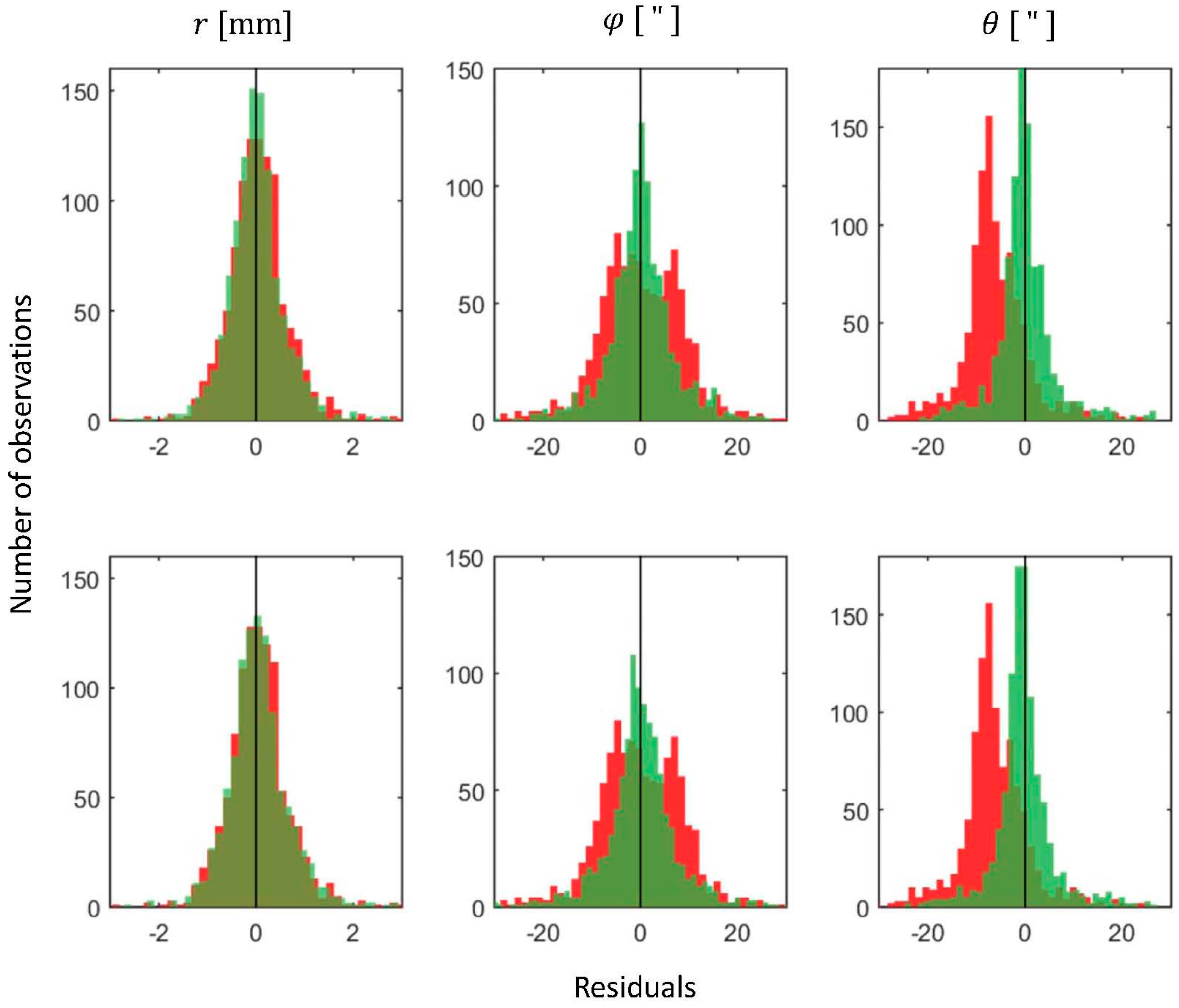
Figure 9 presents the histograms of the measurement residuals of both registrations against the histogram of the measurement residuals of the registration without any calibration.
As it can be seen, both sets of calibration parameters successfully reduced the visible systematic trends in the horizontal and vertical angle measurements, while the range measurements did not present any noticeable trend even in the reference data. The values of the estimated measurement precision (
) are presented in
Table 7.
Again, the improvements achieved using the parameters estimated from all scanner stations do not noticeably differ from the improvements achieved using the parameters estimated from only one scanner station. Finally, the percentage of the improvements is depicted on
Figure 10.
The highest difference between two realizations can be seen in the case of the range measurements. This is expected, because the most influential range parameter—rangefinder offset, was not estimated from a single scanner station. This can be solved by incorporating reference values in the adjustment, as explained in
Section 2.2. The other improvements are comparable, indicating that the calibration from a single scanner station can indeed produce similar results to the self-calibration using the full network configuration.
In the end, one more thing should be highlighted: most of the previous calibration strategies suggested that two consecutive scans from a single scanner station should be rotated around the z axis by 60°, 90° or 120° in order to improve the estimates of the calibration parameters (e.g., [
16,
20,
21,
33]). However, from this experiment, another assumption could be derived. In the case of panoramic terrestrial laser scanners, the best influence on the parameter estimates was the inclusion of two consecutive scans rotated by 180° around the
z axis.