Mechanics Based Tomography: A Preliminary Feasibility Study
Abstract
:1. Introduction
2. Inverse Algorithms Using Limited Boundary Displacements
3. Numerical Results with Simulated Experiments
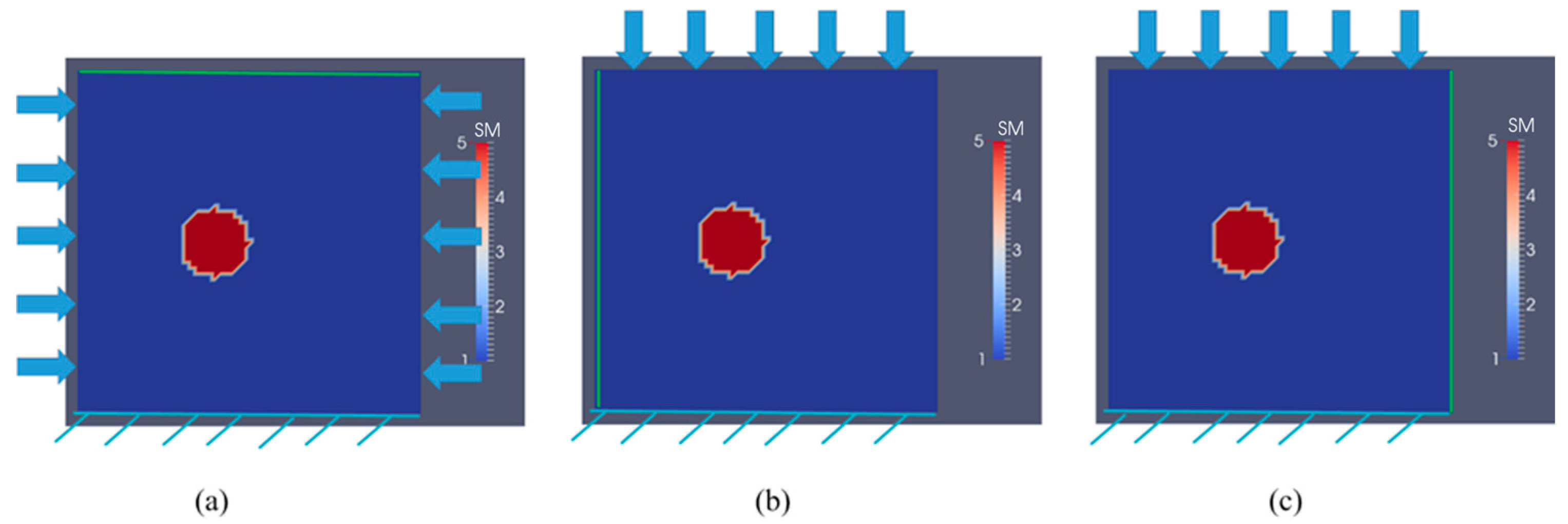
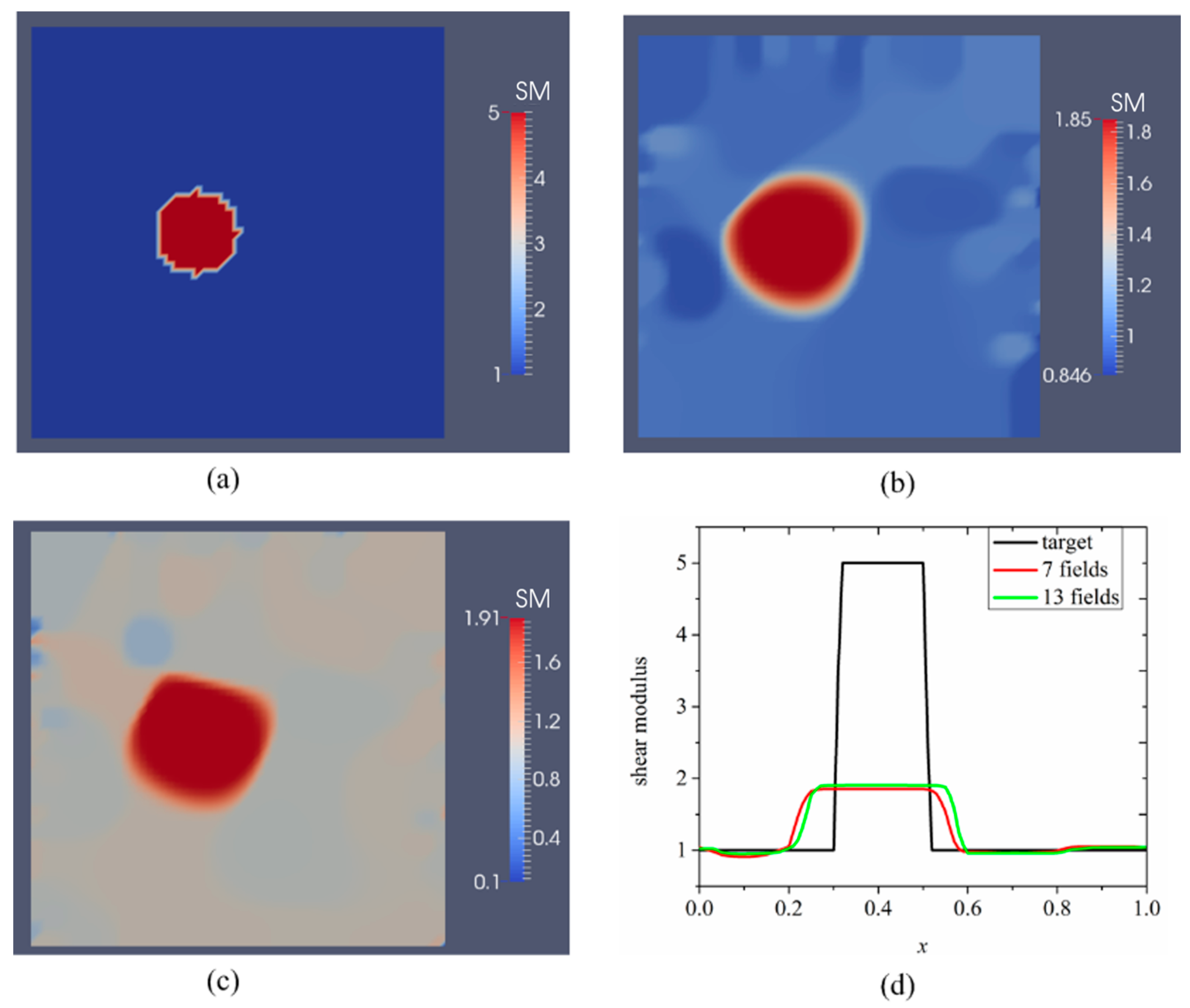
3.1. Case 1: A Square Model with a Small Inclusion
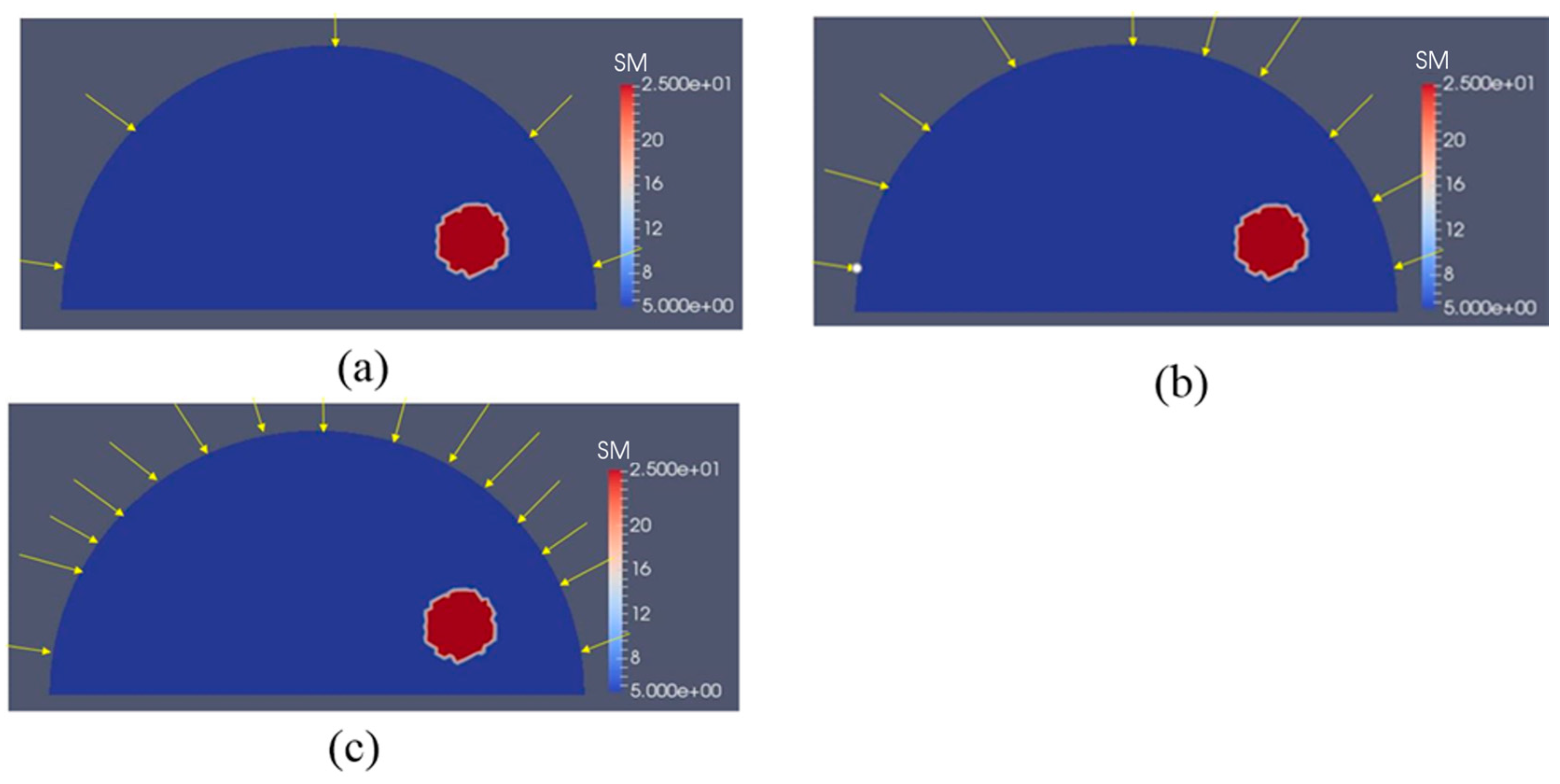
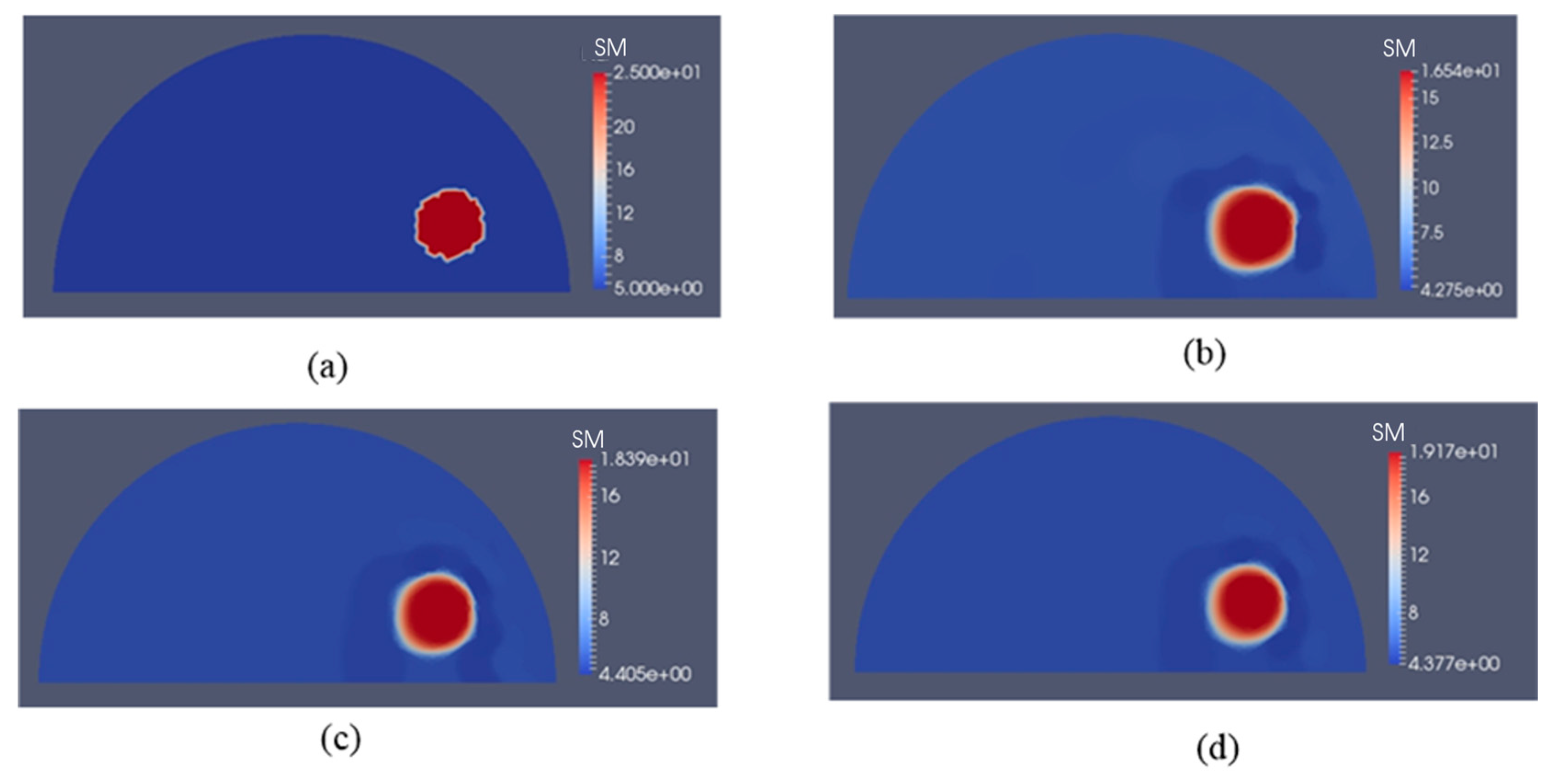
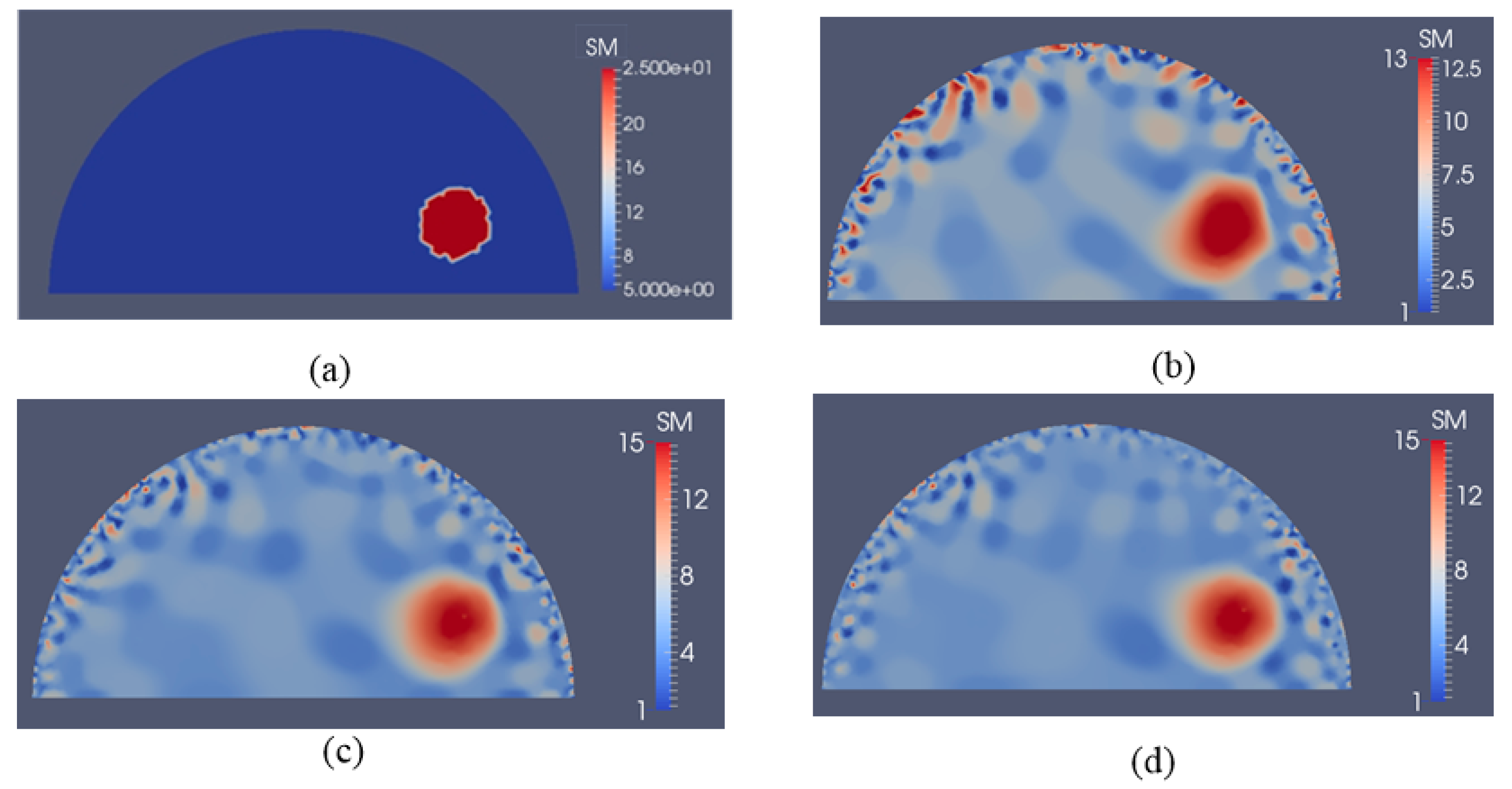
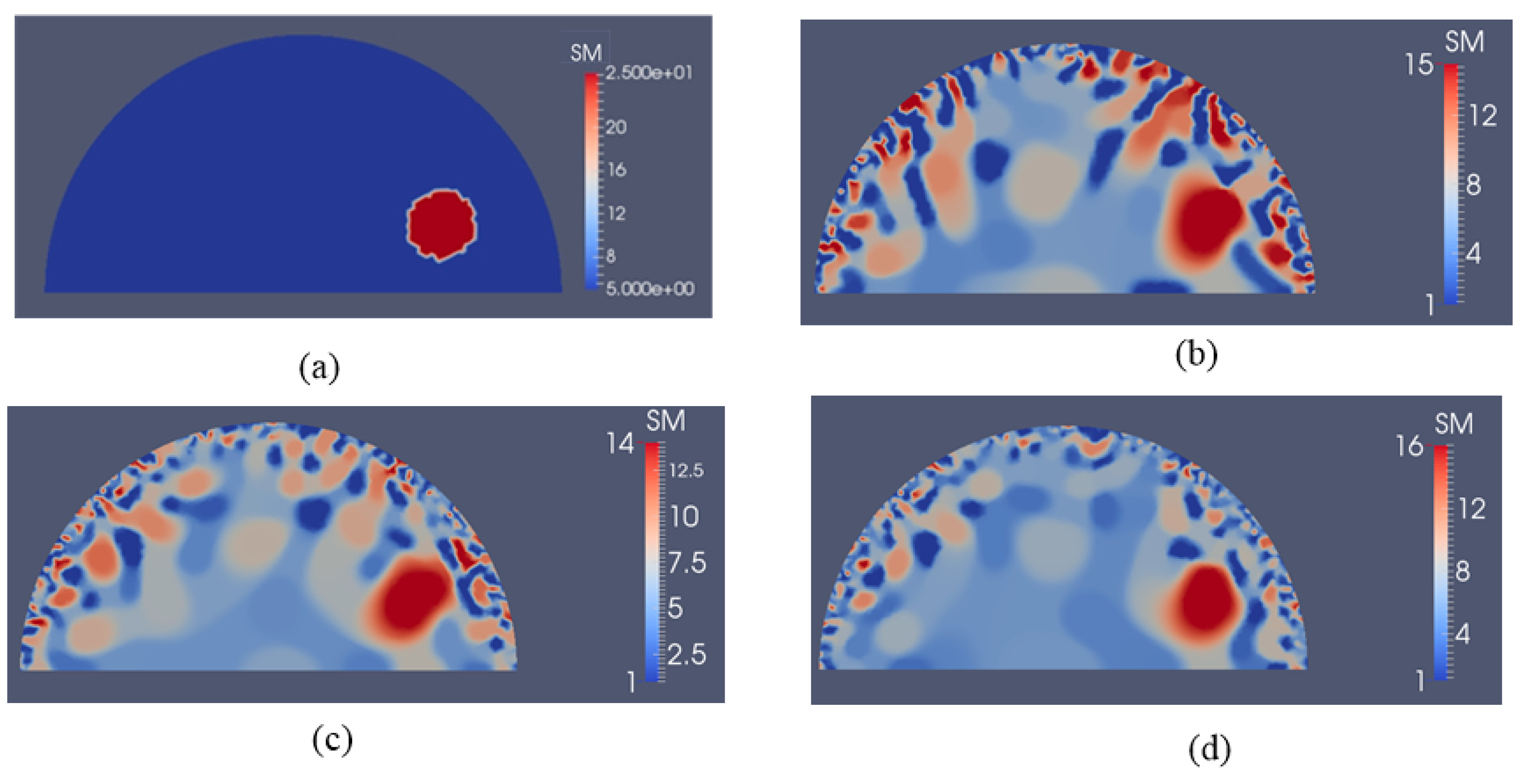
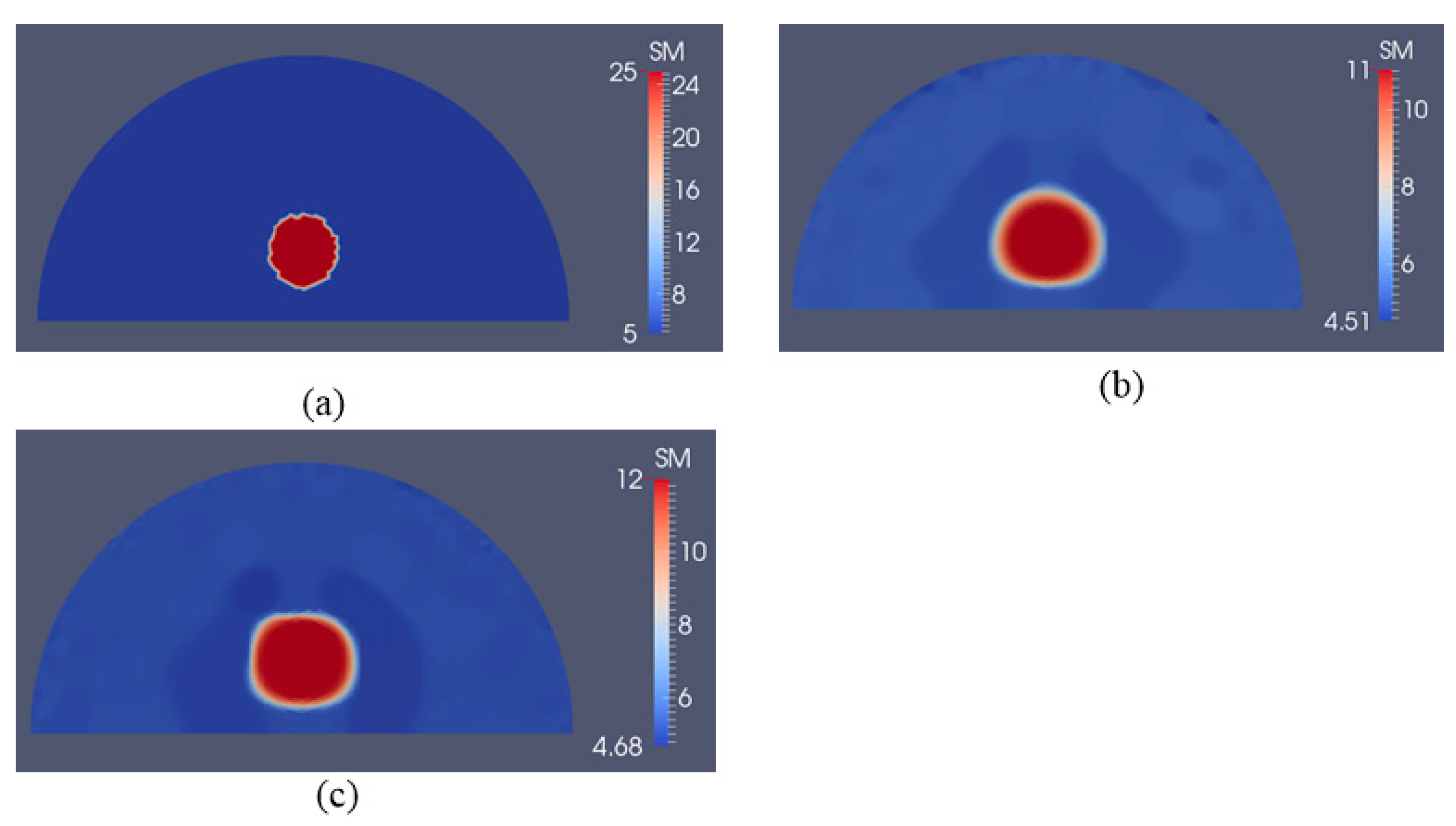
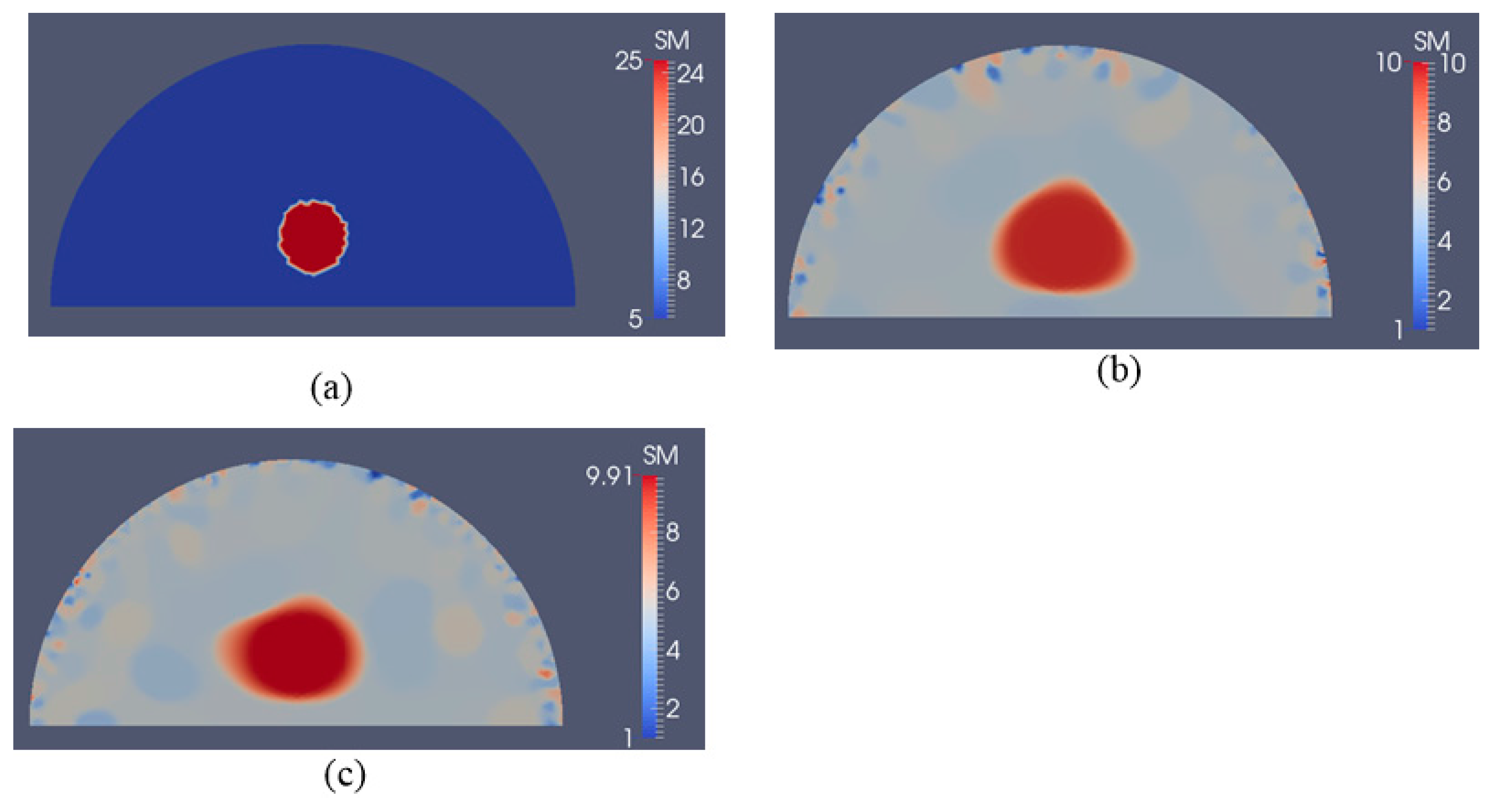
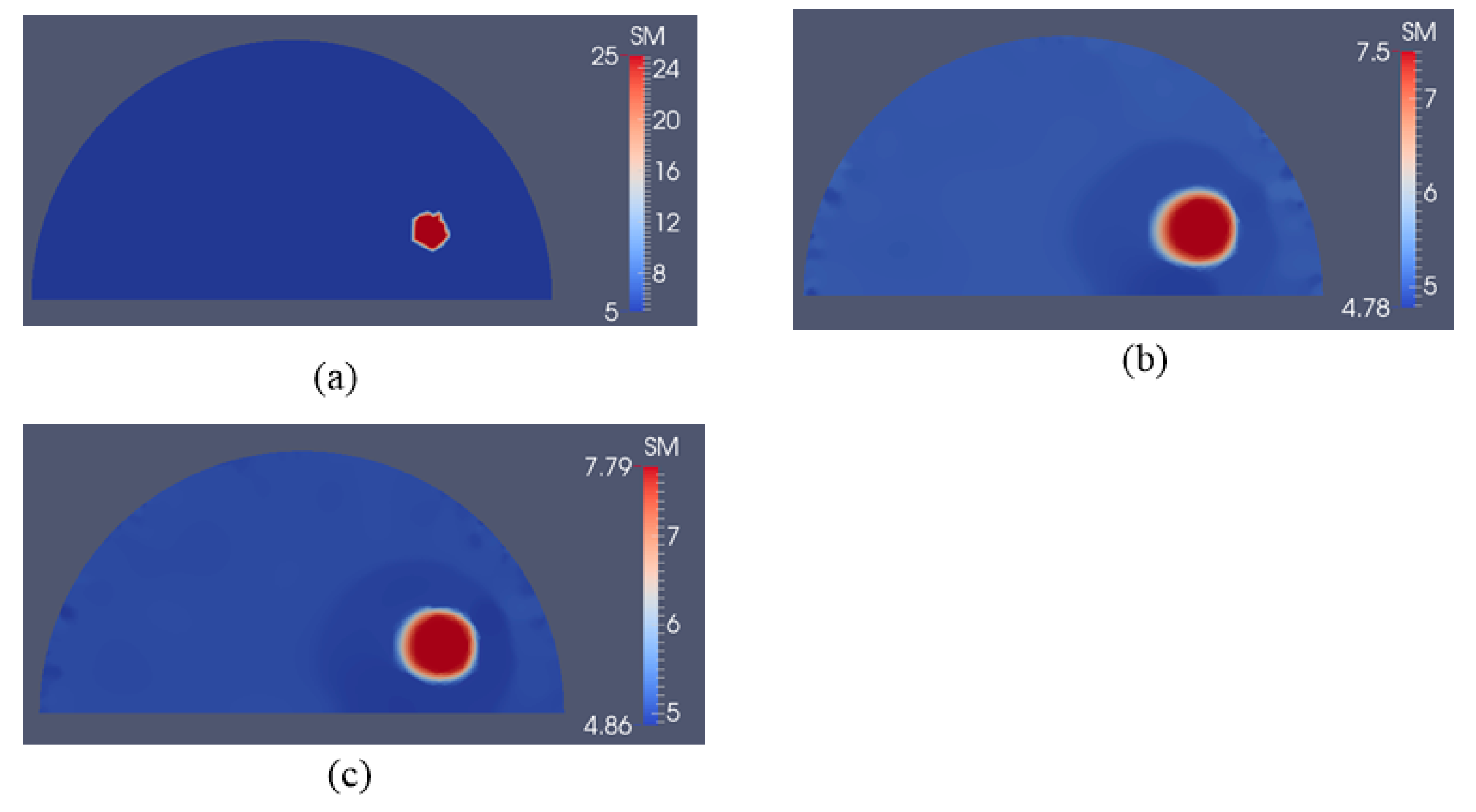
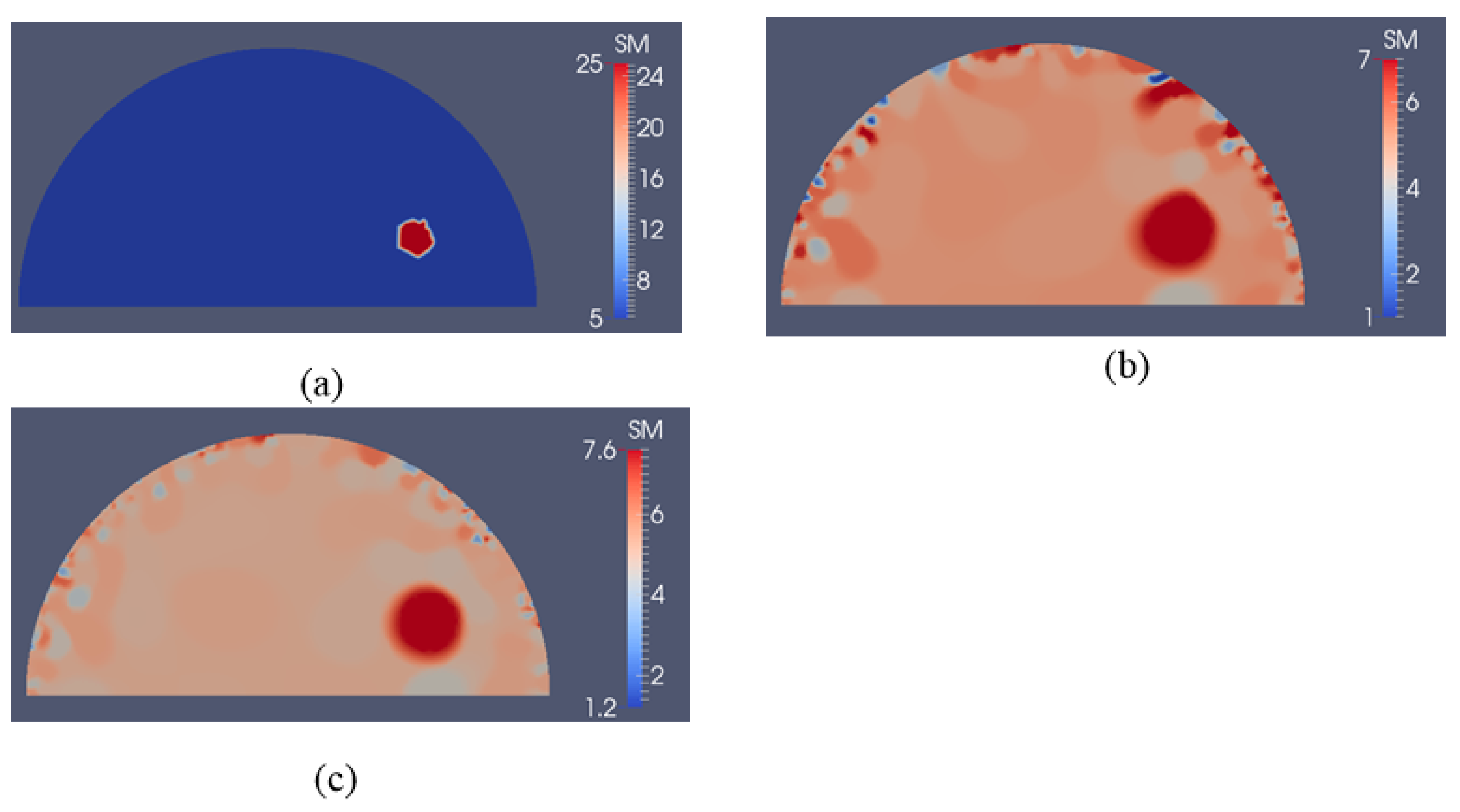
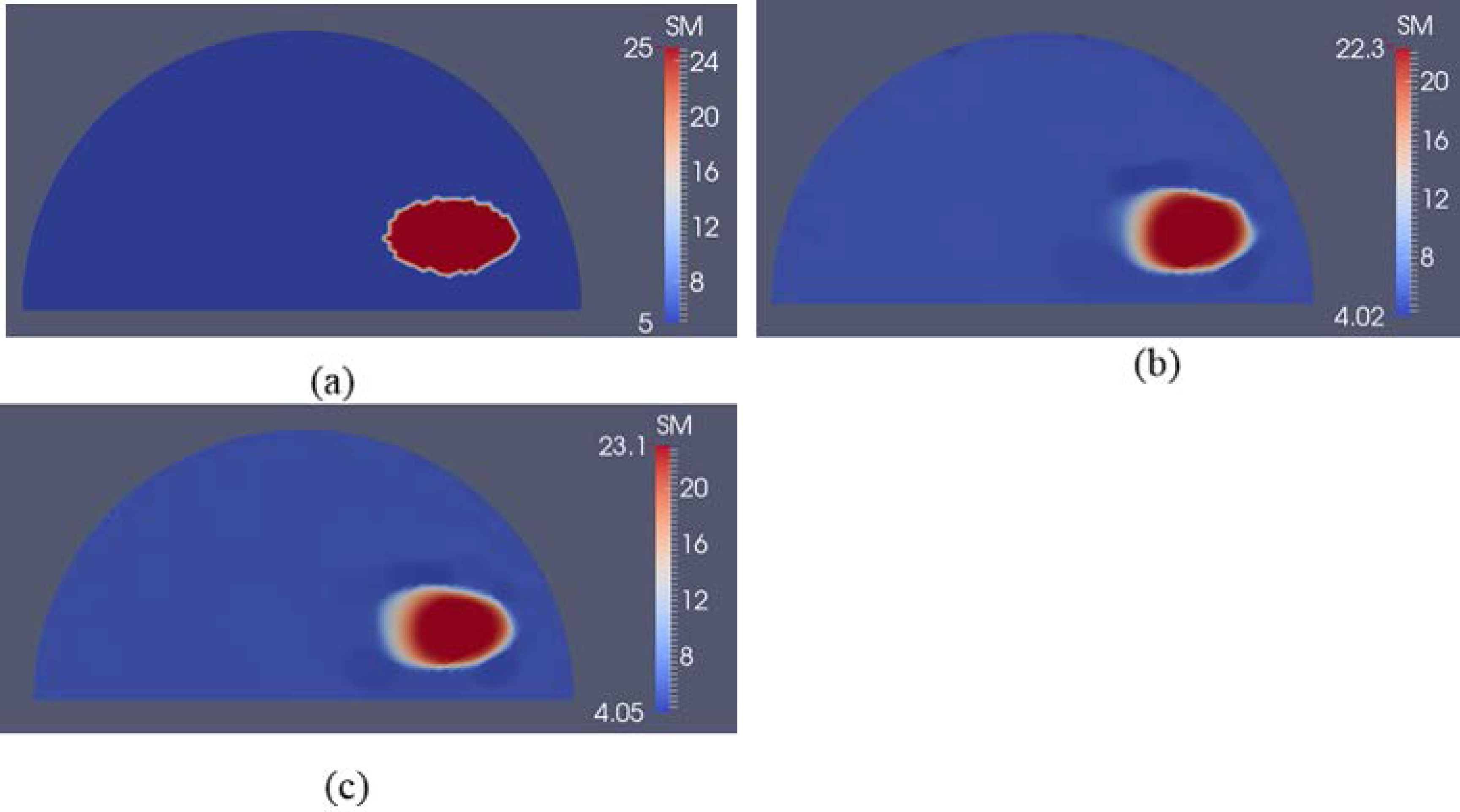
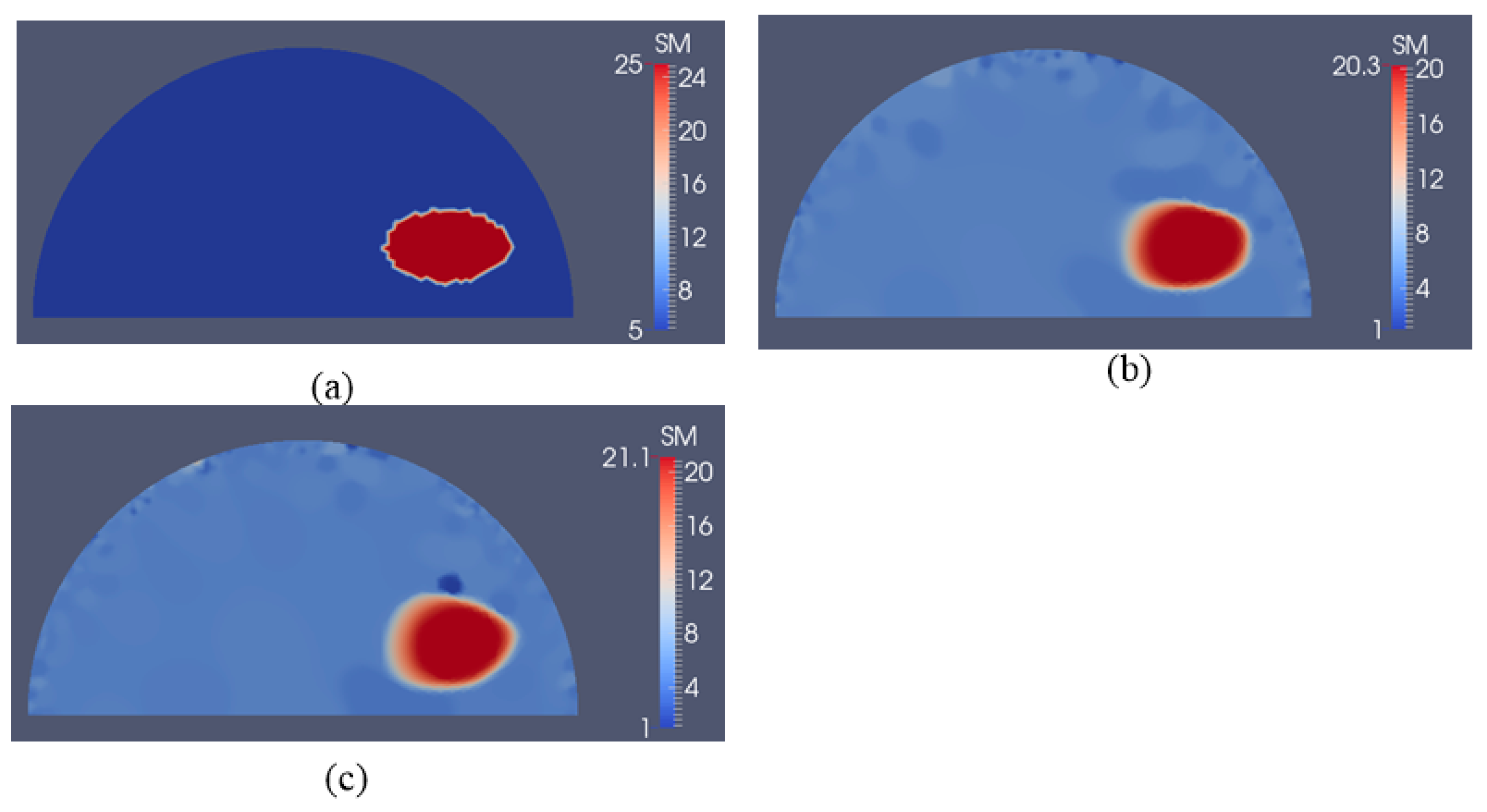
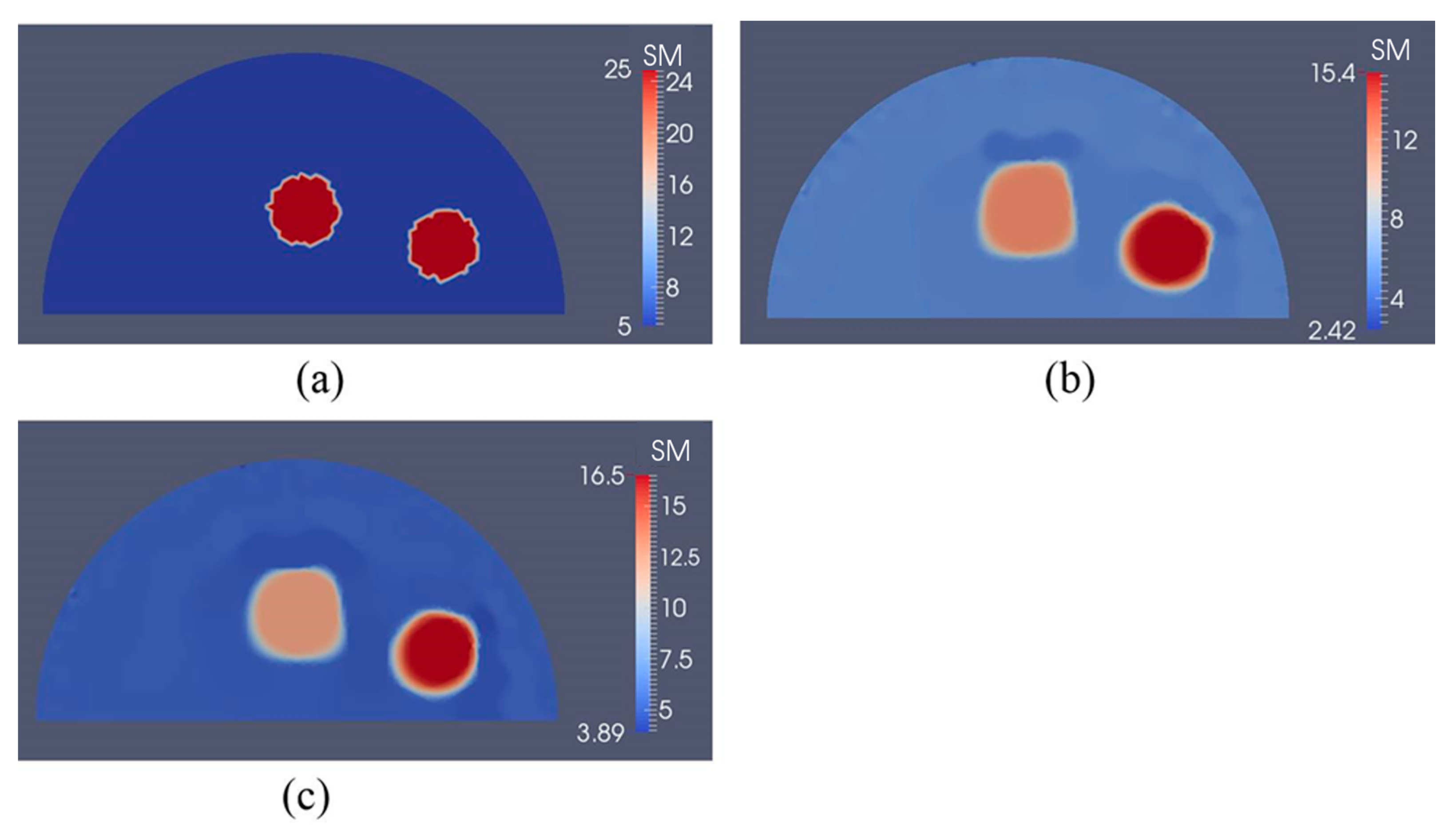
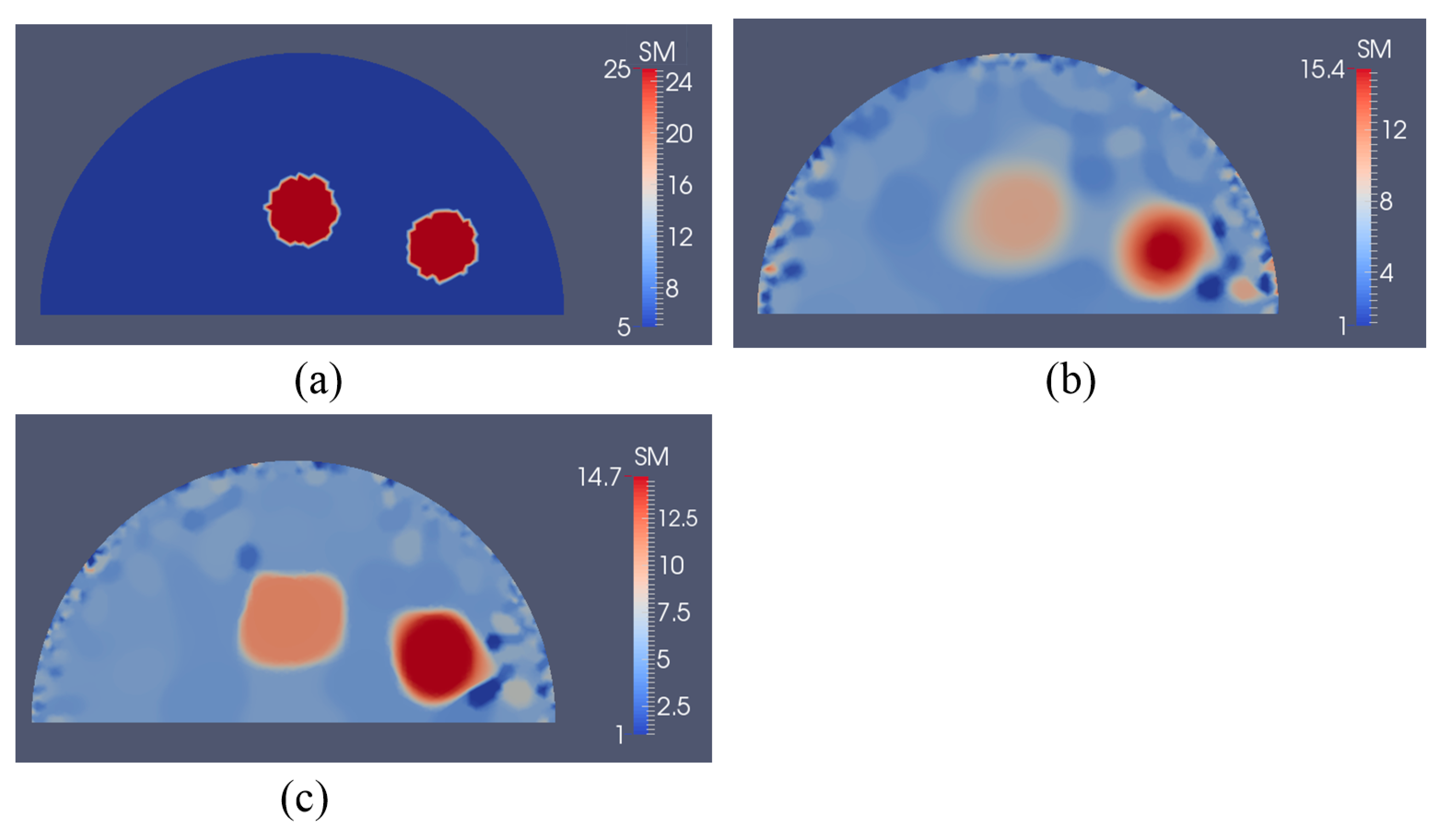
3.2. Case 2: A Semi-Circle Model with One or Two Inclusions
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, H.; Weiss, W.; Medved, M.; Abe, H.; Newstead, G.M.; Karczmar, G.S.; Giger, M.L. Breast density estimation from high spectral and spatial resolution MRI. J. Med. Imaging 2016, 3, 044507. [Google Scholar] [CrossRef] [PubMed]
- Aguilo, M.A.; Aquino, W.; Brigham, J.C.; Fatemi, F. An inverse problem approach for elasticity imaging through vibroacoustics. IEEE Trans. Med. Imaging 2010, 29, 1012–1021. [Google Scholar] [CrossRef] [PubMed]
- Goenezen, S. Inverse Problems in Finite Elasticity: An Application to Imaging the Nonlinear Elastic Properties of Soft Tissues. Ph.D. Thesis, Rensselaer Polytechnic Institute, Troy, NY, USA, 2011. [Google Scholar]
- Goenezen, S.; Barbone, P.; Oberai, A.A. Solution of the nonlinear elasticity imaging inverse problem: The incompressible case. Comput. Methods Appl. Mech. Eng. 2011, 200, 1406–1420. [Google Scholar] [CrossRef] [PubMed]
- Goenezen, S.; Dord, J.F.; Sink, Z.; Barbone, P.; Jiang, J.; Hall, T.J.; Oberai, A.A. Linear and nonlinear elastic modulus imaging: An application to breast cancer diagnosis. IEEE Trans. Med. Imaging 2012, 31, 1628–1637. [Google Scholar] [CrossRef] [PubMed]
- Goenezen, S.; Oberai, A.A.; Dord, J.; Sink, Z.; Barbone, P. Nonlinear elasticity imaging Bioengineering Conference (NEBEC). In Proceedings of the 2011 IEEE 37th Annual Northeast, Troy, NY, USA, 1–3 April 2011; pp. 1–2. [Google Scholar]
- Grediac, M.; Pierron, F.; Avril, S.; Toussaint, E. The virtual fields method for extracting constitutive parameters from full-field measurements: A review. Strain 2006, 42, 233–253. [Google Scholar] [CrossRef]
- Hansen, H.H.G.; Richards, M.S.; Doyley, M.M.; de Korte, C.L. Noninvasive vascular displacement estimation for relative elastic modulus reconstruction in transversal imaging planes. Sensors 2013, 13, 3341–3357. [Google Scholar] [CrossRef] [PubMed]
- Mei, Y.; Goenezen, S. Spatially weighted objective function to solve the inverse problem in elasticity for the elastic property distribution. In Computational Biomechanics for Medicine: New Approaches and New Applications; Doyle, B., Miller, K., Wittek, A., Nielsen, P.M.F., Eds.; Springer: New York, NY, USA, 2015. [Google Scholar]
- Mei, Y.; Goenezen, S. Parameter identification via a modified constrained minimization procedure. In Proceedings of the 24th International Congress of Theoretical and Applied Mechanics, Montreal, QC, Canada, 21–26 August 2016. [Google Scholar]
- Mei, Y.; Kuznetsov, S.; Goenezen, S. Reduced boundary sensitivity and improved contrast of the regularized inverse problem solution in elasticity. J. Appl. Mech. 2015, 83. [Google Scholar] [CrossRef]
- Richards, M.S.; Barbone, P.E.; Oberai, A.A. Quantitative three-dimensional elasticity imaging from quasi-static deformation: A phantom study. Phys. Med. Biol. 2009, 54, 757–779. [Google Scholar] [CrossRef] [PubMed]
- Dickinson, R.J.; Hill, C.R. Measurement of soft-tissue motion using correlation between A-scans. Ultrasound Med. Biol. 1982, 8, 263–271. [Google Scholar] [CrossRef]
- Hall, T.; Barbone, P.E.; Oberai, A.A.; Jiang, J.; Dord, J.; Goenezen, S.; Fisher, T. Recent results in nonlinear strain and modulus imaging. Curr. Med. Imaging Rev. 2011, 7, 313–327. [Google Scholar] [CrossRef] [PubMed]
- Hall, T.J.; Bilgen, M.; Insana, M.F.; Krouskop, T.A. Phantom materials for elastography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1997, 44, 1355–1365. [Google Scholar] [CrossRef]
- Hall, T.J.; Zhu, Y.; Spalding, C.S. In vivo real-time freehand palpation imaging. Ultrasound Med. Biol. 2003, 29, 427–435. [Google Scholar] [CrossRef]
- Ophir, J.; Cespedes, I.; Ponnekanti, H.; Yazdi, Y.; Li, X. Elastography: A quantitative method for imaging the elasticity of biological tissues. Ultrason. Imaging 1991, 13, 111–134. [Google Scholar] [CrossRef] [PubMed]
- Wilson, L.S.; Robinson, D.E. Ultrasonic measurement of small displacements and deformations of tissue. Ultrason. Imaging 1982, 4, 71–82. [Google Scholar] [CrossRef] [PubMed]
- Bayat, M.; Denis, M.; Gregory, A.; Mehrmohammadi, M.; Kumar, V.; Meixner, D.; Fazzio, R.T.; Fatemi, M.; Alizad, A. Diagnostic features of quantitative comb-push shear elastography for breast lesion differentiation. PLoS ONE 2017, 12, e0172801. [Google Scholar] [CrossRef] [PubMed]
- Bayat, M.; Ghosh, S.; Alizad, A.; Aquino, W.; Fatemi, M. A generalized reconstruction framework for transient elastography. J. Acoust. Soc. Am. 2016, 139, 2028. [Google Scholar] [CrossRef]
- Wang, M.; Dutta, D.; Kim, K.; Brigham, J.C. A computationally efficient approach for inverse material characterization combining Gappy POD with direct inversion. Comput. Methods Appl. Mech. Eng. 2015, 286, 373–393. [Google Scholar] [CrossRef]
- Mei, Y.; Fulmer, R.; Raja, V.; Wang, S.; Goenezen, S. Estimating the non-homogeneous elastic modulus distribution from surface deformations. Int. J. Solids Struct. 2016, 83, 73–80. [Google Scholar] [CrossRef]
- Mei, Y.; Goenezen, S. Non-Destructive characterization of heterogeneous solids from limited surface measurements. In Proceedings of the 24th International Congress of Theoretical and Applied Mechanics, Montreal, QC, Canada, 21–26 August 2016. [Google Scholar]
- Gupta, S.; Parameswaran, V.; Sutton, M.A.; Shukla, A. Study of dynamic underwater implosion mechanics using digital image correlation. Proc. R. Soc. A 2014, 470. [Google Scholar] [CrossRef]
- Robert, L.; Nazaret, F.; Cutard, T.; Orteu, J.J. Use of 3-D digital image correlation to characterize the mechanical behavior of a fiber reinforced refractory castable. Exp. Mech. 2007, 47, 761–773. [Google Scholar] [CrossRef]
- Mei, Y.; Tajderi, M.; Goenezen, S. Regularizing biomechanical maps for partially known material propertiese. Int. J. Appl. Mech. 2017, 9. [Google Scholar] [CrossRef]
- Maniatty, A.M.; Liu, Y.; Klaas, O.; Shephard, M.S. Higher order stabilized finite element method for hyperelastic finite deformation. Comput. Methods Appl. Mech. Eng. 2002, 191, 1491–1503. [Google Scholar] [CrossRef]
- Vogel, C.R. Non-convergence of the L-curve regularization parameter selection method. Inverse Probl. 1996, 12, 535–547. [Google Scholar] [CrossRef]
- Vogel, C.R. Computational Methods for Inverse Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002. [Google Scholar]
- Anzengruber, S.; Ramlau, R. Morozov’s discrepancy principle for Tikhonov-type functionals with nonlinear operators. Inverse Probl. 2010, 26. [Google Scholar] [CrossRef]
- Bonesky, T. Morozov’s discrepancy principle and Tikhonov-type functionals. Inverse Probl. 2009, 25. [Google Scholar] [CrossRef]
- Zhu, C.; Byrd, R.H.; Lu, P.; Nocedal, J. L-BFGS-B: FORTRAN Subroutines for Large Scale Bound Constrained Optimization’; Technical Report, NAM-11; EECS Department, Northwestern University: Evanston, IL, USA, 1994. [Google Scholar]
- Zhu, C.; Byrd, R.H.; Lu, P.; Nocedal, J. L-BFGS-B: A limited Memory FORTRAN Code for Solving Bound Constrained Optimization Problems; Technical Report, NAM-11; EECS Department, Northwestern University: Evanston, IL, USA, 1994. [Google Scholar]
- Dorn, O.; Bertete-Aguirre, H.; Berryman, J.G.; Papanicolaou, G.C. A nonlinear inversion method for 3D electromagnetic imaging using adjoint fields. Inverse Probl. 1999, 15, 1523–1558. [Google Scholar] [CrossRef]
- Oberai, A.A.; Gokhale, N.H.; Feijóo, G.R. Solution of inverse problems in elasticity imaging using the adjoint method. Inverse Probl. 2003, 19, 297. [Google Scholar] [CrossRef]





| Noise Level | Relative L2 Error | |
|---|---|---|
| 7 Displacement Datasets | 13 Displacement Datasets | |
| 0.1% | 41.51% | 40.39% |
| 1% | 43.89% | 43.48% |
| Noise Level | Relative L2 Error | ||
|---|---|---|---|
| 5 Displacement Datasets | 10 Displacement Datasets | 15 Displacement Datasets | |
| 0% | 28.68% | 23.91% | 22.52% |
| 1% | 45.40% | 40.66% | 38.30% |
| 5% | 69.26% | 56.25% | 50.78% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, Y.; Wang, S.; Shen, X.; Rabke, S.; Goenezen, S. Mechanics Based Tomography: A Preliminary Feasibility Study. Sensors 2017, 17, 1075. https://doi.org/10.3390/s17051075
Mei Y, Wang S, Shen X, Rabke S, Goenezen S. Mechanics Based Tomography: A Preliminary Feasibility Study. Sensors. 2017; 17(5):1075. https://doi.org/10.3390/s17051075
Chicago/Turabian StyleMei, Yue, Sicheng Wang, Xin Shen, Stephen Rabke, and Sevan Goenezen. 2017. "Mechanics Based Tomography: A Preliminary Feasibility Study" Sensors 17, no. 5: 1075. https://doi.org/10.3390/s17051075
APA StyleMei, Y., Wang, S., Shen, X., Rabke, S., & Goenezen, S. (2017). Mechanics Based Tomography: A Preliminary Feasibility Study. Sensors, 17(5), 1075. https://doi.org/10.3390/s17051075





