Public Auditing with Privacy Protection in a Multi-User Model of Cloud-Assisted Body Sensor Networks
Abstract
:1. Introduction
- A novel service model supporting a multi-user model in cloud-assisted WBSNs is presented. This service model enhances the user experience of WBSNs services in a community hospital environment.
- An improved scheme for supporting public auditing and to protect user‘s data privacy simultaneously (under the assumption that the cloud server is not trusted) is implemented. The multi-user model ensures cloud data access only to authorized members from the same group using a secret group key. Furthermore, our mechanism revokes group members exhibiting illegal actions and achieves system forward security by updating the group key. Experimental evaluations prove that our scheme is secure under the Random Oracle Model (ROM) and outperforms existing schemes in cloud-assisted WBSNs applications.
2. Preliminaries
2.1. Bilinear Map
- Bi-linearity: for all P, Q ∈ R G and a, b ∈ R Zq*, e (a∙P, b∙Q) = e(P, Q)ab.
- Non-degeneracy: there exist P, Q ∈ R G such that e (a∙P, b∙Q) ≠ 1GT.
- Computability: for all P, Q ∈ R G, there exists an efficient algorithm to compute e (a∙P, b∙Q).
2.2. Elliptic Curve Cryptosystem
2.3. ECDLP and CDHP
2.4. System Model
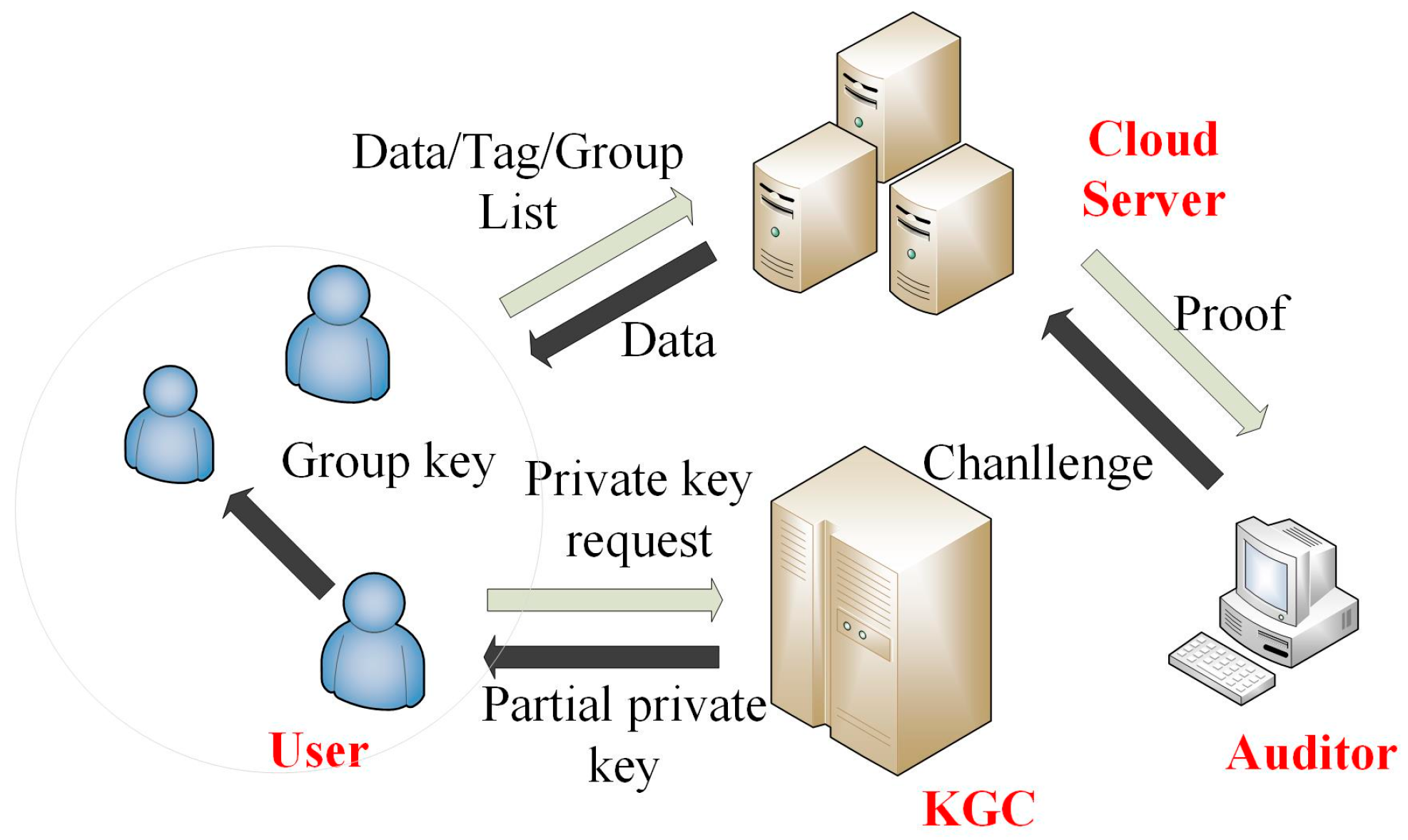
- Cloud server: The cloud server in our scheme is a semi-trusted entity; the user will upload medical data to the cloud server for storage. Assuming that the cloud server is not fully trusted, user sensitive data stored in the cloud are vulnerable for unauthorized accesses. The cloud server can facilitate the necessary computing power and storage capacity for the WBSNs devices.
- Key generating centre: KGC is used to generate public parameters for the system and to generate partial public/private keys for users. KGC is a trusted entity.
- Auditor: The auditor is semi-trusted third party and undertakes the task of data integrity checking. When the user needs to check the integrity of the stored data, the user will request this service through the auditor, and the cloud server runs an interactive algorithm with the auditor to achieve the goal of integrity checking. In this process, the user’s data would not be obtained by the auditor.
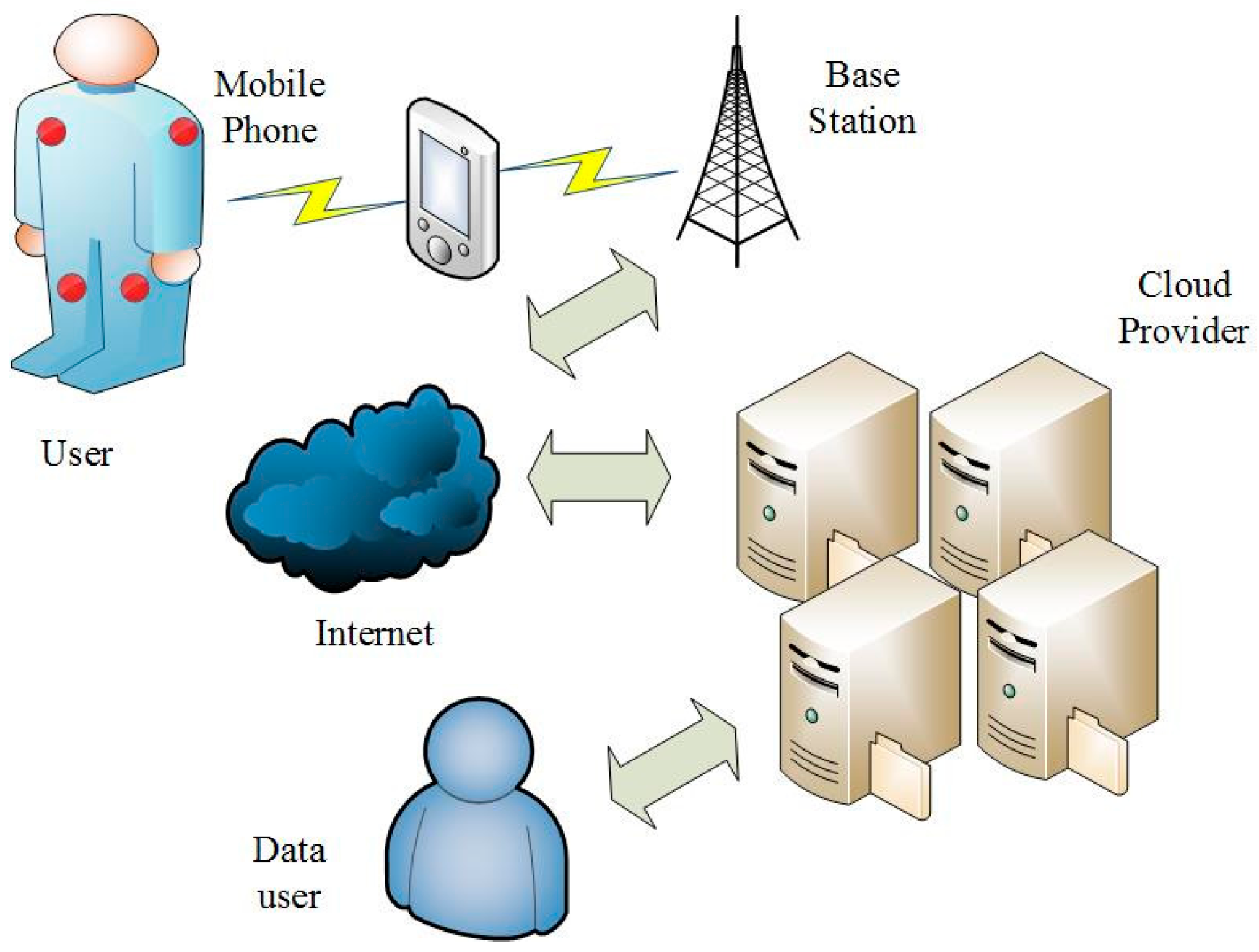
- User: In our scheme, the user is a cloud-assisted WBSN service user. Users use the sensor devices to obtain their own physiological information and to upload the collected physiological information to the cloud server after generating the tag (a signature on the message that is used for checking the integrity of the data) on the collected data and form a historical archive. Users and other group users (such as their community doctors) form a group to share the data stored on the cloud server. Because physiological information is individual private information, users would like to keep their information confidential and do not want any other parties to obtain their data, except the authorized group members. The relationship among these entities is shown in Figure 2.
2.5. Security Requirements
- (1)
- Public verifiability: The stored data on the cloud server should be publicly verified by the third party auditor.
- (2)
- Privacy protecting: The uploaded data should not be accessed by the cloud server or auditor even while uploading or auditing.
- (3)
- Multi-user model: Different users can form a group to share the data stored in the cloud server. No other entities except the legal group users can obtain the data stored on the cloud.
- (4)
- Revocability: When users in the group perform illegal operations, the illegal user should be removed from the group by the group manager.
- (5)
- Forward security: In order to ensure forward security, when the illegal user is revoked, the group key should be updated.
3. Proposed Scheme
| Algorithm 1. Setup. |
| Input: a security parameter l Output: the system parameters (q, G1,G2, P, h1, h2, H, e, Q, QKGC) 1) The KGC chooses a large prime number q > 2l. 2) Chooses an additive group < G1, +>, a multiplicative group < G2, >, a generator P of G1, a bilinear paring e:G1 × G1 → G2, a point Q on G1. 3) Chooses three hash functions h1: {{0,1}*, G1} → Zq*, h2: {{0,1}*, {0,1}*,G1, G1} → Zq*, H: {0,1}* → G1. 4) Choose a random number sKGC ∈ Zq* as the master key and generates QKGC = sKGC · P as public key. Returns (q, G1, G2, P, h1, h2, H, e, Q, QKGC). |
| Algorithm 2. PartialPrivateKeyExtract. |
| Input: the user’s identity IDU Output: the partial key of {PKU,1, SKU,1} 1) The KGC generates a random number tU ∈ Zq*. 2) Computes PKU,1 = tU · P. 3) Computes vU = h1(IDU, PKU,1). 4) Computes SKU,1 = tU + sKGC · vU mod q. Returns {PKU,1, SKU,1}. |
| Algorithm 3. TagGen. |
| Input: SKO, PKO, mi, idi, IDG, IDO, QKGC, Q Output: the tag Si 1) The data owner computes vO = h2 (IDG, IDO, PKO, QKGC). 2) Computes Si = (SKO,1 + vO · SKO,2) · (H(idi) + m i · Q). Returns Si. |
| Algorithm 4. Challenge. |
| Input: NULL Output: the challenge {(ij,rj)}j∈S 1) The auditor generates a random subset S = {i1, i2,..., ic} from the set Zn*(1,2,..., n) and any two elements are not equal. 2) For every element ij ∈ S, the auditor generates a random number rj ∈ Zq*. Returns {(ij,rj)}j∈S. |
| Algorithm 5. ProofGen. |
| Input: , , {(ij,rj)}j∈S Output: the proof {mPro, SPro} 1) The cloud server computes . 2) Computes mod q. Returns {mPro, SPro}. |
| Algorithm 6. ProofVerify. |
| Input: {mPro, SPro}, {(ij,rj)}j∈S, IDO, PKO, Q, QKGC Output: TRUE or FALSE 1) The auditor computes v1 = h1 (IDO, PKO,1). 2) Computes v2 = h2 (IDO, IDG, PKO, QKGC). 3) Then third-party auditor can check the integrity of the stored data by verifying whether equation e(SPro, P) = e(mPro · Q + rj · H(), PKO,1 + v1 · QKGC + v2 · PKO,2) holds. If holds, returns TRUE, Else, returns FALSE. |
- Update the group members list LG (the illegal user’s identity information is removed from the LG). Then, the group organizer sends the updated group members list LG' to the cloud server.
- The organizer chooses a new random number xg' ∈ Zq* as a new group encryption key and distributes the key to all other legal group members. The new group key distributing method is same as that in the algorithm JoinGroup.
4. The Proven Security of Our Proposed Scheme
4.1. The Basic Concept of Proven Security
- (1)
- The formal definition of cryptographic protocols: the original scheme should be abstracted into a conversion scheme, which can deduced a difficult problem (“extremely primitive”).
- (2)
- (3)
- The establishment of the security model: The establishment of security model is mainly to determine the attacker’s attacking purpose and attacking ability. For example, in the digital signature protocol, the adversary’s target is to obtain the ability to forge the signature of any messages or to obtain the private key of the signer. Attacking ability is a description of the attacking steps in order to achieve the goal. As in the digital signature scheme, the adversary can choose any message other than the challenge identity to ask the signature of the signature machine.
- (4)
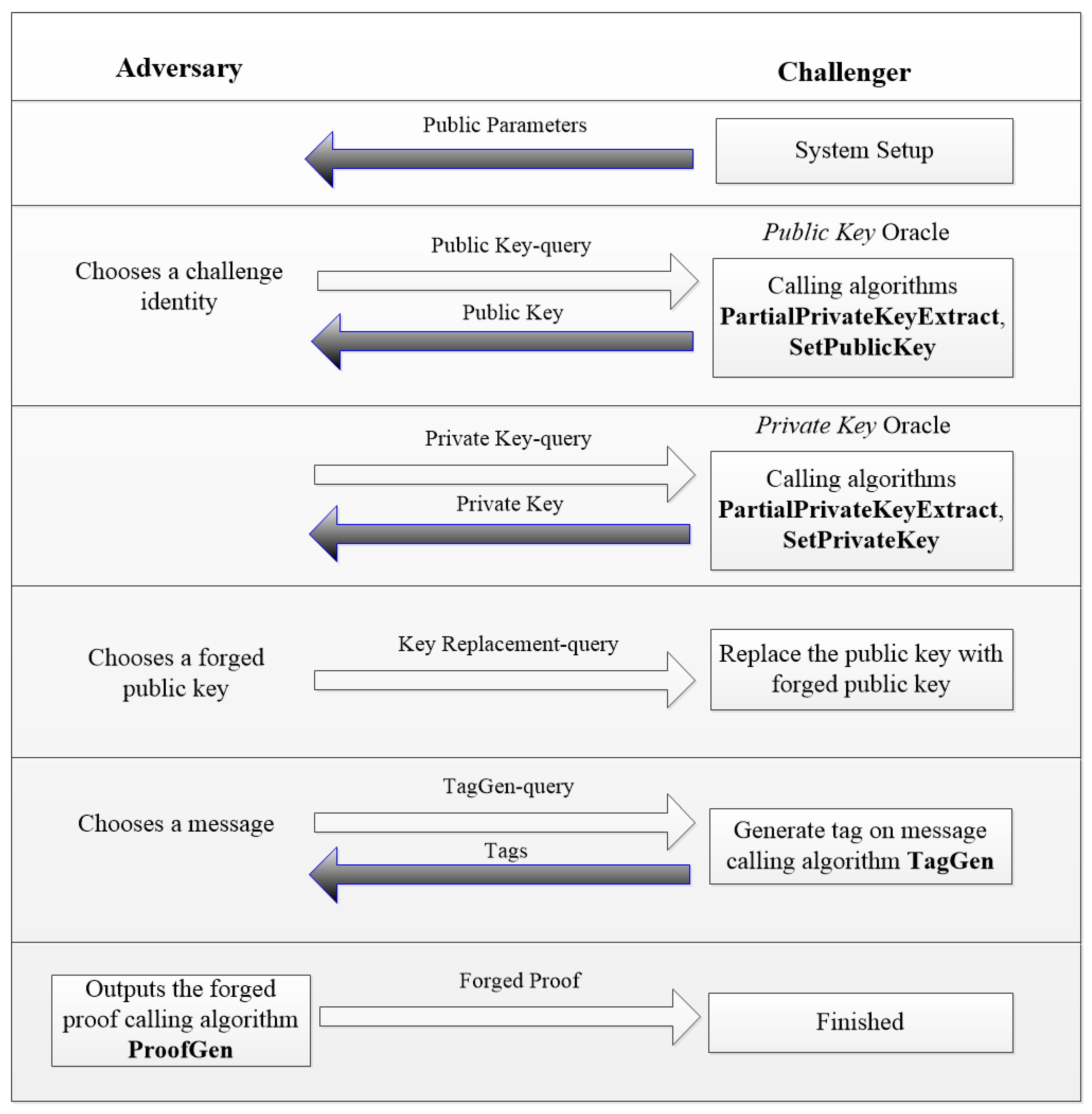
- Formal proof: This process is the core technology of provable security theory. Proven by formal methods to establish an attacking game between analogue rival and challenger to inverse the attacking process, then it converts to solving difficult problems, such as the large prime factorization problem, the discrete logarithm problem in a finite field, etc., thus completing the proof. Many existing cryptographic schemes have been proven secure in the random oracle model [30,33,34,41,43]. The flowchart of the attacking games in our security proof is shown in Figure 3.
4.2. Security Model
4.3. Security Proof
5. Security Analysis
6. Experimental Evaluation
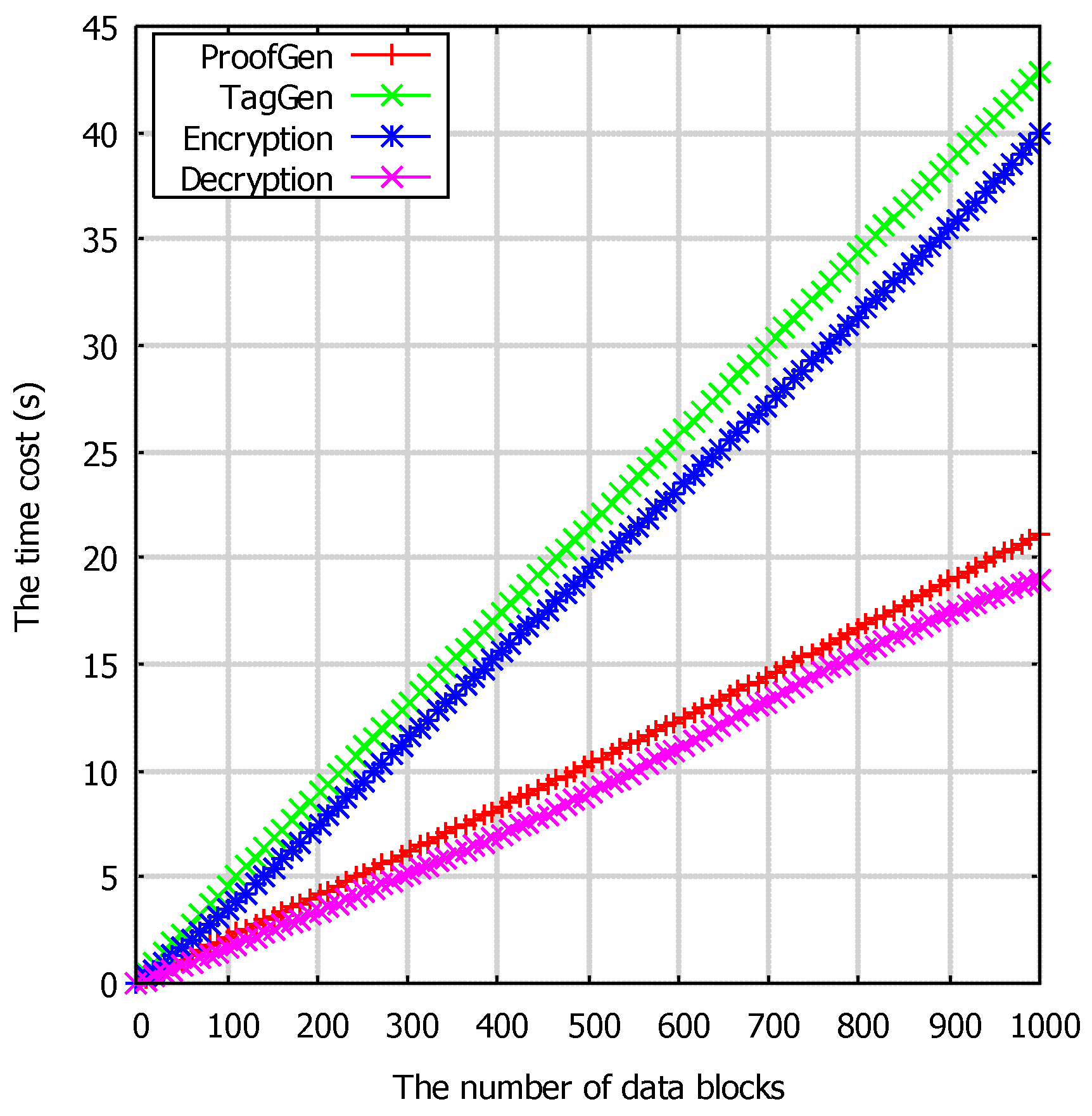
6.1. Experimental Parameters
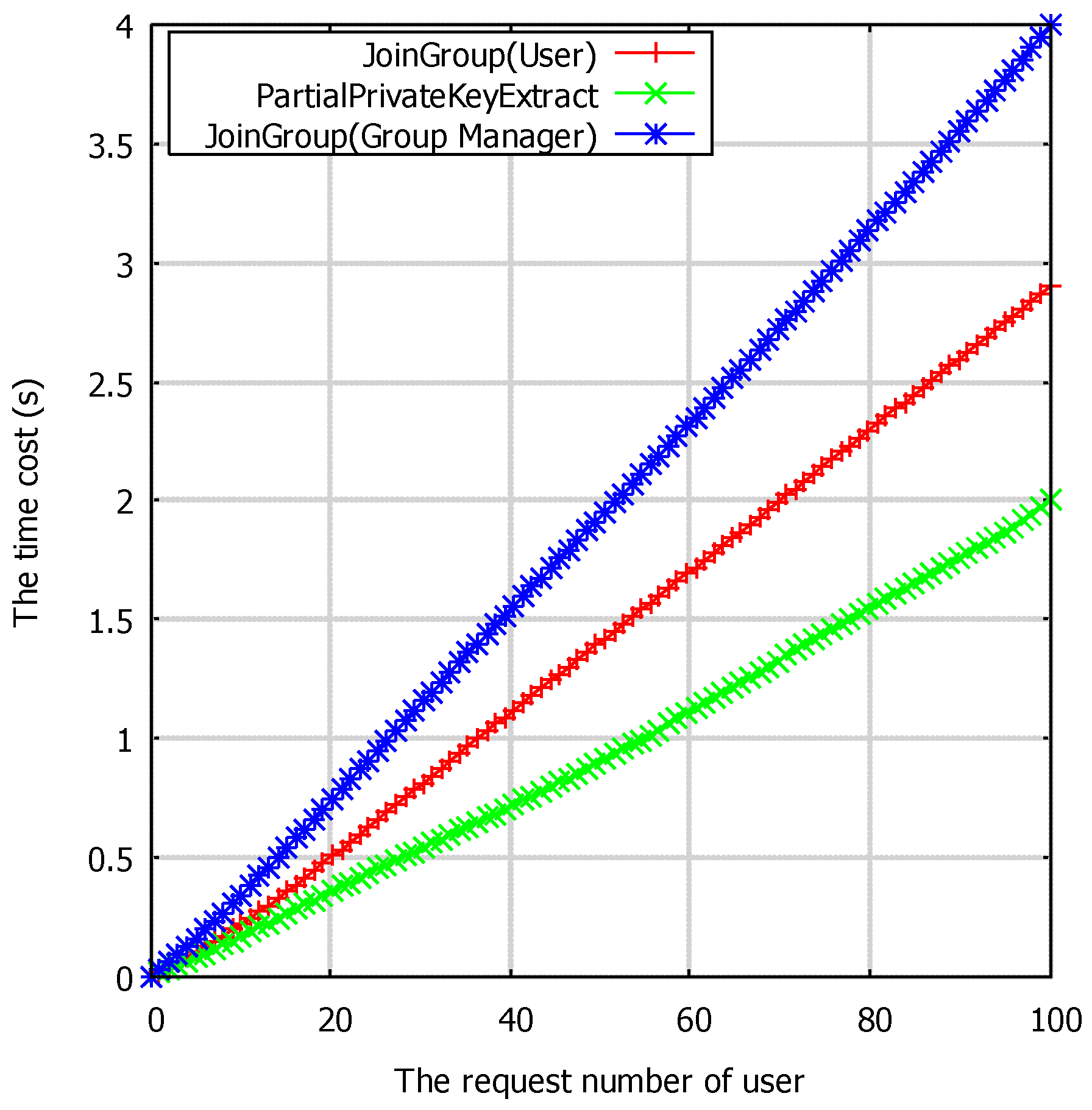
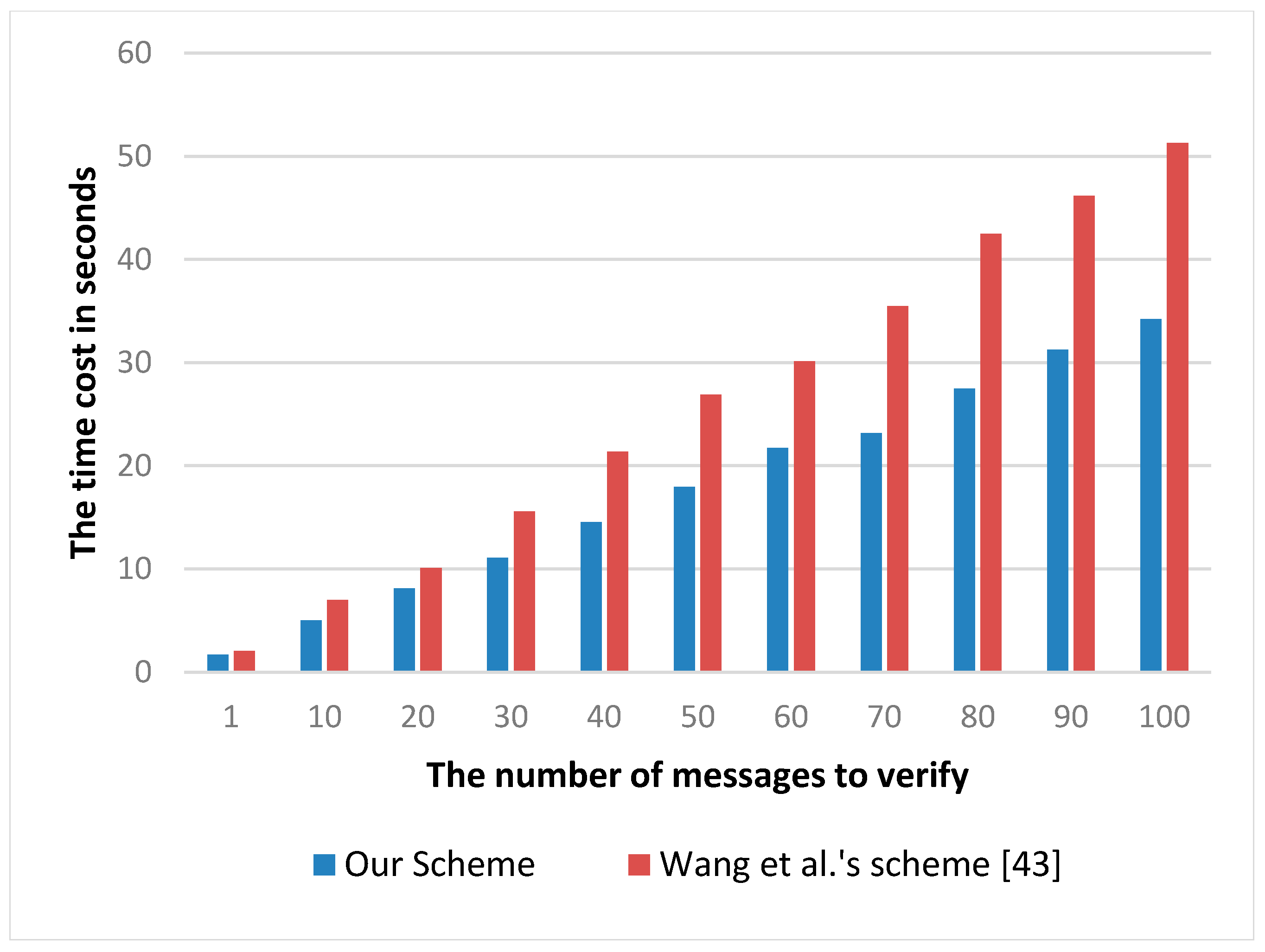
6.2. Experimental Analysis
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yick, J.; Mukherjee, B.; Ghosal, D. Wireless sensor network survey. Comput. Netw. 2008, 52, 2292–2330. [Google Scholar] [CrossRef]
- Jovanov, E.; Milenkovic, A.; Otto, C.; Groen, P.C. A wireless body area network of intelligent motion sensors for computer assisted physical rehabilitation. J. Neuro Eng. Rehabil. 2005, 2, 1–10. [Google Scholar]
- Cao, H.; Leung, V.; Chow, C.; Chan, H. Enabling technologies for wireless body area networks: A survey and outlook. IEEE Commun. Mag. 2009, 47, 84–93. [Google Scholar] [CrossRef]
- Seyedi, M.H.; Kibret, B.; Lai, D.T.H.; Faulkner, M. A survey on intrabody communications for body area network applications. IEEE Trans. Biomed. Eng. 2013, 60, 2067–2079. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Gonzalez, S.; Vasilakos, A.; Cao, H.; Leung, V.C.M. Body area networks: A survey. Mob. Net. Appl. 2011, 16, 171–193. [Google Scholar] [CrossRef]
- Lin, W.; Zhang, R.; Brittelli, J.; Lehmann, C. Wireless Infant Monitoring Device for the prevention of sudden infant death syndrome. In Proceedings of the 2014 11th International Conference & Expo on Emerging Technologies for a Smarter World, Melville, NY, USA, 29–30 October 2014. [Google Scholar]
- Shnayder, V.; Chen, B.; Lorincz, K.; Fulford-Jones, T.R.F.; Welsh, M. Sensor Networks for Medical Care. Available online: https://dash.harvard.edu/bitstream/handle/1/24829604/tr-08-05.pdf?sequence=1 (accessed on 2 May 2017).
- Ivanov, S.; Foley, C.; Balasubramaniam, S.; Botvich, D. Virtual groups for patient WBSNs monitoring in medical environment. IEEE Trans. Biomed. Eng. 2012, 59, 3238–3246. [Google Scholar] [CrossRef] [PubMed]
- Gao, T.; Massey, T.; Selavo, L.; Crawford, D.; Chen, B.; Lorincz, K.; Shnayder, V.; Hauenstein, L.; Dabiri, F.; Jeng, J.; et al. The advanced health and disaster aid network: A light-weight wireless medical system for triage. IEEE Trans. Biomed. Circuits Syst. 2007, 1, 203–216. [Google Scholar] [CrossRef] [PubMed]
- Jovanov, E.; Milenkovic, A.; Otto, C.; Groen, P.D.; Johnson, B.; Warren, S.; Taibi, G. A WBAN system for ambulatory monitoring of physical activity and health status: applications and challenges. In Proceedings of the 27th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Shanghai, China, 17–18 January 2006. [Google Scholar]
- Baronti, P.; Pillai, P.; Chook, V.W.C.; Chessa, S.; Gotta, A.; Hu, Y.F. Wireless sensor networks: A survey on the state of the art and the 802.15. 4 and ZigBee standards. Comput. Commun. 2007, 30, 1655–1695. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Wang, C.; Fang, H. Interference mitigation for cyber-physical wireless body area network system using social networks. IEEE Trans. Emerg. Top. Comput. 2013, 1, 121–132. [Google Scholar] [CrossRef] [PubMed]
- Kwak, K.S.; Ullah, S.; Ullah, N. An overview of IEEE 802.15. 6 standard. In Proceedings of the 2010 3rd International Symposium on Applied Sciences in Biomedical and Communication Technologies, Rome, Italy, 7–10 November 2010. [Google Scholar]
- Poon, C.C.Y.; Zhang, Y.T.; Bao, S.D. A novel biometrics method to secure wireless body area sensor networks for telemedicine and m-health. IEEE Commun. Mag. 2006, 44, 73–81. [Google Scholar] [CrossRef]
- Bao, S.D.; Zhang, Y.T.; Shen, L.F. Physiological signal based entity authentication for body area sensor networks and mobile healthcare systems. In Proceedings of the 2005 IEEE Engineering in Medicine and Biology 27th Annual Conference, Shanghai, China, 17–18 January 2006. [Google Scholar]
- Venkatasubramanian, K.K.; Banerjee, A.; Gupta, S.K.S. EKG-based key agreement in body sensor networks. In Proceedings of the 27th Conference on Computer Communications, Phoenix, AZ, USA, 13–18 April 2008. [Google Scholar]
- CherUKuri, S.; Venkatasubramanian, K.K.; Gupta, S.K.S. Biosec: A biometric based approach for securing communication in wireless networks of biosensors implanted in the human body. In Proceedings of the 2003 International Conference on Parallel Processing Workshops, Kaohsiung, Taiwan, 6–9 October 2003. [Google Scholar]
- Juels, A.; Sudan, M. A fuzzy vault scheme. In Proceedings of the 2002 IEEE International Symposium on Information Theory, Lausanne, Switzerland, 30 June–5 July 2002. [Google Scholar]
- Wu, L.; Yuan, S. A face based fuzzy vault scheme for secure online authentication. In Proceedings of the 2010 Second International Symposium on Data, Privacy, and E-Commerce, Buffalo, NY, USA, 13–14 September 2010. [Google Scholar]
- Meenakshi, V.S.; Padmavathi, G. Security analysis of hardened retina based fuzzy vault. In Proceedings of the 2009 International Conference on Advances in Recent Technologies in Communication and Computing, Kerala, India, 27–28 October 2009. [Google Scholar]
- Kim, A.Y.; Lee, S.H. Authentication protocol using fuzzy eigenface vault based on moc. In Proceedings of the 9th International Conference on Advanced Communication Technology, Okamoto, Japan, 12–14 Februry 2007. [Google Scholar]
- Venkatasubramanian, K.K.; Banerjee, A.; Gupta, S.K.S. PSKA: USAble and secure key agreement scheme for body area networks. IEEE Trans. Inf. Technol. Biomed. 2010, 14, 60–68. [Google Scholar] [CrossRef] [PubMed]
- Miao, F.; Bao, S.D.; Li, Y. A modified fuzzy vault scheme for biometrics-based body sensor networks security. In Proceedings of the 2010 IEEE Global Telecommunications Conference, Miami, FL, USA, 6–10 December 2010. [Google Scholar]
- Liu, H.; Sun, D.; Xiong, K.; Qiu, Z. A new fuzzy vault method using cubic spline interpolation. In Proceedings of the 2010 International Conference on Artificial Intelligence and Computational Intelligence, Sanya, China, 23–24 October 2010. [Google Scholar]
- Dodis, Y.; Reyzin, L.; Smith, A. Fuzzy extractors: How to generate strong keys from biometrics and other noisy data. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2–6 May 2004. [Google Scholar]
- Biel, L.; Pettersson, O.; Philipson, L.; Wide, P. ECG analysis: A new approach in human identification. IEEE Trans. Instrum. Meas. 2001, 50, 808–812. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Vasilakos, A.V.; Fang, H. ECG-cryptography and authentication in body area networks. IEEE Trans. Inf. Technol. Biomed. 2012, 16, 1070–1078. [Google Scholar] [CrossRef] [PubMed]
- Shamir, A. Identity-based cryptosystems and signature schemes. In Proceedings of the Workshop on the Theory and Application of Cryptographic Techniques, Paris, France, 9–11 April 1984. [Google Scholar]
- Al-Riyami, S.S.; Paterson, K.G. Certificateless public key cryptography. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Taipei, Taiwan, 30 November–4 December 2003. [Google Scholar]
- Liu, J.; Zhang, Z.; Chen, X.; Kwak, K.S. Certificateless remote anonymous authentication schemes for wirelessbody area networks. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 332–342. [Google Scholar] [CrossRef]
- Zhao, Z. An efficient anonymous authentication scheme for wireless body area networks using elliptic curve cryptosystem. J. Med. Syst. 2014, 38, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Zhang, Y. New authentication scheme for wireless body area networks using the bilinear pairing. J. Med. Syst. 2015, 39, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Xiong, H. Cost-effective scalable and anonymous certificateless remote authentication protocol. IEEE Trans. Inf. Forensics Secur. 2014, 9, 2327–2339. [Google Scholar] [CrossRef]
- Xiong, H.; Qin, Z. Revocable and scalable certificateless remote authentication protocol with anonymity for wireless body area networks. IEEE Trans. Inf. Forensics Secur. 2015, 10, 1442–1455. [Google Scholar] [CrossRef]
- Zhou, J.; Cao, Z.; Dong, X.; Xiong, N.; Vasilakosd, A.V. 4S: A secure and privacy-preserving key management scheme for cloud-assisted wireless body area network in m-healthcare social networks. Inf. Sci. 2015, 314, 255–276. [Google Scholar] [CrossRef]
- Lu, R.; Lin, X.; Shen, X. SPOC: A secure and privacy-preserving opporTunistic computing framework for mobile-healthcare emergency. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 614–624. [Google Scholar] [CrossRef]
- Lee, C.C.; Hsu, C.W.; Lai, Y.M.; Vasilakos, A. An enhanced mobile-healthcare emergency system based on extended chaotic maps. J. Med. Syst. 2013, 37, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Yi, X.; Bouguettaya, A.; Georgakopoulos, D.; Song, A.; Willemson, J. Privacy protection for wireless medical sensor data. IEEE Trans. Dependable Secur. Comput. 2016, 13, 369–380. [Google Scholar] [CrossRef]
- Wan, J.; Zou, C.; Ullah, S.; Lai, C.F.; Zhou, M.; Wang, X. Cloud-enabled wireless body area networks for pervasive healthcare. IEEE Netw. 2013, 27, 56–61. [Google Scholar] [CrossRef]
- Han, N.D.; Han, L.; Tuan, D.M.; In, H.P.; Jo, M. A scheme for data confidentiality in Cloud-assisted Wireless Body Area Networks. Inf. Sci. 2014, 284, 157–166. [Google Scholar] [CrossRef]
- He, D.; Zeadally, S.; Wu, L. Certificateless public auditing scheme for cloud-assisted wireless body area networks. IEEE Syst. J. 2015, 99, 1–10. [Google Scholar] [CrossRef]
- Li, S.; Zhong, H.; Cui, J. Public auditing scheme for cloud-based wireless body area network. In Proceedings of the 9th International Conference on Utility and Cloud Computing, Shanghai, China, 6–9 December 2016. [Google Scholar]
- Wang, B.; Li, B.; Li, H.; Li, F. Certificateless public auditing for data integrity in the cloud. In Proceedings of the 2013 IEEE Conference on Communications and Network Security, National Harbor, MD, USA, 14–16 October 2013. [Google Scholar]
- Miller, V.S. Use of elliptic curves in cryptography. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Linz, Austria, 9–11 April 1985. [Google Scholar]
- Koblitz, N. Elliptic curve cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Gura, N.; Patel, A.; Wander, A.; Eberle, H.; Shantz, S.H. Comparing elliptic curve cryptography and RSA on 8-bit CPUs. In Proceedings of the International Workshop on Cryptographic Hardware and Embedded Systems, Cambridge, MA, USA, 11–13 August 2004. [Google Scholar]
- Hoffstein, J.; Pipher, J.; Silverman, J.H. An Introduction to Mathematical Cryptography; Springer: New York, NY, USA, 2008. [Google Scholar]
- Bos, J.W.; Halderman, J.A.; Heninger, N.; Moore, J.; Naehrig, M.; Wustrow, E. Elliptic curve cryptography in practice. In Proceedings of the International Conference on Financial Cryptography and Data Security, Christ Church, Barbados, 3–7 March 2014. [Google Scholar]
- Caro, A.D.; Iovino, V. jPBC: Java pairing based cryptography. In Proceedings of the Sixteenth IEEE symposium on Computers and Communications, Kerkyra, Greece, 28 June–1 July 2011. [Google Scholar]
| Symbol | The Meaning of the Symbol |
|---|---|
| l | A security parameter |
| q | A large prime number q > 2l |
| e | A bilinear pairing e: G1 × G1 → G2 |
| sKGC | The master key |
| QKGC | The public key of KGC |
| IDU | The identity of user |
| PKU,2 | The partial public key generated by user self |
| PKU,1 | The partial public key generated by KGC |
| SKU,2 | The partial secret key generated by user self |
| SKU,1 | The partial secret key generated by KGC |
| xg | The group shared encryption key |
| LG | The group member list |
| h1 | The hash functions {{0,1}*, G1} → Zq* |
| h2 | The hash functions {{0,1}*, {0,1}*,G1, G1} → Zq* |
| H | The hash functions {0,1}* → G1 |
| Property | Wang et al.’s Scheme [43] | He et al.’s Scheme [41] | Our Scheme |
|---|---|---|---|
| Public verifiability | √ | √ | √ |
| Multi-user sharing | × | × | √ |
| Revocability | N/A | N/A | √ |
| Forward security | √ | √ | √ |
| Privacy protection | × | × | √ |
| Batch authentication | √ | √ | √ |
| Proven security | √ | √ | √ |
| Key replacement resistant | × | √ | √ |
| PartialPrivateKeyExtract | JoinGroup (Group Manager) | JoinGroup (User) | Encryption | TagGen | ProofGen | ProofVerify | Decryption |
|---|---|---|---|---|---|---|---|
| 1 PM + 1 H | 2 PM | 1 PM | 2 PM | 2n PM + n H | n PM | 2E + (n + 3) PM + n H | 1 PM |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Cui, J.; Zhong, H.; Liu, L. Public Auditing with Privacy Protection in a Multi-User Model of Cloud-Assisted Body Sensor Networks. Sensors 2017, 17, 1032. https://doi.org/10.3390/s17051032
Li S, Cui J, Zhong H, Liu L. Public Auditing with Privacy Protection in a Multi-User Model of Cloud-Assisted Body Sensor Networks. Sensors. 2017; 17(5):1032. https://doi.org/10.3390/s17051032
Chicago/Turabian StyleLi, Song, Jie Cui, Hong Zhong, and Lu Liu. 2017. "Public Auditing with Privacy Protection in a Multi-User Model of Cloud-Assisted Body Sensor Networks" Sensors 17, no. 5: 1032. https://doi.org/10.3390/s17051032
APA StyleLi, S., Cui, J., Zhong, H., & Liu, L. (2017). Public Auditing with Privacy Protection in a Multi-User Model of Cloud-Assisted Body Sensor Networks. Sensors, 17(5), 1032. https://doi.org/10.3390/s17051032







