A New Method for Single-Epoch Ambiguity Resolution with Indoor Pseudolite Positioning
Abstract
:1. Introduction
2. Method Introduction
2.1. DD Observation Equation with Pseudolite System
2.2. Ambiguity Function Method Overview
2.3. Improved Ambiguity Function Method
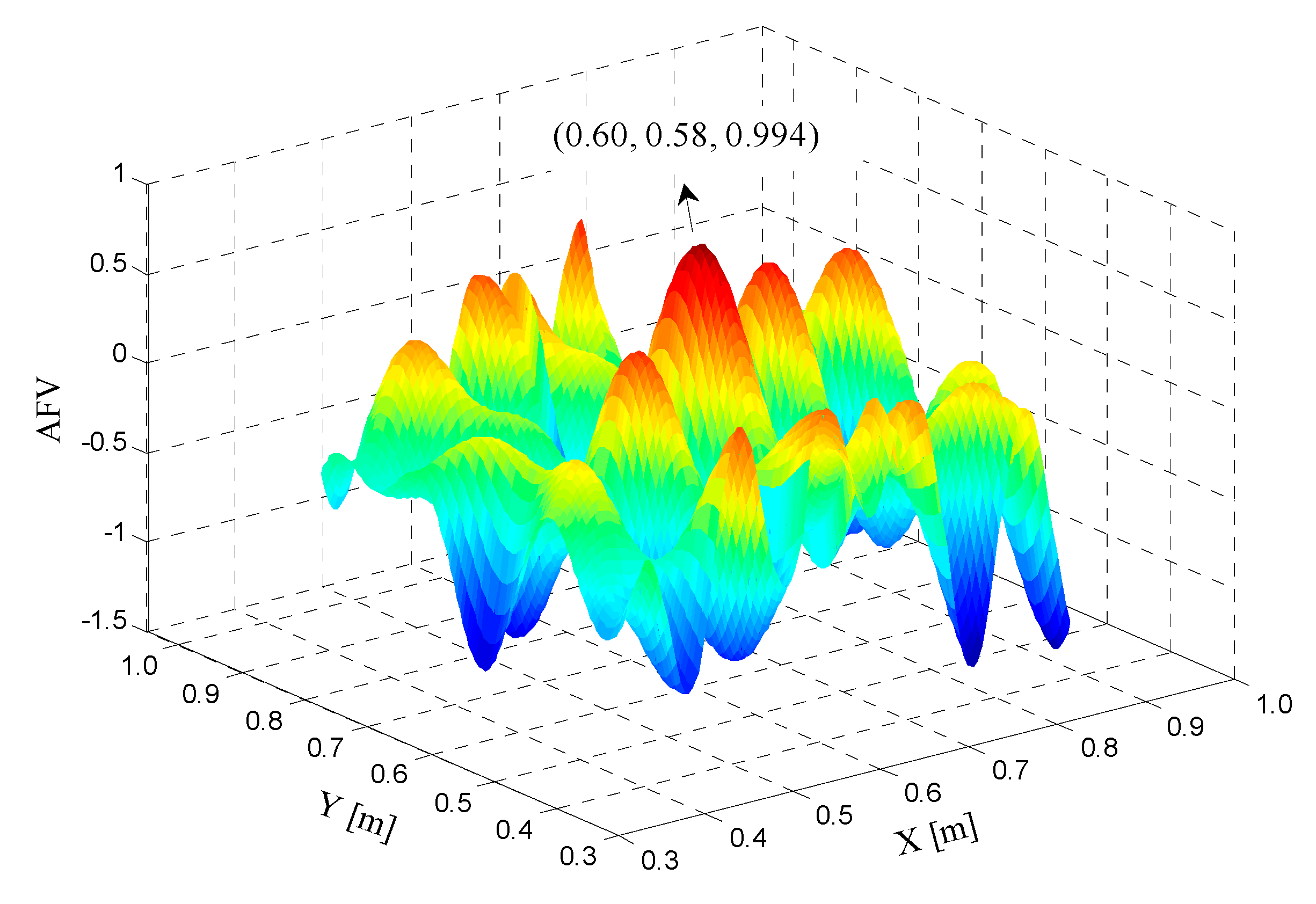
2.3.1. Extended AFM with IPSO for Improving Efficiency
- (1)
- Parameter setting: , , , .
- (2)
- In the search space with a given coordinate domain, generate 60 initial particles at a random distribution (include position and speed). According to Equation (3), calculate the fitness function value of every particle and make a fitness evaluation. The larger the AFV is, the higher the fitness value.
- (3)
- Update the and based on the result of the fitness evaluation above.
- (4)
- Update the position and speed for every particle according to Equation (4).
- (5)
- Based on the fitness function value, divide the population into three groups, namely, the optimal, suboptimal, and poor population . According to Equation (5), make a Gauss mutation for .
- (6)
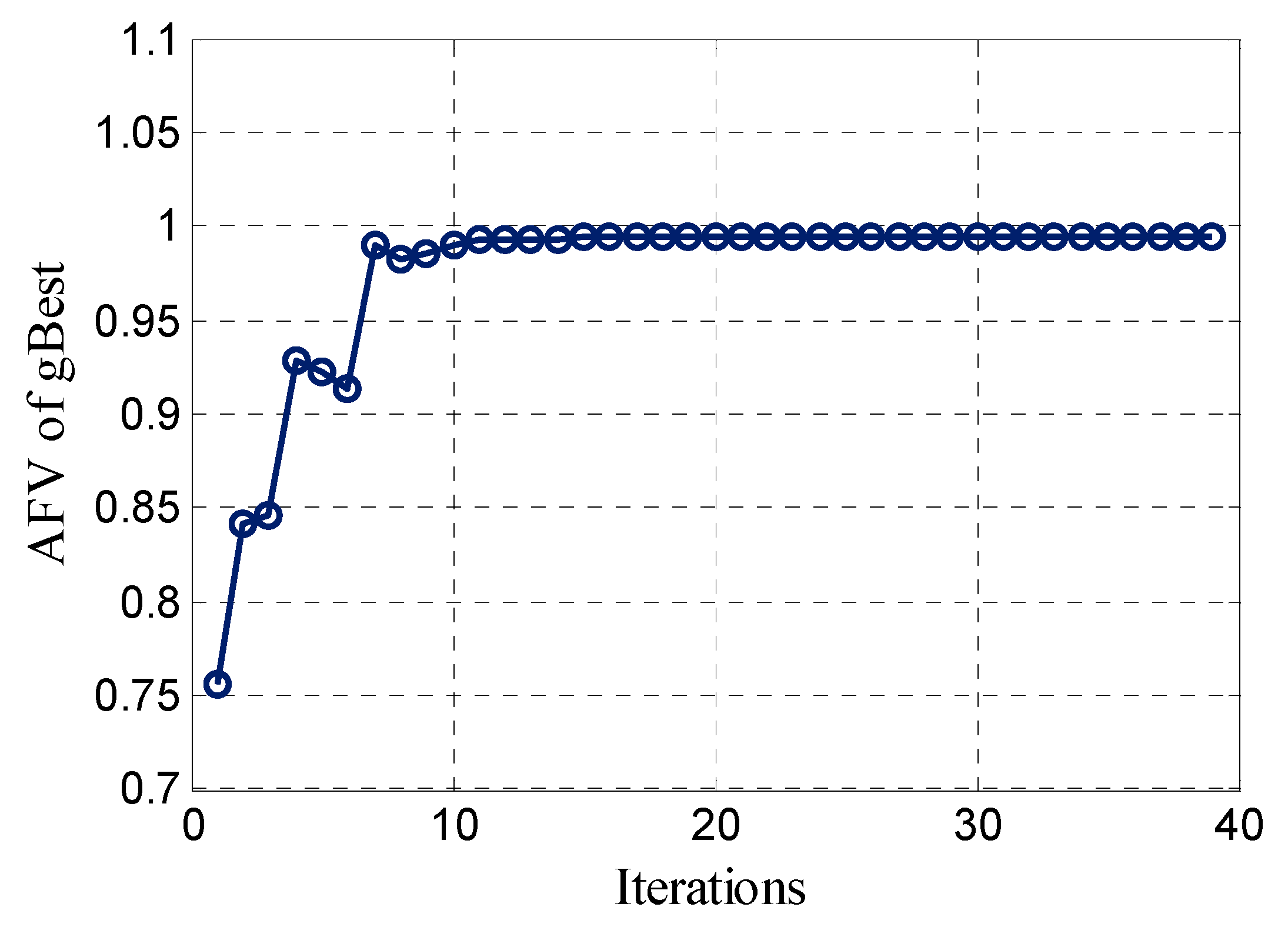
- If the global optimal value or its corresponding fitness function value difference between the last two iterations is less than a certain threshold, exit the iteration; otherwise, repeat steps (2) to (5).
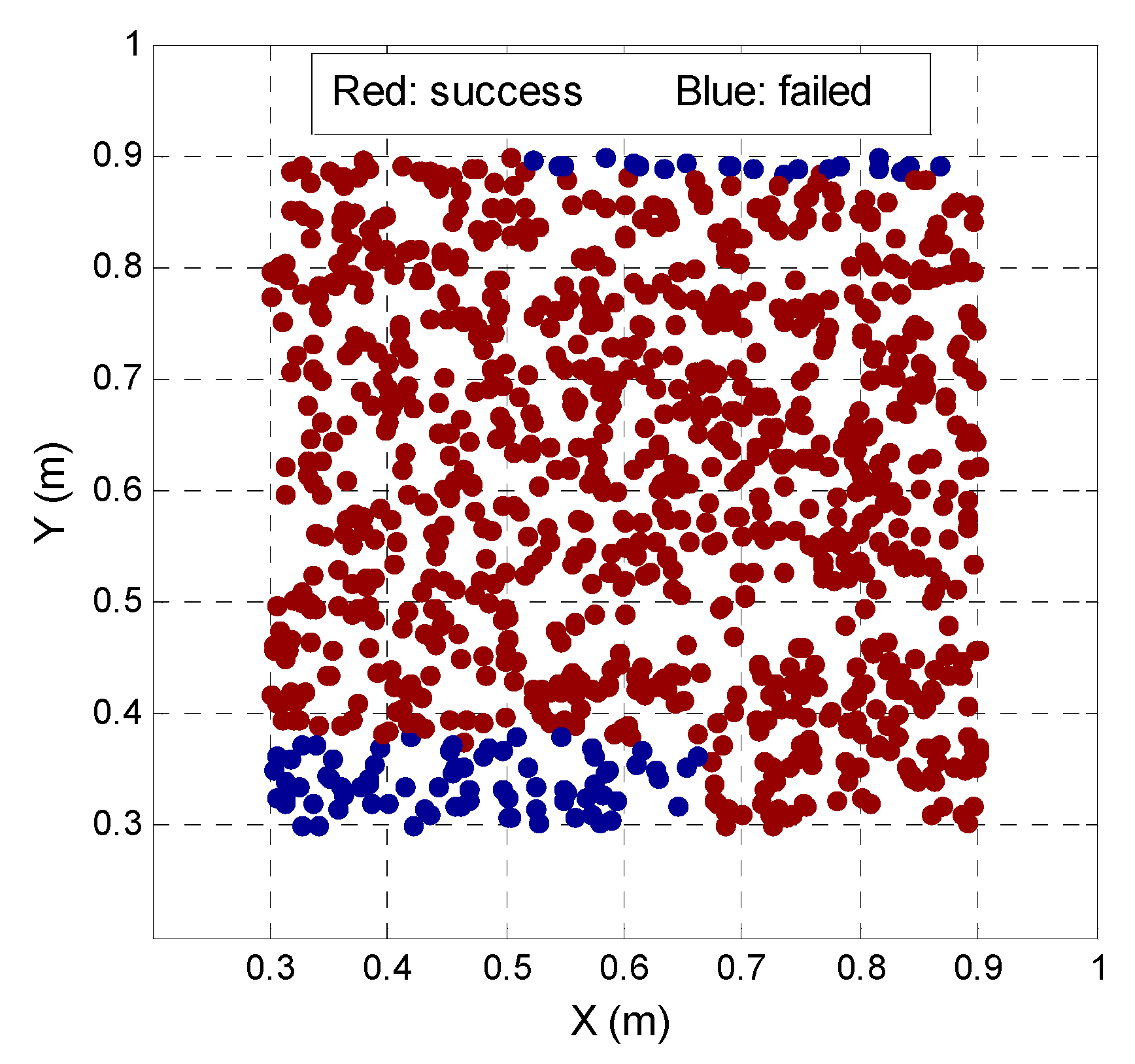
2.3.2. Strategies for Improving AFM Reliability
3. Results and Analysis
3.1. Experimental Platform
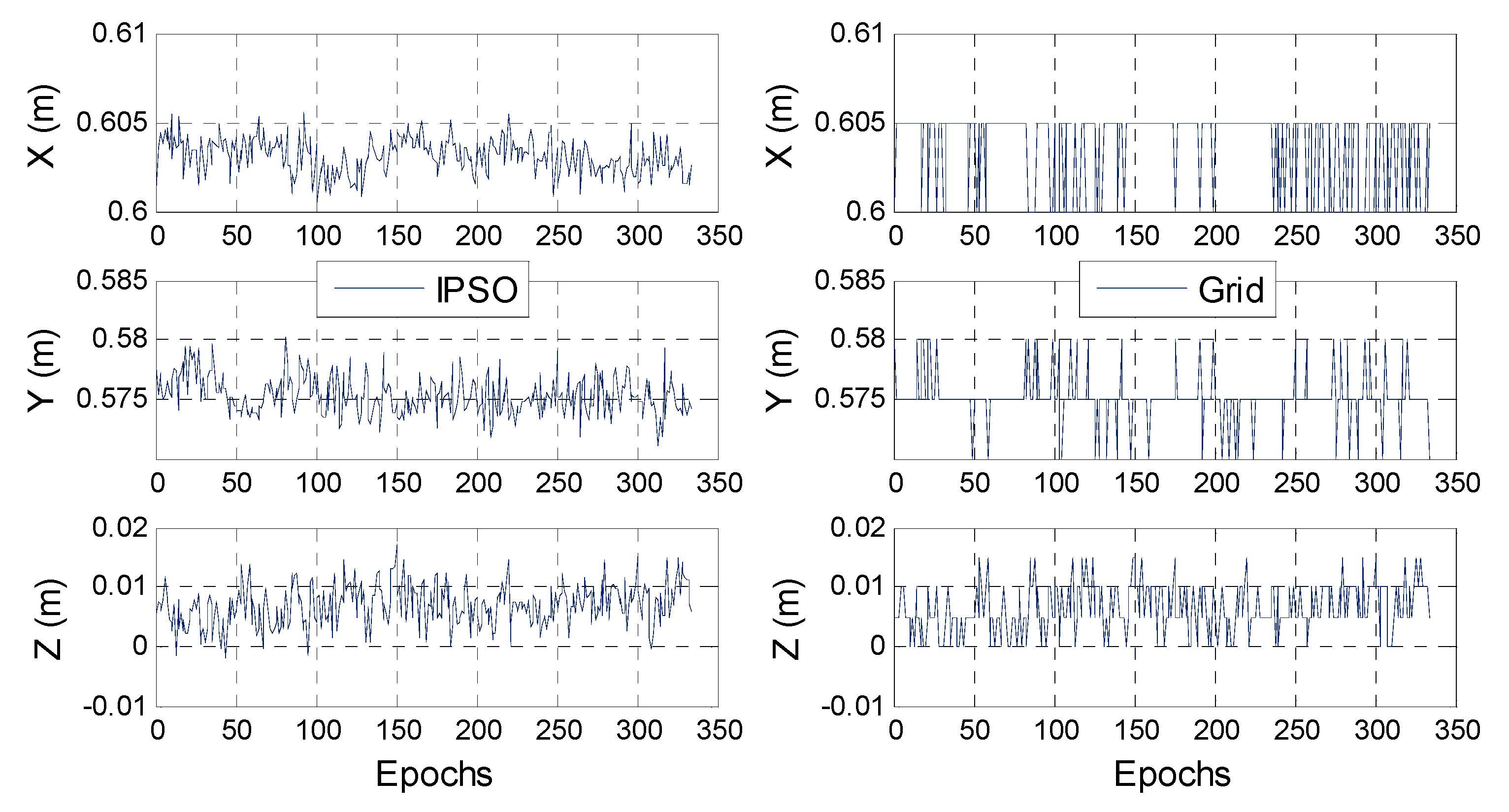
3.2. Performance Analysis of the Proposed AR Method with Pseudolite System
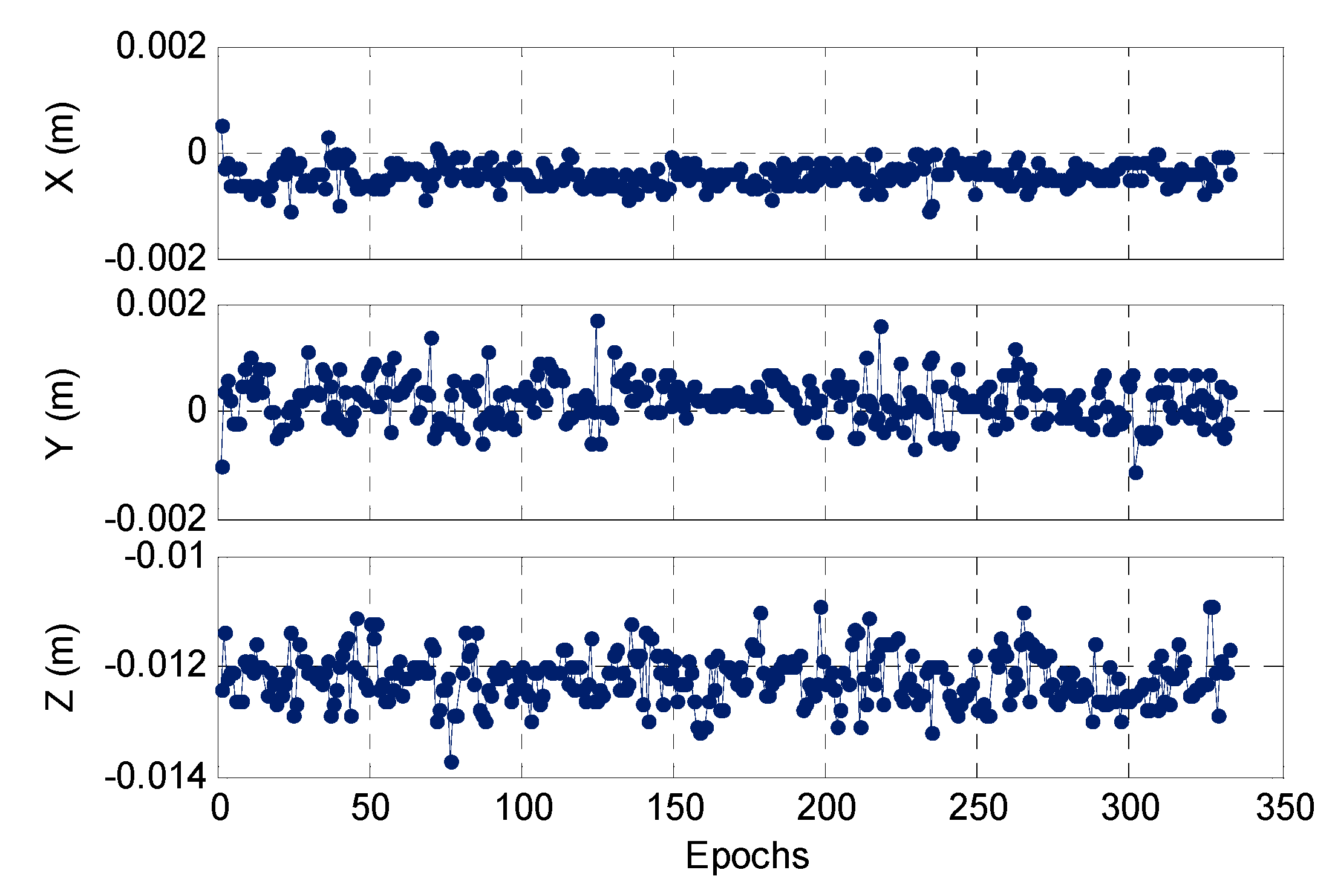
3.2.1. Static Test
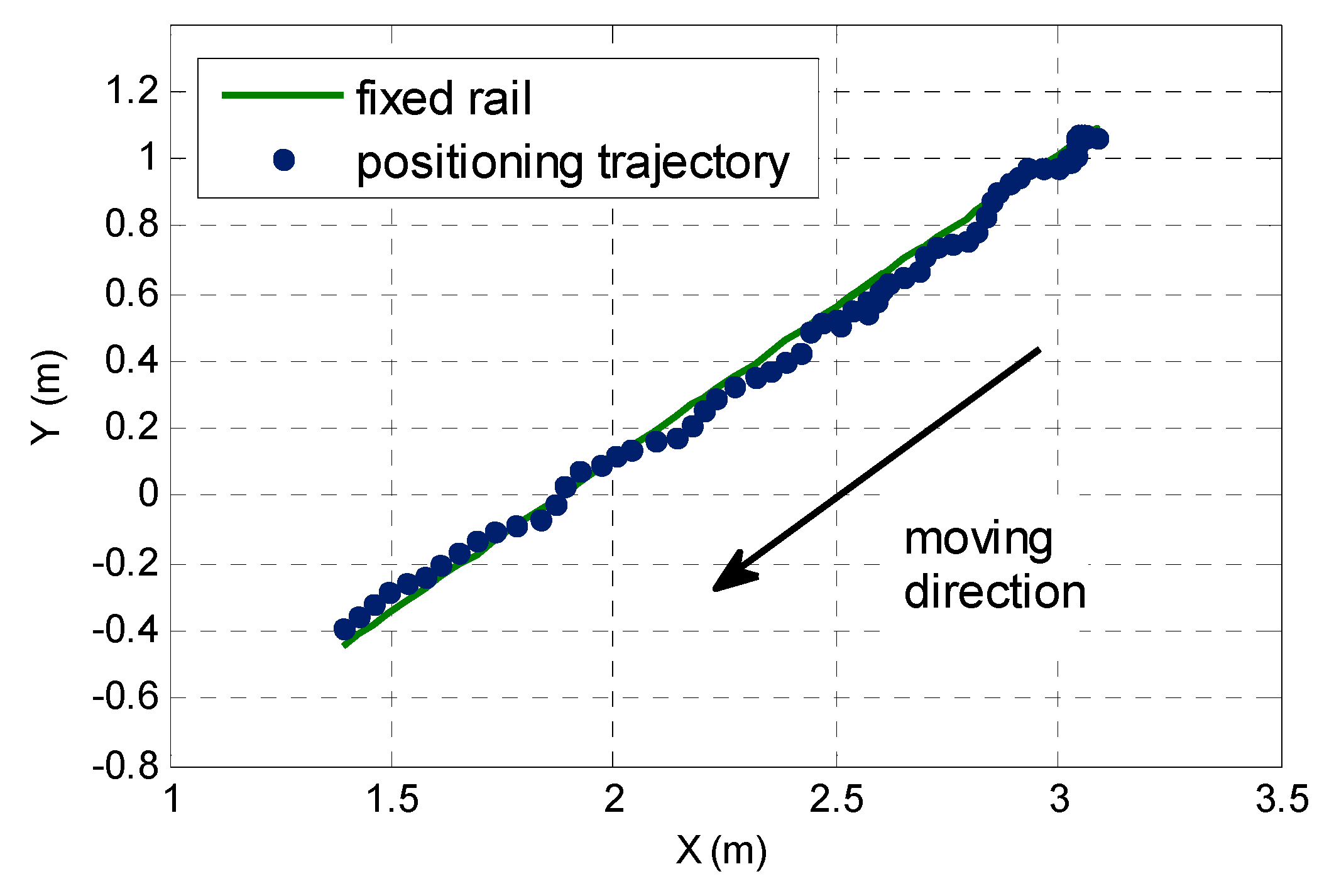
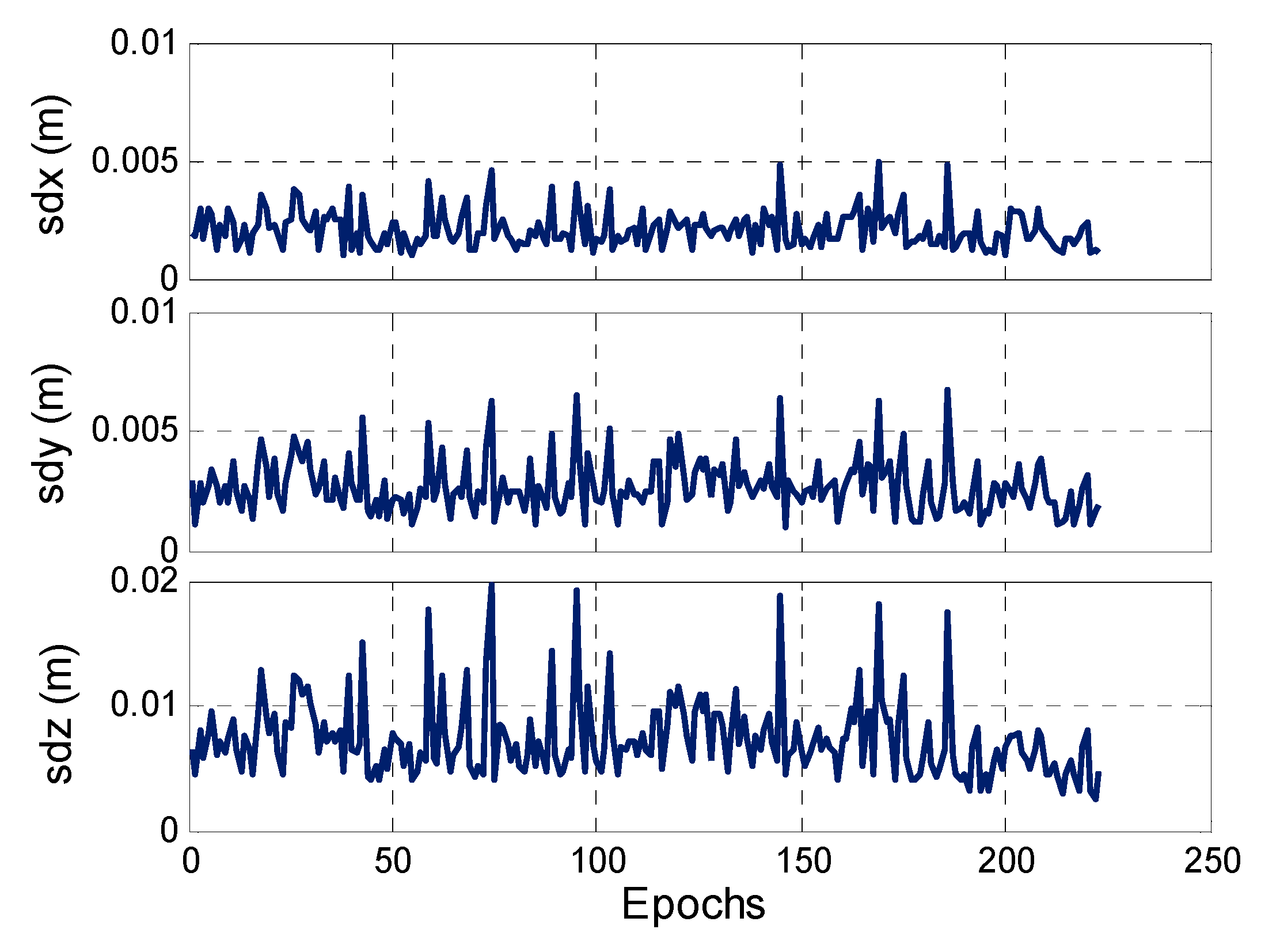
3.2.2. Kinematic Test
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Collins, J. Global Positioning System: Theory and Practice, 5th ed.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 43–50. [Google Scholar]
- Wang, J. Pseudolite Applications in Positioning and Navigation Progress and Problems. J. Glob. Position. Syst. 2002, 1, 48–56. [Google Scholar] [CrossRef]
- Rizos, C.; Barnes, J.; Small, D.; Voigt, G.; Gambale, N. A New Pseudolite-Based Positioning Technology for High Precision Indoor and Outdoor Positioning. In Proceedings of the International Symposium and Exhibition on Geoinformation, Shah Alam, Malaysia, 13–14 October 2003. [Google Scholar]
- Dai, L.; Wang, J.; Rizos, C.; Han, S. Pseudo-Satellite Applications in Deformation Monitoring. GPS Solut. 2002, 5, 80–87. [Google Scholar] [CrossRef]
- Kim, C.; So, H.; Lee, T.; Kee, C. A pseudolite-based positioning system for legacy GNSS receivers. Sensors 2014, 14, 6104–6123. [Google Scholar] [CrossRef] [PubMed]
- Xu, R.; Chen, W.; Xu, Y.; Ji, S. A new indoor positioning system architecture using GPS signals. Sensors 2015, 15, 10074–10087. [Google Scholar] [CrossRef] [PubMed]
- Rizos, C.; Roberts, G.; Barnes, J.; Gambale, N. Experimental results of Locata: A high accuracy indoor positioning system. In Proceedings of the 2010 International Conference on Indoor Positioning and Indoor Navigation, Zurich, Switzerland, 15−17 September 2010. [Google Scholar]
- Kurz, O.; Mongrédien, C.; Rohmer, G. A New Multipath Detection and Mitigation Approach for Pseudolite Systems. In Proceedings of the 26th International Technical Meeting of the ION Satellite Division (ION GNSS+ 2013), Nashville, TN, USA, 16–20 September 2013. [Google Scholar]
- Zhang, P.; Sun, F.; Xu, Y.; Wang, J. Indoor Pseudolite Positioning Based on Interferometric Measurement of Carrier Phase. In China Satellite Navigation Conference (CSNC) 2016 Proceedings: Volume I, Changsha, China, 18–20 May 2016; Sun, J., Liu, J., Fan, S., Wang, F., Eds.; Springer: Singapore, 2016. [Google Scholar]
- Wan, X.; Zhai, C.; Zhan, X. The pseudolite-based indoor navigation system using Ambiguity Resolution on the Fly. In Proceedings of the 3rd International Symposium on Systems and Control in Aeronautics and Astronautics, Harbin, China, 8–10 June 2010; pp. 212–217. [Google Scholar]
- Gioia, C.; Borio, D. Stand-alone and hybrid positioning using asynchronous pseudolites. Sensors 2014, 15, 166–193. [Google Scholar] [CrossRef] [PubMed]
- Borio, D.; Gioia, C.; Baldini, G. Asynchronous pseudolite navigation using C/N0 measurements. J. Navig. 2015, 1, 1–20. [Google Scholar] [CrossRef]
- Dai, L.; Zhang, J.; Rizos, C.; Han, S.; Wang, J. GPS and pseudolite integration for deformation monitoring applications. In Proceedings of the 13th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 2000), Salt Lake City, UT, USA, 19–22 September 2000; pp. 1–8. [Google Scholar]
- Kee, C.; Kim, J.; So, H.; Jun, H.; Parkinson, B.; Hansen, W.W. Effect of the error in line of sight unit vector on the accuracy of GPS and pseudolite navigation system. Comput. Math. Appl. 2004, 48, 779–787. [Google Scholar] [CrossRef]
- Nie, Z.; Wang, Z.; Ou, J.; Ji, S. On the Effect of Linearization and Approximation of Nonlinear Baseline Length Constraint for Ambiguity Resolution. Acta Geod. Cartograph. Sin. 2015, 44, 168–173. [Google Scholar]
- Fujii, K.; Sakamoto, Y.; Wang, W.; Arie, H.; Schmitz, A.; Sugano, S. Hyperbolic positioning with antenna arrays and multi-channel pseudolite for indoor localization. Sensors 2015, 15, 25157–25175. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Langley, R.B. GPS Ambiguity Resolution and Validation: Methodologies, Trends and Issues. In Proceedings of the 7th GNSS Workshop—International Symposium on GPS/GNSS, Seoul, Korea, 30 November–2 December 2000. [Google Scholar]
- Teunissen, P.J.G. Least-Squares Estimation of the Integer GPS ambiguities. Invited Lecture, Section IV Theory and Methodology. In Proceedings of the IAG General Meeting, Beijing, China, 6–13 August 1993. [Google Scholar]
- Teunissen, P.J.G. The least-squares ambiguity decorrelation adjustment: a method for fast GPS integer ambiguity estimation. J. Géod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- De Jonge, P.J.; Tiberius, C. The LAMBDA Method for Integer Ambiguity Estimation: Implementation Aspects; No. 12 of LGR-Series; Delft Geodetic Computing Centre: Delft, The Netherlands, 1996. [Google Scholar]
- Verhagen, S.; Li, B.; Teunissen, P.J.G. Ps-LAMBDA: Ambiguity success rate evaluation software for interferometric applications. Comput. Geosci. 2013, 54, 361–376. [Google Scholar] [CrossRef]
- Chang, X.; Yang, X.; Zhou, T. MLAMBDA: A modified LAMBDA method for integer least-squares estimation. J. Géod. 2005, 79, 552–565. [Google Scholar] [CrossRef]
- Wan, X.G.; Zhan, X.Q.; Du, G. Carrier Phase Method for Indoor Pseudolite Positioning System. Appl. Mech. Mater. 2011, 130–134, 2064–2067. [Google Scholar] [CrossRef]
- Li, T.; Wang, J.; Huang, J. Analysis of ambiguity resolution in precise pseudolite positioning. In Proceedings of the 2012 International Conference on Indoor Positioning and Indoor Navigation, Sydney, Australia, 13–15 November 2012; pp. 1–7. [Google Scholar]
- Counselman, C.C.; Gourevitch, S.A. Miniature interferometer terminals for earth surveying: Ambiguity and multipath with Global Positioning System. IEEE Trans. Geosci. Remote Sens. 1981, GE-19, 244–252. [Google Scholar] [CrossRef]
- Remondi, B.W. Pseudo-kinematic GPS results using the ambiguity function method. Navigation 1991, 38, 17–36. [Google Scholar] [CrossRef]
- Mader, G.L. Ambiguity function techniques for GPS phase initialization and kinematic solutions. In Proceedings of the 2nd International Symposium on Precise Positioning with the Global Positioning System, Ottawa, ON, Canada, 3–7 September 1990. [Google Scholar]
- Han, S.; Rizos, C. Improving the computational efficiency of the ambiguity function algorithm. J. Géod. 1996, 70, 330–341. [Google Scholar] [CrossRef]
- Han, S. Ambiguity function method with constrained conditions and its application in GPS kinematic positioning. J. Wuhan Tech. Univ. Surv. Mapp. 1994, 19, 7–14. [Google Scholar]
- Rinen, A.; Oja, E. A fast fixed-point algorithm for independent component analysis. Neural Comput. 2000, 10, 1–8. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the 1995 IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Clerc, M.; Kennedy, J. The particle swarm—Explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evol. Comput. 2010, 6, 58–73. [Google Scholar] [CrossRef]
- Van den Bergh, F.; Engelbrecht, A.P. A study of particle swarm optimization particle trajectories. Inf. Sci. 2006, 176, 937–971. [Google Scholar] [CrossRef]
- Liang, J.J.; Qin, A.K.; Suganthan, P.N.; Baskar, S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evol. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]
- Eling, C.; Zeimetz, P.; Kuhlmann, H. Single-Epoch Ambiguity Resolution for kinematic GNSS Positioning. In Proceedings of the 3rd International Conference on Machine Control & Guidance, Stuttgart, Germany, 27–29 March 2012. [Google Scholar]
- Hedgecock, W.; Maroti, M.; Ledeczi, A.; Volgyesi, P.; Banalagay, R. Accurate real-time relative localization using single-frequency GPS. In Proceedings of the 12th ACM Conference on Embedded Network Sensor Systems, Memphis, TN, USA, 3–6 November 2014. [Google Scholar]
- Eling, C.; Zeimetz, P.; Kuhlmann, H. Development of an instantaneous GNSS/MEMS attitude determination system. GPS Solut. 2013, 17, 129–138. [Google Scholar] [CrossRef]
- Zhao, X.; Wei, J.; Zhai, L.; Liu, H. Improved ambiguity function method based on analytical resolution for GPS attitude determination. Meas. Sci. Technol. 2007, 18, 2985–2990. [Google Scholar]
- Cellmer, S.; Wielgosz, P.; Rzepecka, Z. Modified ambiguity function approach for GPS carrier phase positioning. J. Géod. 2010, 84, 267–275. [Google Scholar] [CrossRef]
- Hatch, R.R. Pseudolite-Aided Method for Precision Kinematic Positioning. U.S. Patent 5,177,489, 5 January 1993. [Google Scholar]
- Cobb, H.S. GPS pseudolites: Theory, design, and applications. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1997. [Google Scholar]
- Chen, H.; Li, S.; Liu, J.; Liu, F.; Suzuki, M. A Novel Modification of PSO Algorithm for SML Estimation of DOA. Sensors 2016, 16, 2188. [Google Scholar] [CrossRef] [PubMed]
- Dong, N.; Wu, C.H.; Ip, W.H.; Chen, Z.Q.; Chan, C.Y.; Yung, K.L. An opposition-based chaotic GA/PSO hybrid algorithm and its application in circle detection. Comput. Math. Appl. 2012, 64, 1886–1902. [Google Scholar] [CrossRef]
- Xu, S.H.; Liu, J.P.; Zhang, F.H.; Wang, L.; Sun, L.J. A Combination of Genetic Algorithm and Particle Swarm Optimization for Vehicle Routing Problem with Time Windows. Sensors 2015, 15, 21033–21053. [Google Scholar] [CrossRef] [PubMed]
- Pluhacek, M.; Senkerik, R.; Davendra, D.; Kominkova Oplatkova, Z.; Zelinka, I. On the behavior and performance of chaos driven PSO algorithm with inertia weight. Comput. Math. Appl. 2013, 66, 22–134. [Google Scholar] [CrossRef]
- Ren, Z.H. New adaptive particle swarm optimization algorithm with dynamically changing inertia weight. Comput. Sci. 2009, 2, 227–229. [Google Scholar]
- Shi, X.H.; Liang, Y.C.; Lee, H.P.; Lu, C.; Wang, L.M. An improved GA and a novel PSO-GA-based hybrid algorithm. Inf. Process. Lett. 2005, 93, 255–261. [Google Scholar] [CrossRef]
- Higashi, N.; Iba, H. Particle swarm optimization with Gaussian mutation. In Proceedings of the 2003 IEEE Swarm Intelligence Symposium (Sis ’03), Indianapolis, IN, USA, 24–26 April 2003; pp. 72–79. [Google Scholar]
- Kubo, N. Advantage of velocity measurements on instantaneous RTK positioning. GPS Solut. 2009, 13, 271–280. [Google Scholar] [CrossRef]
- Freda, P.; Angrisano, A.; Gaglione, S.; Troisi, S. Time-differenced carrier phases technique for precise GNSS velocity estimation. GPS Solut. 2015, 19, 335–341. [Google Scholar] [CrossRef]




| ICB (m) | LAMBDA Method (Ratio Threshold: 3) | Proposed AR Method | ||||
|---|---|---|---|---|---|---|
| Best Candidate (✓/×) | Ratio | Success (Y/N) | Time (ms) | Success (Y/N) | Time (ms) | |
| 0.05 | ✓ | 4.6 | Y | 2 | Y | 23 |
| 0.10 | ✓ | 2.3 | N | 2 | Y | 22 |
| 0.15 | × | 1.6 | N | 2 | Y | 25 |
| 0.20 | × | 1.5 | N | 2 | Y | 26 |
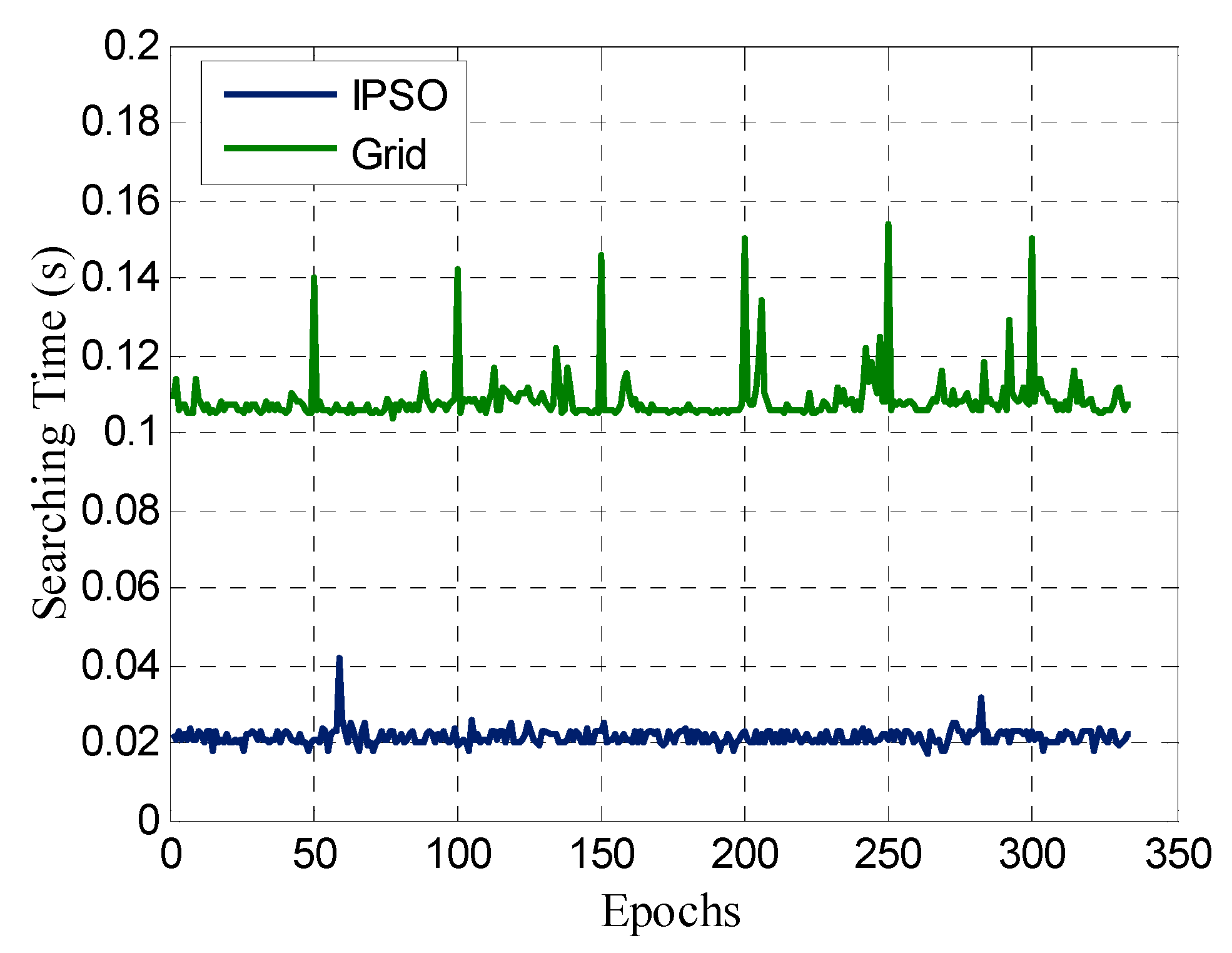
| IPSO | Grid | |||
|---|---|---|---|---|
| Search Step (m) | ||||
| Search Space (m) | / | 0.01 | 0.005 | 0.001 |
| 0.1 | 0.0211 | 0.0154 | 0.1486 | 13.9678 |
| 0.2 | 0.0265 | 0.1166 | 0.8923 | / |
| 0.3 | 0.0343 | 0.3809 | 3.0126 | / |
| Initial Coordinates | Total Epochs | Pseudolites Number | PDOP | |
|---|---|---|---|---|
| Point #1 | (0.6, −0.6, 0.01) | 545 | 5 | 3.5 |
| Point #2 | (0.6, −1.2, 0.01) | 536 | 4 | 4.1 |
| Point #3 | (0.0, 0.0, 0.01) | 342 | 5 | 3.1 |
| Point #4 | (0.0, 0.6, 0.01) | 298 | 5 | 3.2 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhang, P.; Guo, J.; Wang, J.; Qiu, W. A New Method for Single-Epoch Ambiguity Resolution with Indoor Pseudolite Positioning. Sensors 2017, 17, 921. https://doi.org/10.3390/s17040921
Li X, Zhang P, Guo J, Wang J, Qiu W. A New Method for Single-Epoch Ambiguity Resolution with Indoor Pseudolite Positioning. Sensors. 2017; 17(4):921. https://doi.org/10.3390/s17040921
Chicago/Turabian StyleLi, Xin, Peng Zhang, Jiming Guo, Jinling Wang, and Weining Qiu. 2017. "A New Method for Single-Epoch Ambiguity Resolution with Indoor Pseudolite Positioning" Sensors 17, no. 4: 921. https://doi.org/10.3390/s17040921
APA StyleLi, X., Zhang, P., Guo, J., Wang, J., & Qiu, W. (2017). A New Method for Single-Epoch Ambiguity Resolution with Indoor Pseudolite Positioning. Sensors, 17(4), 921. https://doi.org/10.3390/s17040921






