Robot-Beacon Distributed Range-Only SLAM for Resource-Constrained Operation
Abstract
:1. Introduction
- development of a distributed robot-beacon tool that selects the most informative measurements that are integrated in SLAM fulfilling the resource consumption bound;
- extension to 3D SLAM, integration and experimentation of the scheme with an octorotor UAS;
- new experimental performance evaluation and comparison with existing methods;
- new subsection with experimental robustness evaluation;
- extension and more detailed related work. Furthermore, the paper has been restructured and all sections have been completed and rewritten for clarity.
2. Related Work
2.1. Range Only SEIF SLAM in a Nutshell
2.2. Integration of Range Measurements
3. Problem Formulation
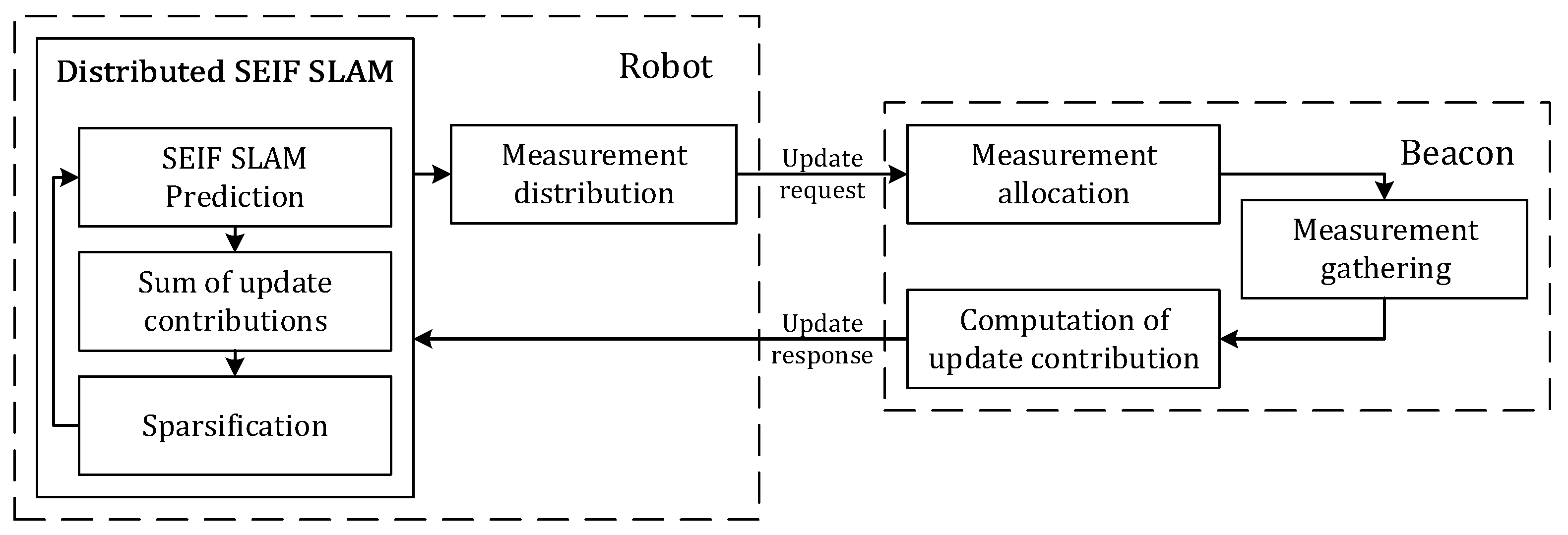
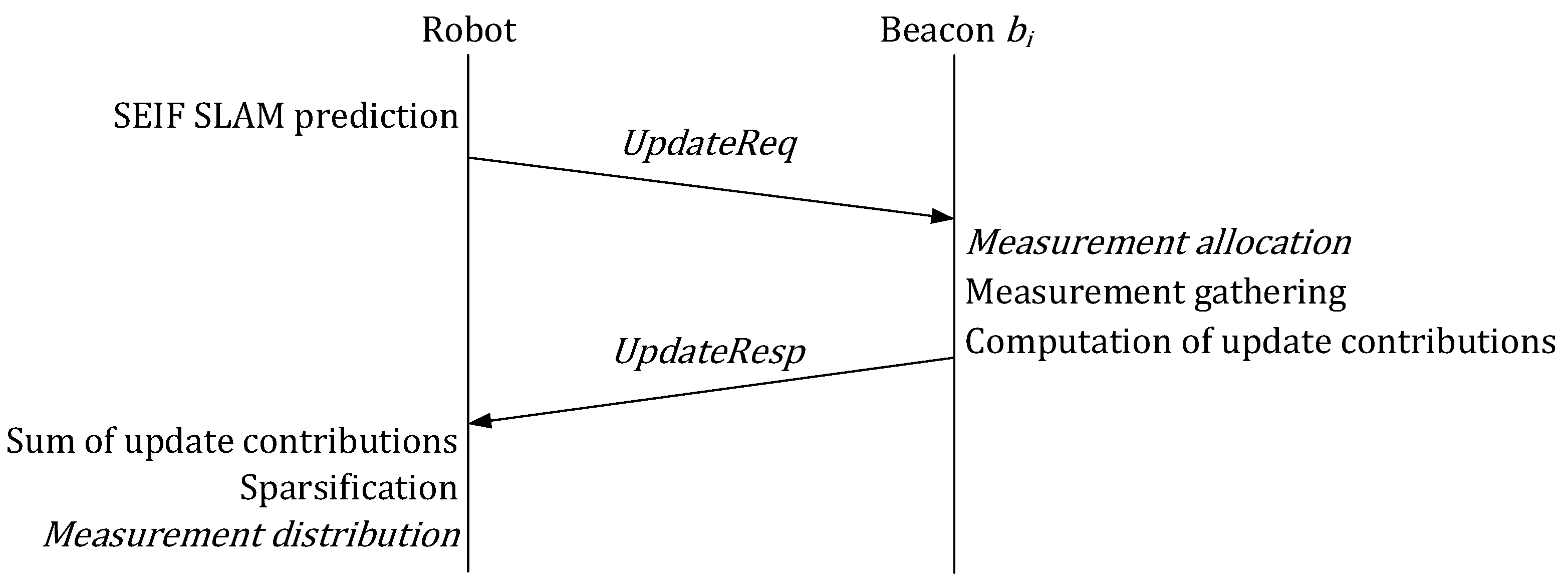
4. Operation of the Robot
| Algorithm 1: Summary of the operation of the robot. |
Require:
|
5. Operation of Beacons
| Algorithm 2: Summary of the operation of beacon |
|
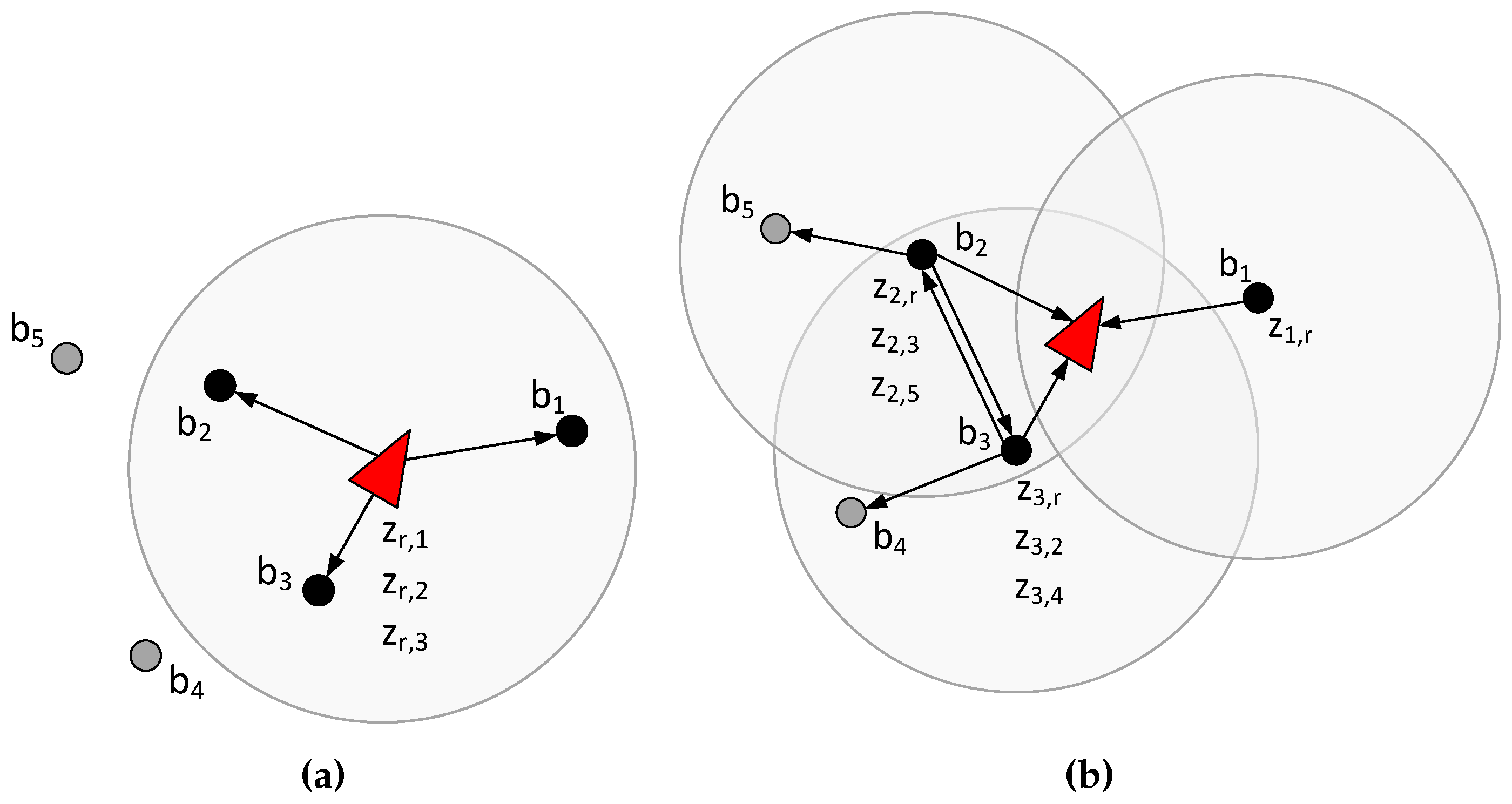
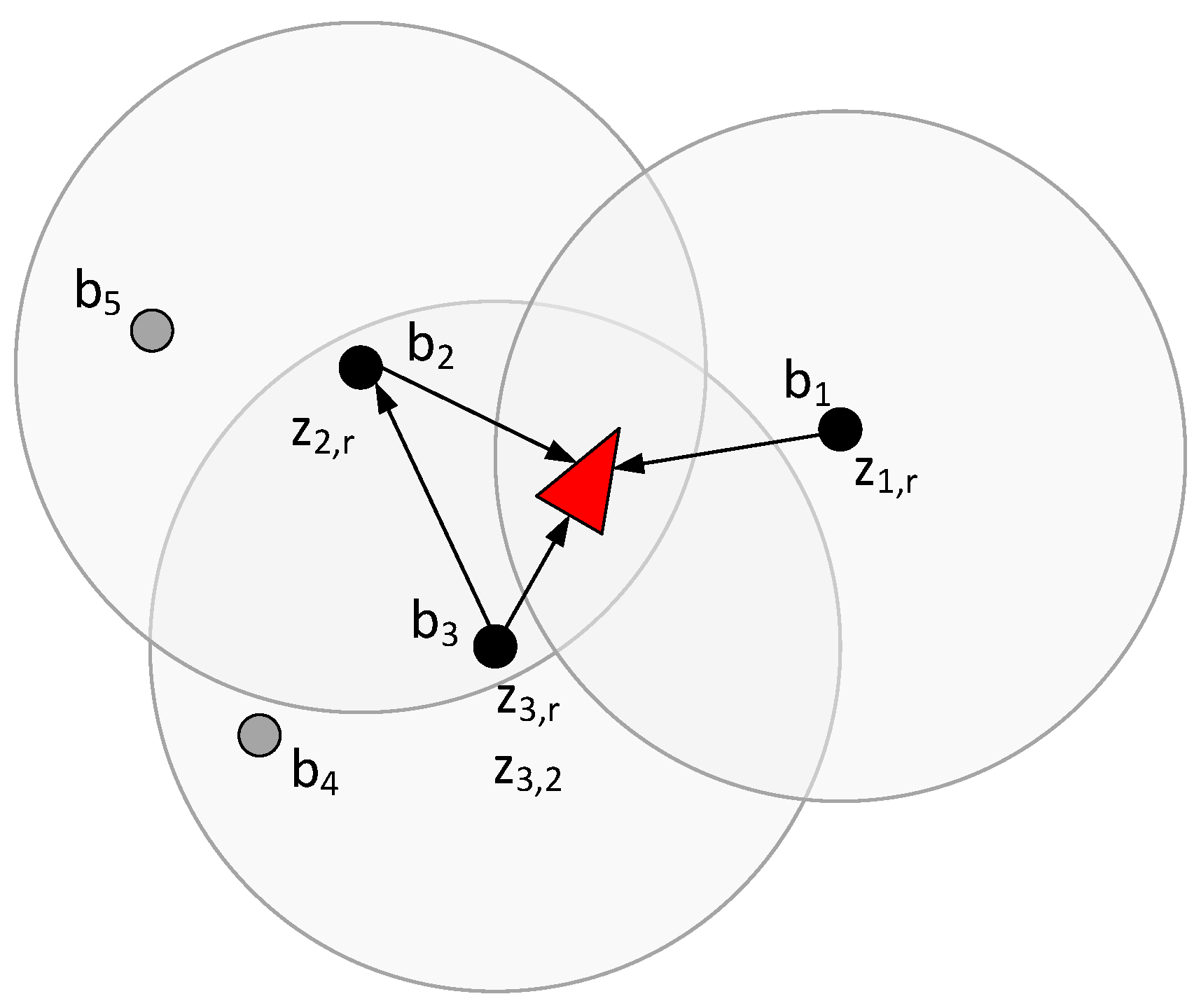
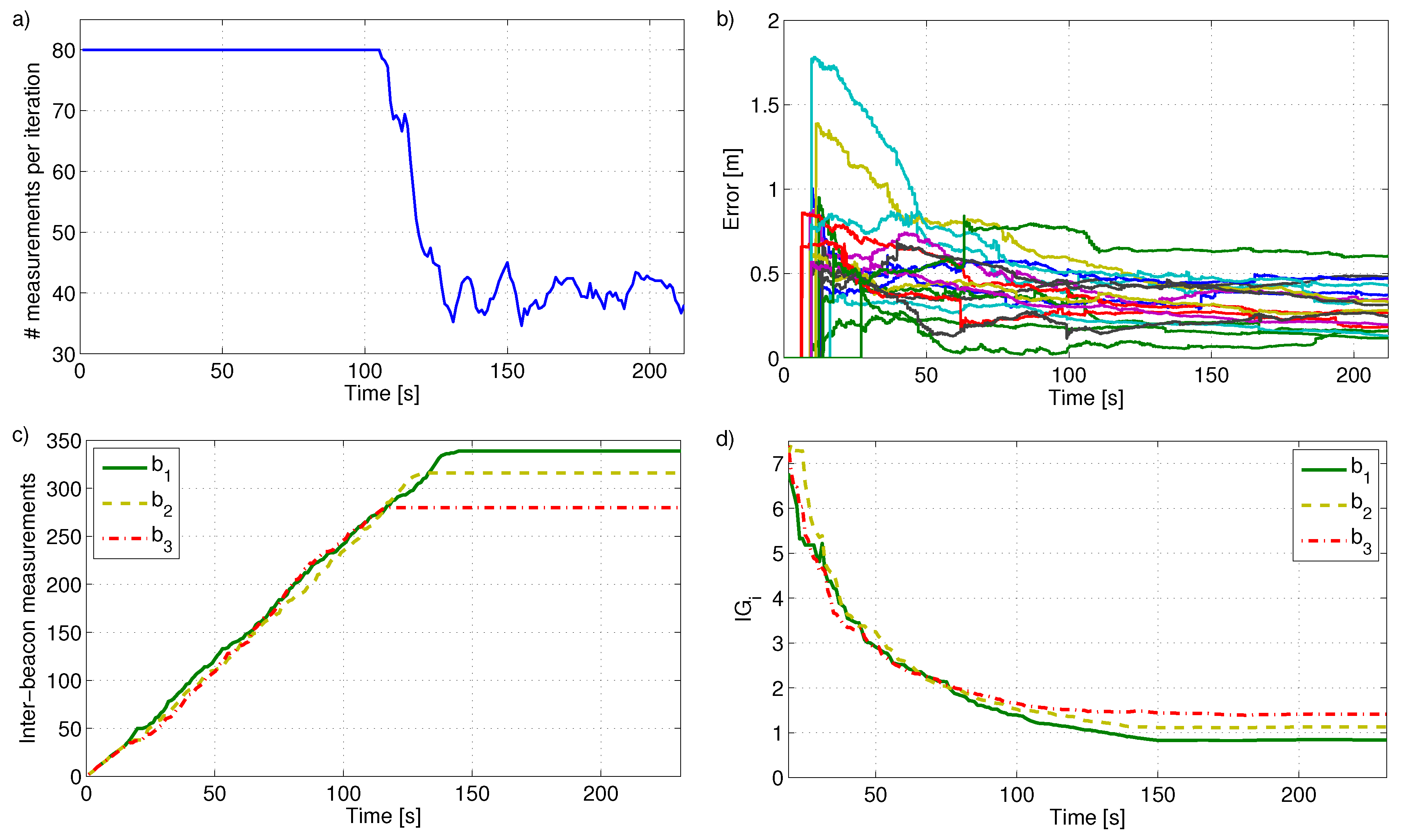
5.1. Measurement Allocation
5.2. Integration of Measurements
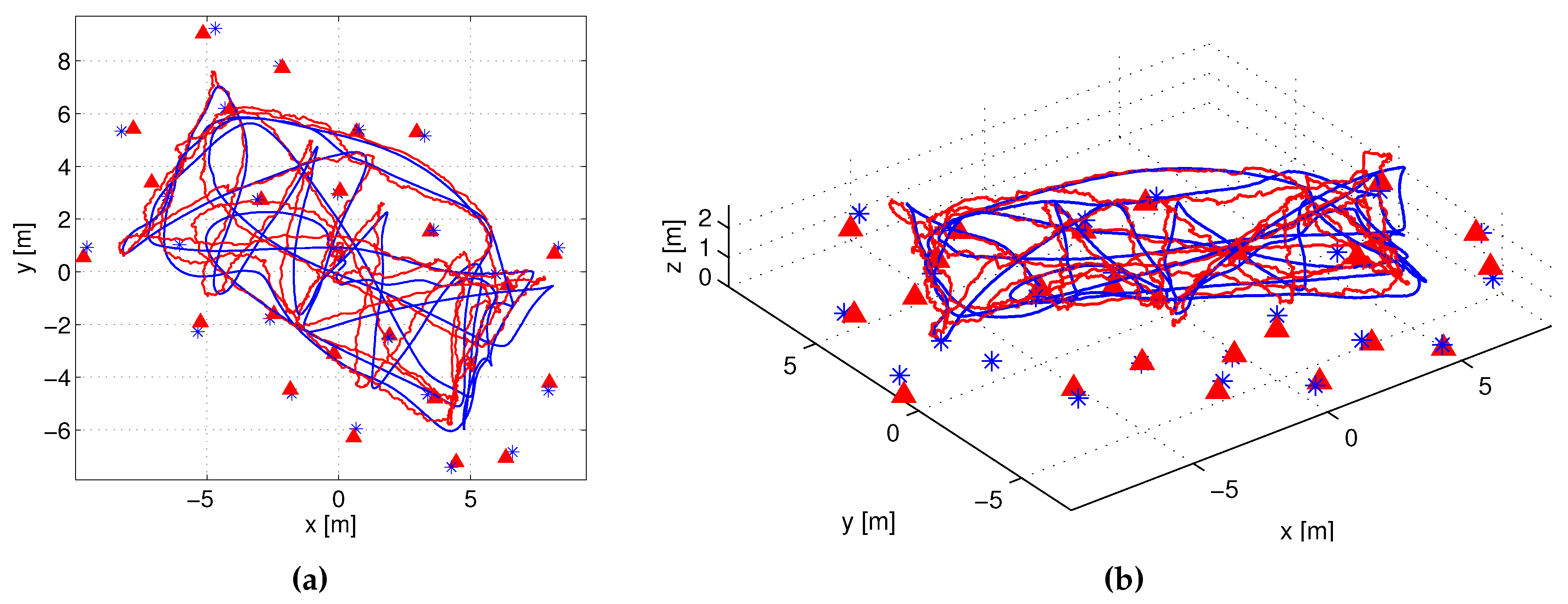
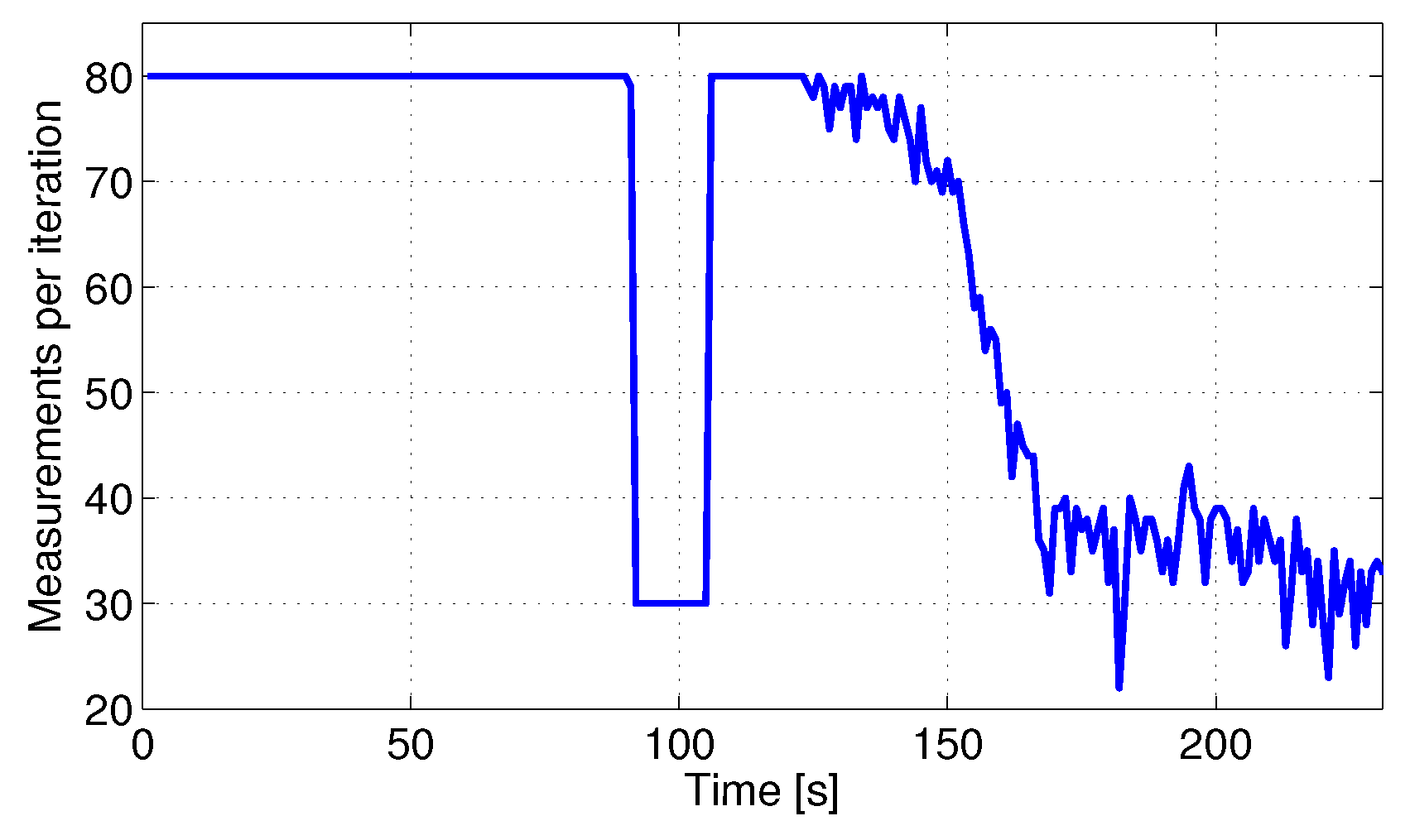
6. Experiments
6.1. Validation
6.2. Performance Comparison
6.3. Discussion
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Covariance matrix of the SLAM global state at time t | |
| Mean of the SLAM global state at time t | |
| Updated information matrix of the SLAM global state at time t | |
| Updated Information vector of the SLAM global state at time t | |
| Predicted information matrix and predicted information vector of the SLAM global state for time t | |
| Update contribution of beacon to | |
| Measurement gathered by the robot to beacon . Measurement gathered by beacon to | |
| Observation models for robot-beacon and inter-beacon measurements | |
| Jacobians of the observation models for robot-beacon and inter-beacon measurements | |
| Sets of the beacons that are currently within the sensing region of the robot and beacon , respectively | |
| List with the number of measurements assigned to each beacon in in measurement distribution | |
| Set of measurements gathered by beacon | |
| Maximum number of measurements that can be gathered and integrated per SLAM iteration | |
| Utility function for measurement | |
| Reward and cost for measurement | |
| Weighting factor between reward and cost |
References
- Brunner, C.J.; Peynot, T.; Vidal-Calleja, T.A.; Underwood, J.P. Selective Combination of Visual and Thermal Imaging for Resilient Localization in Adverse Conditions: Day and Night, Smoke and Fire. J. Field Robot. 2013, 30, 641–666. [Google Scholar] [CrossRef]
- Banatre, M.; Marron, P.; Ollero, A.; Wolisz, A. Cooperating Embedded Systems and Wireless Sensor Networks; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Corke, P.; Hrabar, S.; Peterson, R.; Rus, D.; Saripalli, S.; Sukhatme, G. Deployment and Connectivity Repair of a Sensor Net with a Flying Robot. In Experimental Robotics IX; Springer: Berlin/Heidelberg, Germany, 2006; Volume 21, pp. 333–343. [Google Scholar]
- Maza, I.; Caballero, F.; Capitan, J.; Martinez-de Dios, J.R.; Ollero, A. A distributed architecture for a robotic platform with aerial sensor transportation and self-deployment capabilities. J. Field Robot. 2011, 28, 303–328. [Google Scholar] [CrossRef]
- Martinez-de Dios, J.; Lferd, K.; de San Bernabe, A.; Nunez, G.; Torres-Gonzalez, A.; Ollero, A. Cooperation Between UAS and Wireless Sensor Networks for Efficient Data Collection in Large Environments. J. Intell. Robot. Syst. 2013, 70, 491–508. [Google Scholar] [CrossRef]
- Cobano, J.A.; Martínez-de Dios, J.R.; Conde, R.; Sánchez-Matamoros, J.M.; Ollero, A. Data retrieving from heterogeneous wireless sensor network nodes using UAVs. J. Intell. Robot. Syst. 2010, 60, 133–151. [Google Scholar] [CrossRef]
- Todd, M.; Mascarenas, D.; Flynn, E.; Rosing, T.; Lee, B.; Musiani, D.; Dasgupta, S.; Kpotufe, S.; Hsu, D.; Gupta, R.; et al. A different approach to sensor networking for SHM: Remote powering and interrogation with unmanned aerial vehicles. In Proceedings of the 6th International Workshop on Structural Health Monitoring (Citeseer), Stanford, CA, USA, 11–13 September 2007. [Google Scholar]
- Challa, S.; Leipold, F.; Deshpande, S.; Liu, M. Simultaneous Localization and Mapping in Wireless Sensor Networks. In Proceedings of the Intelligent Sensors, Sensor Networks and Information Processing Conference, Melbourne, Australia, 5–8 December 2005; pp. 81–87. [Google Scholar]
- Menegatti, E.; Zanella, A.; Zilli, S.; Zorzi, F.; Pagello, E. Range-only SLAM with a mobile robot and a Wireless Sensor Networks. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Kobe, Japan, 12–17 May 2009; pp. 8–14. [Google Scholar]
- Sun, D.; Kleiner, A.; Wendt, T. Multi-robot Range-Only SLAM by Active Sensor Nodes for Urban Search and Rescue. In RoboCup 2008: Robot Soccer World Cup XII; Iocchi, L., Matsubara, H., Weitzenfeld, A., Zhou, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5399, pp. 318–330. [Google Scholar]
- Nogueira, M.; Sousa, J.; Pereira, F. Cooperative Autonomous Underwater Vehicle localization. In Proceedings of the IEEE Oceans, Sydney, Australia, 24–27 May 2010; pp. 1–9. [Google Scholar]
- Djugash, J.; Singh, S.; Kantor, G.; Zhang, W. Range-only SLAM for robots operating cooperatively with sensor networks. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Orlando, FL, USA, 15–19 May 2006; pp. 2078–2084. [Google Scholar]
- Torres-González, A.; Martinez-de Dios, J.; Ollero, A. Efficient Robot-Sensor Network Distributed SEIF Range-Only SLAM. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA 2014), Hong Kong, China, 31 May–7 June 2014; pp. 1319–1326. [Google Scholar]
- Menegatti, E.; Danieletto, M.; Mina, M.; Pretto, A.; Bardella, A.; Zanconato, S.; Zanuttigh, P.; Zanella, A. Autonomous discovery, localization and recognition of smart objects through WSN and image features. In Proceedings of the IEEE GLOBECOM 2010, Miami, FL, USA, 6–10 December 2010; pp. 1653–1657. [Google Scholar]
- Olson, E.; Leonard, J.; Teller, S. Robust range-only beacon localization. In Proceedings of the IEEE/OES Autonomous Underwater Vehicles, Sebasco, ME, USA, 17–18 June 2004; pp. 66–75. [Google Scholar]
- Blanco, J.L.; Fernandez-Madrigal, J.A.; Gonzalez, J. Efficient probabilistic Range-Only SLAM. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, IROS’08, Nice, France, 22–26 September 2008; pp. 1017–1022. [Google Scholar]
- Torres-González, A.; Martinez-de Dios, J.; Ollero, A. Integrating Internode Measurements in Sum of Gaussians Range Only SLAM. In ROBOT2013: First Iberian Robotics Conference; Springer International Publishing: Basel, Switzerland, 2014; pp. 473–487. [Google Scholar]
- Thrun, S.; Liu, Y.; Koller, D.; Ng, A.Y.; Ghahramani, Z.; Durrant-Whyte, H. Simultaneous Localization and Mapping with Sparse Extended Information Filters. Int. J. Robot. Res. 2004, 23, 693–716. [Google Scholar] [CrossRef]
- Djugash, J.; Singh, S.; Grocholsky, B. Decentralized mapping of robot-aided sensor networks. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA 2008), Pasadena, CA, USA, 19–23 May 2008; pp. 583–589. [Google Scholar]
- Ila, V.; Porta, J.; Andrade-Cetto, J. Information-Based Compact Pose SLAM. IEEE Trans. Robot. 2010, 26, 78–93. [Google Scholar] [CrossRef]
- Vidal-Calleja, T.A.; Sanfeliu, A.; Andrade-Cetto, J. Action selection for single-camera SLAM. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2010, 40, 1567–1581. [Google Scholar] [CrossRef] [PubMed]
- Torres-González, A.; Martinez-de Dios, J.R.; Ollero, A. An Adaptive Scheme for Robot Localization and Mapping with Dynamically Configurable Inter-Beacon Range Measurements. Sensors 2014, 14, 7684–7710. [Google Scholar] [CrossRef] [PubMed]
- Thrun, S.; Burgard, W.; Fox, D. Probabilistic Robotics, 3rd ed.; The MIT Press: Cambridge, UK, 2005. [Google Scholar]
- Baccour, N.; Koubâa, A.; Mottola, L.; Zúñiga, M.A.; Youssef, H.; Boano, C.A.; Alves, M. Radio link quality estimation in wireless sensor networks: A survey. ACM Trans. Sens. Netw. (TOSN) 2012, 8, 34. [Google Scholar] [CrossRef]
- Stachniss, C.; Grisetti, G.; Burgard, W. Information Gain-based Exploration Using Rao-Blackwellized Particle Filters. Robot. Sci. Syst. 2005, 2, 65–72. [Google Scholar]
- Boers, Y.; Driessen, H.; Bagchi, A.; Mandal, P. Particle filter based entropy. In Proceedings of the IEEE Conference on Information Fusion (FUSION 2010), Edinburgh, UK, 26–29 July 2010. [Google Scholar]
- Heredia, G.; Jiménez-Cano, A.; Sánchez, M.; Llorente, D.; Vega, V.; Braga, J.; Acosta, J.; Ollero, A. Control of a Multirotor Outdoor Aerial Manipulator. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2014), Chicago, IL, USA, 14–18 September 2014. [Google Scholar]
- Nanotron nanoPAN 5375. Available online: http://nanotron.com/EN/PR_ic_modules.php (accessed on 6 April 2017).
- Torres-González, A.; Martinez-de Dios, J.R.; Jiménez-Cano, A.; Ollero, A. An Efficient Fast-Mapping SLAM Method for UAS Applications Using Only Range Measurements. Unmanned Syst. 2016, 4, 155–165. [Google Scholar]



| M1 | M2 | M3 | Proposed | |
|---|---|---|---|---|
| Map RMS error (m) | 0.49 | 0.33 | 0.34 | 0.34 |
| Robot RMS error (m) | 0.59 | 0.49 | 0.50 | 0.51 |
| PF convergence times (s) | 25.2 | 5.4 | 5.6 | 5.7 |
| # of measurements/iteration | 33.2 | 206.9 | 80 | 61.7 |
| Beacon energy consumption (J) | 43.7 | 272.2 | 105.2 | 81.1 |
| Robot CPU time (% of M1) | 100 | 65.6 | 265.5 | 58.6 |
| Map RMS error (m) | 0.35 | 0.346 | 0.34 |
| Robot RMS error (m) | 0.52 | 0.51 | 0.51 |
| PF convergence times (s) | 15.8 | 9.5 | 5.7 |
| # of measurements/iteration | 40 | 56.5 | 61.7 |
| Map RMS error (m) | 0.34 | 0.34 | 0.37 |
| Robot RMS error (m) | 0.51 | 0.51 | 0.52 |
| PF convergence times (s) | 5.7 | 5.7 | 5.9 |
| # of measurements/iteration | 78.9 | 61.7 | 49.3 |
| PRR = 40 | PRR = 60 | PRR = 80 | PRR = 100 | |
|---|---|---|---|---|
| Map RMS error (m) | 0.4 | 0.37 | 0.35 | 0.35 |
| Robot RMS error (m) | 0.57 | 0.53 | 0.52 | 0.51 |
| PF convergence times (s) | 9.6 | 7.1 | 6.4 | 5.7 |
| # of measurements/iteration | 44.8 | 51.4 | 57.1 | 61.7 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torres-González, A.; Martínez-de Dios, J.R.; Ollero, A. Robot-Beacon Distributed Range-Only SLAM for Resource-Constrained Operation. Sensors 2017, 17, 903. https://doi.org/10.3390/s17040903
Torres-González A, Martínez-de Dios JR, Ollero A. Robot-Beacon Distributed Range-Only SLAM for Resource-Constrained Operation. Sensors. 2017; 17(4):903. https://doi.org/10.3390/s17040903
Chicago/Turabian StyleTorres-González, Arturo, Jose Ramiro Martínez-de Dios, and Anibal Ollero. 2017. "Robot-Beacon Distributed Range-Only SLAM for Resource-Constrained Operation" Sensors 17, no. 4: 903. https://doi.org/10.3390/s17040903
APA StyleTorres-González, A., Martínez-de Dios, J. R., & Ollero, A. (2017). Robot-Beacon Distributed Range-Only SLAM for Resource-Constrained Operation. Sensors, 17(4), 903. https://doi.org/10.3390/s17040903







