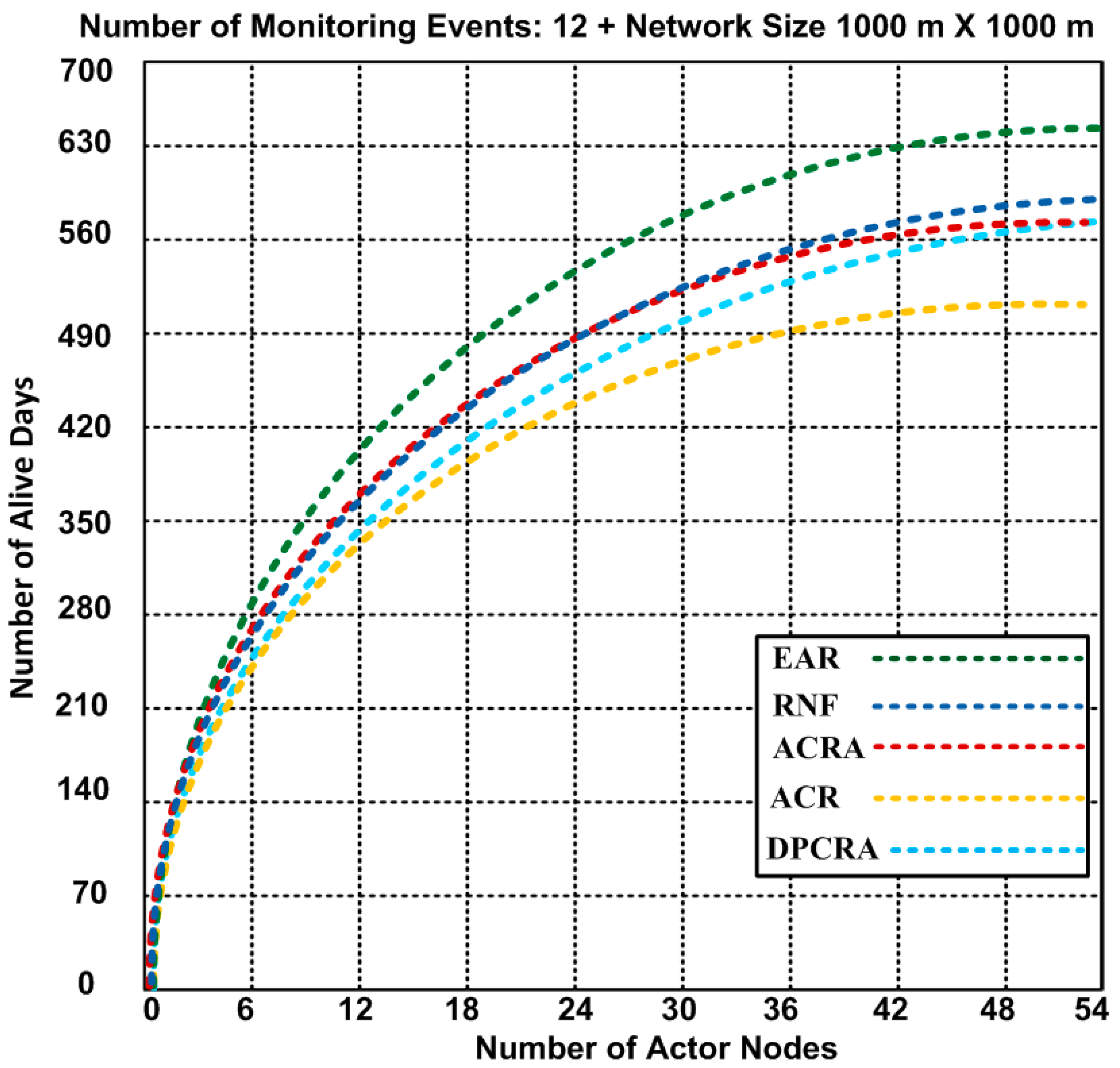
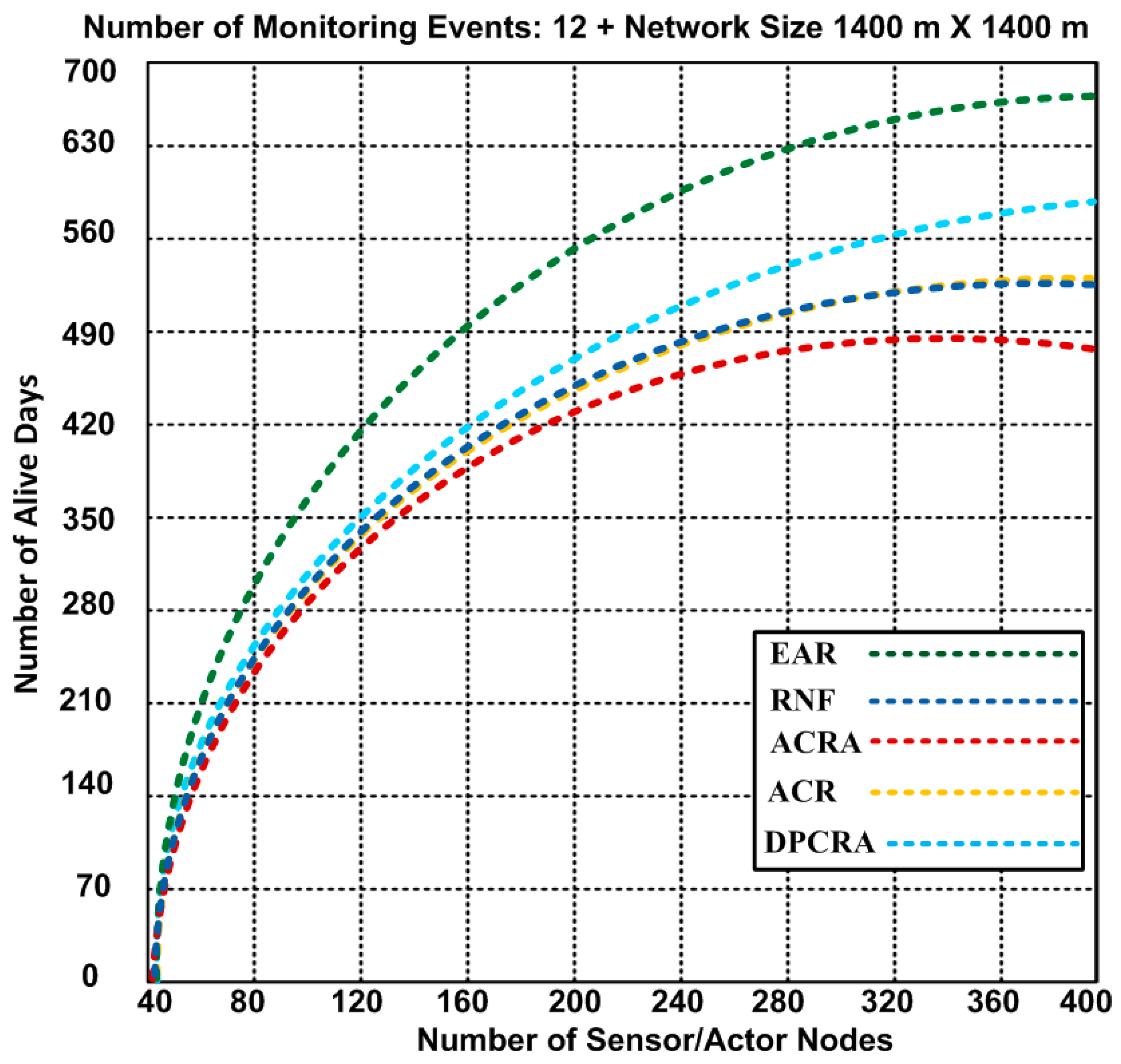
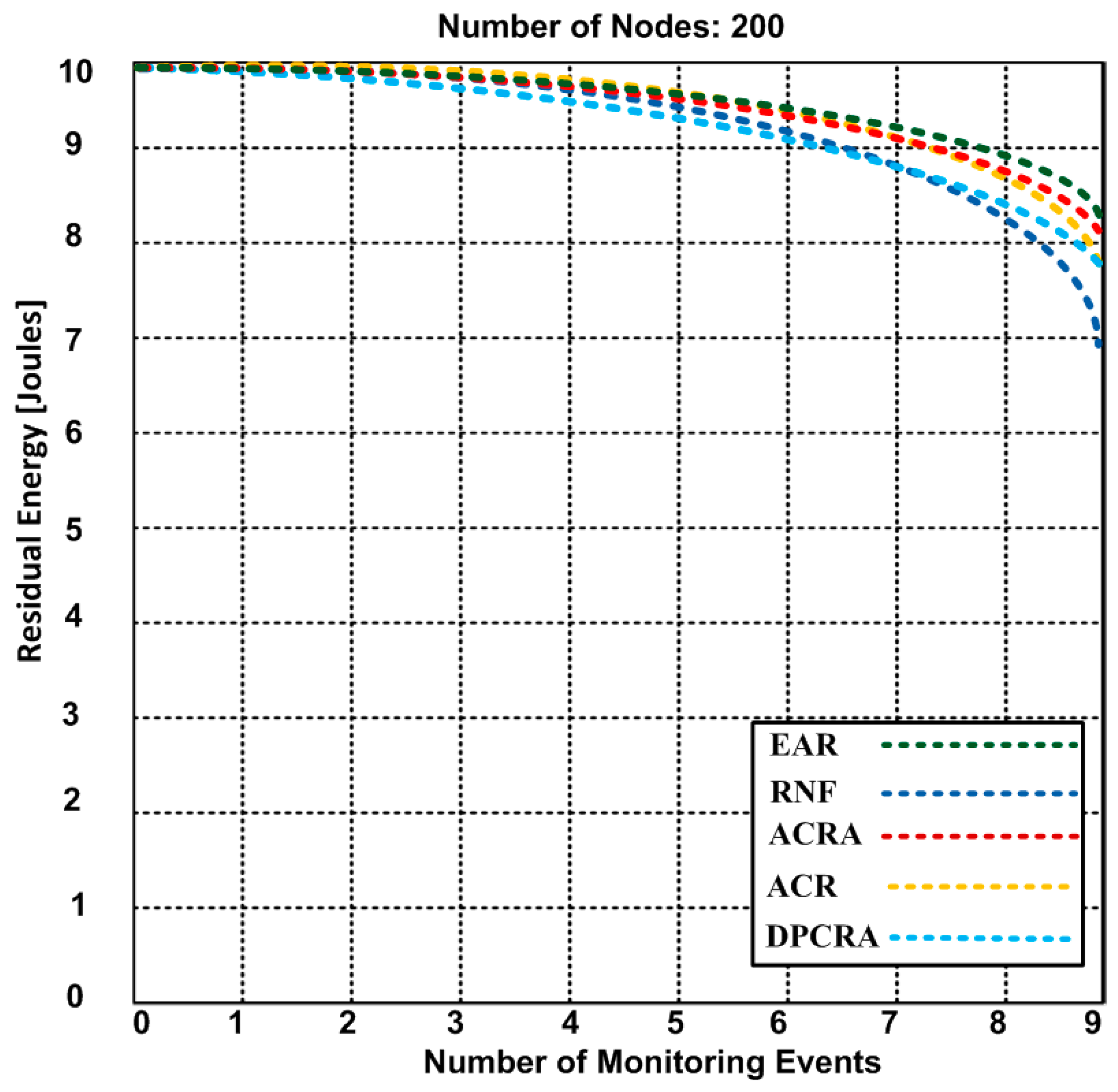
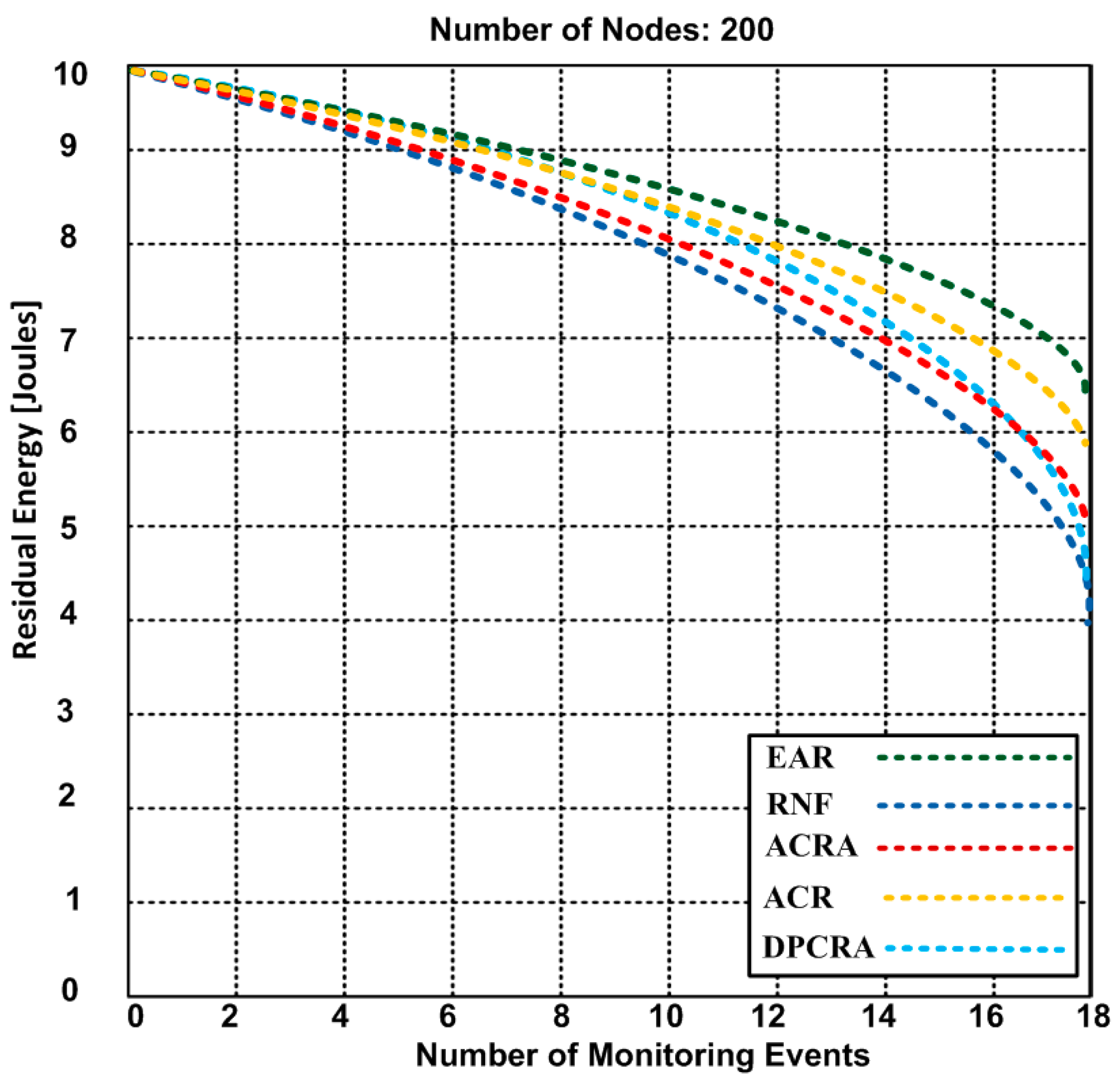
4.1. Problem Formulation
WSANs comprise actors with powerful resources and sensor nodes with limited computation, power, and communication capabilities. The sensors and actors in WSANs collaborate together to monitor and respond to the surrounding world. WSANs can be applied to a wide range of applications, like health or environmental monitoring, chemical attack detection, battlefield surveillance, space missions, intrusion detection, etc. However, WSANs are greatly affected due to environmental changes, frequent changes in event-detection and actor failure processes. The failure of an actor node can result in partitioning of the WSAN and may limit event detection and handling. Actors may fail due to hardware failure, attacks, energy depletion, or communication link issues. Sensor node failure may cause loss of event detection of the assigned environment covered by the sensor. The probability of the actor failure is less than that of sensor failure and can be controlled through the relocation of mobile nodes due to their powerful characteristics; however, actor failure can cause more damage than sensor failure. Actor failure can cause a loss of coordination and connectivity between nodes, limitation in event handling, and can lead to a disjoint WSAN.
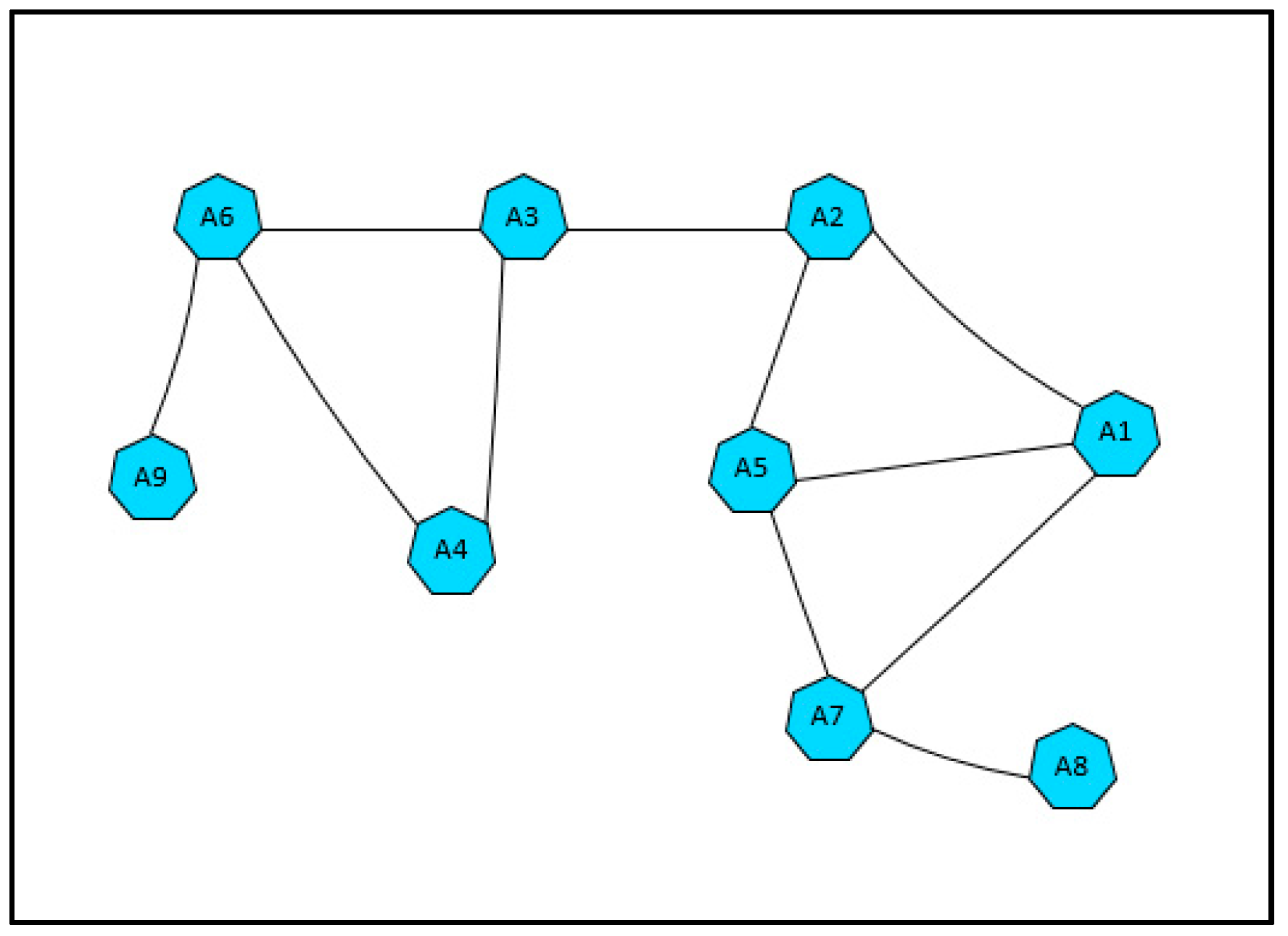
The actor failure occurrence is very critical as it degrades the network performance. The failure of a critical actor may cause high impact to the whole network. Critical actor nodes refer to actors which their failure cause network partitioning.
Figure 2 illustrates the concept of critical actor nodes. Assume that actor A3 failed. Its failure will cause the network to disjoint. Thus, A3 is a critical node. Actor nodes A2, A6, and A7 are critical nodes as well.
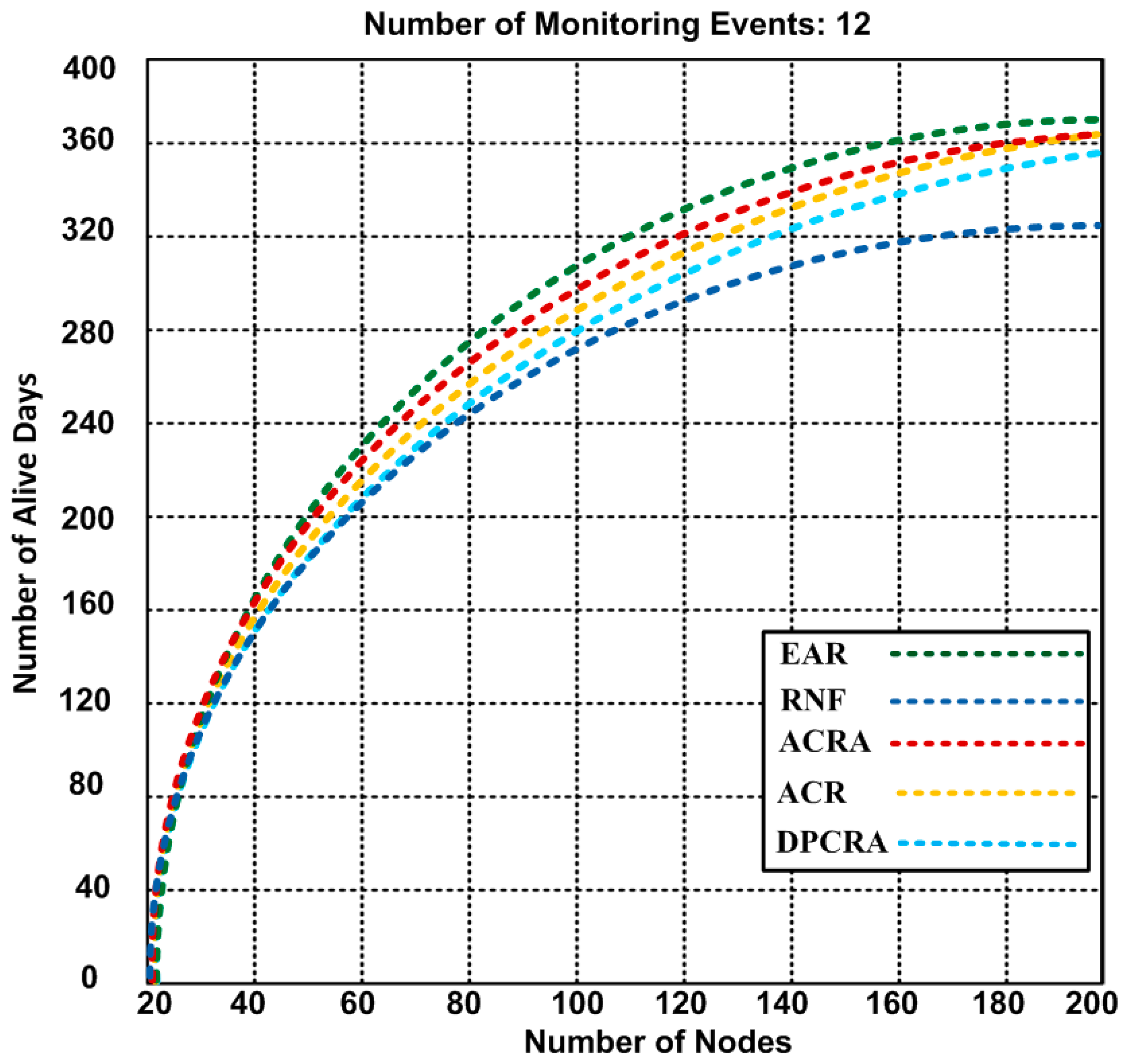
Most of the existing approaches attempted to replace the critical node with another backup node, but they failed to maintain the QoS parameters and energy consumption. For instance RNF manage to handle failure by moving a small block of neighbor actors toward the failed node in order to recover the communication among them. Even though this manages the recovery of the network but it enlarges the recovery scope and cascade relocation. Such behavior should be eliminated in recovery algorithms. In addition, due to the fact that WSANs are deployed in harsh areas and require long term monitoring/acting process, proposed methods should offer robust self-healing failure detection/ recovery techniques which ensure that the network lifetime is maximized as much as possible while maintaining QoS.
In WSANs, the nodes track their neighbors by using heart beat messages to avoid any possible interruption. Moreover, algorithms are used to define the critical nodes using 1-hop or 2-hop message exchange information [
8,
36,
40]. In addition, they identify the actor node failure by the interaction of those heartbeat messages with this particular actor node. Thus, there is possibility of interruption due to losing the trail of heart beat messages. Monitoring actor failure detection using 2-hop neighbor list is efficient once it is combined with QoS measurement capabilities, i.e., packet delivery and forwarding techniques should support efficient packet handling and forwarding. Also, we should minimize the through critical actor nodes. Thus, in our proposed model, we assume that each actor node stores the information up to 2-hops to keep the extended trail information. This helps determine the forwarding capability of the actor nodes. The model aims to ensure the contention-free forwarding capability that minimizes the loss of packets in case of node failure. To determine the actor’s forwarding capability, each actor conveys the group of beacon messages using different power strengths. Furthermore, the neighbor of each actor listens and returns the value in response. After the neighbor actor receives the message, it starts calculating its RSSI value and sends it back to the sender actor. The RSSI model is used to calculate the distance. It has also been combined with further techniques for better accuracy and to find the relative error. Equations (1)–(5) illustrate applying RSSI in actor nodes [
55]. RSSI can also be used to determine the link quality measurement in wireless sensor networks [
56].The RSSI shows the relationship between the received energy of the wireless signals and transmitted energy and the required distance among the actor-sensor nodes. This process helps determine failure node recovery process given in Definition 1. The relationship is given by Equation (1):
where
: Received energy of wireless signals,
: transmitted energy of wireless signals,
: Distance between forwarding and receiving node, and
: Path loss transmission factor whose value depends on the environment.
Taking the logarithm of Equation (1) provides:
where
: Description of energy that could be converted into
.
Therefore, Equation (2) can be converted to its
form as:
where
: transmission parameter.
Here, and represent the relationship between the strength of the received signals and the distance of the signal transmission among sensor-to-sensor, actor-to-sensor or actor-to-actor.
RSSI propagation models cover free-space model, log-normal shadow model and ground bidirectional [
20]. In this study free space model is used due to following conditions.
- ▪
The transmission distance is larger than carrier wavelength and antenna size.
- ▪
There is no obstacle between forwarding actor and either receiving actor or sensor.
The transmission energy of the wireless signals and the energy of the received signals of sensor nodes located at distance of ‘
r’ can be obtained by Equations (4) and (5):
where
: 1/Frequency of the actor node,
: An antenna gains,
: failure factor of the actor and
: distance of the node:
Equation (5) represents the signal attenuation using a logarithmic expression. Assume a field with k actor nodes
,
,
,...,
. The coordinates of the actor nodes are
for
i = 1, 2,…,
k. The actor nodes transmit the information regarding their location with their signal strength to the sensor nodes {
}. The locations of the sensor nodes are unknown. The estimated distances of the actor nodes are calculated from the received signals. In the proposed model, the actor nodes broadcast signals to all sensors. The actor nodes are also responsible for estimating the distances between them and sensor nodes. Let
be an actor node located at
and sensor node is located at
. Focusing on the relative error
relating to
, suppose that the actor node reads a distance
, but the correct distance is
. Therefore, the relative error can be obtained by Equation (6):
The relation between actual distance and the measured distance can be obtained by Equation (7):
which can be reduced to Equation (8):
The probability distribution of the location of the actor node based on beacon messages is described in the following definition.
Definition 1. Let be an actor node located at that sends information to a sensor using RSSI model with standard deviation and path loss .
Let be the calculated distance from the actor node at the sensor node. The probability density function for correct location of the sensor node is obtained by Equation (9): Probability distribution can be simplified due to an actor with Equation (10): This can further be extended by using finite set of actors , , ,…, } that produces Definition 2.
Definition 2. Let , , ,..., } be the set of the actors sending information to the set of sensor nodes using RSSI model with path loss exponent .
If the calculated distance from the actor node at the sensor nodes S =
{}, then the probability density function of correct location of the sensor nodes can be obtained by: where : probability distribution because of an actor . Definition 3. Assume an actor node ai reads a sample distance , using beacon messages , that is modeled with RSSI with path loss and standard deviation .
If ‘R’ provides the mean sample distances and is the mean standard deviation, then the square of the actual distance from actor to sensor using beacons can be determined as: Furthermore, square standard deviation can be found as: The definition shows that the actual distance is greatly dependent on the distribution of the measured ranges.
Hence, our proposed formulas for RSSI-based wireless node location are optimized and modified. They are different from the original RSSI-based formulas. We focused particularly on the energy consumed for transmission and receiving the data including determining the distance between actor-sensor nodes and error rate for finding location of the node that helps identifying the accurate position of the deployed actor nodes for events. Thus, the previous model is used by our proposed algorithm in order to identify the node locations during deployment in addition to during the network lifetime.
4.2. Optimized Deterministic Actor Recovery System Model
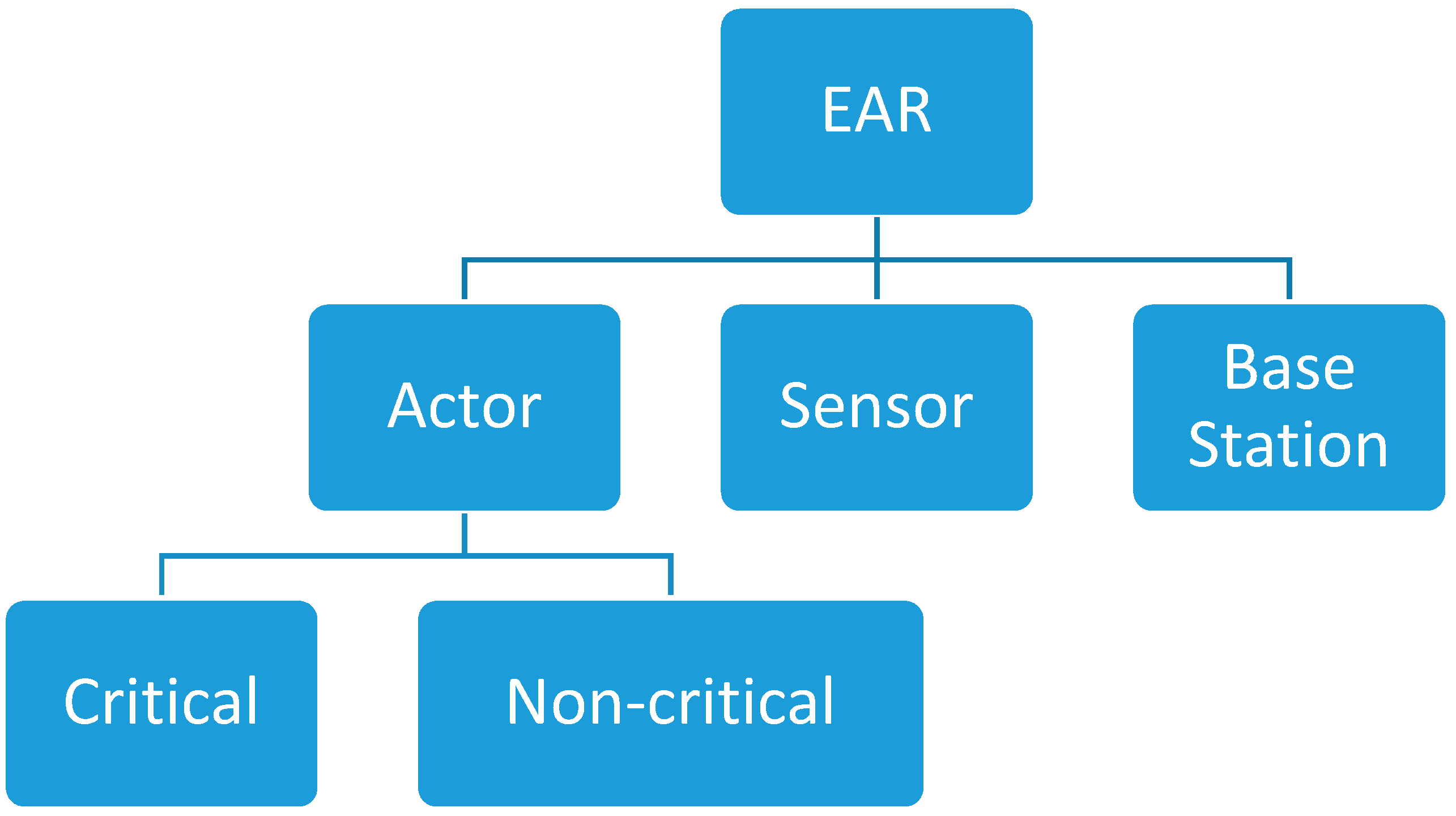
The network consists of multiple actors and sensor nodes that are structured with the hierarchical structure of the nodes. The hierarchical structure of the nodes provides an efficient, fast and logical packet forwarding patterns. It also determines the features of all nodes connected with WSANs. Another advantage of the hierarchical structure is that it helps to start with little multiplexing process for intra-domain routing. As the packets travel further from the source node the model helps to develop higher degree of multiplexing. The nodes of different categories in WSAN as depicted in
Figure 3 possess the assorted nodes types. The network aims to use the resources efficiently for each packet forwarded by an actor node. In addition, it reduces the latency while keeping the network more stable.
Definition 4. Critical actor node is the actor node which its failure cause network partitioning.
Definition 5. Non-critical nodes (NCNs) are regular actor nodes.
Definition 6. Cut Vertex Nodes (CVNs) are nodes which have a cut-vertex link with a critical node, i.e., neighbors of critical node.
Definition 7. The Critical Backup Nodes (CBNs) are actor nodes that are assigned to be the backup nodes for a critical node.
The EAR consists of actor nodes, sensor nodes, and base station. Actor node can be critical or non-critical. Critical actor node is the actor node which its failure causes network partitioning. Non-critical nodes are regular actor node. Sensors node are used to monitor the network for event detection.
In this topology, Cut Vertex Nodes (CVNs) are responsible for the removal of the paths that lead to the critical nodes. When the actor node becomes a critical node, then it is necessary to redirect the traffic of the neighbor nodes to the non-critical nodes. Thus, this task is done by removing the vertex (a path leading to critical nodes) and redirecting the traffic, as it further helps improving the throughput performance and reduces the latency. The Critical Backup Nodes (CBNs) replace the actor nodes when the actor nodes become the critical nodes. We assume that the number of critical backup nodes are more than actor nodes in the network. If all the actor nodes become critical nodes, then replacement should be much easier to avoid any kind of interruption or data loss. There could a possibility of disconnecting the direct communication links of the actor nodes towards the backup nodes when the actor nodes start moving. Thus, we also assume that the links of the actor nodes lead to the backup nodes are always stable despite the mobility. Therefore, there is a high possibility to easily replace the critical nodes with CVNs. The actor node has a privilege to collect the data from event-monitoring nodes (sensor nodes), then it forwards the packets to either base station or sensor /actor nodes in the network. On the other hand, the least degree Non Critical Nodes (NCNs) are preferred to be labeled as backup nodes for event-monitoring nodes.
A neighbor node that is available in Node Distance range (ND) has a similar Cut Vertex Node Distance (CVND). This helps reduce the recovery time and overhead which is important for resource-constrained mission-critical applications.
In the network, each actor node maintains its 2-hop neighbors’ information using heartbeat messages. This information helps to maintain the network state, defining critical actor; as well as assigning backup node for the critical actor. Each actor node saves its neighbors information which includes node ID, RSSI value, number of neighbors which is denoted by the degree of node, node criticality (critical actor/non-critical actor), and node distance. Once a critical node is detected, the backup assignment process is executed in-order to assign a backup node for this critical node. The 2-hop node information is used in the process of backup node selection. Depending on RSSI value (extracted from mathematical model), the non-critical node with the least node degree is preferred to be chosen as a backup node. In case there is more than one neighbor with the same node degree, the neighbor with the least distance is preferred. For each critical actor, a pre-assigned backup actor node is selected which is called Critical Backup Nodes CBN. Consequently, CBN monitors its critical node through heartbeats messages and handles the backup process in case the failure of its critical node. Missing a number of successive heartbeats messages at CBN indicates the failure of the primary.
The topology of the WSAN can be changed during the network lifetime due to the mobility feature of actors, actor node failure, or event handling. Backup nodes are subject to failure as well. Therefore, there are primary backup nodes that select other backup nodes in case of primary backup nodes fail or move beyond the range of ND. To ensure the effectiveness and availability of backup node, we introduce novel backup node selection process in case of primary backup is either failed or in critical condition given in Algorithm 1. Algorithm 1 shows the backup selection process. In this process, the condition of primary backup node is checked. If a primary backup node is in critical condition or ready to move, then a secondary backup node is chosen. However, if a secondary backup node is in critical condition or ready to move, then tertiary backup node Tb is notified to play a role as primary backup node. If the tertiary backup node is in critical condition then the backup assignment algorithm executes and a backup node is assigned.
Since actor nodes are rich-resource nodes, we further use the least square approximation formulation to identify the power strength. This involves little computational overhead which can be easily attuned in an actor so that we identify the power strength because there is a probability of the node to mislay the power at some particular time.
| Algorithm 1: Backup Node Selection Process |
: Primary Backup; : Critical Primary Backup; : Moving Primary Backup; : Secondary Backup; : Critical Secondary Backup; : Moving Secondary Backup; : Tertiary Backup. Input: () Output: () If = || //The condition of primary backup node is checked. Notify and Set (,//Secondary backup node is assigned as primary backup node end if If == || //The condition of Secondary backup node is checked. Notify and Set (,//Tertiary backup node is notified to play a role as primary backup node end if
|
We use node monitoring process to monitor the node pre-failure causes, the post-failure causes and allocates the recovery options. Once each critical actor node picks a suitable backup, then it is informed through regular heartbeat messages (Special signals are sent to neighbor node to play a role as backup node for critical node). Furthermore, the pre-designated backup initiates monitoring its primary actor node through heartbeats. If a number of consecutive heartbeats are missed from the primary actor, then it notifies that the primary actor failed. Thus, a backup node replacement process is started as given in algorithm 1. Before substantiating the post failure process, we must ensure that connection is not interrupted because of the network. In addition, any redundant action of the network must be controlled to avoid any possible increase of the network overhead. The pre-failure backup node process is given in Algorithm 2.
| Algorithm 2: Node Monitoring and Critical Node Detection (NMCND) process |
{
: Pre-Failure; : Post-Failure; : Recovery process; : Critical node; : Backup node; : Primary actor; : Message heartbeat; : Sink node} Input: {;;} Output: {; ;} Set //Number of actor nodes are set as primary actors in the network broadcasts //Sink node broadcasts the message to all primary actor nodes If then// Determine //Initiate critical node discovery process If ∀ : ∈ then assigns Set = end if If NotDelivered then Set for data delivery end if Process //Primary actor node recovery process is conducted end if
|
As shown in Algorithm 2, represents the number of actor nodes in the network. Then, the sink node broadcasts the message to all primary actor nodes to determine pre-failure actor nodes. If primary actor is not identified as pre-failure, then the process of determining the critical actor node will be started in order to choose the backup node. Next, the critical node discovery process is initiated. For each primary node, if the primary node is found as critical node then this node will be defined as critical node and a backup node selection is assigned. The critical node will broadcast a message to its neighbors which includes the information of its backup node. This information is stored by the neighbors and it is used when starting the network recovery process in case the neighbors detect the failure of their critical actor neighbor. If consecutive heartbeat messages are not received from the critical node, then back node starts replacing the critical node to avoid any kind of packet-forwarding delay. In addition, neighbors of the critical node will use stored information to communicate with the backup node in order to restore connectivity. In conclusion, the recovery process is conducted.
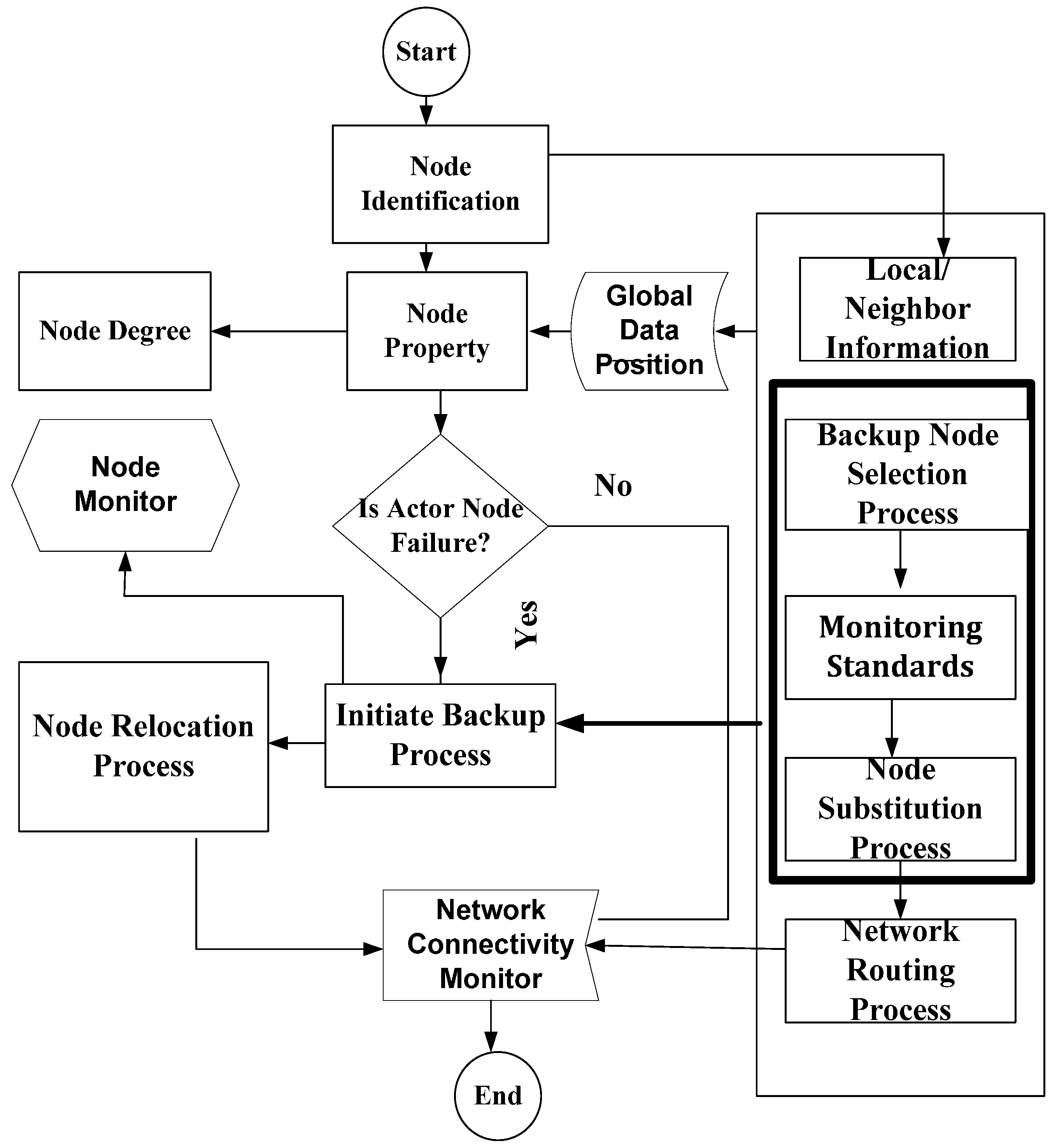
After the node monitoring process is executed, we proceed further with checking the backup assignment and the critical back up assignment of the nodes. This allows to maintain the network connectivity without generating any disjoint procedure of the network. The possibility of the recovery depends on the cut vertex node. If the backup is a non-critical node, then it simply substitutes the primary actor node, and the recovery process is initiated to confirm the backup actor node. If the backup is also a critical node, then a cut vertex node replacement is completed. The pre-assigned backup actor node instantly activates a recovery process once it senses the failure of its primary actor node. The complete node monitoring including failure, recovery and replacement processes are depicted in
Figure 4. In complete node monitoring process, first, the node identification process is initiated. The node is identified based on local neighbor information (LNI) that involves global data position, node property and node degree. The critical node selection process is decided using Algorithms 1 and 2. Once a critical node is identified, it will be assigned a backup node; second, the backup node selection process is started if an actor node fails. The selection process is decided based on monitoring the algorithms explained earlier. Once the backup node selection process is complete, then the backup process starts working in case of node failure. If an actor node does not fail, then the node connectivity monitoring process is started and routing connectivity metrics are checked to ensure whether there is no problem of the router.
After completion of the actor node failure and node assignment processes, the actor nodes should be linked to forward the collected data to the base station. In response, the base station sends its identity (ID) using network integration message (NIM). When an actor node receives NIM from the base station, it saves the destination address of the base station for packet forwarding (PF). Subsequently, NIM is broadcasted in the network among all the actors. At least one actor node is within the range of the base station to avoid any bottlenecks. Otherwise, the base station receives the data through sensor nodes that could be the cause of packet delay and loss. The actor node saves the information of the first actor node from which it receives NIM to use PF process and further forwards NIM with its ID. If an actor gets NIM from multiple actors, then it stores the identity of additional actors in the buffer list. Identity of the saved actors is used in case of topology changes due to mobility or node failure. The detailed process of an actor node that receives NIM is presented in Algorithm 3.
| Algorithm 3: Network Integration and Message Forwarding Process |
{
: Base Station; NIM: Network integration message; PF: packet forwarding; : Node identity; : Actor node; : Node buffer} Input: {, } Output: {NIM, PF} Set NIM//Network integration message is set to interconnect the entire network Set PF//it saves the destination address of the Base station for packet forwarding If PF = then//If a base station is saved as the destination address Decline NIM//If base station is found, then NIM is declined else if NIM // Set PF= // Data forwarding packet is given ID transmitted to Base station Transmit NIM else if NIM then//It will be considered that NIM is forwarded by an actor node end if end else If PF //If it is validated that data packet is forwarded by an actor node, t stores into //When actor node receives NIM from multiple actors Set PF = //Data forwarding packet is given ID Transmit NIM//NIM is transmitted by an actor node End if end else else if NIM then//NIM message is broadcasted by the Base station. If PF then//If data forwarding packets is from an actor Decline NIM//If actor node is found, then NIM is declined else PF = //Each forwarded data packet is given identify from an actor Transmit NIM//network integration message is transmitted by an actor node end else end else end if
|
Our protocol applies a simple algorithm to process the NIM. The actor node first transmits NIM to its higher hop neighbor actors/sensors. When it gets the first NIM from the higher hop actor/sensor, then it forwards to its lower-hop neighbor actors/sensors to ensure the transmission of NIMs in the entire network. All other NIMs are then dropped by the actor nodes. Therefore, if each actor is ensured to be in the communication range of at least one actor, then the NIMs should not require to be managed at sensor nodes.
Let us assume that an actor node transmits the number of bits in each packet that uses encoding mechanism to reduce the complexity of each packet. The sensor nodes monitor the events which check its contribution table that specify the important events. If events are of the significant interest, then the sensor nodes generate the packets and forward to the actor node. The complete process of monitoring the events and forwarding the routing of the data packets is given in Algorithm 4.
| Algorithm 4: Priority-Based Routing for Node Failure Avoidance Process |
{: Packet rate; : Actor node; : Significant; : First interest, : Sharing capacity of node; P: Packet; : remaining output capacity of the node; : Efficient packet rate; : Flag of interest; : Flag of uninterested;: Node failure}Input: {, P } Output: {, } If received by //If actor node receives the packet If then//If the received packet is of significant interest Set //If condition in step-4 is satisfied, received first packet is considered as significant of interest. Set +1 & decrease //Sharing capacity of the node is increased end if end if If > 0 then//Determine the power of node Forw//Received packet is forwarded Set //Flag of interest is set in the buffer Else if < 0 then Process > & P //Showing that packet rate is higher than efficient packet rate Increase / remaining capacity of the actor node is increased Reduce //When capacity of the node is increased, less possibility of node failure end else end if
|