1. Introduction
Seed viability assessment is a key component of agricultural production and commercialization. Seed viability can be affected by several factors, including overheating, physical damage and natural aging. Assurances of high seed productivity are necessary for seed users in agricultural production, and meanwhile high seed viability needs to be guaranteed in agricultural commercialization to ensure the business optimization of seed companies. Hence, both the seed users and seed supply companies are required to invest in seed viability test and classification technologies.
In seed viability assessment, many conventional methods including the standard germination test, electrical conductivity test, seedling growth test, accelerated aging test and triphenyltetrazolium chloride (TTC) quantitative analysis have been proposed [
1,
2]. However, several shortcomings still exist in these methods, such as invasiveness, huge amount of test work needed, long test periods, low accuracy and obvious subjective effects [
3]. Therefore, fast and nondestructive diagnosis methods are urgently required in seed viability assessment. In view of this, several optical techniques, such as infrared thermography, Fourier transform infrared, Fourier transform near-infrared, bio-speckle, nuclear magnetic resonance, ultraviolet-visible and Raman spectroscopy and hyperspectral imaging have been developed to estimate the seed viability [
4,
5,
6,
7,
8,
9,
10].
Although these methods have the merits of being non-contact and providing rapid inspection, they also have limitations, such as the high cost of hyperspectral imaging and nuclear magnetic resonance devices, low throughput in Fourier transform infrared, Fourier transform near-infrared and ultraviolet-visible spectroscopy, Raman spectroscopy and bio-speckle. By contrast, infrared thermography shows the advantages of relatively low cost and high assessment throughput, so considering all the factors, infrared thermography is a proper technique in seed viability assessment [
11,
12,
13,
14,
15].
Recently, many researchers have paid special attention to the application of infrared thermography. As a noninvasive diagnosis method, infrared thermography has been applied in various fields including medical tests, fault diagnosis, remote sensing, plant diseases and insect pest detection, fruit quality and seed viability assessment [
13,
14,
15]. In these applications, seed viability estimation with infrared thermography is what we are most concerned about. In previous studies, the variation of seed heat flow has been proved to be affected by water imbibition, respiration, decomposition of nutrients and other biochemical, physical, chemical reactions correlated with seed viability during the germination processes [
16,
17]. The surface of seeds measured by infrared thermal cameras can be recorded as the temperature data for non-destructive seed viability evaluation. Hence, the infrared thermography technique has great potential in seed quality assessment.
Microcalorimetry techniques have been used to depict the variation of seed heat flow and it is proved that gross metabolism is associated with germination processes [
18,
19,
20]. However, a closed system is needed in microcalorimeter measurements to prevent the dissipation of heat and gas. This closed system can induce the perturbation of potential and lead to confounding seed metabolism feedback. In comparison, infrared thermography can capture thermal activity in the phase of seed imbibition thanks to its large-area scanning advantage. This technique was first used to evaluate the germination capacity of leguminous seeds in 2003, and the results demonstrated that temperature changes in seeds with germination showed a considerable decrease in radiation temperature (more than 1 °C) during the first 12 h [
21]. Further studies about seed viability assessment with the infrared thermography technique found that whether seeds would germinate or not could be predicted in the first three hours of the water uptake period, when the seeds could be redried and stored again [
22].
In seed viability detection with infrared thermography, a temperature-time curve for every seed is generally plotted by using temperature values in time sequence in the acquired thermal images. As the main classification method in previous studies, the minimum distance algorithm is widely adopted to evaluate the seed viability. However, this algorithm is easily affected by the selection of experimental samples. In terms of classification problems, many intelligent algorithms including decision trees, Bayesian classification, KNN (K-nearest neighbors) and artificial neural net were introduced [
23]. Based on the statistical theory, these classification methods need quite a large amount of samples that cannot be satisfied in practical problems. Compared with these methods, the target of support vector machine (SVM) is structural risk minimization instead of empirical risk minimization [
24,
25]. Therefore, the SVM method has the advantages of global optimization and generalization ability, which is suitable for seed viability assessment where a small amount of samples are classified with infrared thermography.
As a new technique in seed viability assessment, it is important to investigate the relationship between the seed heat flows detected by infrared thermography and the seed viability. Considering its non-destructiveness, the infrared thermography technique can be used during the whole sample germination process. It can detect the seed viability during the period of water uptake and improve the accuracy of viable seed assessment by virtue of the temperature change curves of thermography images.
The objectives of the present study included: (1) investigation of the differences in temperature curves of highly viable, aged and dead seeds during the germination period; (2) exploration of the vital parameters of temperature curves; (3) development of a method that can distinguish the viable seeds and unviable seeds before germination.
2. Materials and Methods
2.1. Plant Materials
Pisum sativum L. seeds were selected as the experimental samples, and submitted to standard germination tests for quality control. A total of 120 seeds were divided into two groups, namely A class and B class, for different treatments (80 seeds for A class and 40 seeds for B class). The seeds of class A were stored at 5 °C for three days while the seeds of class B were treated at 100 °C for three days. To be specific, A class seeds were put in a refrigerator at 5 °C for three days, while B class seeds were treated at 100 °C (±1 °C) with a draught drying cabinet. Root lengths of each individual seed were then measured by a Vernier caliper on the fifth day after imbibition so as to qualify the seed viability.
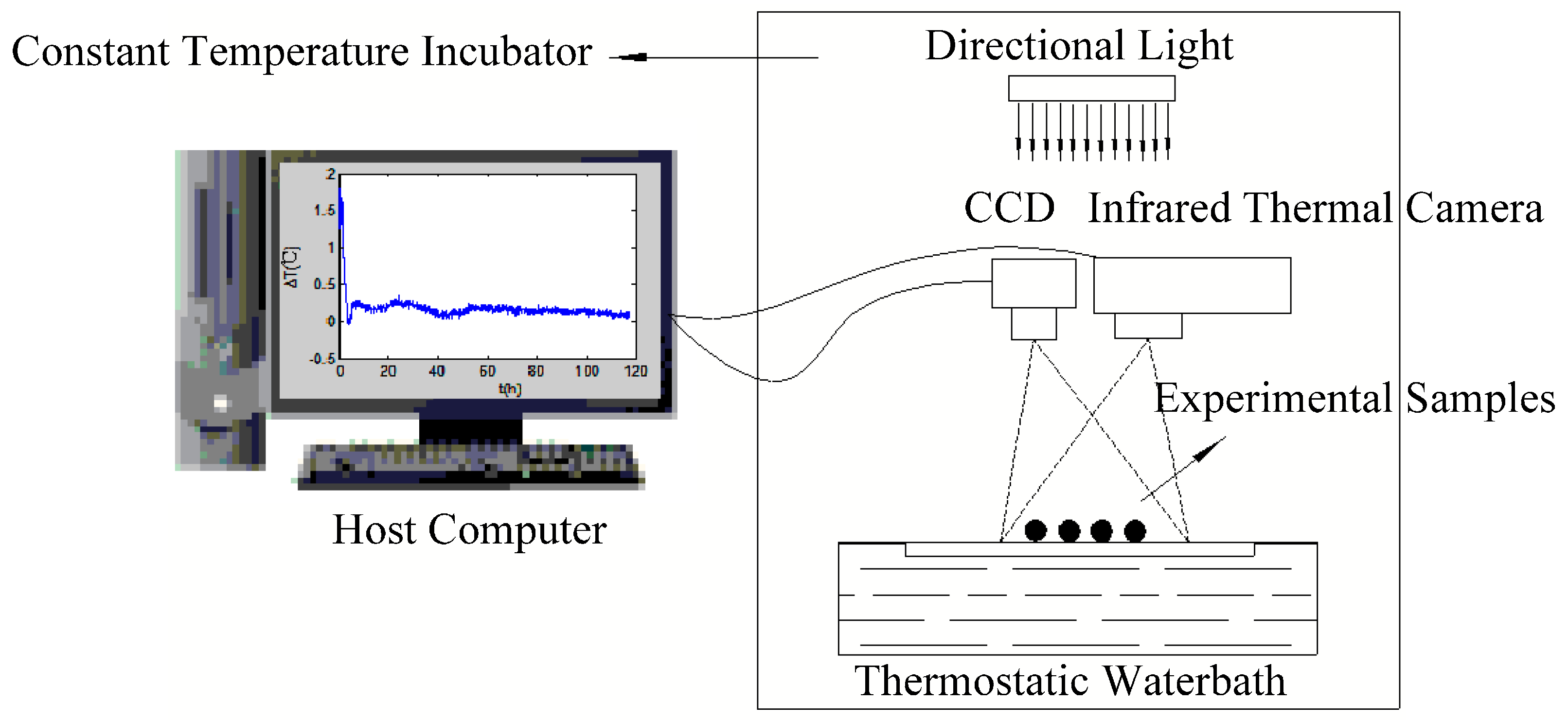
Polycarbonate plates (cryogenic vial holders with holes) were used as the Petri dish in the germination experiment. The polycarbonate plate was placed in a water bath and covered with filter paper. Every seed was placed above the well of the polycarbonate plate with a little well-hydrated dip formed under the seeds. Ambient temperature, including both air and water temperature, was maintained constant at 24 °C with minimal convection to reduce the environment impact on seeds. The infrared thermography system, including a light source, infrared thermal camera, charge coupled device (CCD) and waterbath was put in the constant temperature incubator. The visible and thermal images that captured by infrared camera and CCD respectively, are shown in
Figure 1. During the standard germination test, the temperature incubator has held constant at 24 °C (±0.4 °C) and the seeds continuously exposed to light till the end of the experiment.
2.2. Image Analysis
Figure 2 shows a schematic of the infrared thermography system used to capture and analyze the thermal and visible images of the seeds. This system consists of an infrared thermal camera, a digital color charge-coupled device (CCD) camera, a directional light source, a constant temperature incubator, a thermostatic waterbath, and a host computer. A resolution of 320 × 240 pixels thermal images were registered by the infrared thermal camera Ti55 (Fluke, Everett, WA, USA) with a sensitivity of 0.02 °C and preliminarily processed with the Smartview software (Fluke Systems). Visible images with a resolution of 900 × 600 pixels acquired from the CCD were digitized to 8 bit (256 grey levels) data and stored. Both thermal and visible images were stored every 5 mins over five days and could be exported as individual images or as a series of images in time sequence. Afterwards, these thermal and visible images were analyzed with the software MATLAB (MathWorks, Natick, MA, USA) for post-processing.
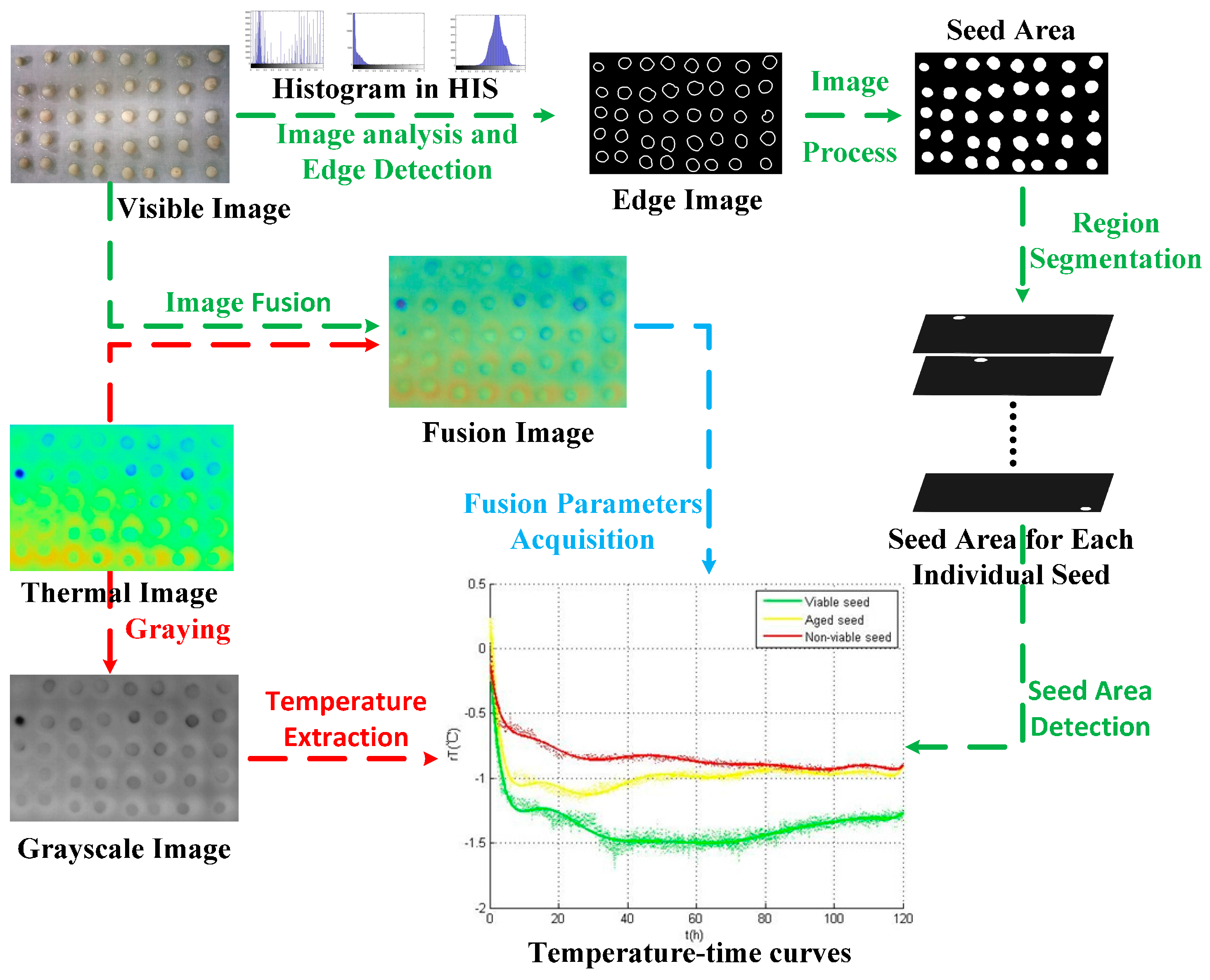
As shown in
Figure 3, due to the effect of water uptake and respiration, heat convection between the seeds and the ambient (both air and water) lasts during the whole germination period until the end of the experiment. Under the impact of this convection, the edges of the seeds in the profiles merge into the background, but in the visible images, the unabridged edges can be detected. By the image fusion technology, the temperature information of seed areas restricted by the shapes in the visible images could be acquired to plot the curves of seeds in the different viability categories during the germination period.
Regarding the characteristics of visible images, we propose an image processing flow to acquire each individual seed areas in the images. As a pre-processing approach, background subtraction can eliminate any non-uniform brightness areas and reflection points in the visible images. The edges of individual seeds were detected by the edge extraction method, and a region growing method was introduced to form the segmented regions. A disk whose area was approximately one-third of the seed area was placed in the center of each seed and defined as the seed area.
Thermal images obtained during the experiment were displayed as pseudo-color images and were transformed into grayscale images which recorded the temperature as gray values. Maximum (grey level is 255) and minimum (grey level is 0) gray values corresponded respectively to the preset maximum (27 °C) and minimum (21 °C) temperature value before the experiment.
Image fusion technology was adopted to extract seed regions in the thermal images with the disk areas in the visible images. Then, the temperature data of each individual seed was obtained through multiplication of thermal images and visible images. The average over all pixels of the seed region was calculated as the resulting temperature value
T and the value can be expressed as the follow equation (Equation (1)):
where
Ii is the grey value of the
i pixel in the thermal image,
n represents the total pixel number of the seed region.
Tmax and
Tmin are the pre-set maximum and minimum temperature values. 255 and 0 are the maximum and minimum grey values in the thermal image.
For the purpose of correcting the temperature value, the temperature of filter paper area around each individual seed area was defined as the environmental temperature of the seed. This ambient area temperature was then introduced into the calculation. Similar to the calculation of temperature value in the seed area, the environment temperature can be calculated by (Equation (1)). Define
rT as the temperature difference between the seed area and the environment area, namely. This difference was expressed in the equation (Equation (2)):
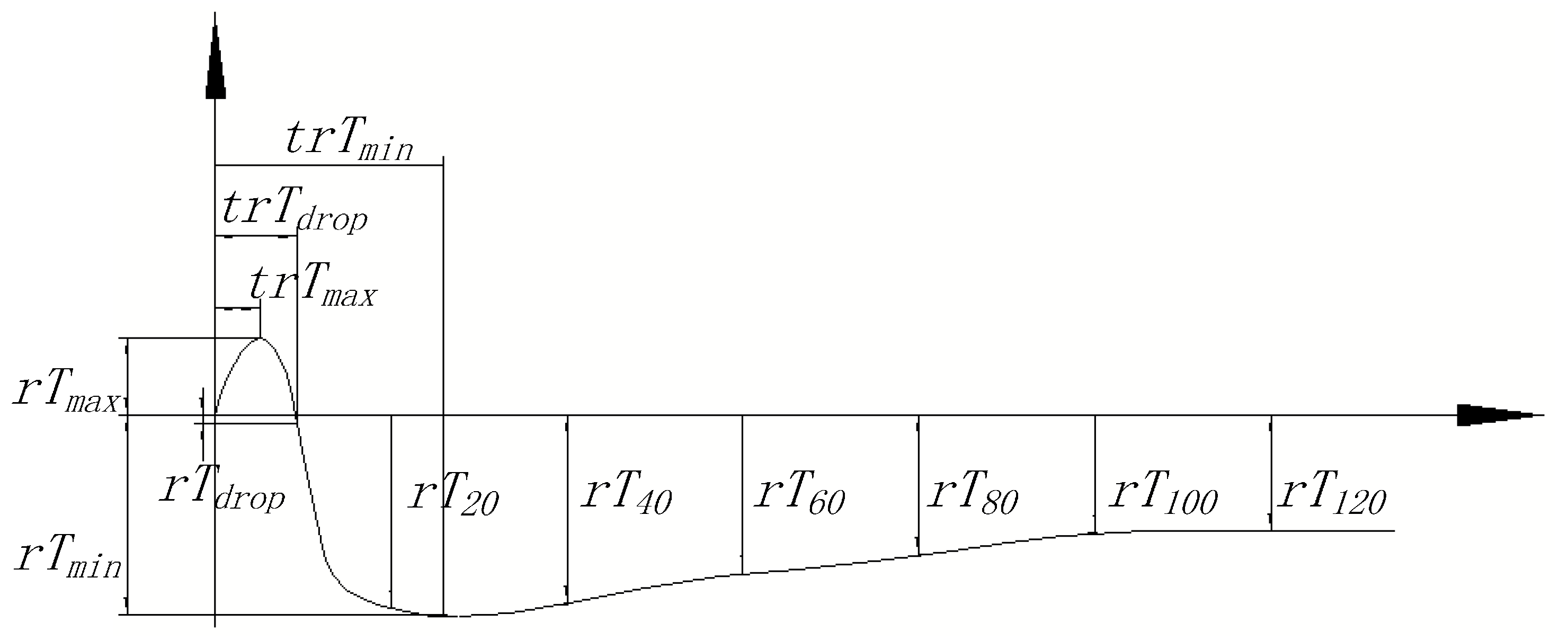
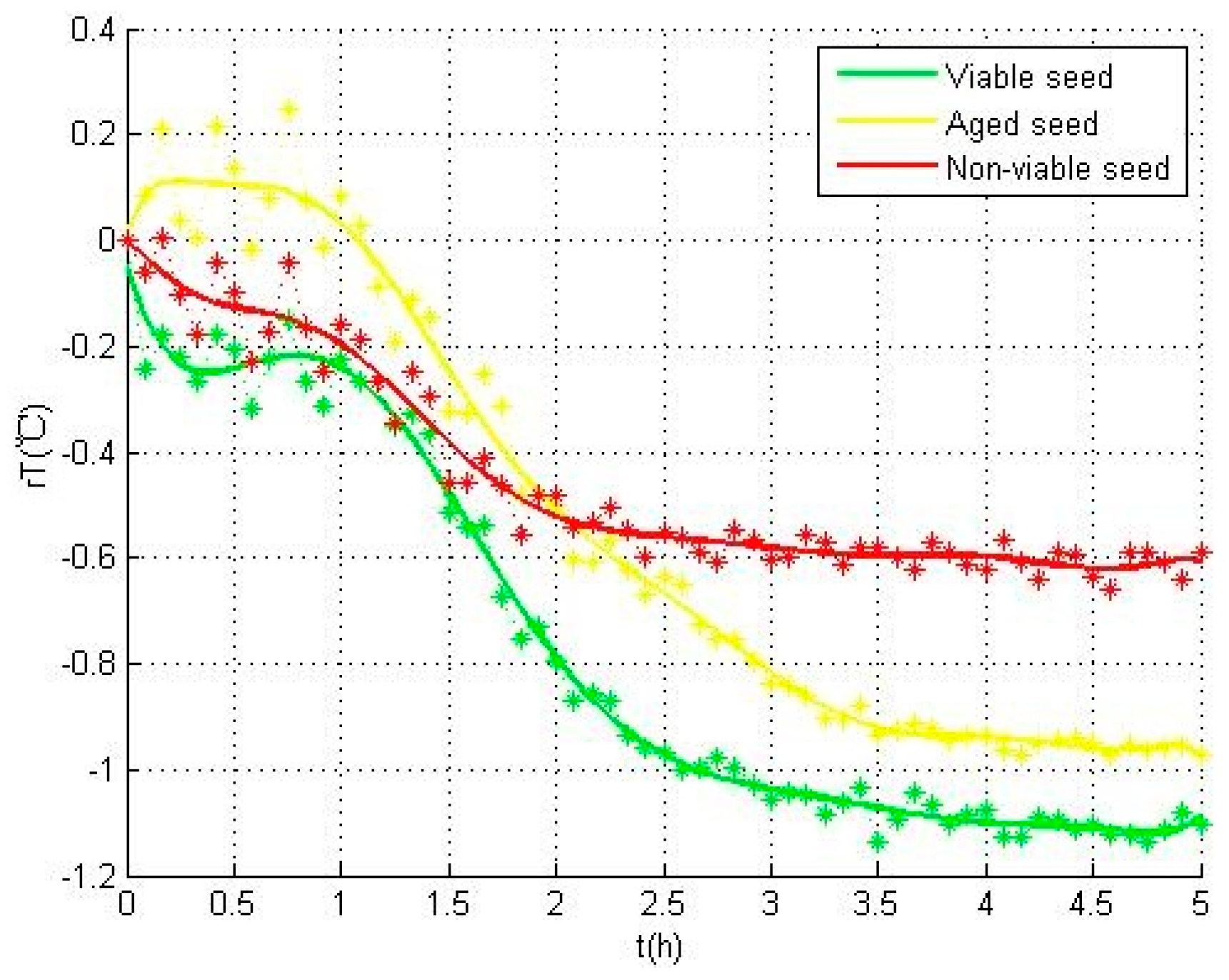
A total number of 1440 thermal images were used to describe the temperature variation for each individual seed during the experiment. This variation was analyzed by the software MATLAB to obtain the temperature curve of each individual seed.
The temperature-time curve of each seed was analysis to extract its characteristic parameters. Then, these parameters were measured by Least Significant Difference (LSD) multiple comparison analysis method. LSD method is used to analyze the multiple comparisons as follows: calculate the ratio of absolute temperature value of two variables
and its standard error of mean difference. The standard error of the mean difference was calculated using the following equation (Equation (3)):
where
MSe is mean square error in F test,
n is number of variables.
The ratio would be compared with the critical value of 2-tailed samples T-test (
α = 0.05). The equation
LSDα could be transformed into the equation (Equation (4)) as:
The results shows that and have a significant difference in α level if the ratio is higher than LSDα. Conversely, the difference between and is not significant.
2.3. Classification Algorithm
Support vector machine (SVM) was first introduced by Cortes as a universal feed-forward classification algorithm. The SVM approach is a supervised method based on the statistical learning theory and structural risk minimization principle, and can be used to analyze data and recognize images. The strategy of SVM classification is to find an optimal separating hyperplane between classes by focusing on training samples that locate at the edge of the class distributions. The main characteristics of SVM are as follows:
- (1)
SVM can be generalized in high-dimensional spaces with only a small amount of training samples.
- (2)
The optimum result can be given by SVM through transforming the problem into a quadratic programming problem.
- (3)
SVM can simulate nonlinear functional relationships.
A brief description of the SVM classification is given below. In a binary classification problem, the aim is to develop a classifier that generalizes accurately for predicting the membership of a class yi (−1, +1) from m-dimensional input data represented by a vector X = {x1, x2, …, xm}. In the case of seed viability assessment based on infrared thermography, m represents the number of the characters of the temperature variation curve during the germination. Before prediction, it is necessary to train a data set containing the characters corresponding to n experimental samples of a known class.
The core of SVM algorithm is to search the optimal hyperplane that separates different classes. This hyperplane can be described as the follow equation (Equation (5)):
where
w is the normal vector of the hyperplane and
b is the offset. During the training process, SVM tries to find the hyperplane that can not only maximize the shortest distance from this hyperplane to the closest training sample of each class (the class
yi = +1 and the class
yi = −1), but also minimize the classification error. The support vectors of the two classes lie on two hyperplanes that are parallel to the optimal hyperplane. The distance between these two planes is defined as the margin associated with the separating hyperplane. The optimization of this margin can be converted into a constrained quadratic optimization problem as follow equation (Equation (6)):
where
ξi represents the classification error for the distance between the misclassified sample
i and the corresponding margin hyperplane and
C is the regularization meta- parameter controls the trade-off between the two conflicting objectives, i.e., margin maximization and error minimization. When
C is small, margin maximization is emphasized; whereas when
C is large, error minimization is predominant. According to the Lagrangian dual formulation, the optimal hyperplane can be expressed as a liner combination of the training observations in the following equation (Equation (7)):
where
αi is a Lagrange multiplier that corresponds to a coefficient associated with each object. The magnitude of
αi is related to the parameter
C and varies between 0 and
C.
For nonlinear classification problems, the input data are mapped into a high dimensional space through a mapping function. Then the data can be separated with a linear SVM. In the dual representation, a kernel, the inner product of two vectors of
u(
x1) and
u(
x2) is used as the mapping function. In this study, the radial basis function (RBF) kernel is used for its advantage of good performance in obtaining almost all boundary shapes. The RBF kernel function is given as the following equation (Equation (8)):
where
φ(
X1) and
φ(
X2) are the mapping functions of the objects
X1 and
X2 respectively;
σ is the kernel parameter determined by the kernel width meta-parameter.
As a conclusion, the two meta-parameters regularization parameter C and kernel parameter G need to be selected properly as they determine the boundary complexity and the observed classification rate.
The multi classifier is integrated by a single classifier with a certain difference. In this work, a multi classifier y (viable seeds, aged seeds, non-viable seeds) consisted of three two-class classifiers y1 (viable seeds, aged seeds) y2 (viable seeds, non-viable seeds) and y3 (aged seeds, non-viable seeds). To combine these classifiers, the weighted voting algorithm is adopted. The resultant class is given by choosing the class voted by the majority of the classifiers. Only samples from two classed of each individual classifier are used for training.
To be specific, all the classifiers were regarded as a voter with a weight value to produce classification results. The performance differences of the base classifiers was introduced by assign a weight value to each base classifier, and the equation (Equation (9)) is shown as follows:
where
αi is the weight value of
i based classifier.
pi represents the average accuracy of the training set of the
i based classifier.
4. Conclusions
In this study, the infrared thermography technique was proposed as a viability assessment method for pea seeds based on their temperature variations. The temperature on the surfaces of experimental samples was measured in a non-destructive and non-contact way by this technique, and the viability of seeds of different categories were obtained by artificial aging. The thermal profiles of the seeds were recorded during the germination experiment, and the temperature curve for each individual seed was plotted by the method of image processing and image fusion. Finally, the SVM model, as a multi-classification method, was used to classify the seeds into viable, aged and non-viable types according to the root length.
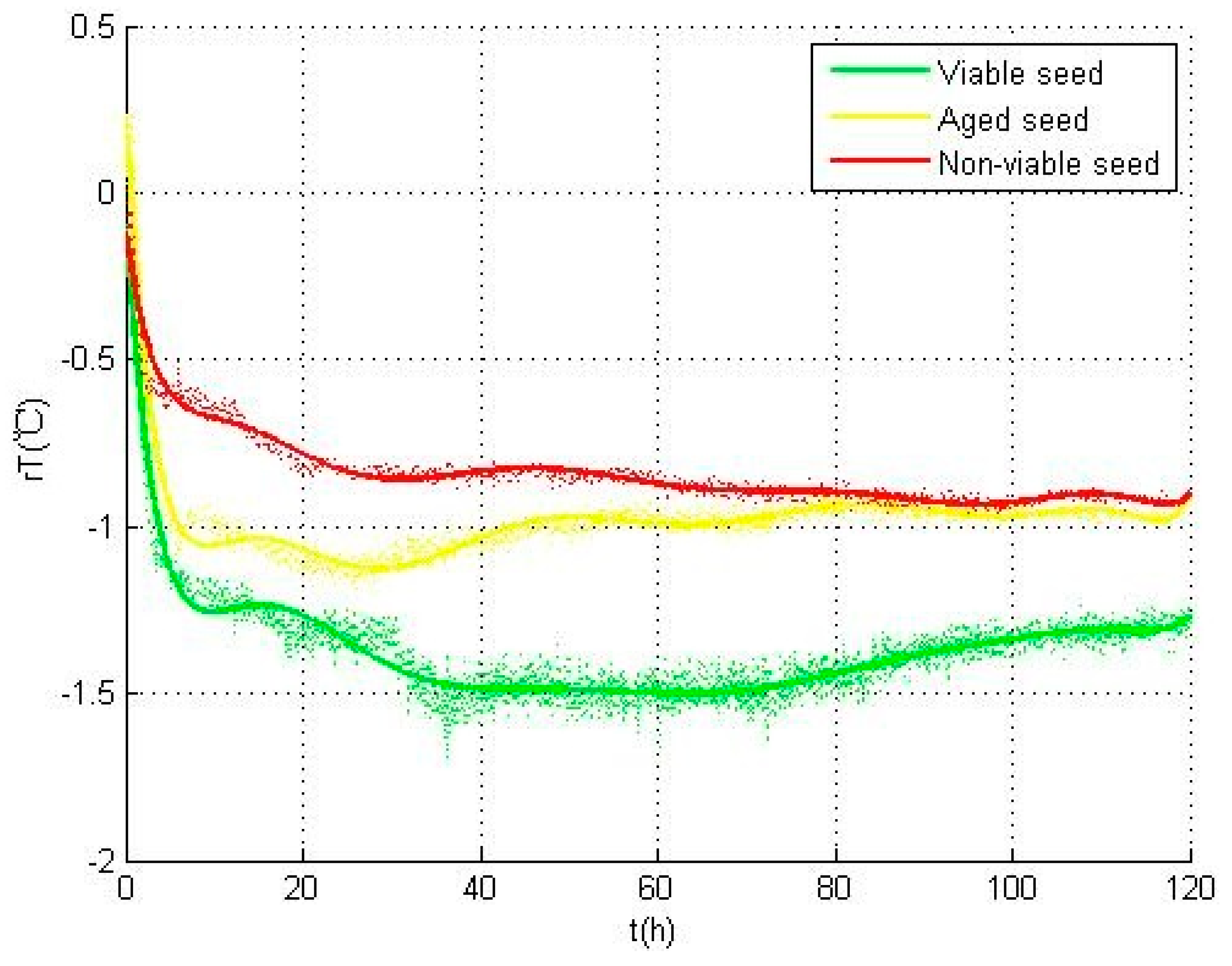
The results showed that there are significant differences between the parameters used for characterizing the temperature variations of seeds depended on the seed viability. With these parameters, SVM was used to classify the seed samples into three categories, and the classification accuracy rate was 95%. On this basis, another SVM model was proposed to predict the seed viability in the first three hours when the seeds can be redried and stored again, and result in an overall accuracy rate of 91.67%.
Our work indicates that the infrared thermography technique can be used as a fast, non-invasive method in seed viability assessment, and has great potential in the viability assessment for various agricultural specimens. In the future, more data from extensive experiments are required to illuminate the relationship between the temperature variations and the specific biophysical and biochemical activities.