Model-Based Estimation of Ankle Joint Stiffness
Abstract
:1. Introduction
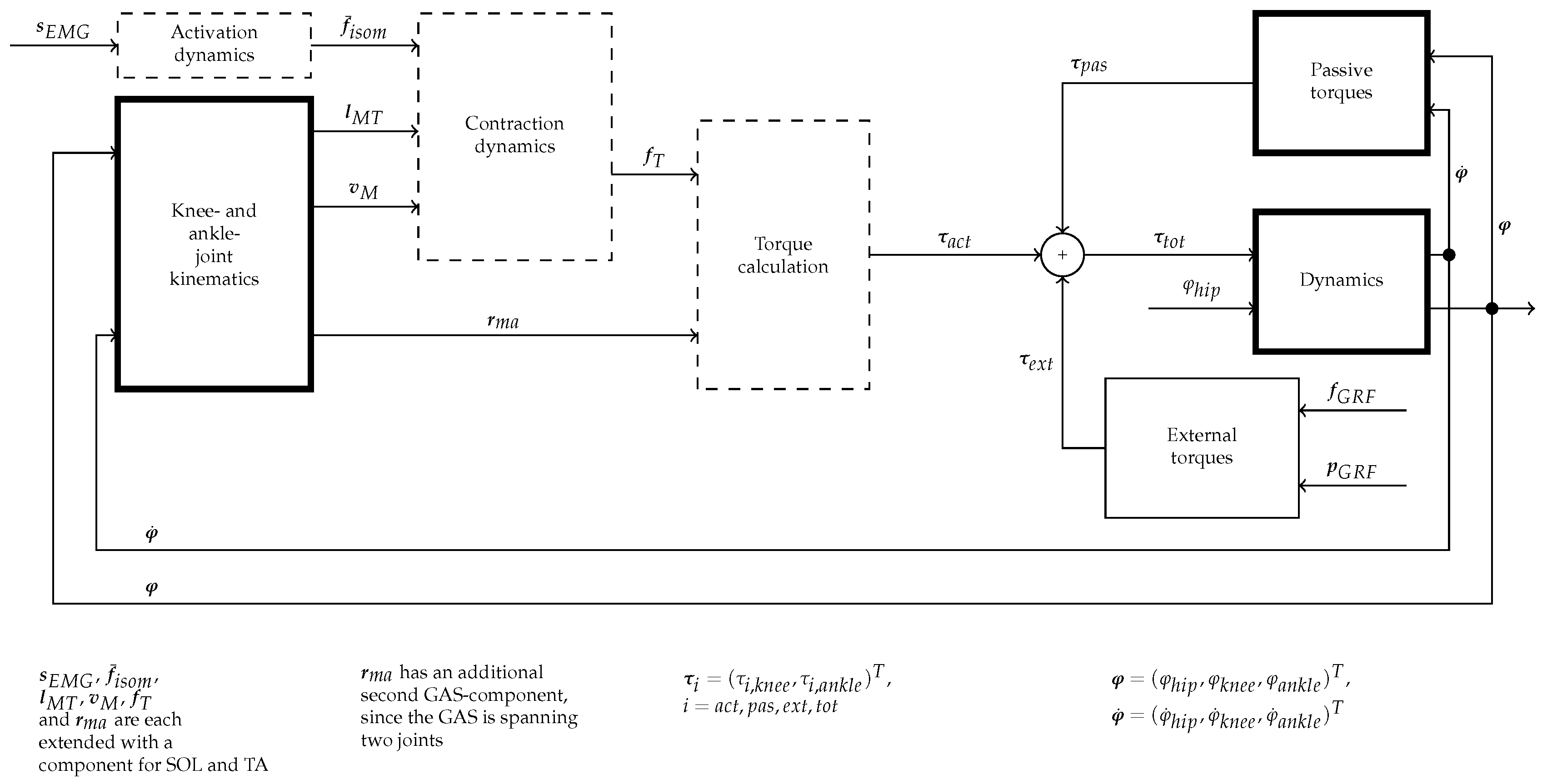
2. Dynamic Lower Extremity Modelling
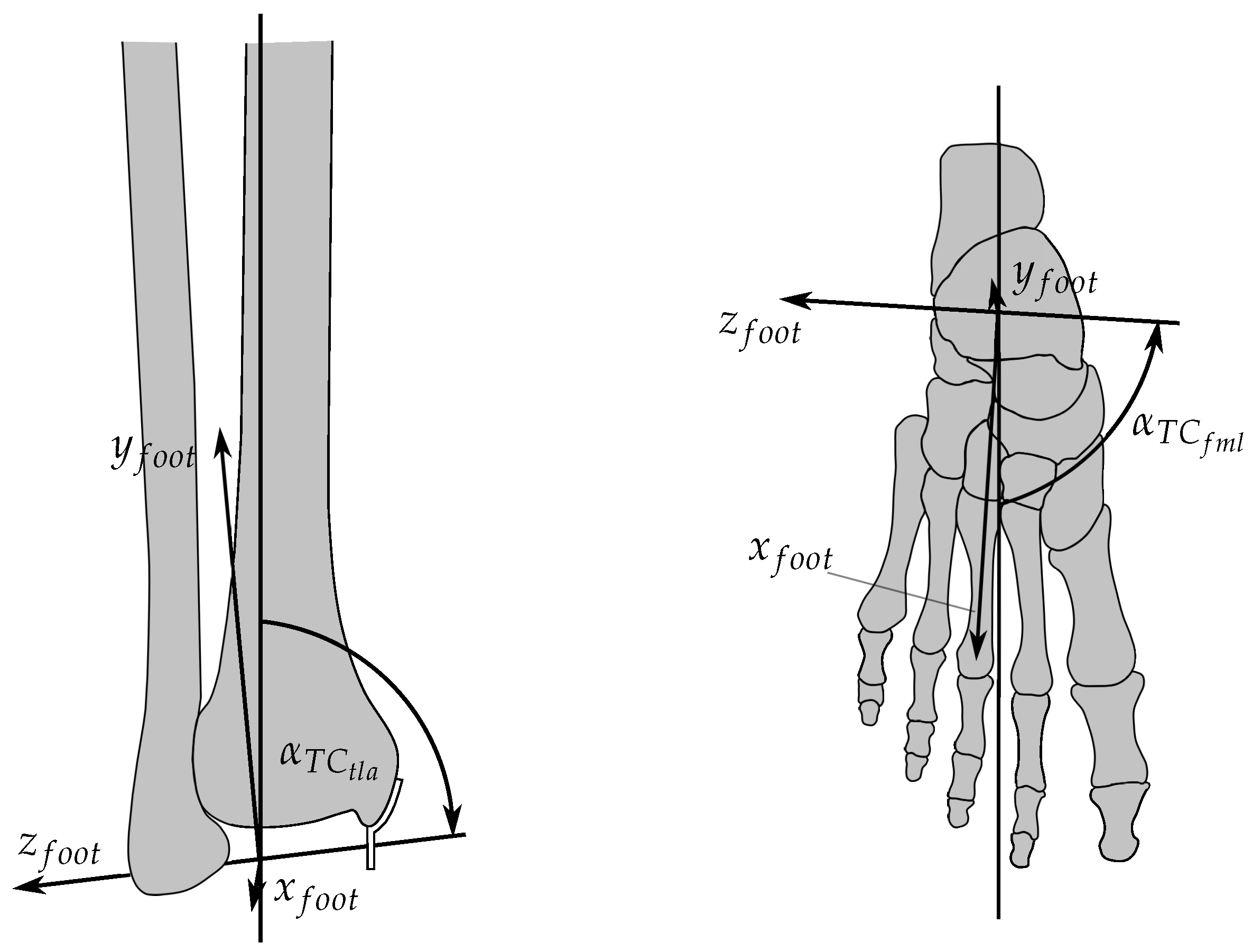
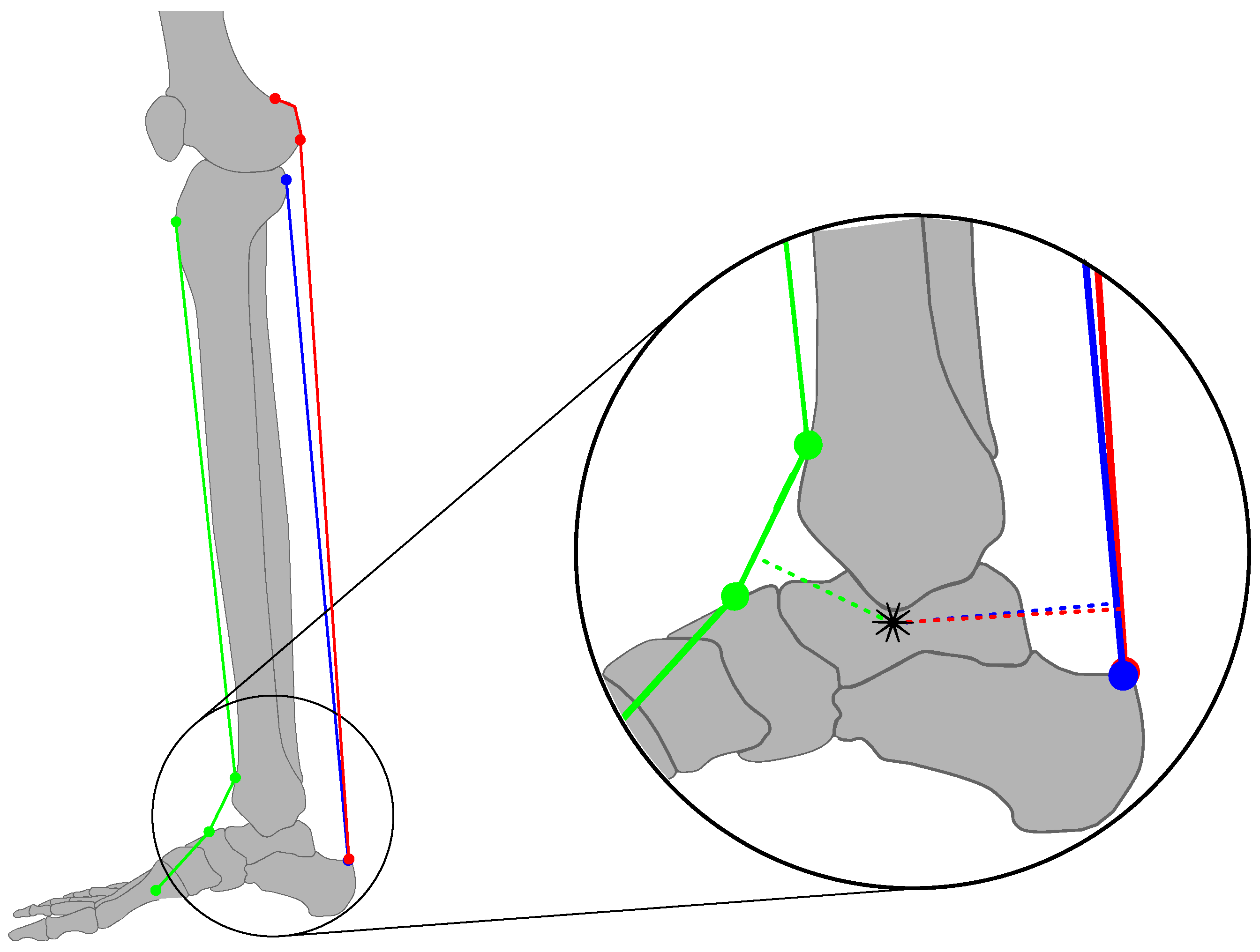
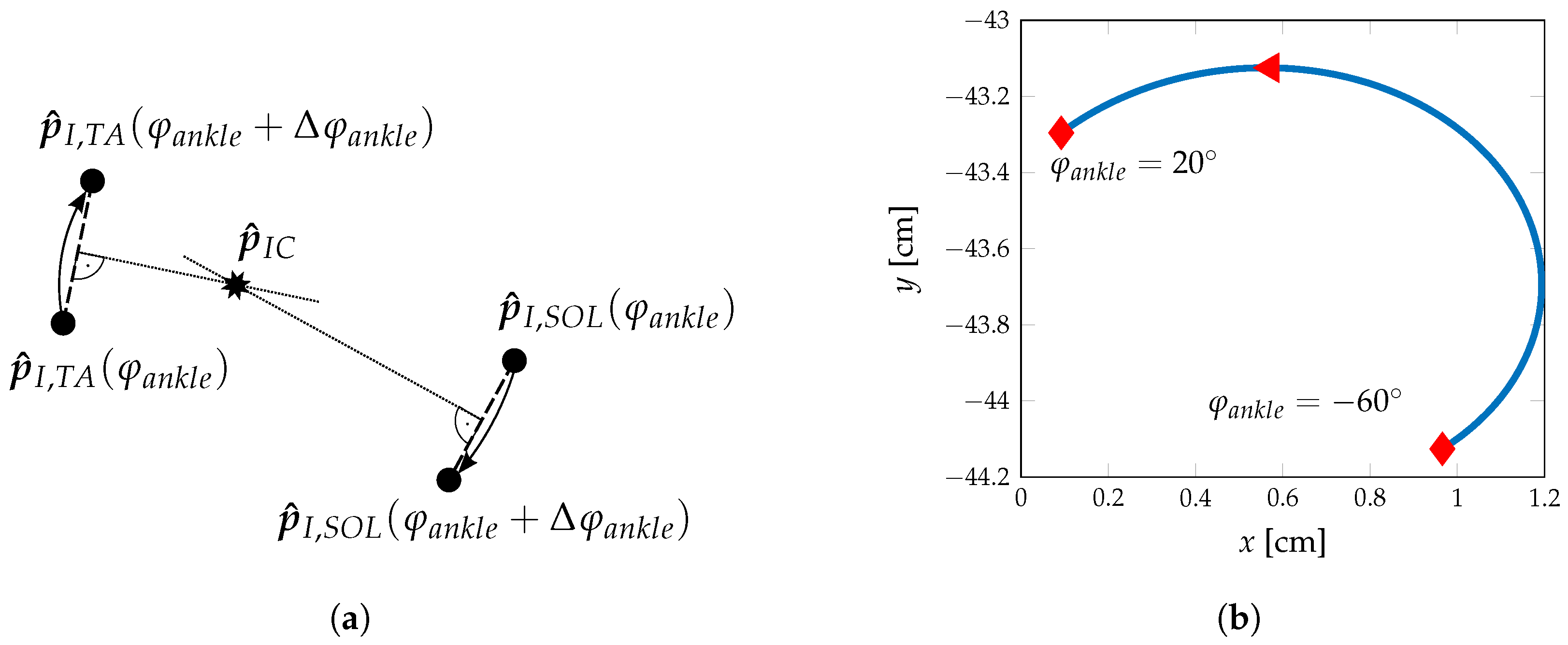
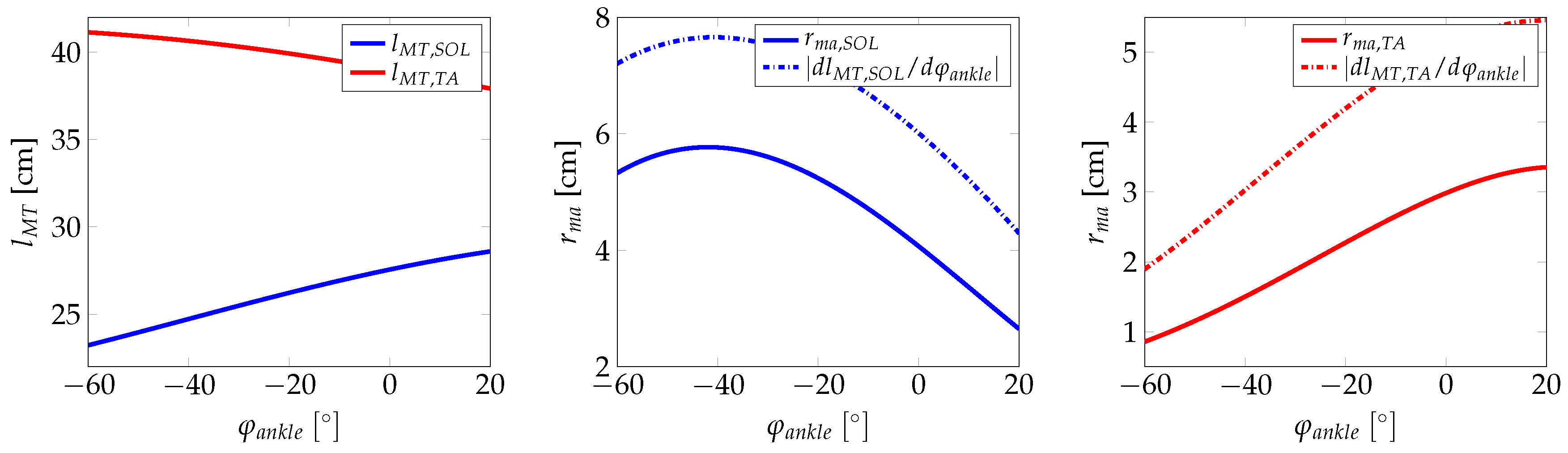
2.1. Ankle Kinematic Model
2.2. Hip Kinematic Model
2.3. Lower Extremity Dynamics
3. Methods and Material
3.1. Cubature Kalman Filter and Square-Cubature Kalman Filter
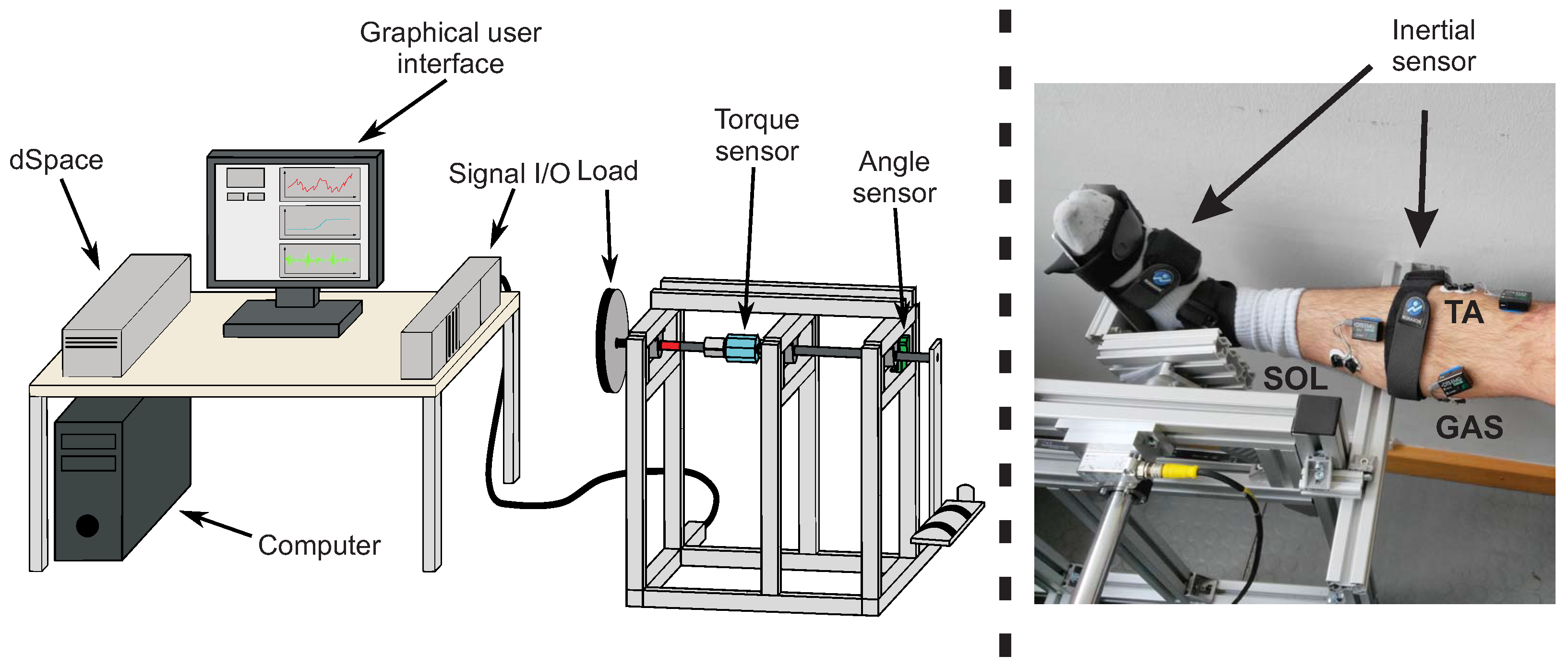
3.2. Experimental Setup
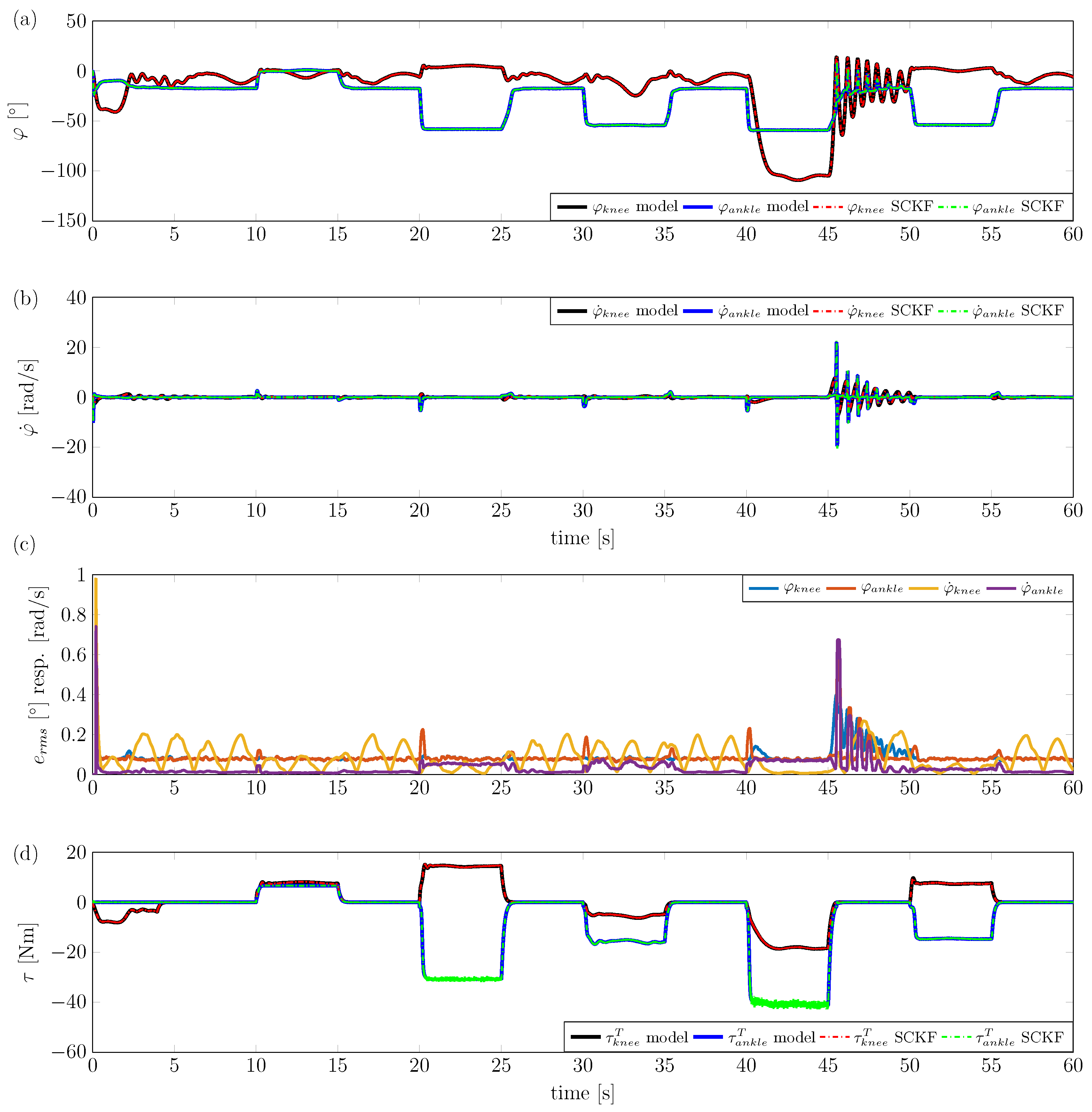
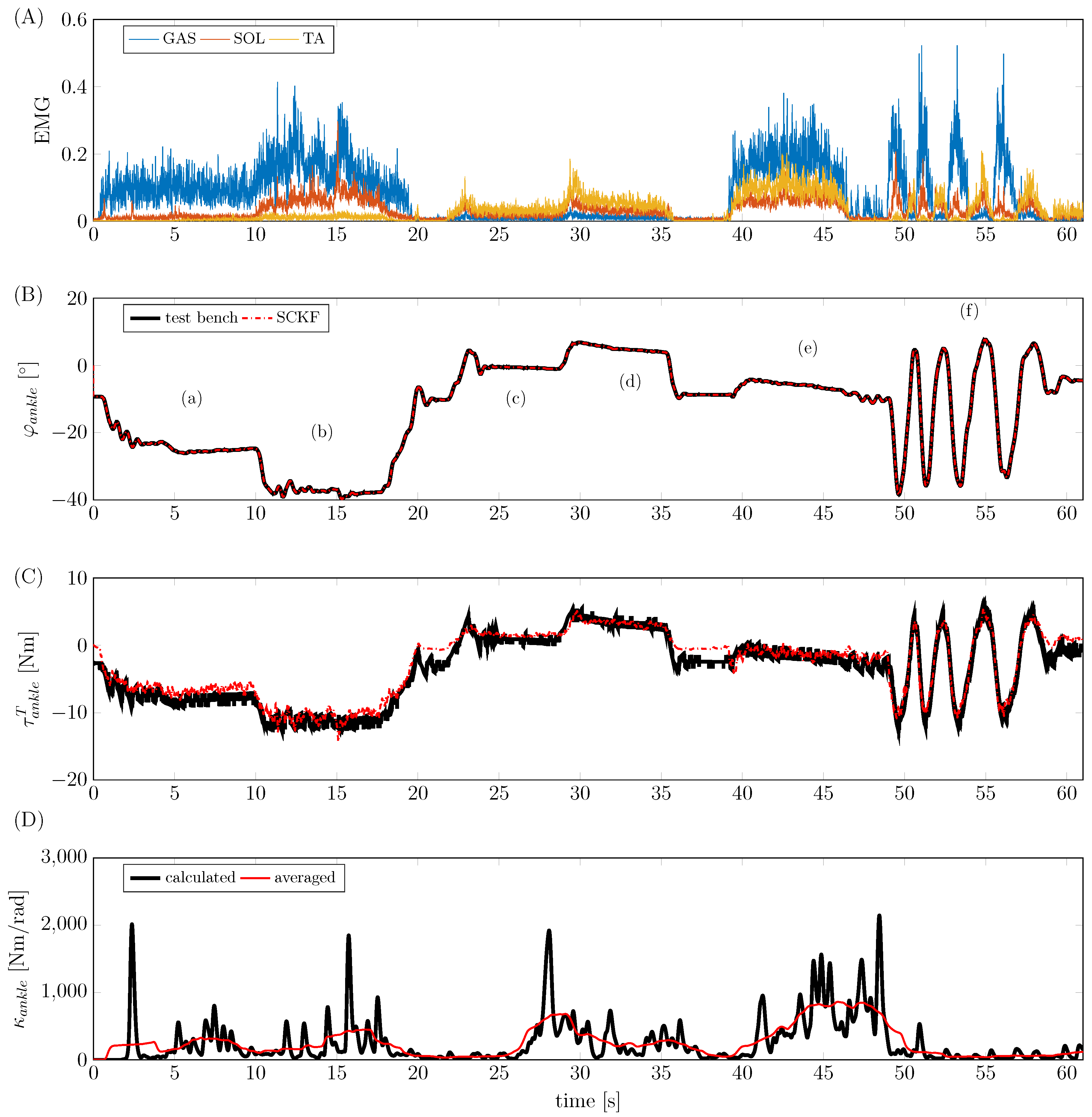
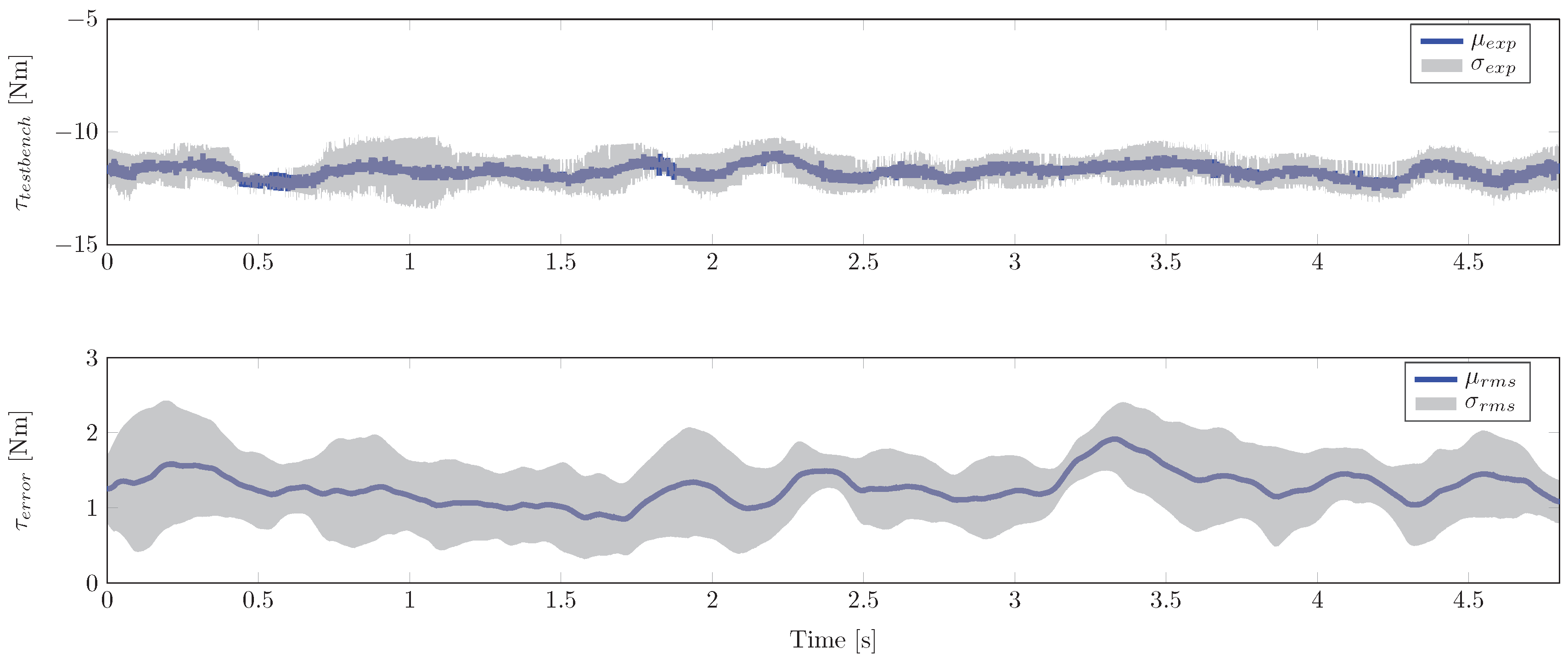
4. Simulation and Experimental Results
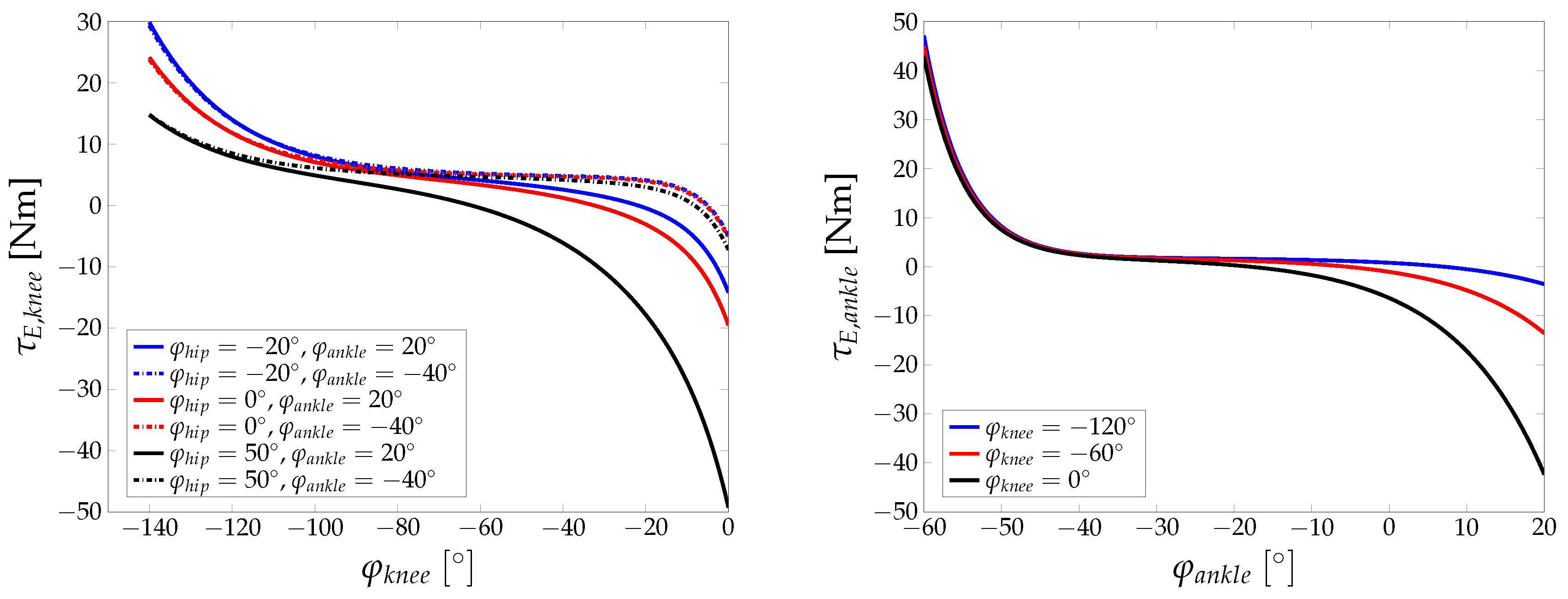
4.1. Simulation Study
4.2. Experimental Study
5. Discussion and Conclusions
Author Contributions
Conflicts of Interest
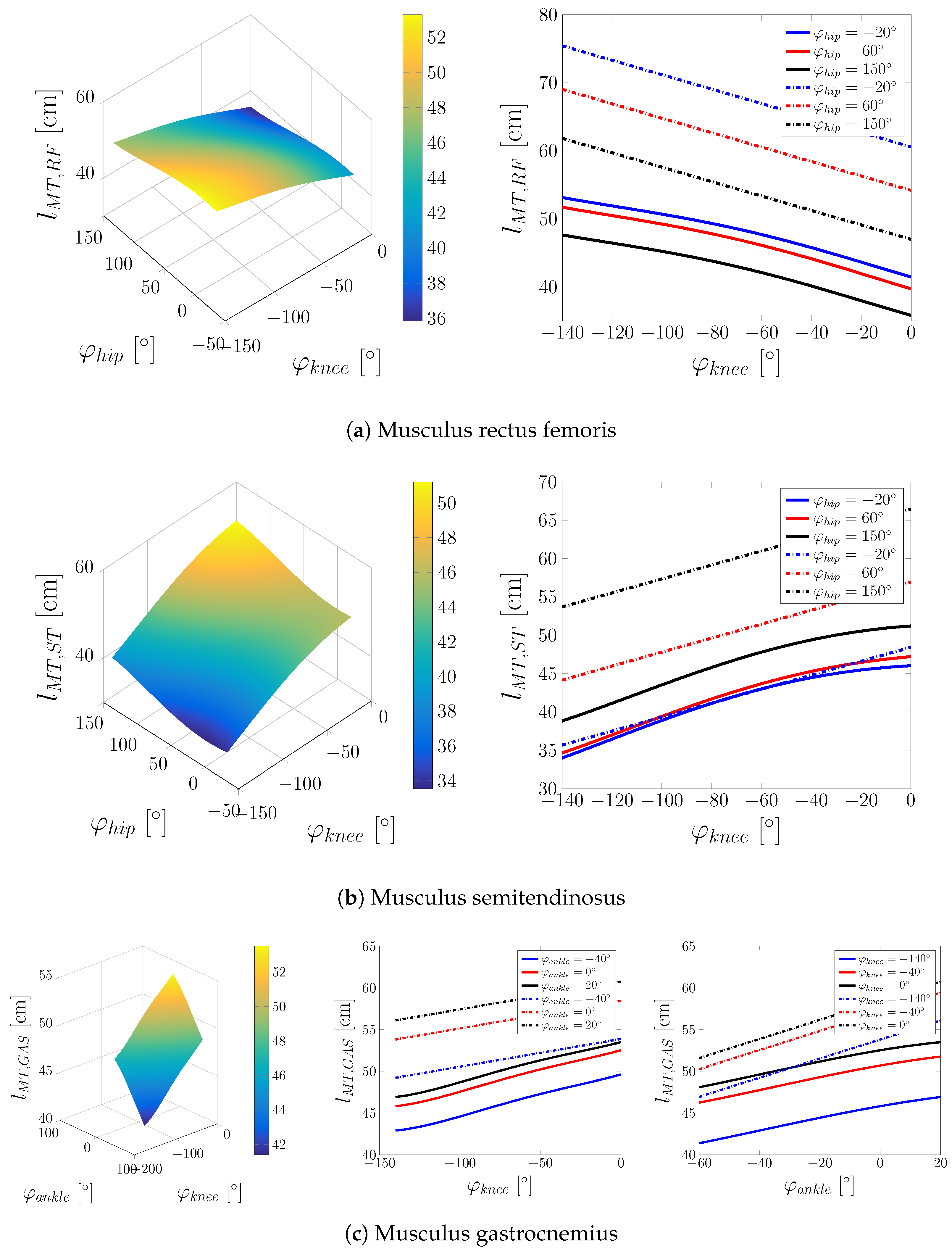
Appendix A. Additional Figures
Appendix B. Experimental Protocol
| Movement | Description | Approximate Duration (s) | |
|---|---|---|---|
| 0 | Maximum voluntary contraction | Maximum voluntary contraction of involved muscles | 5 |
| 1 | Plantar flexion | Loose stretching of the foot | 5 |
| 2 | Maximal plantar flexion | Stretching the foot as far as possible | 5 |
| 3 | Dorsiflexion | Loose upward flexion of the foot | 5 |
| 4 | Maximal dorsiflexion | Flexing the foot upward as far as possible | 5 |
| 5 | Coactivation | Tensing of all muscles around the ankle, thereby locking foot in a fixed position | 10 |
| 6 | Dynamic plantar/dorsiflexion | Dynamic switching between stretching and upward flexion | 10 |
Appendix C. Experimental Performance
| ID | Peak Error (Nm) | Test-Bench Torque at Peak (Nm) | Peak Error Excluding Dynamic Movement (Nm) | Test-Bench Torque at Peak Excluding Dynamic Movement (Nm) |
|---|---|---|---|---|
| 001 | 6.7238 | −11.0530 | 3.6368 | 10.5838 |
| 002 | 6.4308 | 12.3142 | 4.6228 | 21.2717 |
| 003 | 5.6401 | 12.4584 | 5.6401 | 12.4584 |
| 004 | 4.0512 | −4.6143 | 4.0512 | −4.6143 |
| 006 | 8.1544 | 22.45 | 8.1544 | 22.45 |
Appendix D. Model Parameters
| Parameter | Descriptionri | Value | Source |
|---|---|---|---|
| Pennation angle of RF | 13.9 | [55] | |
| Pennation angle of HAMS, represented here by the semimembranosus | 15.1 | [55] | |
| Pennation angle of GAS, represented here by the medial head of GAS | 9.9 | [55] | |
| Pennation angle of VM | 29.6 | [55] | |
| Pennation angle of SOL | 28.3 | [55] | |
| Pennation angle of TA | 9.6 | [55] | |
| Maximum contraction speed of RF | 0.76 m/s | [55] | |
| Maximum contraction speed of HAMS, represented here by the semimembranosus | 0.69 m/s | [55] | |
| Maximum contraction speed of GAS, represented here by the medial head of GAS | 0.51 m/s | [55] | |
| Maximum contraction speed of VM | 0.97 m/s | [55] | |
| Maximum contraction speed of SOL | 0.44 m/s | [55] | |
| Maximum contraction speed of TA | 0.68 m/s | [55] | |
| Length of thigh | individual | Reg. Equations from [62] | |
| Length of shank | individual | Reg. Equations from [62] | |
| Length of foot | individual | Reg. Equations from [62] | |
| Distance from distal end of thigh to its centre of mass | individual | Reg. Equations from [47] | |
| Distance from distal end of shank to its centre of mass | individual | Reg. Equations from [47] | |
| Length of dorsum | individual | Based on [46] | |
| x coordinate of centre of mass of foot with respect to the foot reference frame | individual | Based on [46] | |
| y coordinate of centre of mass of foot with respect to the foot reference frame | individual | Based on [46] | |
| Mass of thigh | individual | Reg. Equations from [47] | |
| Mass of shank | individual | Reg. Equations from [47] | |
| Mass of foot | individual | Reg. Equations from [47] | |
| Principal moments of inertia of thigh | individual | Reg. Equations from [47] | |
| Principal moments of inertia of shank | individual | Reg. Equations from [47] | |
| Principal moments of inertia of foot | individual | Reg. Equations from [47] |
| Parameter | Descriptionri | Value | Source |
|---|---|---|---|
| Angle between talocrural joint axis and midline of foot, projected onto the horizontal plane | 84 | [34] | |
| Angle between talocrural joint axis and long axis of tibia | 80 | [34] | |
| a | Principle axis length of the femur condyle ellipse | 3.31 cm | [63] |
| b | Semi-axis length of the femur condyle ellipse | 2.71 cm | [63] |
| Angle between femur axis and femur condyle semi-axis | 14 | [63] | |
| Tibia plateau length | 5.3 cm | [63] | |
| Angle between perpendicular with respect to tibia axis and tibia plateau | 3 | [63] | |
| Distance between tibia plateau edge and tibial tuberosity | 4.5 cm | [63] | |
| Angle between tibia axis and tibial tuberosity appendage | 15 | [63] | |
| Patella tendon length | 6.5 cm | [63] | |
| Patella length | 3.94 cm | [64] | |
| Patella width | 1.63 cm | [64] | |
| Coordinates of origin of SOL in shank reference frame [cm] | [−2.92, 24.67, 0.06] | [43] | |
| Coordinates of insertion of SOL in foot reference frame [cm] | [−3.65, −2.88, 0.56] | [43] | |
| Coordinates of insertion of GAS in foot reference frame [cm] | [−3.68, −2.89, 0.28] | [43] | |
| Coordinates of origin of TA in shank reference frame [cm] | [−1.55, 21.75, 1.34] | [43] | |
| Coordinates of effective origin of TA in shank reference frame [cm] | [2.56, 2.57, −0.93] | [43] | |
| Coordinates of insertion of TA in foot reference frame [cm] | [18.50, −5.10, −3.30] | [43] | |
| Coordinates of effective insertion of TA in foot reference frame [cm] | [7.57, −4.20, −1.96] | [44] | |
| Maximum isometric force of muscle i | individual | Exp. det. | |
| Parameters of passively generated viscoelastic torques | individual | Exp. det. |
References
- Marchal-Crespo, L.; Reinkensmeyer, D.J. Review of control strategies for robotic movement training after neurologic injury. J. Neuroeng. Rehabil. 2009, 6, 20. [Google Scholar] [CrossRef] [PubMed]
- Vanderborght, B.; Albu-Schäffer, A.; Bicchi, A.; Burdet, E.; Caldwell, D.G.; Carloni, R.; Catalano, M.; Eiberger, O.; Friedl, W.; Ganesh, G.; et al. Variable impedance actuators: A review. Robot. Auton. Syst. 2013, 61, 1601–1614. [Google Scholar] [CrossRef]
- Misgeld, B.; Lüken, M.; Heitzmann, D.; Wolf, S.; Leonhardt, S. Body Sensor Network-Based Spasticity Detection. IEEE J. Biomed. Health Inf. 2016, 20, 748–755. [Google Scholar] [CrossRef] [PubMed]
- Burdet, E.; Osu, R.; Franklin, D.W.; Milner, T.E.; Kawato, M. The central nervous system stabilizes unstable dynamics by learning optimal impedance. Nature 2001, 414, 446–449. [Google Scholar] [CrossRef] [PubMed]
- Hogan, N. Adaptive Control of Mechanical Impedance by Coactivation of Antagonist Muscles. IEEE Trans. Autom. Control 1984, 29, 681–690. [Google Scholar] [CrossRef]
- Franklin, D.W.; Osu, R.; Burdet, E.; Kawato, M.; Milner, T.E. Adaptation to stable and unstable dynamics achieved by combined impedance control and inverse dynamics model. J. Neurophysiol. 2003, 90, 3270–3282. [Google Scholar] [CrossRef] [PubMed]
- Scheidt, R.A.; Dingwell, J.B.; Mussa-Ivaldi, F.A. Learning to move amid uncertainty. J. Neurophysiol. 2001, 86, 971–985. [Google Scholar] [PubMed]
- Rouse, E.J.; Gregg, R.D.; Hargrove, L.J.; Sensinger, J.W. The Difference Between Stiffness and Quasi-Stiffness in the Context of Biomechanical Modeling. IEEE Trans. Biomed. Eng. 2013, 60, 562–568. [Google Scholar] [CrossRef] [PubMed]
- Kearney, R.; Hunter, I. Dynamics of human ankle stiffness: Variation with displacement amplitude. J. Biomech. 1982, 15, 753–756. [Google Scholar] [CrossRef]
- Winters, J.M.; Stark, L. Analysis of fundamental human movement patterns through the use of in-depth antagonistic muscle models. IEEE Trans. Biomed. Eng. 1985, 36, 826–839. [Google Scholar] [CrossRef] [PubMed]
- Wynarsky, G.T.; Greenwald, A.S. Mathematical model of the human ankle joint. J. Biomech. 1983, 16, 241249–247251. [Google Scholar]
- Apkarian, J.; Naumann, S.; Cairns, B. A three-dimensional kinematic and dynamic model of the lower limb. J. Biomech. 1989, 22, 143–155. [Google Scholar] [CrossRef]
- Glitsch, U.; Baumann, W. The three-dimensional determination of internal loads in the lower extremity. J. Biomech. 1997, 30, 1123–1131. [Google Scholar] [CrossRef]
- Pizzolato, C.; Lloyd, D.G.; Sartori, M.; Ceseracciu, E.; Besier, T.F.; Fregly, B.J.; Reggiani, M. CEINMS: A toolbox to investigate the influence of different neural control solutions on the prediction of muscle excitation and joint moments during dynamic motor tasks. J. Biomech. 2015, 48, 3929–3936. [Google Scholar] [CrossRef] [PubMed]
- Riener, R.; Edrich, T. Identification of passive elastic joint moments in the lower extremities. J. Biomech. 1999, 32, 539–544. [Google Scholar] [CrossRef]
- Lee, H.; Krebs, H.I.; Hogan, N. Multivariable dynamic ankle mechanical impedance with active muscles. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 971–981. [Google Scholar] [CrossRef] [PubMed]
- Van Eesbeek, S.; Van Der Helm, F.; Verhaegen, M.; De Vlugt, E. LPV subspace identification of time-variant joint impedance. In Proceedings of the 6th International IEEE/EMBS Conference on Neural Engineering (NER 2013), San Diego, CA, USA, 6–8 November 2013; pp. 343–346. [Google Scholar]
- Kearney, R.E.; Stein, R.B.; Parameswaran, L. Identification of intrinsic and reflex contributions to human ankle stiffness dynamics. IEEE Trans. Biomed. Eng. 1997, 44, 493–504. [Google Scholar] [CrossRef] [PubMed]
- Sartori, M.; Reggiani, M.; Farina, D.; Lloyd, D.G. EMG-driven forward-dynamic estimation of muscle force and joint moment about multiple degrees of freedom in the human lower extremity. PLoS ONE 2012, 7, e52618. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, D.G.; Besier, T.F. An EMG-driven musculoskeletal model to estimate muscle forces and knee joint moments in vivo. J. Biomech. 2003, 36, 765–776. [Google Scholar] [CrossRef]
- Sartori, M.; Maculan, M.; Pizzolato, C.; Reggiani, M.; Farina, D. Modeling and simulating the neuromuscular mechanisms regulating ankle and knee joint stiffness during human locomotion. J. Neurophysiol. 2015, 114, 2509–2527. [Google Scholar] [CrossRef] [PubMed]
- Buchanan, T.S.; Lloyd, D.G. Muscle activity is different for humans performing static tasks which require force control and position control. Neurosci. Lett. 1995, 194, 61–64. [Google Scholar] [CrossRef]
- Pfeifer, S.; Vallery, H.; Hardegger, M.; Riener, R.; Perreault, E.J. Model-based estimation of knee stiffness. IEEE Trans. Biomed. Eng. 2012, 59, 2604–2612. [Google Scholar] [CrossRef] [PubMed]
- Rouse, E.J.; Hargrove, L.J.; Perreault, E.J.; Kuiken, T.A. Estimation of human ankle impedance during the stance phase of walking. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 870–878. [Google Scholar] [PubMed]
- Blaya, J.A.; Herr, H. Adaptive control of a variable-impedance ankle-foot orthosis to assist drop-foot gait. IEEE Trans. Neural Syst. Rehabil. Eng. 2004, 12, 24–31. [Google Scholar] [CrossRef] [PubMed]
- Eilenberg, M.F.; Geyer, H.; Herr, H. Control of a powered ankle–foot prosthesis based on a neuromuscular model. IEEE Trans. Neural Syst. Rehabil. Eng. 2010, 18, 164–173. [Google Scholar] [CrossRef] [PubMed]
- Arasaratnam, I.; Haykin, S. Cubature Kalman Filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef]
- Misgeld, B.J.E.; Lueken, M.; Riener, R.; Leonhardt, S. Observer-based human knee stiffness estimation. IEEE Trans. Biomed. Eng. 2017. Epub ahead of print. [Google Scholar] [CrossRef] [PubMed]
- Lundberg, A.; Goldie, I.; Kalin, B.; Selvik, G. Kinematics of the ankle/foot complex: plantarflexion and dorsiflexion. Foot Ankle Int. 1989, 9, 194–200. [Google Scholar]
- Leardini, A.; O’connor, J.; Catani, F.; Giannini, S. A geometric model of the human ankle joint. J. Biomech. 1999, 32, 585–591. [Google Scholar] [CrossRef]
- Sheehan, F.T. The instantaneous helical axis of the subtalar and talocrural joints: A non-invasive in vivo dynamic study. J. Foot Ankle Res. 2010, 3, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Barnett, C.; Napier, J. The axis of rotation at the ankle joint in man. Its influence upon the form of the talus and the mobility of the fibula. J. Anat. 1952, 86, 1. [Google Scholar] [PubMed]
- Hicks, J. The mechanics of the foot: I. The joints. J. Anat. 1953, 87, 345. [Google Scholar] [PubMed]
- Isman, R.E.; Inman, V.T. Anthropometric studies of the human foot and ankle. Bull. Prosthet. Res. 1969, 11, 97–108. [Google Scholar]
- Siegler, S.; Chen, J.; Schneck, C. The three-dimensional kinematics and flexibility characteristics of the human ankle and subtalar joints—Part I: Kinematics. J. Biomech. Eng. 1988, 110, 364–373. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.K.; Starkweather, K.D.; Hollister, A.M.; Jatana, S.; Lupichuk, A.G. Kinematics of the ankle: A hinge axis model. Foot Ankle Int. 1992, 13, 439–446. [Google Scholar] [CrossRef]
- Procter, P.; Paul, J. Ankle joint biomechanics. J. Biomech. 1982, 15, 627–634. [Google Scholar] [CrossRef]
- Dul, J.; Johnson, G. A kinematic model of the human ankle. J. Biomed. Eng. 1985, 7, 137–143. [Google Scholar] [PubMed]
- Scott, S.H.; Winter, D.A. Talocrural and talocalcaneal joint kinematics and kinetics during the stance phase of walking. J. Biomech. 1991, 24, 743–752. [Google Scholar] [CrossRef]
- Van Den Bogert, A.J.; Smith, G.D.; Nigg, B.M. In vivo determination of the anatomical axes of the ankle joint complex: an optimization approach. J. Biomech. 1994, 27, 1477–1488. [Google Scholar] [CrossRef]
- Leitch, J.; Stebbins, J.; Zavatsky, A.B. Subject-specific axes of the ankle joint complex. J. Biomech. 2010, 43, 2923–2928. [Google Scholar] [CrossRef] [PubMed]
- Riegger, C.L. Anatomy of the ankle and foot. Phys. Ther. 1988, 68, 1802–1814. [Google Scholar] [CrossRef] [PubMed]
- Hoy, M.G.; Zajac, F.E.; Gordon, M.E. A musculoskeletal model of the human lower extremity: The effect of muscle, tendon, and moment arm on the moment-angle relationship of musculotendon actuators at the hip, knee, and ankle. J. Biomech. 1990, 23, 157–169. [Google Scholar] [CrossRef]
- Yamaguchi, G.; Sawa, A.; Moran, D.; Fessler, M.; Winters, J. A survey of human musculotendon actuator parameters. In Multiple Muscle Systems: Biomechanics and Movement Organization; Springer: New York, NY, USA, 1990; pp. 717–773. [Google Scholar]
- Delp, S.L.; Loan, J.P.; Hoy, M.G.; Zajac, F.E.; Topp, E.L.; Rosen, J.M. An interactive graphics-based model of the lower extremity to study orthopaedic surgical procedures. IEEE Trans. Biomed. Eng. 1990, 37, 757–767. [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, G.T.; Zajac, F.E. Restoring Unassisted Natural Gait to Paraplegics via Functional Neuromuscular Stimulation: A Computer Simulation Study. IEEE Trans. Biomed. Eng. 1990, 37, 886–902. [Google Scholar] [CrossRef] [PubMed]
- De Leva, P. Adjustments to Zatsiorsky-Seluyanov’s segment inertia parameters. J. Biomech. 1996, 29, 1223–1230. [Google Scholar] [CrossRef]
- Riener, R.; Fuhr, T. Patient-driven control of FES-supported standing up: a simulation study. IEEE Trans. Rehabil. Eng. 1998, 6, 113–124. [Google Scholar] [CrossRef] [PubMed]
- Amankwah, K.; Triolo, R.J.; Kirsch, R. Effects of spinal cord injury on lower-limb passive joint moments revealed through a nonlinear viscoelastic model. J. Rehabil. Res. Dev. 2004, 41, 15. [Google Scholar] [PubMed]
- Zajac, F.E. Muscle and tendon: properties, models, scaling, and application to biomechanics and motor control. Crit. Rev. Biomed. Eng. 1988, 17, 359–411. [Google Scholar]
- Günther, M.; Schmitt, S.; Wank, V. High-frequency oscillations as a consequence of neglected serial damping in Hill-type muscle models. Biol. Cybern. 2007, 97, 63–79. [Google Scholar] [CrossRef] [PubMed]
- Julier, S.J.; Uhlmann, J.K. Unscented filtering and nonlinear estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef]
- Hermens, H.J.; Freriks, B.; Disselhorst-Klug, C.; Rau, G. Development of recommendations for SEMG sensors and sensor placement procedures. J. Electromyogr. Kinesiol. 2000, 10, 361–374. [Google Scholar] [CrossRef]
- Misgeld, B.J.; Lüken, M.; Leonhardt, S. Identification of isolated biomechanical parameters with a wireless body sensor network. In Proceedings of the 13th IEEE International Conference on Wearable and Implantable Body Sensor Networks (BSN), San Francisco, CA, USA, 14–17 June 2016; pp. 37–42. [Google Scholar]
- Arnold, E.M.; Ward, S.R.; Lieber, R.L.; Delp, S.L. A model of the lower limb for analysis of human movement. Ann. Biomed. Eng. 2010, 38, 269–279. [Google Scholar] [CrossRef] [PubMed]
- Rugg, S.; Gregor, R.; Mandelbaum, B.; Chiu, L. In vivo moment arm calculations at the ankle using magnetic resonance imaging (MRI). J. Biomech. 1990, 23, 495499–497501. [Google Scholar]
- Maganaris, C.N. Imaging-based estimates of moment arm length in intact human muscle-tendons. Eur. J. Appl. Physiol. 2004, 91, 130–139. [Google Scholar] [CrossRef] [PubMed]
- Ito, M.; Akima, H.; Fukunaga, T. In vivo moment arm determination using B-mode ultrasonography. J. Biomech. 2000, 33, 215–218. [Google Scholar] [CrossRef]
- Morasso, P.G.; Sanguineti, V. Ankle Muscle Stiffness Alone Cannot Stabilize Balance During Quiet Standing. J. Neurophysiol. 2002, 88, 2157–2162. [Google Scholar] [PubMed]
- Weiss, P.; Hunter, I.; Kearney, R. Human ankle joint stiffness over the full range of muscle activation levels. J. Biomech. 1988, 21, 539–544. [Google Scholar] [PubMed]
- Hawkins, D.; Hull, M. A method for determining lower extremity muscle-tendon lengths during flexion/extension movements. J. Biomech. 1990, 23, 487–494. [Google Scholar] [CrossRef]
- Winter, D.A. Biomechanics and Motor Control of Human Movement; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Riener, R. Neurophysiologische und Biomechanische Modellierung zur Entwicklung Geregelter Neuroprothesen. Master’s Thesis, Technische Universität München, München, Germany, 1997. [Google Scholar]
- Yamaguchi, G.T.; Zajac, F.E. A planar model of the knee joint to characterize the knee extensor mechanism. J. Biomech. 1989, 22, 1–10. [Google Scholar] [CrossRef]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Misgeld, B.J.E.; Zhang, T.; Lüken, M.J.; Leonhardt, S. Model-Based Estimation of Ankle Joint Stiffness. Sensors 2017, 17, 713. https://doi.org/10.3390/s17040713
Misgeld BJE, Zhang T, Lüken MJ, Leonhardt S. Model-Based Estimation of Ankle Joint Stiffness. Sensors. 2017; 17(4):713. https://doi.org/10.3390/s17040713
Chicago/Turabian StyleMisgeld, Berno J. E., Tony Zhang, Markus J. Lüken, and Steffen Leonhardt. 2017. "Model-Based Estimation of Ankle Joint Stiffness" Sensors 17, no. 4: 713. https://doi.org/10.3390/s17040713
APA StyleMisgeld, B. J. E., Zhang, T., Lüken, M. J., & Leonhardt, S. (2017). Model-Based Estimation of Ankle Joint Stiffness. Sensors, 17(4), 713. https://doi.org/10.3390/s17040713






