Terrestrial Water Storage in African Hydrological Regimes Derived from GRACE Mission Data: Intercomparison of Spherical Harmonics, Mass Concentration, and Scalar Slepian Methods
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Theory and Practice
2.2.1. GRACE-Estimated Errors and Scale Factors
2.2.2. Scalar Slepian Localization
2.3. GRACE Data and Processing
2.4. Analysis and Model
3. Results
3.1. GRACE Errors and CLM4.0 Scale Factor in African Regimes
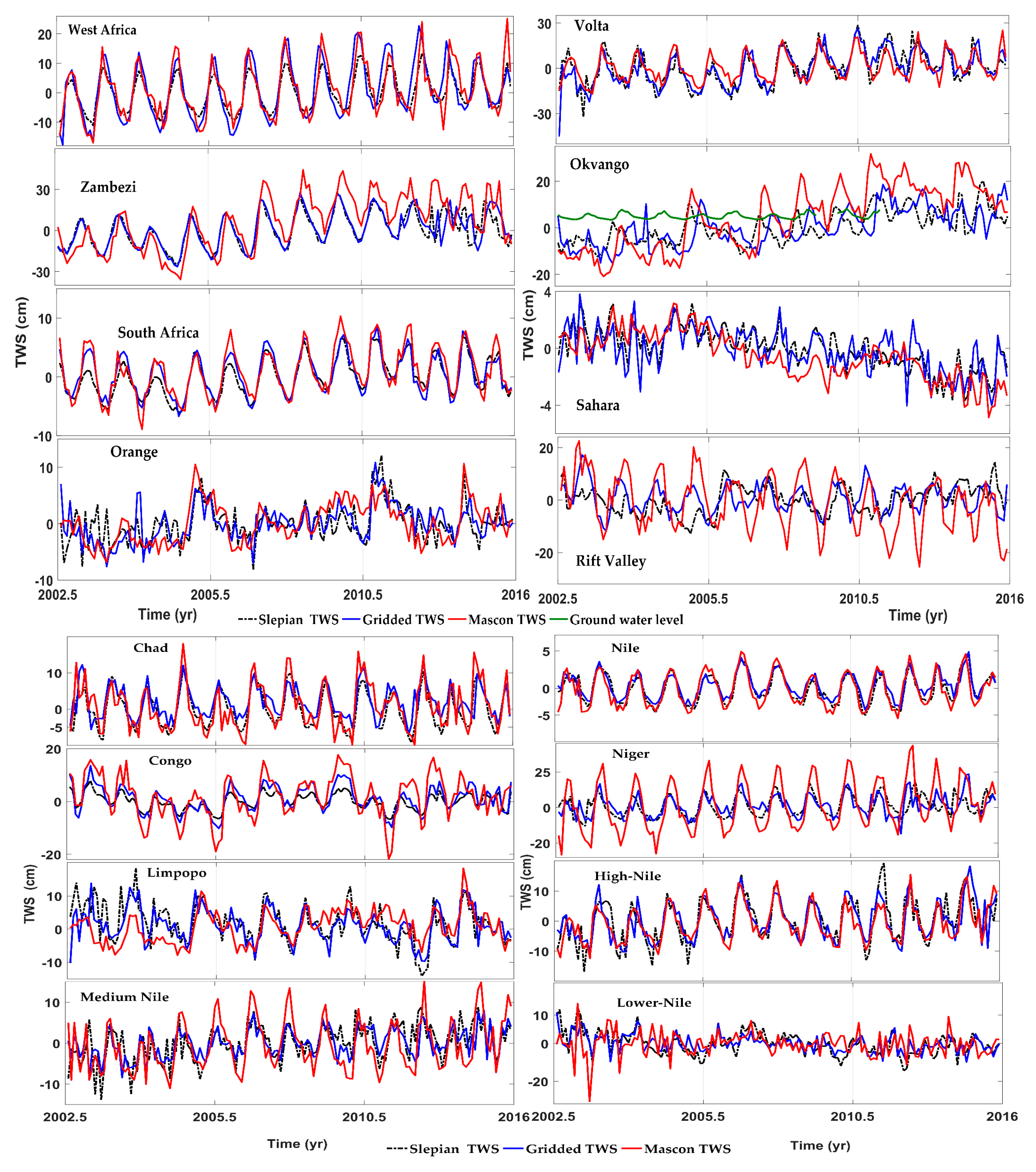
3.2. Statistical Performance of the TWS Estimates
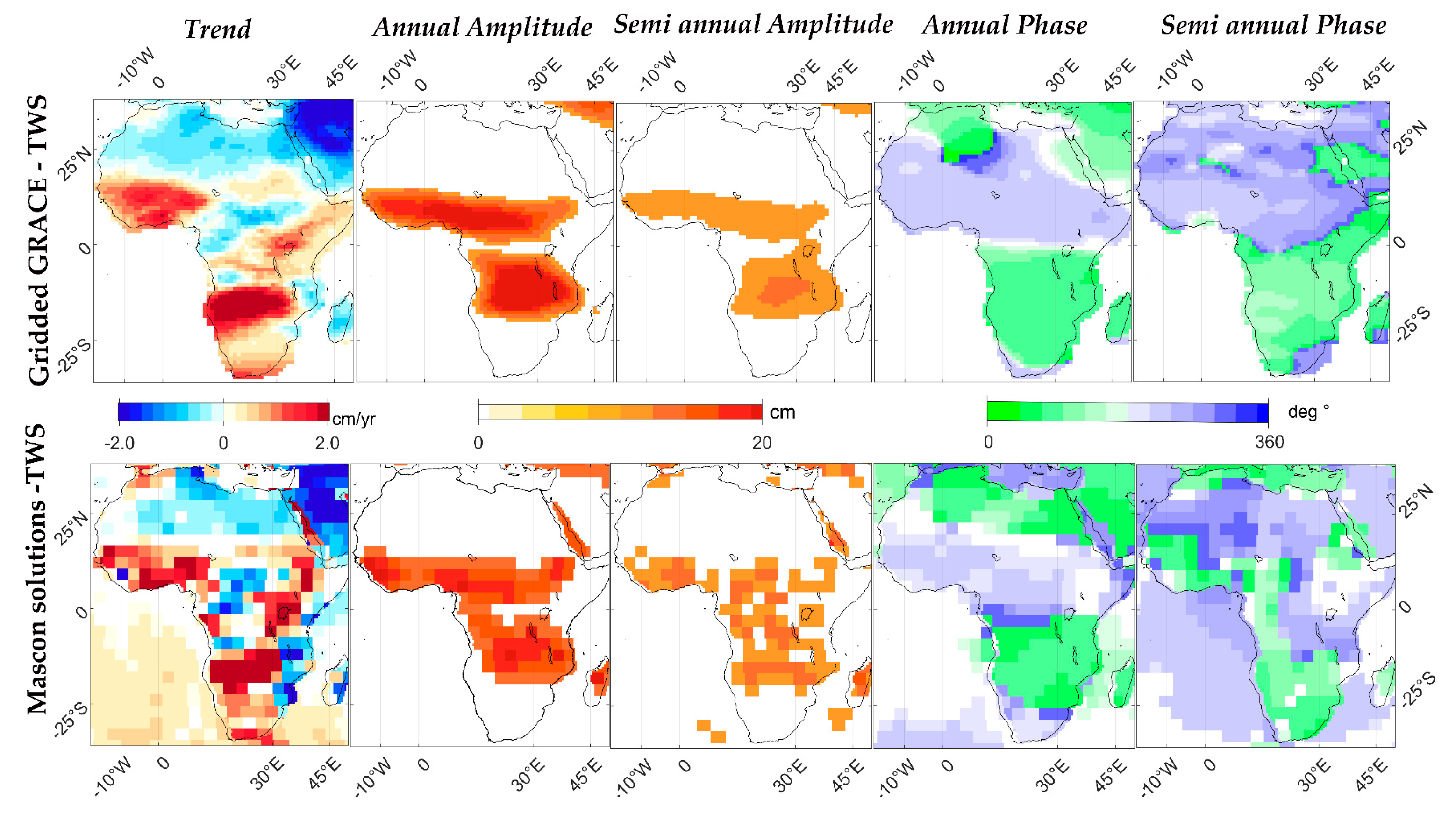
3.3. TWS Variations in Africa
4. Discussion
4.1. GRACE Error Assessment at African Hydrological Regimes
4.2. Comparison of SH-TWS, SL-TWS, and MSC-TWS
4.3. TWS Recharge and Depletion in Africa
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE measurements of mass variability in the earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Sol. Ea 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Syed, T.H.; Famiglietti, J.S.; Rodell, M.; Chen, J.; Wilson, C.R. Analysis of terrestrial water storage changes from GRACE and GLDAS. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Ramillien, G.; Famiglietti, J.S.; Wahr, J. Detection of continental hydrology and glaciology signals from GRACE: A review. Surv. Geophys. 2008, 29, 361–374. [Google Scholar] [CrossRef]
- Schmidt, R.; Schwintzer, P.; Flechtner, F.; Reigber, C.; Guntner, A.; Doll, P.; Ramillien, G.; Cazenave, A.; Petrovic, S.; Jochmann, H.; et al. GRACE observations of changes in continental water storage. Glob. Planet. Chang. 2006, 50, 112–126. [Google Scholar] [CrossRef]
- Rodell, M.; Chen, J.L.; Kato, H.; Famiglietti, J.S.; Nigro, J.; Wilson, C.R. Estimating groundwater storage changes in the Mississippi River Basin (USA) using GRACE. Hydrogeol. J. 2007, 15, 159–166. [Google Scholar] [CrossRef]
- Yeh, P.J.F.; Swenson, S.C.; Famiglietti, J.S.; Rodell, M. Remote sensing of groundwater storage changes in Illinois using the gravity recovery and climate experiment (GRACE). Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Voss, K.A.; Famiglietti, J.S.; Lo, M.; Linage, C.; Rodell, M.; Swenson, S.C. Groundwater depletion in the Middle East from GRACE with implications for transboundary water management in the Tigris-Euphrates-Western Iran region. Water Resour. Res. 2013, 49, 904–914. [Google Scholar] [CrossRef] [PubMed]
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [PubMed]
- Rodell, M.; Famiglietti, J.S.; Chen, J.; Seneviratne, S.I.; Viterbo, P.; Holl, S.; Wilson, C.R. Basin scale estimates of evapotranspiration using GRACE and other observations. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Ramillien, G.; Frappart, F.; Guntner, A.; Ngo-Duc, T.; Cazenave, A.; Laval, K. Time variations of the regional evapotranspiration rate from gravity recovery and climate experiment (GRACE) satellite gravimetry. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D. The 2009 exceptional amazon flood and interannual terrestrial water storage change observed by GRACE. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Thomas, A.C.; Reager, J.T.; Famiglietti, J.S.; Rodell, M. A GRACE-based water storage deficit approach for hydrological drought characterization. Geophys. Res. Lett. 2014, 41, 1537–1545. [Google Scholar] [CrossRef]
- Reager, J.T.; Thomas, B.F.; Famiglietti, J.S. River basin flood potential inferred using GRACE gravity observations at several months lead time. Nat. Geosci. 2014, 7, 589–593. [Google Scholar] [CrossRef]
- Syed, T.H.; Famiglietti, J.S.; Chambers, D.P. GRACE-based estimates of terrestrial freshwater discharge from basin to continental scales. J. Hydrometeorol. 2009, 10, 22–40. [Google Scholar] [CrossRef]
- Syed, T.; Famiglietti, J.; Chen, J.; Rodell, M.; Seneviratne, S.; Viterbo, P.; Wilson, C. Total basin discharge for the Amazon and Mississippi River basins from GRACE and a land-atmosphere water balance. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Tang, J.S.; Cheng, H.W.; Liu, L. Assessing the recent droughts in southwestern China using satellite gravimetry. Water Resour. Res. 2014, 50, 3030–3038. [Google Scholar] [CrossRef]
- Liu, R.; Li, J.; Fok, H.S.; Shum, C.K.; Li, Z. Earth surface deformation in the north China plain detected by joint analysis of GRACE and GPS data. Sensors 2014, 14, 19861–19876. [Google Scholar] [CrossRef] [PubMed]
- Zou, R.; Wang, Q.; Freymueller, J.T.; Poutanen, M.; Cao, X.; Zhang, C.; Yang, S.; He, P. Seasonal hydrological loading in southern Tibet detected by joint analysis of GPS and GRACE. Sensors 2015, 15, 30525–30538. [Google Scholar] [CrossRef] [PubMed]
- Van Dam, T.; Wahr, J.; Lavallée, D. A comparison of annual vertical crustal displacements from GPS and gravity recovery and climate experiment (GRACE) over Europe. J. Geophys. Res. Sol. Ea 2007, 112. [Google Scholar] [CrossRef]
- Lo, M.H.; Famiglietti, J.S.; Yeh, P.J.F.; Syed, T.H. Improving parameter estimation and water table depth simulation in a land surface model using GRACE water storage and estimated base flow data. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Guntner, A. Improvement of global hydrological models using GRACE data. Surv. Geophys. 2008, 29, 375–397. [Google Scholar] [CrossRef]
- Tapley, B.D.; Schutz, B.E.; Born, G.H. Statistical Orbit Determination; Elsevier Academic Press: Amsterdam, The Netherlands, 2004; p. 547. [Google Scholar]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.N.; Boening, C.; Landerer, F.W. Improved methods for observing earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Sol. Ea 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Rowlands, D.D.; Luthcke, S.B.; McCarthy, J.J.; Klosko, S.M.; Chinn, D.S.; Lemoine, F.G.; Boy, J.P.; Sabaka, T.J. Global mass flux solutions from GRACE: A comparison of parameter estimation strategies-mass concentrations versus stokes coefficients. J. Geophys. Res. Sol. Ea 2010, 115. [Google Scholar] [CrossRef]
- Wahr, J.; Swenson, S.; Velicogna, I. Accuracy of GRACE mass estimates. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Longuevergne, L.; Scanlon, B.R.; Wilson, C.R. GRACE hydrological estimates for small basins: Evaluating processing approaches on the high plains aquifer, USA. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Jekeli, C. Alternative Methods to Smooth the Earth's Gravity Field; Ohio State University: Columbus, OH, USA, 1981; p. 54. [Google Scholar]
- Werth, S.; Guntner, A.; Schmidt, R.; Kusche, J. Evaluation of GRACE filter tools from a hydrological perspective. Geophys. J. Int. 2009, 179, 1499–1515. [Google Scholar] [CrossRef]
- Swenson, S.C.; Wahr, J.M. Estimating signal loss in regularized GRACE gravity field solutions. Geophys. J. Int. 2011, 185, 693–702. [Google Scholar] [CrossRef]
- Klees, R.; Zapreeva, E.; Winsemius, H.; Savenije, H. The bias in GRACE estimates of continental water storage variations. Hydrol. Earth Syst. Sci. 2006, 3, 3557–3594. [Google Scholar] [CrossRef]
- Landerer, F.W.; Swenson, S.C. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Harig, C.; Simons, F.J. Mapping greenland’s mass loss in space and time. Proc. Natl. Acad. Sci. USA 2012, 109, 19934–19937. [Google Scholar] [CrossRef] [PubMed]
- Simons, F.J.; Dahlen, F.A. Spherical slepian functions and the polar gap in geodesy. Geophys. J. Int. 2006, 166, 1039–1061. [Google Scholar] [CrossRef]
- Wang, L.; Shum, C.K.; Simons, F.J.; Tapley, B.; Dai, C.L. Coseismic and postseismic deformation of the 2011 Tohoku-Oki earthquake constrained by GRACE gravimetry. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Han, S.C.; Riva, R.; Sauber, J.; Okal, E. Source parameter inversion for recent great earthquakes from a decade-long observation of global gravity fields. J. Geophys. Res. Sol. Ea 2013, 118, 1240–1267. [Google Scholar] [CrossRef]
- Wiese, D.N.; Nerem, R.S.; Han, S.C. Expected improvements in determining continental hydrology, ice mass variations, ocean bottom pressure signals, and earthquakes using two pairs of dedicated satellites for temporal gravity recovery. J. Geophys. Res. Sol. Ea 2011, 116. [Google Scholar] [CrossRef]
- Plattner, A.; Simons, F.J. High-resolution local magnetic field models for the Martian South Pole from Mars Global Surveyor Data. J. Geophys. Res. Planets 2015, 120, 1543–1566. [Google Scholar] [CrossRef]
- Vorosmarty, C.J.; Green, P.; Salisbury, J.; Lammers, R.B. Global water resources: Vulnerability from climate change and population growth. Science 2000, 289, 284–288. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Progress on Sanitation and Drinking Water: 2014 Update; 9241507241; World Health Organization: Paris, France, 2014. [Google Scholar]
- FAO. World Map of the Major Hydrological Basins. Available online: http://www.fao.org/geonetwork/ (accessed on 25 September 2016).
- Trabucco, A.; Zomer, R. Global Aridity Index (Global-Aridity) and Global Potential Evapo-Transpiration (Global-Pet) Geospatial Database. Available online: http://www.cgiar-csi.org/ (accessed on 25 September 2016).
- Trabucco, A.; Zomer, R.J.; Bossio, D.A.; van Straaten, O.; Verchot, L.V. Climate change mitigation through afforestation/reforestation: A global analysis of hydrologic impacts with four case studies. Agric Ecosyst. Environ. 2008, 126, 81–97. [Google Scholar] [CrossRef]
- GRACE Tellus. Available online: http://GRACE.Jpl.Nasa.Gov/mission/GRACE/ (accessed on 25 September 2016).
- Simons, F.J.; Dahlen, F.A.; Wieczorek, M.A. Spatiospectral concentration on a sphere. SIAM Rev. 2006, 48, 504–536. [Google Scholar] [CrossRef]
- Simons, F.J.; Hawthorne, J.C.; Beggan, C.D. Efficient analysis and representation of geophysical processes using localized spherical basis functions. Proc. SPIE 2009, 7446, 74460G. [Google Scholar]
- Simons, F. Slepian functions and their use in signal estimation and spectral analysis. In Handbook of Geomathematics; Freeden, W., Nashed, M.Z., Sonar, T., Eds.; Springer: Heidelberg, Germany, 2010; pp. 891–923. [Google Scholar]
- Cheng, M.K.; Ries, J.C.; Tapley, B.D. Variations of the earth’s figure axis from satellite laser ranging and GRACE. J. Geophys. Res. Sol. Ea 2011, 116. [Google Scholar] [CrossRef]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. Sol. Ea 2008, 113. [Google Scholar] [CrossRef]
- Geruo, A.; Wahr, J.; Zhong, S.J. Computations of the viscoelastic response of a 3-d compressible earth to surface loading: An application to glacial isostatic adjustment in Antarctica and Canada. Geophys. J. Int. 2013, 192, 557–572. [Google Scholar]
- Jolliffe, I. Principal Component Analysis; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Okavango Basin Information System (OBIS). Available online: http://leutra.Geogr.Uni-jena.De/obis/metadata/start.Php (accessed on 25 September 2016).
- Long, D.; Longuevergne, L.; Scanlon, B.R. Global analysis of approaches for deriving total water storage changes from GRACE satellites. Water Resour. Res. 2015, 51, 2574–2594. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Famiglietti, J.S.; Rodell, M. Attenuation effect on seasonal basin-scale water storage changes from GRACE time-variable gravity. J. Geod. 2007, 81, 237–245. [Google Scholar] [CrossRef]
- Dutt Vishwakarma, B.; Devaraju, B.; Sneeuw, N. Minimizing the effects of filtering on catchment scale GRACE solutions. Water Resour. Res. 2016, 52, 5868–5890. [Google Scholar] [CrossRef]
- Wiese, D.N.; Landerer, F.W.; Watkins, M.M. Quantifying and reducing leakage errors in the JPL RL05M GRACE mascon solution. Water Resour. Res. 2016, 52, 7490–7502. [Google Scholar] [CrossRef]
- Sultan, M.; Ahmed, M.; Wahr, J.; Yan, E.; Emil, M. Monitoring aquifer depletion from space: Case studies from the saharan and arabian aquifers. In Remote Sensing of the Terrestrial Water Cycle; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014; pp. 347–366. [Google Scholar]
- Ramillien, G.; Frappart, F.; Seoane, L. Application of the regional water mass variations from GRACE satellite gravimetry to large-scale water management in Africa. Remote Sens. 2014, 6, 7379–7405. [Google Scholar] [CrossRef]
- Goncalves, J.; Petersen, J.; Deschamps, P.; Hamelin, B.; Baba-Sy, O. Quantifying the modern recharge of the “fossil” Sahara aquifers. Geophys. Res. Lett. 2013, 40, 2673–2678. [Google Scholar] [CrossRef]
- Foster, S.; Loucks, D.P. Non-Renewable Groundwater Resources: A Guidebook on Socially-Sustainable Management for Water-Policy Makers; Unesco: Paris, France, 2006. [Google Scholar]
- Gleeson, T.; VanderSteen, J.; Sophocleous, M.A.; Taniguchi, M.; Alley, W.M.; Allen, D.M.; Zhou, Y.X. Groundwater sustainability strategies. Nat. Geosci. 2010, 3, 378–379. [Google Scholar] [CrossRef]
- Sultan, B.; Janicot, S. Abrupt shift of the ITCZ over West Africa and intra-seasonal variability. Geophys. Res. Lett. 2000, 27, 3353–3356. [Google Scholar] [CrossRef]
- Asnani, G. Tropical Mmeteorology; GC Asnani Pune: New Delhi, India, 1993. [Google Scholar]
- Ferreira, V.G.; Andam-Akorful, S.A.; He, X.-F.; Xiao, R.-Y. Estimating water storage changes and sink terms in volta basin from satellite missions. Water Sci. Eng. 2014, 7, 5–16. [Google Scholar]
- Awange, J.L.; Forootan, E.; Kusche, J.; Kiema, J.B.K.; Omondi, P.A.; Heck, B.; Fleming, K.; Ohanya, S.O.; Goncalves, R.M. Understanding the decline of water storage across the Ramser-Lake Naivasha using satellite-based methods. Adv. Water Resour. 2013, 60, 7–23. [Google Scholar] [CrossRef]
- Becker, M.; LLovel, W.; Cazenave, A.; Guntner, A.; Cretaux, J.F. Recent hydrological behavior of the East African great lakes region inferred from GRACE, satellite altimetry and rainfall observations. C. R. Geosci. 2010, 342, 223–233. [Google Scholar] [CrossRef]
- Gan, T.; Ito, M.; Huelsmann, S.; Qin, X.; Lu, X.; Liong, S.; Rutschman, P.; Disse, M.; Koivosalo, H. Possible climate change/variability and human impacts, vulnerability of african drought prone regions, its water resources and capacity building. Hydrol. Sci. J. 2015. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Monitoring the water balance of Lake Victoria, East Africa, from space. J. Hydrol. 2009, 370, 163–176. [Google Scholar] [CrossRef]
- Deus, D.; Gloaguen, R.; Krause, P. Water balance modeling in a semi-arid environment with limited in situ data using remote sensing in Lake Manyara, East African Rift, Tanzania. Remote Sens. 2013, 5, 1651–1680. [Google Scholar] [CrossRef]
- Harig, C.; Lewis, K.W.; Plattner, A.; Simons, F.J. A suite of software analyzes data on the sphere. Eos 2015, 96. [Google Scholar] [CrossRef]
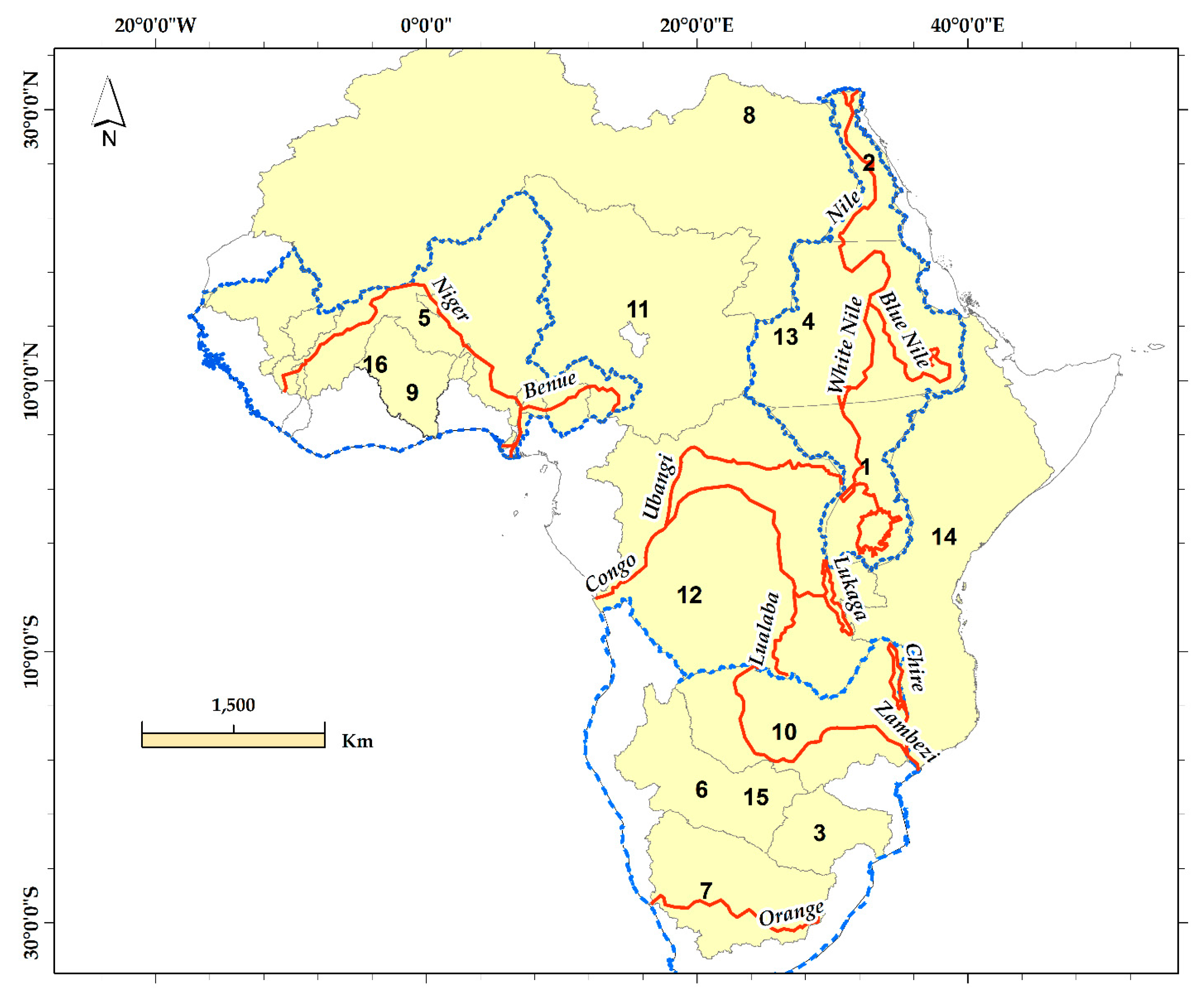


| ROI ID | ROI Name | A (km2) | AI | Cl | l (mm) | m (mm) | Total Errors (mm) | kSH | kMS |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Higher Nile | 1,030,026 | 0.48 | DSH | 5.36 | 10.43 | 11.63 | 1.17 | 0.96 |
| 2 | Lower Nile | 455,637 | 0.15 | A | 13.25 | 25.43 | 28.62 | 0.38 | 0.88 |
| 3 | Limpopo | 415,017 | 0.33 | SA | 8.32 | 17.21 | 19.25 | 1.31 | 0.98 |
| 4 | Middle Nile | 1,901,388 | 0.28 | SA | 6.46 | 18.45 | 19.58 | 1.87 | 0.99 |
| 5 | Niger | 2,118,387 | 0.32 | SA | 5.74 | 12.34 | 13.54 | 1.16 | 1.59 |
| 6 | Okavango | 530,021 | 0.45 | SA | 6.85 | 16.86 | 18.15 | 1.12 | 1.23 |
| 7 | Orange | 973,218 | 0.31 | SA | 7.46 | 15.82 | 17.42 | 1.11 | 0.75 |
| 8 | Sahara | 6,907,746 | 0.02 | HA | 5.42 | 11.24 | 12.41 | 0.85 | 0.62 |
| 9 | Volta | 407,391 | 0.59 | DSH | 5.81 | 13.61 | 15.95 | 1.36 | 1.34 |
| 10 | Zambezi | 1,391,230 | 0.54 | SH | 7.41 | 16.42 | 17.93 | 1.11 | 1.01 |
| 11 | Chad | 2,662,435 | 0.19 | A | 4.92 | 10.82 | 11.82 | 0.99 | 1.05 |
| 12 | Congo | 4,014,741 | 0.89 | H | 5.38 | 10.83 | 12.36 | 1.24 | 1.09 |
| 13 | Nile | 3,241,937 | 0.29 | SA | 6.25 | 13.44 | 14.75 | 1.15 | 0.97 |
| 14 | Rift valley | 2,976,053 | 0.29 | SA | 5.34 | 9.53 | 10.91 | 0.96 | 0.72 |
| 15 | South Africa | 5,992,256 | 0.35 | SA | 4.55 | 12.82 | 13.53 | 0.49 | 0.28 |
| 16 | West Africa | 4,251,507 | 0.53 | DSH | 6.55 | 13.68 | 15.33 | 0.98 | 0.98 |
| ROI ID | ROI Name | NSE | R | No. of EOF | No. of Basis ≥ 0.6 | ||||
|---|---|---|---|---|---|---|---|---|---|
| NSE1 | NSE2 | NSE3 | R1 | R2 | R3 | ||||
| 1 | Higher Nile | 0.62 | 0.64 | 0.65 | 0.82 | 0.83 | 0.87 | 3 | 6 |
| 2 | Lower Nile | 0.53 | −0.42 | −1.02 | 0.75 | 0.25 | 0.38 | 2 | 2 |
| 3 | Limpopo | 0.46 | 0.03 | 0.08 | 0.73 | 0.52 | 0.52 | 2 | 2 |
| 4 | Middle Nile | 0.32 | −0.32 | −0.22 | 0.65 | 0.53 | 0.73 | 4 | 11 |
| 5 | Niger | 0.33 | 0.40 | 0.55 | 0.68 | 0.62 | 0.74 | 4 | 13 |
| 6 | Okavango | 0.42 | 0.21 | −0.55 | 0.73 | 0.85 | 0.82 | 3 | 4 |
| 7 | Orange | 0.36 | −0.07 | −0.07 | 0.62 | 0.56 | 0.53 | 3 | 5 |
| 8 | Sahara | 0.52 | 0.31 | 0.09 | 0.77 | 0.74 | 0.64 | 2 | 35 |
| 9 | Volta | 0.67 | 0.52 | 0.64 | 0.85 | 0.78 | 0.75 | 3 | 2 |
| 10 | Zambezi | 0.73 | −0.28 | −0.10 | 0.89 | 0.73 | 0.78 | 3 | 8 |
| 11 | Chad | 0.57 | −0.07 | −0.07 | 0.82 | 0.85 | 0.74 | 3 | 14 |
| 12 | Congo | 0.60 | 0.50 | 0.30 | 0.88 | 0.87 | 0.73 | 4 | 29 |
| 13 | Nile | 0.80 | 0.70 | 0.40 | 0.92 | 0.96 | 0.88 | 3 | 19 |
| 14 | Rift Valley | 0.27 | −3.09 | −1.35 | 0.29 | 0.23 | 0.63 | 4 | 17 |
| 15 | South Africa | 0.82 | 0.60 | 0.70 | 0.95 | 0.92 | 0.93 | 3 | 35 |
| 16 | West Africa | 0.42 | 0.43 | 0.62 | 0.96 | 0.93 | 0.78 | 4 | 26 |
| ROI ID | ROI Name | SL-TWS | SH-TWS | MSC-TWS | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Trend (cm/year) | AA (cm) | SA (cm) | Trend (cm/year) | AA (cm) | SA (cm) | Trend (cm/year) | AA (cm) | SA (cm) | ||
| 1 | Higher Nile | 0.51 | 6.83 | 5.51 | 0.48 | 6.83 | 3.85 | 0.53 | 7.23 | 4.86 |
| 2 | Lower Nile | −2.36 | 2.34 | 1.35 | −2.10 | 2.14 | 0.57 | −1.52 | 1.24 | 0.25 |
| 3 | Limpopo | −0.54 | 3.82 | 1.65 | −0.52 | 4.38 | 1.55 | −0.43 | 4.65 | 1.76 |
| 4 | Middle Nile | 1.87 | 5.84 | 1.48 | 1.29 | 4.05 | 0.54 | 1.44 | 6.77 | 2.28 |
| 5 | Niger | 1.74 | 9.35 | 1.46 | 1.55 | 9.15 | 2.56 | 1.82 | 11.92 | 4.84 |
| 6 | Okavango | 1.44 | 3.72 | 1.84 | 1.63 | 3.67 | 0.64 | 1.50 | 6.89 | 0.45 |
| 7 | Orange | 0.35 | 1.65 | 0.52 | 0.31 | 1.65 | 1.25 | 0.34 | 1.64 | 2.11 |
| 8 | Sahara | −1.02 | 0.44 | 0.14 | −0.83 | 1.24 | 0.47 | −1.31 | 0.09 | 0.32 |
| 9 | Volta | 2.82 | 14.30 | 3.45 | 4.75 | 13.9 | 1.69 | 4.83 | 13.21 | 0.27 |
| 10 | Zambezi | 1.35 | 14.91 | 3.27 | 1.45 | 9.98 | 3.28 | 1.64 | 14.34 | 3.58 |
| 11 | Chad | 0.05 | 8.53 | 0.65 | 0.06 | 6.52 | 1.84 | 0.07 | 8.79 | 1.49 |
| 12 | Congo | 0.05 | 5.64 | 2.18 | 0.05 | 5.13 | 1.55 | 0.01 | 5.76 | 3.57 |
| 13 | Nile | 0.13 | 3.25 | 0.27 | 0.26 | 2.65 | 0.17 | 0.28 | 3.92 | 1.17 |
| 14 | Rift valley | 0.06 | 1.64 | 1.46 | 0.07 | 1.54 | 2.35 | 0.08 | 1.53 | 1.66 |
| 15 | South Africa | 1.27 | 4.82 | 0.43 | 0.73 | 5.96 | 1.84 | 1.29 | 6.48 | 0.82 |
| 16 | West Africa | 1.71 | 9.89 | 0.45 | 1.63 | 12.5 | 0.81 | 1.73 | 13.24 | 3.95 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rateb, A.; Kuo, C.-Y.; Imani, M.; Tseng, K.-H.; Lan, W.-H.; Ching, K.-E.; Tseng, T.-P. Terrestrial Water Storage in African Hydrological Regimes Derived from GRACE Mission Data: Intercomparison of Spherical Harmonics, Mass Concentration, and Scalar Slepian Methods. Sensors 2017, 17, 566. https://doi.org/10.3390/s17030566
Rateb A, Kuo C-Y, Imani M, Tseng K-H, Lan W-H, Ching K-E, Tseng T-P. Terrestrial Water Storage in African Hydrological Regimes Derived from GRACE Mission Data: Intercomparison of Spherical Harmonics, Mass Concentration, and Scalar Slepian Methods. Sensors. 2017; 17(3):566. https://doi.org/10.3390/s17030566
Chicago/Turabian StyleRateb, Ashraf, Chung-Yen Kuo, Moslem Imani, Kuo-Hsin Tseng, Wen-Hau Lan, Kuo-En Ching, and Tzu-Pang Tseng. 2017. "Terrestrial Water Storage in African Hydrological Regimes Derived from GRACE Mission Data: Intercomparison of Spherical Harmonics, Mass Concentration, and Scalar Slepian Methods" Sensors 17, no. 3: 566. https://doi.org/10.3390/s17030566
APA StyleRateb, A., Kuo, C.-Y., Imani, M., Tseng, K.-H., Lan, W.-H., Ching, K.-E., & Tseng, T.-P. (2017). Terrestrial Water Storage in African Hydrological Regimes Derived from GRACE Mission Data: Intercomparison of Spherical Harmonics, Mass Concentration, and Scalar Slepian Methods. Sensors, 17(3), 566. https://doi.org/10.3390/s17030566








