Enhanced Passive RF-DC Converter Circuit Efficiency for Low RF Energy Harvesting
Abstract
:1. Introduction
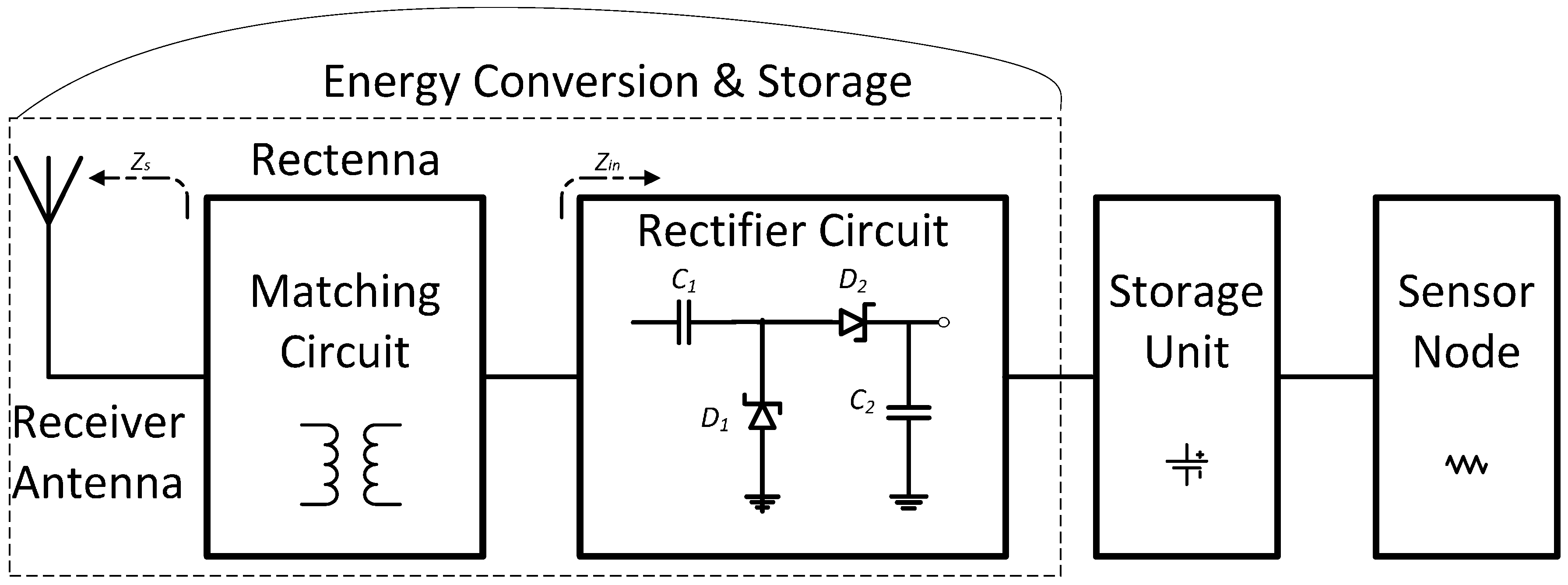
2. RF Energy Conversion and Storage
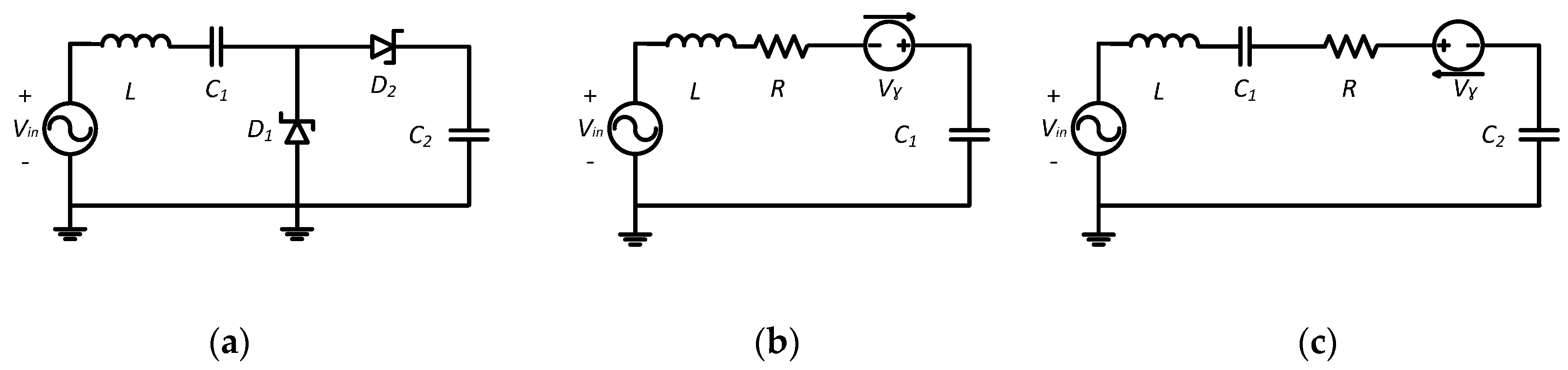
3. Basic Rectifier Circuit for RF Applications
4. Novel Approach for an RF-DC Converter Based on Voltage Multiplier Circuit
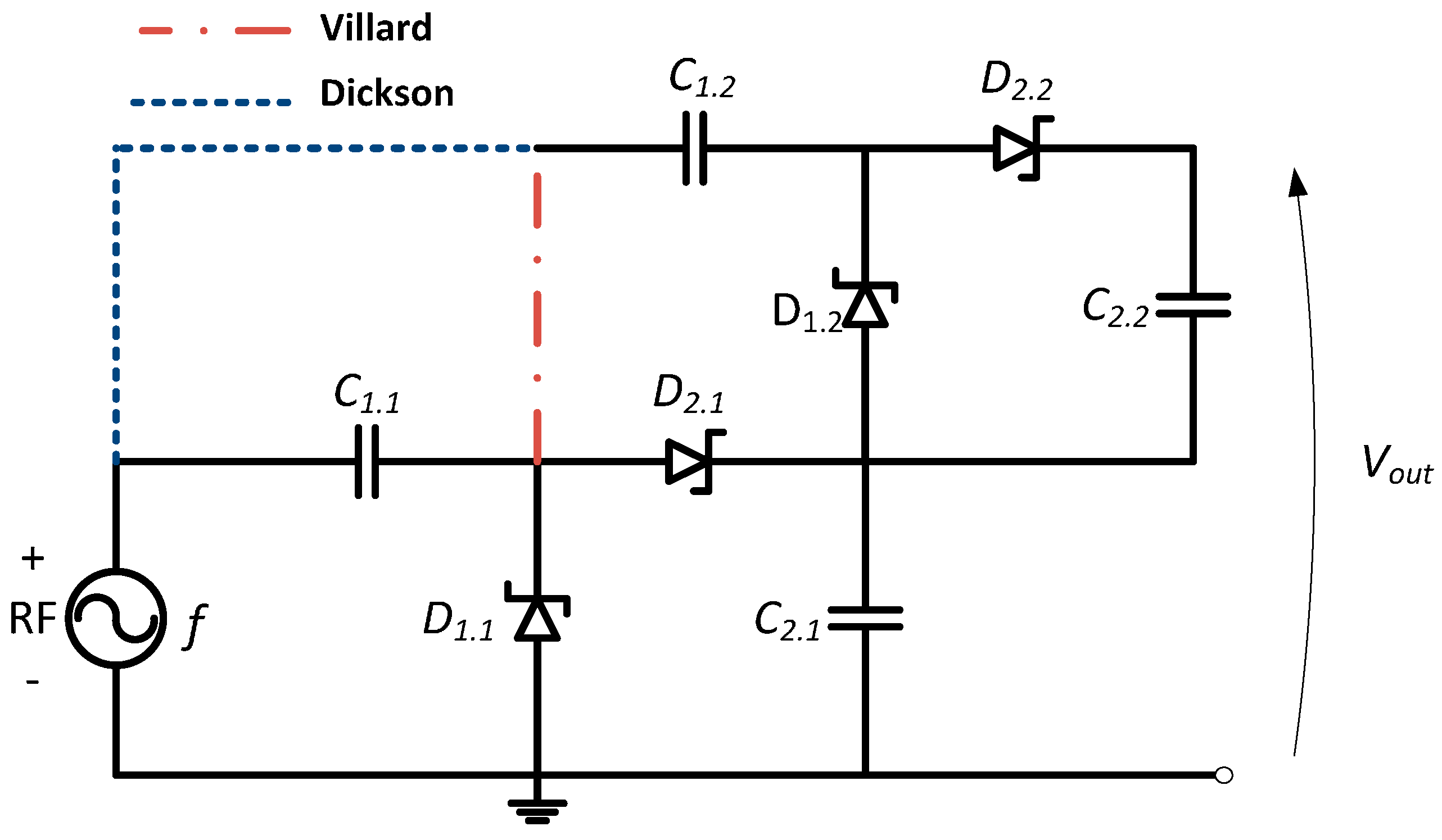
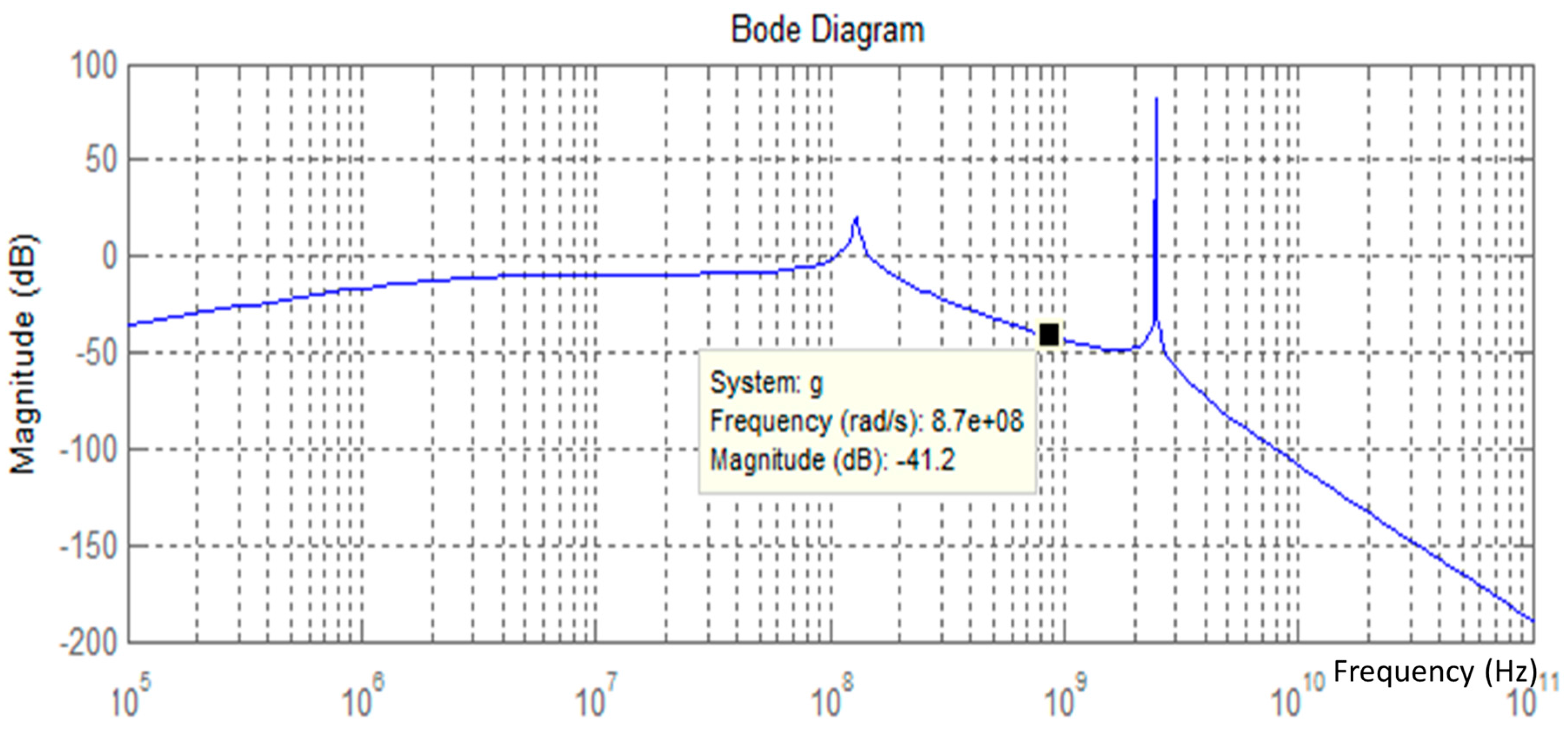
4.1. Novel Approach for a Signal Voltage Multiplier Circuit
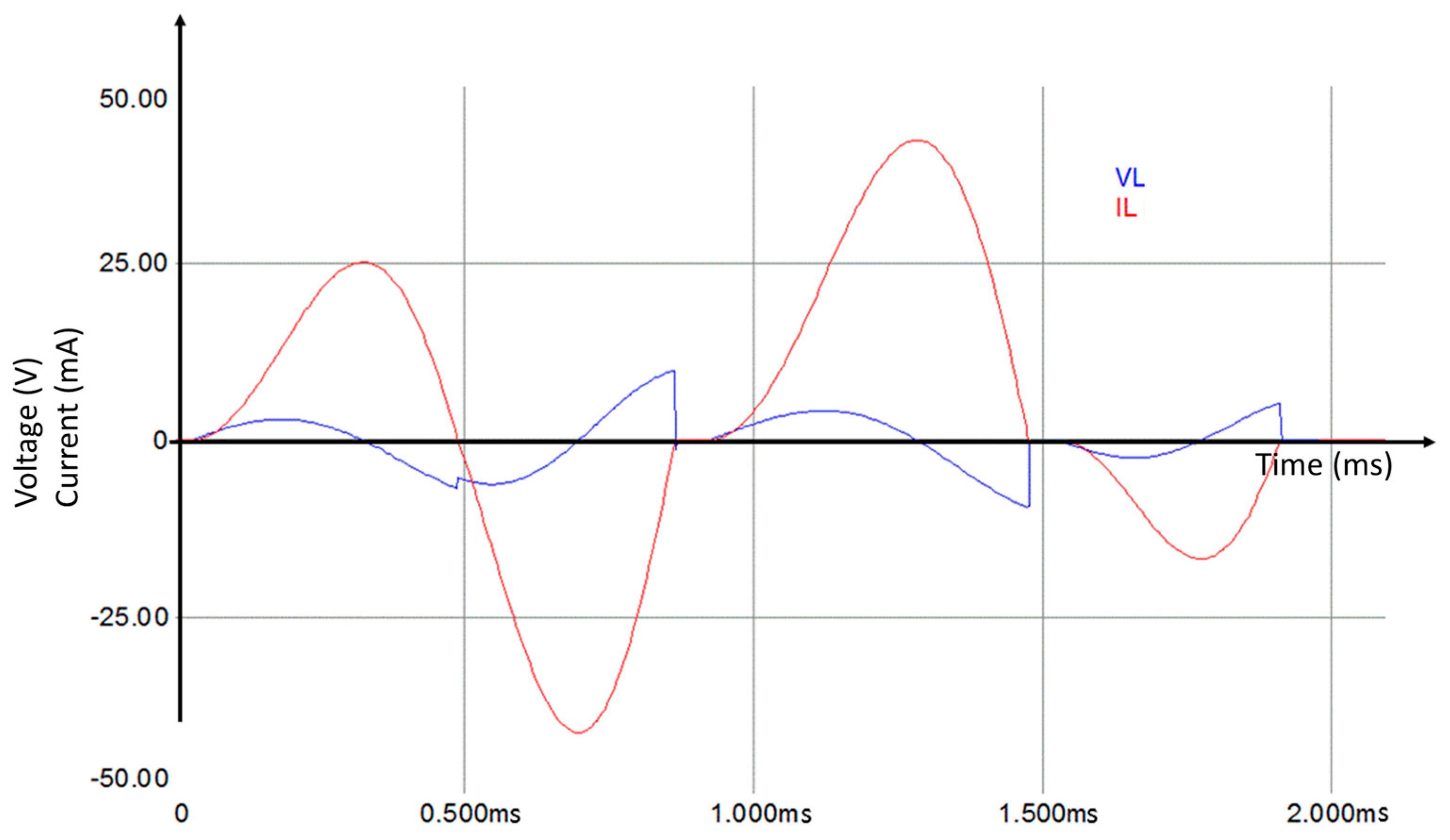
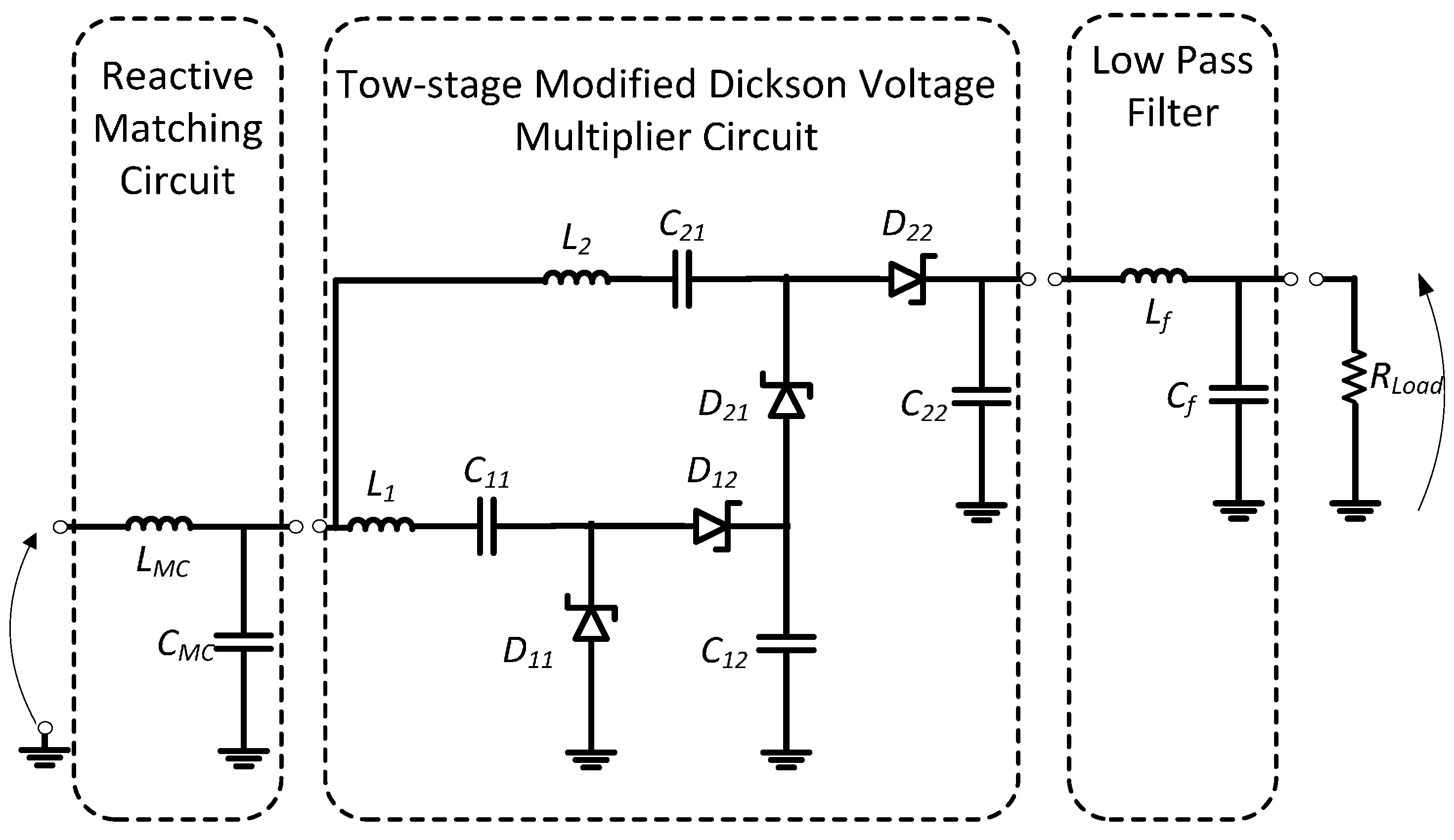
4.2. Proposed Signal Voltage Multiplier Circuit
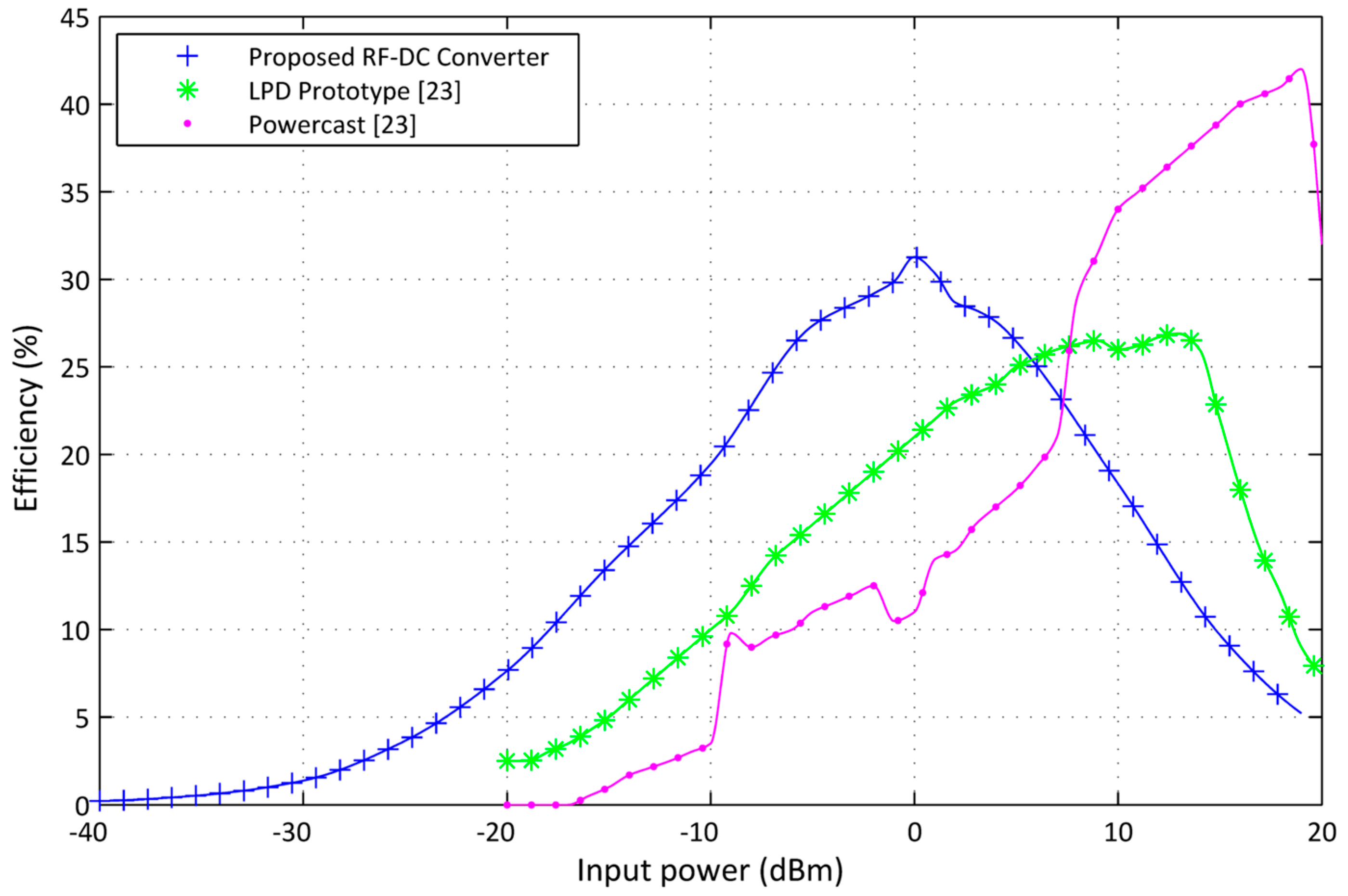
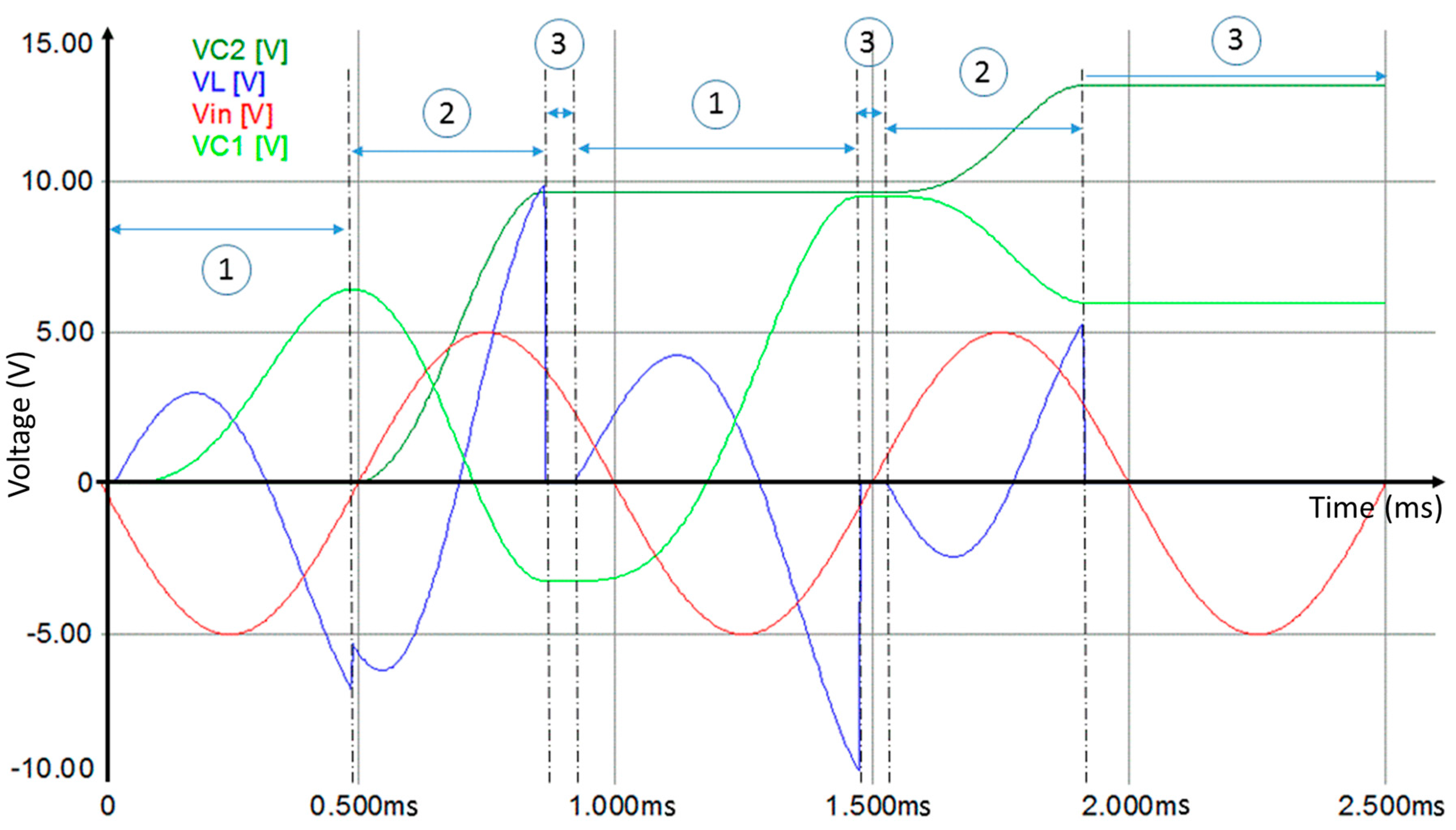
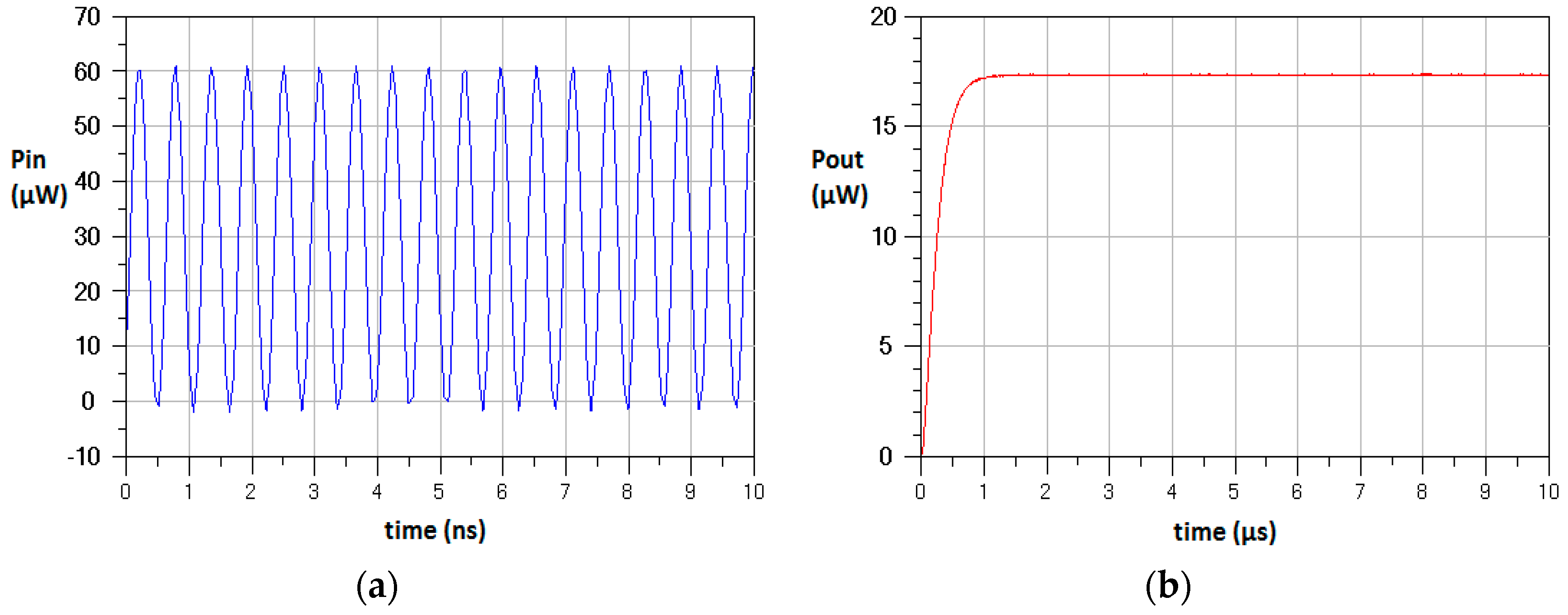
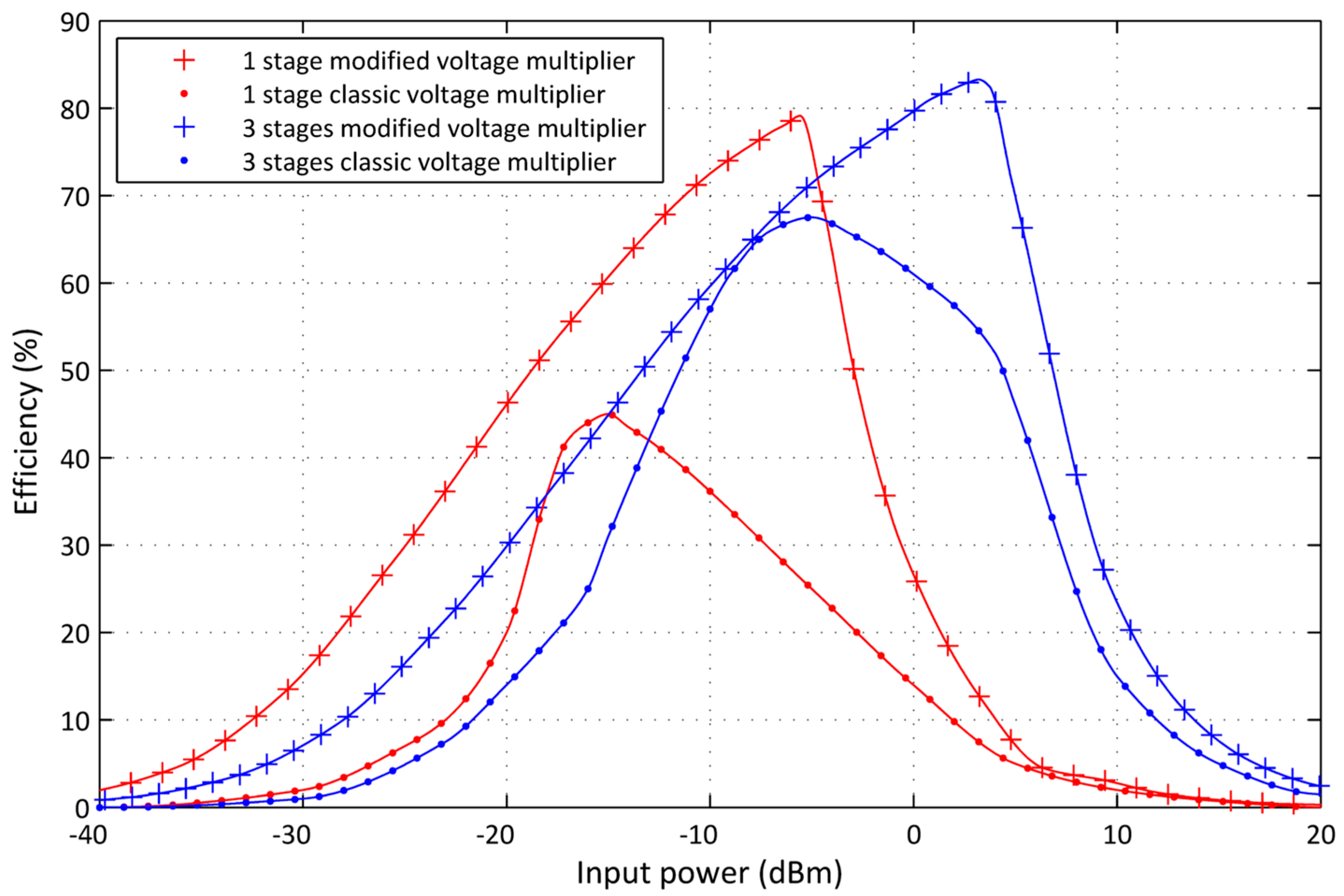
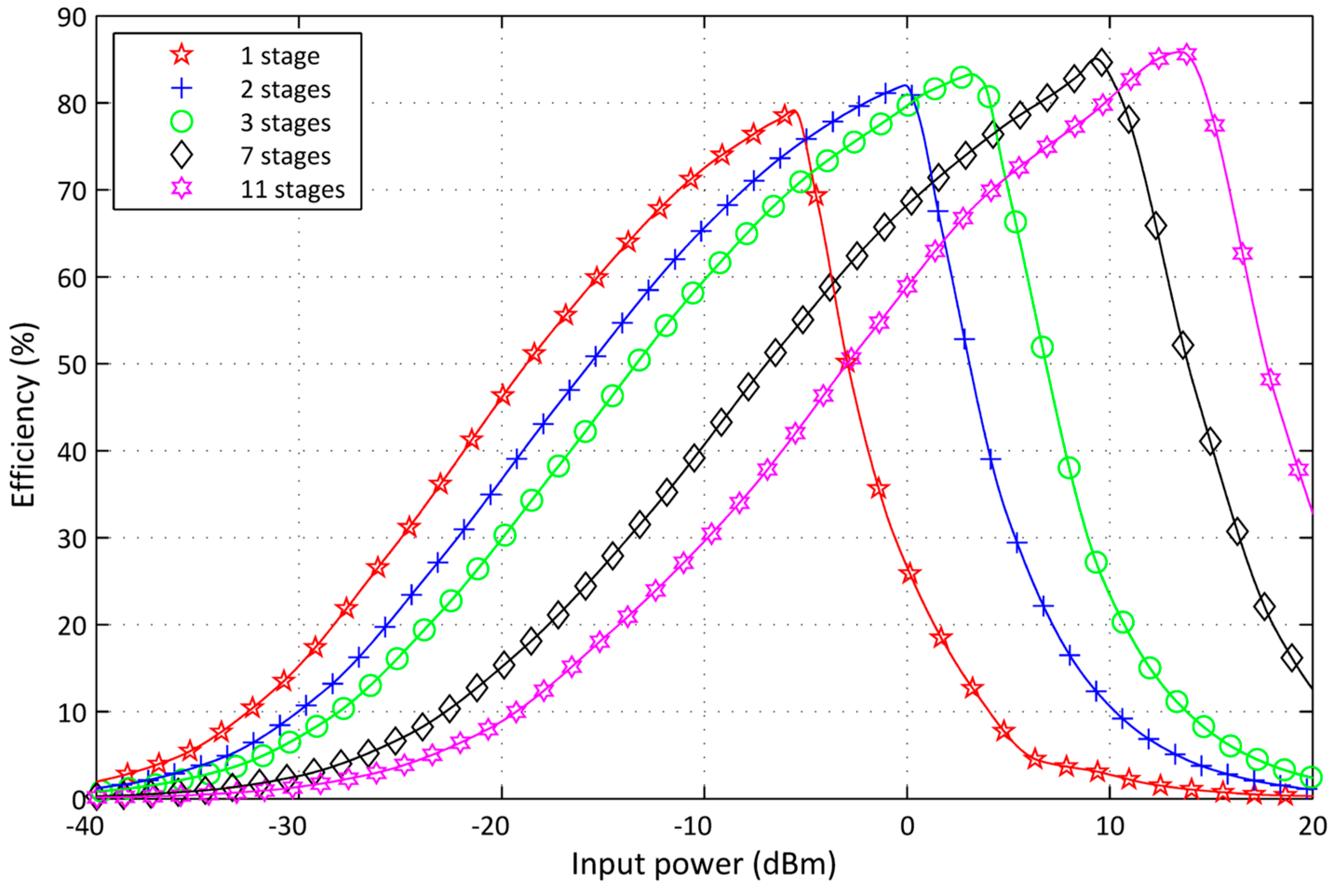
4.3. Simulations for a Modified Voltage Multiplier Circuit
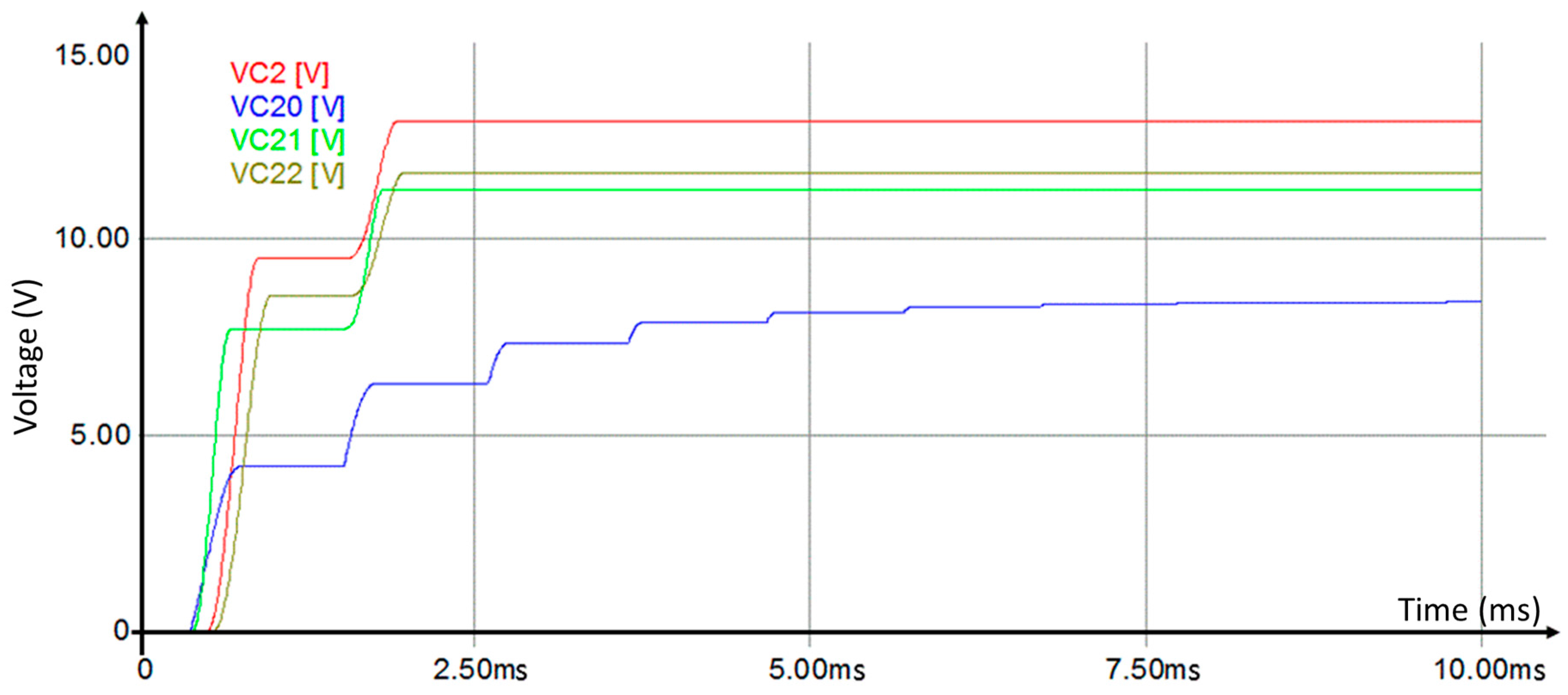
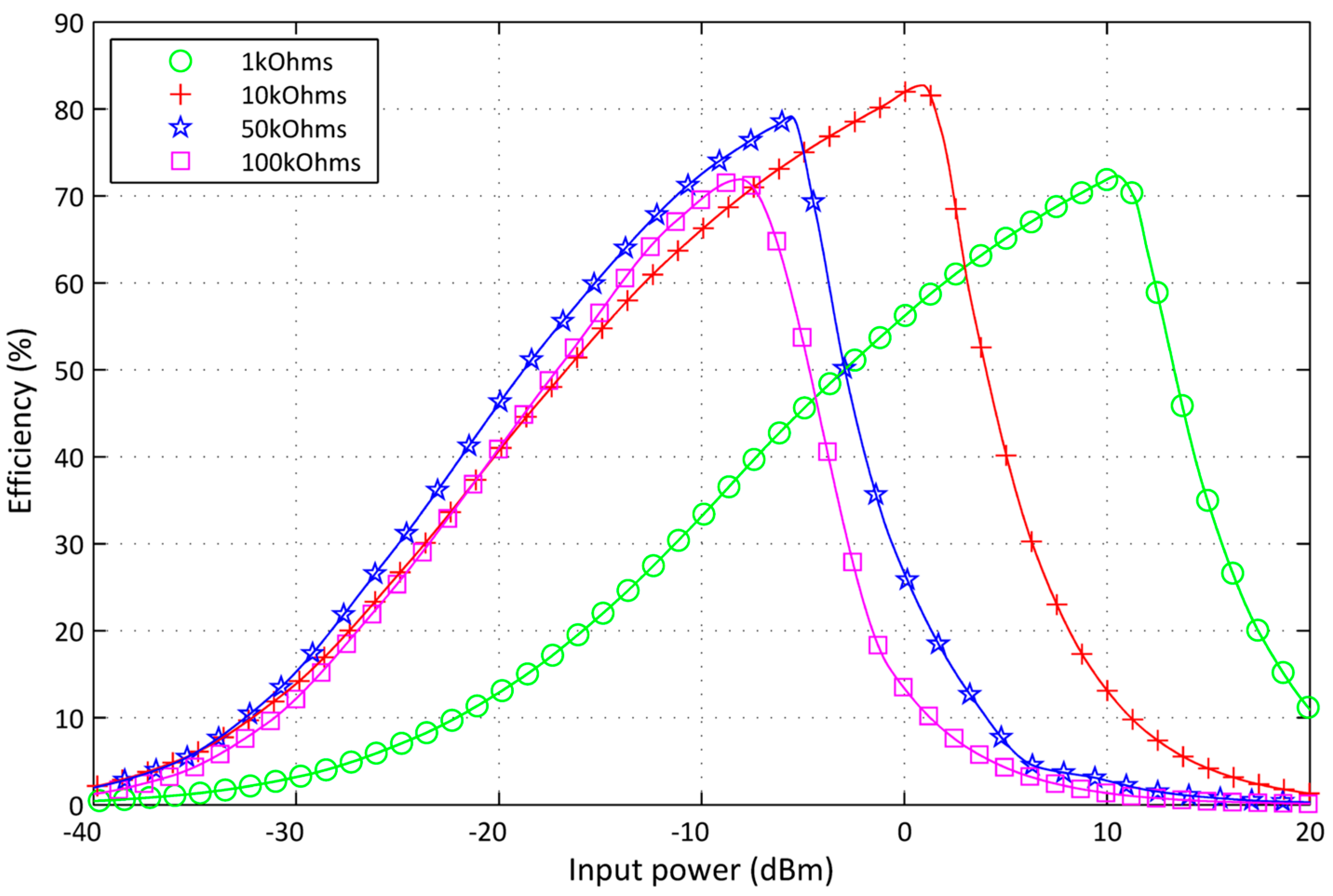
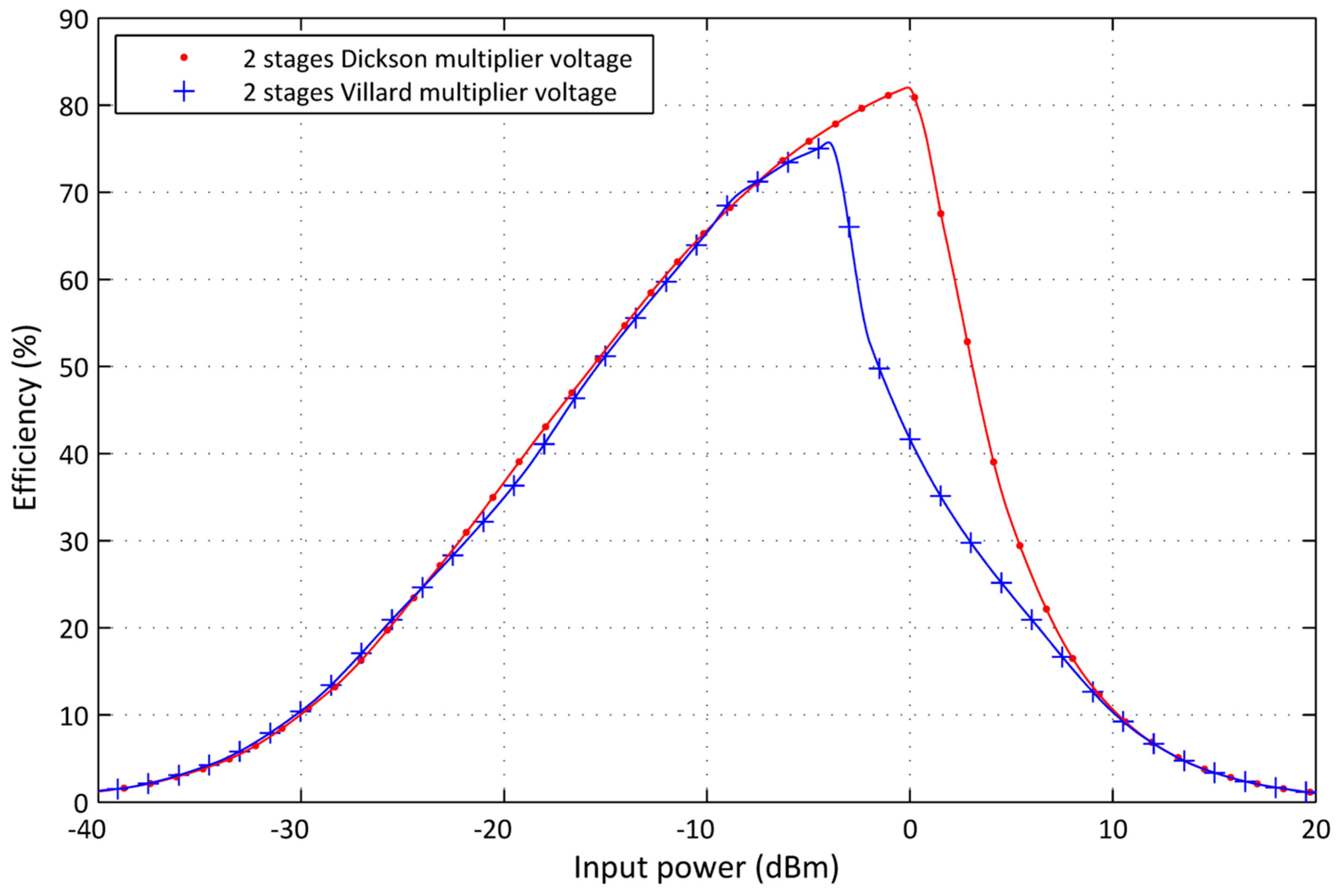
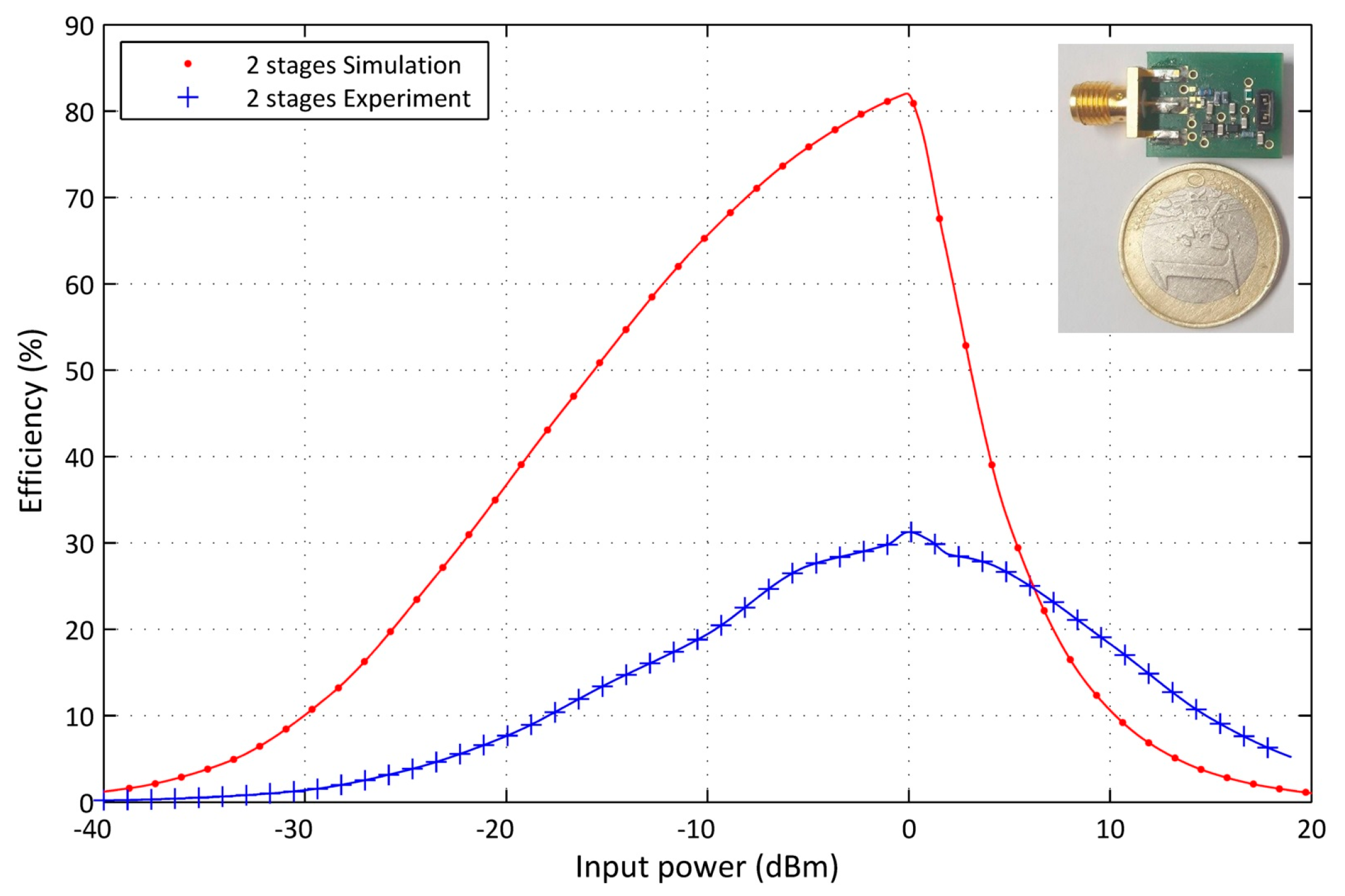
4.4. Design and Experiment Setup for a Modified Dual Stages Voltage Multiplier Circuit
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kawasaki, S. The Green Energy Harvesting Winds by the RF/Microwave Power Transmission. In Proceedings of the 2013 Wireless Power Transfer, Perugia, Italy, 15–16 May 2013; pp. 111–114.
- Patel, A.C.; Vaghela, M.P.; Bajwa, H.; Patra, P.K. Power Harvesting for Low Power Wireless Sensor Network. In Proceedings of the Antennas & Propagation Conference, Loughborough, UK, 16–17 November 2009; pp. 633–636.
- Zhao, W.; Choi, K.; Bauman, S.; Salter, T.; Lowy, D.A.; Peckerar, M.; Khandani, M.K. An Energy Harvesting System Surveyed for a Variety of Unattended Electronic Applications. Solid State Electron. 2013, 79, 233–237. [Google Scholar] [CrossRef]
- Masuch, J.; Delgado-Restituto, M.; Milosevic, D.; Baltus, P. Co-Integration of an RF Energy Harvester into a 2.4 GHz Transceiver. IEEE J. Solid State Circuits 2013, 48, 1565–1574. [Google Scholar] [CrossRef]
- Shadmehr, H.; Grimaccia, F.; Gruosso, G.; Mussetta, M.; Zich, R. Optimized Antenna for Low UHF Range Wireless Power Transfer. Int. J. Commun. Antenna Propag. 2013, 3, 21. [Google Scholar]
- Dolgov, A.; Zane, R.; Popovic, Z. Power Management System for Online Low Power RF Energy Harvesting Optimization. IEEE Trans. Circuits Syst. 2010, 57, 1802–1811. [Google Scholar] [CrossRef]
- Nariman, M.; Shirinfar, F.; Toda, A.P.; Pamarti, S.; Rofougaran, A.; Flaviis, F. A Compact 60-GHz Wireless Power Transfer System. IEEE Trans. Microwave Theory Tech. 2016, 64, 2664–2677. [Google Scholar] [CrossRef]
- Olgun, U.; Chen, C.; Volakis, J. Investigation of Rectenna Array Configurations for Enhanced RF Power Harvesting. IEEE Antennas Wirel. Propag. Lett. 2011, 10, 262–265. [Google Scholar] [CrossRef]
- Visser, H.; Vullers, R.M. RF Energy Harvesting and Transport for Wireless Sensor Network Applications: Principles and Requirements. Proc. IEEE 2013, 101, 1410–1423. [Google Scholar] [CrossRef]
- ERC/REC 70-03. Recommendation Adopted by the Frequency Management, Regulatory Affairs and Spectrum Engineering Working Groups. Available online: http://www.arcep.fr/fileadmin/reprise/dossiers/frequences/ERC-REC-70-03E-version02.PDF (accessed on 3 March 2017).
- Federal Communications Commission. Code of Federal Regulations; Federal Communications Commission: Washington, DC, USA, 2002. [Google Scholar]
- Nishimoto, H.; Kawahara, Y.; Asami, T. Prototype Implementation of Ambient RF Energy Harvesting Wireless Sensor Networks. In Proceedings of the IEEE Sensor Conference, Waikoloa, HI, USA, 1–4 November 2010; pp. 1282–1287.
- Curty, J.; Joehl, N.; Dehollain, C.; Declercq, M. Remotely powered addressable UHF RFID integrated system. IEEE J. Solid State Circuits 2005, 40, 2193–2202. [Google Scholar] [CrossRef]
- Lorenz, C.H.P.; Hemour, S.; Wu, K. Physical Mechanism and Theoretical Foundation of Ambient RF Power Harvesting Using Zero-Bias Diodes. IEEE Trans. Microwave Theory Tech. 2016, 64, 2146–2158. [Google Scholar] [CrossRef]
- Devi, K.; Din, N.; Chakrabarty, C. Optimization of the Voltage Doubler Stages in an RF-DC Convertor Module for Energy Harvesting. Circuits Syst. 2012, 3, 216–222. [Google Scholar] [CrossRef]
- Dickson, J.F. On-chip high-voltage generation in MNOS integrated circuits using an improved voltage multiplier technique. IEEE J. Solid State Circuits 1976, 11, 374–378. [Google Scholar] [CrossRef]
- Tanzawa, T.; Tanaka, T. A dynamic analysis of the Dickson charge pump circuit. IEEE J. Solid State Circuits 2013, 32, 1231–1240. [Google Scholar] [CrossRef]
- Yan, H.; Montero, J.M.; Akhnoukh, A.; Burghartz, J.N. An integration scheme for RF power harvesting. In Proceedings of the STW Annual Workshop on Semiconductor Advances for Future Electronics and Sensors, Utrecht, The Netherlands, 17–18 November 2005; pp. 17–18.
- Chaour, I.; Bdiri, S.; Fakhfakh, A.; Kanoun, O. Modified rectifier circuit for high efficiency and low power RF energy harvester. In Proceedings of the International Multi-Conference on Systems, Signals & Devices (SSD), Leipzig, Germany, 21–24 March 2016; pp. 619–623.
- Henderson, A. Continuity of Inductor Currents and Capacitor Voltages in Linear Networks Containing Switches. Int. J. Electron. 1971, 31, 579–587. [Google Scholar] [CrossRef]
- Nimo, A.; Grgić, D.; Reindl, L.M. Optimization of Passive Low Power Wireless Electromagnetic Energy Harvesters. Sensors 2012, 12, 13636–13663. [Google Scholar] [CrossRef] [PubMed]
- Texas Instruments MSP430L092. Available online: http://www.ti.com/product/msp430l092 (accessed on 3 April 2015).
- Nintanavongsa, P.; Muncuk, U.; Richard Lewis, D.; Chowdhury, K. Design Optimization and Implementation for RF Energy Harvesting Circuits. IEEE J. Emerg. Sel. Top. Circuits Syst. 2012, 2, 24–33. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaour, I.; Fakhfakh, A.; Kanoun, O. Enhanced Passive RF-DC Converter Circuit Efficiency for Low RF Energy Harvesting. Sensors 2017, 17, 546. https://doi.org/10.3390/s17030546
Chaour I, Fakhfakh A, Kanoun O. Enhanced Passive RF-DC Converter Circuit Efficiency for Low RF Energy Harvesting. Sensors. 2017; 17(3):546. https://doi.org/10.3390/s17030546
Chicago/Turabian StyleChaour, Issam, Ahmed Fakhfakh, and Olfa Kanoun. 2017. "Enhanced Passive RF-DC Converter Circuit Efficiency for Low RF Energy Harvesting" Sensors 17, no. 3: 546. https://doi.org/10.3390/s17030546
APA StyleChaour, I., Fakhfakh, A., & Kanoun, O. (2017). Enhanced Passive RF-DC Converter Circuit Efficiency for Low RF Energy Harvesting. Sensors, 17(3), 546. https://doi.org/10.3390/s17030546