Image-Based Multi-Target Tracking through Multi-Bernoulli Filtering with Interactive Likelihoods
Abstract
:1. Introduction
- a novel interactive likelihood (ILH) method for sequential Monte Carlo (SMC) image-based trackers that can be computed non-iteratively to preclude the tracker from sampling from areas that belong to different targets;
- this interactive likelihood method is integrated with the multi-Bernoulli filter, a state-of-the-art RFS tracker, which is referred to as MBFILH;
- the deep learning technique for pedestrian detection proposed in [25] is combined with the MBFILH; and
- an extensive evaluation is carried out using several publicly available datasets and standard evaluation metrics.
2. Related Work
2.1. Common Multi-Target Tracking Algorithms
2.2. Current Trends
3. Method
3.1. Image-Based Multi-Bernoulli Filter
3.2. Bayes’ Recursion
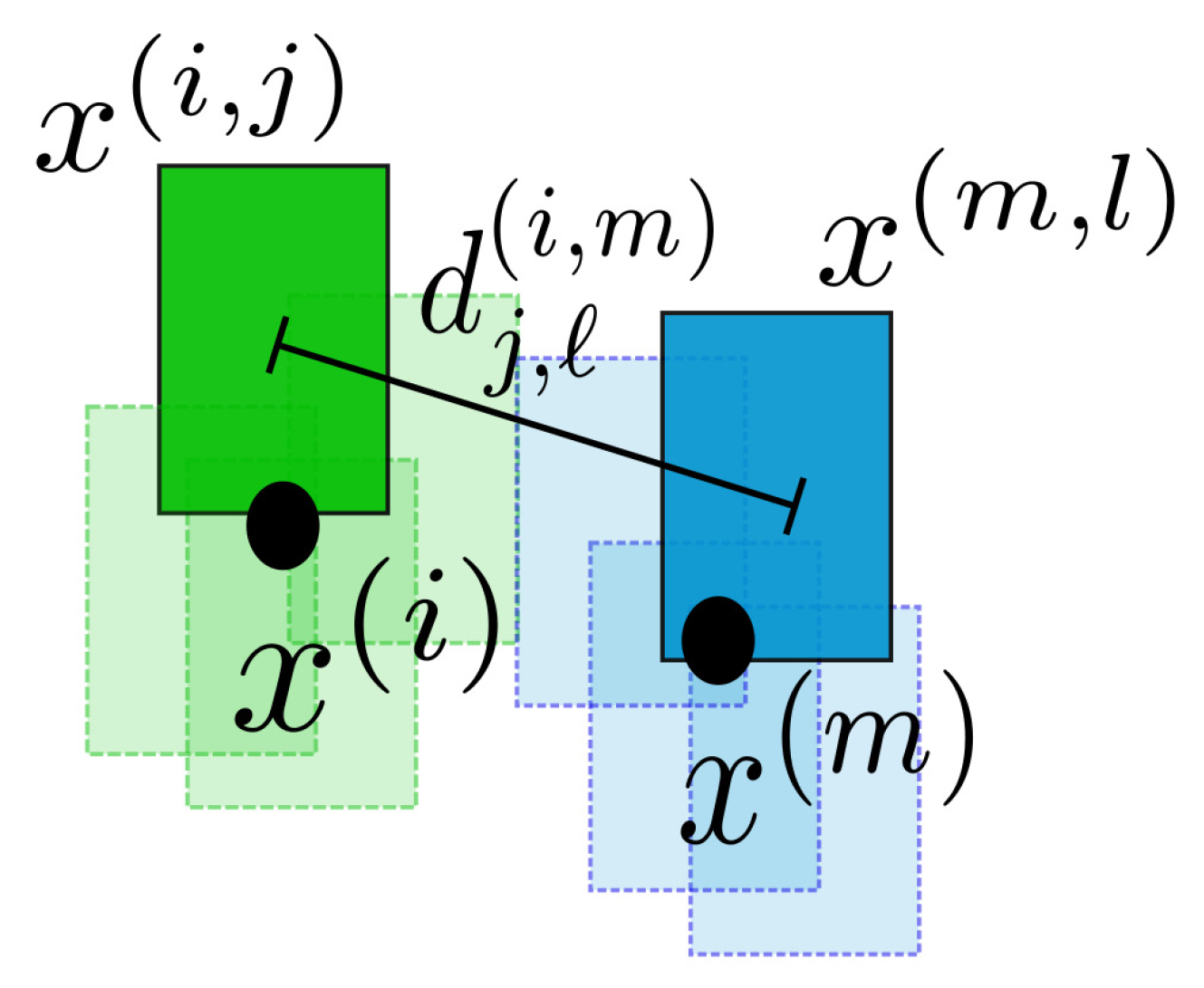
3.3. Likelihood Functions
3.4. Particle Filter Implementation
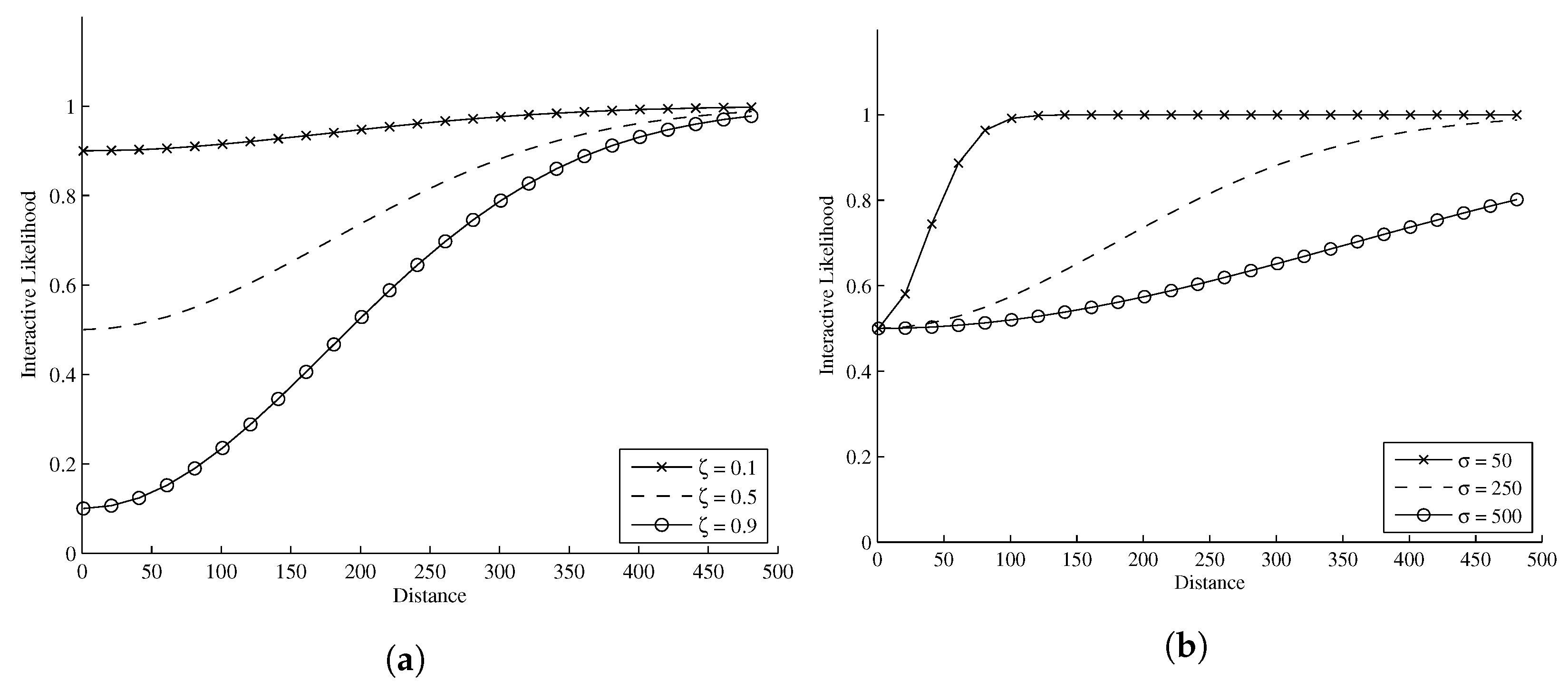
4. Interactive Likelihood
4.1. Deep Learning for Pedestrian Detection
- Channel 1 input = the Y channel of the resized (to 84 × 28) YUV converted image.
- Channel 2 input = the Y, U and V channels of the 84 × 28 image resized to 42 × 14, concatenated and zero padded to achieve the overall dimensions of 84 × 28.
- Channel 3 input = three edge maps (horizontal and vertical) obtained from each channel of the YUV converted image using a Sobel edge detector, resized to be 42 × 14 and concatenated along with the maximum values of these three edge maps into an image of overall size 84 × 28.
5. Experiments and Results
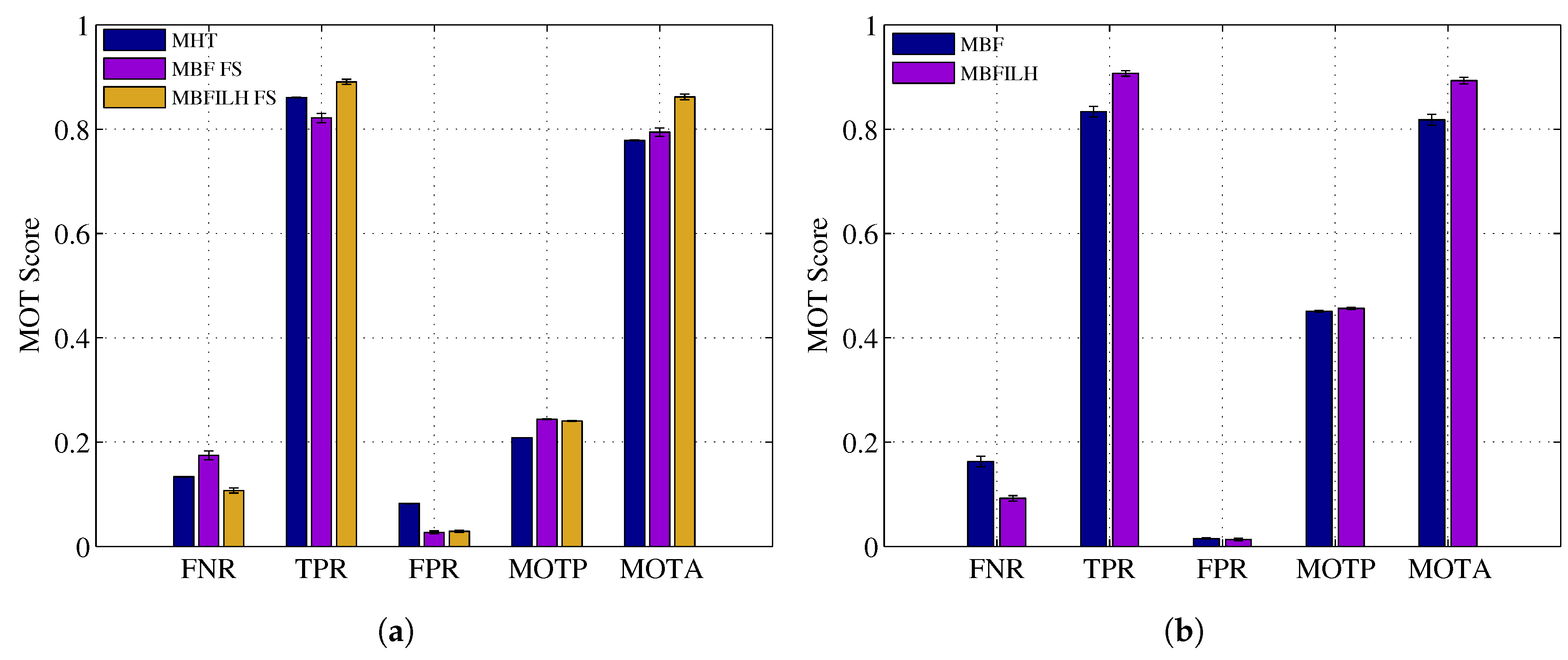
- 2003 PETS INMOVE: (the 2003 PETS INMOVE dataset was originally obtained from ftp://ftp.cs.rdg.ac.uk/pub/VS-PETS/) In this dataset, the performance of the multi-Bernoulli filter without (MBF) the ILH, with the ILH (MBFILH), an implementation of the multiple hypothesis tracking (MHT) method [67], the multi-Bernoulli filter without the ILH and with a fixed target size (MBF FS), and the multi-Bernoulli filter with the ILH with a fixed target size (MBFILH FS) is evaluated; the HSV-based likelihood function in Equation (8) is used for all RFS filter configurations (MBF, MBFILH, MBF FS and MBFILH FS) within this dataset.
- Empirically-determined interactive likelihood parameters: ζ = 0.15 and σ = 5.
- Australian Rules Football League (AFL) [68]: In this dataset, the MBF and the MBFILH filter configurations use the likelihood function in Equation (8).
- Empirically-determined interactive likelihood parameters: ζ = 0.15 and σ = 5 in reduced resolution images and ζ = 0.15 and σ = 10 in full resolution images.
- TUD-Stadtmitte [69]: in this dataset, the pedestrian detector-based likelihood function in Equation (10) is used with the multi-Bernoulli filter without the ILH (MBF PD) and with the ILH (MBFILH PD).
- Empirically-determined interactive likelihood parameters: ζ = 0.45 and σ = 150.
- Empirically-determined pedestrian detector parameters: ζ = 0.30.
5.1. 2003 PETS INMOVE
- FNR: false negative rate (↓).
- TPR: true positive rate (↑).
- FPR: false positive rate (↓).
- TP: number of true positives (↑).
- FN: number of false negatives (↓).
- FP: number of false positives (↓).
- IDSW: number of i.d. switches (↓).
- MOTP: multi-object tracking precision (↑).
- MOTA: multi-object tracking accuracy (↑).
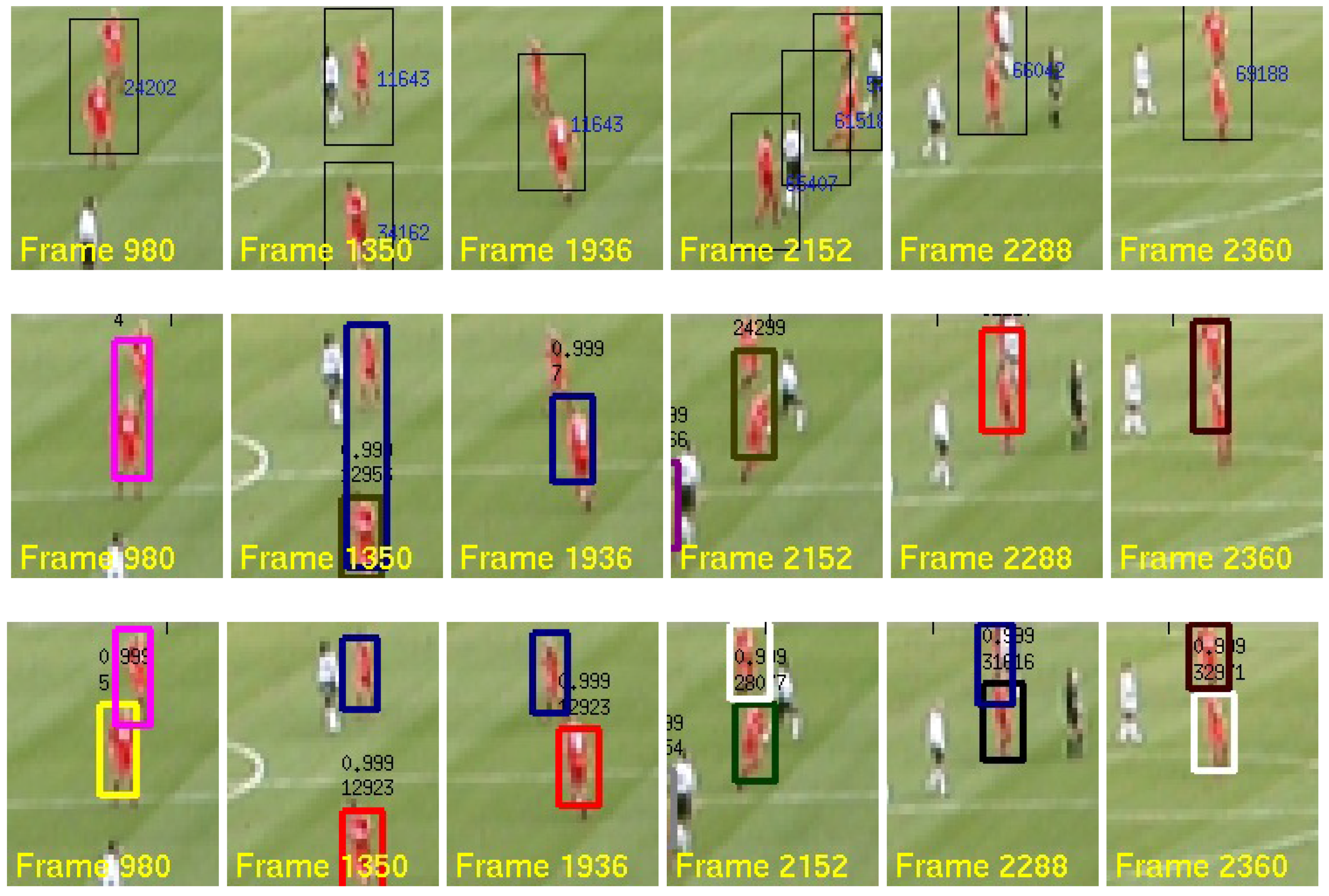
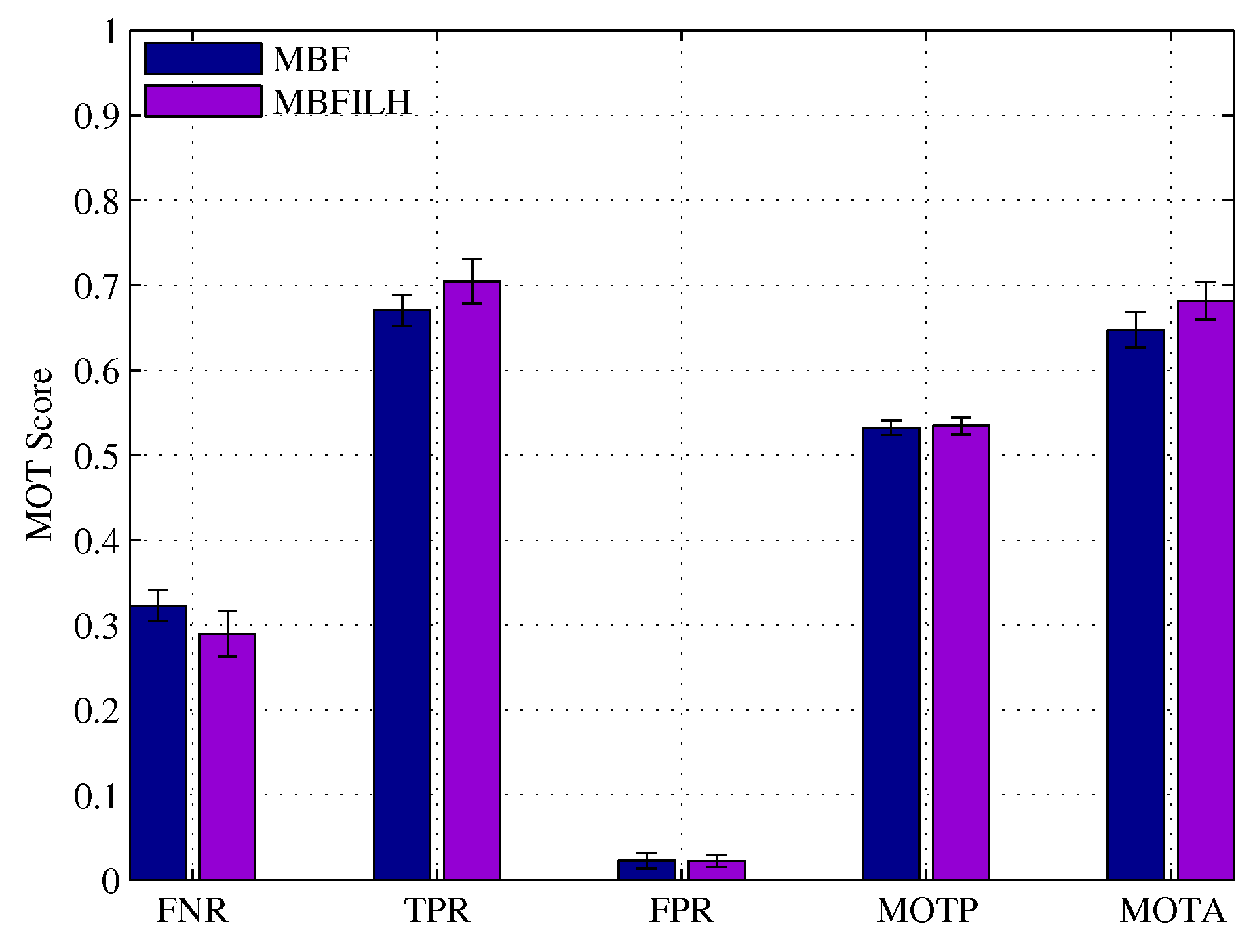
5.2. Australian Rules Football League
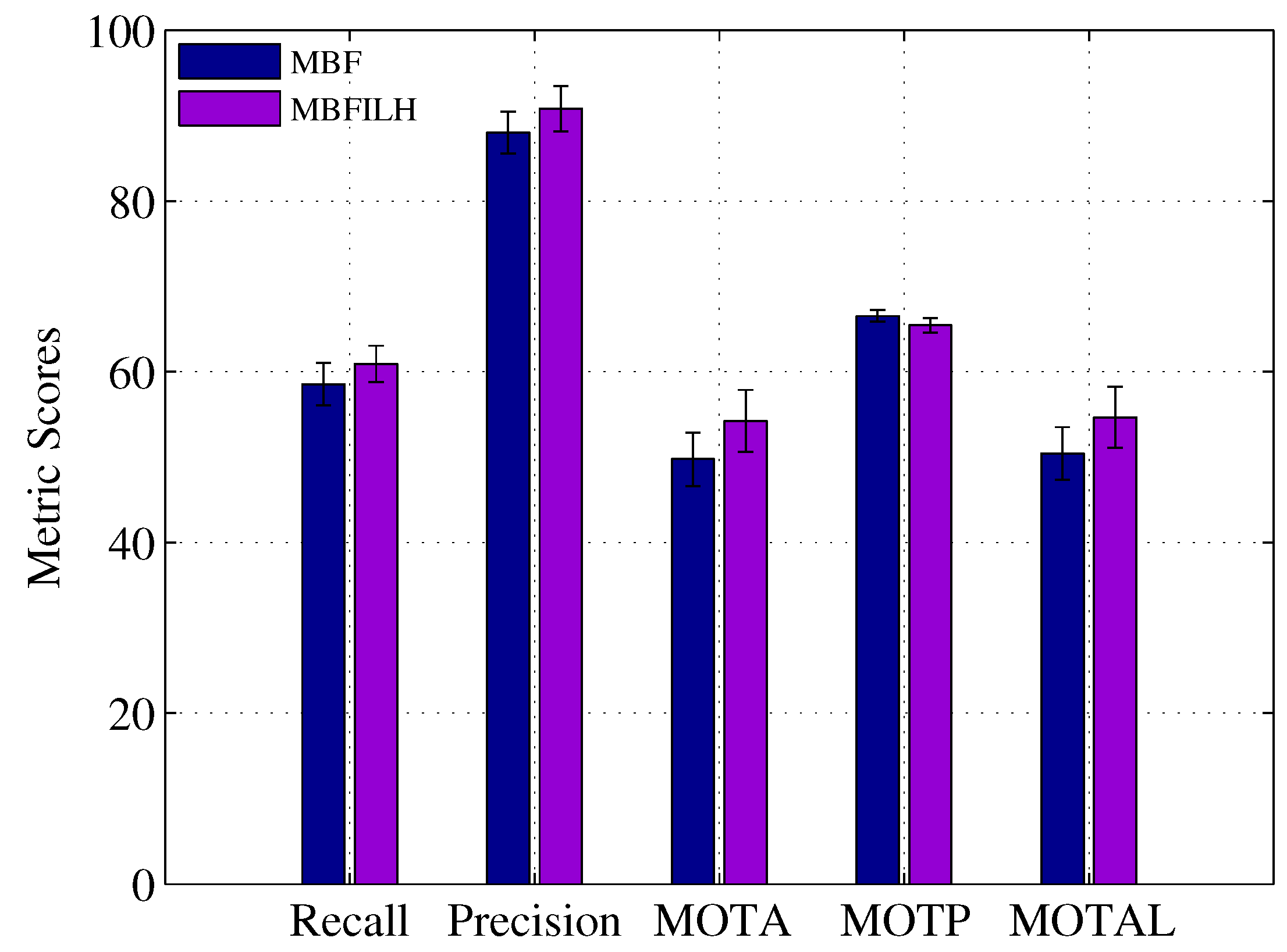
5.3. TUD-Stadtmitte
- Rcll: recall, the percentage of detected targets (↑).
- Prcn: precision, the percentage of correctly detected targets (↑).
- FAR: number of false alarms per frame (↓).
- GT: number of ground truth trajectories.
- MT: number of mostly tracked trajectories (↑).
- PT: number of partially-tracked trajectories.
- ML: number of mostly lost trajectories (↓).
- FP: number of false positives (↓).
- FN: number of false negatives (↓).
- IDs: number of i.d. switches (↓).
- FM: number of fragmentations (↓).
- MOTA: multi-object tracking accuracy in [0, 100] (↑).
- MOTP: multi-object tracking precision in [0, 100] (↑).
- MOTAL: multi-object tracking accuracy in [0, 100] with log10 (IDs) (↑).
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mallick, M.; Vo, B.N.; Kirubarajan, T.; Arulampalam, S. Introduction to the issue on multitarget tracking. IEEE J. Sel. Top. Signal Process. 2013, 7, 373–375. [Google Scholar] [CrossRef]
- Stone, L.D.; Streit, R.L.; Corwin, T.L.; Bell, K.L. Bayesian Multiple Target Tracking; Artech House: Norwood, MA, USA, 2013. [Google Scholar]
- Milan, A.; Leal-Taixé, L.; Schindler, K.; Reid, I. Joint tracking and segmentation of multiple targets. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5397–5406.
- Reid, D.B. An algorithm for tracking multiple targets. IEEE Trans. Autom. Control 1979, 24, 843–854. [Google Scholar] [CrossRef]
- Hwang, I.; Balakrishnan, H.; Roy, K.; Tomlin, C. Multiple-target tracking and identity management in clutter, with application to aircraft tracking. In Proceedings of the American Control Conference, Boston, MA, USA, 30 June–2 July 2004; pp. 3422–3428.
- Bar-Shalom, Y. Multitarget-Multisensor Tracking: Applications and Advances; Artech House, Inc.: Norwood, MA, USA, 2000. [Google Scholar]
- Bobinchak, J.; Hewer, G. Apparatus and Method for Cooperative Multi Target Tracking And Interception. U.S. Patent 7,422,175, 9 September 2008. [Google Scholar]
- Soto, C.; Song, B.; Roy-Chowdhury, A.K. Distributed multi-target tracking in a self-configuring camera network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 1486–1493.
- Wang, X. Intelligent multi-camera video surveillance: A review. Pattern Recognit. Lett. 2013, 34, 3–19. [Google Scholar] [CrossRef]
- Kamath, S.; Meisner, E.; Isler, V. Triangulation based multi target tracking with mobile sensor networks. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 3283–3288.
- Coue, C.; Fraichard, T.; Bessiere, P.; Mazer, E. Using Bayesian programming for multi-sensor multi-target tracking in automotive applications. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA ’03), Taipei, Taiwan, 14–19 September 2003; pp. 2104–2109.
- Ong, L.; Upcroft, B.; Bailey, T.; Ridley, M.; Sukkarieh, S.; Durrant-Whyte, H. A decentralised particle filtering algorithm for multi-target tracking across multiple flight vehicles. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 4539–4544.
- Premebida, C.; Nunes, U. A multi-target tracking and GMM-classifier for intelligent vehicles. In Proceedings of the 2006 IEEE Intelligent Transportation Systems Conference, Toronto, ON, Canada, 17–20 September 2006; pp. 313–318.
- Jia, Z.; Balasuriya, A.; Challa, S. Recent developments in vision based target tracking for autonomous vehicles navigation. In Proceedings of the 2006 IEEE Intelligent Transportation Systems Conference, Toronto, ON, Canada, 17–20 September 2006; pp. 765–770.
- Choi, J.; Ulbrich, S.; Lichte, B.; Maurer, M. Multi-target tracking using a 3D-Lidar sensor for autonomous vehicles. In Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems (ITSC 2013), The Hague, The Netherlands, 6–9 October 2013; pp. 881–886.
- Ristic, B.; Vo, B.N.; Clark, D.; Vo, B.T. A Metric for Performance Evaluation of Multi-Target Tracking Algorithms. IEEE Trans. Signal Process. 2011, 59, 3452–3457. [Google Scholar] [CrossRef]
- Mahler, R.P. Statistical Multisource-Multitarget Information Fusion; Artech House, Inc.: Norwood, MA, USA, 2007. [Google Scholar]
- Vo, B. T.; Vo, B. N.; Cantoni, A. The Cardinality Balanced Multi-Target Multi-Bernoulli Filter and Its Implementations. IEEE Trans. Signal Process. 2009, 57, 409–423. [Google Scholar]
- Reuter, S.; Vo, B.T.; Vo, B.N.; Dietmayer, K. Multi-object tracking using labeled multi-Bernoulli random finite sets. In Proceedings of the 17th International Conference on Information Fusion (FUSION), Salamanca, Spain, 7–10 July 2014; pp. 1–8.
- Vo, B.T.; Vo, B.N. Labeled Random Finite Sets and Multi-Object Conjugate Priors. IEEE Trans. Signal Process. 2013, 61, 3460–3475. [Google Scholar] [CrossRef]
- Reuter, S.; Vo, B.T.; Vo, B.N.; Dietmayer, K. The Labeled Multi-Bernoulli Filter. IEEE Trans. Signal Process. 2014, 62, 3246–3260. [Google Scholar]
- Vo, B.N.; Vo, B.T.; Phung, D. Labeled Random Finite Sets and the Bayes Multi-Target Tracking Filter. IEEE Trans. Signal Process. 2014, 62, 6554–6567. [Google Scholar] [CrossRef]
- Papi, F.; Vo, B.N.; Vo, B.T.; Fantacci, C.; Beard, M. Generalized Labeled Multi-Bernoulli Approximation of Multi-Object Densities. IEEE Trans. Signal Process. 2015, 63, 5487–5497. [Google Scholar] [CrossRef]
- Vo, B.N.; Vo, B.T.; Hoang, H.G. An Efficient Implementation of the Generalized Labeled Multi-Bernoulli Filter. IEEE Trans. Signal Process. 2017, 65, 1975–1987. [Google Scholar] [CrossRef]
- Ouyang, W.; Wang, X. Joint deep learning for pedestrian detection. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Sydney, Australia, 1–8 December 2013; pp. 2056–2063.
- Fortmann, T.E.; Bar-Shalom, Y.; Scheffe, M. Multi-target tracking using joint probabilistic data association. In Proceedings of the 19th IEEE Conference on Decision and Control including the Symposium on Adaptive Processes, Albuquerque, NM, USA, 10–12 December 1980; pp. 807–812.
- Hoseinnezhad, R.; Vo, B.N.; Vo, B.T.; Suter, D. Visual tracking of numerous targets via multi-Bernoulli filtering of image data. Pattern Recognit. 2012, 45, 3625–3635. [Google Scholar] [CrossRef]
- Ristic, B.; Vo, B.T.; Vo, B.N.; Farina, A. A Tutorial on Bernoulli Filters: Theory, Implementation and Applications. IEEE Trans. Signal Process. 2013, 61, 3406–3430. [Google Scholar] [CrossRef]
- Vo, B.N.; Vo, B.T.; Pham, N.T.; Suter, D. Joint Detection and Estimation of Multiple Objects From Image Observations. IEEE Trans. Signal Process. 2010, 58, 5129–5141. [Google Scholar] [CrossRef]
- Vo, B.N.; Vo, B.T.; Pham, N.T.; Suter, D. Bayesian multi-object estimation from image observations. In Proceedings of the 12th International Conference on Information Fusion (FUSION ’09), Seattle, WA, USA, 6–9 July 2009; pp. 890–898.
- Vo, B.T.; Vo, B.N. A random finite set conjugate prior and application to multi-target tracking. In Proceedings of the 2011 Seventh International Conference on Intelligent Sensors, Sensor Networks and Information Processing (ISSNIP), Adelaide, Australia, 6–9 December 2011; pp. 431–436.
- Hoseinnezhad, R.; Vo, B.N.; Vo, B.T. Visual Tracking in Background Subtracted Image Sequences via Multi-Bernoulli Filtering. IEEE Trans. Signal Process. 2013, 61, 392–397. [Google Scholar] [CrossRef]
- Hoseinnezhad, R.; Vo, B.N.; Suter, D.; Vo, B.T. Multi-object filtering from image sequence without detection. In Proceedings of the 2010 IEEE International Conference on Acoustics Speech and Signal Processing (ICASSP), Dallas, TX, USA, 14–19 March 2010; pp. 1154–1157.
- Maggio, E.; Taj, M.; Cavallaro, A. Efficient Multitarget Visual Tracking Using Random Finite Sets. IEEE Trans. Circuits Syst. Video Technol. 2008, 18, 1016–1027. [Google Scholar] [CrossRef]
- Rezatofighi, S.H.; Milan, A.; Zhang, Z.; Shi, Q.; Dick, A.; Reid, I. Joint probabilistic data association revisited. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 3047–3055.
- Lee, H.; Grosse, R.; Ranganath, R.; Ng, A.Y. Convolutional deep belief networks for scalable unsupervised learning of hierarchical representations. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; pp. 609–616.
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105.
- Sermanet, P.; Kavukcuoglu, K.; Chintala, S.; LeCun, Y. Pedestrian detection with unsupervised multi-stage feature learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 22–28 June 2013; pp. 3626–3633.
- Ouyang, W.; Wang, X. A discriminative deep model for pedestrian detection with occlusion handling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 3258–3265.
- Ouyang, W.; Zeng, X.; Wang, X. Modeling mutual visibility relationship in pedestrian detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 22–28 June 2013; pp. 3222–3229.
- Zeng, X.; Ouyang, W.; Wang, X. Multi-stage contextual deep learning for pedestrian detection. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 121–128.
- Luo, P.; Tian, Y.; Wang, X.; Tang, X. Switchable deep network for pedestrian detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 899–906.
- Milan, A.; Rezatofighi, S.H.; Dick, A.R.; Schindler, K.; Reid, I.D. Online Multi-target Tracking using Recurrent Neural Networks. arXiv, 2016; arXiv:1604.03635. [Google Scholar]
- Chen, X.; Qin, Z.; An, L.; Bhanu, B. An online learned elementary grouping model for multi-target tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014.
- Tang, S.; Andres, B.; Andriluka, M.; Schiele, B. Subgraph decomposition for multi-target tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015.
- Shafique, K.; Shah, M. A noniterative greedy algorithm for multiframe point correspondence. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 51–65. [Google Scholar] [CrossRef] [PubMed]
- Bar-Shalom, Y.; Daum, F.; Huang, J. The probabilistic data association filter. IEEE Control Syst. 2009, 29, 82–100. [Google Scholar] [CrossRef]
- Oh, S.; Russell, S.; Sastry, S. Markov Chain Monte Carlo Data Association for Multi-Target Tracking. IEEE Trans. Autom. Control 2009, 54, 481–497. [Google Scholar]
- Choi, W. Near-online multi-target tracking with aggregated local flow descriptor. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 3029–3037.
- Wang, B.; Wang, G.; Chan, K.L.; Wang, L. Tracklet Association by Online Target-Specific Metric Learning and Coherent Dynamics Estimation. arXiv, 2015; arXiv:1511.06654. [Google Scholar]
- Bewley, A.; Ge, Z.; Ott, L.; Ramos, F.; Upcroft, B. Simple Online and Realtime Tracking. arXiv, 2016; arXiv:1602.00763. [Google Scholar]
- Kim, C.; Li, F.; Ciptadi, A.; Rehg, J.M. Multiple hypothesis tracking revisited. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 4696–4704.
- Milan, A.; Schindler, K.; Roth, S. Multi-Target Tracking by Discrete-Continuous Energy Minimization. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 2054–2068. [Google Scholar] [CrossRef] [PubMed]
- Leal-Taixé, L.; Milan, A.; Reid, I.; Roth, S.; Schindler, K. MOTchallenge 2015: Towards a benchmark for multi-target tracking. arXiv, 2015; rXiv:1504.01942. [Google Scholar]
- Milan, A.; Leal-Taixe, L.; Reid, I.; Roth, S.; Schindler, K. MOT16: A Benchmark for Multi-Object Tracking. arXiv, 2016; arXiv:1603.00831. [Google Scholar]
- Dehghan, A.; Tian, Y.; Torr, P.H.S.; Shah, M. Target identity-aware network flow for online multiple target tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1146–1154.
- Porikli, F. Needle picking: A sampling based Track-before-detection method for small targets. Proc. SPIE 2010, 7698, 769803. [Google Scholar]
- Davey, S.; Rutten, M.; Cheung, B. A comparison of detection performance for several track-before-detect algorithms. EURASIP J. Adv. Signal Process. 2008. [Google Scholar] [CrossRef]
- Mahler, R. Random Set Theory for Target Tracking and Identification; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Mahler, R.P.S. “Statistics 101” for multisensor, multitarget data fusion. IEEE Aerosp. Electron. Syst. Mag. 2004, 19, 53–64. [Google Scholar] [CrossRef]
- Vo, B.N.; Singh, S.; Doucet, A. Sequential Monte Carlo methods for multitarget filtering with random finite sets. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1224–1245. [Google Scholar]
- Qu, W.; Schonfeld, D.; Mohamed, M. Real-Time Distributed Multi-Object Tracking Using Multiple Interactive Trackers and a Magnetic-Inertia Potential Model. IEEE Trans. Multimedia 2007, 9, 511–519. [Google Scholar] [CrossRef]
- Xiao, J.; Oussalah, M. Collaborative Tracking for Multiple Objects in the Presence of Inter-Occlusions. IEEE Trans. Circuits Syst. Video Technol. 2016, 26, 304–318. [Google Scholar] [CrossRef]
- Yang, B.; Yang, R. Interactive particle filter with occlusion handling for multi-target tracking. In Proceedings of the 12th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD), Zhangjiajie, China, 15–17 August 2015; pp. 1945–1949.
- Dollar, P.; Wojek, C.; Schiele, B.; Perona, P. Pedestrian detection: A benchmark. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 304–311.
- Antunes, D.M.; de Matos, D.M.; Gaspar, J. A Library for Implementing the Multiple Hypothesis Tracking Algorithm. arXiv, 2011; arXiv:1106.2263. [Google Scholar]
- Milan, A.; Gade, R.; Dick, A.; Moeslund, T.B.; Reid, I. Improving global multi-target tracking with local updates. In Proceedings of the Workshop on Visual Surveillance and Re-Identification, Zurich, Switzerland, 6–7 September 2014.
- Andriluka, M.; Roth, S.; Schiele, B. Monocular 3D pose estimation and tracking by detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), San Francisco, CA, USA, 13–18 June 2010; pp. 623–630.
- Schuhmacher, D.; Vo, B.T.; Vo, B.N. A Consistent Metric for Performance Evaluation of Multi-Object Filters. IEEE Trans. Signal Process. 2008, 56, 3447–3457. [Google Scholar] [CrossRef]
- Bernardin, K.; Stiefelhagen, R. Evaluating multiple object tracking performance: The CLEAR MOT metrics. J. Image Video Process. 2008, 2008, 246309. [Google Scholar] [CrossRef]
- Dicle, C.; Camps, O.; Sznaier, M. The way they move: Tracking multiple targets with similar appearance. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 2304–2311.
- Milan, A.; Schindler, K.; Roth, S. Detection- and trajectory-level exclusion in multiple object tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland, OR, USA, 23–28 June 2013; pp. 3682–3689.
- Park, J.; Tabb, A.; Kak, A.C. Hierarchical data structure for real-time background subtraction. In Proceedings of the IEEE International Conference on Image Processing, Atlanta, GA, USA, 8–11 October 2006; pp. 1849–1852.
- Ristic, B.; Clark, D.; Vo, B.N.; Vo, B.T. Adaptive Target Birth Intensity for PHD and CPHD Filters. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 1656–1668. [Google Scholar] [CrossRef]
- Yuan, C.; Wang, J.; Lei, P.; Bi, Y.; Sun, Z. Multi-Target Tracking Based on Multi-Bernoulli Filter with Amplitude for Unknown Clutter Rate. Sensors 2015, 15, 29804. [Google Scholar] [CrossRef] [PubMed]
- Zea, A.; Faion, F.; Baum, M.; Hanebeck, U.D. Level-set random hypersurface models for tracking non-convex extended objects. In Proceedings of the 16th International Conference on Information Fusion, Istanbul, Turkey, 9–12 July 2013; pp. 1760–1767.
- Beard, M.; Reuter, S.; Granström, K.; Vo, B.T.; Vo, B.N.; Scheel, A. Multiple Extended Target Tracking with Labeled Random Finite Sets. IEEE Trans. Signal Process. 2016, 64, 1638–1653. [Google Scholar] [CrossRef]


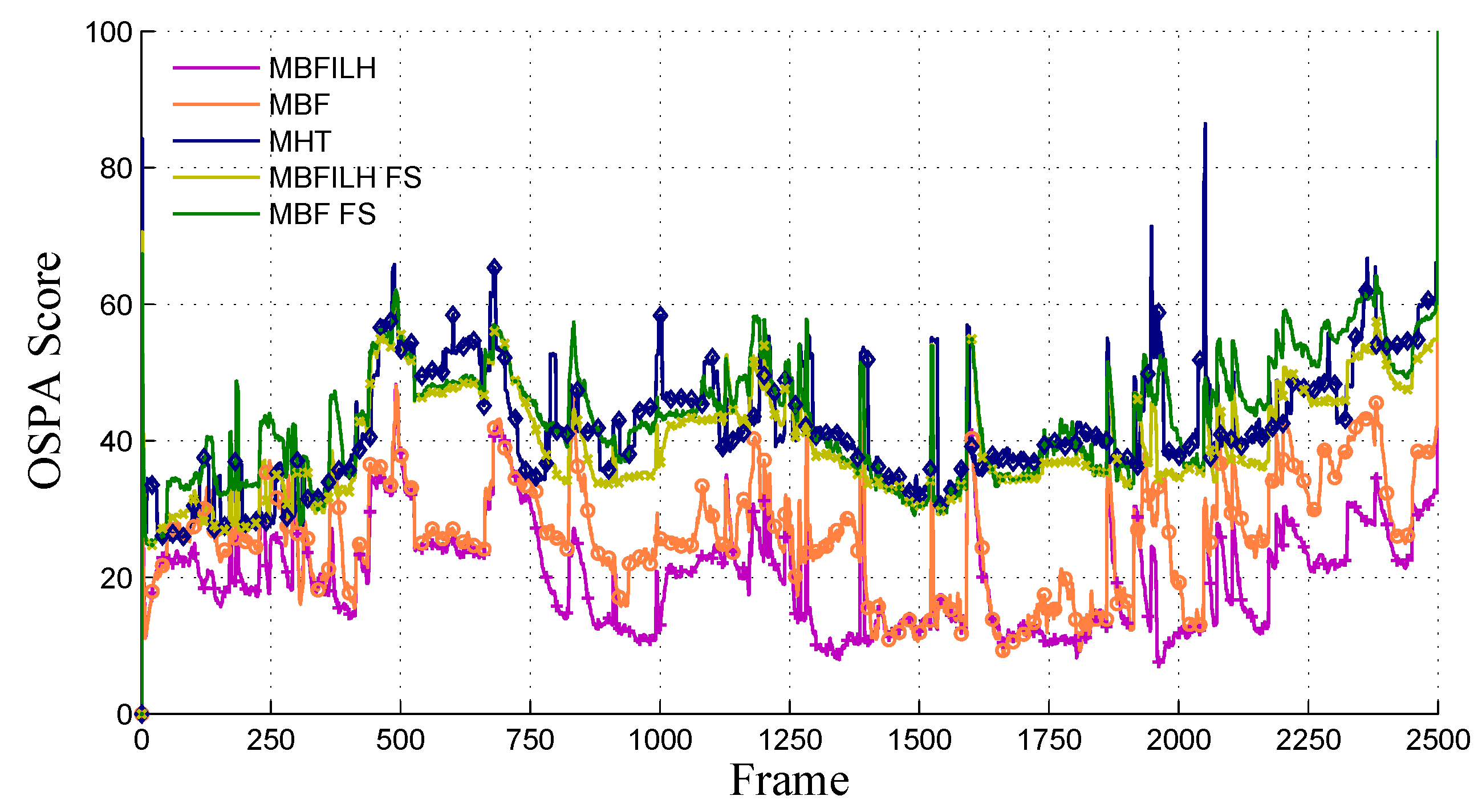


| Method | Mean OSPA Scores |
|---|---|
| MHT | 42.30 |
| MBF FS | 43.57 |
| MBFILH FS | 40.02 |
| MBF | 26.29 |
| MBFILH | 20.39 |
| Method | FNR | TPR | FPR | TP | FN | FP | IDSW | MOTP | MOTA |
|---|---|---|---|---|---|---|---|---|---|
| MHT | 13.3% | 86.0% | 8.2% | 14,789 | 2293 | 1415 | 104 | 20.9% | 77.8% |
| MBF FS | 17.4% | 82.1% | 2.7% | 14,117 | 3004 | 465 | 65 | 24.4% | 79.4% |
| MBFILH FS | 10.7% | 89.1% | 2.9% | 15,308 | 1846 | 496 | 33 | 24.0% | 86.2% |
| MBF | 16.3% | 83.3% | 1.5% | 14,322 | 2803 | 264 | 62 | 45.1% | 81.8% |
| MBFILH | 9.2% | 90.7% | 1.4% | 15,583 | 1585 | 234 | 20 | 45.7% | 89.3% |
| Method | MOTP | MOTA |
|---|---|---|
| SMOT [72] | 60.8% | 16.7% |
| DCO [73] | 63.3% | 29.7% |
| [68] (no init) | 64.1% | 32.0% |
| [68] (no LDA) | 63.6% | 39.0% |
| [68] (full) | 63.6% | 41.4% |
| MBFILH | 52.8% | 66.3% |
| Method | Rcll | Prcn | FAR | MT | PT | ML | FP | FN | IDs | FM | MOTA | MOTP | MOTAL |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MBF PD | 58.54% | 88.00% | 0.52 | 3.10 | 6.70 | 0.20 | 92.7 | 479.30 | 8.8 | 12.10 | 49.76% | 66.53% | 50.43% |
| MBFILH PD | 60.91% | 90.79% | 0.40 | 3.70 | 6.10 | 0.20 | 71.50 | 451.90 | 5.70 | 12.90 | 54.23% | 65.44% | 54.65% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoak, A.; Medeiros, H.; Povinelli, R.J. Image-Based Multi-Target Tracking through Multi-Bernoulli Filtering with Interactive Likelihoods. Sensors 2017, 17, 501. https://doi.org/10.3390/s17030501
Hoak A, Medeiros H, Povinelli RJ. Image-Based Multi-Target Tracking through Multi-Bernoulli Filtering with Interactive Likelihoods. Sensors. 2017; 17(3):501. https://doi.org/10.3390/s17030501
Chicago/Turabian StyleHoak, Anthony, Henry Medeiros, and Richard J. Povinelli. 2017. "Image-Based Multi-Target Tracking through Multi-Bernoulli Filtering with Interactive Likelihoods" Sensors 17, no. 3: 501. https://doi.org/10.3390/s17030501
APA StyleHoak, A., Medeiros, H., & Povinelli, R. J. (2017). Image-Based Multi-Target Tracking through Multi-Bernoulli Filtering with Interactive Likelihoods. Sensors, 17(3), 501. https://doi.org/10.3390/s17030501








