Dynamic Context-Aware Event Recognition Based on Markov Logic Networks
Abstract
:1. Introduction
2. Related Work
3. Preliminaries
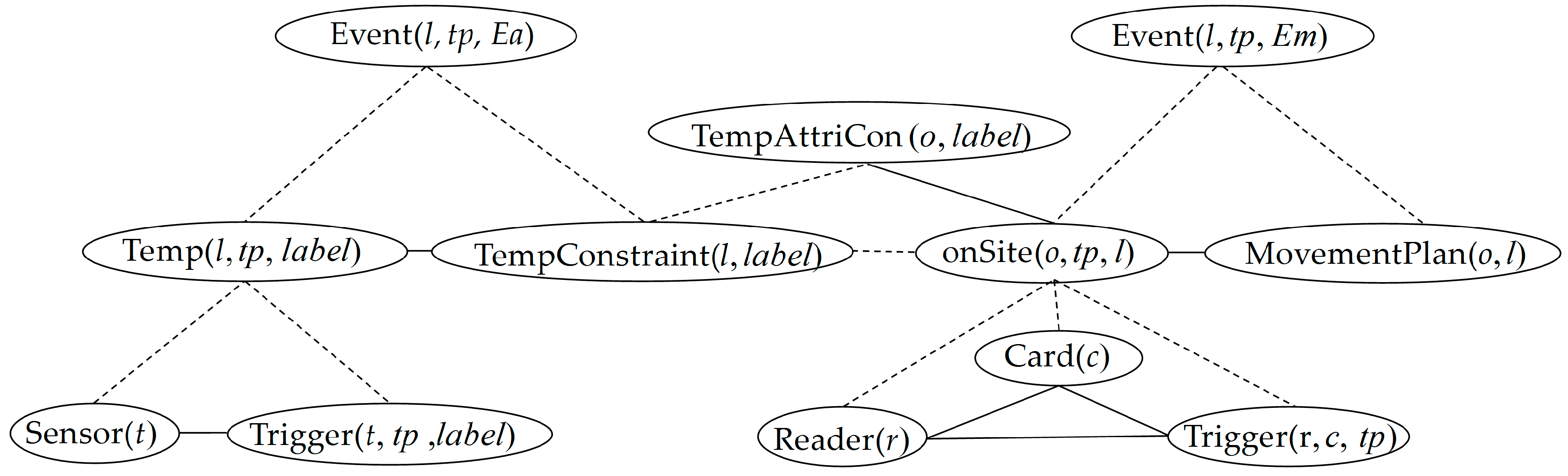
4. Our MLNs-Based Approach for Event Recognition
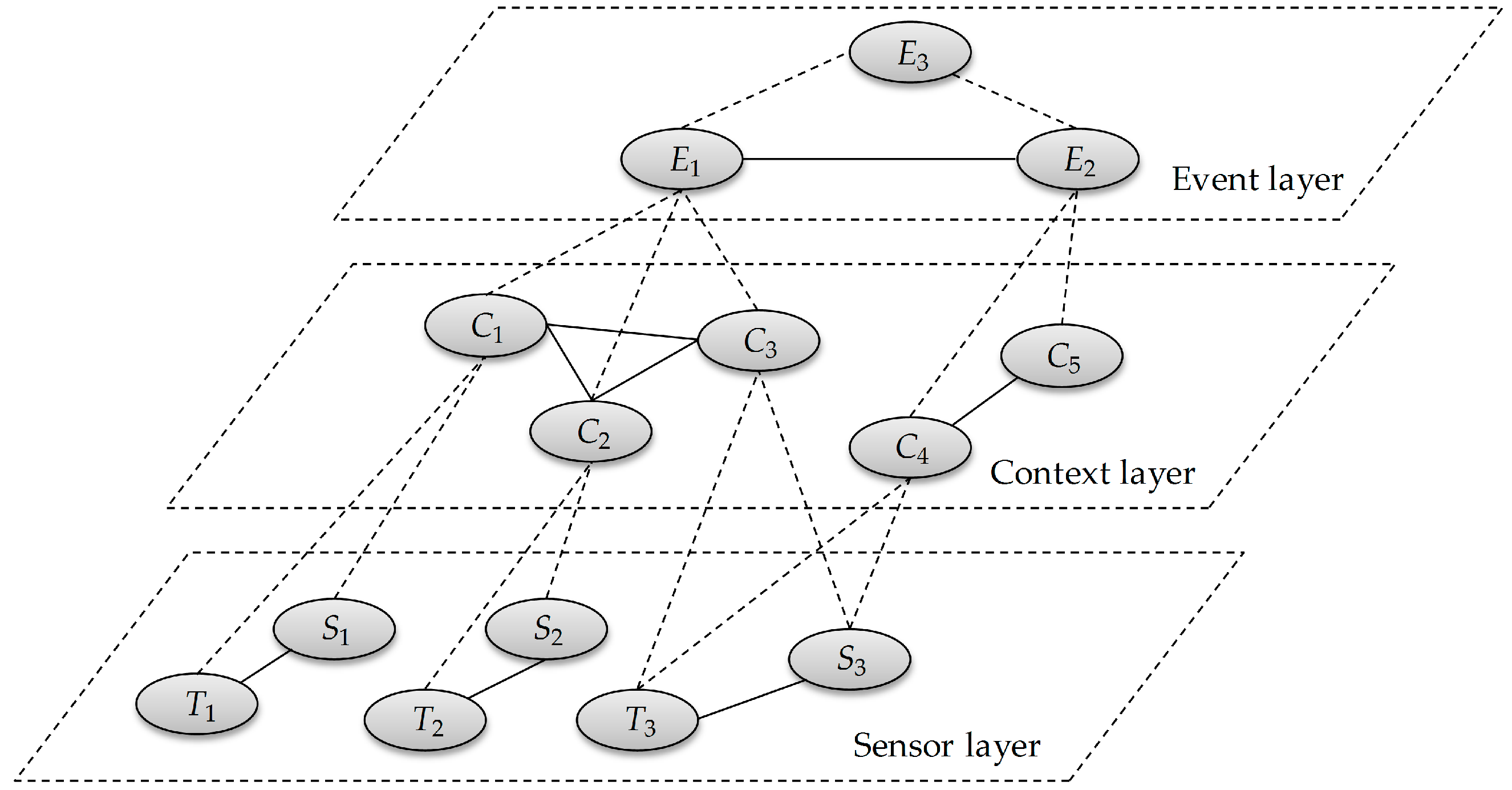
4.1. Multi-Level Information Fusion Model
- Normal (n): a storage object does not validate against its constraints on the movement plan and attributes.
- Violation of movement plan (m): a storage object is deviated from its movement plan to an unscheduled location.m1: Violating the movement plan in the goods-in phase;m2: Violating the movement plan in the inventorying phase;m3: Violating the movement plan in the goods-out phase.
- Violation of attribute constraints (a): this state is activated when any property value of a storage object is beyond the range of its attribute constraints.a1: Violating the temperature attributes;a2: Violating the humidity attributes.
4.2. Statistical Learning Method for Formula Weights
4.3. Dynamic Weight Updating Algorithm
| Algorithm 1. Dynamic Weight Updating Algorithm |
| Input: |
| A Markov logic network , the number of time slices N, an event set consisting of incorrectly recognized events , a dataset consisting of testing data used before the current timestamp, . |
| Output: updated |
| Step 1: ← the factor sensors in terms of events in . |
| Step 2: and ← the relevant rules and weights with respect to factor sensors in . |
| Step 3: if the size of (, then |
| ← the data on the N nearest time slices in . |
| else ← . |
| Step 4: achieve from by the statistical learning method in Section 4.2. |
| Step 5: obtain with updated . |
| Return: |
5. Experiments
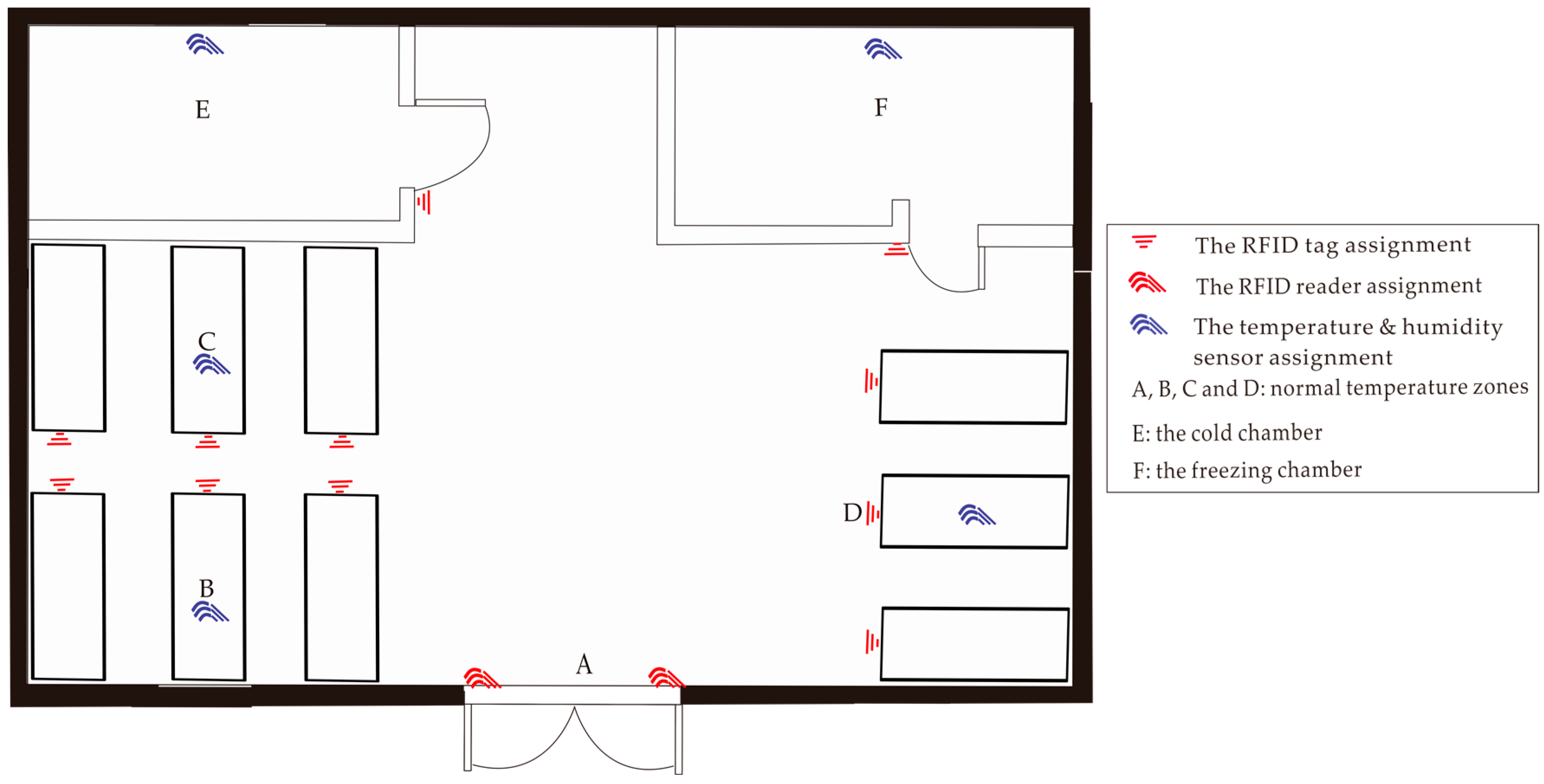
5.1. Datasets
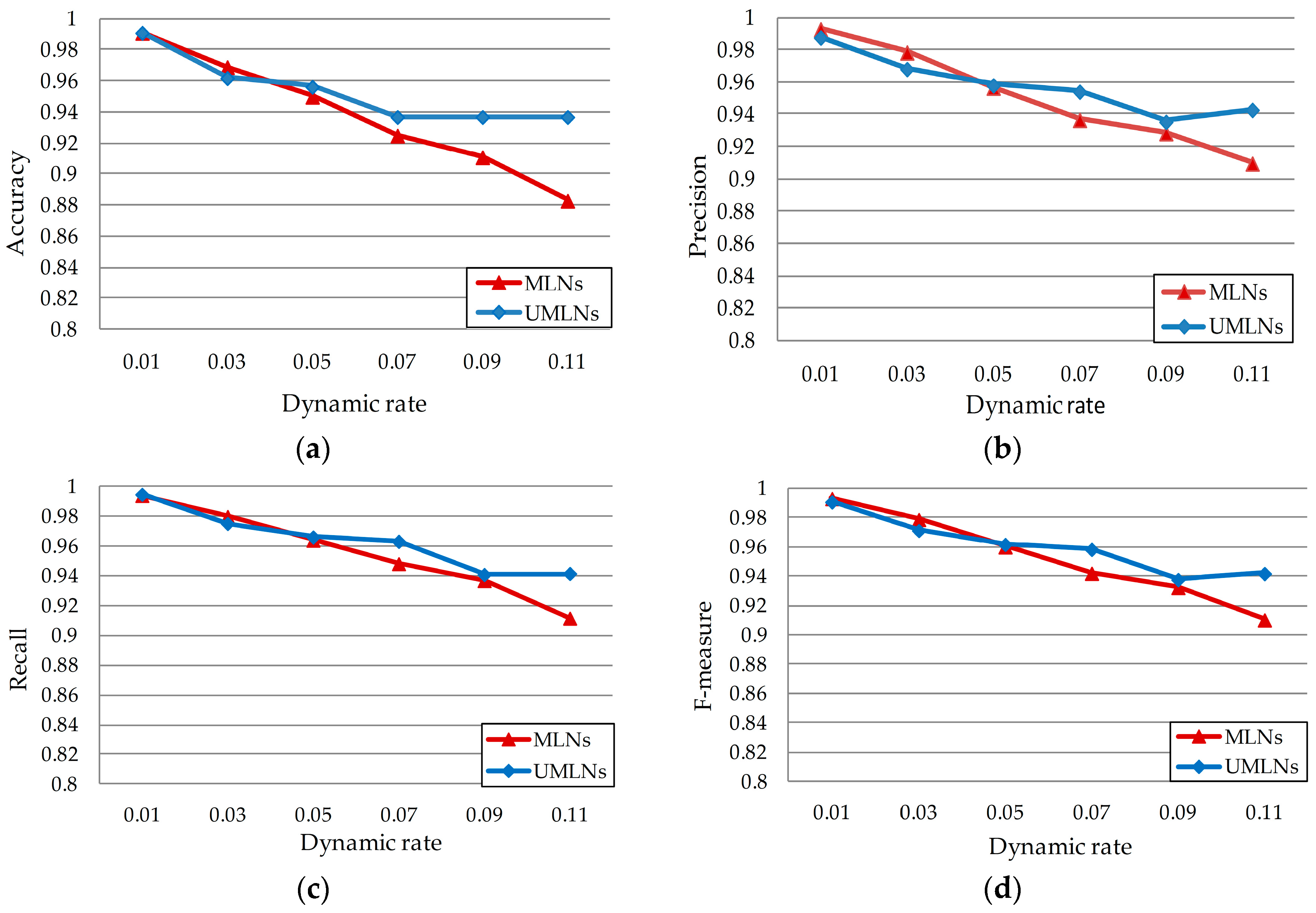
5.2. Results and Analysis
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, H.; Gao, J.; Su, S.; Zhang, X.; Wang, Z. A Visual-Aided Wireless Monitoring System Design for Total Hip Replacement Surgery. IEEE Trans. Biomed. Circ. Syst. 2015, 9, 227–236. [Google Scholar] [CrossRef] [PubMed]
- Ye, J.; Dasiopoulou, S.; Stevenson, G.; Meditskos, G.; Kontopoulos, E.; Kompatsiaris, I.; Dobson, S. Semantic web technologies in pervasive computing: A survey and research roadmap. Pervasive Mob. Comput. 2015, 23, 1–25. [Google Scholar] [CrossRef]
- Barnaghi, P.; Wang, W.E.I.; Henson, C.; Taylor, K. Semantics for the Internet of Things: Early progress and back to the future. Int. J. Semant. Web Inf. Syst. 2012, 8, 1–21. [Google Scholar] [CrossRef]
- Yurur, O.; Liu, C.H.; Moreno, W. A survey of context-aware middleware designs for human activity recognition. IEEE Commun. Mag. 2014, 52, 24–31. [Google Scholar] [CrossRef]
- Yurur, O.; Liu, C.H.; Sheng, Z.; Leung, V.C.M.; Moreno, W.; Leung, K.K. Context-awareness for mobile sensing: A survey and future directions. IEEE Commun. Surv. Tutor. 2016, 18, 68–93. [Google Scholar] [CrossRef]
- Perera, C.; Zaslavsky, A.; Christen, P.; Georgakopoulos, D. Context aware computing for the internet of things: A survey. IEEE Commun. Surv. Tutor. 2014, 16, 414–454. [Google Scholar] [CrossRef]
- Skillen, K.L.; Chen, L.; Nugent, C.D.; Donnelly, M.P.; Burns, W.; Solheim, I. Ontological user modelling and semantic rule-based reasoning for personalisation of Help-On-Demand services in pervasive environments. Future Gener. Comput. Syst. 2014, 34, 97–109. [Google Scholar] [CrossRef]
- Yang, Q. Activity recognition: Linking low-level sensors to high-level intelligence. In Proceedings of the IJCAI International Joint Conference on Artificial Intelligence, Pasadena, CA, USA, 11–17 July 2009; pp. 20–25.
- Yurur, O.; Liu, C.-H.; Moreno, W. Unsupervised posture detection by smartphone accelerometer. Electron. Lett. 2013, 49, 562–564. [Google Scholar] [CrossRef]
- Wang, X.; Ji, Q. Context augmented Dynamic Bayesian Networks for event recognition. Pattern Recognit. Lett. 2014, 43, 62–70. [Google Scholar] [CrossRef]
- Lukasiewicz, T.; Straccia, U. Managing uncertainty and vagueness in description logics for the Semantic Web. Web Semant. 2008, 6, 291–308. [Google Scholar] [CrossRef]
- Almeida, A.; López-de-Ipiña, D. Assessing ambiguity of context data in intelligent environments: Towards a more reliable context managing system. Sensors 2012, 12, 4934–4951. [Google Scholar] [CrossRef] [PubMed]
- Nottelmann, H.; Fuhr, N. Adding Probabilities and Rules to OWL Lite Subsets Based on Probabilistic Datalog. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2006, 14, 17–41. [Google Scholar] [CrossRef]
- Da Costa, P.C.G.; Laskey, K.B.; Laskey, K.J. PR-OWL: A Bayesian Ontology Language for the Semantic Web. Uncertain. Reason. Semant. Web I 2008, 5327, 88–107. [Google Scholar]
- Ding, Z.; Peng, Y.; Pan, R. BayesOWL: Uncertainty Modeling in Semantic Web Ontologies. Soft Comput. Ontol. Semant. Web 2006, 29, 3–29. [Google Scholar]
- Chen, L.; Hoey, J.; Nugent, C.D.; Cook, D.J.; Yu, Z. Sensor-based activity recognition. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2012, 42, 790–808. [Google Scholar] [CrossRef]
- Van Kasteren, T.L.M.; Englebienne, G.; Kröse, B.J.A. Human Activity Recognition from Wireless Sensor Network Data: Benchmark and Software. Act. Recognit. Pervasive Intell. Environ. 2011, 4, 165–186. [Google Scholar]
- Veenendaal, A.; Daly, E.; Jones, E.; Gang, Z.; Vartak, S.; Patwardhan, R.S. Sensor Tracked Points and HMM Based Classifier for Human Action Recognition. Comput. Sci. Emerg. Res. J. 2016, 5, 1–5. [Google Scholar]
- Gaikwad, K.; Narawade, V. HMM Classifier for Human Activity Recognition. Comput. Sci. Eng. 2012, 2, 27–36. [Google Scholar]
- Wang, L.; Gu, T.; Tao, X.; Chen, H.; Lu, J. Recognizing multi-user activities using wearable sensors in a smart home. Pervasive Mob. Comput. 2011, 7, 287–298. [Google Scholar] [CrossRef]
- Raman, N.; Maybank, S.J. Activity recognition using a supervised non-parametric hierarchical HMM. Neurocomputing 2016, 199, 163–177. [Google Scholar] [CrossRef]
- Chiang, Y.T.; Hsu, K.C.; Lu, C.H.; Fu, L.C.; Hsu, J.Y.J. Interaction models for multiple-resident activity recognition in a smart home. In Proceedings of the IEEE/RSJ 2010 International Conference on Intelligent Robots and Systems, IROS 2010—Conference Proceedings, Taipei, Taiwan, 18–22 October 2010; pp. 3753–3758.
- Nazerfard, E.; Das, B.; Holder, L.B.; Cook, D.J. Conditional random fields for activity recognition in smart environments. In Proceedings of the 1st ACM International Health Informatics Symposium, Arlington, TX, USA, 11–12 November 2010; pp. 282–286.
- Tapia, E.M.; Intille, S.S.; Larson, K. Activity Recognition in the Home Using Simple and Ubiquitous Sensors. Pervasive Comput. 2004, 3001, 158–175. [Google Scholar]
- Hsueh, Y.-L.; Lin, N.-H.; Chang, C.-C.; Chen, O.T.-C.; Lie, W.-N. Abnormal event detection using Bayesian networks at a smart home. In Proceedings of the 2015 8th International Conference on Ubi-Media Computing (UMEDIA), Colombo, Sri Lanka, 24–26 August 2015; pp. 273–277.
- Patwardhan, A.S. Walking, Lifting, Standing Activity Recognition using Probabilistic Networks. Int. Res. J. Eng. Technol. 2015, 3, 667–670. [Google Scholar]
- Magherini, T.; Fantechi, A.; Nugent, C.D.; Vicario, E. Using Temporal Logic and Model Checking in Automated Recognition of Human Activities for Ambient-Assisted Living. Hum. Mach. Syst. IEEE Trans. 2013, 43, 509–521. [Google Scholar] [CrossRef]
- Chen, L.; Nugent, C.; Mulvenna, M.; Finlay, D.; Hong, X.; Poland, M. Using event calculus for behaviour reasoning and assistance in a smart home. In Proceedings of the 6th International Conference on Smart Homes and Health Telematics, Ames, IA, USA, 28 June–2 July 2008; pp. 81–89.
- Kapitanova, K.; Son, S.H.; Kang, K.-D. Using fuzzy logic for robust event detection in wireless sensor networks. Ad Hoc Netw. 2012, 10, 709–722. [Google Scholar] [CrossRef]
- Bouchard, B.; Giroux, S.; Bouzouane, A. A logical approach to ADL recognition foralzheimer’s patients. In Proceedings of the 4th International Conference on Smart Homes and Health Telematic, Belfast, Ireland, 26–28 June 2006; pp. 122–129.
- Brendel, W.; Fern, A.; Todorovic, S. Probabilistic event logic for interval-based event recognition. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 3329–3336.
- Snidaro, L.; Visentini, I.; Bryan, K. Fusing uncertain knowledge and evidence for maritime situational awareness via Markov Logic Networks. Inf. Fusion 2015, 21, 159–172. [Google Scholar] [CrossRef]
- Gomez-Romero, J.; Serrano, M.A.; Garcia, J.; Molina, J.M.; Rogova, G. Context-based multi-level information fusion for harbor surveillance. Inf. Fusion 2015, 21, 173–186. [Google Scholar] [CrossRef]
- Chahuara, P.; Fleury, A.; Vacher, M. Using Markov Logic Network for On-Line Activity Recognition from Non-visual Home Automation Sensors. Ambient Intell. 2012, 7683, 177–192. [Google Scholar]
- Skarlatidis, A.; Paliouras, G.; Artikis, A.; Vouros, G.A. Probabilistic Event Calculus for Event Recognition. ACM Trans. Comput. Log. 2015, 16, 1–37. [Google Scholar] [CrossRef]
- Richardson, M.; Domingos, P. Markov logic networks. Mach. Learn. 2006, 62, 107–136. [Google Scholar] [CrossRef]
- Woo, S.H.; Choi, J.Y.; Kwak, C.; Kim, C.O. An active product state tracking architecture in logistics sensor networks. Comput. Ind. 2009, 60, 149–160. [Google Scholar] [CrossRef]
- Singla, P.; Domingos, P. Discriminative Training of Markov Logic Networks. In Proceedings of the 20th National Conference on Artificial Intelligence, Pittsburgh, PA, USA, 9–13 July 2005; pp. 868–873.
- Lowd, D.; Domingos, P. Efficient Weight Learning for Markov Logic Networks. In Proceedings of the 11th European Conference Principles Practice Knowledge Discovery Databases, Warsaw, Poland, 17–21 September 2007; pp. 200–211.
- Poon, H.; Domingos, P. Sound and Efficient Inference with Probabilistic and Deterministic Dependencies. In Proceedings of the AAAI’06, Boston, MA, USA, 16–20 July 2006; pp. 458–463.
- Niu, F.; Ré, C.; Doan, A.; Shavlik, J. Tuffy: Scaling up Statistical Inference in Markov Logic Networks using an RDBMS. Proc. VLDB Endow. 2011, 4, 373–384. [Google Scholar] [CrossRef]
- Van Kasteren, T.; Noulas, A. Accurate activity recognition in a home setting. In Proceedings of the 10th International Conference on Ubiquitous Computing (UbiComp), Seoul, Korea, 21–24 September 2008; pp. 1–9.


| Event | State Transition | Description | |
|---|---|---|---|
| En | N → n | Transition between normal states | |
| Em1 | n → m | n → m1 | Violating the movement plan in the goods-in phase |
| Em2 | n → m2 | Violating the movement plan in the inventorying phase | |
| Em3 | n → m3 | Violating the movement plan in the goods-out phase | |
| Ea1 | n → a | n → a1 | Violating constraints on the temperature attribute |
| Ea2 | n → a2 | Violating constraints on the humidity attribute | |
| # | Rules |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 |
| HMM | MLNs | CRF | |
|---|---|---|---|
| Accuracy | 94.5% | 95.5% | 95.6% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, F.; Deng, D.; Li, P. Dynamic Context-Aware Event Recognition Based on Markov Logic Networks. Sensors 2017, 17, 491. https://doi.org/10.3390/s17030491
Liu F, Deng D, Li P. Dynamic Context-Aware Event Recognition Based on Markov Logic Networks. Sensors. 2017; 17(3):491. https://doi.org/10.3390/s17030491
Chicago/Turabian StyleLiu, Fagui, Dacheng Deng, and Ping Li. 2017. "Dynamic Context-Aware Event Recognition Based on Markov Logic Networks" Sensors 17, no. 3: 491. https://doi.org/10.3390/s17030491
APA StyleLiu, F., Deng, D., & Li, P. (2017). Dynamic Context-Aware Event Recognition Based on Markov Logic Networks. Sensors, 17(3), 491. https://doi.org/10.3390/s17030491





