Error-Based Observer of a Charge Couple Device Tracking Loop for Fast Steering Mirror
Abstract
:1. Introduction
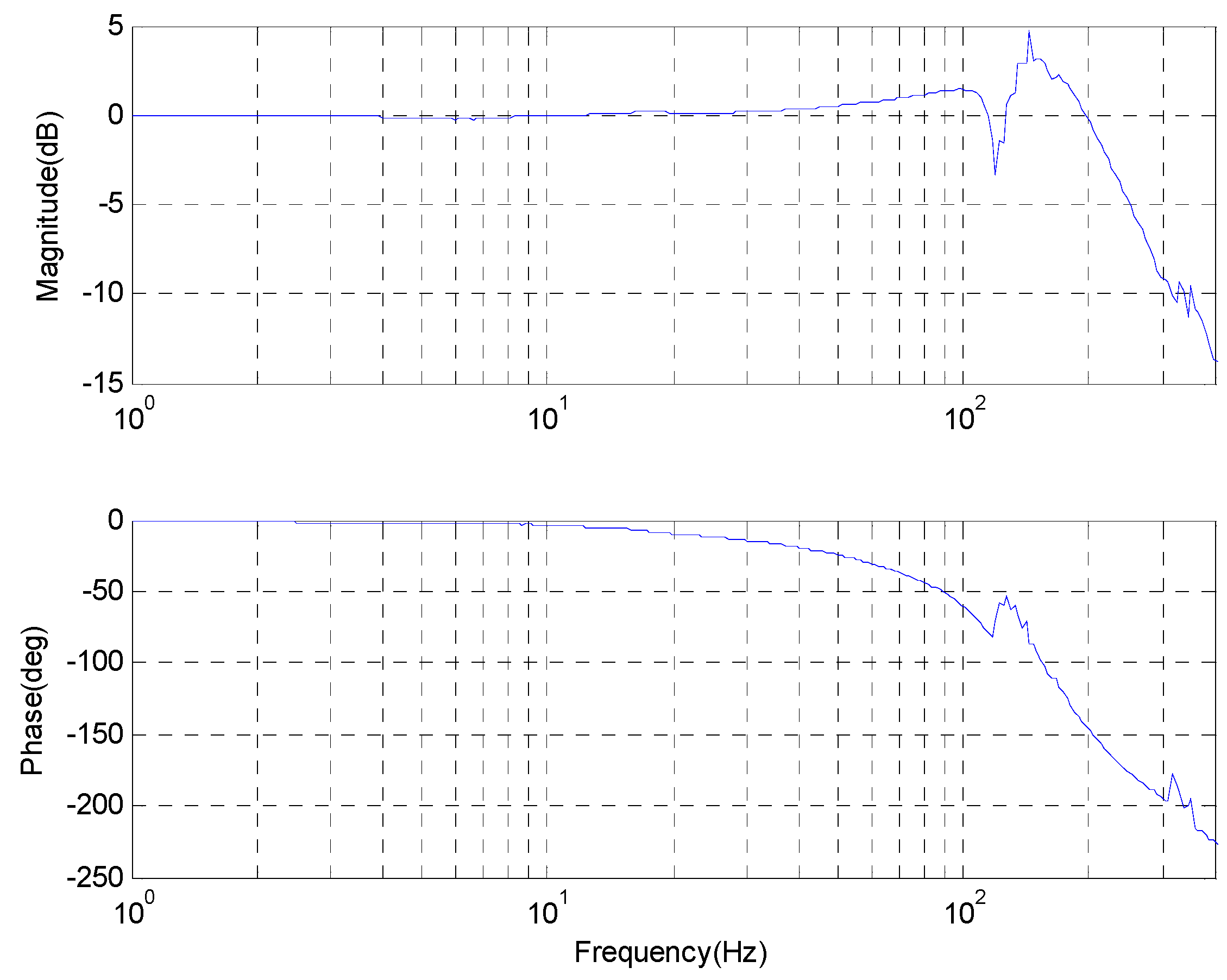
2. The Model of CCD-Based FSM System
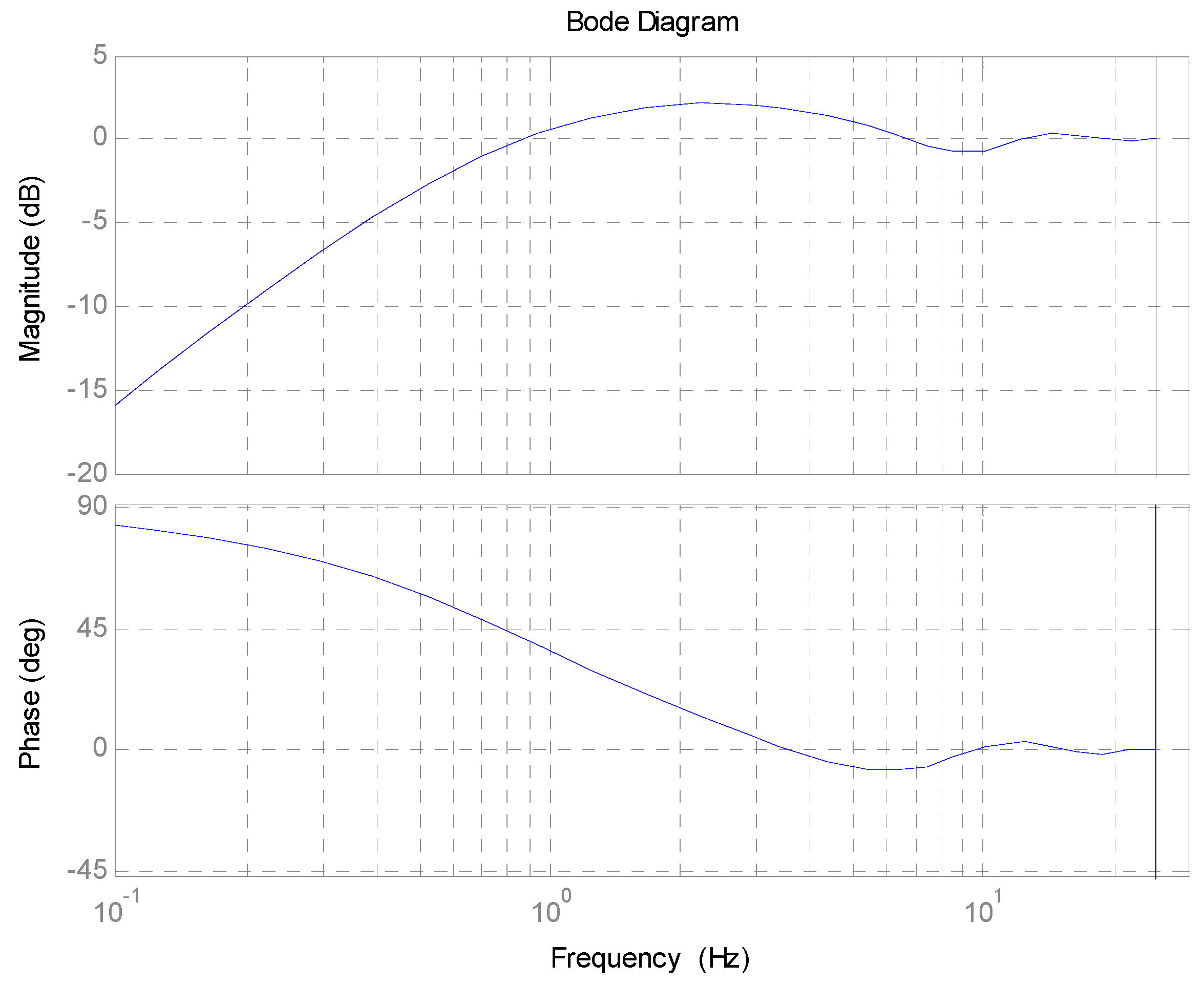
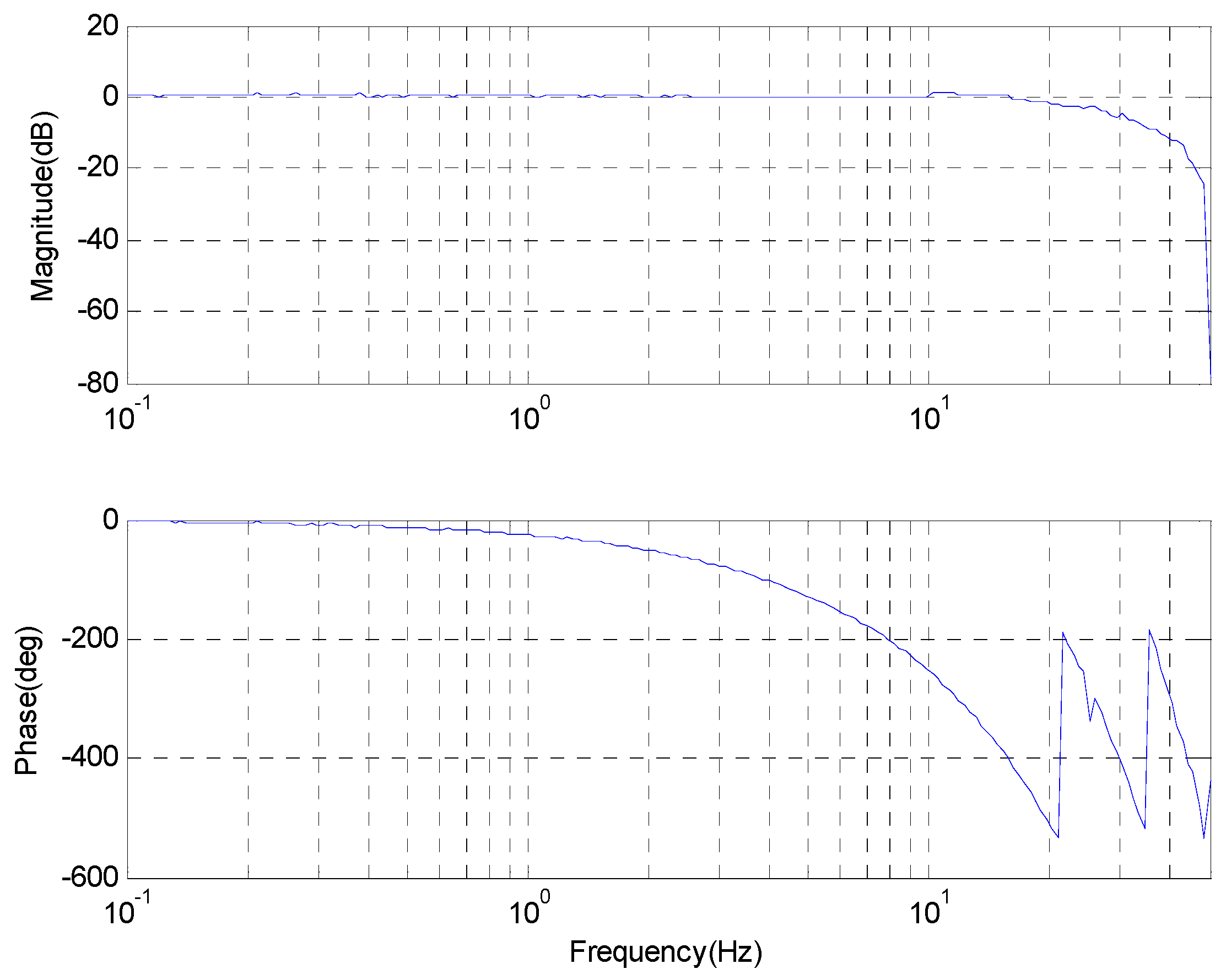
3. Parameters Design
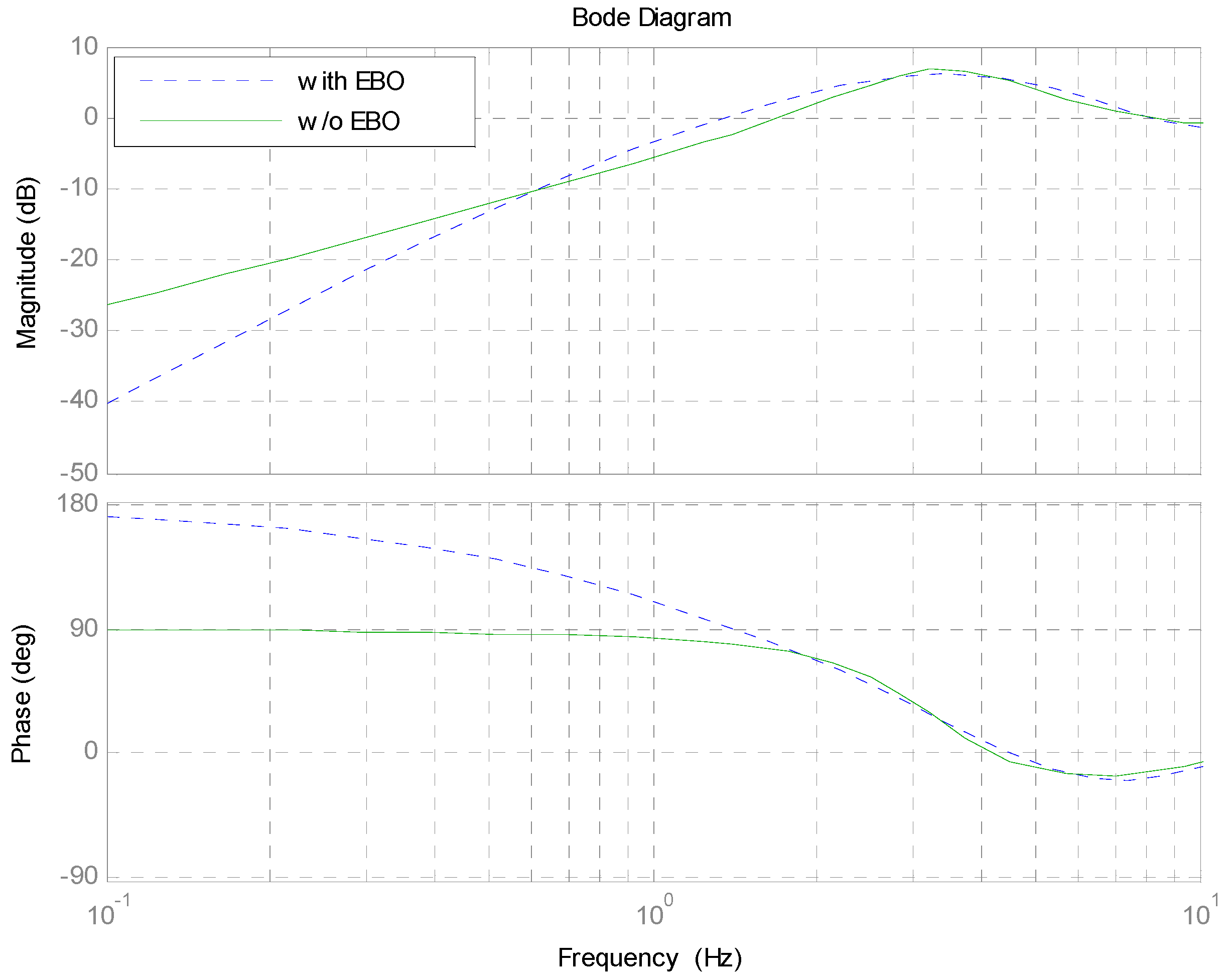
4. Performance Analysis
5. Experimental Setup
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tian, J.; Yang, W.; Peng, Z.; Tang, T.; Li, Z. Application of MEMS Accelerometers and Gyroscopes in Fast Steering Mirror Control Systems. Sensors 2016, 16, 440. [Google Scholar] [CrossRef] [PubMed]
- Hilkert, J.M. A comparison of inertial line-of-sight stabilization techniques using mirrors. Proc. SPIE 2004, 5430. [Google Scholar] [CrossRef]
- Ares, J. Position and displacement sensing with Shack-Hartmann wave-front sensors. Appl. Opt. 2000, 39, 1511–1520. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Hu, L.; Wang, Y.; Wang, S.; Mu, Q. Time delay compensation method for tip–tilt control in adaptive optics system. Appl. Opt. 2015, 54, 3383–3388. [Google Scholar] [CrossRef] [PubMed]
- Gaffard, J.P.; Boyer, C. Adaptive optics: Effect of sampling rate and time lags on the closed loop bandwidth. Proc. SPIE 1990, 1271, 33–50. [Google Scholar]
- Portillo, A.A.; Ortiz, G.G.; Racho, C. Fine pointing controlfor optical communications. In Proceedings of the 2001 IEEE Aerospace Conference, Big Sky, MT, USA, 10–17 March 2001; pp. 1541–1550.
- Southwood, D.M. CCD based optical tracking loop design trades. Proc. SPIE 1992, 1635, 286–299. [Google Scholar]
- Dessenne, C.; Madec, P.-Y.; Rabaud, D.; Fleury, B. First sky tests of adaptive optics predictive control. In Proceedings of the ESO/OSA Topical Meeting on Astronomy with Adaptive Optics, Garching, Germany, 7–11 September 1998.
- Tang, T.; Zhang, T.; Du, J.-F.; Ren, G. Acceleration feedback of a current-following synchronized control algorithm for telescope elevation axis. Res. Astron. Astrophys. 2016, 16, 165. [Google Scholar] [CrossRef]
- Tang, T.; Ma, J.; Ren, G.; Fu, C. Compensating for some errors related to time delay in a charge-coupled-device-based fast steering mirror control system using a feedforward loop. Opt. Eng. 2010, 49, 073005. [Google Scholar] [CrossRef]
- Kazuhiko, A.; Hidehiko, K.; Hideaki, M.; Toshihiro, K. Wide-range Fine Pointing Mechanism for Optical Inter-satellite Communications. NEC Res. Dev. 2001, 42, 193–198. [Google Scholar]
- Tang, T.; Ma, J.; Ren, G. PID-I controller of charge coupled device–based tracking loop for fast-steering mirror. Opt. Eng. 2011, 50, 043002. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering, 4th ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1997; pp. 544–545. [Google Scholar]
- Youla, D.; Jabr, H.; Bongiorno, J., Jr. Modern Wiener-Hopf design of optimal controllers Part II: The multivariable case. IEEE Trans. Autom. Control 1976, 21, 319–338. [Google Scholar] [CrossRef]
- Horowitz, R.; Li, Y.; Oldham, K.; Kon, S.; Huang, X.H. Dual-stage servo systems and vibration compensation in computer hard disk drives. Control Eng. Pract. 2007, 15, 291–305. [Google Scholar] [CrossRef]
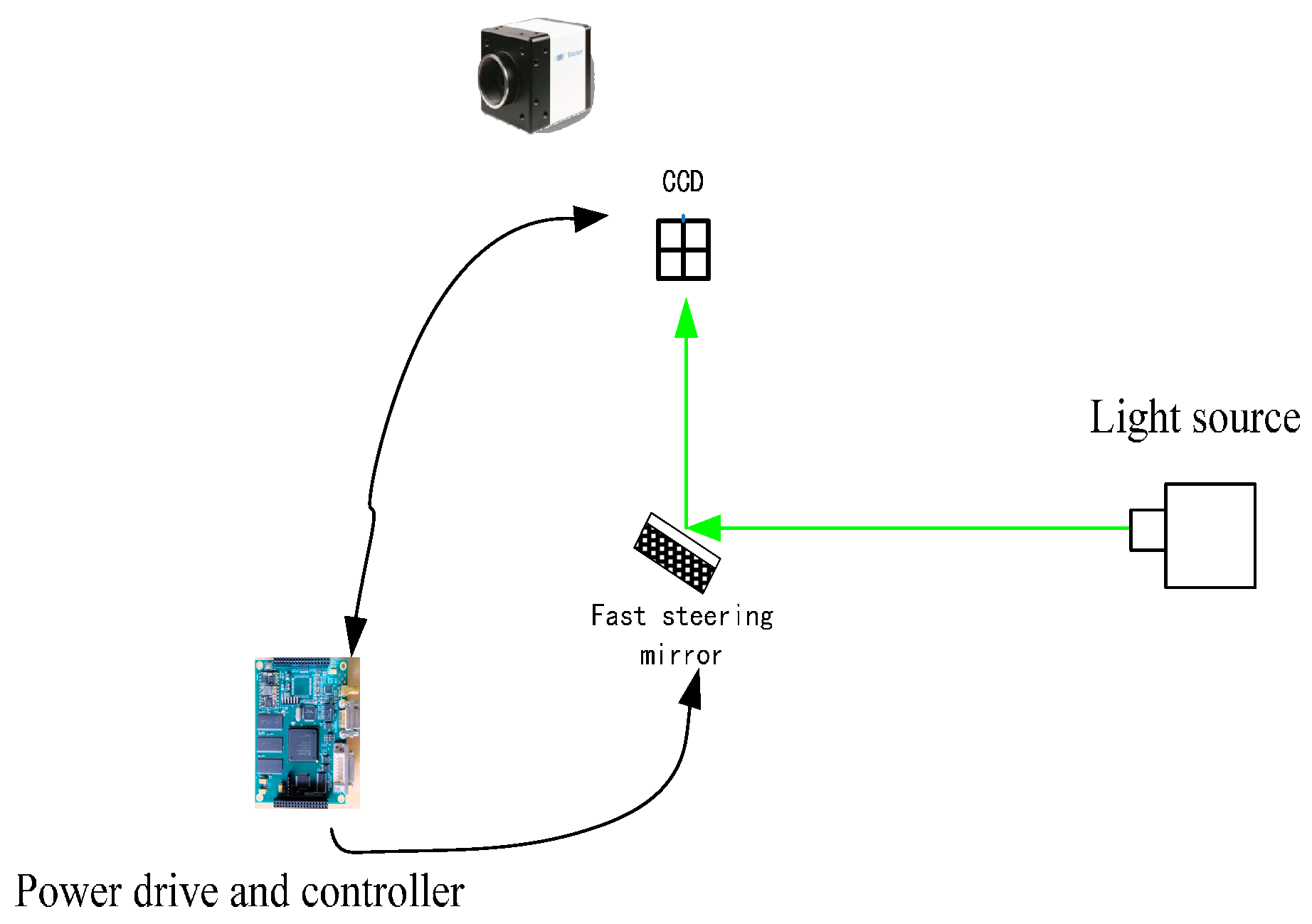



| Frame frequency | 50 Hz |
| Pixels | 640 × 512 |
| Pixel size | 5.5 μm |
| Focus length | 500 mm–1000 mm |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, T.; Deng, C.; Yang, T.; Zhong, D.; Ren, G.; Huang, Y.; Fu, C. Error-Based Observer of a Charge Couple Device Tracking Loop for Fast Steering Mirror. Sensors 2017, 17, 479. https://doi.org/10.3390/s17030479
Tang T, Deng C, Yang T, Zhong D, Ren G, Huang Y, Fu C. Error-Based Observer of a Charge Couple Device Tracking Loop for Fast Steering Mirror. Sensors. 2017; 17(3):479. https://doi.org/10.3390/s17030479
Chicago/Turabian StyleTang, Tao, Chao Deng, Tao Yang, Daijun Zhong, Ge Ren, Yongmei Huang, and Chengyu Fu. 2017. "Error-Based Observer of a Charge Couple Device Tracking Loop for Fast Steering Mirror" Sensors 17, no. 3: 479. https://doi.org/10.3390/s17030479
APA StyleTang, T., Deng, C., Yang, T., Zhong, D., Ren, G., Huang, Y., & Fu, C. (2017). Error-Based Observer of a Charge Couple Device Tracking Loop for Fast Steering Mirror. Sensors, 17(3), 479. https://doi.org/10.3390/s17030479





