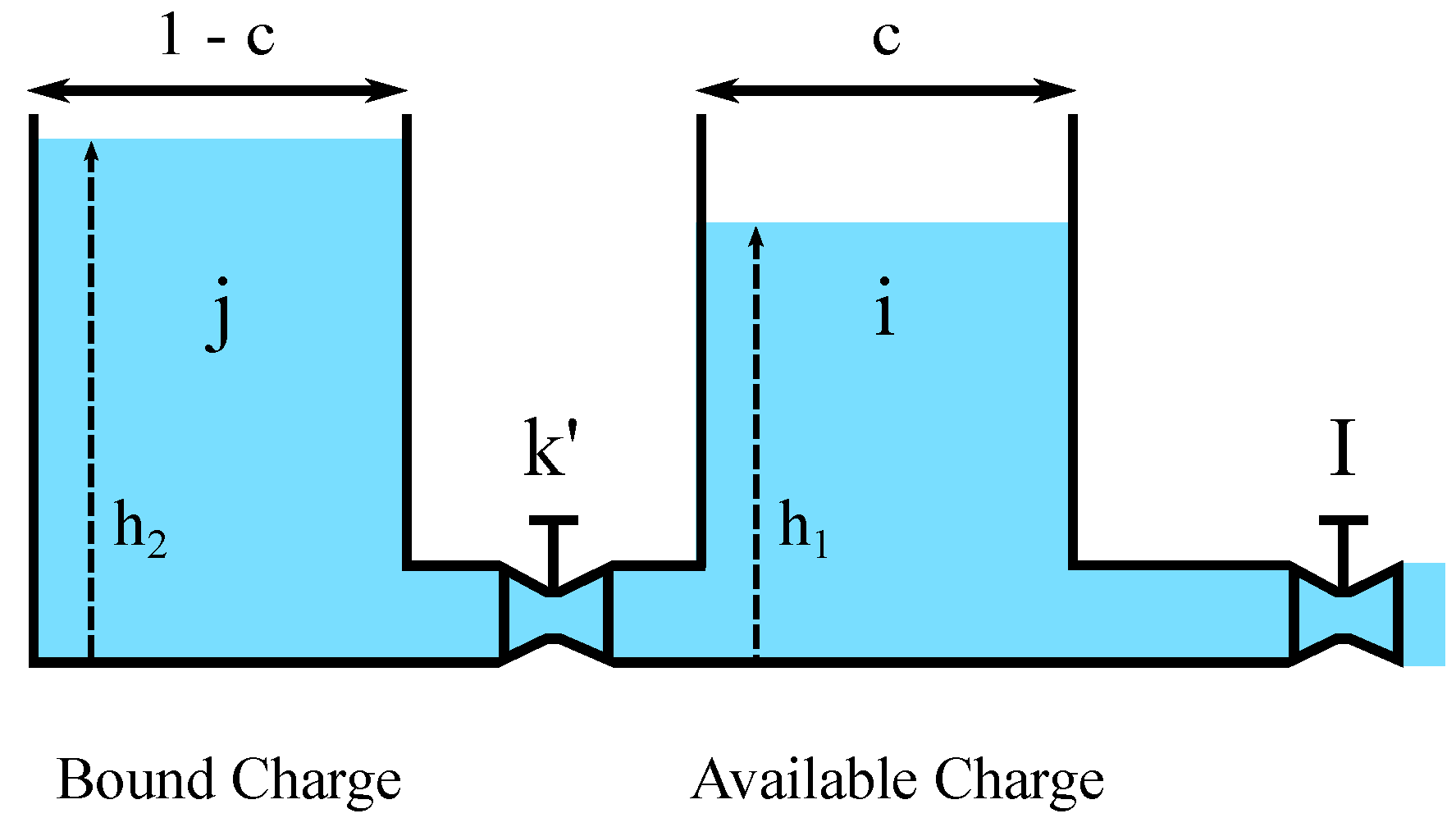
The target of this section is to detail the integration of the Arrhenius equation with KiBaM. The resulting analytical model, Temperature-Dependent KiBaM (T-KiBaM), is able to integrate the effect of temperature on the battery operating behavior, particularly upon both its voltage behavior and its lifetime. Consider the proposition below.
A set of experimental assessments was performed to validate this procedure and to illustrate how to use the proposed T-KiBaM. Briefly, a set of experiments with Ni-MH batteries were performed to obtain the T-KiBaM parameters, c and k. Then, the described methodology was applied to obtain the Arrhenius constants, and A. Finally, the proposed approach was validated by comparing the experimental results against the results obtained with the analytical T-KiBaM. This methodology is presented below. Note that, except when explicitly stated, all presented graphs contain interpolated voltage curves upon the experimental data, in order to clearly present the obtained results.
4.1. Finding Activation Energy () and the Upper-Bound of the Reaction Rate (A)
The experimental assessment was done using a set of twelve Panasonic batteries, Model HHR-4MRT/2BB (2xAAA, Ni-MH, 2.4 V, 750 mAh). The batteries were fully charged at the beginning of the experiments, being discharged until reaching the cut-off value of 2.0 V. The time required for reaching this voltage level defines the battery lifetime in each experimental assessment. Note that this cut-off value is commonly used in experimental tests with Ni-MH batteries, in order to prevent the internal damage that could occur if the voltage level went below 2.0 V [
29]. The recharging time was around eight hours, by using a common Ni-MH battery charger (output: 1.2 V
DC, 250 mA). The batteries stayed at rest during, at least, 60 min before the start of each experiment.
A test-bed has been specifically developed for this experimental assessment, which includes a discharge-controlled circuit and an Arduino UNO [
33]. This test-bed allows setting up controlled discharge currents to the batteries and collecting the experimental data for further analysis.
Figure 4 presents a photo of the test-bed circuit, and
Figure 5 illustrates the interconnection of its main blocks.
The discharge-controlled circuit is able to consume currents in the range of 30
A–30 mA, commonly found in COTS low-power WSN nodes, e.g., MICAz from Crossbow [
34]. It is possible to select among 256 consumed current values, by using a digital potentiometer (AD5206, Analog Devices, Inc., Norwood, MA, USA) [
35]. The discharge-controlled circuit guarantees a constant discharge current from the batteries, by using a controlled current source. The batteries’ board also includes a temperature sensor (Maxim 18B20) [
36] for temperature measurements.
An Arduino UNO controls all circuit components and collects the experimental data from the batteries’ board: battery voltage and temperature. The UNO board has analog inputs with 10-bit resolution, the data log interval being adjustable. For the performed assessments, data were recorded every 10 s. A computer receives the collected data from the UNO board through a USB connection using CoolTerm [
37], which stores all data in a TXT file for further analysis.
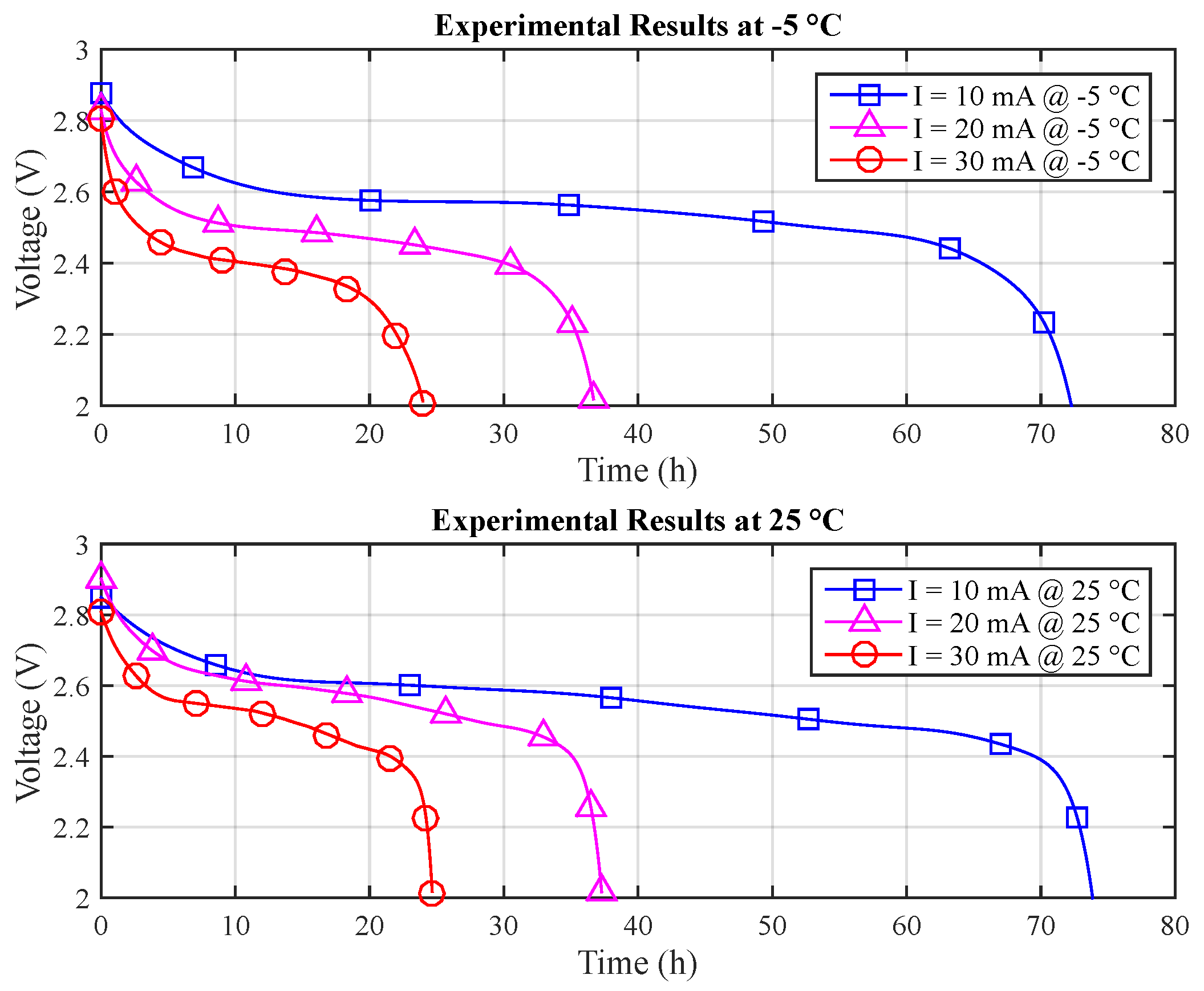
The experiments were performed at a set of different temperatures, with a 15 °C step, −5, 10, 25 and 40 °C, using thermally-insulated equipment with temperature control. A complementary full experiment was performed for 32.5 °C, as this temperature was found to be the most relevant outlier between the assessed temperature values. For all of the experiments, only the batteries (including the temperature sensor) remained inside the thermally-insulated equipment, at a controlled temperature.
Three experimental assessments were performed for each of the above-mentioned temperature values and for each of the following discharge current values: 10, 20 and 30 mA (actually, due to the available 256 resistance values obtained from the digital potentiometer, the considered current values were: 10.424, 20.303 and 30.242 mA). A total of 45 experiments were performed, three for each current/temperature pair. Thus, average lifetime/voltage values from three experiments were considered for each measurement presented in this paper.
For the estimation of the T-KiBaM parameters, only two temperature values are required. Therefore, just the measurements for −5 and 25 °C were considered for this purpose. It is possible to obtain the capacity provided by the battery using
. As the discharge current is constant, the capacity is obtained by just multiplying the current value by the experimental lifetime, i.e.,
.
Table 1 shows the obtained results for both temperature ranges.
Figure 6 depicts the discharge curves for each temperature.
The obtained set of experimental measurements (numerical values are represented with up to five significant figures, whenever available) allows the evaluation of the T-KiBaM parameters, as previously explained in
Section 3.3:
Note that being that
, this indicates that the reaction rate is slower at lower temperatures. By using Equation (
18), it is possible to obtain the activation energy value,
, which is equal to
. Through the activation energy (
),
and temperature (
) values, it is possible to obtain an upper-bound for the reaction rate (
A):
The new values for
k are then obtained by combining Equation (
19) with the obtained values of
A,
,
R and
T. Thus,
k values vary with temperature, defining the T-KiBaM dependence on temperature as shown by Proposition 1. Finally,
A and
values are constant values for a given battery type and do not depend on the temperature value.
Table 2 depicts the relationship between
k and temperature.
Note that it is possible to extrapolate the values of
k beyond the temperature range at which the parameters were obtained, due to the chemical kinetics concepts modeled by the Arrhenius equation.
Table 2 shows the behavior of the reaction rate (
k) between −12.5 and 47.5 °C. However, it is also worth mentioning that the operating limits of the battery must be taken into account for these extrapolations. The indicated temperature range for the discharge of Ni-MH batteries varies from −10 to 45 °C [
29].
4.2. Calibrating T-KiBaM for Battery-Specific Characteristics
Temperature also affects the battery capacity. Typically, batteries provide higher effective capacities at higher temperatures [
2] and lower effective capacities when used at lower temperatures [
38]. Within this context, it is crucial to adjust T-KiBaM to the technology of the battery being modeled (e.g., Ni-MH or Li-ion).
Therefore, in this section, we present a method for adjusting the T-KiBaM parameters accordingly. Briefly, through a set of experimental assessments, it is possible to evaluate the losses and gains of the battery capacity according to the temperature variation. Such knowledge is incorporated in T-KiBaM to model the initial battery capacity under different temperature conditions.
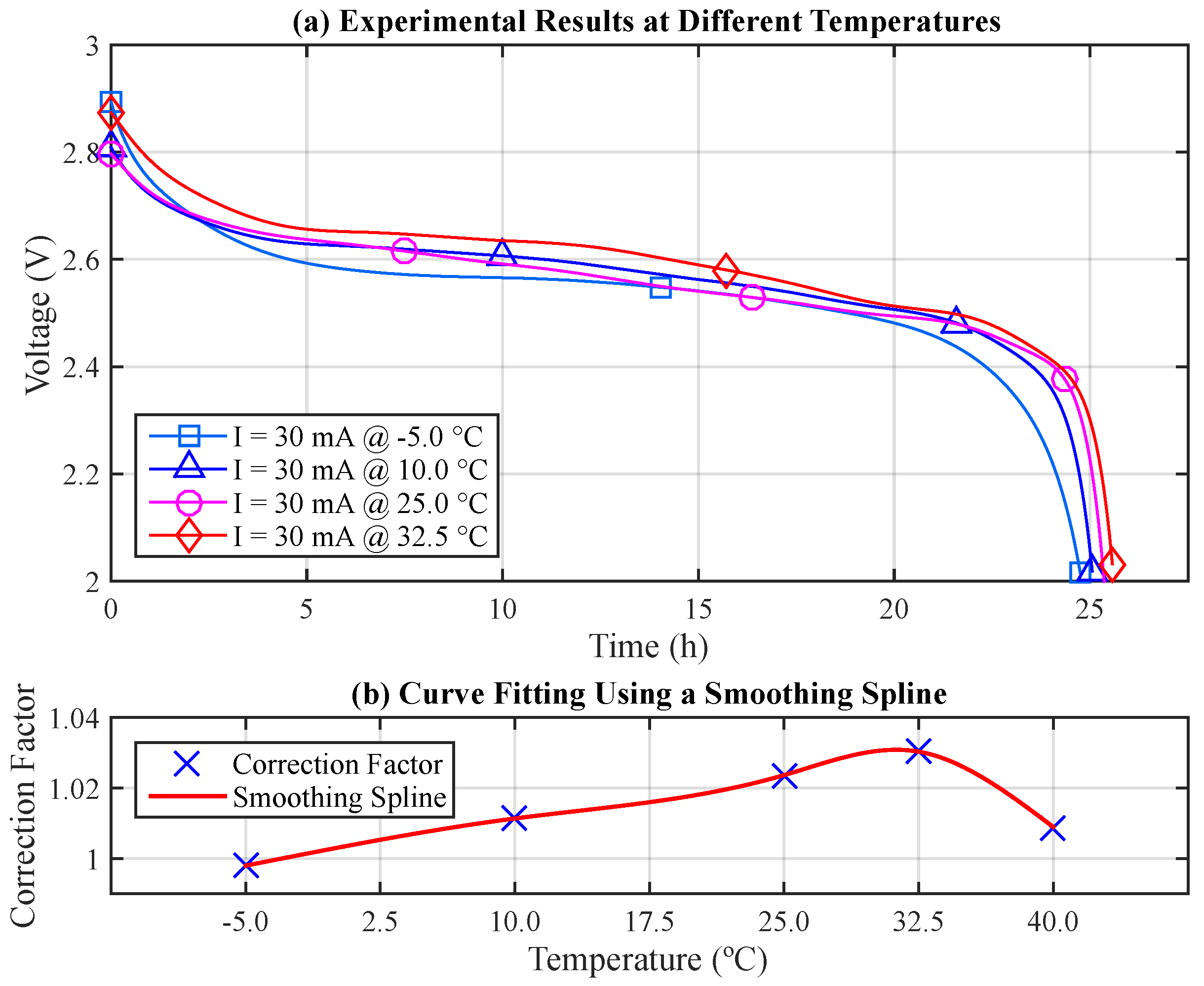
First, fifteen experiments were performed with the same discharge current, 30 mA, under five different temperatures: −5, 10, 25, 32.5 and 40 °C (three experiments for each temperature). Each of the following average lifetimes was obtained from three battery pairs: 24.749, 25.087, 25.385, 25.560 and 25.022 h, respectively.
Figure 7a illustrates the related discharge curves,
(for the sake of clarity, the results at 40 °C were not included). Note the non-linearity of these voltage curves throughout the experiments with different curves for different temperatures, even using the same discharge current.
As previously mentioned, the capacity provided by the battery can be evaluated by integrating its discharge current over time. From the obtained results, it becomes possible to evaluate the losses and gains of the battery capacity at different temperatures, in order to establish the Correction Factor (CF) of the initial battery capacity (
) for each situation. The losses and gains of the battery capacity are evaluated with respect to the battery nominal capacity, which was 750 mAh for this case.
Table 3 presents the obtained results.
After establishing the correction factor, which indicates the gain or loss of the initial battery capacity (
) at different temperatures, it is possible to find a function that properly fits the data.
Figure 7 (b) depicts the CF data points and the fitted curve. A smoothing spline (piecewise polynomial function of degree three) [
39] with
and
fits the obtained data points:
where
.
Table 4 presents the coefficients for each segment. Note that this function enables the adjustment of the initial battery capacity according to the selected temperature and is valid only within the aforementioned temperature range, i.e., from −5 to 40 °C, which represents the case for most part of the applications within the WSN context (e.g., from snow [
40] to industrial [
41] monitoring applications).
4.3. Modeling the Voltage Behavior for Ni-MH Batteries
Voltage is important output information from the battery modeling, as it provides a perspective on how the battery behaves over time. In this sense, it is valuable to model variable
during the discharge process, in order to understand the ability of the battery to maintain its nominal voltage. The original KiBaM offers this possibility (Equation (
14)), though inaccurately since it does not model the exponential voltage decrease at the beginning of the discharge curve, nor the “knee” at the end of the discharge curve (as will be illustrated later, in this section), which can be observed in real experiments with Ni-MH batteries (cf.
Figure 7). Thus, it becomes necessary to improve the voltage model that has been used in KiBaM.
Tremblay and Dessaint [
42,
43] developed a voltage model for different battery technologies, e.g., lead-acid, Ni-MH, Ni-Cd and Li-ion. Although being able to handle both charge and discharge curves for each battery type, only the Ni-MH battery discharge model is presented in this paper.
The Tremblay–Dessaint voltage model can accurately represent the voltage dynamics with varying current values. Besides, it considers the Open Circuit Voltage (OCV) as a function of the State of Charge (SoC). Thus, the battery voltage may be obtained as follows:
where
is the battery voltage (V),
is the battery constant reference voltage (V),
is the polarization resistance (Ω),
Q is the battery capacity (Ah),
is the actual battery charge (Ah),
is the exponential zone amplitude (V),
B is the exponential zone time constant inverse (Ah)
−1,
is the internal resistance (Ω),
i is the discharge current (A) and
is the filtered current (A). For further details, please refer to [
42,
43].
Equation (
21) is valid only for Li-ion batteries, as it presents an exponential term that is not observed in other battery types, such as lead-acid, Ni-MH and Ni-Cd. These batteries exhibit a hysteresis phenomenon between the charge and discharge processes, which occurs only at the beginning of the discharge curve, regardless of their SoC. This phenomenon can be represented by a non-linear dynamic system:
where
is the exponential zone voltage (V),
is the discharge current (A) and
is the charge/discharge mode. The exponential voltage relies on its initial value
and the charge (
) or discharge (
) mode.
Briefly, the final form for the discharge equation of the voltage model for Ni-MH and Ni-Cd batteries is as follows:
However, this voltage model presents an inconsistency at the end of the analytical evaluation (cf. Figure 4 of [
42]), where the following problems arise: (P1) the analytical lifetimes are smaller than the experimental lifetimes at the battery voltage cut-off point; and (P2) the model returns voltage values below zero for time instants close to the end of the analytical evaluation.
Temperature-Dependent Voltage Model (TVM)
In this section, we propose the Temperature-Dependent Voltage Model (TVM) model, an extension of the Tremblay–Dessaint model, which is able to attenuate the above described problems (P1 and P2) and appropriately represent the influence of the temperature on the curve during the battery discharge.
In order to increase the accuracy of the Tremblay–Dessaint voltage model, i.e., attenuating P1 and P2, a smoothing constant,
, has been added. This
value multiplies the terms that relate current and time, i.e.,
and
. Therefore, Equations (
22) and (
23) should be rewritten as follows:
All parameters (
,
B,
,
Exp,
,
Q,
and
) can be obtained using the battery data-sheet or by performing experimental measurements [
43]. Considering an experiment at −5 °C, for example, the following values can be obtained:
| V | |
| V | (Ah) |
| V |
| Ah·CF. |
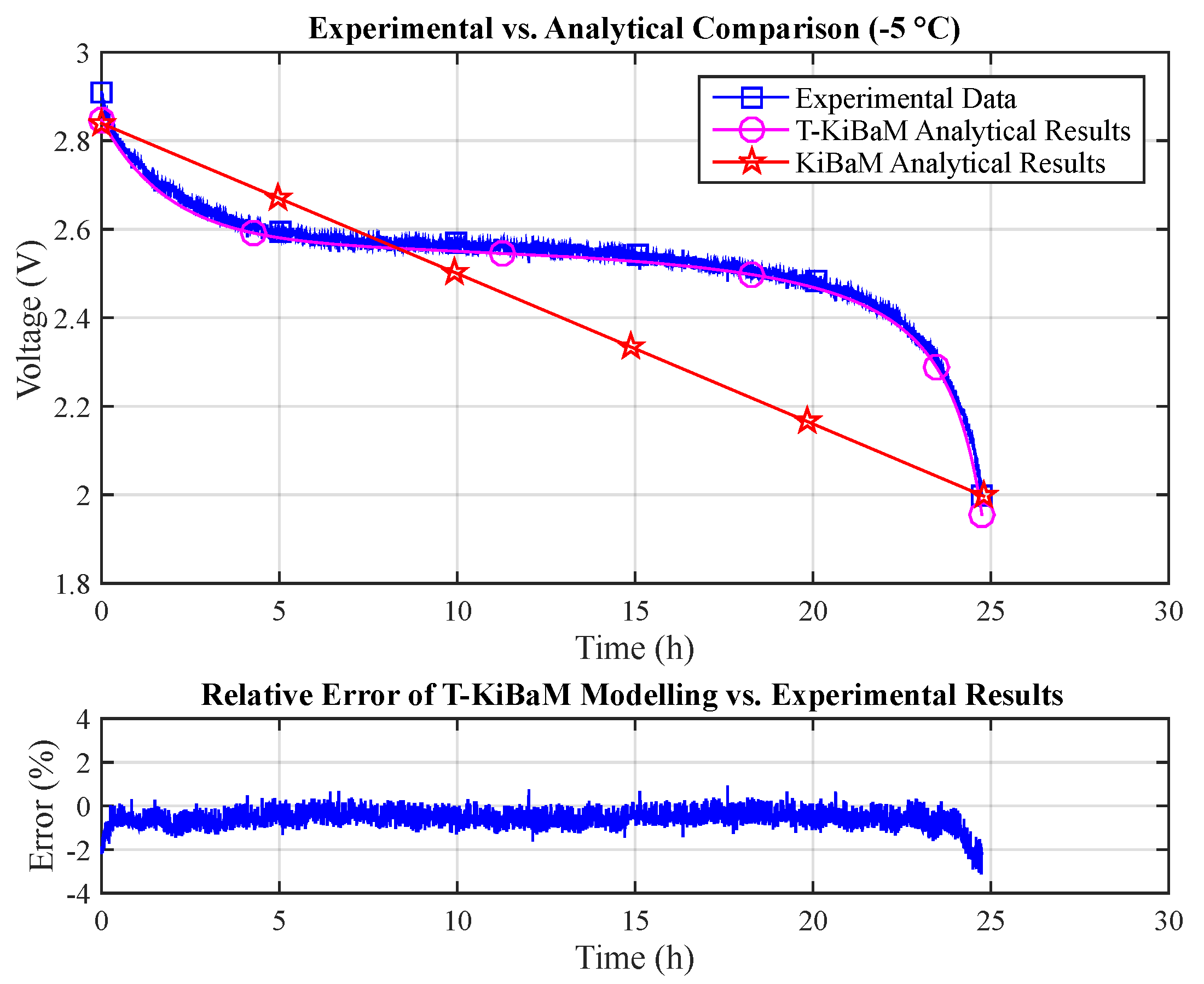
Figure 8 compares data obtained through the experimental assessment (
T = −5 °C,
I = 30 mA) with both the T-KiBaM (Equation (
25)) and the original KiBaM analytical results (Equation (
14)). The raw experimental data are then used to make a point-to-point comparison with just the T-KiBaM analytical curve, as the original KiBaM linear results are clearly inaccurate along the time scale. Note that a reduced steady-state relative error is obtained for most of the T-KiBaM analytical results. The following absolute errors were obtained for T-KiBaM values: 3.1% (max) and 0.6% (mean).
Experiments performed for different temperature values enabled the extraction of the voltage model parameters.
Table 5 illustrates the Arrhenius constants obtained for each parameter, as well as the values of all parameters at each temperature.
Finally, it becomes possible to represent the values obtained from the T-KiBaM analytical voltage model adapted to different temperatures, using the set of parameters represented in
Table 5, along with their respective constants
A and
, using the Arrhenius equation.
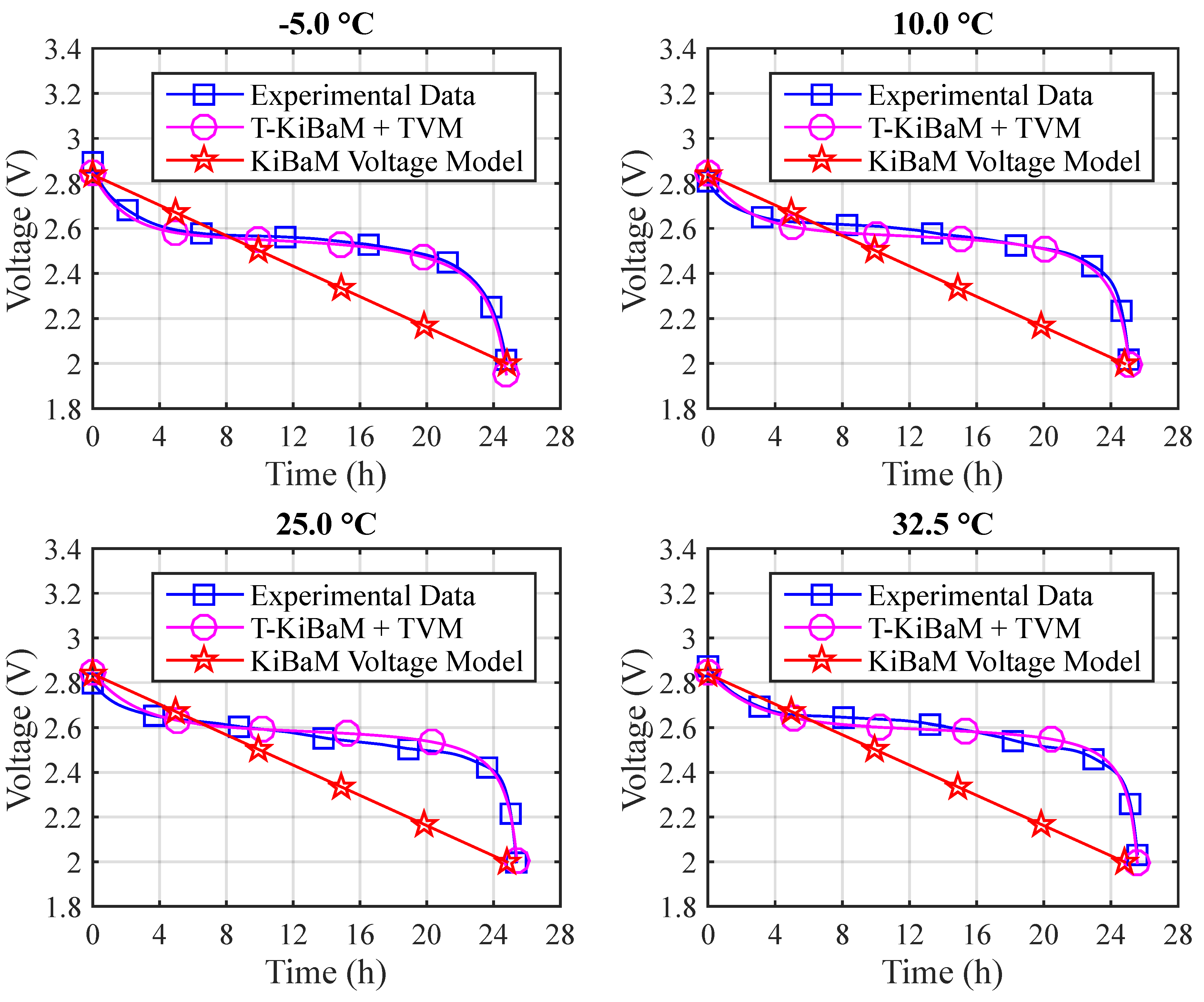
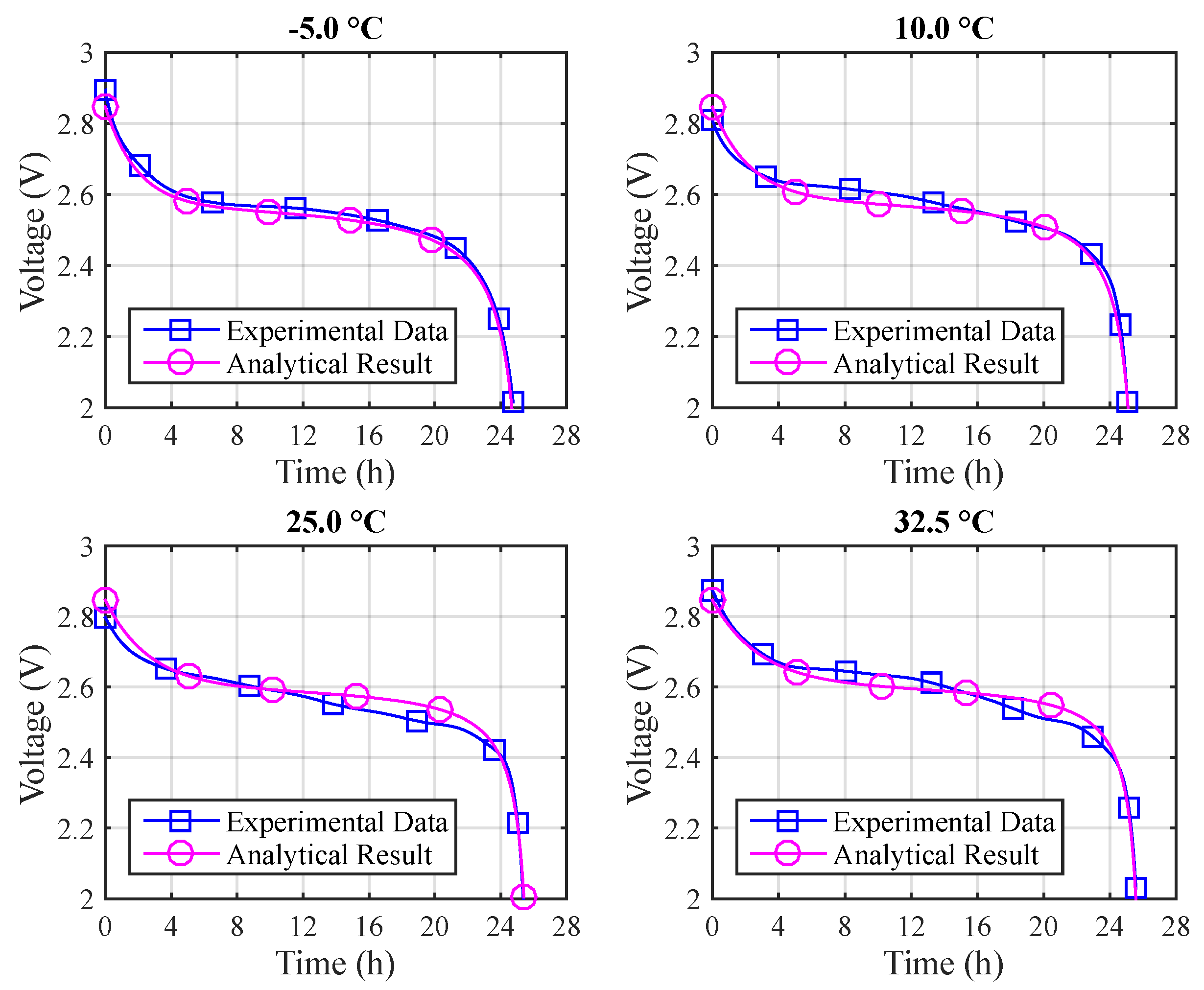
Figure 9 depicts the voltage results for the different temperatures using Arrhenius constants. The absolute errors are: (a)
T = −5 °C: 3.1% (max) and 0.6% (mean); (b)
T = 10 °C: 2.9% (max) and 0.7% (mean); (c)
T = 25 °C: 2.0% (max) and 0.9% (mean); (d)
T = 32.5 °C: 6.7% (max) and 1.2% (mean).
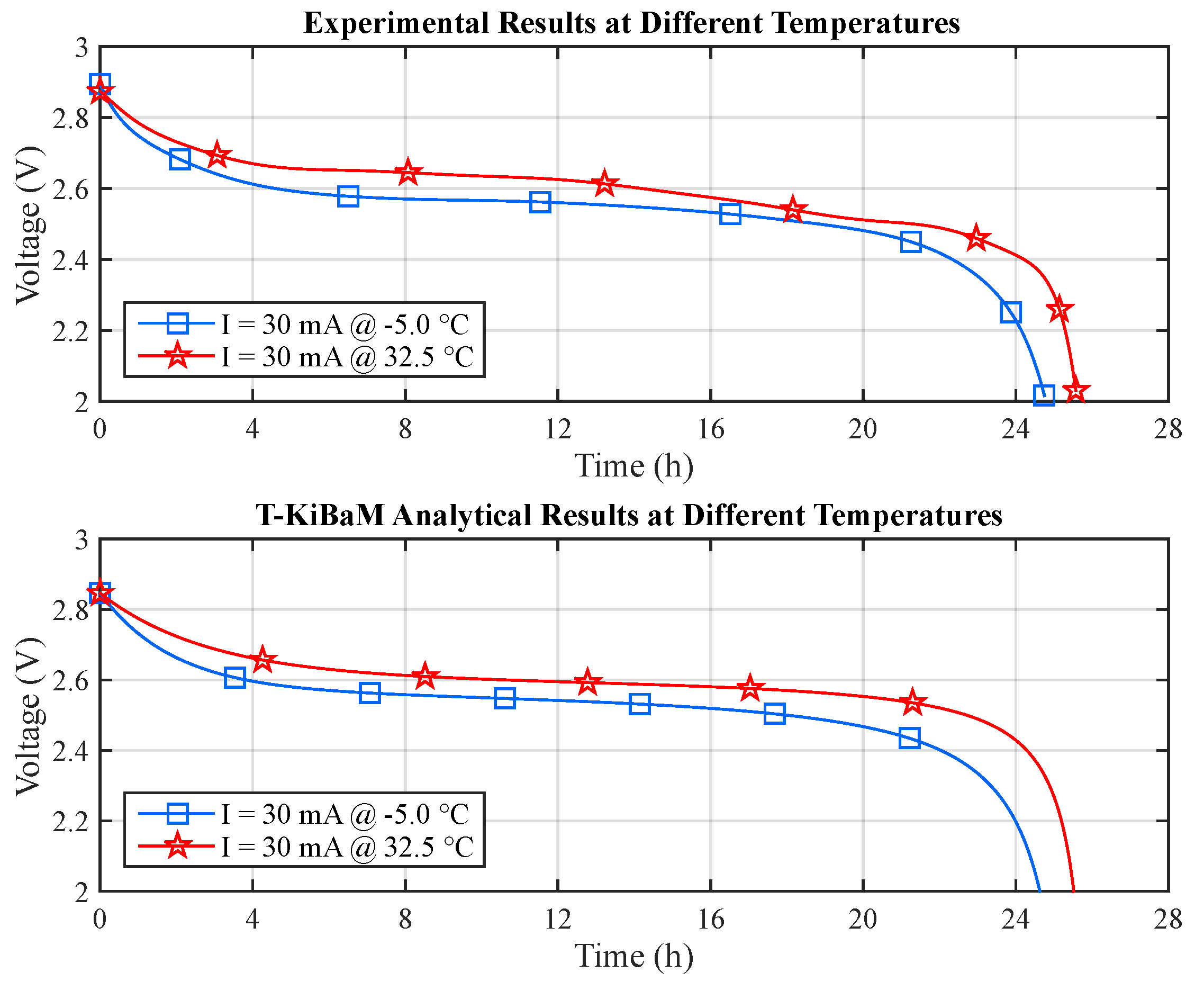
Figure 10 depicts a comparison between the experimental and the T-KiBaM analytical results, regarding the voltage levels at different temperatures.
The modified voltage model, which is called TVM, was integrated into T-KiBaM, as it satisfactorily represents the battery discharge behavior regarding the voltage level, for the case of Ni-MH batteries at different temperatures.