A Sensor Data Fusion System Based on k-Nearest Neighbor Pattern Classification for Structural Health Monitoring Applications
Abstract
:1. Introduction
2. Theoretical Background
2.1. Piezoelectric Sensors
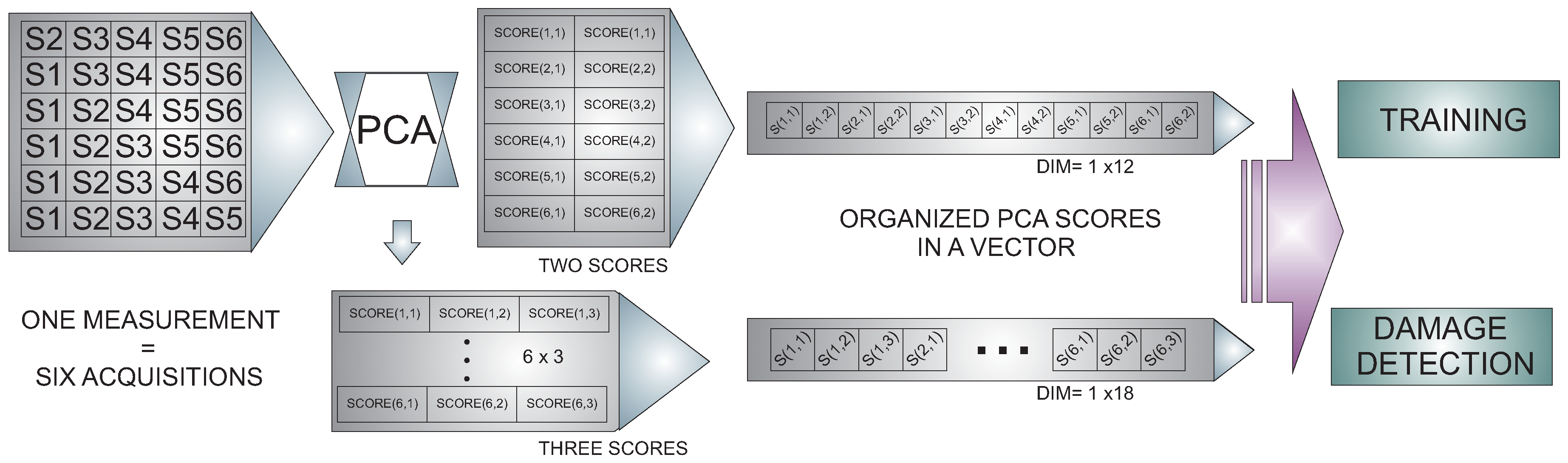
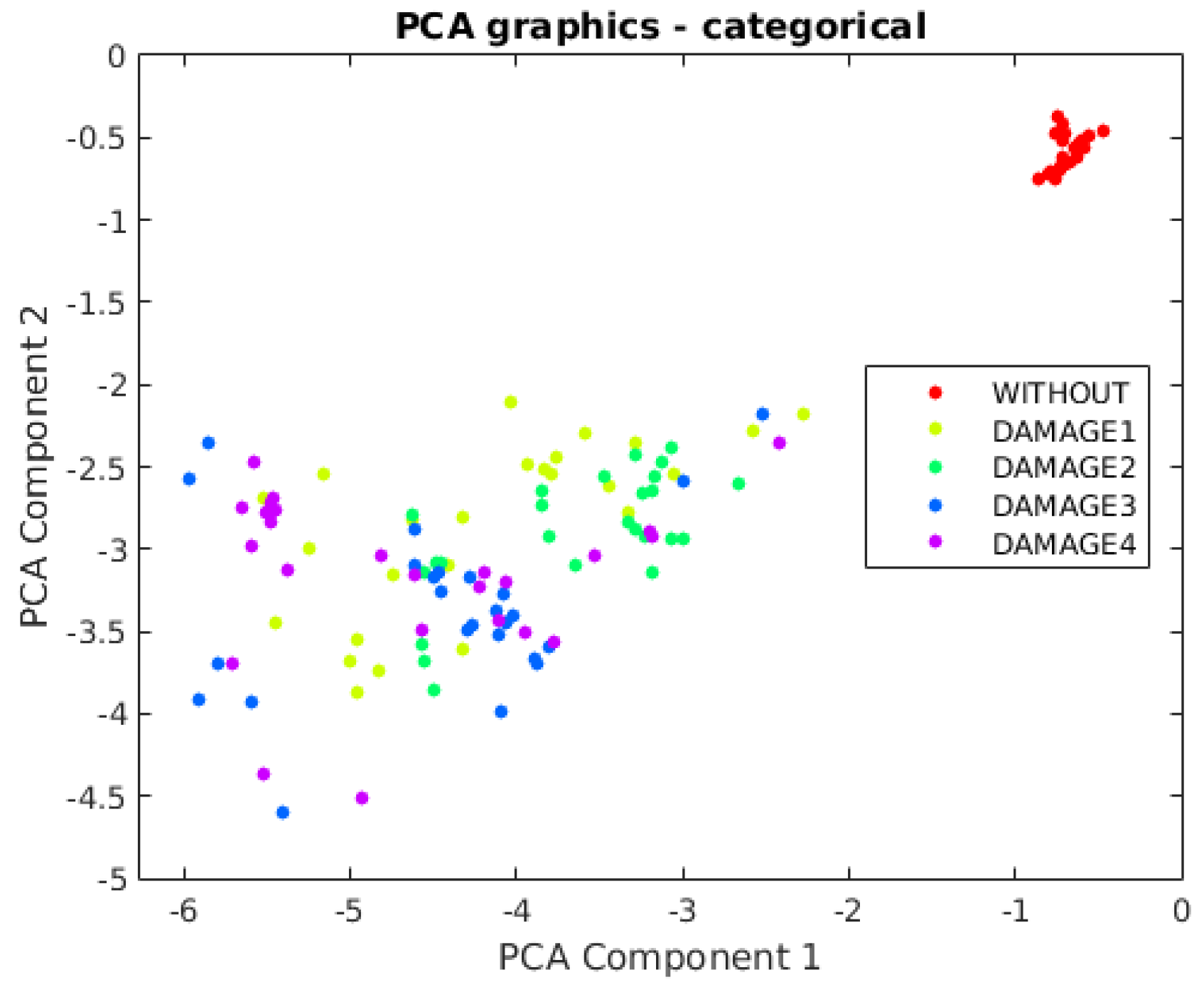
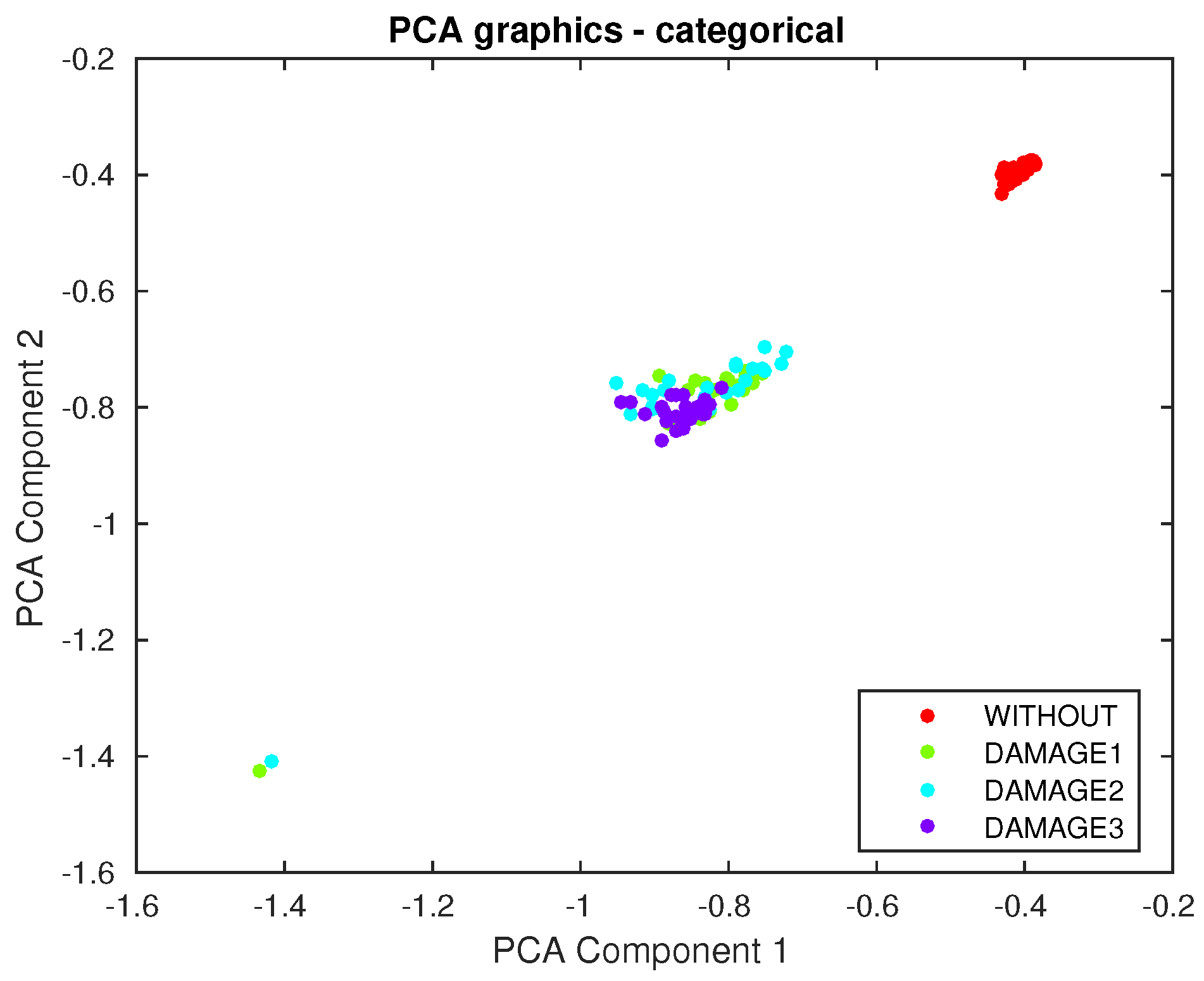
2.2. Principal Component Analysis
2.2.1. PCA Modeling
2.2.2. Normalization: Group Scaling
2.2.3. Projection of New Data onto the PCA Model
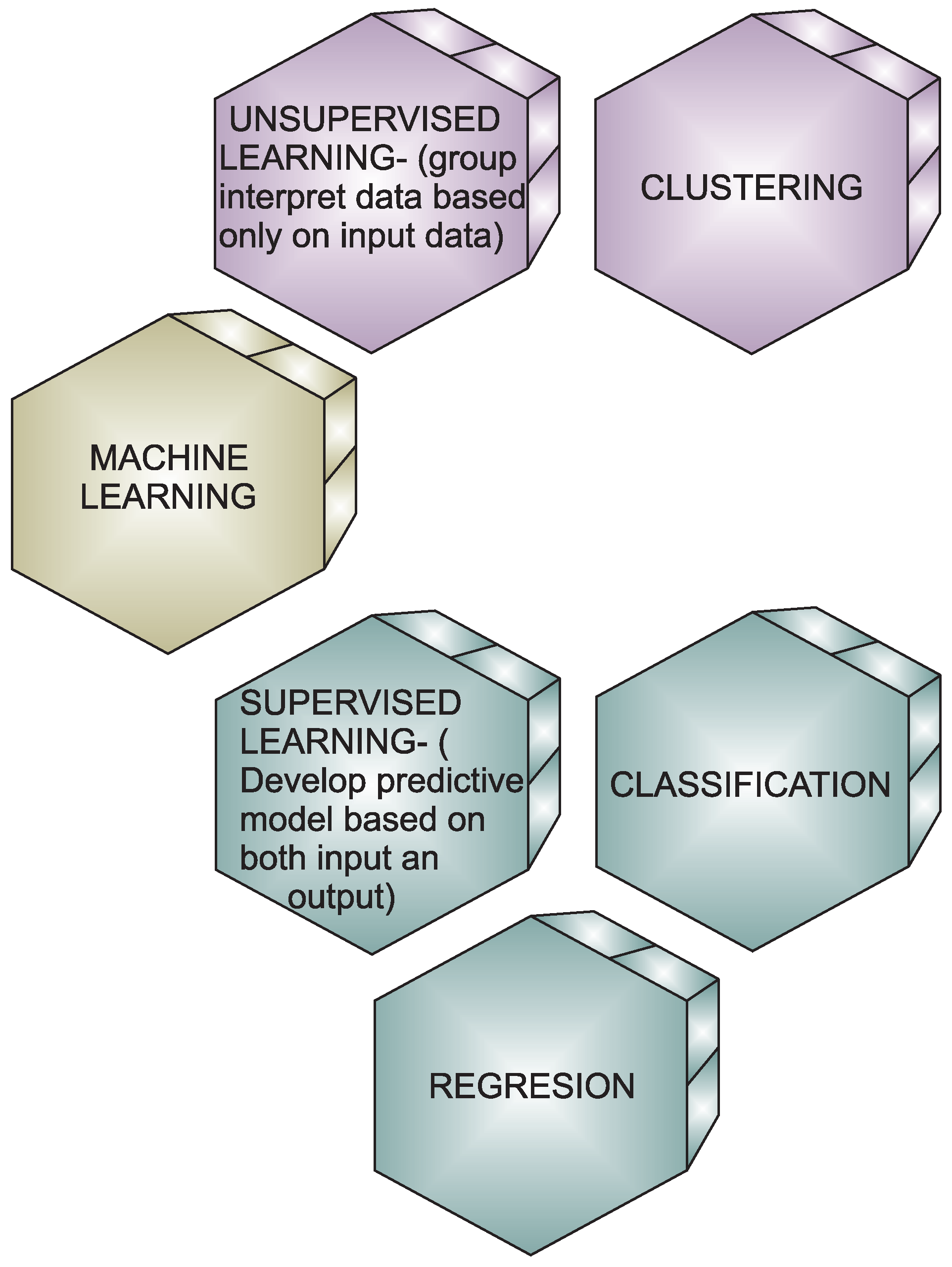
2.3. Machine Learning
2.4. Nearest Neighbor Pattern Classification
- Fine k-NN: A nearest neighbor classifier that makes finely detailed distinctions between classes with the number of neighbors set to one.
- Medium k-NN: A nearest neighbor classifier with fewer distinctions than a fine k-NN with the number of neighbors set to 10.
- Coarse k-NN: A nearest neighbor between classes, with the number of neighbors set to 100.
- Cosine k-NN: A nearest neighbor classifier that uses the cosine distance metric. The cosine distance between two vectors u and v is defined as:that is, one minus the ratio of the inner product of u and v over the product of the norms of u and v.
- Cubic k-NN: A nearest neighbor classifier that uses the cubic distance metric. The cubic distance between two n-dimensional vectors u and v is defined as:
- Weighted k-NN: A nearest neighbor classifier that uses distance weighting. The weighted Euclidean distance between two n-dimensional vectors u and v is defined as:where and .
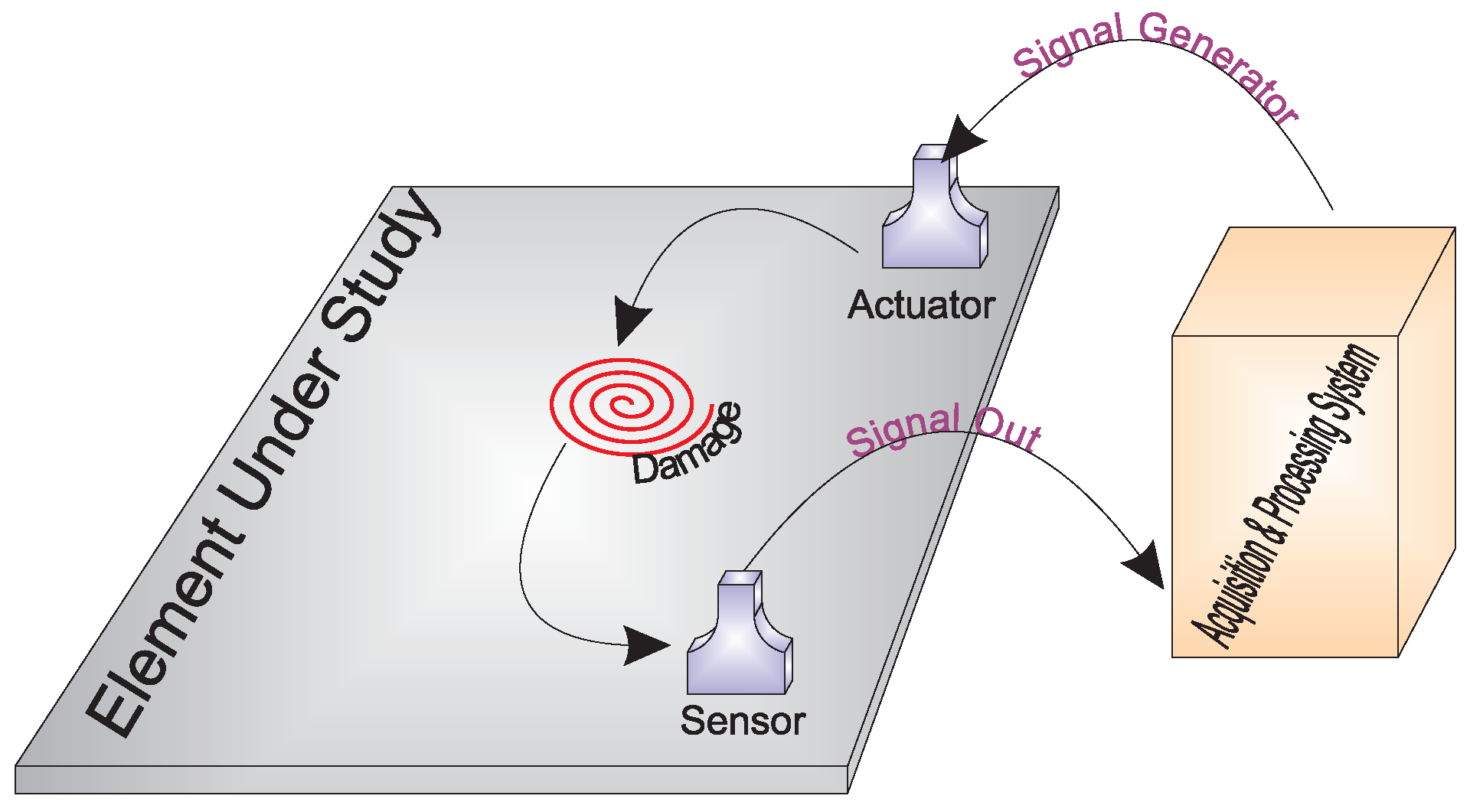
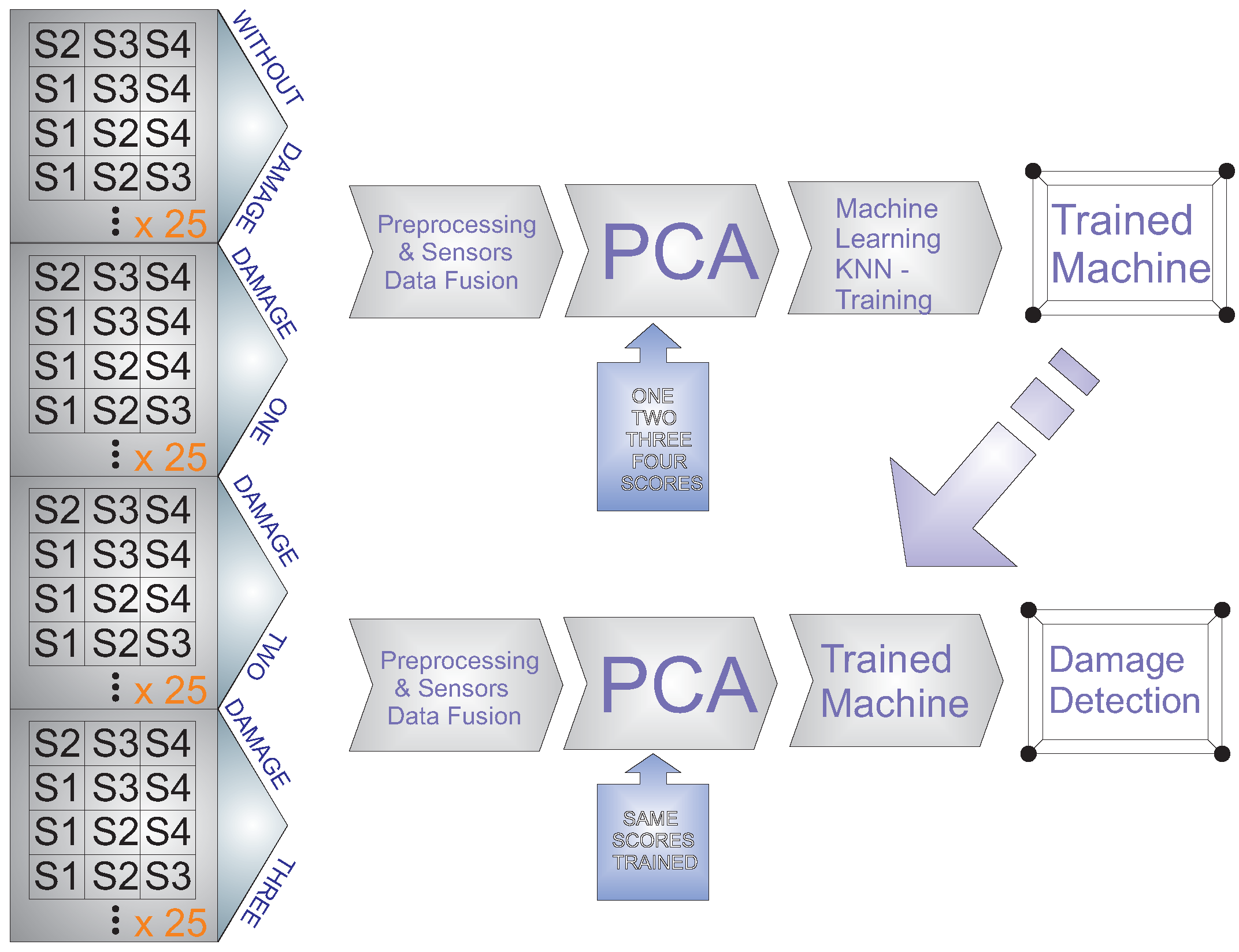
3. Structural Health Monitoring System
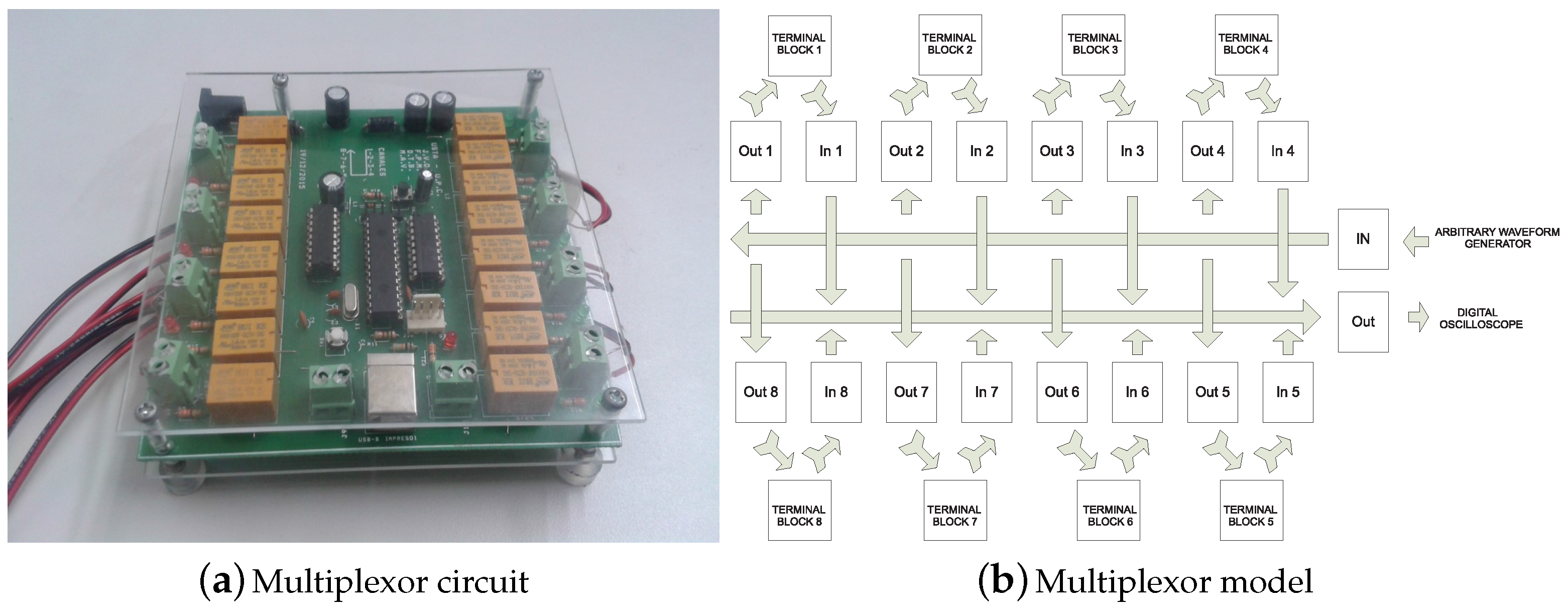
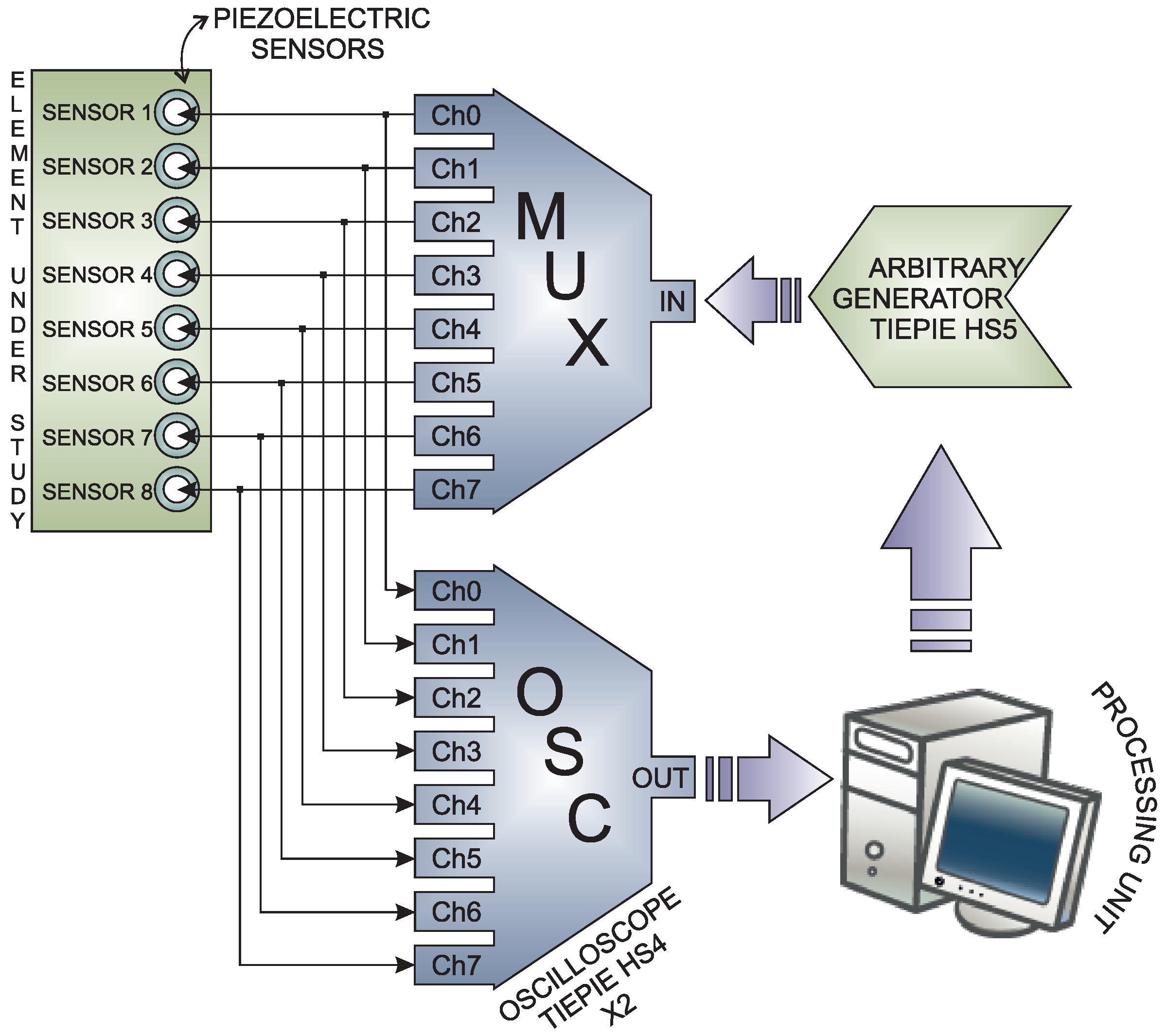
3.1. Hardware of the SHM System
3.2. Software of the SHM System
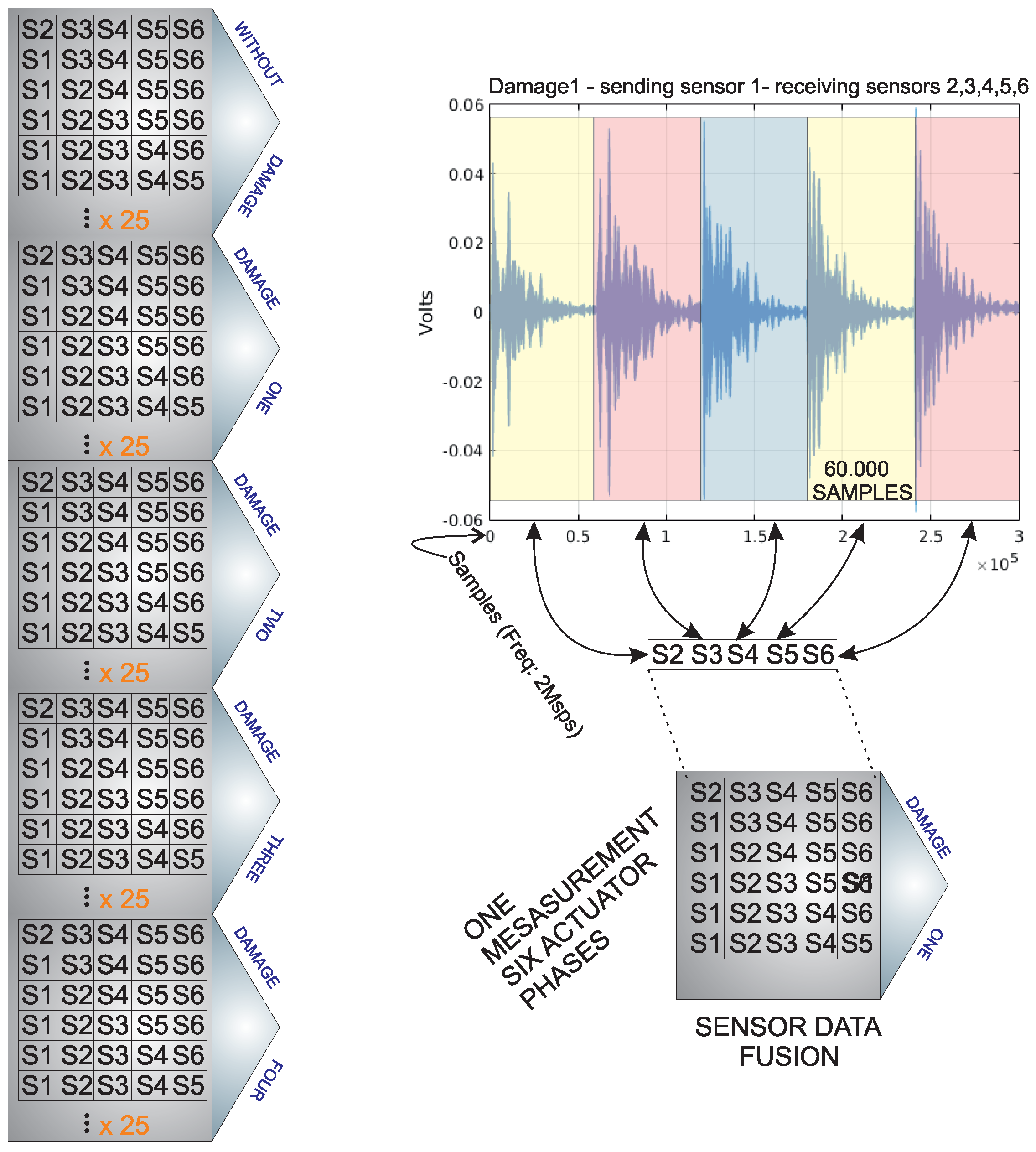
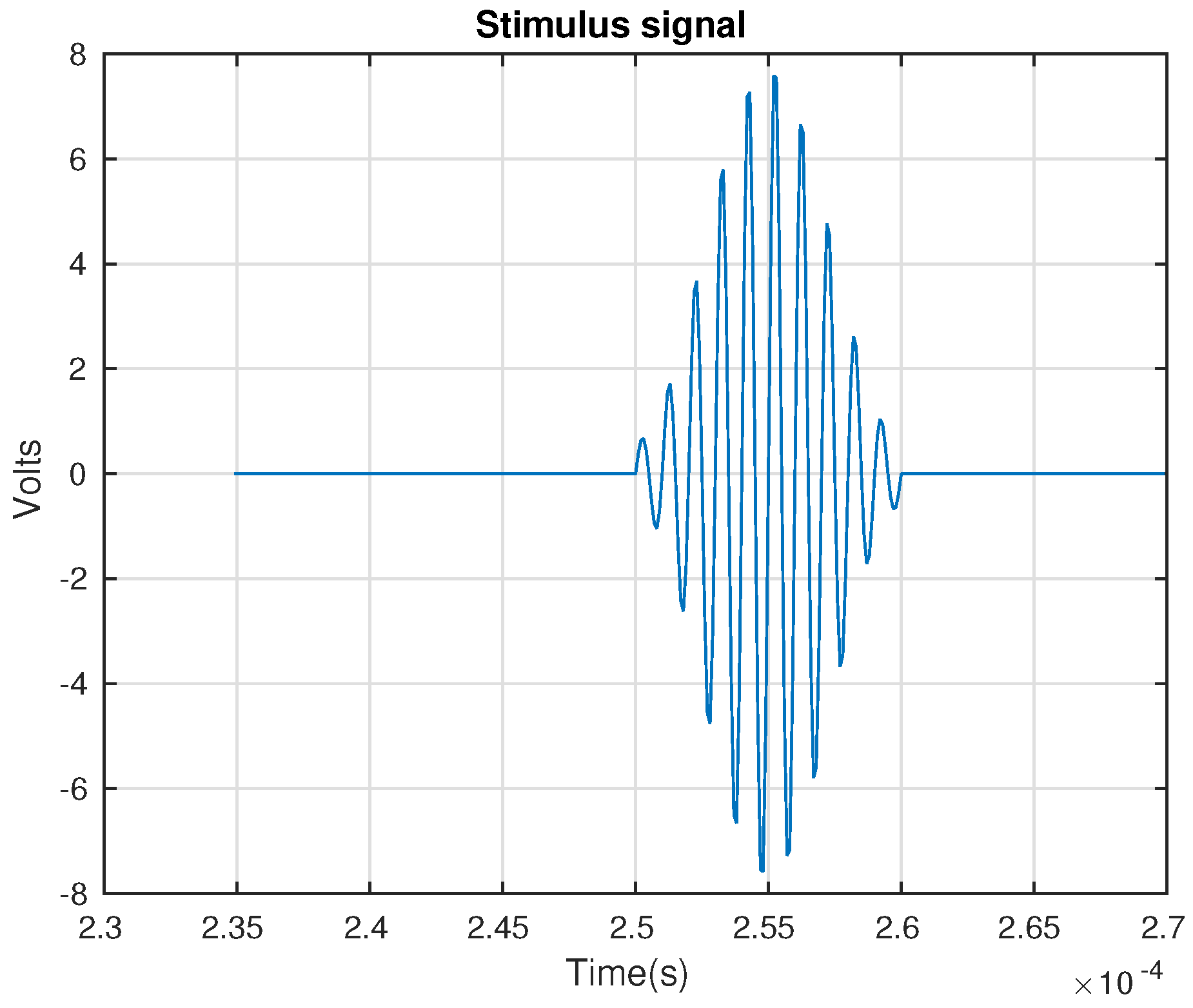
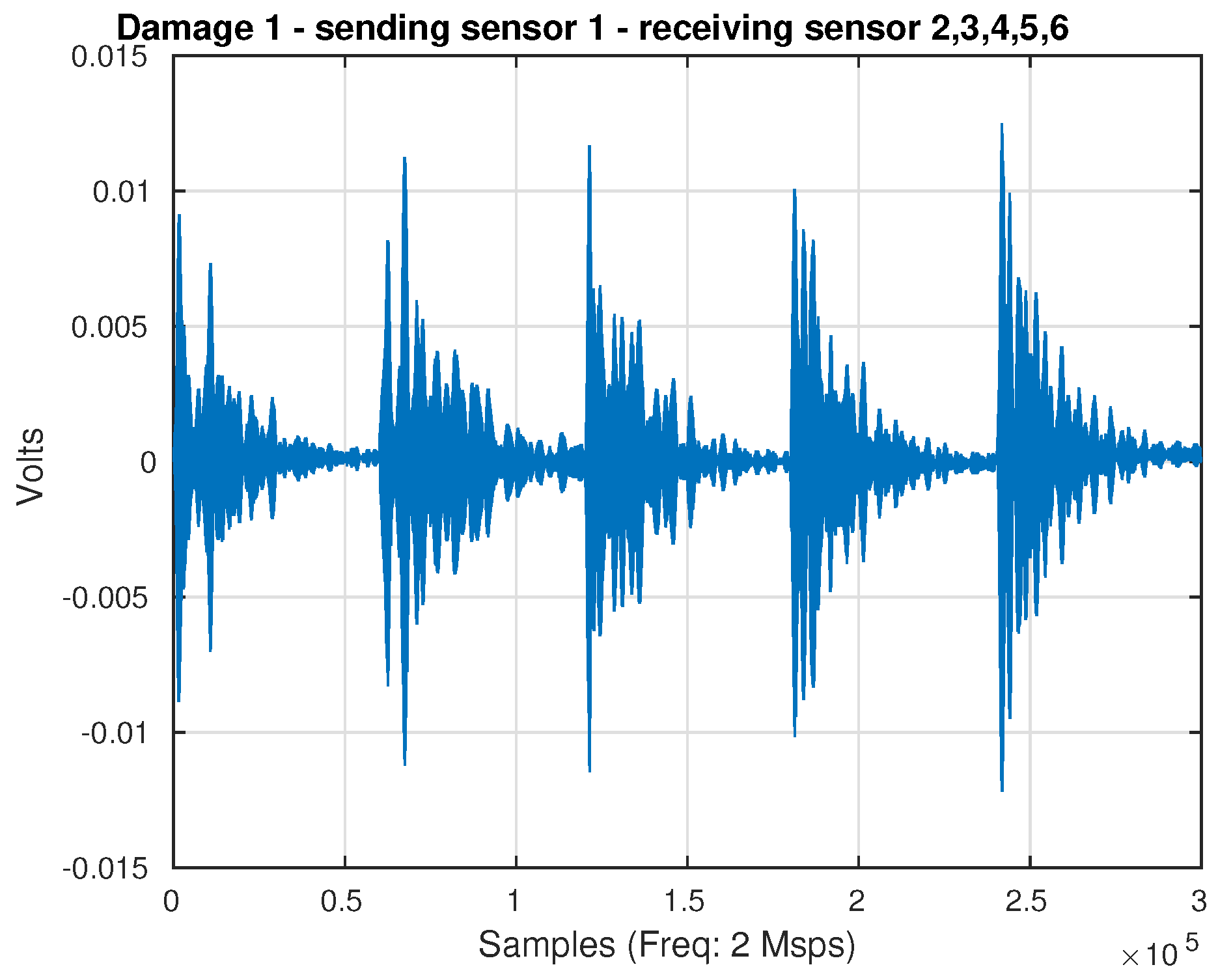
4. Experimental Setup and Results
- (i)
- An aluminum rectangular profile with a sensor network formed by six piezoelectric transducers bonded on both sides of the profile; see Figure 12;
- (ii)
- An aluminum plate with four piezoelectric transducers;
- (iii)
- Composite plate of carbon fiber polymer with six piezoelectric transducers;
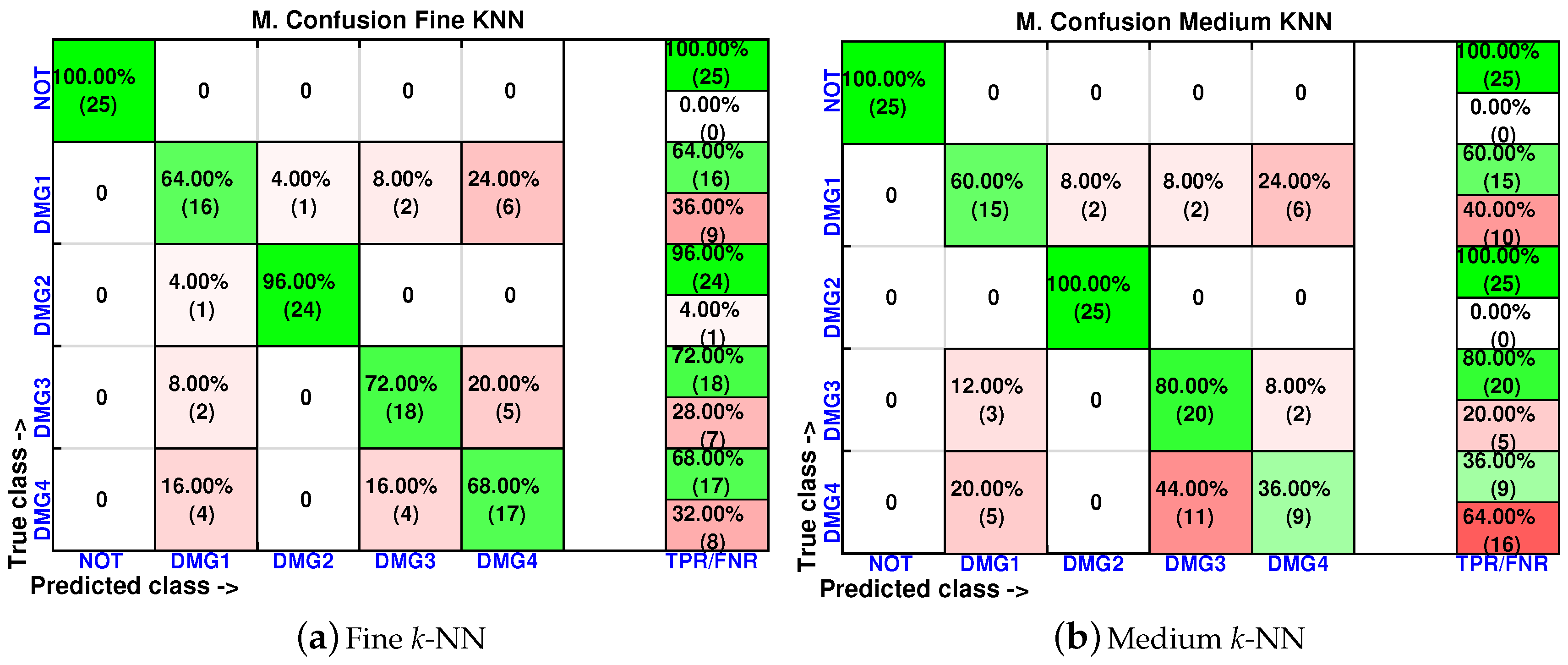
- Fine k-NN
- Medium k-NN
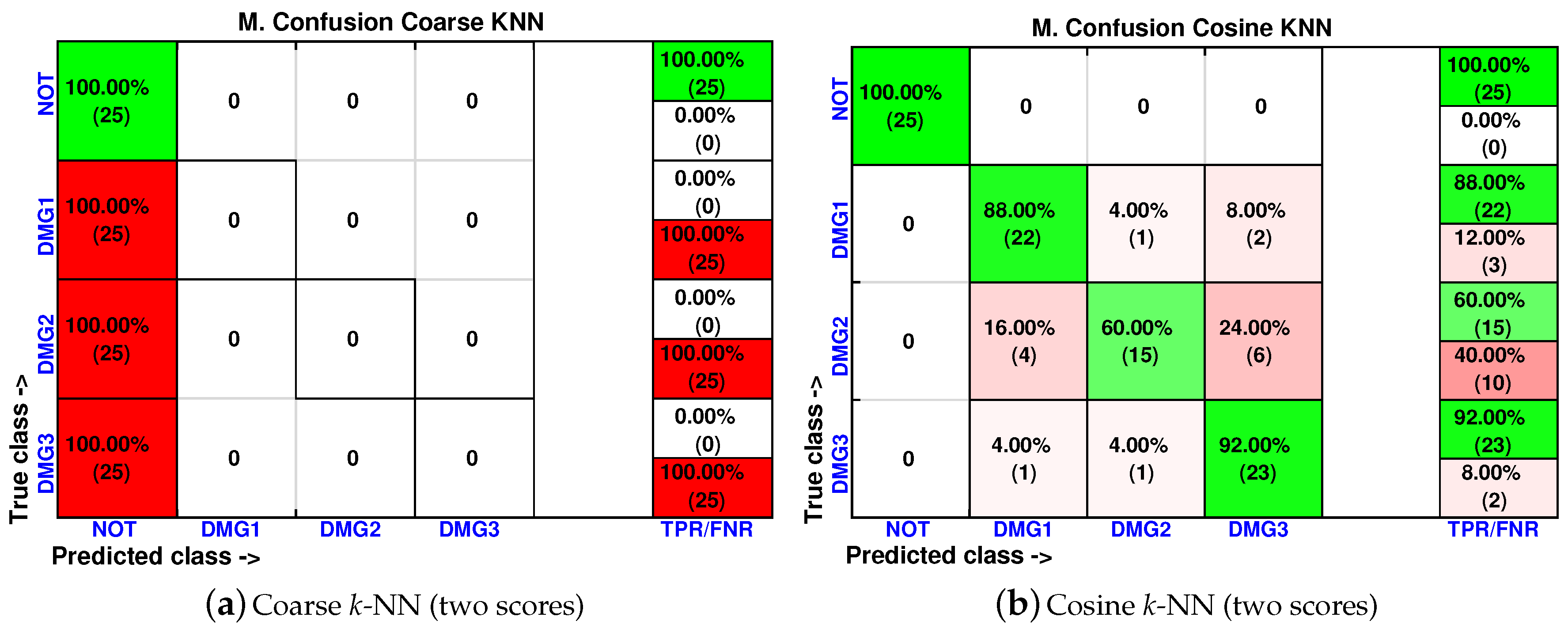
- Coarse k-NN
- Cosine k-NN
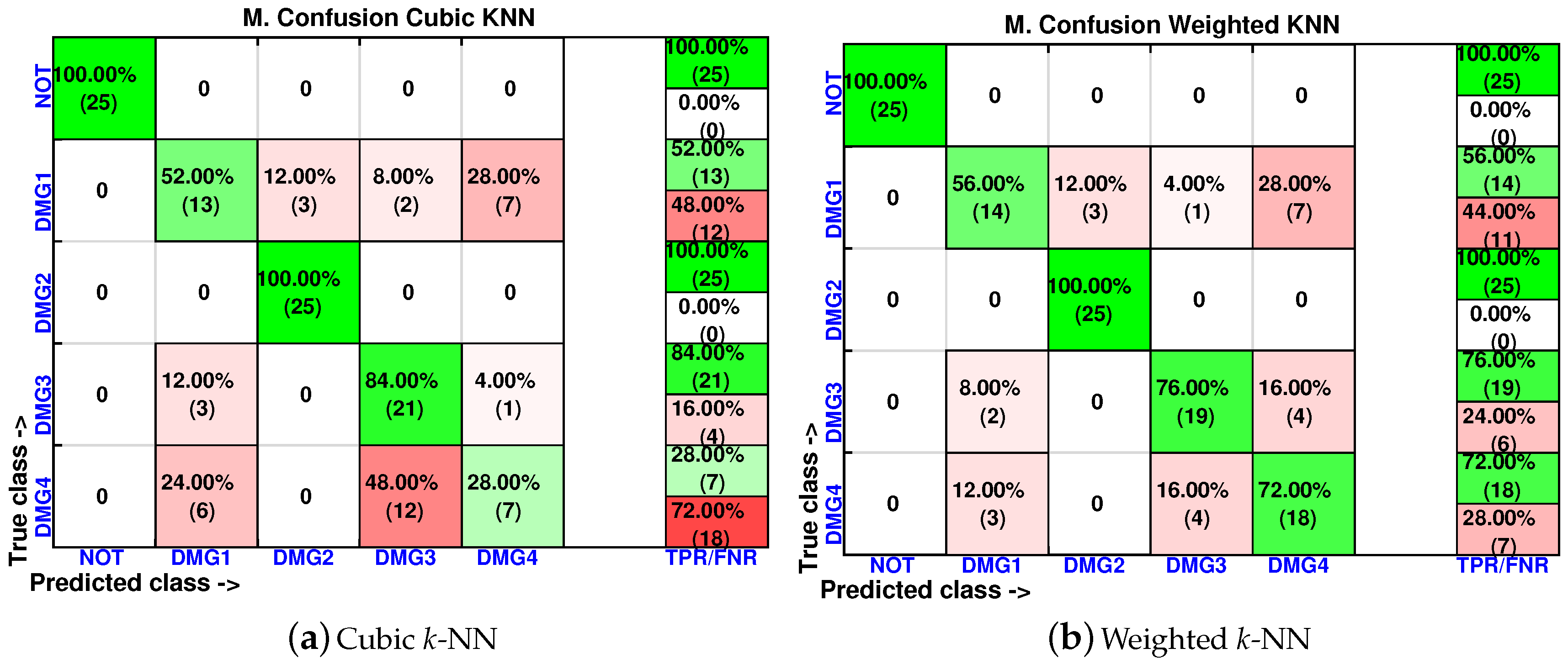
- Cubic k-NN
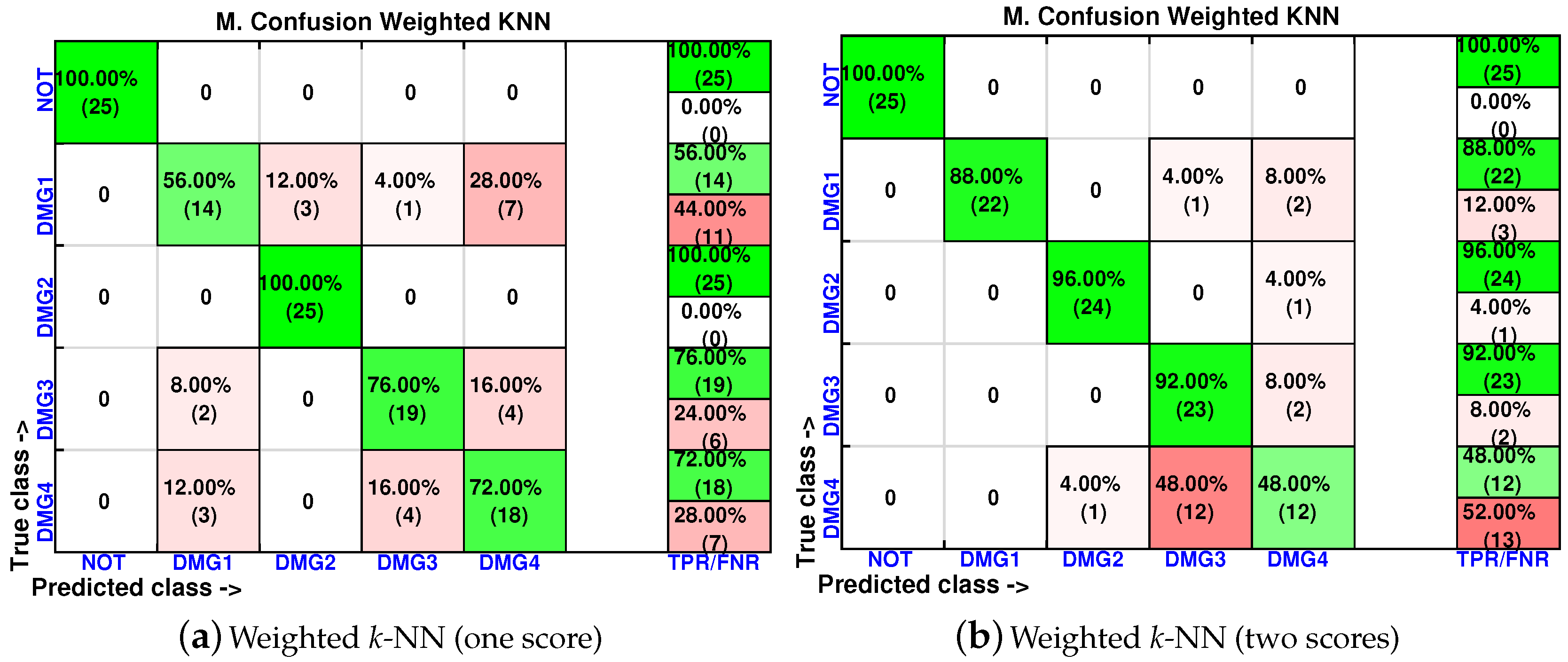
- Weighted k-NN
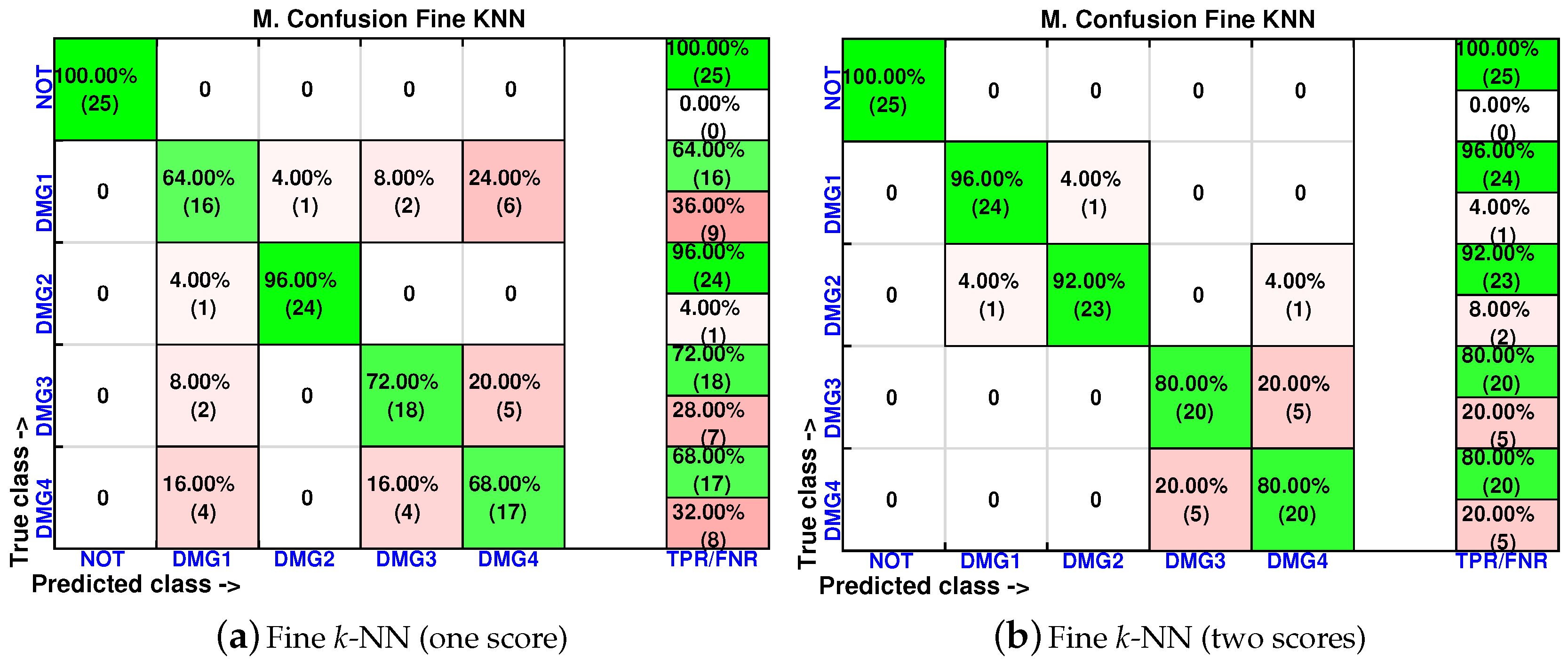
4.1. First Specimen: Aluminum Rectangular Profile
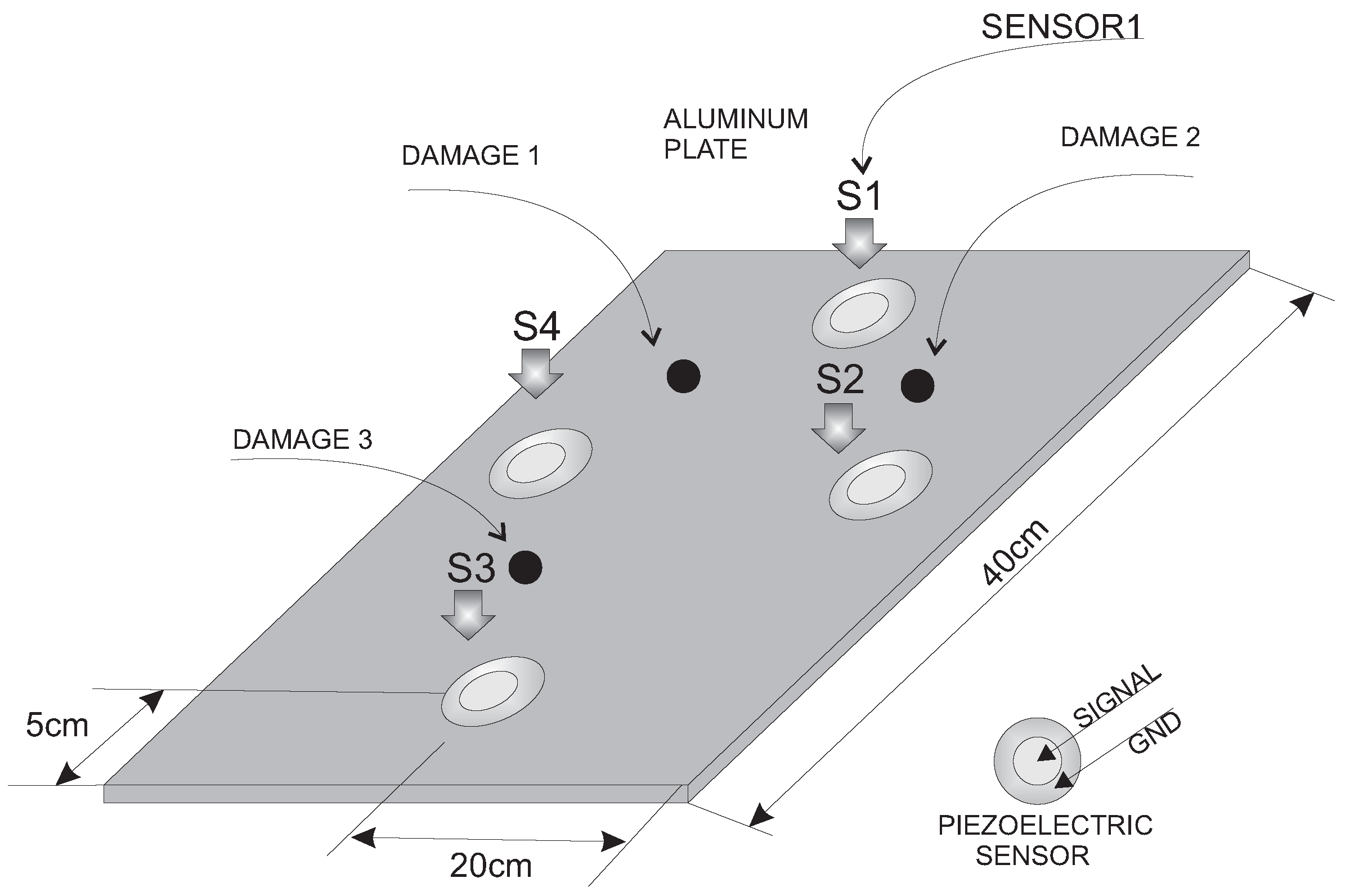
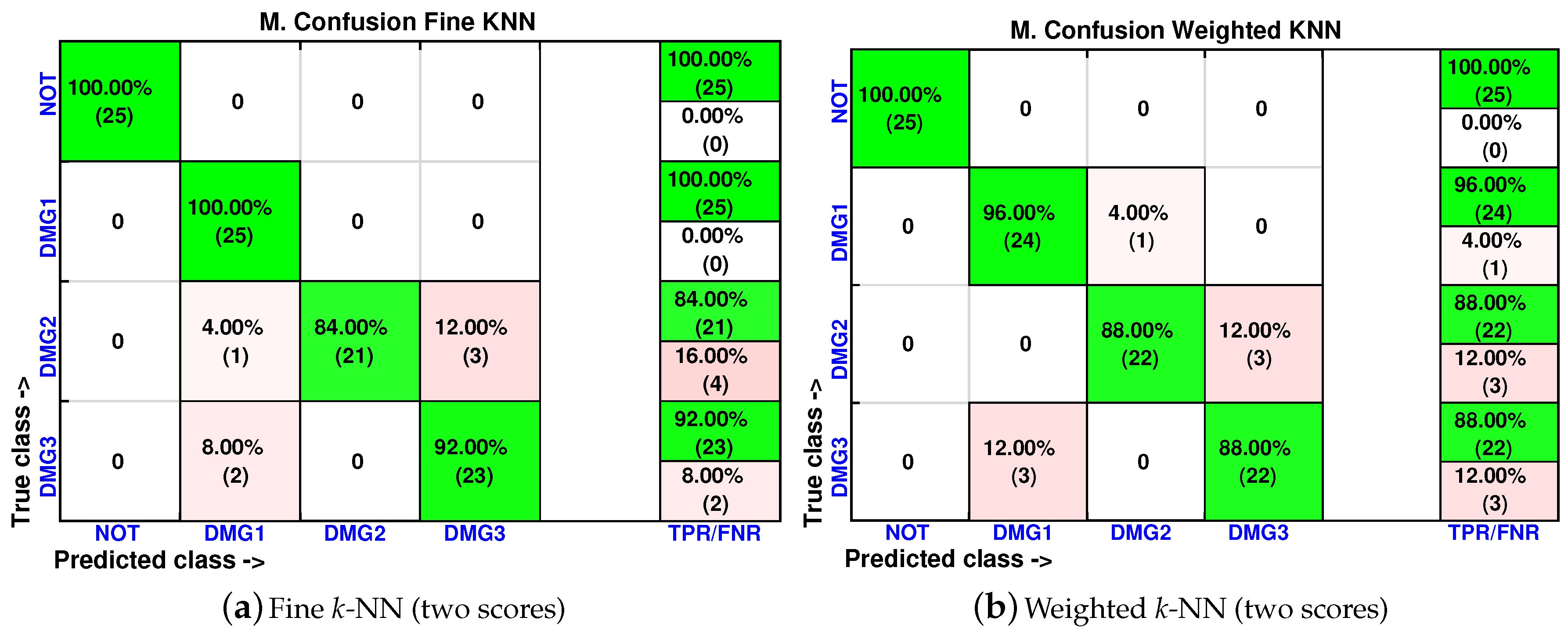
4.2. Second Specimen: Aluminum Plate
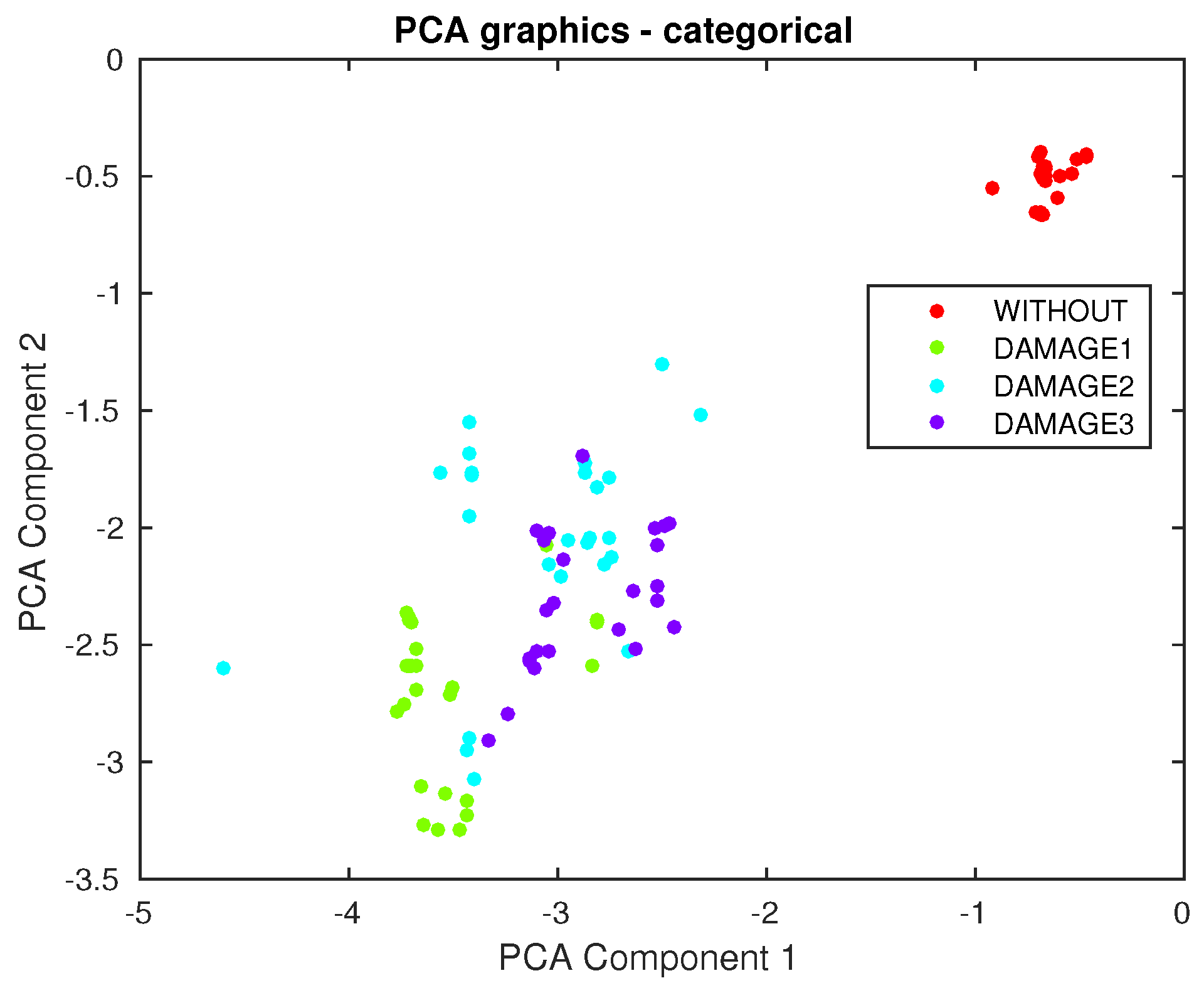
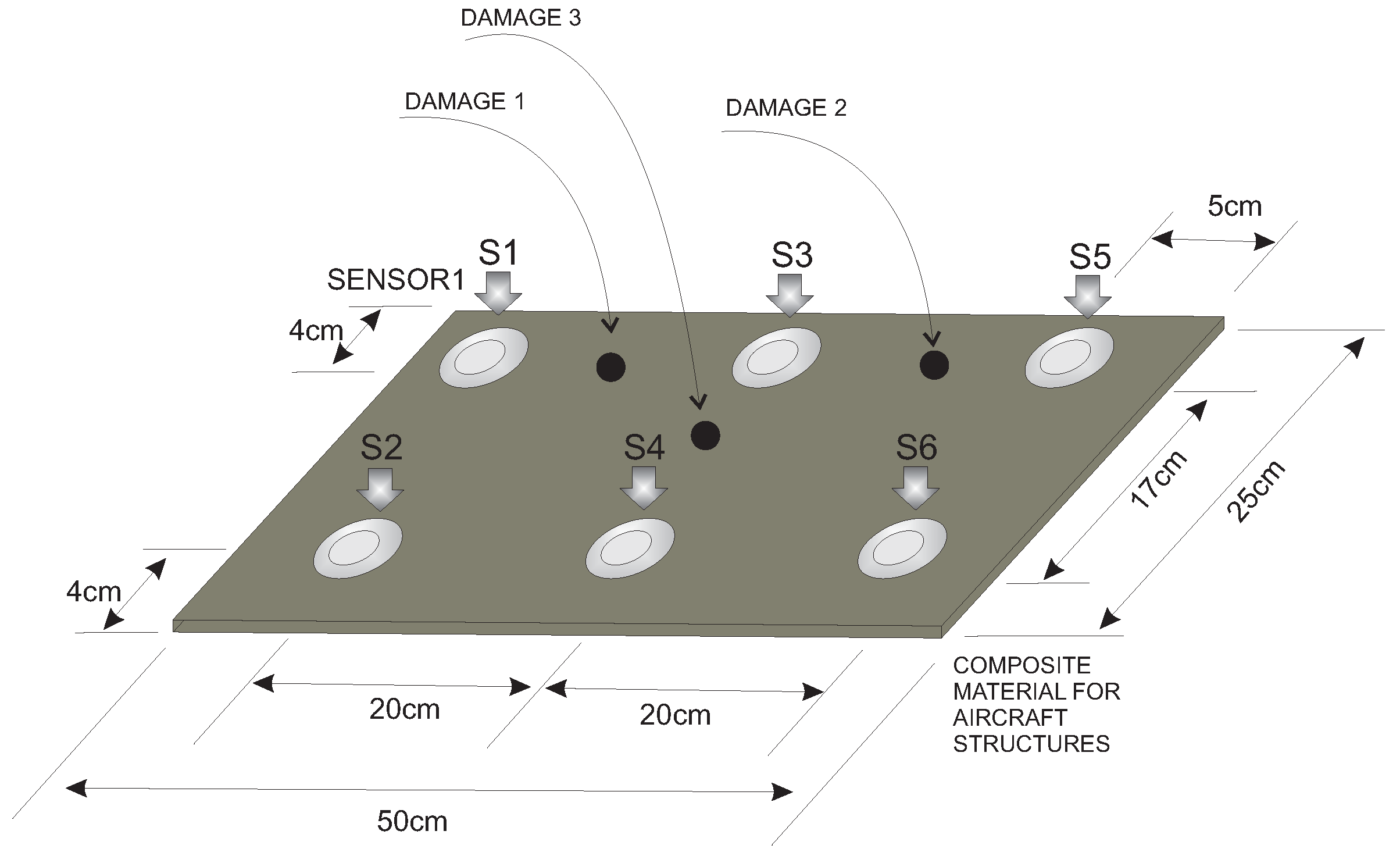
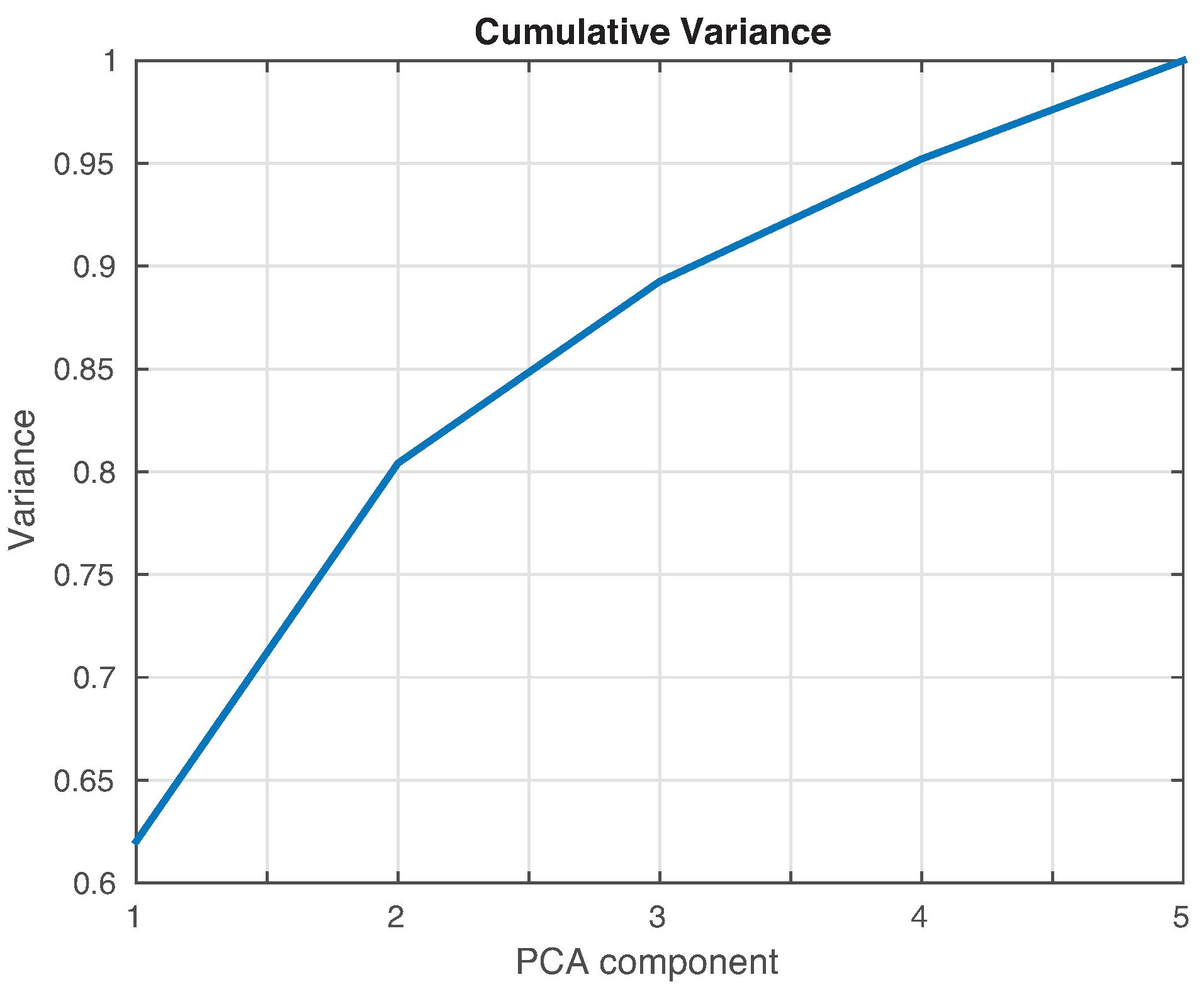
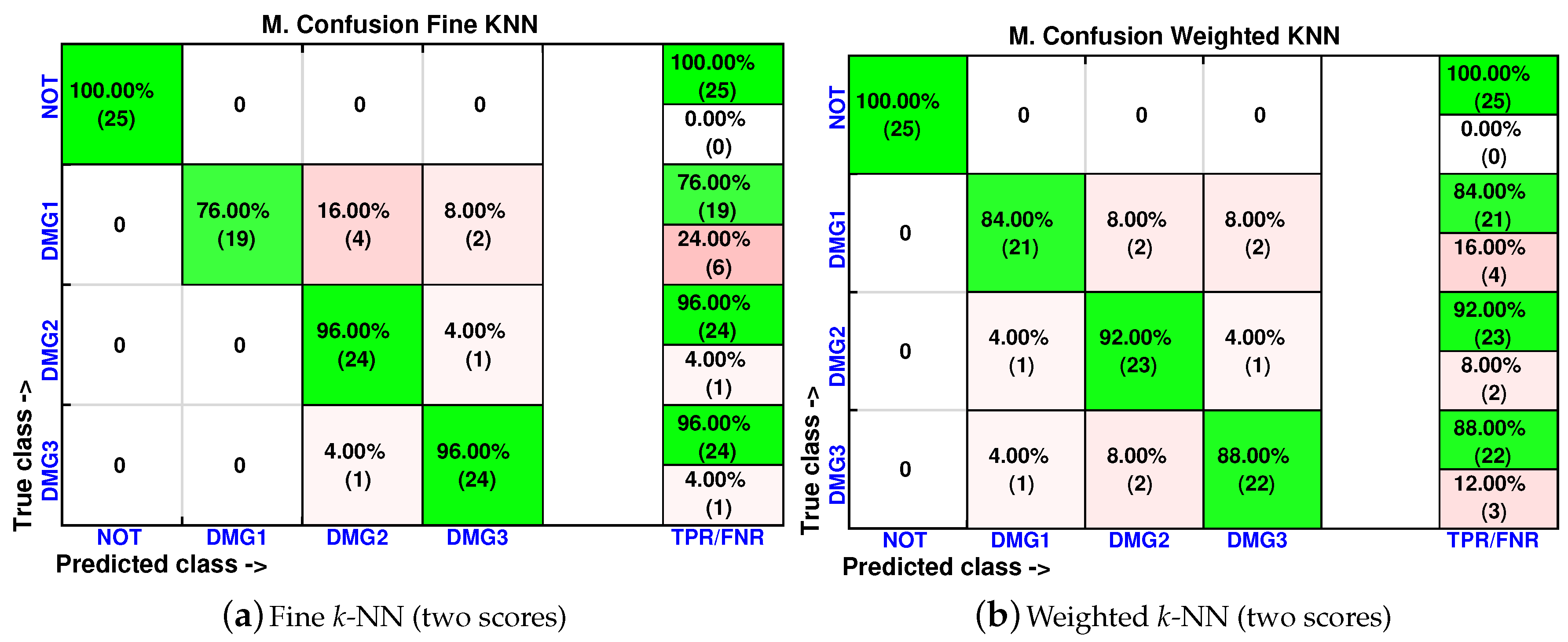
4.3. Third Specimen: Composite Plate, Carbon Fiber
5. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| k-NN | k-nearest neighbors algorithm |
| PCA | Principal component analysis |
| PZT | Lead-zirconate-titanate |
| SHM | Structural health monitoring |
References
- Anaya, M.; Tibaduiza, D.; Torres, M.A.; Pozo, F.; Ruiz, M.; Mujica, L.E.; Rodellar, J.; Fritzen, C.P. Data-driven methodology to detect and classify structural changes under temperature variations. Smart Mater. Struct. 2014, 23, 045006. [Google Scholar] [CrossRef]
- Tibaduiza, D.; Anaya, M.; Forero, E.; Castro, R.; Pozo, F. A sensor fault detection methodology applied to piezoelectric active systems in structural health monitoring applications. IOP Conf. Ser. Mater. Sci. Eng. 2016, 138, 012016. [Google Scholar] [CrossRef]
- Buethe, I.; Fritzen, C.P. Investigation on sensor fault effects of piezoelectric transducers on wave propagation and impedance measurements. In Proceedings of the 2013 COMSOL Conference, Rotterdam, The Netherlands, 23–25 October 2013.
- Gharibnezhad, F. Robust Damage Detection in Smart Structures. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2014. [Google Scholar]
- Dervilis, N.; Worden, K.; Cross, E.J. On robust regression analysis as a means of exploring environmental and operational conditions for SHM data. J. Sound Vib. 2015, 347, 270–296. [Google Scholar] [CrossRef]
- Zhang, H.; Guo, J.; Xie, X.; Bie, R.; Sun, Y. Environmental Effect Removal Based Structural Health Monitoring in the Internet of Things. In Proceedings of the 2013 Seventh International Conference on Innovative Mobile and Internet Services in Ubiquitous Computing (IMIS), Taichung, Taiwan, 3–5 July 2013.
- Langone, R.; Reynders, E.; Mehrkanoon, S.; Suykens, J.A.K. Automated structural health monitoring based on adaptive kernel spectral clustering. Mech. Syst. Signal Process. 2017, 90, 64–78. [Google Scholar] [CrossRef]
- He, Q.P.; Wang, J. Fault detection using the k-nearest neighbor rule for semiconductor manufacturing processes. IEEE Trans. Semicond. Manuf. 2007, 20, 345–354. [Google Scholar] [CrossRef]
- Mulligan, K.R.; Quaegebeur, N.; Ostiguy, P.-C.; Masson, P.; Letourneau, S. Comparison of metrics to monitor and compensate for piezoceramic debonding in structural health monitoring. Struct. Health Monit. 2012, 12, 153–168. [Google Scholar] [CrossRef]
- Gui, G.; Pan, H.; Lin, Z.; Li, Y.; Yuan, Z. Data-driven support vector machine with optimization techniques for structural health monitoring and damage detection. KSCE J. Civ. Eng. 2017, 21, 523–534. [Google Scholar] [CrossRef]
- Nick, W.; Shelton, J.; Asamene, K.; Esterline, A. A Study of Supervised Machine Learning Techniques for Structural Health Monitoring. In Proceedings of the 26th Modern Artificial Intelligence and Cognitive Science Conference (MAICS 2015), Greensboro, NC, USA, 25–26 April 2015.
- Torres, M.A.; Buethe, I.; Tibaduiza, D.; Rodellar, J.; Fritzen, C.P. Damage detection and classification in pipework using acousto-ultrasonics and non-linear data-driven modeling. J. Civ. Struct. Health Monit. 2013, 3, 297–306. [Google Scholar] [CrossRef]
- Tibaduiza, D.A.; Mujica, L.E.; Anaya, M.; Rodellar, J.; Güemes, A. Independent component analysis for detecting damages on aircraft wing skeleton. In Proceedings of the 5th European Conference on Structural Control (EACS 2012), Genoa, Italy, 18–20 June 2012.
- Gautschi, G. Piezoelectric Sensorics: Force Strain Pressure Acceleration and Acoustic Emission Sensors Materials and Amplifiers; Springer: Berlin, Germany, 2002. [Google Scholar]
- Anaya, M. Design and Validation of a Structural Health Monitoring System Based on Bio-inspired Algorithms. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2016. [Google Scholar]
- Jollife, I. Principal Component Analysis; Springer: New York, NY, USA, 2002. [Google Scholar]
- Anaya, M.; Tibaduiza, D.A.; Pozo, F. A bioinspired methodology based on an artificial immune system for damage detection in structural health monitoring. Shock Vib. 2015, 2015, 648097. [Google Scholar] [CrossRef]
- Tibaduiza, D.A. Design and Validation of a Structural Health Monitoring System for Aeronautical Structures. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2012. [Google Scholar]
- Jeong, D.H.; Ziemkiewicz, C.; Fisher, B.; Ribarsky, W.; Chang, R. iPCA: An interactive system for PCA based visual analytics. Comput. Graph. Forum 2009, 28, 767–774. [Google Scholar] [CrossRef]
- Pozo, F.; Vidal, Y. Wind turbine fault detection through principal component analysis and statistical hypothesis testing. Energies 2016, 9, 3. [Google Scholar] [CrossRef]
- Farrar, C.; Worden, K. Structural Health Monitoring: A Machine Learning Perspective; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Ciang, C.C.; Lee, J.-R.; Bang, H.-J. Structural health monitoring for a wind turbine system: A review of damage detection methods. Meas. Sci. Technol. 2008, 19, 122001. [Google Scholar] [CrossRef]
- Cover, T.M.; Hart, P.E. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Dhanabal, S.; Chandramathi, S. A review of various K-nearest neighbor query processing techniques. Int. J. Comput. Appl. Technol. 2011, 31, 14–22. [Google Scholar]
- Yang, J.; Sun, Z.; Chen, Y. Fault detection using the clustering-kNN rule for gas sensor arrays. Sensors 2016, 16, 2069. [Google Scholar] [CrossRef] [PubMed]
- Johnson, J.; Yadav, A. Fault Detection and Classification Technique for HVDC Transmission Lines Using kNN. In Proceedings of the International Conference on ICT for Sustainable Development (ICT4SD), Panaji, India, 1–2 July 2016.
- Statistics and Machine Learning Toolbox for Matlab; MathWorks: Natick, MA, USA, 2015; Available online: https://es.mathworks.com/help/pdf_doc/stats/stats.pdf (accessed on 17 February 2017).
- Deng, Z.; Zhu, X.; Cheng, D.; Zong, M.; Zhang, S. Efficient kNN classification algorithm for big data. Neurocomputing 2016, 195, 143–148. [Google Scholar] [CrossRef]
- Oh, S.; Byon, Y.; Yeo, H. Improvement of search strategy with k-nearest neighbors approach for traffic state prediction. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1146–1156. [Google Scholar] [CrossRef]
- Tibaduiza, D.A.; Mujica, L.E.; Rodellar, J. Damage classification in structural health monitoring using principal component analysis and self-organizing maps. Struct. Control Health Monit. 2012, 20, 1303–1316. [Google Scholar] [CrossRef]
- Mujica, L.E.; Ruiz, M.; Pozo, F.; Rodellar, J.; Güemes, A. A structural damage detection indicator based on principal component analysis and statistical hypothesis testing. Smart Mater. Struct. 2014, 23, 025014. [Google Scholar] [CrossRef]
- Pozo, F.; Arruga, I.; Mujica, L.E.; Ruiz, M.; Podivilova, E. Detection of structural changes through principal component analysis and multivariate statistical inference. Struct. Health Monit. 2016, 15, 127–142. [Google Scholar] [CrossRef]












© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vitola, J.; Pozo, F.; Tibaduiza, D.A.; Anaya, M. A Sensor Data Fusion System Based on k-Nearest Neighbor Pattern Classification for Structural Health Monitoring Applications. Sensors 2017, 17, 417. https://doi.org/10.3390/s17020417
Vitola J, Pozo F, Tibaduiza DA, Anaya M. A Sensor Data Fusion System Based on k-Nearest Neighbor Pattern Classification for Structural Health Monitoring Applications. Sensors. 2017; 17(2):417. https://doi.org/10.3390/s17020417
Chicago/Turabian StyleVitola, Jaime, Francesc Pozo, Diego A. Tibaduiza, and Maribel Anaya. 2017. "A Sensor Data Fusion System Based on k-Nearest Neighbor Pattern Classification for Structural Health Monitoring Applications" Sensors 17, no. 2: 417. https://doi.org/10.3390/s17020417
APA StyleVitola, J., Pozo, F., Tibaduiza, D. A., & Anaya, M. (2017). A Sensor Data Fusion System Based on k-Nearest Neighbor Pattern Classification for Structural Health Monitoring Applications. Sensors, 17(2), 417. https://doi.org/10.3390/s17020417







