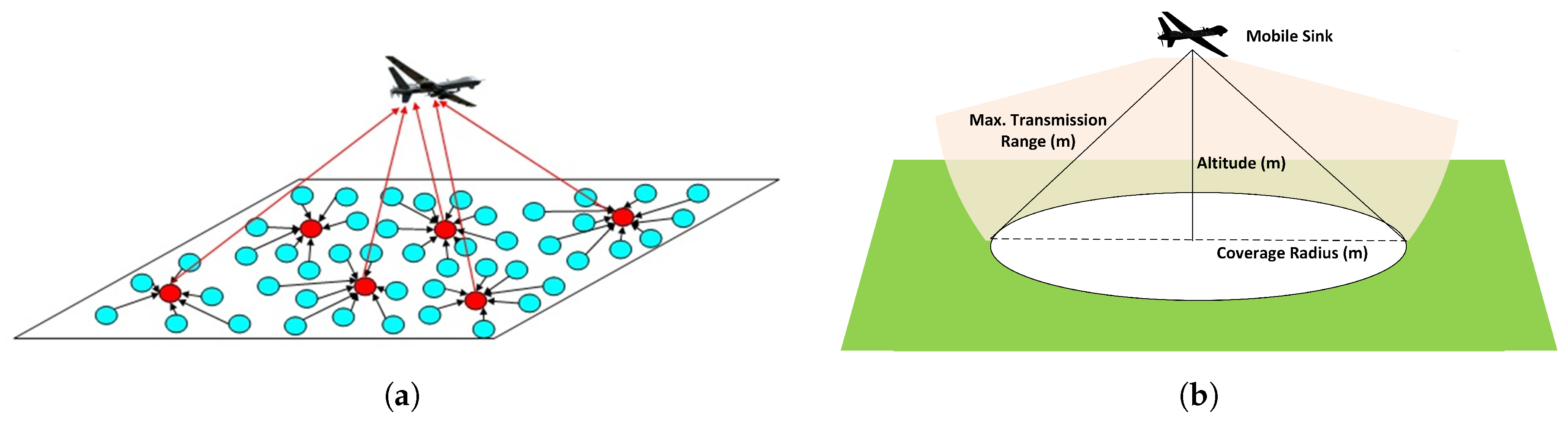
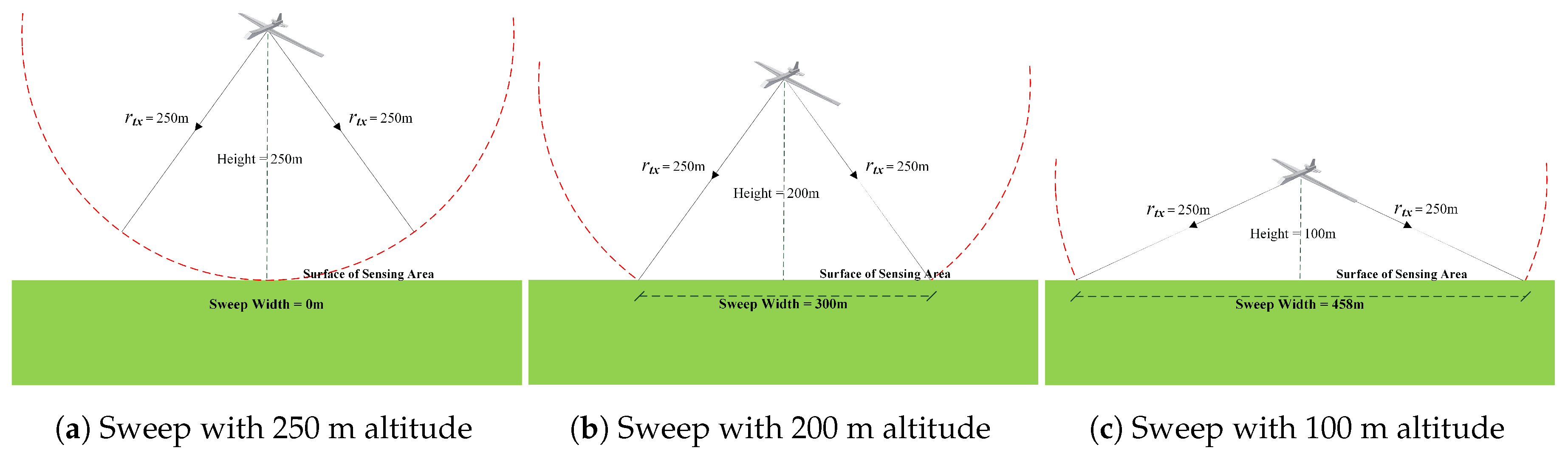
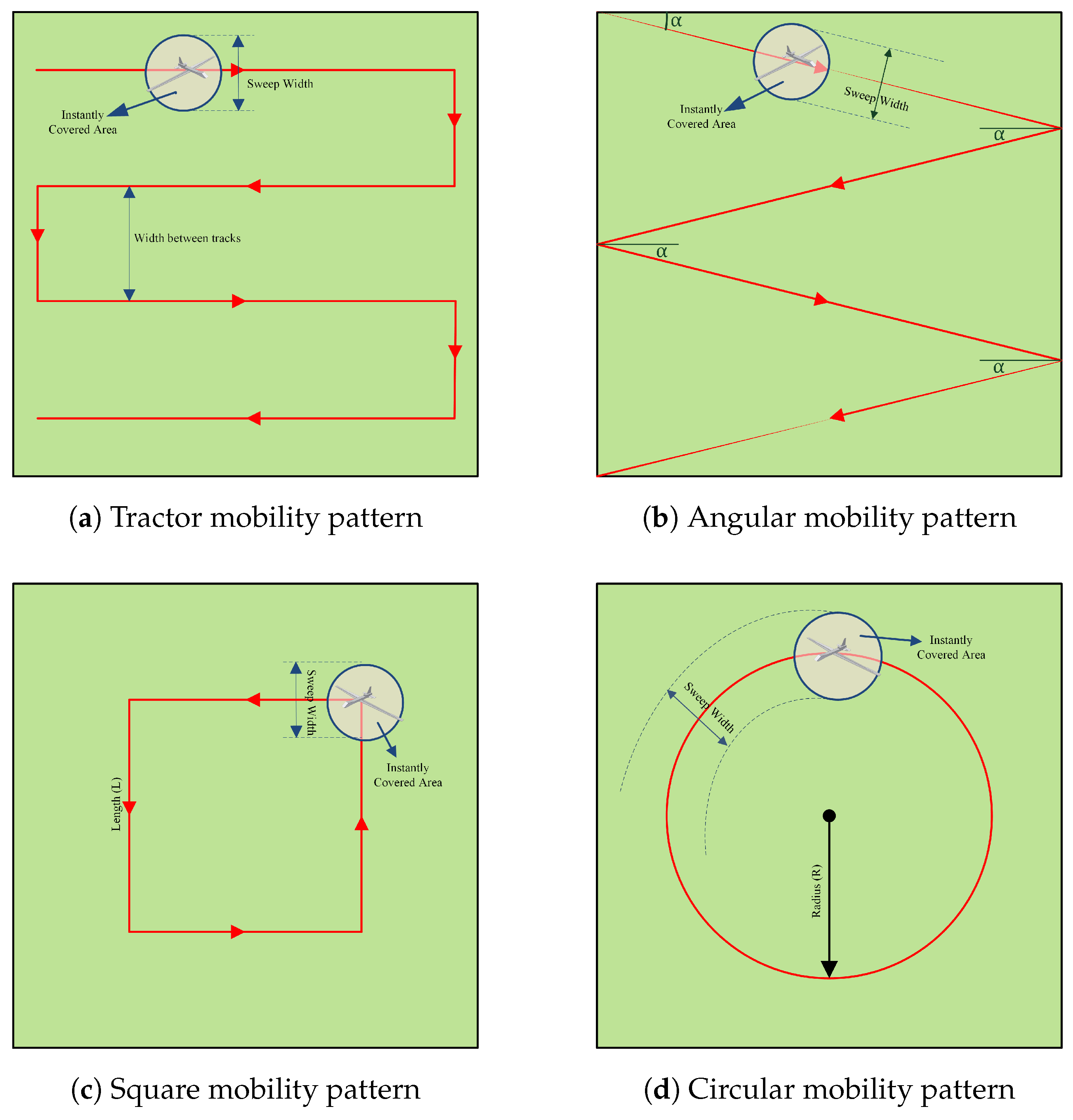
In making decision to select the best appropriate mobility pattern to apply in the operation area, there could be two main objectives: (1) covering the maximum number of nodes; (2) spending less time in the operation area with maximum utilization. Therefore, the performance results are based on the measurements to observe the effects of mobility patterns on these objectives.
4.3.1. Coverage
The number of cluster heads represents the number of clusters formed. Although a smaller number of clusters is admired in WSN, in such large-scale operation areas where the coverage is the major problem, fewer clusters may indicate a high number of uncovered nodes. Therefore, although the number of cluster heads gives some valuable information, it has to be evaluated together with the number of covered nodes.
The coverage in the Tractor mobility pattern depends on the width between the parallel tracks. Coverage with track mobility is tested with various track widths between 200 m and 2000 m. With 2000 m width, the UAV crosses the operation area at the center from one end to the other. As the track width narrows, the number of tracks increases, which leads to an increase in the UAV path length. Longer paths also lead to the coverage of more sensor nodes and the formation of more clusters closer to the UAV path. On the other hand, with fewer tracks, gaps are expected to exist with some uncovered nodes between tracks. As expected,
Figure 4a shows that increasing the width of the tracks leads to a decrease in the number of CHs. The maximum number of CHs with UAV access is seen at width value 200 m with the UAV altitude value 100 m. For the 250 m altitude, the number of clusters are at a minimum, and only the sensor nodes under the exact projection of the UAV path can be the CHs. Although the number of CHs is a good indicator of coverage, more accurate results are obtained by the number of covered nodes.
Figure 4b shows the number of covered nodes in the Tractor mobility pattern. It is seen that when the track width is narrow, the number of covered nodes are very close to each other for each altitude. However, when the track width increases to more than 400 m, the number of covered nodes decreases sharply (except with 100 m altitude), with fewer covered nodes for higher altitudes. When the two figures are compared, it is seen that the number of covered nodes are not directly proportional to the number of CHs. Although the number of CHs for altitude 250 m is steadily low for all width values, the number of covered nodes does not present similar results. The reason is that selected CHs form clusters with their member nodes, which are considered to have indirect access to the UAV through the CHs. Therefore, altitude 250 m performs results closer to other altitudes when the track width is narrow. The clustering algorithm plays a key role in the formation of clusters based on the UAV path. This leads to more nodes being covered, even though they might not have direct access to the UAV. This characteristic is also seen at altitude 100 m. Although the number of CHs decreases sharply when the width is about 500 m, the number of covered nodes does not decrease sharply, almost having steady and similar results. It is also seen in
Figure 4b that for altitudes other than 100 m, as the width grows to 1000 m, the number of covered nodes decreases sharply, but after 1000 m it starts to decrease slightly. The reason is related to the gaps between the tracks. When the width is small, there is no gap between the tracks where the UAV covers most of the nodes. As the width grows, gaps get larger, causing the decrease in the number of covered nodes.
In the Angular mobility pattern, the UAV is reflected from the border with the defined angle value when the UAV impinges on the border of the operation area. Therefore, the coverage in the Angular mobility pattern depends on the angle value. The mobility pattern is tested with four different angle values: 5, 10, 15, and 25. It is seen in
Figure 4c that increasing the angle value leads to a decrease in the number of CHs. With smaller angles, the number of legs on the path is increased; therefore, more clusters are formed closer to the UAV path. On the other hand, it is expected to see some gaps between the legs when the angle gets larger (
Figure 3b). The maximum number of CHs with UAV access is seen at an angle value of 5
. On the other hand, decreasing the altitude also leads to an increase in the number of CHs. This is related to the coverage and sweep width, as illustrated in
Figure 2. At low altitudes, more nodes receive the signals from the UAV to compete to be CHs.
Figure 4d shows the number of covered nodes in the Angular mobility pattern. It is seen that the number of covered nodes decreases as the angle value increases. Smaller angle values cause fewer UAV legs to be constructed over the operation are, which leads the UAV to sweep less of an area. At the angle value 5
and altitude 100 m, 197 out of 200 nodes are covered with the maximum value. For all angle values except 25
, the number of covered nodes are very close to each other. However, at the angle value 25
, the number of covered nodes reduced significantly—especially for the altitudes 250 m and 200 m. When the covered nodes are compared according to the altitude, it is clearly seen that low altitude covers more nodes. Very similar to the Tractor mobility pattern results, the number of covered nodes are not directly proportional to the number of CHs. There is a sharp decrease in the number of CHs between angles 5
and 10
, but the number of clustered nodes does not change much. The reason is related to the clustering algorithm. Although the number of clusters is reduced with higher angle values, clustering algorithms are able to connect member nodes to the UAV with the use of CHs. Therefore, the number of covered nodes is not affected much with respect to the CHs when the angle value is small. On the contrary, when the angle value is very large (e.g., 25), the number of covered nodes reduces due to the gaps between legs.
The coverage in the Square mobility pattern depends on the length of the edge of the square, where the center of the square is the center of the operation area. The mobility pattern was tested with 10 different square side lengths, starting from 200 m to 2000 m, with 200 m increase at each step. With 2000 m side length, the UAV follows the borders (edges) of the square-shaped operation area. It is important to see the effects of gaps in the center when the square is large and the effects of gaps at the outside of the square-shaped sweep region when the square is small. With a wider square, the length of the path is increased; therefore, more clusters are formed closer to the UAV path. The maximum number of CHs with UAV access is seen at side length value 1600 m at all altitude values, and the maximum is reached with altitude 100 m (
Figure 4e).
Figure 4f shows the number of covered nodes in the Square mobility pattern. At side length 1200 m and altitude 100 m, most of the 200 nodes are covered. It is seen that as the square path increases, the number of covered nodes increases until the side length value 1200 m, and then decreases slightly. The reason is related to the gaps inside and outside of the square. When the side lengths (and therefore the squares) are small, there are gaps outside of the square where the UAV cannot cover any node in that region. As the size of the square grows, gaps outside of the square get smaller. On the other hand, after 1200 m, the gaps outside of the square are at a minimum or no gap exists, but new gaps appear at the center of the square. This is why the number of covered nodes increases until side length value 1200 m and decreases after that. When the altitudes are compared with each other, it is seen that all altitudes perform similarly, with some constant difference between each other. It is also noticeable that the performance of the Square mobility pattern is very similar to the Circular mobility pattern.
The coverage in the Circle mobility pattern depends on the radius value
R, where the center of the circle is the center of the operation area. It is seen in
Figure 4g that increasing the radius of the circling UAV leads to an increase in the number of CHs. With a larger circle, the length of the path is increased; therefore, more clusters are formed closer to the UAV path. On the other hand, it is expected to see some gaps at the corners of the area when the circle gets smaller, and gaps at the center of the area when the circle gets larger. These gaps increase the number of standalone CHs (CHs without a cluster member) and uncovered nodes. The maximum number of CHs is seen at radius values 800 m and 900 m. As the altitude decreases, the UAV sweeps a greater area; therefore, the highest number of clusters is observed at 100 m with 800 m circling radius.
Figure 4h shows the number of covered nodes. It is seen that as the circular path grows, the number of covered nodes increases until the radius value 700 m, and then decreases slightly. The number of covered nodes is proportional to the number of CHs. Similar to the Square mobility pattern, when the altitudes are compared with each other, it is seen that all altitudes perform similarly with some constant difference between each other.
When all mobility patterns are compared, the maximum number of covered nodes is seen at the altitude of 100 m. In the Angular mobility pattern, the number of covered nodes is not affected as much as other mobility patterns due to the varying performance parameters, altitude, circle radius, etc.
4.3.2. Time Efficiency and Utilization
On data collection in the WSN, one main aim is to collect the data from as many nodes as possible, and the other aim is to collect the data as quickly as possible to reduce the operation time. In large-scale WSN deployments, every node in the network might not be accessed without leaving a gap in the network. Accessing each sensor and retrieving its data is usually the main aim. However, this approach might introduce additional UAV operation time to be spent in the operation area. Covering each sensor node may cause unnecessary cost, which might even not be fulfilled by the UAV capabilities. Therefore, it is essential to observe the time efficiency to gather the required information from the WSN. It is essential to know how much more time is required to cover some more nodes. If the time required to cover a few more nodes will increase the overall time too much (in other words, if the benefit remains marginal), the intention of covering some more nodes might be prevented to keep the cost at an acceptable level and to utilize the time and cost more efficiently. For the time efficiency, the Time Spent per Covered Node metric is defined, and is formulated as follows:
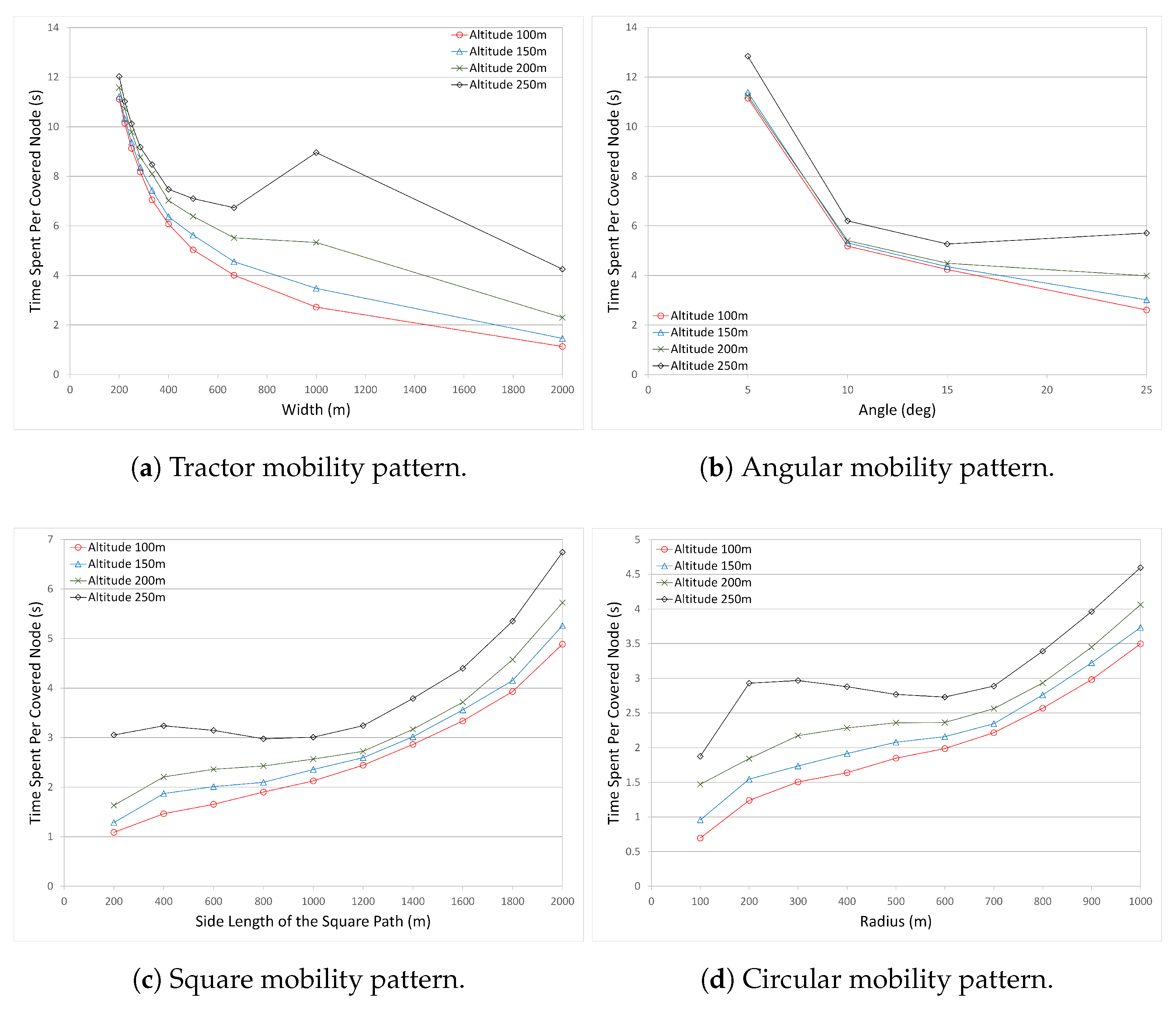
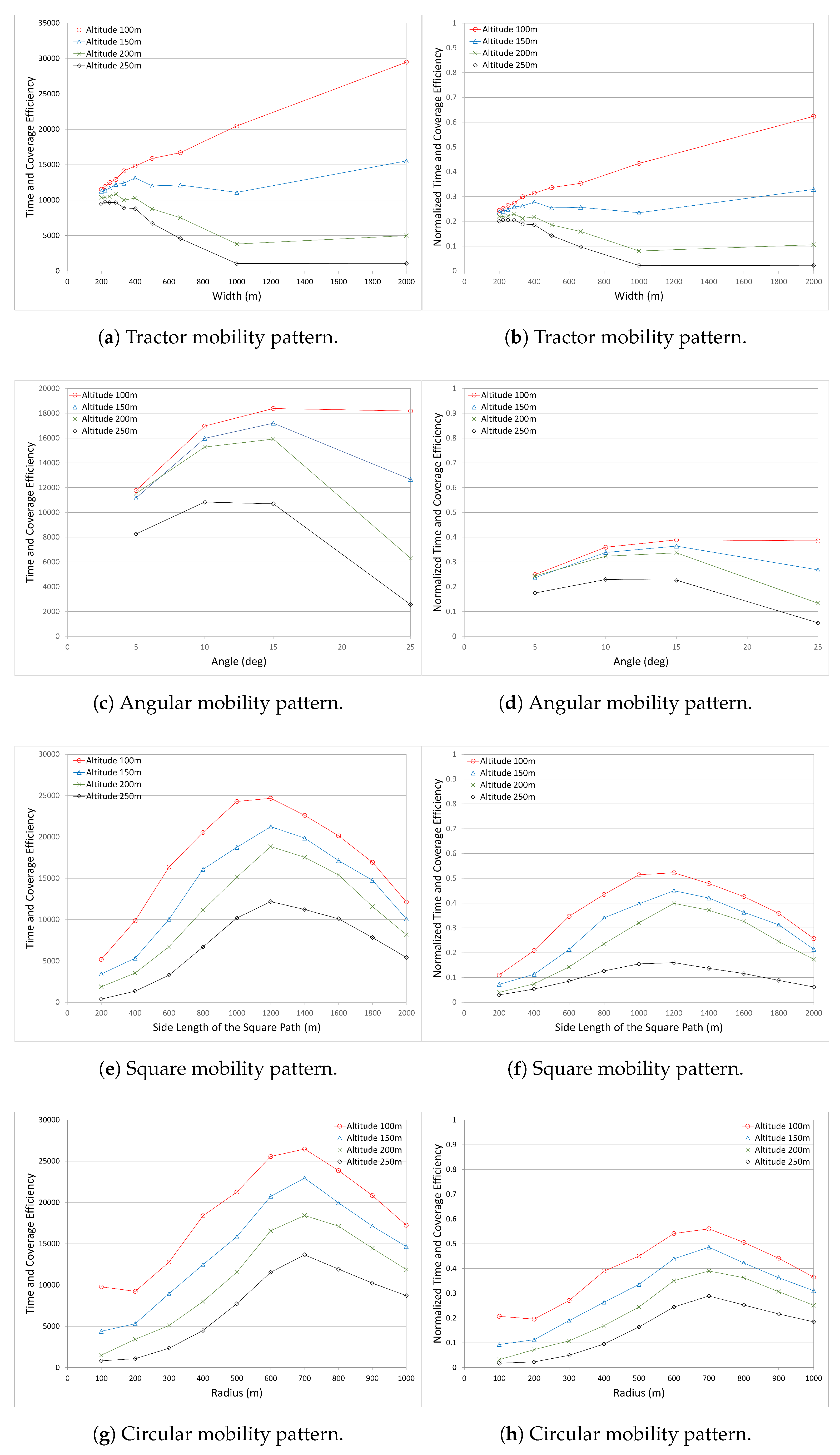
Figure 5 shows the time spent per covered node for all mobility models with various altitudes.
Figure 5a shows the time spent to cover a single node in the Tractor mobility pattern. In the Tractor mobility pattern, as the path length decreases (the width between the tracks increases), the time spent to cover a single node decreases sharply until width value 500 m, between 500 m–1000 m, there is a moderate decrease, and after 1000 m, the time spent per covered node starts to decrease slightly. The results for altitude 250 m differ from the other altitudes. At altitude 250 m, the time spent per covered node decreases sharply, then starts to increase again at 700 m, and starts to decrease after 1000 m. It is related with the number of covered nodes. According to these results, the time spent per covered node is very small at the width value 2000 m, but it is most probably an inadvisable parameter to use when the number of covered nodes is also considered.
Figure 5b shows the time spent to cover a single node in the Angular mobility pattern. It is seen that as the angle value increases (path length decreases), the time spent to cover a single node decreases sharply, and then continues to decrease slightly after angle value 10
for all altitude values. At angle value 25
and altitude 100 m, the time spent to cover a single node is at a minimum. Except altitude 250 m, all altitudes present similar results. Results for 250 m are much higher compared to the others. The reason is related to the number of covered nodes. On the other hand, it is seen that the minimum time spent per covered nodes is observed at angle value 25
at all altitudes. However, when we compared with the number of covered nodes, angle value 25
performs the worst in terms of the number of covered nodes. In this case, there is a dilemma in choosing the best mobility model and pattern; that is, whether the number of covered nodes or the time spent per covered node should be selected as the decision metric. Therefore, a new metric Time and Coverage Efficiency is defined, and will be presented later.
Figure 5c shows the time spent to cover a single node in the Square mobility pattern. It can be seen that when the side length (and therefore the path length) increases, the time spent to cover a single node increases slightly until length value 1200 m, and then starts to increase sharply. The results for the Square mobility pattern are very similar to the results of the Circular mobility pattern, for which the results will be discussed in further detail.
Figure 5d shows the time spent to cover a single node in the Circular mobility pattern. When the UAV follows a path (i.e., circle), the path length depending on the mobility type becomes important. As the path length increases, the UAV will spend more time in the air. However, depending on the clustering algorithms and the UAV path, more stable and balanced clusters can be formed. Therefore, a preferred pattern can be selected based on the time per node. Here, as is seen in
Figure 5d, when he circular path length increases, the time spent to cover a single node increases, then the increase rate slows down due to more covered nodes, and then increases again. The minimum time spent per covered node is observed at the radius 100 m. However, the same decision issue arises again. With the radius 100 m, the Circular mobility pattern performs the worst with respect to the number of covered nodes. Therefore, as mentioned in angular mobility, the number of covered nodes and the time spent to cover these nodes have to be considered together. According to these results, at radius between 500 m and 700 m, more nodes are covered within a shorter time. If we consider only the number of covered nodes, the altitude 700 m is the best choice in circular mobility.
Among all mobility patterns, the Square mobility pattern and the Circular mobility pattern have lower and more stable values for the time spent per covered node. It is also seen that the rate of change in the Square and Circular mobility patterns is lower than the Tractor and Angular mobility patterns.
When all mobility patterns are compared, the time spent per covered node in Angular and Tractor mobility patterns is very high for some values of angle and track width (i.e., angle value 5 in Angular mobility pattern and track width value 200 m in Tractor mobility pattern). On the other hand, depending on the parameter values, the time spent per covered node reduces to very small values (i.e., for angle value 25 in Angular and track width value 2000 m in Tractor mobility patterns). For these small values, it is questionable to use these parameters in the data collection of such a large-scale WSN. When we look at the number of covered nodes for the scenarios with these small values of time spent per covered node, it is seen that very few nodes are covered. So, it is the network operator’s responsibility to consider multiple metrics depending on the objectives. There is a tradeoff whether to use the parameters with more covered nodes or the parameters with short time to cover a single node. Altitudes affect the number of covered nodes at each mobility pattern, and the time spent per covered node is directly related to the number of covered nodes. This tradeoff introduces the utilization metric, which is considered as a measure for the performance of the system.
In the literature, there are many performance metrics defined to measure the performance of the system. Three of them are very close to each other. These are the utilization, the efficiency, and the productivity metrics. Their corresponding formulas are given below.
Productivity (
4) is the inverse of the performance metric “The Time Spent per Covered Node” (
1). Therefore, the results for the productivity will not be given because we have already given the results for the time spent per covered node.
The Utilization (
2) and the Efficiency (
3) are very close to each other, giving similar results and the same curve pattern in the graphs. Their y-scales range between 0 and 1. Therefore, rather than using both metrics, we have used only utilization in the evaluations. Previously, the results for the performance metric “the number of covered nodes” were presented. It is clear that the utilization metric is the normalization of “the number of covered nodes”, where the utilization value varies between 0 and 1.
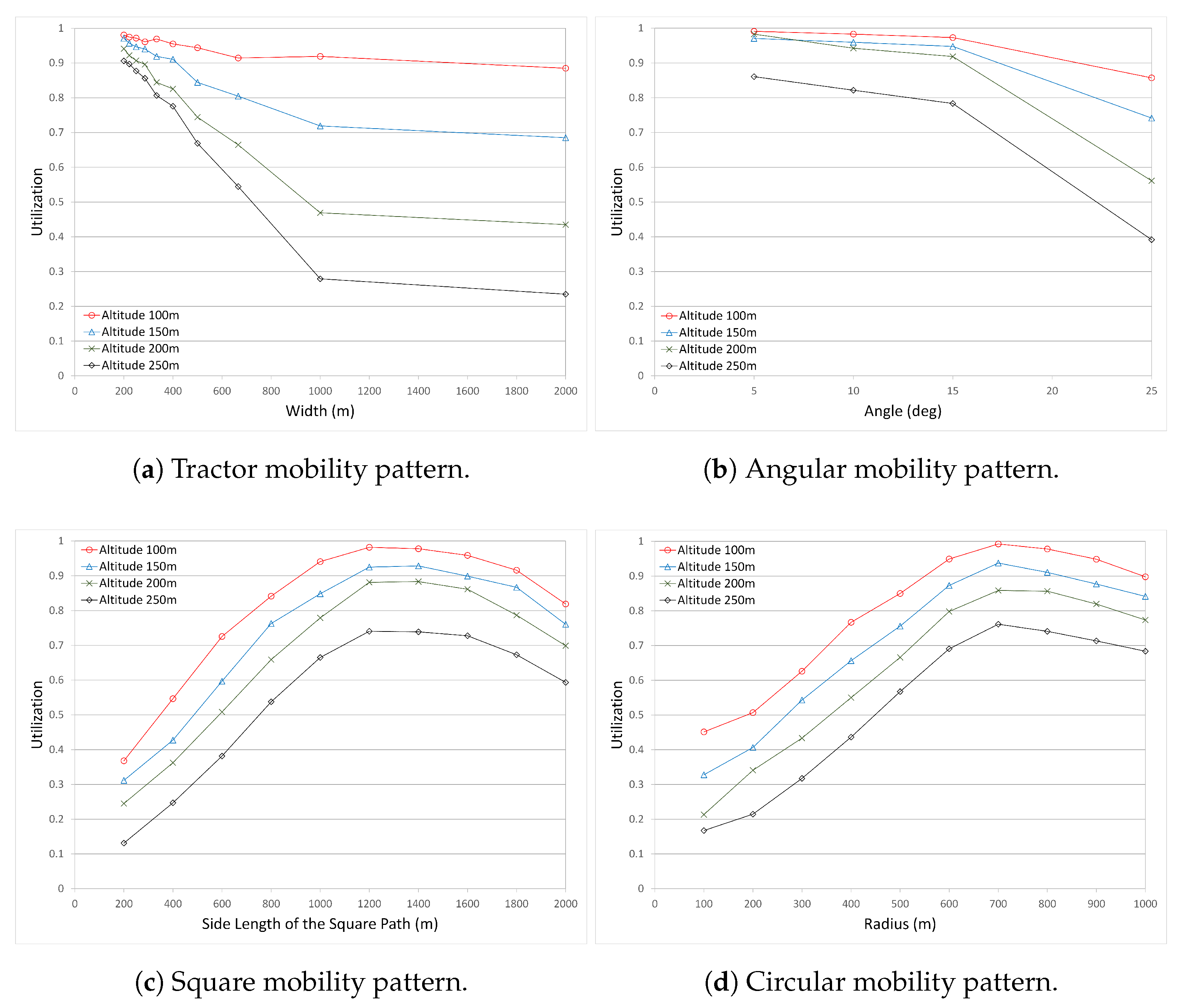
Figure 6 presents the utilization results for all mobility patterns. The graphs for “the number of covered nodes” can be referred to when in need of more detailed information on each graph.
The utilization graphs of Circular and Square mobility patterns are very similar to each other (
6). When the circle or square size is small, the utilization is also low. As the size of the circle and the square grows, the utilization increases. However, in both mobility patterns, the utilization starts to decrease after a peak value. This is because gaps begin to grow in the center of the circle/square.
In the Angular mobility pattern, the utilization is very high when the angle value is small for all altitude values. For the altitude 100 m, the utilization decreases slightly, but is very high compared to the other altitudes. In other altitudes, the utilization decreases slightly until angle value 15
, and decreases more at angle value 25
. Altitude 250 m has the worst utilization results. It is seen in
Figure 6b that the altitude and the angle value affect the utilization. Small angle value and lower altitudes increase the connectivity and accessibility to the UAV.
The Tractor mobility pattern (
Figure 6a) performs similarly to the Angular mobility pattern. For the UAV altitude 100 m, it performs better than other altitudes, and the utilization decreases slightly even as the width between tracks increases. However, other altitudes are affected strongly by the increase in the width of the tracks, and the utilization decreases sharply as the width and altitude increase.
4.3.3. Time vs. Coverage Efficiency
In the metrics presented above, it is seen that considering only the coverage of the nodes or the time elapsed to cover the nodes is not enough, and may lead to false decisions being made. While maximizing the number of nodes is an important metric, minimizing the elapsed time is another important metric. The UAV flying over the operation area may not have enough energy to complete its mission. Or, the UAV may have limited time to collect as much of the necessary data as possible. Therefore, time and coverage metrics have to be analyzed together.
We define a new metric, which is a measure of the time and the coverage. It is named as “Time–Coverage Efficiency”. The aim is to maximize the number of covered nodes while minimizing the operation time. In other words, time spent for a node has to be minimized while maximizing the number of covered nodes. The equation for this new metric is given below:
In (
6), we square the number of covered nodes in the numerator of the fraction, because it must be promoted to higher values as much as possible; we take the square root of the time spent per covered node in the denominator because the time spent per covered node has to be minimized as much as possible. In the evaluation and comparison, scenarios which perform better in terms of these metrics—more number of covered nodes and less time spent per covered node—have to be identified and be recommended for use in the operation area. Therefore, we defined the metric as given in (
6).
Figure 7 shows the Time and Coverage Efficiency in all mobility patterns (in the left column). In the Angular mobility pattern, it is seen that although more nodes are covered with the angle value 5
at all altitudes, it is not the most efficient one because of how long it takes to sweep the operation area. With angle 5
, more legs are constructed, which increases the total length of the UAV path. This leads to the coverage of more nodes, but longer duration. However, as the angle increases, the number of legs decreases, which eventually decreases the path length of the UAV. It thus takes less time to sweep the area. On the other hand, when the number of covered nodes is considered, there is a slight decrease. It means that with a tradeoff allowing a few nodes to be uncovered, the UAV saves time in collecting data. This is true for angles 10
and 15
. For angle 25
, although the UAV has the minimum flight path, there is a sharp decrease in the number of covered nodes, especially for altitude 250 m. When the results of the Angular mobility pattern are considered, angle 15
presents the optimum results for time–coverage efficiency. It is also seen that the performance at altitude 250 m is the worst among the others, and for the altitude 250 m, the angle 10
presents better results than the angle 15
.
In the Circular mobility pattern, it is clearly seen that the Circular mobility pattern with the radius 700 m is better than other radius values at all altitudes. It can also be verified by looking at two other metrics—the number of covered nodes and the time spent per node graphs.
In the Square mobility pattern (very similar to the circular mobility pattern), it is clearly seen that the square mobility pattern with the side length 1200 m is better than other side length values at all altitudes. This information can also be verified by looking at two other metrics—the number of covered nodes and the time spent per node graphs.
The performance of the Tractor mobility pattern is very different compared to the other mobility patterns. For the 100 m altitude, as the width between the parallel tracks gets larger, time–coverage efficiency increases. The reason is related to the reduced flight time of the UAV by decreasing the path while preserving the number of covered nodes. However, the situation is very different at other altitudes. As the width increases, the time–coverage efficiency value follows a stable pattern for the 150 m altitude and decreases sharply for 200 m and 250 m altitudes. Performance at 250 m altitude is very poor compared to the others.
In all mobility patterns, the UAV altitude 100 m performs better than other altitude values. The reasons are explained previously, and are illustrated in
Figure 1b and
Figure 2. However, for a specific mobility pattern and depending on the altitude, the most appropriate performance parameter that presents the highest results may differ. For example, in the Angular mobility pattern, the most appropriate angle value for the best performance is 10
for the altitude 250 m, whereas the most appropriate angle value for the best performance is 15
for the altitude 200 m. Depending on the operation altitude of the UAV and the mobility pattern, the UAV operator can choose the right parameters to get better performance results.
Although the time–coverage efficiency metric provides many valuable information, it is necessary to normalize the results to allow them to be compared with each other. Equation (
7) represents the efficiency of normalized time and the efficiency of normalized coverage of each mobility pattern.
Equation (
7) is similar to (
6), where numerator and the denominator are divided by new values. The numerator is divided by the maximum number of covered nodes among all scenarios, including all mobility patterns and altitudes to normalize this value between 0 and 1. Similarly, the denominator “time spent per covered node” is divided by the minimum time spent per covered node among all scenarios, including all mobility patterns and altitudes to normalize this value. Overall results will be scaled varying between 0 and 1 to let all results be compared in the same scale.
Figure 7 shows the Normalized Time and Coverage Efficiency in all mobility patterns (in the right column). It reveals the details and the hidden points in the comparison. For example, although the results of the Circular and Square mobility patterns are similar to each other where the curves present similar patterns, there are differences in the performance. For these two mobility patterns, the curve pattern similarity is seen in the number of covered nodes graphs. However, we are not able to see the difference and its magnitude in those graphs. With the use of Normalized Time–Coverage Efficiency presented in
Figure 7, we are able to see the differences and their magnitudes. Hence, more accurate decisions can be made by decision makers (e.g., UAV operators).
When the graphs are compared with each other, it is seen that, generally, the Circle and Square mobility patterns are superior to the others, where the Circle mobility pattern is the most superior. The Tractor mobility pattern performs better only at the altitude 100 m. At other altitudes, it does not perform well compared to the others, due to the increases in path length and operation duration in the Tractor mobility pattern.
On the other hand, the graphs in
Figure 7 are very useful to compare the performance of the mobility patterns at each altitude. For example, the question could be “which mobility patterns perform better and at what parameter values for the UAV altitude value 100 m?” The answer will be the tractor mobility with width value 2000 m. However, the UAVs may not fly at this altitude at every area or zone. For the same question, if the altitude is increased to 150 m, then the circle mobility has to be selected with the radius of 700 m. If the altitude is increased to 200 m, either the square mobility with the side length 1200 m or the circular mobility with the radius 700 m can be selected.
If only two mobility patterns are considered (e.g., Angular and Tractor mobility patterns), for some altitudes, the Angular mobility pattern performs better and for the other altitudes the Tractor mobility pattern performs better.
As can be seen, each mobility pattern presents different performance results. In making the decision to select the best and most appropriate mobility pattern for application in the operation area, there could be two main objectives: first, covering the maximum nodes; second, spending less time in the operation area with maximum utilization. By defining the Time–Coverage Efficiency metric, we address this problem by finding the most appropriate mobility pattern with the best performance results.