1. Introduction
New paradigms in sensors and actuators data transmission strategies are topics of interest due to the challenges that the increase in the amount of data presents in a completely inter-communicated world. Cloud computing, Internet of Things (IoT), sensor networks, multimedia, teleoperation, smart-phones and inter-vehicular communications are only a few examples of such a challenge. The most used transmission strategy is the periodic sampling transmission strategy, where sensor or controller data are periodically sent across networks and the parameter to be adjusted is the transmission period. The motivation for this periodic sampling nature is that it is easy to be implemented in computing environments, and there is a well known system theory around it.
On the other hand, amplitude sampling has grown in importance due its efficiency selecting the data to be processed or to be sent across the networks. Basic amplitude sampling is focused on transmitting a data packet when the value of the data deviates from a reference piece of data by a known value called delta value, deadband or threshold. The utility of this sampling strategy is proved by the implementation in real commercial sensors, like the EnOcean sensors [
1], and its use is motivated because it allows for sending much less data, maintaining a similar signal tracking-error performance.
The amplitude sampling technique is mentioned in the literature as the “
send-on-delta“ method [
2], “
deadband“ method [
3], “
event-triggering“, “
event-sampling“ [
4] or even “
Lebesque sampling“ [
5]. From now on, we refer to this strategy as the send-on-delta (SoD) method. The most common SoD method uses a constant delta value (
δ), and the reference data is the last sent one (
); this SoD strategy is called
last-sent SoD or
basic SoD and may be modeled by a send function
like:
where
is the candidate data to be sent at instant
t. In place of using the send function represented in expression (1), some authors [
6] use the function
and employ the term
trigger-function.
Apart from the basic SoD technique, there are some others, like the
relative deadband, presented in [
7], inspired by Weber’s law in human sensibility, where the deadband value is proportional to the value of the last-sent data (
); the
network-based deadband [
8,
9] where the deadband value is selected depending on the network status; the
linear-predicted-data SoD [
10] where the reference data is a linear prediction calculated using the last-sent-data and the previous sampled data. Some other SoD strategies are focused on the trigger function, for example the
IAE-based SoD, where the driver sends a sample if the sampling integral absolute error (IAE) is bigger than the deadband value [
11], or the
Energy-error based SoD, where a data is sent if the energy of the error measured in the last sampling interval is bigger than the deadband threshold [
12]. In parallel, the SoD strategies are used to improve collaborative challenges through data networks [
13,
14].
Periodic-sampling and Send-on-Delta sampling are not the only solutions to deal with the data selection to be sent across the network. In the literature, we also find the ’
adaptive sampling“ solutions. As commented in [
15], send-on-delta solutions differ from the adaptive-sampling in the way that both selects the send instant; adaptive-sampling solutions does not monitor the data to be sent and compares it with others (as done in the SoD solutions), but instead, the data send instant is determined by a timer that is excited when an event occurs. The difference between these two transmission paradigms may be found in the scientific literature under the more technical terms ”event-triggering“ (which refers to the SoD solutions) and ”self-triggering“ (referred to the adaptive-sampling). A complete compilation about event-based sampling is included in the book [
16].
The advantages of using SoD are that it may save network resources maintaining an acceptable application performance. Other resources saved by the SoD strategy are the battery consumption in wireless sensor networks or the CPU load. Besides the savings on network consumption, the SoD strategies may decrease the signal tracking-error [
17,
18], the system-error of control systems [
4] or the estimation-error if an estimator is used in networked control systems [
19]; this would be achieved if the average transmission rate remains the same as the transmission rate of a conforming periodic sampling strategy [
18]. An example of such a situation would occur in 3G/4G commercial data communications, where the network operators sell an amount of data (
D) to be sent monthly, which makes, in practical implementations, a mean available bandwidth. In this case, the conforming periodic sampling strategy would have a constant sampling rate of
bits/s, but the peak bandwidth is much bigger (until 100 Mbps in 4G networks). The SoD sampling strategy may be used to try to reduce significantly the signal tracking error, but maintaining the goal to send
D bytes in one month.
Nevertheless, it is difficult to obtain a delta value for the basic SoD strategy given a desired average transmission rate because it depends on the network performance, on the control system and on the nature of the sampled signal, which is, in most cases, unpredictable. A preliminary attempt to select dynamically a delta value for a simple control system is recently presented in [
20], and, in this paper, we formulate the bases, improve the behavior, and extend the results for general signal tracking.
The paper is organized as follows. This first section was an introduction to present the general concepts of periodic sampling and send-on-delta (SoD) sampling.
Section 2 studies the problems of selecting a delta value if a mean allowable bandwith is given for the basic SoD strategy. The algorithm to select dynamically a delta value is presented in detail in
Section 3. Simulation results and comparative analysis between the proposed solution and a conformant periodic sampling strategy are presented in
Section 4. Finally, in
Section 5, the conclusions and future work are summarized.
2. Problem Statement
Usually, SoD strategies stand to reduce the amount of data that should be transmitted through a network to reduce resources. However, in some cases, the SoD strategy could be utilized by the senders to reduce the tracking error in place of reducing the amount of sent messages. In this work, we demonstrate that the tracking error generated by a basic SoD transmission strategy is in general smaller than the one generated by a conformant periodic transmission strategy.
The problem is that it is very difficult to prevent the throughput λ of an unpredictable signal given a fixed delta value δ, and, by extension, it is very difficult to obtain a fixed delta value given a mean throughput .
From [
17], the throughput
λ of a monotonic continuous-time signal sampled periodically is given by the formula:
where
is the maximum of the absolute value of the signal time derivative and
is the upper bound of the signal tracking error.
For a basic SoD (with delta value
δ) applied to a monotonic continuous signal, the upper bound of the signal tracking error matches the delta value. From [
2], the upper and lower bounds of the basic SoD strategy are given by the Formula (3):
where
ν is the local extrema density, that is, the average number of signal peaks (maxima and minima) in a time unit, and
is the average slope of the signal
after an operation time of
, given by
If the signal is monotonously increasing or decreasing, the limits in Equation (3) match each other, and the relationship between δ and λ is fixed.
From Equation (3), given an average throughput
, the maximum and minimum values for
δ are given by
Assumption 1. From the Expression (4)
, if during the test duration, the signal is monotonically increasing or decreasing, or has only a few maxima and minima per second compared to the average throughput (), equality (5)
holds Proposition 1. Based on Assumption 1, the basic Send-on-Delta transmission strategy generates a smaller tracking error than a periodic transmission strategy with the same mean throughput.
Proof. For a periodic transmission strategy, the average throughput matches the instantaneous throughput (
); therefore, from Equations (2) and (5):
From the properties of the expected value, it is always true that
. Therefore,
☐
This result can be extended to no-monotonous signals by dividing the signal into monotonous zones and maintaining the average throughput constant. If we define for the monotonous zone
i:
as the upper bound in error tracking for the periodic sampling strategy, and
as the upper bound in error tracking for the SoD sampling strategy,
then
.
Intuitively, this means that the basic SoD transmission strategy has in general a smaller tracking error than the periodic transmission strategy for the same mean throughput.
2.1. Obtaining the Transmission-Rate Given a Delta Value.
Equation (5) presents an indeterminacy if due to the continuous nature of the signal . In practical implementations, discretized signals are used.
Assumption 2. Let us assume that the original raw signal is periodically discretized with sampling rate for computational use at the application layer. Samples are represented by .
After that, the sample is delivered to the SoD driver that decides if it should be sent or not according to the send Function (1).
If sent, a packet contains one sample. Figure 1 may help to visualize this assumption. At reception, the SoD driver uses the Zero Order Hold (ZOH) strategy, where the last received data is hold and delivered to the application layer until a new data arrives. Assumption 2 implies some consequences and clarifications:
In contrast to the original sampling rate , we use the term transmission-rate or throughput λ (in packets per second) to define the amount of messages in a time unit that will be sent after the SoD strategy is applied by the SoD driver. Therefore, if there is not a SoD strategy implemented, the transmission and the sampling rates are equivalent ().
Assumption 2 allows for defining the normalized throughput as the number of messages in a time unit divided by the original periodic sampling rate of the signal (). The normalized mean throughput is the mean throughput during the operation time, divided by ().
During the operation time , an amount of N samples are received by the SoD driver from the application layer. Therefore, .
For a discretized signal
, the value of
after
N samples is now
Assumption 2 solves the indeterminacy of Equation (5) when
by imposing operational limits. If we define
and
as
and define
then the relationship between
λ and
δ may be synthesized in Equation (9), where
is the mean normalized throughput after sample
N:
2.2. Obtaining a Delta Value Given a Mean Available Transmission-Rate
From Equation (9), given a normalized available average transmission-rate (
) for an operation time
,
can be expressed like:
3. Practical Implementation
The sampling rate at the application layer is known and the normalized available mean transmission rate is given as the desired final result. Conversely, and, consequently, changes in an unpredictable way and so happens with that may not follow at all. Therefore, should be calculated dynamically to achieve it. Relationship (10) is useful if the signal changes smoothly due to the average value of , but the real nature of is unknown. However, some practical issues should be taken into account.
3.1. Practical δ Limits
It is unfeasible to know the values of
and
based on Equation (7). Therefore, some practical limits should be established. Taking into account that
is
, and, therefore,
, the minimum value of
δ is established as:
The maximum limit of
δ can be established by a
value based on a maximum desired tracking error or on limits given by transparency or stability issues if the
signal has a teleoperation or a control system nature. In these cases, the maximum value of
δ is given by:
3.2. Practical Implementation
The real average throughput after N samples () is given by , where is the number of messages sent after an operation time of time units. On the other side, the desired average throughput () could be given by , where is the allowed number of messages to be sent in . That means that the sender has a quantity of messages to send () in an operation time (); However, since the operating time is not known in advance, the algorithm computations are performed in fixed time windows ().
Assumption 3. The whole operation time is an integer of : Assumption 3 may be fulfilled if is small enough compared to and eliminates unnecessary residual calculations.
Dividing calculations into
K time windows, the average throughputs
and
may be replaced by the amount of messages in
time units, that is:
where
is the amount of sent messages at the end of the
i-th time-window and
the amount of allowed messages to be sent in
. Since
and
are constants, so is
. Therefore,
is replaced by:
Definition 1. The remaining number of messages during the i-th time-window is the difference between: the real number of available messages to be sent at the start of the i-th time-window , and the number of sent messages during the i-th time-window : The real available number of messages to be sent will be defined below.
Definition 2. The container number of messages at the end of the i-th time-window is the sum of: at the end of the i-th time-window, and the remaining number of messages of previous time-windows: Definition 3. The real available number of messages to be sent at the start of the i-th time-window is the sum of: and : Previous definitions have some remarks:
at the start and at the end of each time-window, that is, . Mathematically, , where N is the application sample number and T is the application sampling period (see Assumption 2).
for the first time-window (), and, therefore, .
may have a negative value if . Therefore, may also have a negative value. If there is credit, that is, the sender can send more than the available number of messages and, if , there is debt, that is, the sender should send if possible less than messages.
From Equations (14) and (16),
Remark 1. If, at the end of the operation time, tends to 0, that is,thenwhere .
Taking into account Remark 1 and the central term of Equation (10), during the
i-th time window, the delta value is calculated in real-time as:
where
N matches
.
In practical implementations, it could be recommended that the container messages would not be available to be spent at the start of the time-window, because, in these cases, the calculations may oscillate too much from one window to the other.
To solve this practical issue, we propose a procedure to calculate
presented below, represented as:
where
is a function of the container messages updated every time a new message is sent.
The procedure to calculate is presented in Procedure 1.
Basically, for every time-window at the instant when a new message is sent, the procedure:
does not decrease if there is still a positive value in the container (credit, that is ) and this decreases the container, or
decreases twice if there is a negative value in the container (debt, that is ) and increases the container, or
decreases once if there is 0 in the container ().
The result of the procedure is replaced in Equation (19). Although
may become 0 or a negative value, it does not affect the
results due to the limits in Equation (10).
| Procedure 1 Calculate |
|
|
|
|
| MessSent: |
| if Message sent then |
| |
| | | | | | | | | | | | // remaining messages decreases |
| if then | | | | | | | | | | | // if there are credit |
| | | | | | | | | | | | // remaining messages increases |
| | | | | | | | | | | | // credit decreases |
| goto NewWin. |
| else if then | | | | | | | | | | | // if there are debt |
| | | | | | | | | | | | // remaining messages decreases |
| | | | | | | | | | | | // debt decreases |
|
| NewWin: |
| if then | | | | | | | | | | | // A new time-window starts |
| |
| |
| |
| |
|
|
| goto MessSent. |
3.3. Other Practical Issues
Equation (8) shows that, at the start of the algorithm, the delta value may change too fast following
when
N is small. If, at the start of the algorithm, the signal is in a stationary state for
samples, the
value is small. Therefore, Equation (8) may be rewritten as:
This solution smooths the effect that could happen if, at the start of the algorithm, the signal suddenly changes very fast and grows accordingly.
Another issue is that, from Equation (19), if the
variable grows too much, or if the
variable becomes too small (that is, if the predicted amount of data allowable to be sent is spent before the time-window is finished), it is important to apply upper bounds for the delta value. In this case, if the delta value exceeds the
limit defined in Equation (12), it is reset to the average value of
δ in the
N-th algorithm implementation given by:
In the same way, at the end of the time-window (), from Equation (19), the value of may become too small if there are no messages sent (or too few). In this case, if the delta value is below the limit defined in Equation (11), it is also reset to .
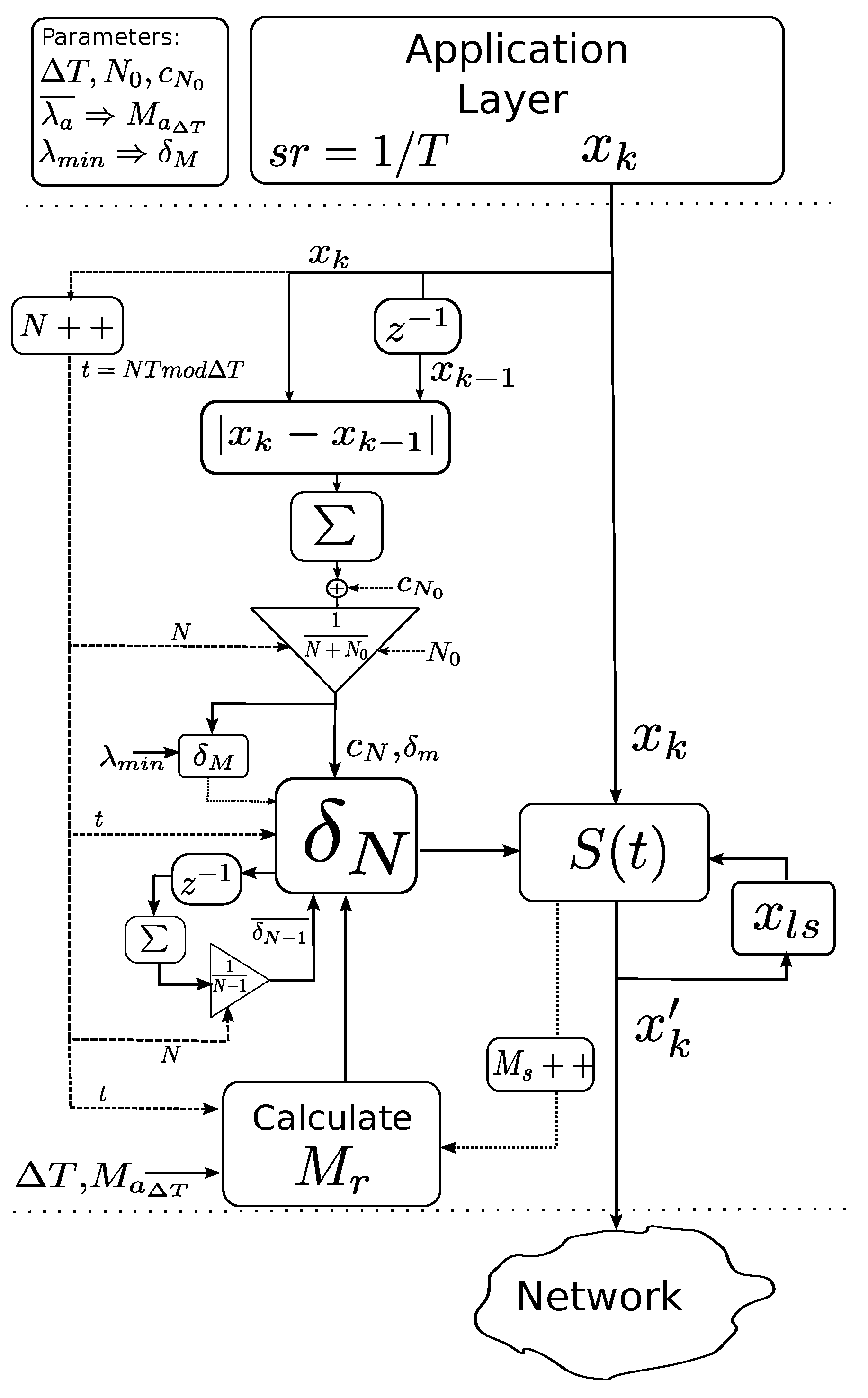
3.4. Summarizing the Algorithm
Expression (23) summarizes the proposed algorithm, where
is given finally by Equation (21):
where
,
is calculated in Equation (21),
is calculated in Equation (22) and
is calculated applying the Procedure 1.
A schematic about the whole algorithm is illustrated in
Figure 2.
4. Simulation
Simulations are performed with two main objectives: on the one side, the results of the simulations have to show that the algorithm gets the desired mean available transmission rate for tested signals, and, on the other side, the proposed algorithm should feature a smaller signal tracking error at reception than a conformant periodic sampling strategy.
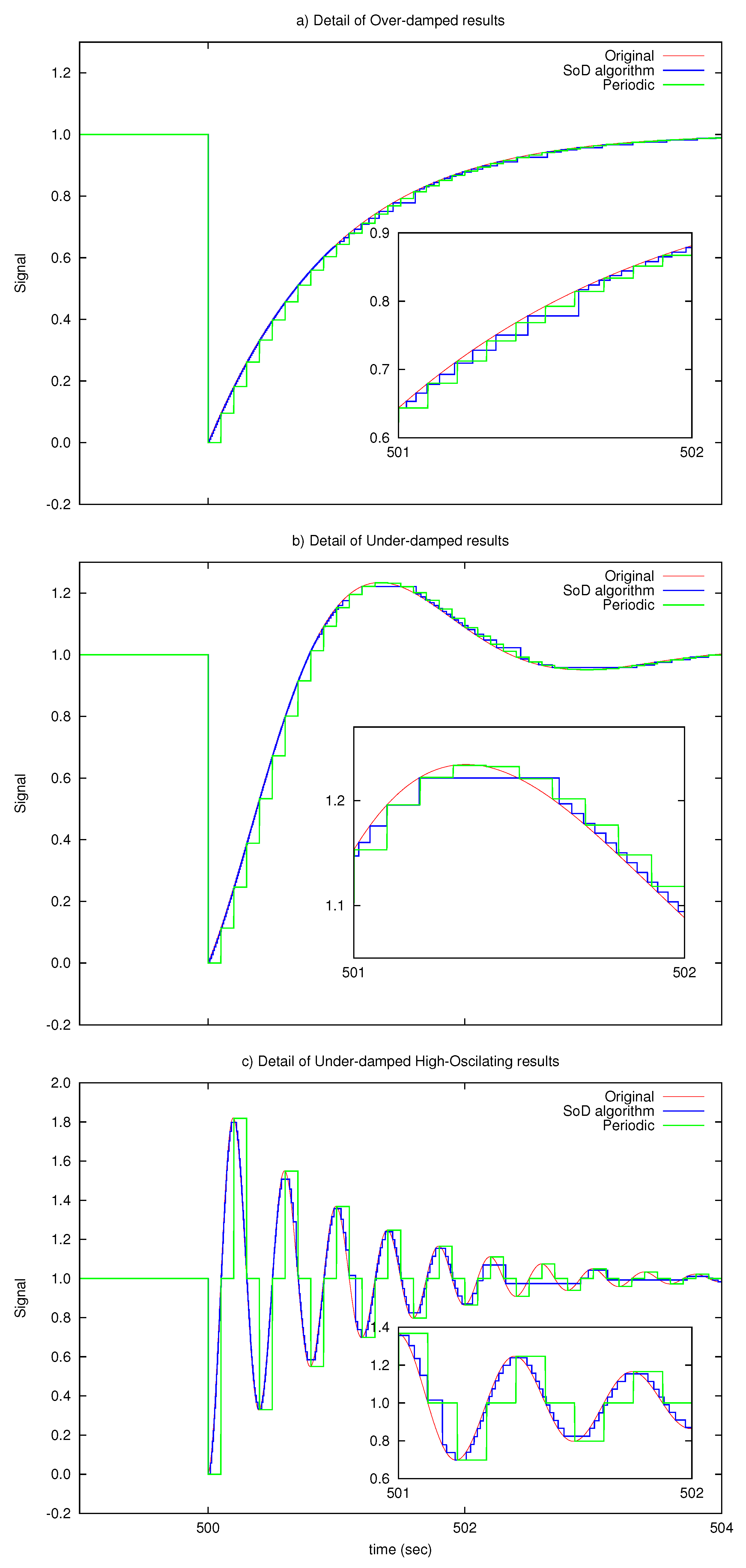
Simulations are applied to three test signals. The signals are selected according to the unit step responses for a second-order control system following Equation (24) with
,
and different
ρ and
μ parameters. Parameter
ρ delimits the asymptotic contention of the overshoot and undershoot, and
μ delimits the number of oscillations before the settling time. For simplicity, we set
ρ to 1 (
) for the three signals:
The first signal is an over-damped step-response, the second one is an under-damped step-response and the last one is also an under-damped step response but with a high-oscillating behaviour. The nature of the signals may have an important effect on the results, reflected not only by the variable but in the number of sent messages () in the time-window. For example, for a signal that changes rapidly during a short period but remains constant during a long period, the proposed SoD sampling should perform significantly better than the periodic one; on the contrary, for a signal that changes during the whole operation time, the proposed SoD sampling should perform worse than before, but, in any case, based on Proposition 1, it has to perform better than the periodic one if the delta value δ is well selected to match the desired throughput.
To observe the algorithm behavior in a long-time operation, the signals are periodically repeated, using a repetition period of s for the main tests. At the end of this section, some results with different repetition periods are presented to observe the behaviour for different kinds of signals.
Simulations are performed using the network simulator NS2. Both extremes are connected through a packet switched network with a bandwith of 10 Mbps and 1 ms delay between hosts. There is no residual traffic in the network. We consider that the available transmission rate for each sender is of 10 kbps and that the senders may take advantage of the whole available transmission rate over 1000 s. The raw original signal is sampled at 1000 pkt/s. We consider that the packet contains residual information (control or other data) in addition to the sensed data. Therefore, the packet size is 125 bytes and the available transmission rate is 10 pkt/s. The simulation parameters are presented in
Table 1.
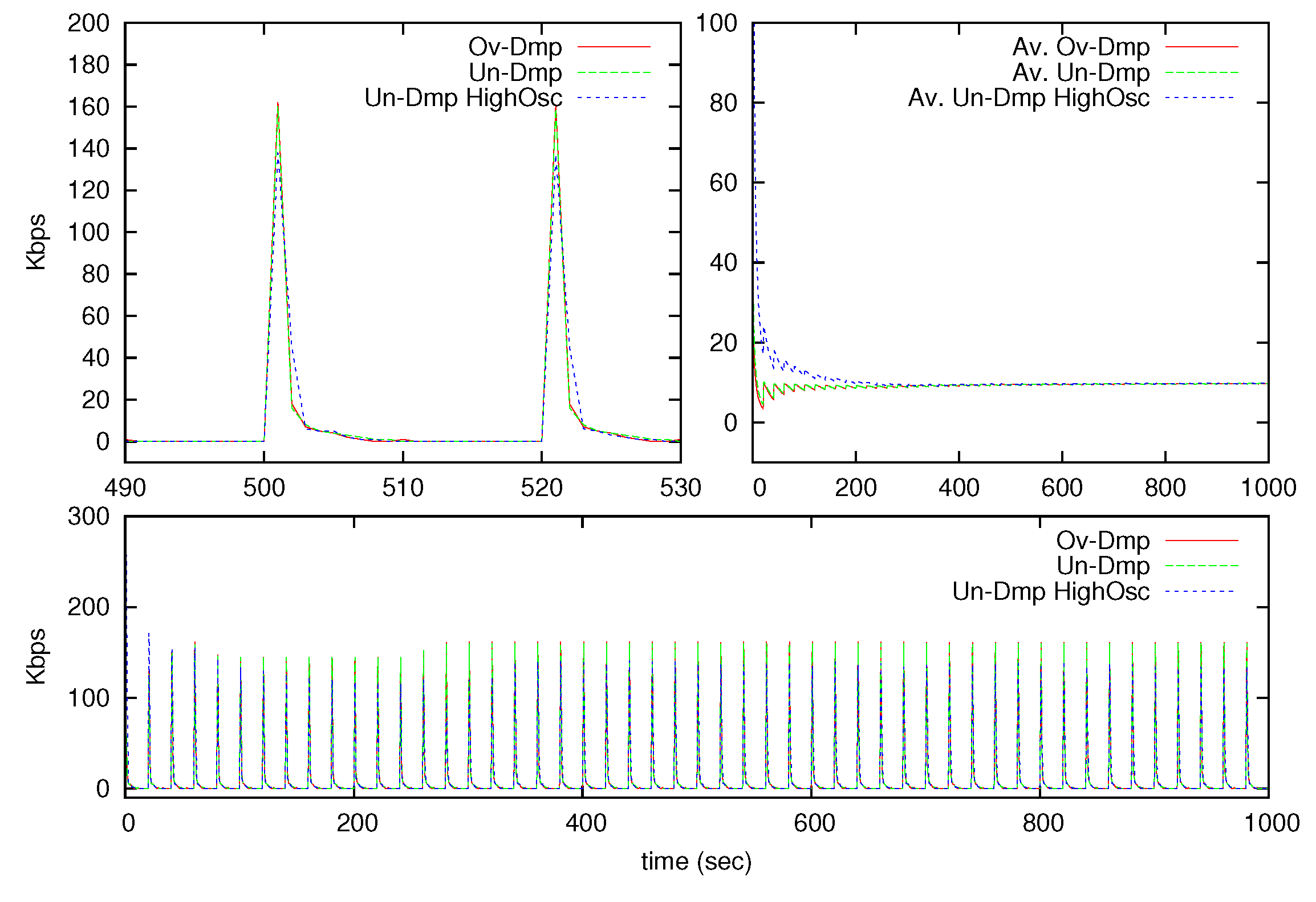
Figure 3 illustrates a detail of the sent signals comparing the periodic transmission with the proposed SoD transmission strategy for
kbps. The graph results show that the proposed SoD algorithm tracks in a more accurate way the original signal for the three proposed test signals.
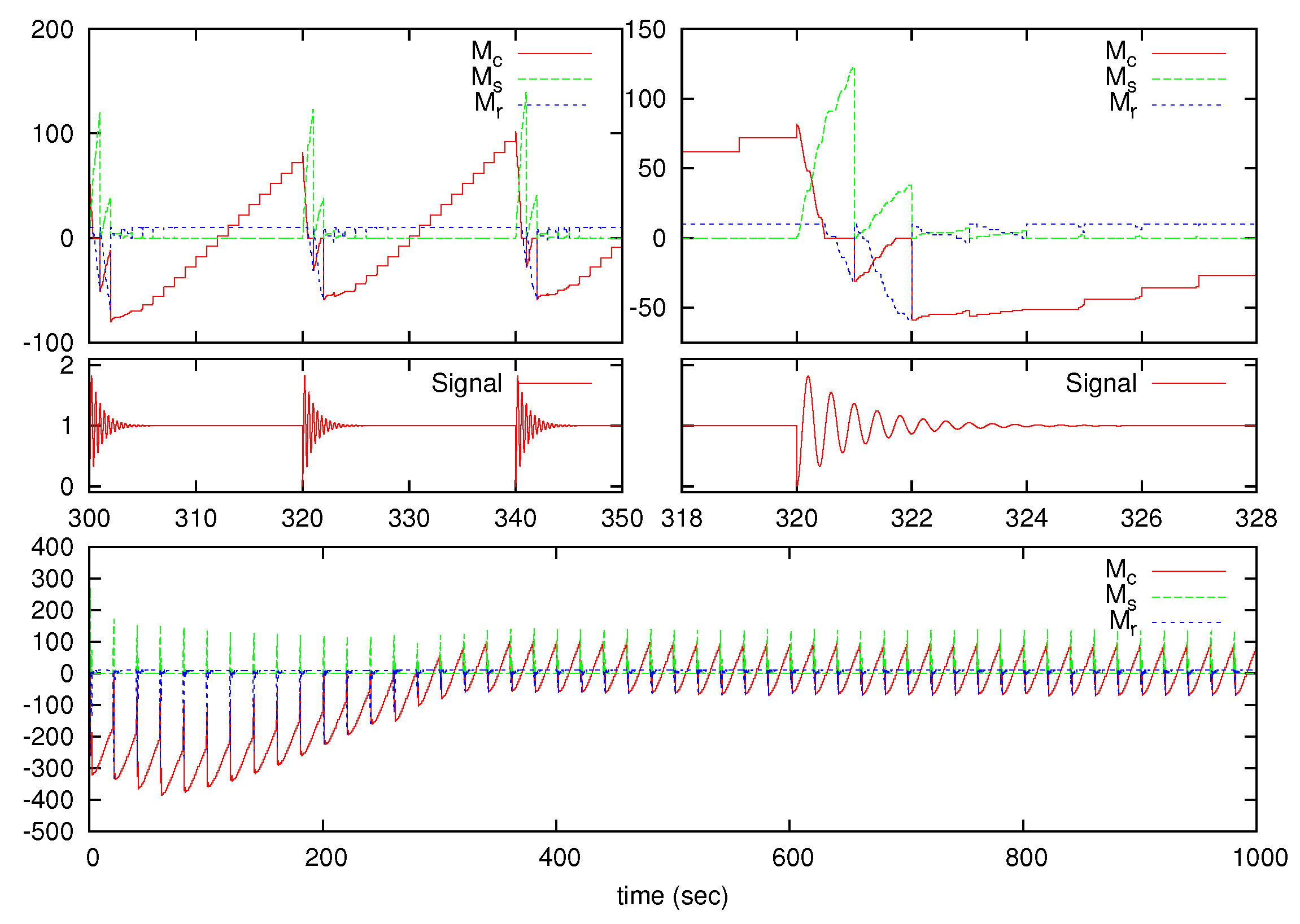
The algorithm behavior is shown in
Figure 4 and
Figure 5 using the under-damped High-Oscillating test signal, which was the worst case.
Figure 4 shows the results from Procedure 1 to calculate
, where variables
and
are also drawn. As seen,
converges to 0 for long-time operation.
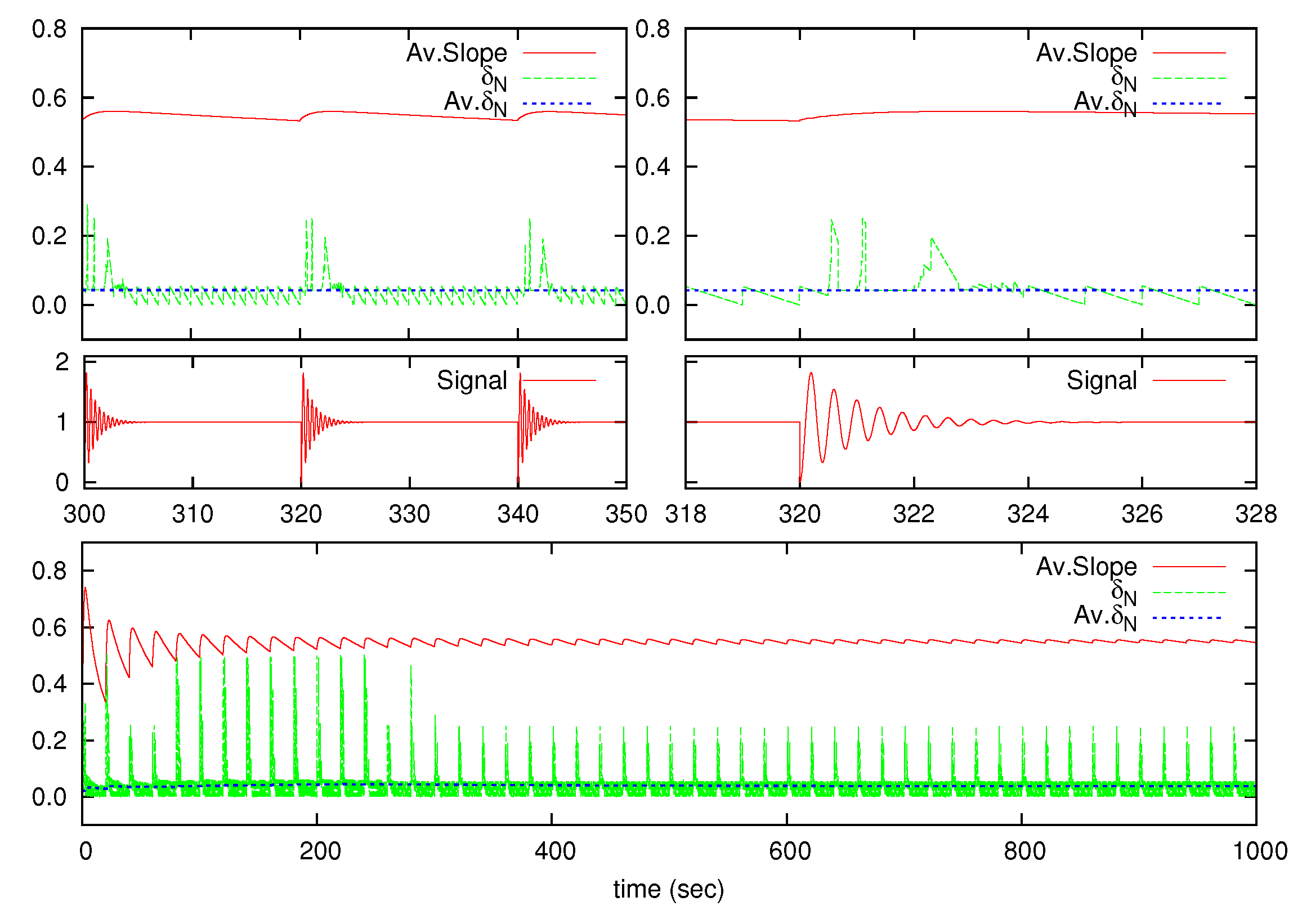
Figure 5 shows the
,
and
variables. Similar results are achieved for the over-damped and under-damped signals.
The throughput and the error are illustrated in
Figure 6 and
Figure 7. The bottom of
Figure 6 shows the throughput behavior during the whole testing time; the upper left corner shows a detail at the middle of the testing time and finally the upper right corner shows the average value of the throughput during the entire testing duration. As expected, the throughput is concentrated at the moments where the signal changes faster, but the average throughput value converges to the desired average throughput in long-time operations as seen in the upper right corner of the figure.
The tracking error is calculated comparing the original signal with the transmitted signal for the two transmission strategies: the proposed SoD strategy and the conformant periodic transmission strategy. That is, for the SoD strategy, the error is given by Expression (25), and, for the periodic sampling strategy, the error is given by Expression (26):
Note that represents the original signal, and stands for the transmitted signal after applying the SoD driver.
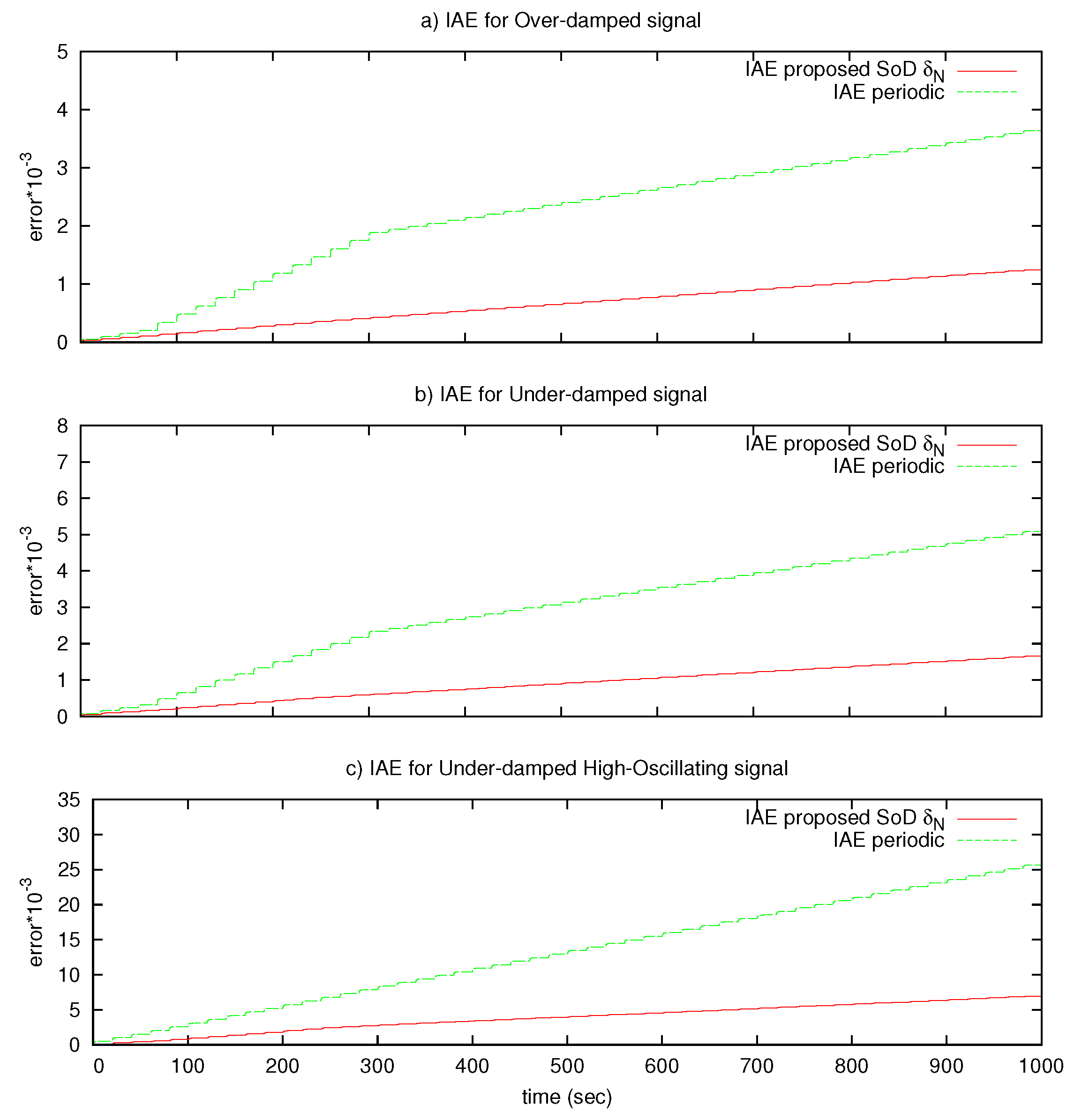
In addition, the Integral Absolute Error (
) is measured and presented in
Figure 7. This figure shows that the error measured using the SoD algorithm is much smaller than the conformant periodic transmission strategy in long-time simulation intervals for the three tested signals.
Despite the graphs showing the effectiveness of the proposed algorithm, some numerical results are given in
Table 2.
Numerical results are calculated for the three signals with a repetition period
of 20 s. These results reveal that the proposed algorithm performs well in long-time operation, and that the tracking error is much smaller than the conformant periodic transmission strategy. However, as mentioned at the start of this section, the nature of the test signals may affect the results, particularly the error results, mainly if the signal spends a lot of time without changes. Therefore,
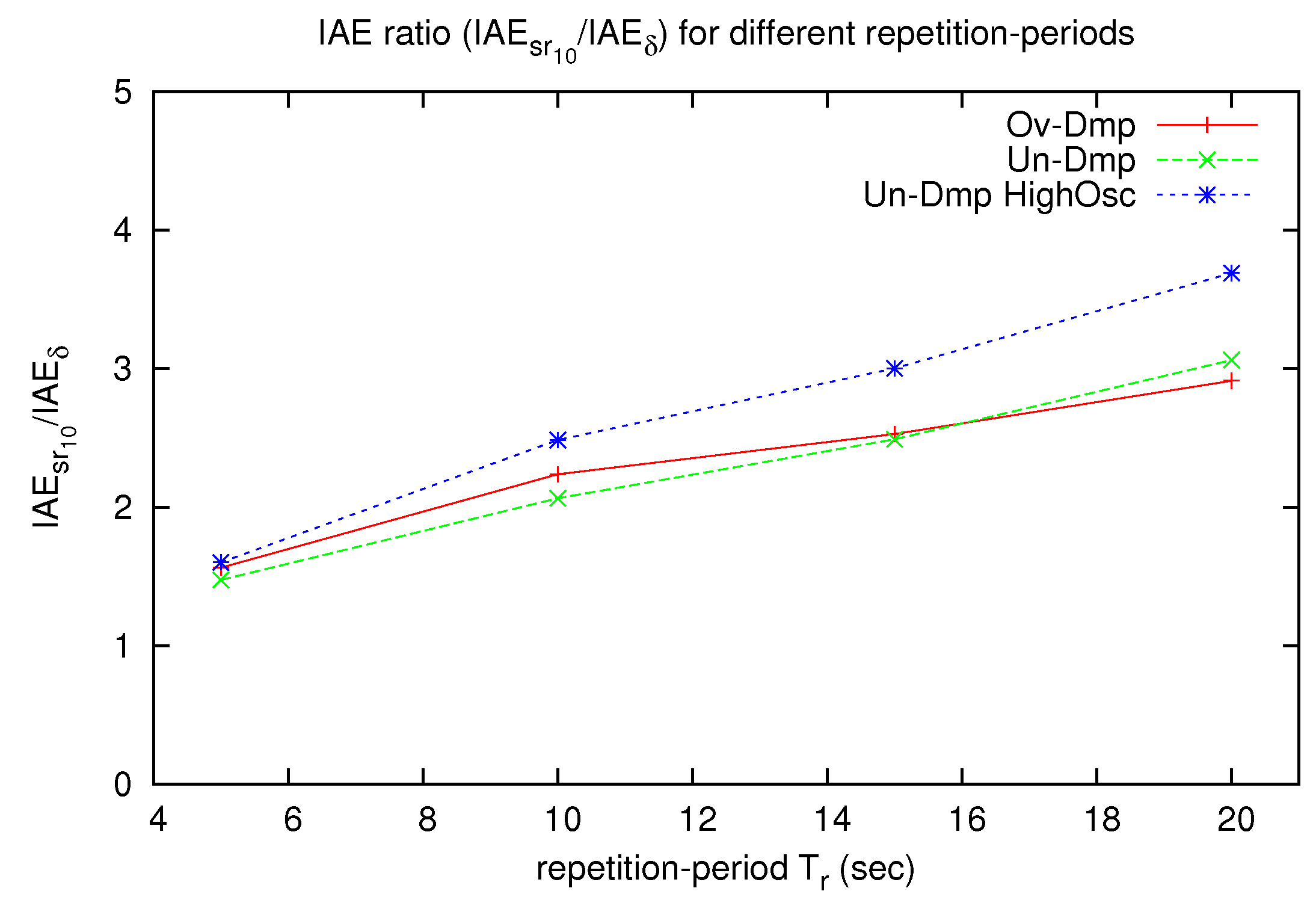
Figure 8 presents an error comparison for the three signals with
s. The vertical axis represents the ratio between the measured IAE of the conformant periodic sampling and the proposed SoD sampling (
).
In all of the cases, the proposed SoD sampling strategy performs better than the conformant periodic sampling. Besides that for shorter repetition periods, the measured IAE for both strategies are closer, the IAE for the periodic one is at least 1.5 times bigger than the proposed SoD, as expected based on Proposition 1.
In spite of these results, the real throughput is difficult to adjust to match exactly the desired throughput, especially at the start of the algorithm. Nevertheless, the results are satisfactory in long-time operation for the three signals, matching more than 90% of the desired throughput 200 s after the start and matching more than 96% of the desired throughput at the end of the test times. These results are very similar for the other repetition periods.
5. Conclusions
This paper presents an algorithm to reduce the signal tracking error taking advantage of the basic Send-on-Delta (SoD) sampling strategy. Given a mean available bandwith, the paper demonstrates that, for continuous signals, the SoD sampling strategy performs better than a conformant (same available bandwith) periodic transmission. The algorithm is tested for three signals based on usual step responses of second order control systems, and is then compared with the periodic transmission. The tests compare two indicators: the tracking-error and the average-throughput. Results show that the tracking-error is definitely smaller with the proposed method and that the average-throughput is achieved in long-time operation. The fact that the average throughput is achieved in long-time operation is due to the proper nature of the SoD technique, where samples are concentrated when the signal changes faster; therefore, the throughput can not be uniform and has to be analyzed as an average throughput in time, with more accurate results the longer the operation-time.
The results invite us to improve the algorithm behavior basically by minimizing the convergence time of the mean throughput to the desired one. This could be achieved by changing some initial parameters, parameters that are actually very few, to simplify the algorithm. Other SoD techniques, such as the linear predicted SoD technique that could be very interesting for continuous signal tracking as seen in [
18], are being studied in order to also develop an algorithm to reduce the tracking-error given a mean available transmission rate.
Finally, one of the main interests in developing the algorithm is to dynamically determine the delta value to reduce the error in place of reducing the throughput if the available transmission rate is dynamically shared by different senders—for example, for distributed sensor networks, multi-agent systems or distributed systems in general.