Novel Hierarchical Fall Detection Algorithm Using a Multiphase Fall Model
Abstract
:1. Introduction
2. Related Work
2.1. Fall Detection Algorithm
2.2.1. Threshold-Based Fall Detection Algorithms
2.2.2. Machine Learning–Based Fall Detection Algorithms
3. Materials and Methods
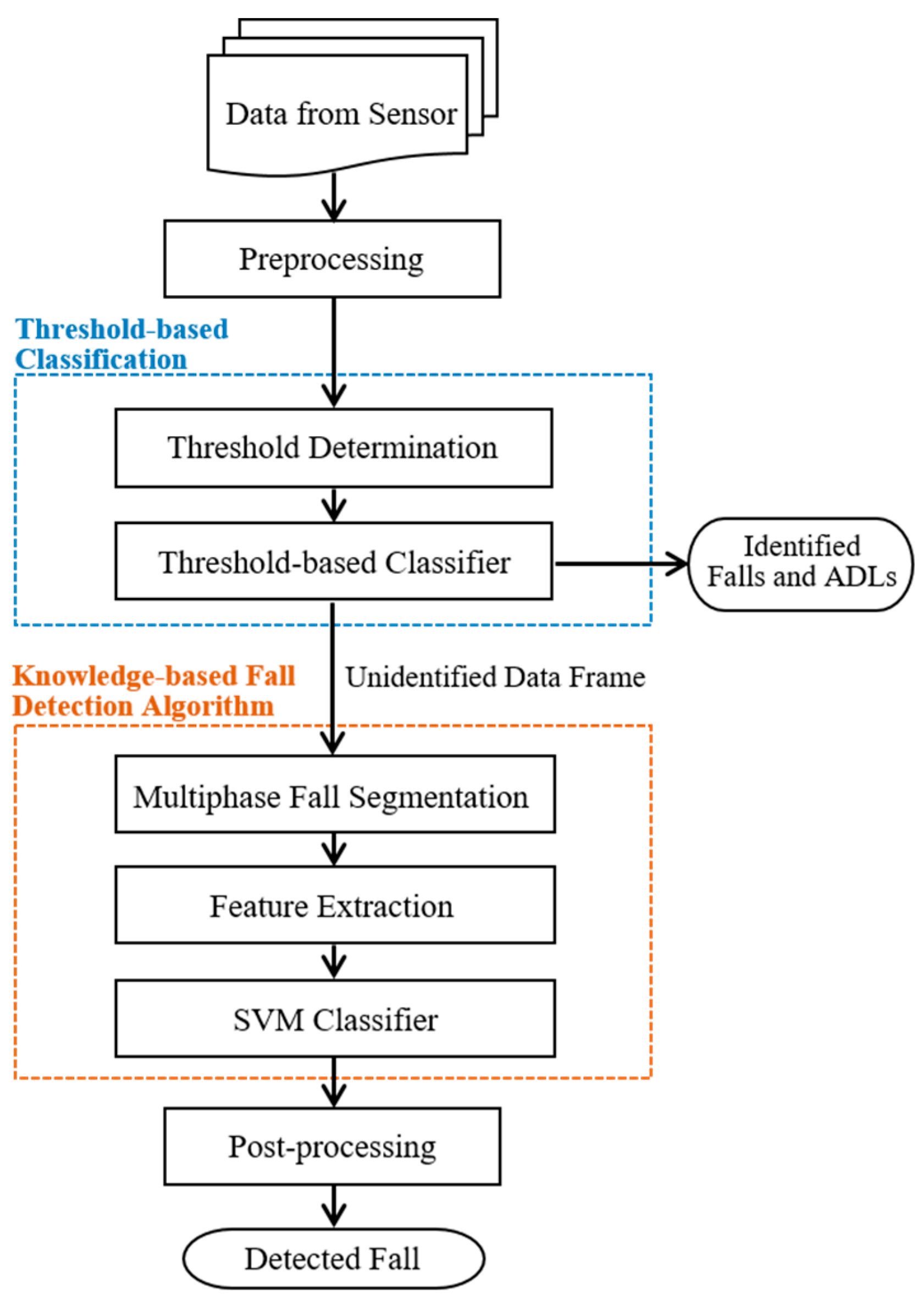
3.1. Hierarchical Fall Detection Algorithm
3.2. Performance Evaluation Criteria
4. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Round | Stand | Stand up | Sit down | Walk | Stoop | Jump | Walk Backward | Stand from Sit | Stand from Squat | Sit (Normal) | Sit (Fast) | Lie (Normal) | Lie (Fast) | Go up Stairs | Go down Stairs | Walk (Normal) | Walk (Fast) | Jump (Ground) | Jump (Bed) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 15 | 15 | 16 | 16 | 15 | 15 | 3 | 6 | 6 | 6 | 6 | 6 | 6 | 7 | 6 | 6 | 6 | 6 | 6 |
| 16 | 15 | 15 | 15 | 15 | 15 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | 8 | 6 | 6 | 6 | 6 | 6 | |
| 15 | 15 | 15 | 15 | 16 | 16 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | 7 | 6 | 6 | 6 | 5 | 6 | |
| 15 | 16 | 15 | 15 | 15 | 15 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | 7 | 6 | 6 | 6 | 6 | 6 | |
| 15 | 15 | 15 | 15 | 15 | 15 | 4 | 6 | 6 | 6 | 6 | 5 | 6 | 8 | 5 | 6 | 6 | 6 | 6 | |
| 2 | 15 | 15 | 15 | 16 | 15 | 15 | 4 | 6 | 6 | 6 | 6 | 5 | 6 | 7 | 5 | 6 | 6 | 6 | 6 |
| 16 | 15 | 15 | 15 | 15 | 16 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | 7 | 6 | 6 | 6 | 5 | 6 | |
| 15 | 16 | 16 | 15 | 15 | 15 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | 8 | 6 | 6 | 6 | 6 | 6 | |
| 15 | 15 | 15 | 15 | 16 | 15 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | 8 | 6 | 6 | 6 | 6 | 6 | |
| 15 | 15 | 15 | 15 | 15 | 15 | 3 | 6 | 6 | 6 | 6 | 6 | 6 | 7 | 6 | 6 | 6 | 6 | 6 | |
| 3 | 15 | 15 | 15 | 15 | 15 | 15 | 3 | 6 | 6 | 6 | 6 | 6 | 6 | 7 | 6 | 6 | 6 | 5 | 6 |
| 15 | 15 | 15 | 16 | 15 | 15 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | 7 | 6 | 6 | 6 | 6 | 6 | |
| 15 | 15 | 15 | 15 | 15 | 16 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | 7 | 6 | 6 | 6 | 6 | 6 | |
| 15 | 16 | 15 | 15 | 16 | 15 | 4 | 6 | 6 | 6 | 6 | 5 | 6 | 8 | 6 | 6 | 6 | 6 | 6 | |
| 16 | 15 | 16 | 15 | 15 | 15 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | 8 | 5 | 6 | 6 | 6 | 6 | |
| 4 | 16 | 15 | 16 | 15 | 15 | 15 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | 8 | 6 | 6 | 6 | 6 | 6 |
| 15 | 16 | 15 | 16 | 15 | 15 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | 7 | 6 | 6 | 6 | 6 | 6 | |
| 15 | 15 | 15 | 15 | 15 | 15 | 3 | 6 | 6 | 6 | 6 | 5 | 6 | 8 | 5 | 6 | 6 | 6 | 6 | |
| 15 | 15 | 15 | 15 | 15 | 15 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | 7 | 6 | 6 | 6 | 6 | 6 | |
| 15 | 15 | 15 | 15 | 16 | 16 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | 7 | 6 | 6 | 6 | 5 | 6 | |
| 5 | 16 | 15 | 15 | 16 | 15 | 15 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | 7 | 6 | 6 | 6 | 6 | 6 |
| 15 | 15 | 16 | 15 | 16 | 15 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | 7 | 5 | 6 | 6 | 6 | 6 | |
| 15 | 15 | 15 | 15 | 15 | 15 | 4 | 6 | 6 | 6 | 6 | 5 | 6 | 7 | 6 | 6 | 6 | 5 | 6 | |
| 15 | 16 | 15 | 15 | 15 | 16 | 4 | 6 | 6 | 6 | 6 | 6 | 6 | 8 | 6 | 6 | 6 | 6 | 6 | |
| 15 | 15 | 15 | 15 | 15 | 15 | 3 | 6 | 6 | 6 | 6 | 6 | 6 | 8 | 6 | 6 | 6 | 6 | 6 | |
| total | 380 | 380 | 380 | 380 | 380 | 380 | 95 | 150 | 150 | 150 | 150 | 145 | 150 | 185 | 145 | 150 | 150 | 145 | 150 |
| Round | Stand | Stand up | Sit down | Walk | Stoop | Jump | Walk Backward | Stand from Sit | Stand from Squat | Sit (Normal) | Sit (Fast) | Lie (Normal) | Lie (Fast) | Go up Stairs | Go down Stairs | Walk (Normal) | Walk (Fast) | Jump (Ground) | Jump (Bed) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | |||||||||||||||||
| 1 | 1 | ||||||||||||||||||
| 1 | |||||||||||||||||||
| 2 | 2 | ||||||||||||||||||
| 1 | |||||||||||||||||||
| 1 | |||||||||||||||||||
| 1 | 1 | ||||||||||||||||||
| 3 | 1 | ||||||||||||||||||
| 1 | |||||||||||||||||||
| 1 | |||||||||||||||||||
| 1 | |||||||||||||||||||
| 1 | 1 | ||||||||||||||||||
| 4 | 1 | ||||||||||||||||||
| 1 | |||||||||||||||||||
| 1 | |||||||||||||||||||
| 1 | |||||||||||||||||||
| 2 | |||||||||||||||||||
| 5 | 1 | 1 | |||||||||||||||||
| 1 | |||||||||||||||||||
| 1 | |||||||||||||||||||
| 1 | |||||||||||||||||||
| total | 0 | 0 | 0 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 8 | 15 | 0 | 0 | 0 | 0 | 0 | 0 |
| Round | Stand | Stand up | Sit down | Walk | Stoop | Jump | Walk Backward | Stand from Sit | Stand from Squat | Sit (Normal) | Sit (Fast) | Lie (Normal) | Lie (Fast) | Go up Stairs | Go down Stairs | Walk (Normal) | Walk (Fast) | Jump (Ground) | Jump (Bed) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 1 | ||||||||||||||||
| 1 | |||||||||||||||||||
| 1 | |||||||||||||||||||
| 1 | |||||||||||||||||||
| 2 | 1 | ||||||||||||||||||
| 1 | 1 | ||||||||||||||||||
| 1 | 2 | 3 | |||||||||||||||||
| 3 | 1 | ||||||||||||||||||
| 1 | |||||||||||||||||||
| 2 | |||||||||||||||||||
| 2 | 2 | ||||||||||||||||||
| 4 | 1 | 2 | |||||||||||||||||
| 1 | |||||||||||||||||||
| 1 | 1 | 1 | 1 | 1 | |||||||||||||||
| 2 | |||||||||||||||||||
| 1 | |||||||||||||||||||
| 5 | 1 | 1 | 1 | ||||||||||||||||
| 1 | 1 | ||||||||||||||||||
| 1 | |||||||||||||||||||
| 3 | |||||||||||||||||||
| 1 | 1 | ||||||||||||||||||
| total | 0 | 0 | 3 | 0 | 8 | 2 | 5 | 0 | 0 | 0 | 4 | 8 | 11 | 0 | 0 | 1 | 4 | 1 |
References
- Bloom, D.E.; Boersch-Supan, A.; McGee, P.; Seike, A. Population aging: Facts, challenges, and responses. Benefits Compens. Int. 2011, 41, 22. [Google Scholar]
- Stevens, J.A.; Corso, P.S.; Finkelstein, E.A.; Miller, T.R. The costs of fatal and non-fatal falls among older adults. Inj. Prev. 2006, 12, 290–295. [Google Scholar] [CrossRef] [PubMed]
- Kannus, P.; Parkkari, J.; Koskinen, S.; Niemi, S.; Palvanen, M.; Jarvinen, M.; Vuori, I. Fall-induced injuries and deaths among older adults. JAMA 1999, 281, 1895–1899. [Google Scholar] [CrossRef] [PubMed]
- Gurley, R.J.; Lum, N.; Sande, M.; Lo, B.; Katz, M.H. Persons found in their homes helpless or dead. N. Engl. J. Med. 1996, 334, 1710–1716. [Google Scholar] [CrossRef] [PubMed]
- Wild, D.; Nayak, U.; Isaacs, B. How dangerous are falls in old people at home? Br. Med. J. (Clin. Res. Ed.) 1981, 282, 266–268. [Google Scholar] [CrossRef]
- Hartholt, K.A.; van Beeck, E.F.; Polinder, S.; van der Velde, N.; van Lieshout, E.M.; Panneman, M.J.; van der Cammen, T.J.; Patka, P. Societal consequences of falls in the older population: Injuries, healthcare costs, and long-term reduced quality of life. J. Trauma Acute Care Surg. 2011, 71, 748–753. [Google Scholar] [CrossRef] [PubMed]
- Shumway-Cook, A.; Ciol, M.A.; Gruber, W.; Robinson, C. Incidence of and risk factors for falls following hip fracture in community-dwelling older adults. Phys. Ther. 2005, 85, 648–655. [Google Scholar] [PubMed]
- Delahoz, Y.S.; Labrador, M.A. Survey on fall detection and fall prevention using wearable and external sensors. Sensors 2014, 14, 19806–19842. [Google Scholar] [CrossRef] [PubMed]
- Tinetti, M.E. Preventing falls in elderly persons. N. Engl. J. Med. 2003, 348, 42–49. [Google Scholar] [CrossRef] [PubMed]
- Prevention, O.F.; Panel, O.S. Guideline for the prevention of falls in older persons. J. Am. Geriatr. Soc. 2001, 49, 664–672. [Google Scholar]
- Zecevic, A.A.; Salmoni, A.W.; Speechley, M.; Vandervoort, A.A. Defining a fall and reasons for falling: Comparisons among the views of seniors, health care providers, and the research literature. Gerontol. 2006, 46, 367–376. [Google Scholar] [CrossRef]
- Igual, R.; Medrano, C.; Plaza, I. Challenges, issues and trends in fall detection systems. Biomed. Eng. Online 2013, 12, 1–66. [Google Scholar] [CrossRef] [PubMed]
- Zigel, Y.; Litvak, D.; Gannot, I. A method for automatic fall detection of elderly people using floor vibrations and sound—Proof of concept on human mimicking doll falls. IEEE Trans. Biomed. Eng. 2009, 56, 2858–2867. [Google Scholar] [CrossRef] [PubMed]
- Stone, E.E.; Skubic, M. Fall detection in homes of older adults using the microsoft kinect. IEEE J. Biomed. Health Inform. 2015, 19, 290–301. [Google Scholar] [CrossRef] [PubMed]
- Daher, M.; Diab, A.; El Najjar, M.E.B.; Khalil, M.; Charpillet, F.; Daher, M.; Diab, A.; El Najjar, M.E.B.; Khalil, M.; Charpillet, F. Automatic fall detection system using sensing floors. Int. J. Comput. Inform. Sci. 2016, 12, 75. [Google Scholar]
- Lin, C.-S.; Hsu, H.C.; Lay, Y.-L.; Chiu, C.-C.; Chao, C.-S. Wearable device for real-time monitoring of human falls. Measurement 2007, 40, 831–840. [Google Scholar] [CrossRef]
- Chen, J.; Kwong, K.; Chang, D.; Luk, J.; Bajcsy, R. Wearable sensors for reliable fall detection. In Proceedings of the 27th Annual International Conference of the Engineering in Medicine and Biology Society, Shanghai, China, 17–18 January 2005; pp. 3551–3554.
- Bourke, A.K.; Lyons, G.M. A threshold-based fall-detection algorithm using a bi-axial gyroscope sensor. Med. Eng. Phys. 2008, 30, 84–90. [Google Scholar] [CrossRef] [PubMed]
- Lamb, S.E.; Jørstad-Stein, E.C.; Hauer, K.; Becker, C. Development of a common outcome data set for fall injury prevention trials: The prevention of falls network europe consensus. J. Am. Geriatr. Soc. 2005, 53, 1618–1622. [Google Scholar] [CrossRef] [PubMed]
- Shinmoto Torres, R.L.; Visvanathan, R.; Hoskins, S.; van den Hengel, A.; Ranasinghe, D.C. Effectiveness of a batteryless and wireless wearable sensor system for identifying bed and chair exits in healthy older people. Sensors 2016, 16, 546. [Google Scholar] [CrossRef] [PubMed]
- Noury, N.; Rumeau, P.; Bourke, A.; ÓLaighin, G.; Lundy, J. A proposal for the classification and evaluation of fall detectors. IRBM 2008, 29, 340–349. [Google Scholar] [CrossRef]
- Becker, C.; Schwickert, L.; Mellone, S.; Bagala, F.; Chiari, L.; Helbostad, J.L.; Zijlstra, W.; Aminian, K.; Bourke, A.; Todd, C.; et al. Proposal for a multiphase fall model based on real-world fall recordings with body-fixed sensors. Zeitschrift für Gerontologie und Geriatrie 2012, 45, 707–715. [Google Scholar] [CrossRef] [PubMed]
- Pannurat, N.; Thiemjarus, S.; Nantajeewarawat, E. Automatic fall monitoring: A review. Sensors 2014, 14, 12900–12936. [Google Scholar] [CrossRef] [PubMed]
- Noury, N.; Fleury, A.; Rumeau, P.; Bourke, A.K.; Laighin, G.O.; Rialle, V.; Lundy, J.E. Fall detection—Principles and methods. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2007, 2007, 1663–1666. [Google Scholar] [PubMed]
- Bourke, A.; O’brien, J.; Lyons, G. Evaluation of a threshold-based tri-axial accelerometer fall detection algorithm. Gait Posture 2007, 26, 194–199. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.N.; Chan, C.T. A zigbee-based location-aware fall detection system for improving elderly telecare. Int. J. Environ. Res. Public Health 2014, 11, 4233–4248. [Google Scholar] [CrossRef] [PubMed]
- Kangas, M.; Konttila, A.; Winblad, I.; Jamsa, T. Determination of simple thresholds for accelerometry-based parameters for fall detection. In Proceedings of the 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBS), Lyon, France, 22–26 August 2007; pp. 1367–1370.
- Kangas, M.; Konttila, A.; Lindgren, P.; Winblad, I.; Jämsä, T. Comparison of low-complexity fall detection algorithms for body attached accelerometers. Gait Posture 2008, 28, 285–291. [Google Scholar] [CrossRef] [PubMed]
- Albert, M.V.; Kording, K.; Herrmann, M.; Jayaraman, A. Fall classification by machine learning using mobile phones. PLoS ONE 2012, 7, e36556. [Google Scholar] [CrossRef] [PubMed]
- Yuwono, M.; Moulton, B.D.; Su, S.W.; Celler, B.G.; Nguyen, H.T. Unsupervised machine-learning method for improving the performance of ambulatory fall-detection systems. BioMed. Eng. Online 2012, 11, 9. [Google Scholar] [CrossRef] [PubMed]
- Ozdemir, A.T.; Barshan, B. Detecting falls with wearable sensors using machine learning techniques. Sensors 2014, 14, 10691–10708. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.; Ralhan, A.; Ko, S. A study on machine learning algorithms for fall detection and movement classification. In Proceedings of the 2011 International Conference on Information Science and Applications (ICISA), Jeju Island, Korea, 27–29 April 2011; pp. 1–8.
- Apdm Waerable Technologies. Available online: http://www.apdm.com/wearable-sensors/ (accessed on 29 August 2016).
- Dinh, A.; Shi, Y.; Teng, D.; Ralhan, A.; Chen, L.; Dal Bello-Haas, V.; Basran, J.; Ko, S.-B.; McCrowsky, C. A fall and near-fall assessment and evaluation system. Open Biomed. Eng. J. 2009, 3, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Chao, P.K.; Chan, H.L.; Tang, F.T.; Chen, Y.C.; Wong, M.K. A comparison of automatic fall detection by the cross-product and magnitude of tri-axial acceleration. Physiol. Meas. 2009, 30, 1027–1037. [Google Scholar] [CrossRef] [PubMed]
- Bourke, A.; Van de Ven, P.; Gamble, M.; O’Connor, R.; Murphy, K.; Bogan, E.; McQuade, E.; Finucane, P.; Olaighin, G.; Nelson, J. Evaluation of waist-mounted tri-axial accelerometer based fall-detection algorithms during scripted and continuous unscripted activities. J. Biomech. 2010, 43, 3051–3057. [Google Scholar] [CrossRef] [PubMed]
- Rescio, G.; Leone, A.; Siciliano, P. Support vector machine for tri-axial accelerometer-based fall detector. In Proceedings of the 2013 5th IEEE International Workshop on Advances in Sensors and Interfaces (IWASI), Bari, Italy, 13–14 June 2013; pp. 25–30.
- Huynh, Q.T.; Nguyen, U.D.; Irazabal, L.B.; Ghassemian, N.; Tran, B.Q. Optimization of an accelerometer and gyroscope-based fall detection algorithm. J. Sens. 2015, 2015, 452078. [Google Scholar] [CrossRef]
- Palmerini, L.; Bagala, F.; Zanetti, A.; Klenk, J.; Becker, C.; Cappello, A. A wavelet-based approach to fall detection. Sensors 2015, 15, 11575–11586. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Hu, C.; Wang, X. A smart device enabled system for autonomous fall detection and alert. Int. J. Distrib. Sens. Netw. 2016, 2016, 2308183. [Google Scholar] [CrossRef]
- Chen, K.-H.; Yang, J.-J.; Jaw, F.-S. Accelerometer-based fall detection using feature extraction and support vector machine algorithms. Instrum. Sci. Technol. 2016, 44, 333–342. [Google Scholar] [CrossRef]
- Gibson, R.M.; Amira, A.; Ramzan, N.; Casaseca-de-la-Higuera, P.; Pervez, Z. Multiple comparator classifier framework for accelerometer-based fall detection and diagnostic. Appl. Soft Comput. 2016, 39, 94–103. [Google Scholar] [CrossRef]
- Klenk, J.; Becker, C.; Lieken, F.; Nicolai, S.; Maetzler, W.; Alt, W.; Zijlstra, W.; Hausdorff, J.; Van Lummel, R.; Chiari, L. Comparison of acceleration signals of simulated and real-world backward falls. Med. Eng. Phys. 2011, 33, 368–373. [Google Scholar] [CrossRef] [PubMed]
- Cleland, I.; Kikhia, B.; Nugent, C.; Boytsov, A.; Hallberg, J.; Synnes, K.; McClean, S.; Finlay, D. Optimal placement of accelerometers for the detection of everyday activities. Sensors 2013, 13, 9183–9200. [Google Scholar] [CrossRef] [PubMed]
- Hsu, C.W.; Lin, C.J. A comparison of methods for multiclass support vector machines. IEEE Trans. Neural Netw. 2002, 13, 415–425. [Google Scholar] [PubMed]
- Anzai, Y. Pattern Recognition & Machine Learning; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Kangas, M.; Vikman, I.; Wiklander, J.; Lindgren, P.; Nyberg, L.; Jamsa, T. Sensitivity and specificity of fall detection in people aged 40 years and over. Gait Posture 2009, 29, 571–574. [Google Scholar] [CrossRef] [PubMed]
- Bagala, F.; Becker, C.; Cappello, A.; Chiari, L.; Aminian, K.; Hausdorff, J.M.; Zijlstra, W.; Klenk, J. Evaluation of accelerometer-based fall detection algorithms on real-world falls. PLoS ONE 2012, 7, e37062. [Google Scholar] [CrossRef] [PubMed]
- Bersch, S.D.; Azzi, D.; Khusainov, R.; Achumba, I.E.; Ries, J. Sensor data acquisition and processing parameters for human activity classification. Sensors 2014, 14, 4239–4270. [Google Scholar] [CrossRef] [PubMed]
- Chawla, N.V. Data mining for imbalanced datasets: An overview. In Data Mining and Knowledge Discovery Handbook; Springer: New York, NY, USA, 2009; pp. 875–886. [Google Scholar]
- Fortino, G.; Gravina, R. Fall-mobileguard: A smart real-time fall detection system. In Proceedings of the 10th EAI International Conference on Body Area Networks, Sydney, Australia, 28–30 September 2015; ICST (Institute for Computer Sciences, Social-Informatics and Telecommunications Engineering): South Portland, ME, USA, 2015; pp. 44–50. [Google Scholar]
- Kangas, M.; Vikman, I.; Nyberg, L.; Korpelainen, R.; Lindblom, J.; Jamsa, T. Comparison of real-life accidental falls in older people with experimental falls in middle-aged test subjects. Gait Posture 2012, 35, 500–505. [Google Scholar] [CrossRef] [PubMed]



| Article (Year) | Detection Algorithm (Methods) | Sensor(s) | Placement | Features Used for Fall Detection | Fall and ADL Types | Results |
|---|---|---|---|---|---|---|
| Kangas et al. (2008) [28] | Threshold-based | Tri-axial accelerometer | Waist Wrist Head | Beginning of the fall (SVTOT) Falling velocity Fall impact (SVTOT, SVD, SVMaxMin, or Z2) Posture after impact | Falls: 9 ADLs: -- | Sn 2: 97% (Waist) Sp 2: 100% (Waist) |
| Dinh et al. (2009) [34] | Machine learning–based (NB, RBF, SVM, C4.5 Ripple down rule learner) | Tri-axial accelerometer Dual-axial gyroscope | Thorax | Acceleration (X, Y and Z axis) Gyroscope (X and Y axis) | Falls: 4 ADLs: 3 | Naïve Bayesian Acc 2: 97.3% Radial Basis Function Acc 2: 95.8% |
| Chao et al. (2009) [35] | Threshold-based | Tri-axial accelerometer | Chest Waist | Acceleration magnitude Acceleration cross-product | Falls: 8 ADLs: 13 | Sn 2: 98.2% (Chest) Sp 2: 92.4% (Chest) Sn 2: 98.2% (Waist) Sp 2: 89.9% (Waist) |
| Bourke et al. (2010) [36] | Threshold-based | Tri-axial accelerometer | Waist | Upper fall threshold Lower fall threshold Vertical velocity | Falls: 8 ADLs: 4 | Velocity + impact + posture Sn 2: 100% Sp 2: 100% Less than 1 false positive a day |
| Choi et al. (2011) [32] | Machine learning–based (NB) | SNA 1: Tri-axial accelerometer, dual-axial gyroscope DNA 1: Tri-axial accelerometer, one-axial gyroscope | SNA 1: Chest DNA 1: Chest, Thigh | SNA 1: Acceleration (X, Y and Z axis) Gyroscope (X and Y axis) DNA 1: Acceleration (X, Y and Z axis) Gyroscope (X axis) | SNA 1: Falls: 4 ADLs: 3 DNA 1: Falls: 4 ADLs: 4 | SNA 1: Acc 2: 99.4% DNA 1: Acc 2: 99.8% |
| Rescio et al. (2013) [37] | Machine learning–based (SVM) | Tri-axial accelerometer | Waist | The product between the value of the acceleration peak and the change in the CPO | -- | Sn 2: 97.7% Sp 2: 94.8% |
| Özdemir et al. (2014) [31] | Machine learning–based (kNN, LSM, SVM, Bayesian Decision Making, Dynamic Time Warping, ANN) | Tri-axial accelerometer Tri-axial gyroscope Tri-axial magnetometer | Head, Chest, Waist, Wrist, Thigh, Ankle | Minimum, Maximum Mean, Variance Skewness Kurtosis Autocorrelation Discrete Fourier transform | Falls: 20 ADLs: 16 | kNN Sn 2: 100% Sp 2: 99.91% |
| Huynh et al. (2015) [38] | Threshold-based | Tri-axial accelerometer Tri-axial gyroscope | Chest | Upper fall threshold Lower fall threshold | Falls: 4 ADLs: 6 | Sn 2: 96.55% Sp 2: 89.50% |
| Palmerini et al. (2015) [39] | Threshold-based | Tri-axial accelerometer | Lower back | Continuous wavelet transform coefficients Upper peak value Lower peak value | Falls: 5 ADLs: -- | Wavelet Sn 2: 90% Sp 2: 89.7% |
| He et al. (2016) [40] | Machine learning–based (kNN, NB, Bayes Net, ANN, Decision Tree, Bagging, Ripper) | Tri-axial accelerometer Tri-axial gyroscope | upper trunk | Resultant acceleration (α) Resultant angular velocity (ω) | Falls: 2 ADLs: 3 | kNN (k = 3) Sn 2: 100% Sp 2: 99.91% Acc 2: 97.8548% |
| Chen et al. (2016) [41] | Machine learning–based (SVM) | Tri-axial accelerometer | Waist | Maximum magnitude of the sum vector Rotation angle Slope Acceleration in the xy-plane Standard deviation of the sun vector | Falls: 6 ADLs: 6 | Sn 2: 95.76% Sp 2: 93.28% Acc 2: 94.58% |
| Gibson et al. (2016) [42] | Machine learning-based (ANN, kNN, RBF, Probabilistic Principal Component Analysis, Linear Discriminant Analysis) | Tri-axial accelerometer | Chest | Discrete wavelet transform | Falls: 6 ADLs: 5 | Radial Basis Function Sn 2: 100% Sp 2: 99.91% Linear Discriminant Analysis Sn 2: 100% Sp 2: 99.91% |
| No. | Activities before Fall | Characteristics | |||
| 1 | Stand | Forward | Backward | Lateral (right and left) | |
| 2 | Stand up | Forward | Backward | Lateral (right and left) | |
| 3 | Sit down | Forward | Backward | Lateral (right and left) | |
| 4 | Stoop | Forward | Backward | Lateral (right and left) | |
| 5 | Walk | Forward | Backward | Lateral (right and left) | |
| 6 | Walk backward | -- | Backward | -- | |
| 7 | Jump | Forward | Backward | Lateral (right and left) | |
| No. | Activities of Daily Living | Characteristic | No. | Activities of Daily Living | Characteristic |
| 1 | Stand up | From sit | 2 | Stand up | From squat |
| 3 | Sit down | Normal | 4 | Sit down | Fast |
| 5 | Lie on the bed | Normal | 6 | Lie on the bed | Fast |
| 7 | Go up stairs | Normal | 8 | Go down stairs | Normal |
| 9 | Walk | Normal | 10 | Walk | Fast |
| 11 | Jump | On the ground | 12 | Jump | On the bed |
| Feature Vector, F = (f1, f2, …, f54) R54 | Feature Description |
|---|---|
| f1~f3 | mean ax(i); mean ay(i); mean ax(i), where i = 1, ..., m 1 |
| f4~f6 | mean anorm(i) 2; mean averti(i) 3; mean ahori(i) 4, where i = 1, ..., m 1 |
| f7~f9 | std ax(i); std ay(i); std ax(i), where i = 1, ..., m 1 |
| f10~f12 | std anorm(i) 2; std averti(i) 3; std ahori(i) 4, where i = 1, ..., m 1 |
| f13~f15 | var ax(i); var ay(i); var ax(i), where i = 1, ..., m 1 |
| f16~f18 | var anorm(i) 2; var averti(i) 3; var ahori(i) 4, where i = 1, ..., m 1 |
| f19~f21 | max ax(i); max ay(i); max ax(i), where i = 1, ..., m 1 |
| f22~f24 | max anorm(i) 2; max averti(i) 3; max ahori(i) 4, where i = 1, ..., m 1 |
| f25~f27 | min ax(i); min ay(i); min ax(i), where i = 1, ..., m 1 |
| f28~f30 | min anorm(i) 2; min averti(i) 3; min ahori(i) 4, where i = 1, ..., m 1 |
| f31~f33 | range ax(i); range ay(i); range ax(i), where i = 1, ..., m 1 |
| f34~f36 | range anorm(i) 2; range averti(i) 3; range ahori(i) 4, where i = 1, ..., m 1 |
| f37~f39 | kurtosis ax(i); kurtosis ay(i); kurtosis ax(i), where i = 1, ..., m 1 |
| f40~f42 | kurtosis anorm(i) 2; kurtosis averti(i) 3; kurtosis ahori(i) 4, where i = 1, ..., m 1 |
| f43~f45 | skewness ax(i); skewness ay(i); skewness ax(i), where i = 1, ..., m 1 |
| f46~f48 | skewness anorm(i) 2; skewness averti(i) 3; skewness ahori(i) 4, where i = 1, ..., m 1 |
| f49 | Correlation coefficient between ax and ay |
| f50 | Correlation coefficient between ax and az |
| f51 | Correlation coefficient between ay and az |
| f52 | Correlation coefficient between anorm 2 and averti 3 |
| f53 | Correlation coefficient between anorm 2 and ahori 4 |
| f54 | Correlation coefficient between averti 3 and ahori 4 |
| Knowledge-Based Fall Detection Algorithm | ||||||
|---|---|---|---|---|---|---|
| Round | 1 | 2 | 3 | 4 | 5 | Mean (Std) |
| Sensitivity (%) | 100 (0) | 99.79 (0.47) | 99.58 (0.57) | 99.79 (0.48) | 99.79 (0.47) | 99.79 (0.43) |
| Specificity (%) | 98.63 (1.36) | 98.62 (1.00) | 98.90 (0.61) | 98.62 (0.98) | 98.91 (0.61) | 98.74 (0.88) |
| Precision (%) | 98.97 (1.03) | 98.96 (0.73) | 99.16 (0.47) | 98.97 (0.72) | 99.17 (0.47) | 99.05 (0.66) |
| Accuracy (%) | 99.41 (0.59) | 99.29 (0.50) | 99.29 (0.26) | 99.28 (0.27) | 99.41 (0.42) | 99.33 (0.40) |
| Machine Learning–Based Fall Detection Algorithm | ||||||
|---|---|---|---|---|---|---|
| Round | 1 | 2 | 3 | 4 | 5 | Mean (Std) |
| Sensitivity (%) | 99.58 (0.58) | 99.16 (1.37) | 99.36 (0.94) | 99.15 (0.89) | 98.95 (0.74) | 99.24 (0.89) |
| Specificity (%) | 98.63 (1.68) | 98.63 (1.66) | 98.63 (2.37) | 97.80 (2.50) | 98.37 (1.48) | 98.41 (1.84) |
| Precision (%) | 98.97 (1.26) | 98.95 (1.29) | 98.99 (1.73) | 98.35 (1.88) | 98.76 (1.10) | 98.81 (1.38) |
| Accuracy (%) | 99.17 (0.90) | 98.93 (1.47) | 99.05 (0.90) | 98.56 (1.02) | 98.69 (0.49) | 98.88 (0.95) |
| Predict Results and Measure Matrix | Fall (Ground Truth) | ADL (Ground Truth) | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Stand | stand up | Sit down | Walk | Stoop | Jump | Walk Backward | Stand from Sit | Stand from Squat | Sit (Normal) | Sit (Fast) | Lie (Normal) | Lie (Fast) | Go up Stairs | Go down Stairs | Walk (Normal) | Walk (Fast) | Jump (Ground) | Jump (Bed) | |
| Fall (Predicted) | 380 | 380 | 380 | 380 | 375 | 380 | 95 | 0 | 0 | 0 | 0 | 8 | 15 | 0 | 0 | 0 | 0 | 0 | 0 |
| ADL (Predicted) | 0 | 0 | 0 | 0 | 5 | 0 | 0 | 150 | 150 | 150 | 150 | 137 | 135 | 185 | 145 | 150 | 150 | 145 | 150 |
| Sensitivity (%) | 100 | 100 | 100 | 100 | 98.68 | 100 | 100 | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| Specificity (%) | -- | -- | -- | -- | -- | -- | -- | 100 | 100 | 100 | 100 | 94.48 | 90 | 100 | 100 | 100 | 100 | 100 | 100 |
| False positive rate (%) | -- | -- | -- | -- | -- | -- | -- | 0 | 0 | 0 | 0 | 5.52 | 10 | 0 | 0 | 0 | 0 | 0 | 0 |
| False negative rate (%) | 0 | 0 | 0 | 0 | 1.32 | 0 | 0 | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| Predict Results and Measure Matrix | Fall (Ground Truth) | ADL (Ground Truth) | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Stand | Stand up | Sit down | Walk | Stoop | Jump | Walk Backward | Stand from Sit | Stand from Squat | Sit (Normal) | Sit (Fast) | Lie (Normal) | Lie (Fast) | Go up Stairs | Go down Stairs | Walk (Normal) | Walk (Fast) | Jump (Ground) | Jump (Bed) | |
| Fall (Predicted) | 380 | 380 | 377 | 380 | 372 | 378 | 90 | 0 | 0 | 0 | 4 | 8 | 11 | 0 | 0 | 1 | 4 | 1 | 0 |
| ADL (Predicted) | 0 | 0 | 3 | 0 | 8 | 2 | 5 | 150 | 150 | 150 | 146 | 137 | 139 | 185 | 145 | 149 | 146 | 144 | 150 |
| Sensitivity (%) | 100 | 100 | 99.21 | 100 | 97.76 | 99.47 | 94.74 | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| Specificity (%) | -- | -- | -- | -- | -- | -- | -- | 100 | 100 | 100 | 97.33 | 94.48 | 91.86 | 100 | 100 | 99.33 | 97.33 | 99.31 | 100 |
| False positive rate (%) | -- | -- | -- | -- | -- | -- | -- | 0 | 0 | 0 | 2.67 | 5.52 | 8.14 | 0 | 0 | 0.67 | 2.67 | 0.69 | 0 |
| False negative rate (%) | 0 | 0 | 0.79 | 0 | 2.1 | 0.53 | 5.26 | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsieh, C.-Y.; Liu, K.-C.; Huang, C.-N.; Chu, W.-C.; Chan, C.-T. Novel Hierarchical Fall Detection Algorithm Using a Multiphase Fall Model. Sensors 2017, 17, 307. https://doi.org/10.3390/s17020307
Hsieh C-Y, Liu K-C, Huang C-N, Chu W-C, Chan C-T. Novel Hierarchical Fall Detection Algorithm Using a Multiphase Fall Model. Sensors. 2017; 17(2):307. https://doi.org/10.3390/s17020307
Chicago/Turabian StyleHsieh, Chia-Yeh, Kai-Chun Liu, Chih-Ning Huang, Woei-Chyn Chu, and Chia-Tai Chan. 2017. "Novel Hierarchical Fall Detection Algorithm Using a Multiphase Fall Model" Sensors 17, no. 2: 307. https://doi.org/10.3390/s17020307
APA StyleHsieh, C.-Y., Liu, K.-C., Huang, C.-N., Chu, W.-C., & Chan, C.-T. (2017). Novel Hierarchical Fall Detection Algorithm Using a Multiphase Fall Model. Sensors, 17(2), 307. https://doi.org/10.3390/s17020307







