Centralized Networks to Generate Human Body Motions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Network Structure
2.1.1. Background on Scale-Free Networks and Centralized Networks
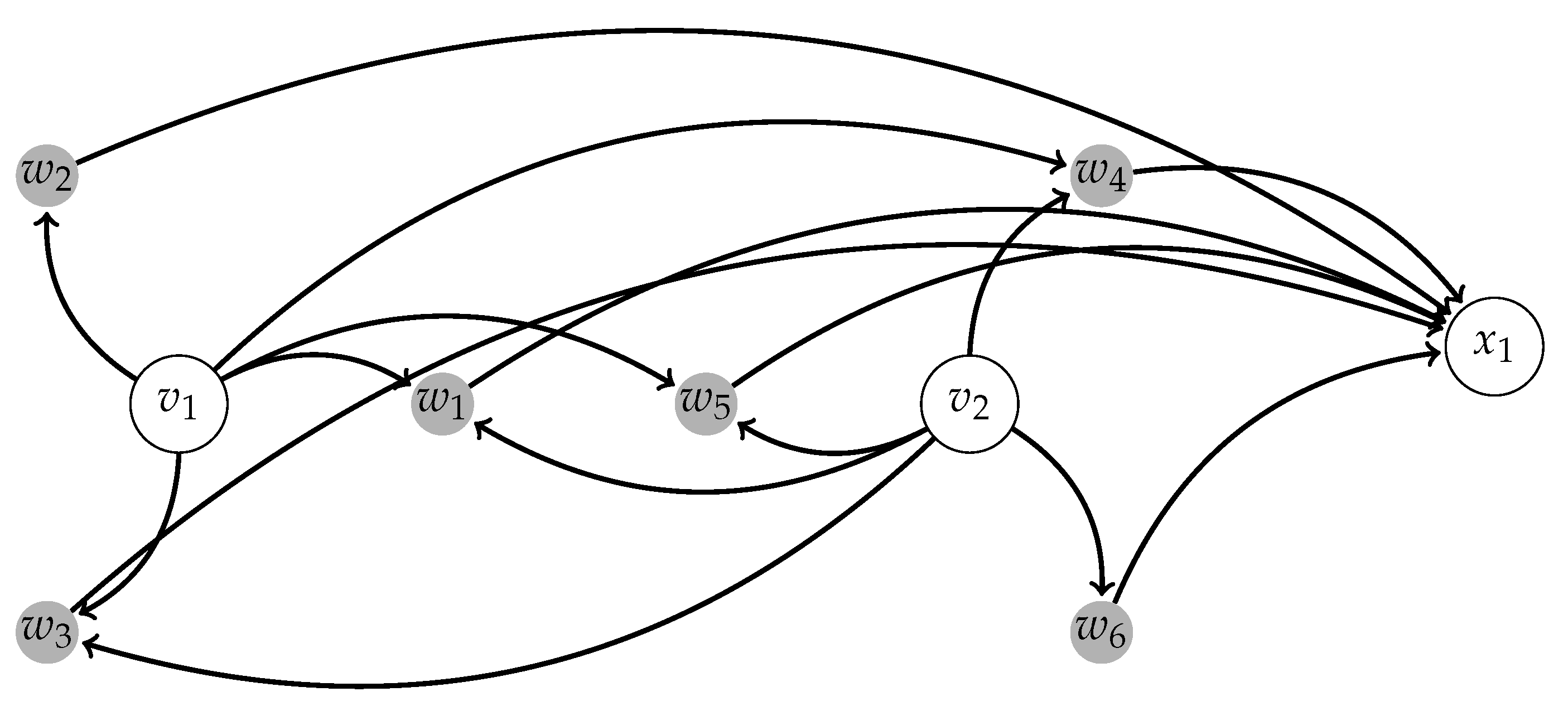
2.1.2. Centralized Networks for Elementary Human Motions
- A
- Harmonic basis. Here we assume thatwhere b is a frequency.
- B
- System of radial basis functions.For the case where a motion consists of many segments and we observe sharp transitions between those segments, we can use radial basis functionswhere is a fixed function, b is a sharpness parameter, and is the vector of centers of radial basis functions with components , where the latter are parameters of the system, and denotes the Euclidian norm of the vector z: . We assume that the radial basis function is well localized at and is smooth. For example, we can take the Gaussian
- C
- Polynomial basis.Here we takeThe basis B has an important advantage: the radial basis functions provide local approximations that are important to approximate complicated motions with sharp transitions.To perform switching in the network, we will also use the sigmoidal functions . They are increasing and smooth (at least twice differentiable) functions such thatTypical examples can be given by
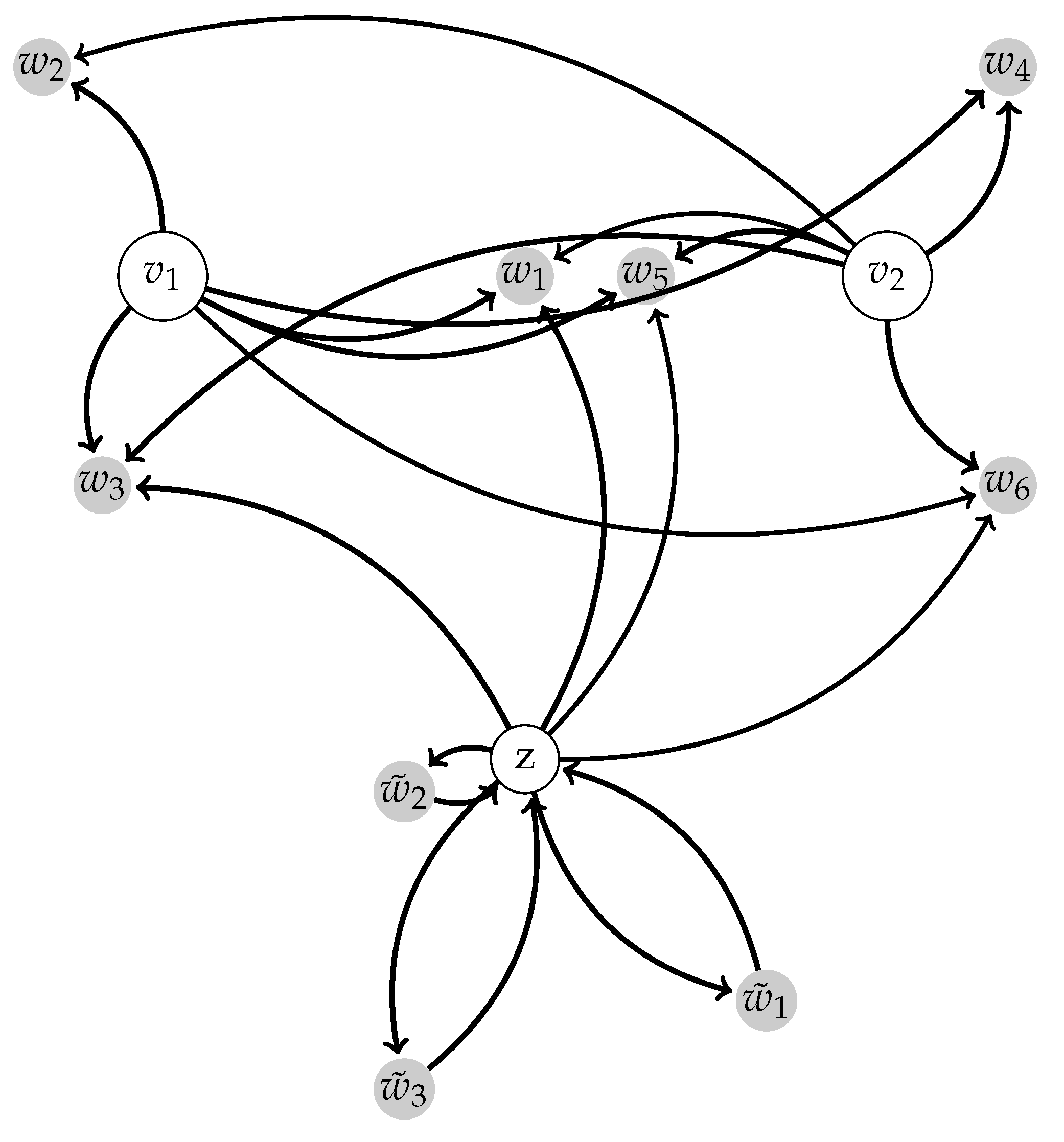
2.1.3. Centralized Networks Generating a Large Class of Human Body Motions
2.2. Switching Module
2.3. Algorithm of Construction of the RBF Network to Generate Human Body Motions
2.3.1. Non-Segmented Motions
2.3.2. Segmented Motions
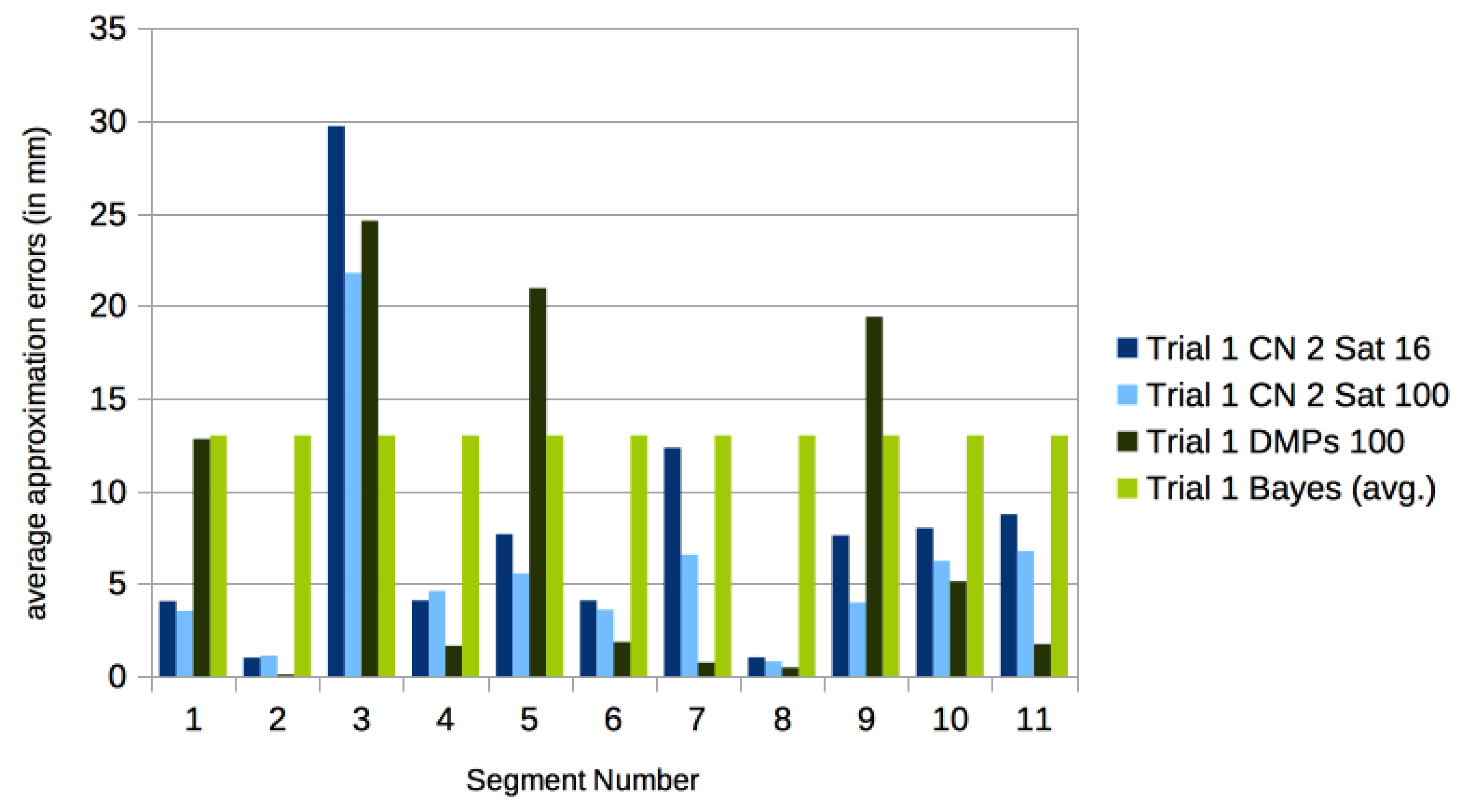
2.4. Comparison with DMPs
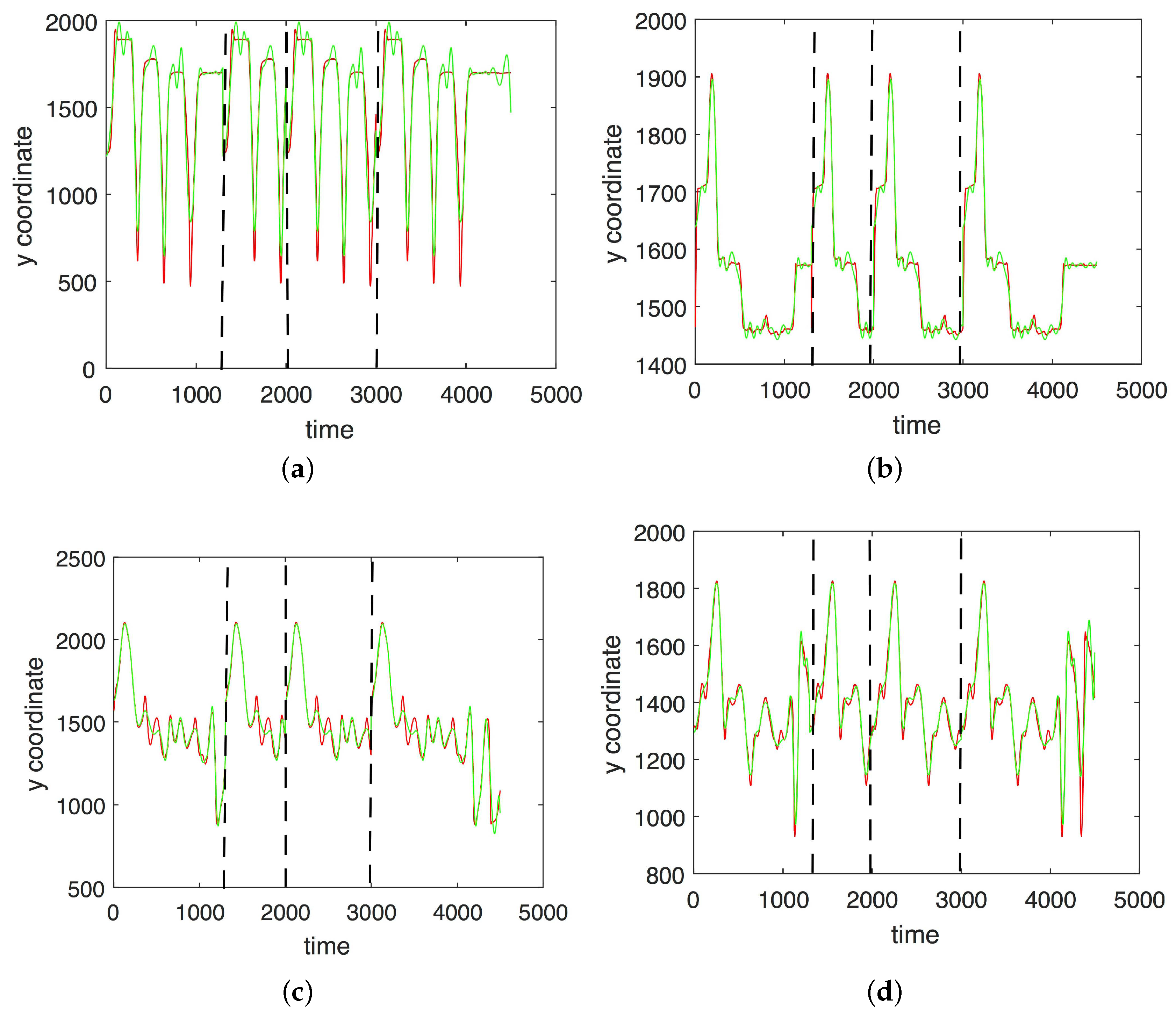
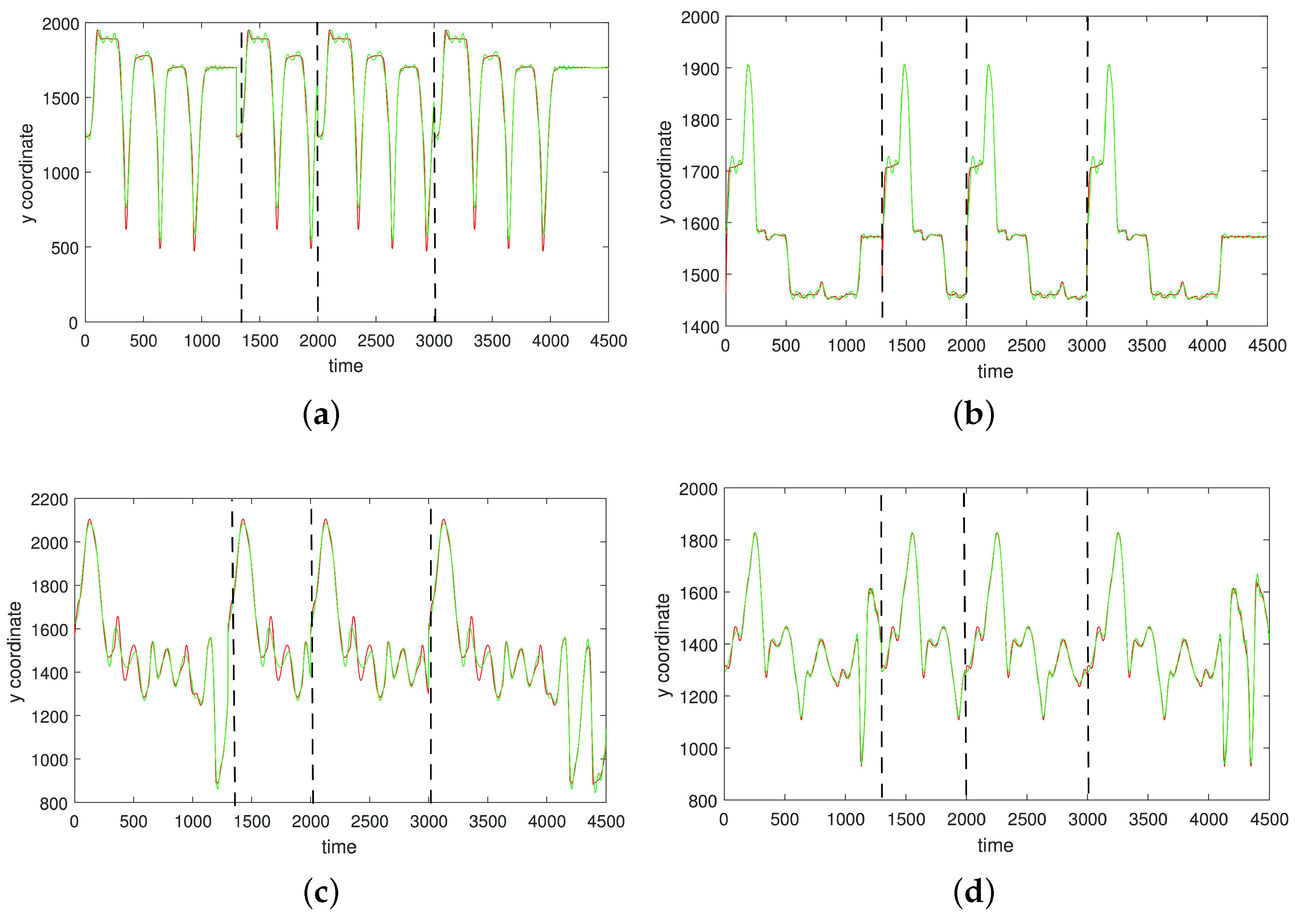
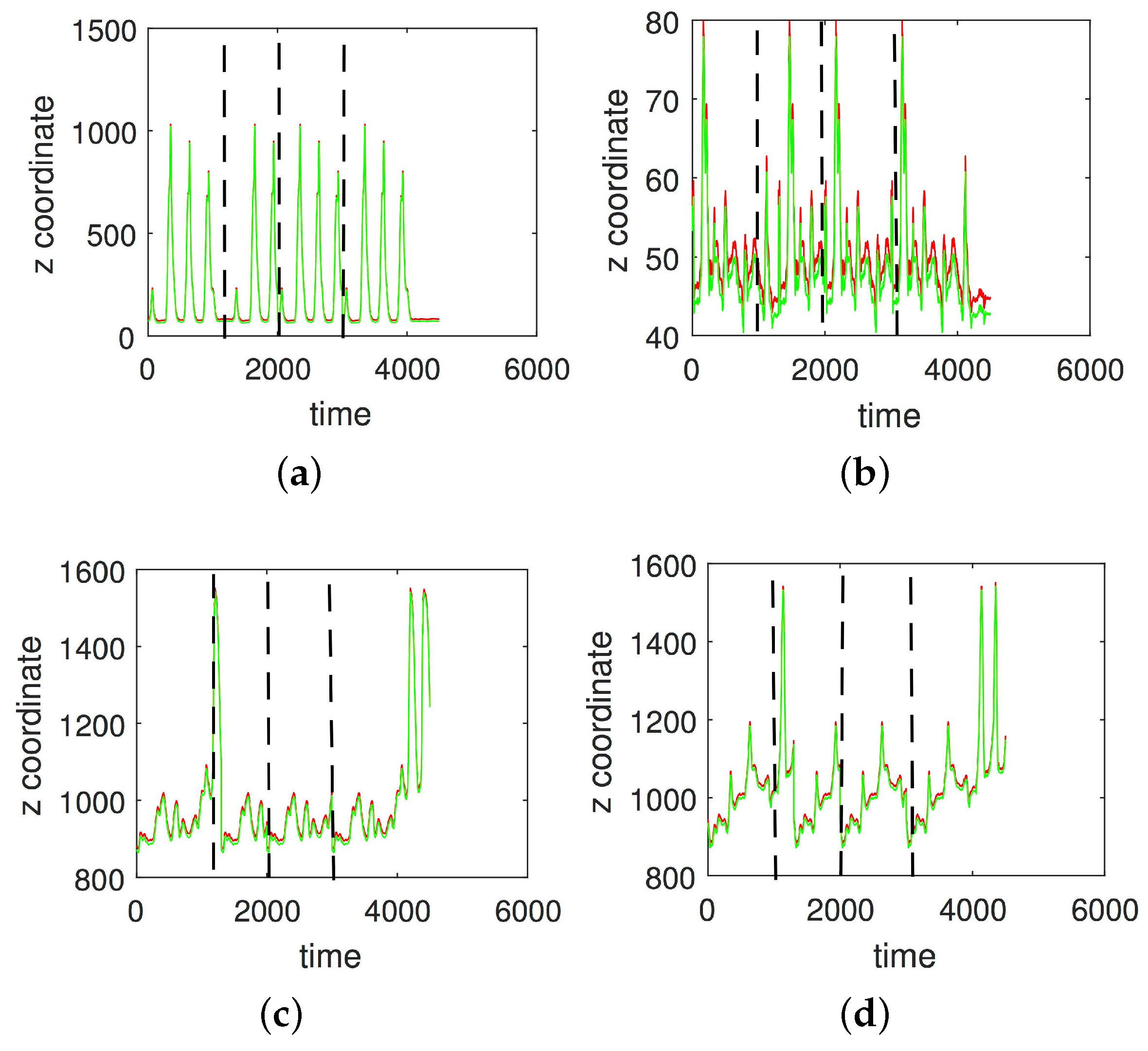
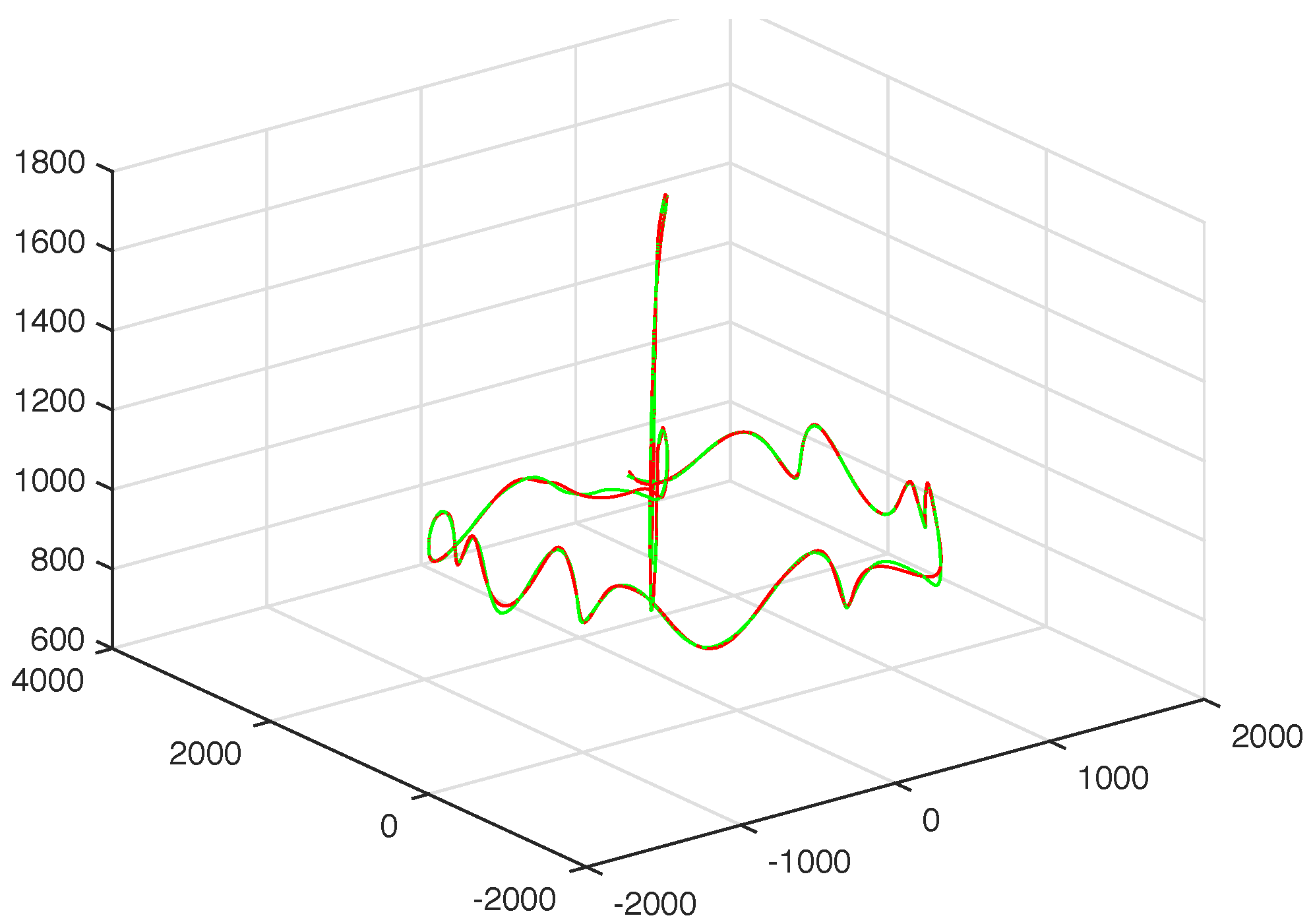
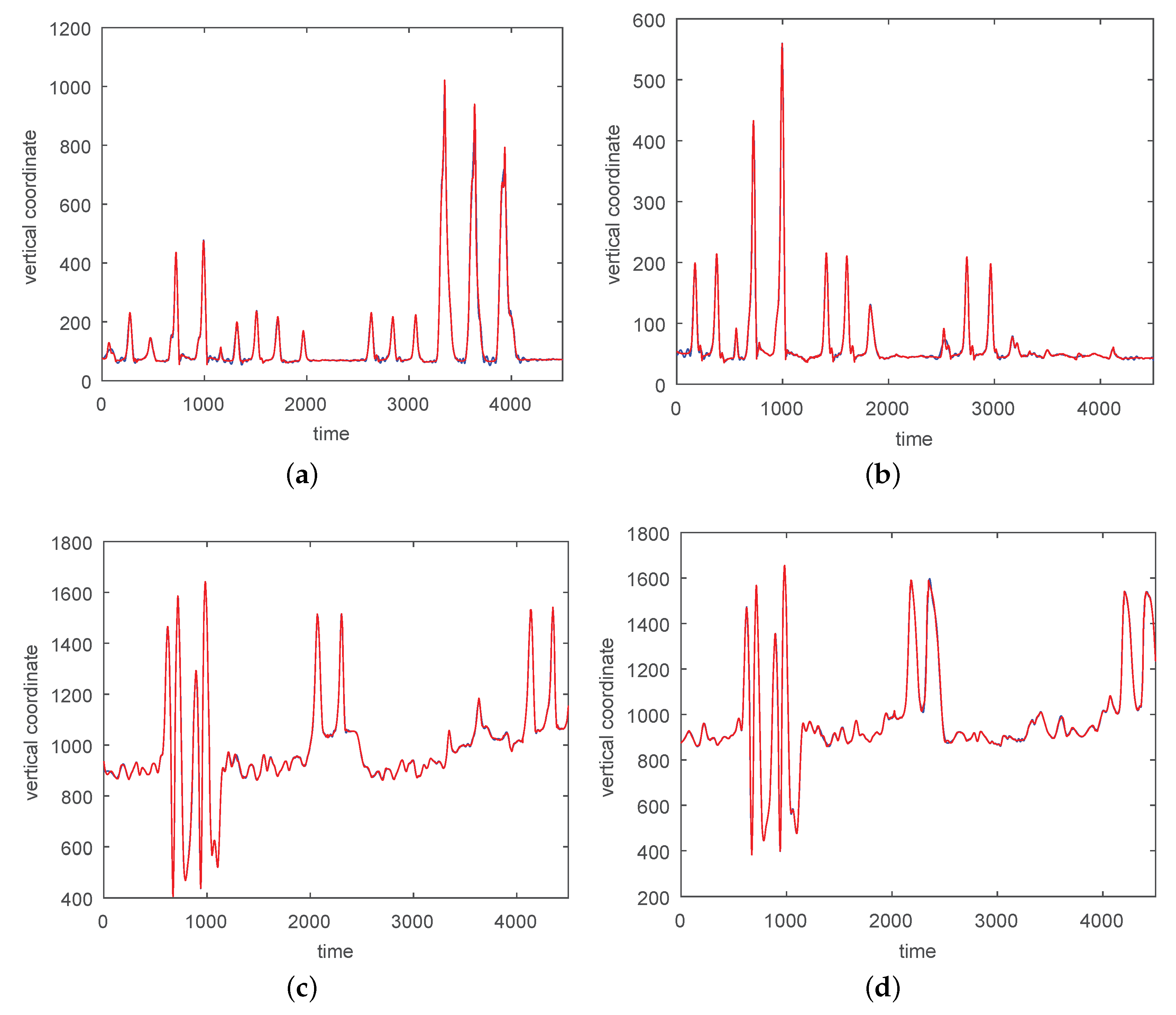
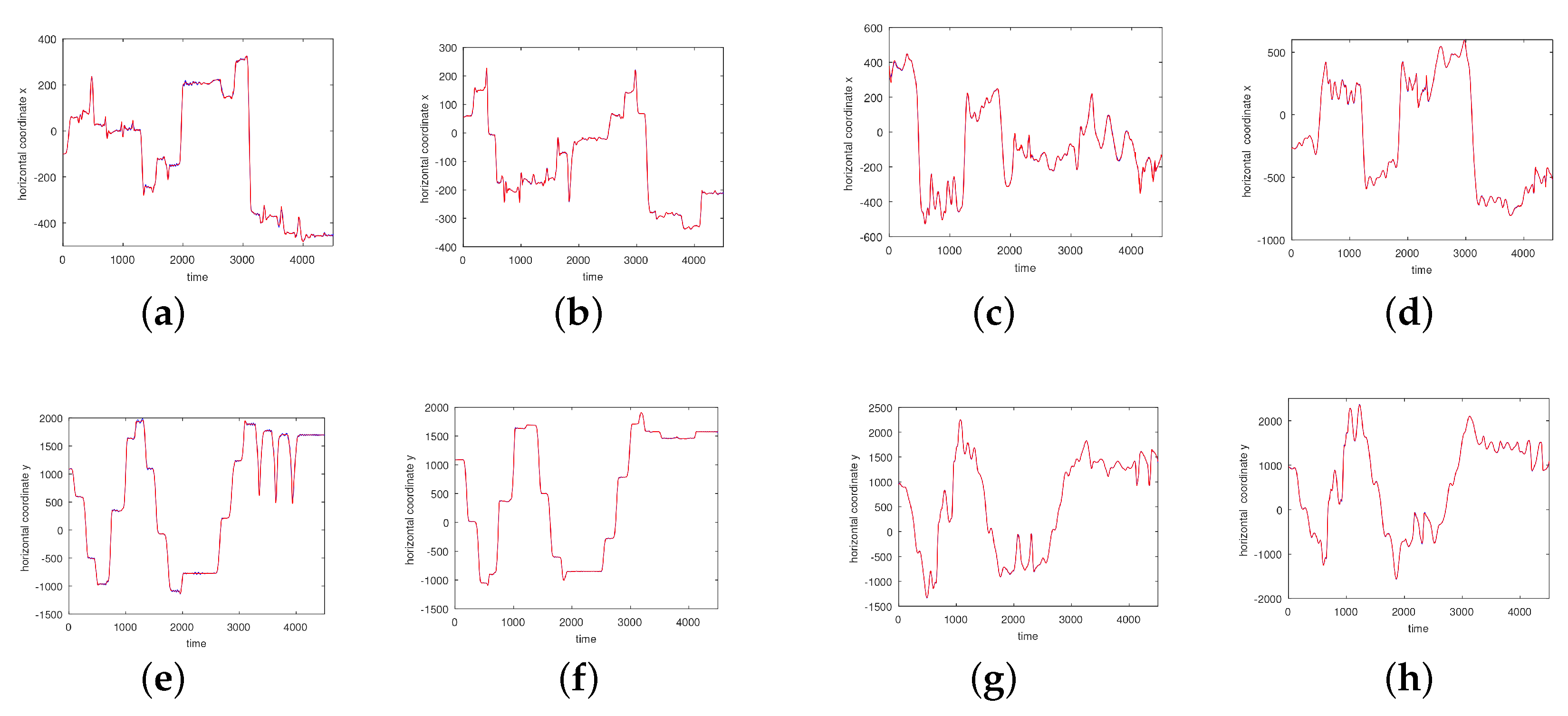
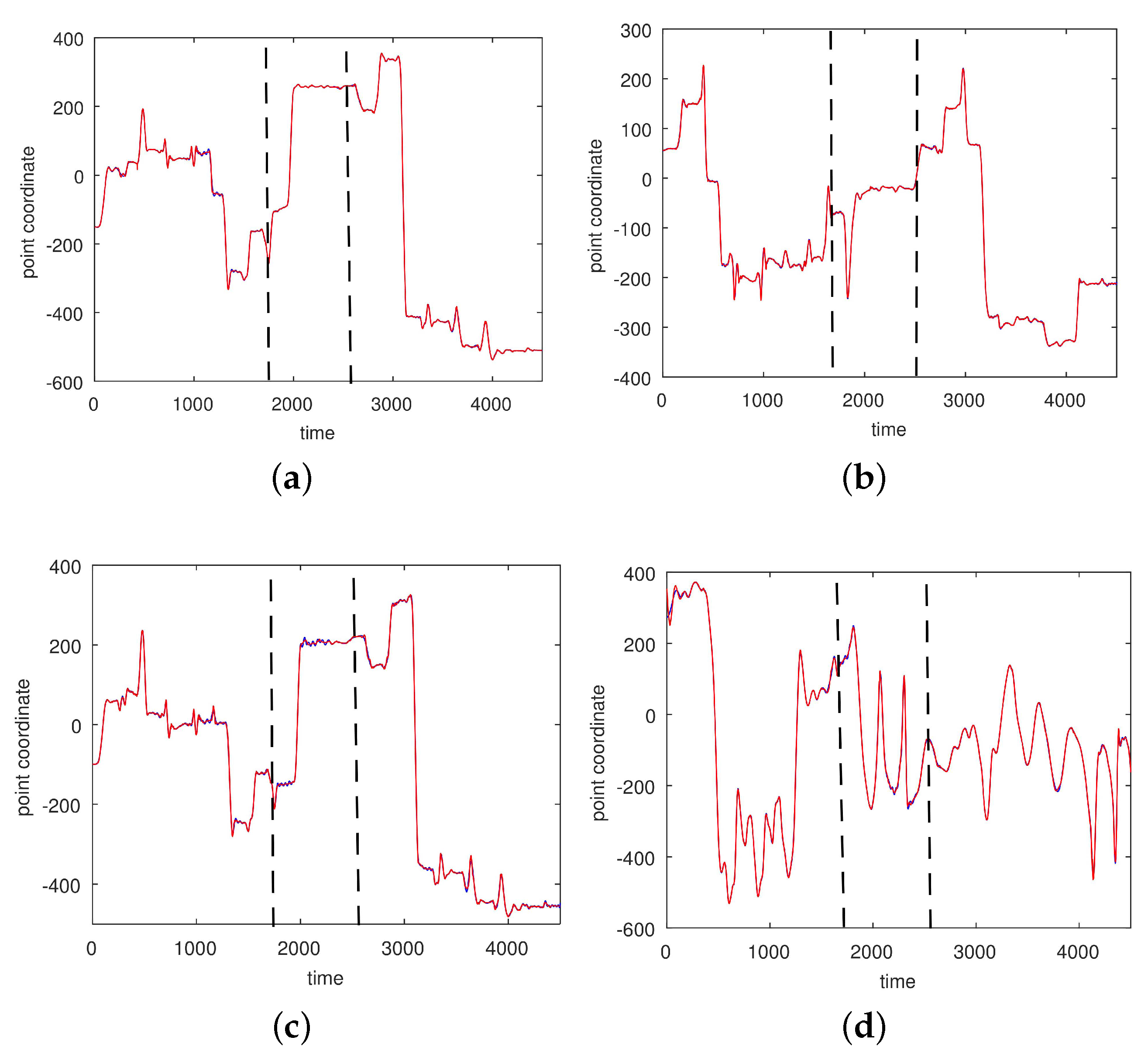
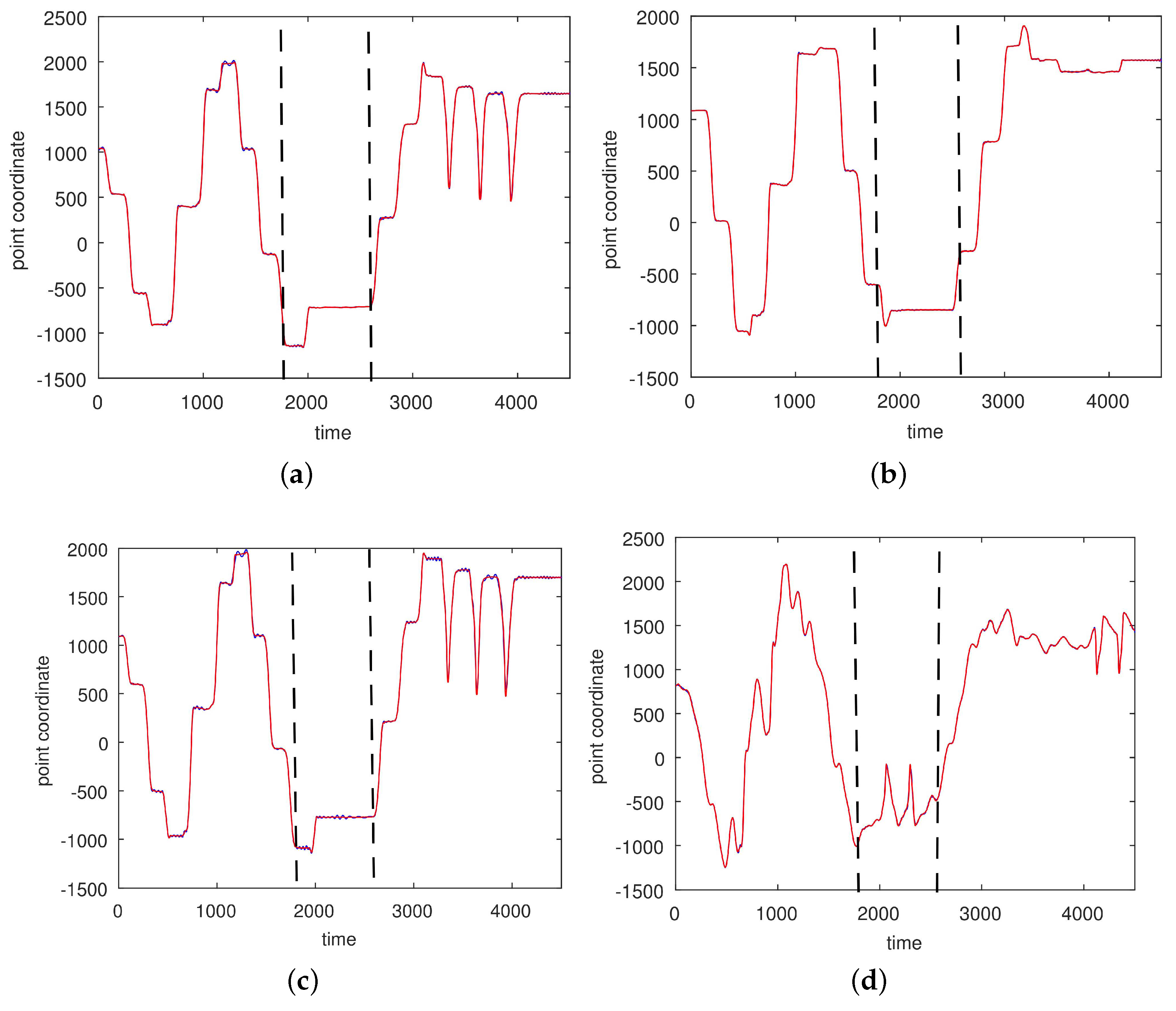
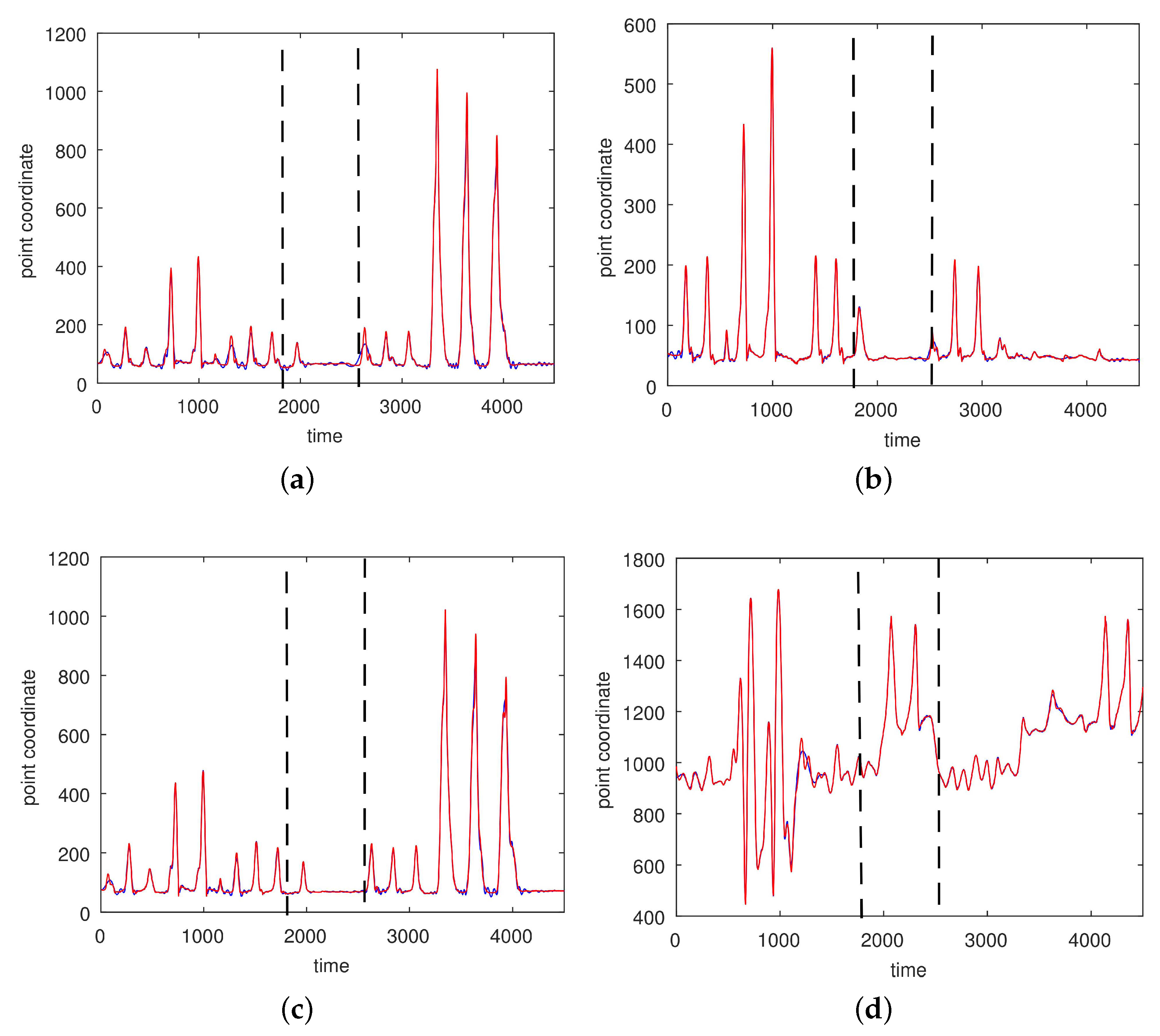
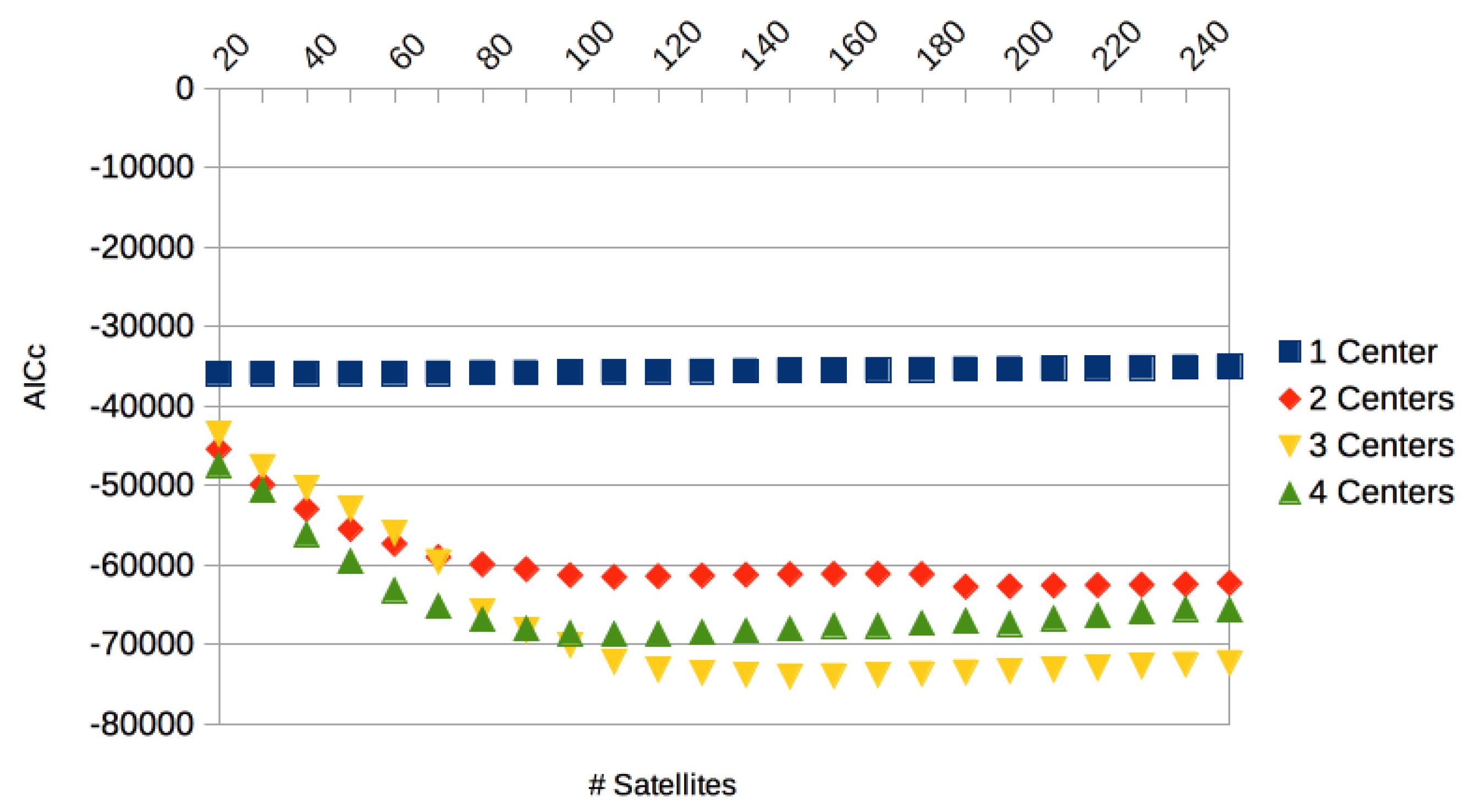
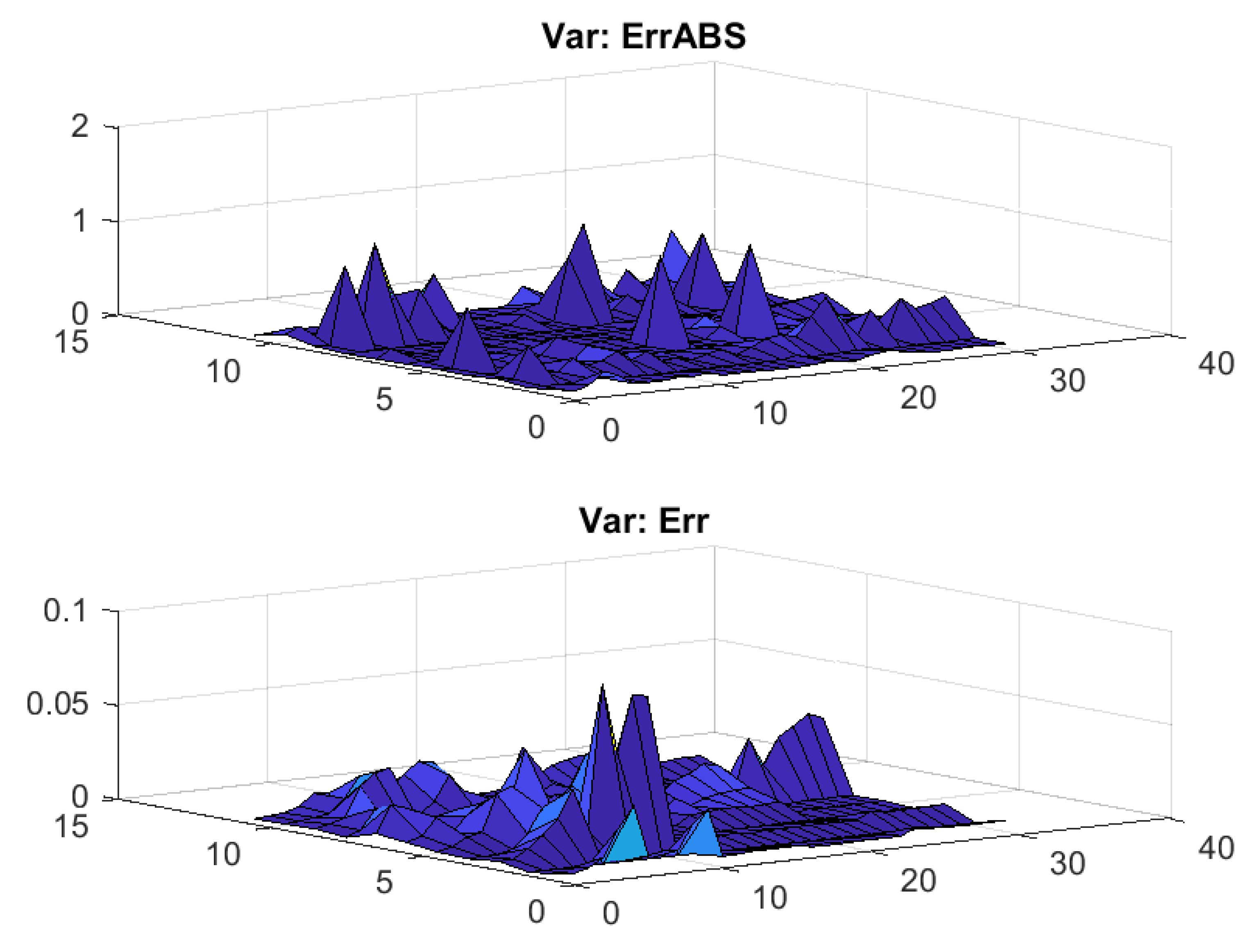
3. Results
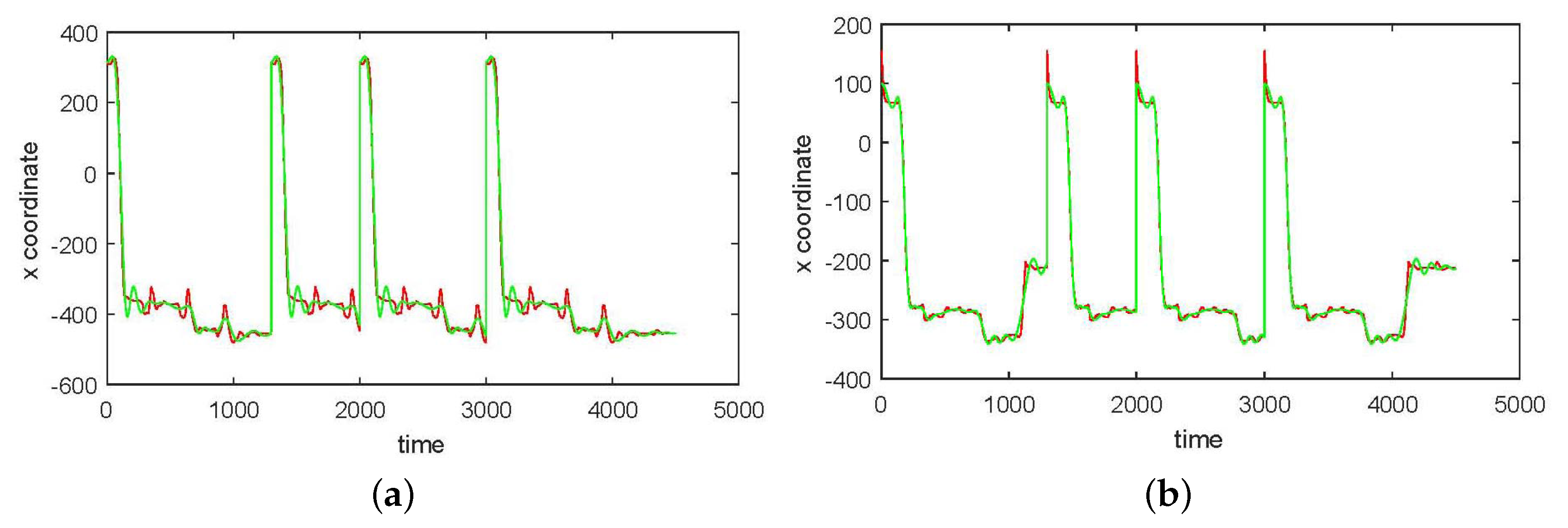
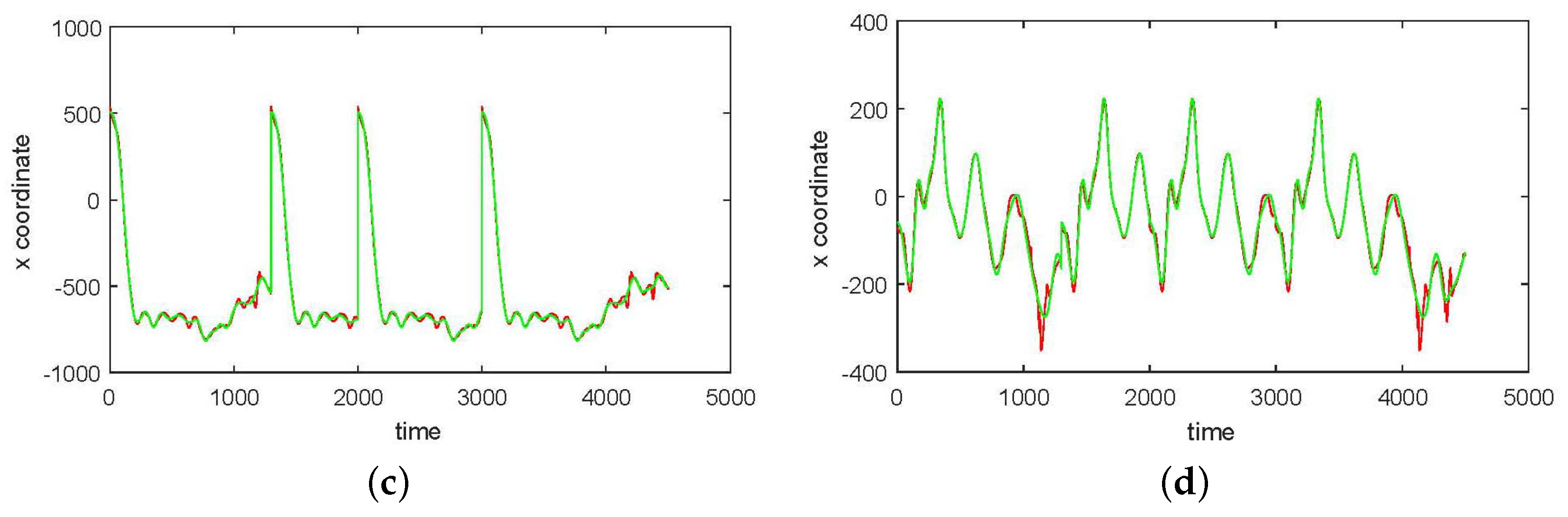
3.1. Results without Segmentation and Ad Hoc Segmentations
3.2. Results Based on Algorithmic Segmentations as Pre-Processing Steps
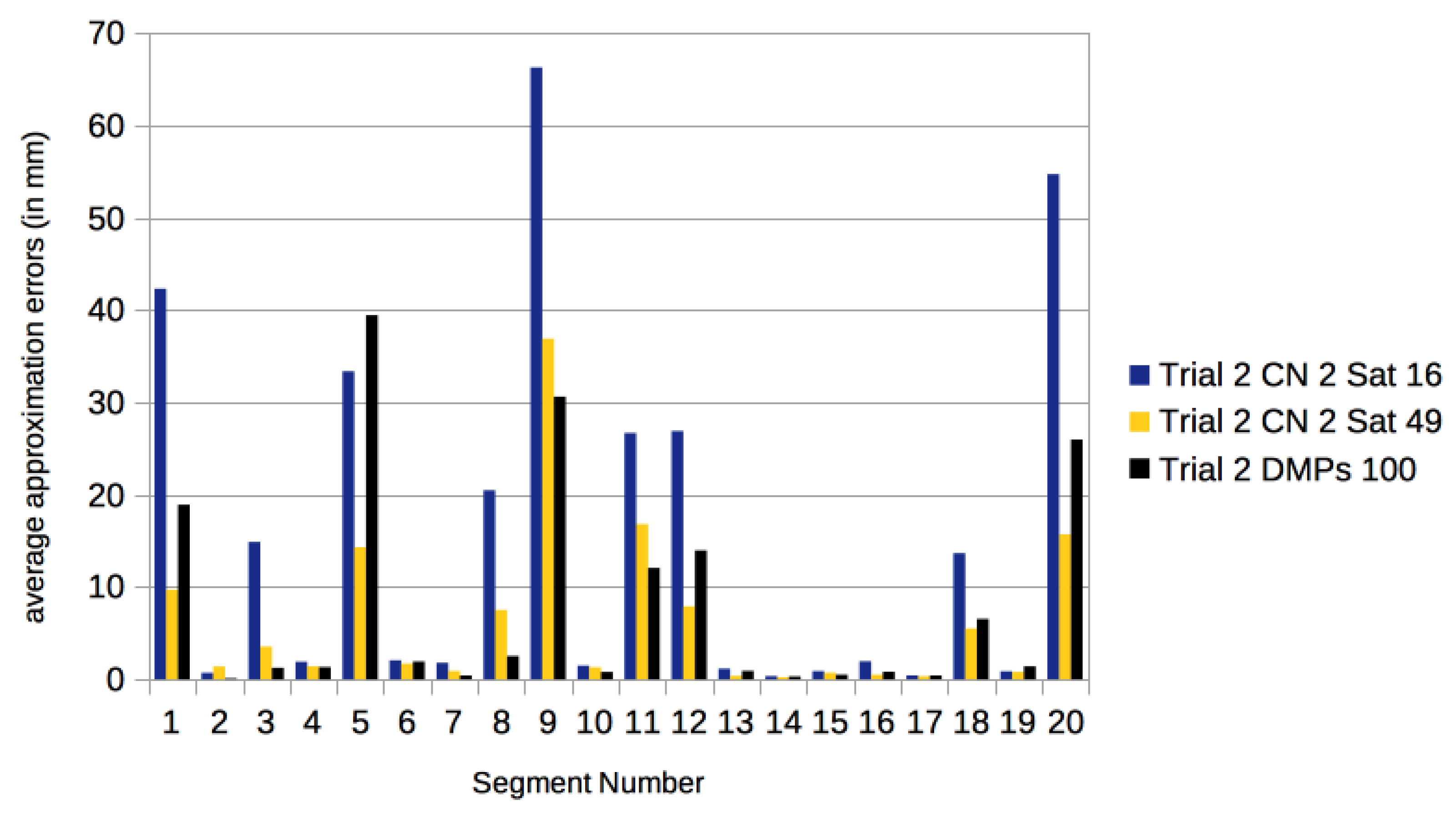
3.3. Comparison with Other Approaches
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ordóñez, F.J.; Roggen, D. Deep convolutional and LSTM recurrent neural networks for multimodal wearable activity recognition. Sensors 2016, 16, 115. [Google Scholar] [CrossRef] [PubMed]
- Holden, D.; Saito, J.; Komura, T. A deep learning framework for character motion synthesis and editing. ACM Trans. Graph. 2016, 35, 1–11. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, Y.; Xiao, S.; He, C.; Li, H. Auto-Conditioned LSTM Network for Extended Complex Human Motion Synthesis. 2017. Available online: http://xxx.lanl.gov/abs/1707.05363 (accessed on 1 September 2017).
- Fragkiadaki, K.; Levine, S.; Felsen, P.; Malik, J. Recurrent Network Models for Human Dynamics. In Proceedings of the 2015 IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 4346–4354. [Google Scholar]
- Holden, D.; Komura, T.; Saito, J. Phase-functioned neural networks for character control. ACM Trans. Graph. 2017, 36. [Google Scholar] [CrossRef]
- Vakulenko, S.; Morozov, I.; Radulescu, O. Maximal switchability of centralized networks. Nonlinearity 2016, 29, 2327–2354. [Google Scholar] [CrossRef]
- Chialvo, D.R. Emergent complex neural dynamics. Nat. Phys. 2010, 6, 744–750. [Google Scholar] [CrossRef]
- Jeong, H.; Tombor, B.; Albert, R.; Oltvai, Z.; Barabási, A. The large-scale organization of metabolic networks. Nature 2000, 407, 651–654. [Google Scholar] [PubMed]
- Jeong, H.; Mason, S.P.; Barabási, A.L.; Oltvai, Z.N. Lethality and centrality in protein networks. Nature 2001, 411, 41–42. [Google Scholar] [CrossRef] [PubMed]
- Rabinovich, M.I.; Varona, P.; Selverston, A.I.; Abarbanel, H.D. Dynamical principles in neuroscience. Rev. Mod. Phys. 2006, 78, 1213–1265. [Google Scholar] [CrossRef]
- Dunne, J.A.; Williams, R.J.; Martinez, N.D. Food-web structure and network theory: The role of connectance and size. Proc. Natl. Acad. Sci. USA 2002, 99, 12917–12922. [Google Scholar] [CrossRef] [PubMed]
- Jordano, P.; Bascompte, J.; Olesen, J.M. Invariant properties in coevolutionary networks of plant–animal interactions. Ecol. Lett. 2003, 6, 69–81. [Google Scholar] [CrossRef]
- Dezső, Z.; Barabási, A.L. Halting viruses in scale-free networks. Phys. Rev. E 2002, 65, 055103. [Google Scholar] [CrossRef] [PubMed]
- Chiel, H.J.; Beer, R.D.; Quinn, R.D.; Espenschied, K.S. Robustness of a distributed neural network controller for locomotion in a hexapod robot. IEEE Trans. Robot. Autom. 1992, 8, 293–303. [Google Scholar] [CrossRef]
- Collins, J.J.; Richmond, S.A. Hard-wired central pattern generators for quadrupedal locomotion. Biol. Cybern. 1994, 71, 375–385. [Google Scholar] [CrossRef]
- Ijspeert, A.J. Central pattern generators for locomotion control in animals and robots: A review. Neural Netw. 2008, 21, 642–653. [Google Scholar] [CrossRef] [PubMed]
- Golubitsky, M.; Stewart, I.; Buono, P.L.; Collins, J. A modular network for legged locomotion. Phys. D Nonlinear Phenom. 1998, 115, 56–72. [Google Scholar] [CrossRef]
- Chen, S.; Cowan, C.F.; Grant, P.M. Orthogonal least squares learning algorithm for radial basis function networks. IEEE Trans. Neural Netw. 1991, 2, 302–309. [Google Scholar] [CrossRef] [PubMed]
- Schilling, R.J.; Carroll, J.J.; Al-Ajlouni, A.F. Approximation of nonlinear systems with radial basis function neural networks. IEEE Trans. Neural Netw. 2001, 12, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Jonic, S.; Jankovic, T.; Gajic, V.; Popvic, D. Three machine learning techniques for automatic determination of rules to control locomotion. IEEE Trans. Biomed. Eng. 1999, 46, 300–310. [Google Scholar] [CrossRef] [PubMed]
- Schaal, S.; Peters, J.; Nakanishi, J. Control, planning, learning, and imitation with dynamic movement primitives. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems (IROS 2003), Las Vegas, NV, USA, 27–31 October 2003; pp. 1–21. [Google Scholar]
- Schaal, S. Dynamic movement primitives—A framework for motor control in humans and humanoid robotics. In Adaptive Motion of Animals and Machines; Springer: Tokyo, Japan, 2006; pp. 261–280. [Google Scholar]
- Tamosiunaite, M.; Nemec, B.; Ude, A.; Wörgötter, F. Learning to pour with a robot arm combining goal and shape learning for dynamic movement primitives. Robot. Auton. Syst. 2011, 59, 910–922. [Google Scholar] [CrossRef]
- Ernesti, J.; Righetti, L.; Do, M.; Asfour, T.; Schaal, S. Encoding of periodic and their transient motions by a single dynamic movement primitive. In Proceedings of the 2012 12th IEEE-RAS International Conference on Humanoid Robots, Osaka, Japan, 29 November–1 December 2012; pp. 57–64. [Google Scholar]
- Ijspeert, A.J.; Nakanishi, J.; Hoffmann, H.; Pastor, P.; Schaal, S. Dynamical movement primitives: Learning attractor models for motor behaviors. Neural Comput. 2013, 25, 328–373. [Google Scholar] [CrossRef] [PubMed]
- Kovar, L.; Gleicher, M. Automated extraction and parameterization of motions in large data sets. ACM Trans. Graph. 2004, 23, 559–568. [Google Scholar] [CrossRef]
- Chai, J.; Hodgins, J.K. Performance animation from low-dimensional control signals. ACM Trans. Graph. 2005, 24, 686–696. [Google Scholar] [CrossRef]
- Krüger, B.; Tautges, J.; Weber, A.; Zinke, A. Fast local and global similarity searches in large motion capture databases. In Proceedings of the Eurographics/ACM SIGGRAPH Symposium on Computer Animation, Madrid, Spain, 2–4 July 2010; pp. 1–10. [Google Scholar]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef]
- Bascompte, J. Networks in ecology. Basic Appl. Ecol. 2007, 8, 485–490. [Google Scholar] [CrossRef]
- Tanizawa, T.; Paul, G.; Cohen, R.; Havlin, S.; Stanley, H.E. Optimization of network robustness to waves of targeted and random attacks. Phys. Rev. E 2005, 71, 047101. [Google Scholar] [CrossRef] [PubMed]
- Albert, R.; Jeong, H.; Barabási, A.L. Error and attack tolerance of complex networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef] [PubMed]
- Bar-Yam, Y.; Epstein, I.R. Response of complex networks to stimuli. Proc. Natl. Acad. Sci. USA 2004, 101, 4341–4345. [Google Scholar] [CrossRef] [PubMed]
- Carlson, J.M.; Doyle, J. Complexity and robustness. Proc. Natl. Acad. Sci. USA 2002, 99, 2538–2545. [Google Scholar] [CrossRef] [PubMed]
- Vakulenko, S.A.; Radulescu, O. Flexible and robust networks. J. Bioinform. Comput. Biol. 2012, 10, 1241011. [Google Scholar] [CrossRef] [PubMed]
- Vakulenko, S.; Radulescu, O. Flexible and robust patterning by centralized gene networks. Fundam. Inform. 2012, 118, 345–369. [Google Scholar]
- Vakulenko, S. A system of coupled oscillators can have arbitrary prescribed attractors. J. Phys. A Gen. Phys. 1994, 27, 2335–2349. [Google Scholar] [CrossRef]
- Carnegie Mellon University Graphics Lab. Motion Capture Database. Available online: http://mocap.cs.cmu.edu (accessed on 1 June 2017).
- Krüger, B.; Vögele, A.; Willig, T.; Yao, A.; Klein, R.; Weber, A. Efficient unsupervised temporal segmentation of motion data. IEEE Trans. Multimed. 2017, 19, 797–812. [Google Scholar] [CrossRef]
- Tautges, J.; Zinke, A.; Krüger, B.; Baumann, J.; Weber, A.; Helten, T.; Müller, M.; Seidel, H.P.; Eberhardt, B. Motion reconstruction using sparse accelerometer data. ACM Trans. Graph. 2011, 30, 18:1–18:12. [Google Scholar] [CrossRef]
- Riaz, Q.; Tao, G.; Krüger, B.; Weber, A. Motion reconstruction using very few accelerometers and ground contacts. Graph. Models 2015, 79, 23–38. [Google Scholar] [CrossRef]
- Anderson, D.R. Model Based Inference in the Life Sciences; Springer: New York, NY, USA, 2008. [Google Scholar]
- Vögele, A.; Zsoldos, R.; Krüger, B.; Licka, T. Novel methods for surface EMG analysis and exploration based on multi-modal gaussian mixture models. PLoS ONE 2016. [Google Scholar] [CrossRef] [PubMed]
- Pullen, K.; Bregler, C. Motion capture assisted animation: Texturing and synthesis. ACM Trans. Graph. 2002, 21, 501–508. [Google Scholar] [CrossRef]
- Lee, Y.; Wampler, K.; Bernstein, G.; Popović, J.; Popović, Z. Motion fields for interactive character locomotion. ACM Trans. Graph. 2010, 29, 138:1–138:8. [Google Scholar] [CrossRef]
| Number of Oscillators | Number of Satellites | Integral Relative Accuracies | |||
|---|---|---|---|---|---|
| Segment 1 | Segment 2 | Segment 3 | Segment 4 | ||
| 1 | 100 | 0.2133 | 0.0827 | 0.423 | 0.0749 |
| 2 | 25 | 0.1207 | 0.0486 | 0.0405 | 0.076 |
| 2 | 50 | 0.0351 | 0.0089 | 0.0084 | 0.0586 |
| 2 | 100 | 0.0189 | 0.0068 | 0.0029 | 0.0299 |
| 3 | 25 | 0.0832 | 0.0253 | 0.0297 | 0.0685 |
| 3 | 100 | 0.0133 | 0.0063 | 0.0031 | 0.0071 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vakulenko, S.; Radulescu, O.; Morozov, I.; Weber, A. Centralized Networks to Generate Human Body Motions. Sensors 2017, 17, 2907. https://doi.org/10.3390/s17122907
Vakulenko S, Radulescu O, Morozov I, Weber A. Centralized Networks to Generate Human Body Motions. Sensors. 2017; 17(12):2907. https://doi.org/10.3390/s17122907
Chicago/Turabian StyleVakulenko, Sergei, Ovidiu Radulescu, Ivan Morozov, and Andres Weber. 2017. "Centralized Networks to Generate Human Body Motions" Sensors 17, no. 12: 2907. https://doi.org/10.3390/s17122907
APA StyleVakulenko, S., Radulescu, O., Morozov, I., & Weber, A. (2017). Centralized Networks to Generate Human Body Motions. Sensors, 17(12), 2907. https://doi.org/10.3390/s17122907





