An Advanced Hybrid Technique of DCS and JSRC for Telemonitoring of Multi-Sensor Gait Pattern
Abstract
1. Introduction
2. Distributed Compressed Sensing for Multi-Sensor Gait Data
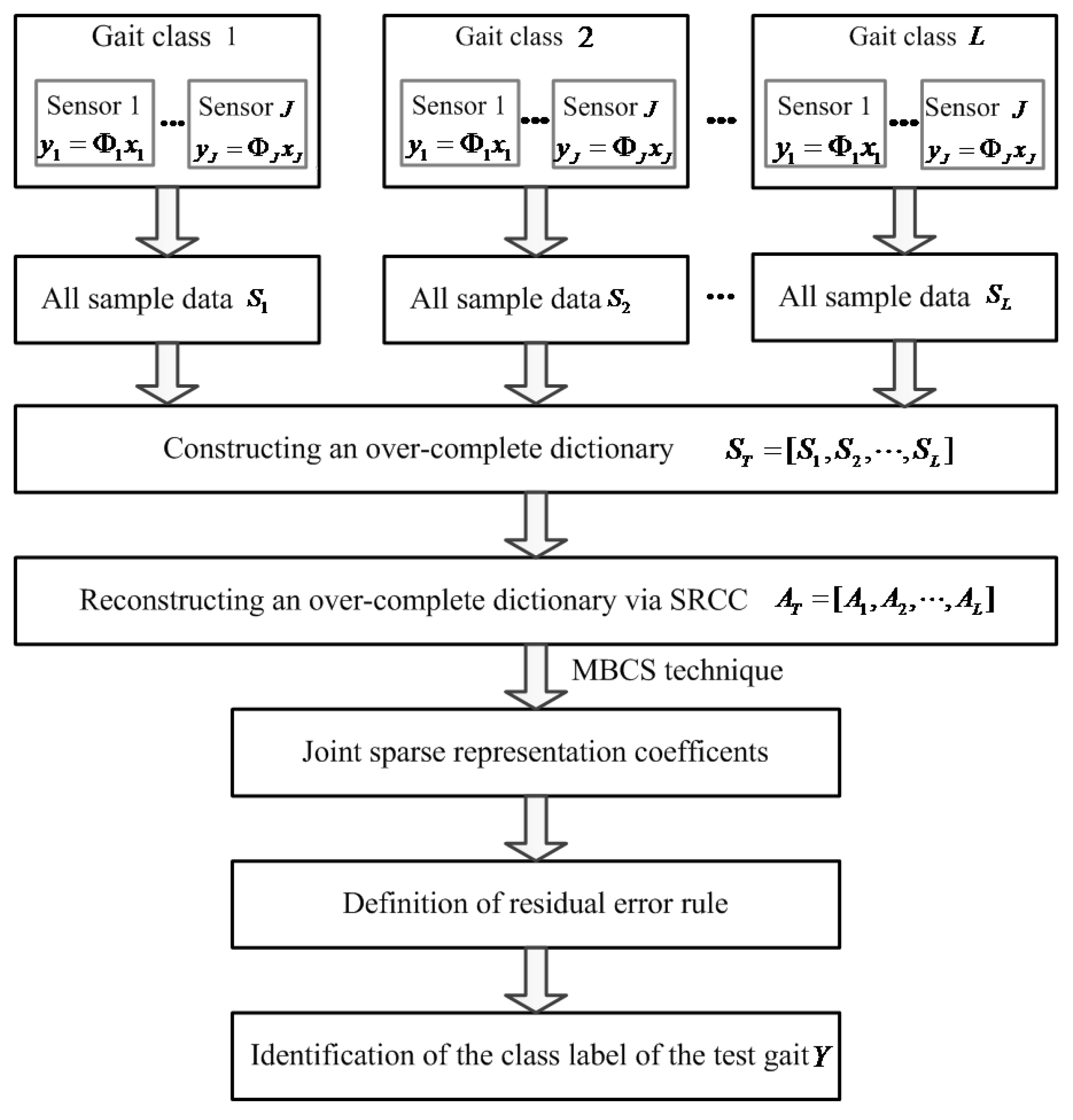
3. A Novel Neighboring JSRC Model for Gait Classification
3.1. Constructing an Over-Complete Dictionary for JSRC
3.2. Reconstructing a New Over-Complete Dictionary for JSRC
3.3. MBCS Technique for Solving Joint Sparse Representation Coefficients
3.4. The Definition of Minimal Residual Error Rule for Gait Classification
4. Materials and Methods
4.1. The Selection of Multi-Sensor Gait Data
4.2. Data Preprocessing
4.3. Training and Testing the Gait-Classification Model
4.4. Evaluation Criteria for the Proposed Technique
5. Results
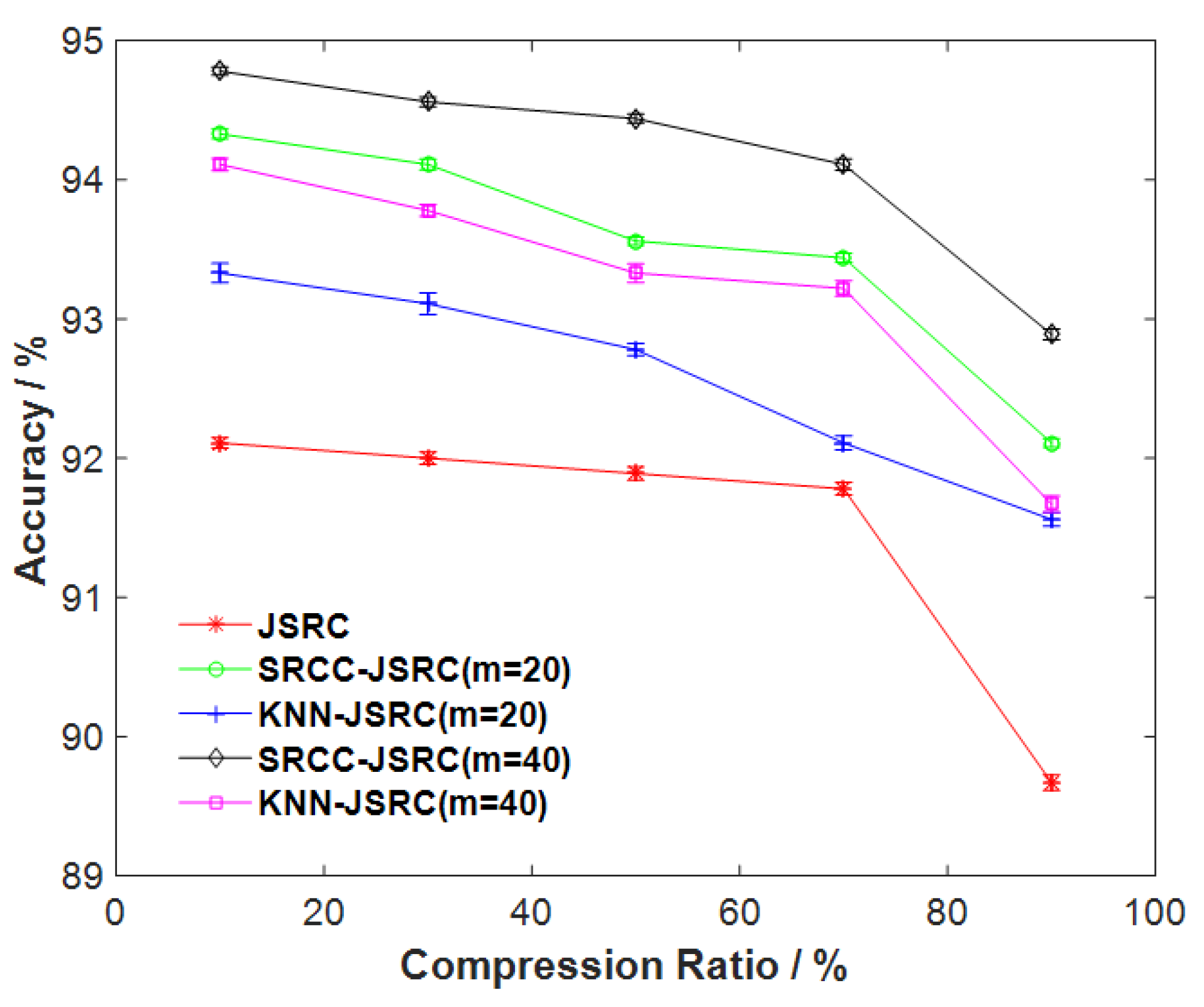
5.1. The Evaluation of the Effect of DCS on the Developed Neighboring JSRC
5.2. The Assessment of Gait-Classification Performance Based on the Different Compression Ratios
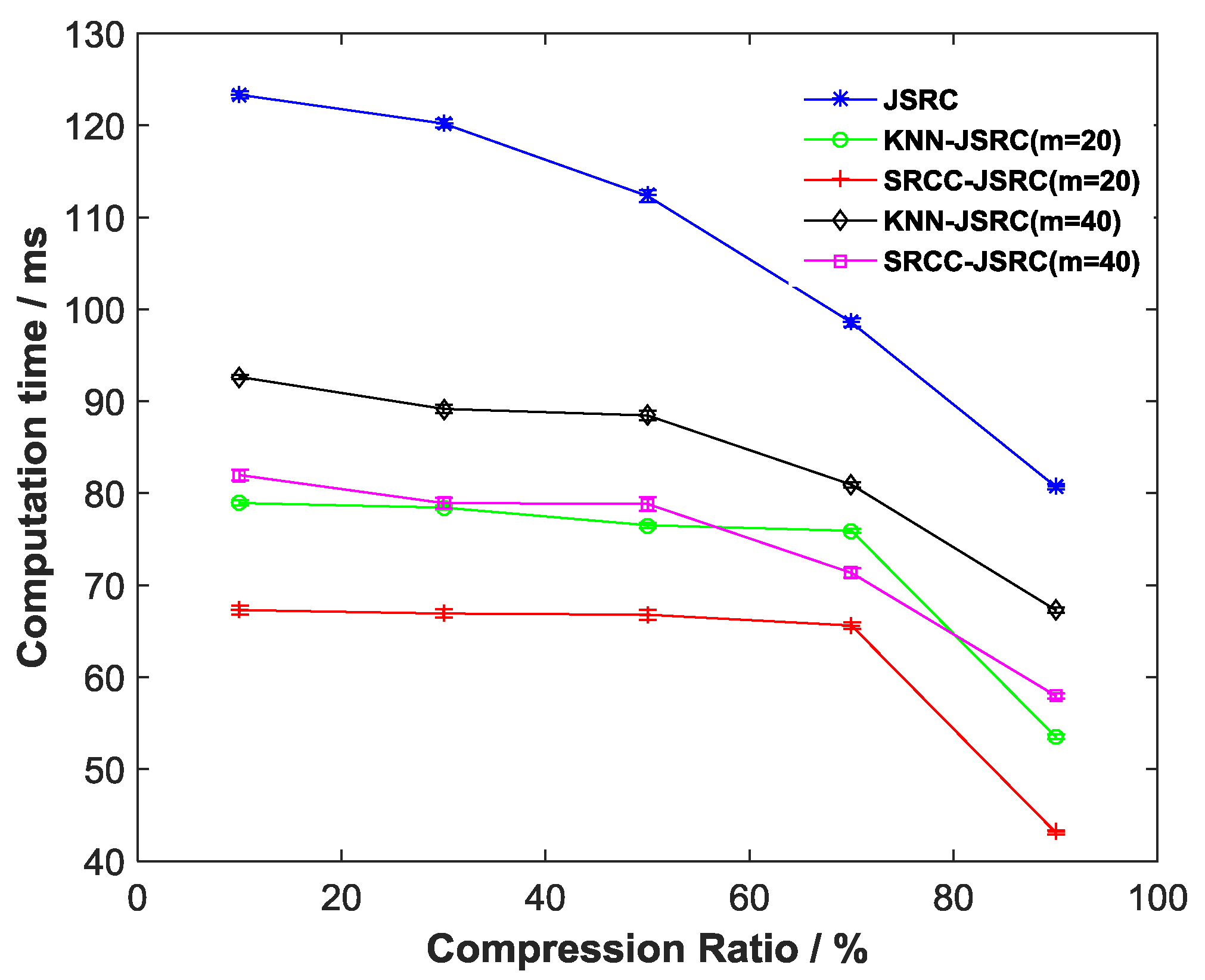
5.3. The Evaluation of Computation Time Cost Based on the Different Compression Ratios
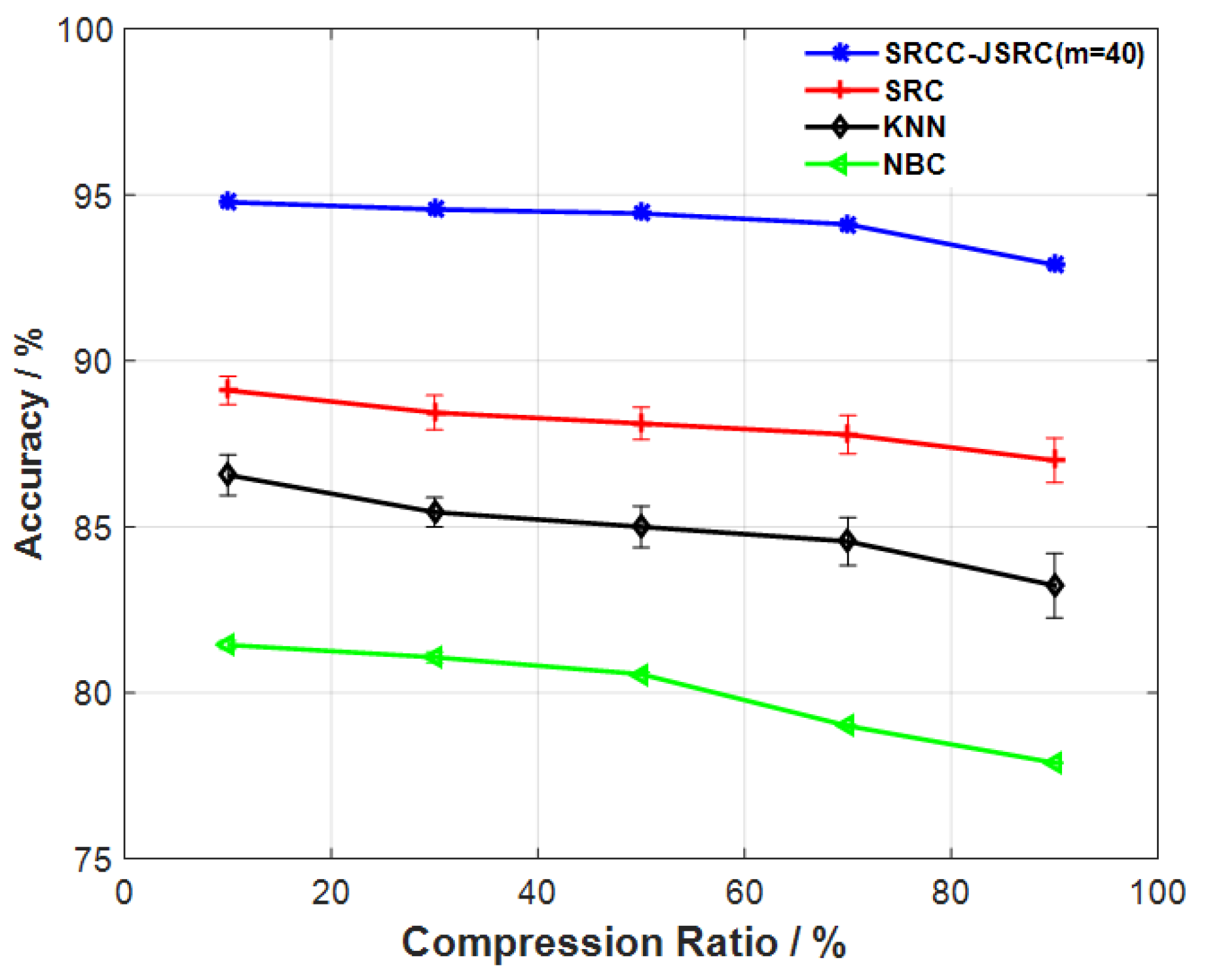
5.4. Evaluation of Our Proposed Model for Gait Telemonitoring
6. Discussion
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Ersoy, H.; Alemdar, C. Wireless sensor networks for healthcare: A survey. Comput. Netw. 2010, 54, 2688–2710. [Google Scholar]
- Latre, B.; Braem, B.; Moerman, I.; Blondia, C.; Demeester, P. A survey on wireless body area networks. Wirel. Netw. 2011, 17, 1–18. [Google Scholar] [CrossRef]
- Chen, M.; Gonzalez, S.; Vasilakos, A.; Cao, H.; Leung, V. Body Area Networks: A Survey. Mob. Netw. Appl. 2011, 16, 171–193. [Google Scholar] [CrossRef]
- Wong, W.Y.; Wong, M.S.; Lo, K.H. Clinical applications of sensors for human posture and movement analysis: A review. Prosthet. Orthot. Int. 2007, 31, 62–75. [Google Scholar] [CrossRef] [PubMed]
- Hao, Y.; Foster, R. Wireless body sensor networks for health-monitoring applications. Physiol. Meas. 2008, 29, 27–56. [Google Scholar] [CrossRef] [PubMed]
- Olivares, A.; Olivares, G.; Mula, F.; Gorriz, J.; Ramirez, J. Wagyromag: Wireless sensor network for monitoring and processing human body movement in healthcare applications. J. Syst. Arch. 2011, 57, 905–915. [Google Scholar] [CrossRef]
- Pantelopoulos, A.; Bourbakis, N.G. A survey on wearable sensor-based systems for health monitoring and prognosis. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2010, 40, 1–12. [Google Scholar] [CrossRef]
- Taleb, T.; Bottazzi, D.; Guizani, M.; Nait-Charif, H. Angelah: A framework for assisting elders at home. IEEE J. Sel. Areas Commun. 2009, 27, 480–494. [Google Scholar] [CrossRef]
- Patel, S.; Park, H.; Bonato, P.; Chan, L.; Rodgers, M. A review of wearable sensors and systems with application in rehabilitation. J. Neuroeng. Rehabil. 2012, 9, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Abdelkrim, H.; Marion, S. Wireless sensor networks for rehabilitation applications: Challenges and opportunities. J. Netw. Comput. Appl. 2013, 36, 1–15. [Google Scholar]
- Ullah, S.; Higgins, H.; Braem, B.; Latre, B.; Blondia, C.; Moerman, I.; Kwak, K.S. A comprehensive survey of wireless body area networks. J. Med. Syst. 2010, 36, 1065–1094. [Google Scholar] [CrossRef] [PubMed]
- Mo, L.F.; Liu, S.P.; Gao, R.X.; John, D.; Staudenmayer, J.W.; Freedson, P.S. Wireless design of a multisensor system for physical activity monitoring. IEEE Trans. Biomed. Eng. 2012, 59, 3230–3237. [Google Scholar] [PubMed]
- Marinkovic, S.J.; Popovici, E.M.; Spagnol, C.; Faul, S.; Marnane, W.P. Energy-efficient low duty cycle MAC protocol for wireless body area networks. IEEE Trans. Inf. Technol. Biomed. 2009, 13, 915–925. [Google Scholar] [CrossRef] [PubMed]
- Donoho, D. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Akimura, D.; Kawahara, Y.; Asami, T. Compressed sensing method for human activity sensing using mobile phone accelerometers. In Proceedings of the Ninth International Conference on Networked Sensing Systems (INSS), Antwerp, Belgium, 6 June 2012; pp. 1–4. [Google Scholar]
- Wu, J.; Xu, H. An advanced scheme of compressed sensing of acceleration data for telemonintoring of human gait. Biomed. Eng. Online 2016, 15, 1–17. [Google Scholar]
- Holmes, C.C.; Adams, N.M. A probabilistic nearest neighbour method for statistical pattern recognition. J. R. Stat. Soc. Ser. B 2002, 64, 295–306. [Google Scholar] [CrossRef]
- Hanson, M.A.; Powell, H.C.; Barth, A.T.; Lach, J.; Brandt-Pearce, M. Neural network gait classification for On-Body inertial sensors. In Proceedings of the 6th International Workshop on Wearable and Implantable Body Sensor Networks, Berkeley, CA, USA, 3–5 June 2009; pp. 181–186. [Google Scholar]
- Burges, C.J. A Tutorial on Support Vector Machines for Pattern Recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Mannini, A.; Sabatini, A.M. Machine Learning methods for classifying human physical activity from on-body accelerometer. Sensors 2010, 10, 1154–1175. [Google Scholar] [CrossRef] [PubMed]
- Taborri, J.; Rossi, S.; Palermo, E.; Patanè, F.; Cappa, P. A novel HMM distributed classifier for the detection of gait phases by means of a wearable inertial sensor network. Sensors 2014, 14, 16212–16234. [Google Scholar] [CrossRef] [PubMed]
- Mannini, A.; Sabatini, A.M.; Intille, S.S. Human gait detection from wrist-worn accelerometer data. Gait Posture 2013, 37 (Suppl. 1), S26–S27. [Google Scholar] [CrossRef]
- Wright, J.; Yang, A.Y.; Ganesh, A.; Sastry, S.S.; Ma, Y. Robust face recognition via sparse representation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 210–227. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Sawchuk, A.A. Human daily activity recognition with sparse representation using wearable sensors. IEEE J. Biomed. Health Inform. 2013, 17, 553–560. [Google Scholar]
- Allen, Y.Y.; Roozbeh, J.; Shankar, S.S.; Ruzena, B. Distributed Recognition of Human Actions Using Wearable Motion Sensor Networks. J. Ambient Intell. Smart Environ. 2009, 1, 103–115. [Google Scholar]
- Giannini, S.; Catani, F.; Benedetti, M.G.; Leardini, L. Gait Analysis: Methodologies and Clinical Applications; IOS Press: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Chau, T. A review of analytical techniques for gait data. Part 1: Fuzzy, statistical and fractal methods. Gait Posture 2001, 13, 49–66. [Google Scholar] [PubMed]
- Chau, T. A review of analytical techniques for gait data. Part 2: Neural network and wavelet methods. Gait Posture 2001, 13, 102–120. [Google Scholar] [PubMed]
- Jeevan, K.; Sridhar, K. Compressive sensing of foot gait signals and its application for the estimation of clinical relevant time series. IEEE Trans. Biomed. Eng. 2015, 63, 1401–1415. [Google Scholar]
- Baron, D.; Wakin, M.B.; Duarte, M.F.; Sarvotham, S.; Baraniuk, R.G. Distributed Compressed Sensing. Available online: http://www.dsp.rice.edu/~rorb/pdf/DCS112005.pdf (accessed on 1 August 2005).
- Duarte, M.F.; Sarvotham, S.; Baron, D.; Wakin, M.; Baraniuk, R.G. Distributed compressed sensing of jointly sparse signals. In Proceedings of the 39th Asilomar Conference on Signal, System and Computer, Pacific Grove, CA, USA, 30 October–2 November 2005; pp. 1537–1541. [Google Scholar]
- Tropp, J.A.; Gilbert, A.C.; Strauss, M.J. Simultaneous sparse approximation via greedy pursuit. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Philadelphia, PA, USA, 19–23 March 2005; pp. 721–724. [Google Scholar]
- Luo, J.; Yang, B.; Chen, Z. Color image restoration via extended joint sparse model. In Communications in Computer and Information Science, Proceedings of the Pattern Recognition, Beijing, China, 24–26 September 2012; Springer: Berlin/Heidelberg, Germany, 2012; Volume 321, pp. 497–504. [Google Scholar]
- Yuan, X.T.; Liu, X.B.; Yan, S.C. Visual classification with multitask joint sparse representation. IEEE Trans. Image Process. 2012, 21, 4349–4360. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Yang, Z. Spatial correlation-based distributed compressed sensing in wireless sensor networks. In Proceedings of the 2010 6th International Conference on Wireless Communications Networking and Mobile Computing (WiCOM), Chengdu, China, 23–25 September 2010; pp. 1–4. [Google Scholar]
- Yang, H.; Huang, L.; Xu, H.; Liu, A. Distributed compressed sensing in wireless local area networks. Int. J. Commun. Syst. 2015, 27, 2723–2743. [Google Scholar] [CrossRef]
- Ying, H.; Schlosser, M.; Schnitzer, A.; Schafer, T.; Schlafke, M.E.; Leonhardt, S.; Schiek, M. Distributed intelligent sensor network for the rehabilitation of Parkinson’s patients. IEEE Trans. Inf. Technol. Biomed. 2011, 15, 268–276. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Luong, H.Q.; Philips, W.; Song, H.; Cui, H. Sparse representation and position prior based face hallucination upon classified over-complete dictionaries. Signal Process. 2012, 92, 2066–2074. [Google Scholar] [CrossRef]
- Dong, W.; Li, X.; Zhang, D.; Shi, G. Sparsity-based image denoising via dictionary learning and structural clustering. In Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011; pp. 457–464. [Google Scholar]
- Sundman, D.; Saikat, C.; Skoglund, M. A greedy pursuit algorithm for distributed compressed sensing. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 2729–2732. [Google Scholar]
- Xiao, L.; Li, R.F.; Luo, J.; Duan, M. Activity recognition via distributed random projection and joint sparse representation in body sensor networks. In Proceedings of the 7th China Conference Advances in Wireless Sensor Networks (CWSN2013), Qingdao, China, 17–19 October 2013; pp. 51–60. [Google Scholar]
- Zhang, Z.; Jung, T.; Makeig, S.; Pi, Z.; Rao, B.D. Spatiotemporal sparse Bayesian learning with applications to compressed sensing of multichannel physiological signals. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 1186–1197. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Nasrabadi, N.M.; Zhang, Y.; Huang, T.S. Multi-Observation Visual Recognition via Joint Dynamic Sparse Representation. In Proceedings of the IEEE International Conference of Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 595–602. [Google Scholar]
- Guha, T.; Ward, R.K. Learning Sparse Representations for Human Action Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1576–1588. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Chen, N.; Peng, J. Nearest regularized joint sparse representation for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2016, 13, 424–428. [Google Scholar] [CrossRef]
- Shekhar, S.; Patel, V.M.; Nasrabadi, N.M.; Chellappa, R. Joint sparse representation for robust multimodal biometrics recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 36, 113–126. [Google Scholar] [CrossRef] [PubMed]
- Sarvotham, S.; Wakin, M.B.; Baron, D.; Duarte, M.F.; Baraniuk, R.G. Analysis of the DCS One-Stage Greedy Algorithm for Common Sparse Supports. Available online: http://www.dsp.rice.edu/sites/dsp.rice.edu/files/publications/report/2005/analysis-ece-2005.pdf (accessed on 1 October 2005).
- Ji, S.; Dunson, D.; Carin, L. Multitask compressive sensing. IEEE Trans. Signal Process. 2009, 57, 92–106. [Google Scholar] [CrossRef]
| All Samples Data Size | ||
|---|---|---|
| All Subjects | Gait Pattern Classes | Window Samples |
| 20 | 9 | 10 |
| Classification Algorithms | Accuracy/% | Computation Time/ms |
|---|---|---|
| JSRC | 91.33 | 132.8510 |
| KNN-JSRC (m = 20) | 94.00 | 77.0239 |
| KNN-JSRC (m = 40) | 94.11 | 87.4365 |
| KNN-JSRC (m = 60) | 94.44 | 102.5404 |
| SRCC-JSRC (m = 20) | 92.67 | 66.1759 |
| SRCC-JSRC (m = 40) | 94.44 | 78.0513 |
| SRCC-JSRC (m = 60) | 94.89 | 90.7440 |
| Algorithms | SRCC-JSRC (m = 40) | SRCC-JSRC (m = 20) | KNN-JSRC (m = 40) | KNN-JSRC (m = 20) | JSRC |
|---|---|---|---|---|---|
| Mean value (%) | 94.58 | 94.23 | 93.31 | 93.13 | 92.11 |
| SD value | (0.043, 0.076) | (0.029, 0.038) | (0.041, 0.066) | (0.042, 0.078) | (0.037, 0.054) |
| Algorithms | SRCC-JSRC (m = 40) | SRCC-JSRC (m = 20) | KNN-JSRC (m = 40) | KNN-JSRC (m = 20) | JSRC |
|---|---|---|---|---|---|
| Mean value (ms) | 77.65 | 65.98 | 88.03 | 76.45 | 132.06 |
| SD value | (0.032, 0.065) | (0.025, 0.034) | (0.036, 0.061) | (0.036, 0.072) | (0.032, 0.049) |
| Standing | Sitting | Walk Forward | Turn Left | Turn Right | Upstairs | Downstairs | Jog | Jump | Total | Recall | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Standing | 186 | 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 200 | 93% |
| Sitting | 6 | 184 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 200 | 92% |
| Walk forward | 4 | 0 | 194 | 0 | 0 | 2 | 0 | 0 | 0 | 200 | 97% |
| Turn left | 4 | 0 | 6 | 188 | 2 | 0 | 0 | 0 | 0 | 200 | 94% |
| Turn right | 6 | 4 | 0 | 0 | 190 | 0 | 0 | 0 | 0 | 200 | 95% |
| Upstairs | 0 | 6 | 0 | 0 | 0 | 196 | 0 | 4 | 0 | 200 | 98% |
| Downstairs | 4 | 2 | 0 | 0 | 0 | 0 | 194 | 0 | 0 | 200 | 97% |
| Jog | 0 | 0 | 0 | 0 | 0 | 4 | 1 | 200 | 0 | 200 | 100% |
| Jump | 0 | 0 | 6 | 0 | 0 | 4 | 6 | 4 | 180 | 200 | 90% |
| Total | 210 | 212 | 216 | 188 | 192 | 206 | 201 | 208 | 180 | ||
| Precision | 88% | 88% | 90% | 100% | 99% | 96% | 97% | 96% | 100% |
| Indices | Compression Ratio | Accuracy | Computation Time | Precision | Recall |
|---|---|---|---|---|---|
| F values | 70.51 | 101.21 | 146.81 | 224.92 | 182.47 |
| Significance values | 0.0235 | 0.0379 | 0.0342 | 0.0288 | 0.0357 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Wang, J.; Ling, Y.; Xu, H. An Advanced Hybrid Technique of DCS and JSRC for Telemonitoring of Multi-Sensor Gait Pattern. Sensors 2017, 17, 2764. https://doi.org/10.3390/s17122764
Wu J, Wang J, Ling Y, Xu H. An Advanced Hybrid Technique of DCS and JSRC for Telemonitoring of Multi-Sensor Gait Pattern. Sensors. 2017; 17(12):2764. https://doi.org/10.3390/s17122764
Chicago/Turabian StyleWu, Jianning, Jiajing Wang, Yun Ling, and Haidong Xu. 2017. "An Advanced Hybrid Technique of DCS and JSRC for Telemonitoring of Multi-Sensor Gait Pattern" Sensors 17, no. 12: 2764. https://doi.org/10.3390/s17122764
APA StyleWu, J., Wang, J., Ling, Y., & Xu, H. (2017). An Advanced Hybrid Technique of DCS and JSRC for Telemonitoring of Multi-Sensor Gait Pattern. Sensors, 17(12), 2764. https://doi.org/10.3390/s17122764





