A Robust High-Accuracy Ultrasound Indoor Positioning System Based on a Wireless Sensor Network
Abstract
:1. Introduction
2. Global Description of the UIPS
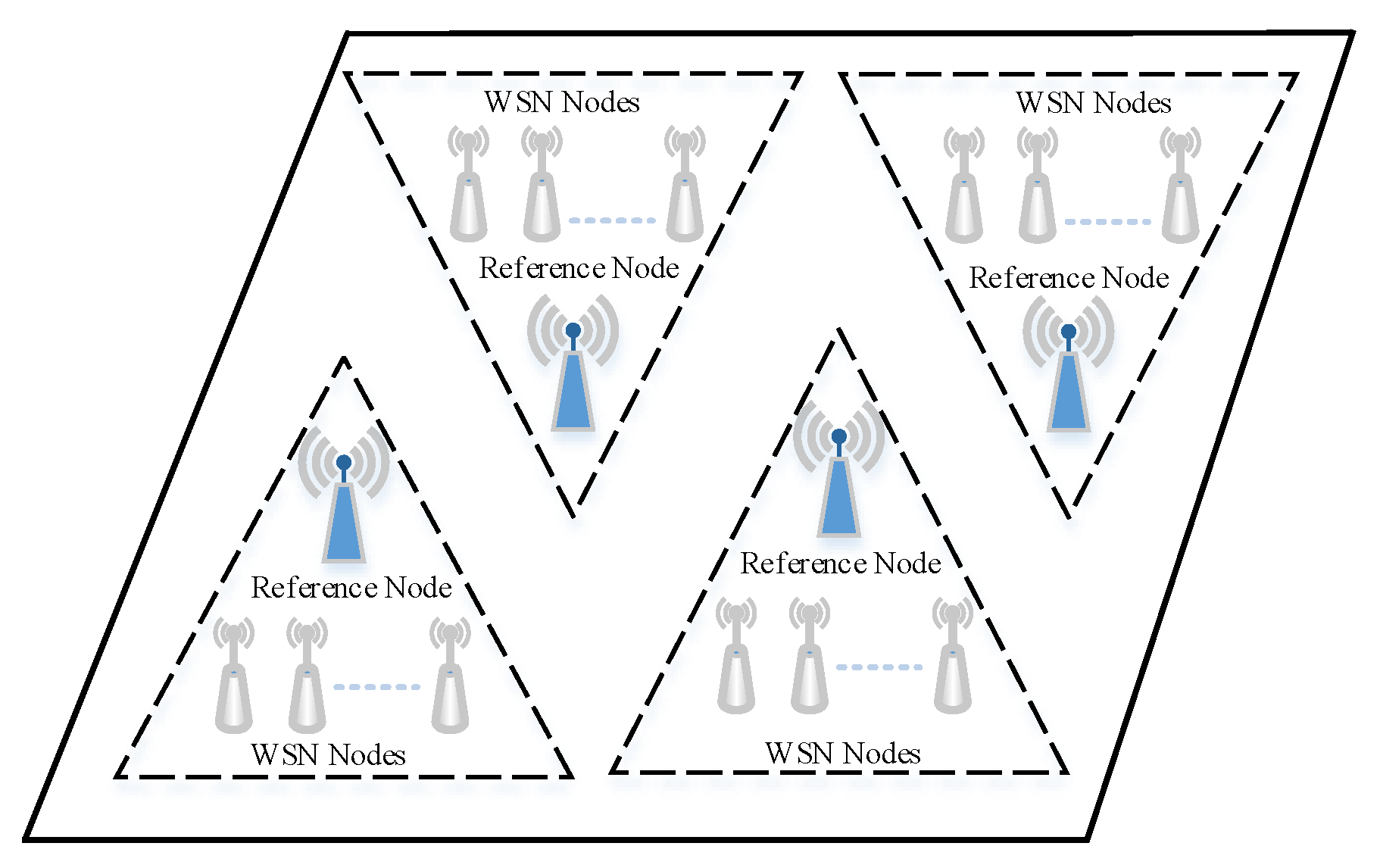
2.1. UIPS Architecture
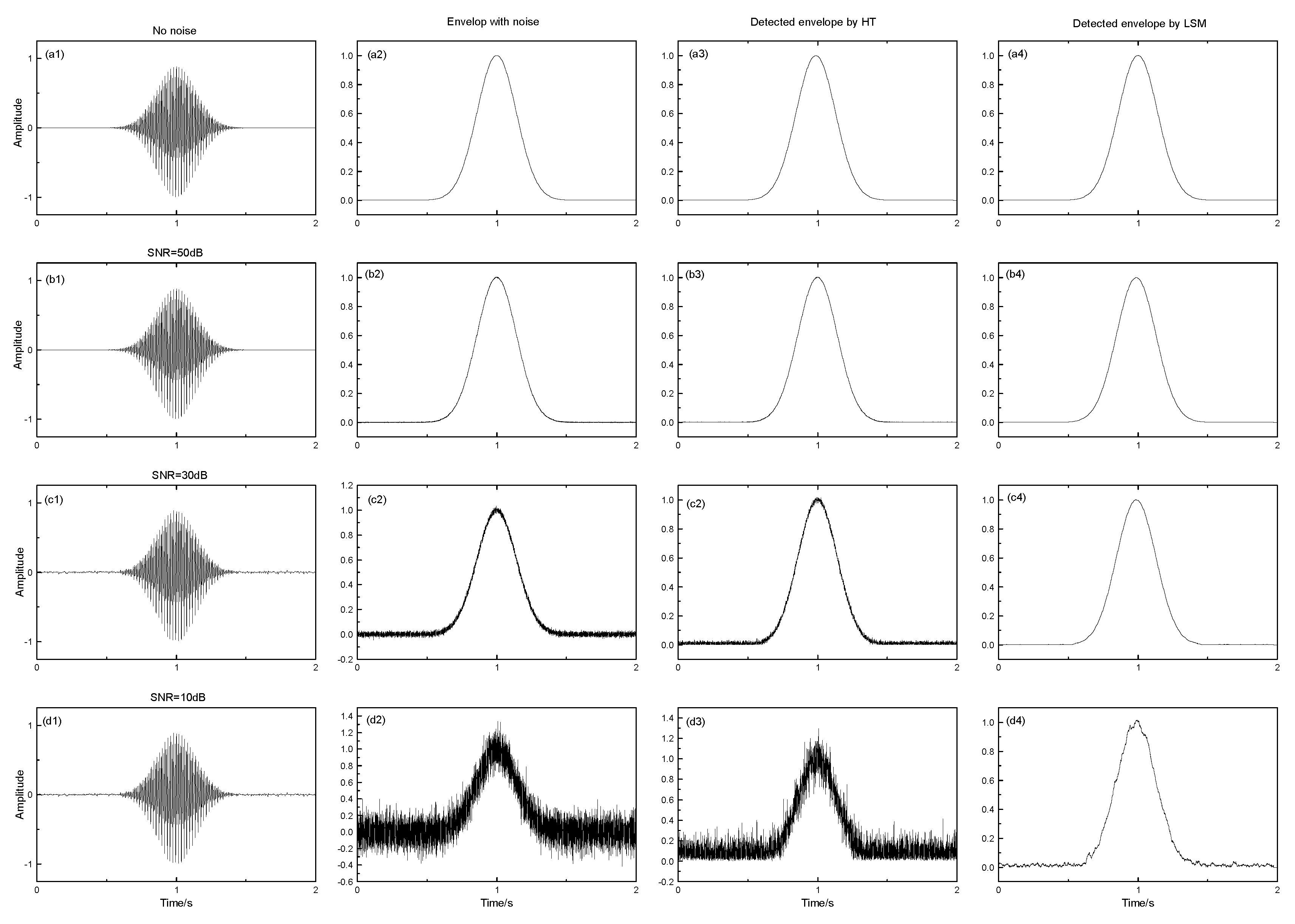
2.2. Ultrasonic Envelope Detection
3. Implementation of Positioning
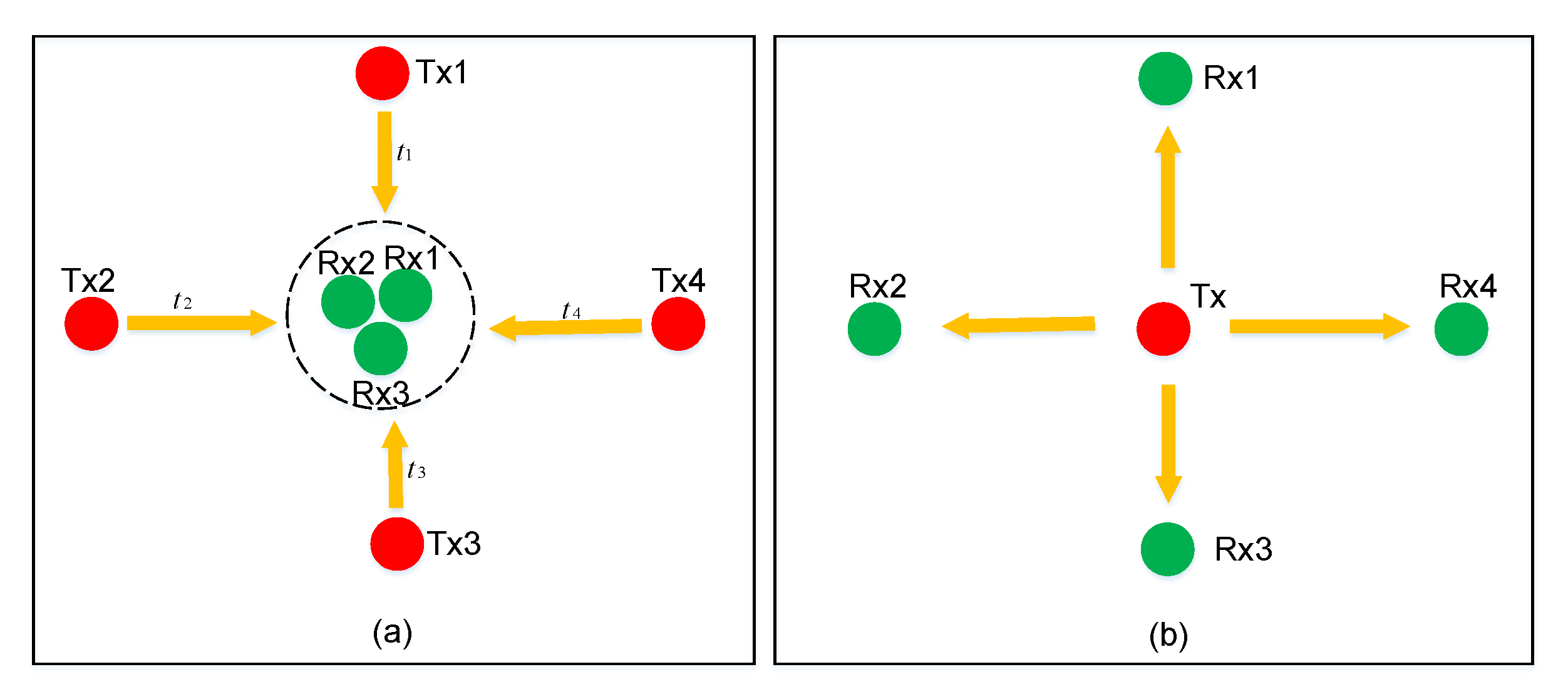
3.1. Time Synchronization
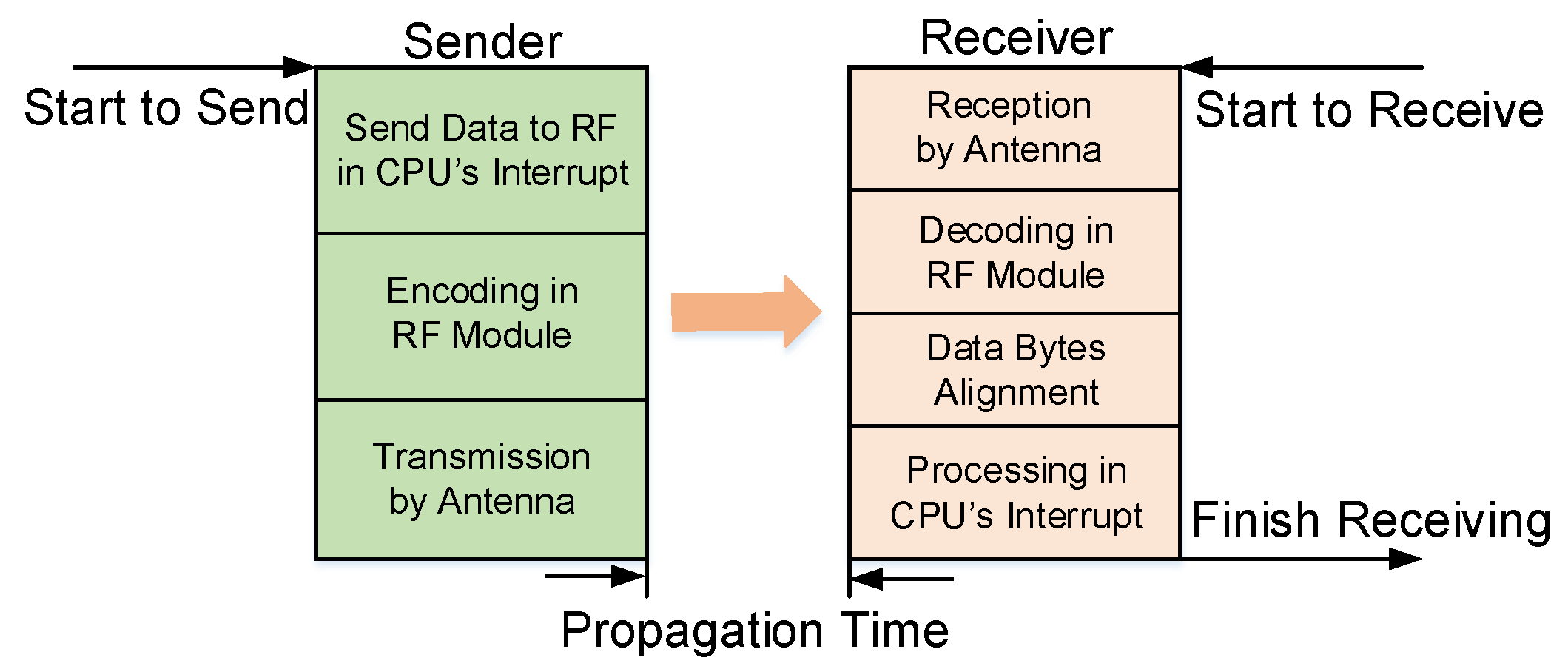
3.2. Ultrasonic TOF Estimation
3.3. Estimation of Distances and Positioning
4. Implementation of the UIPS
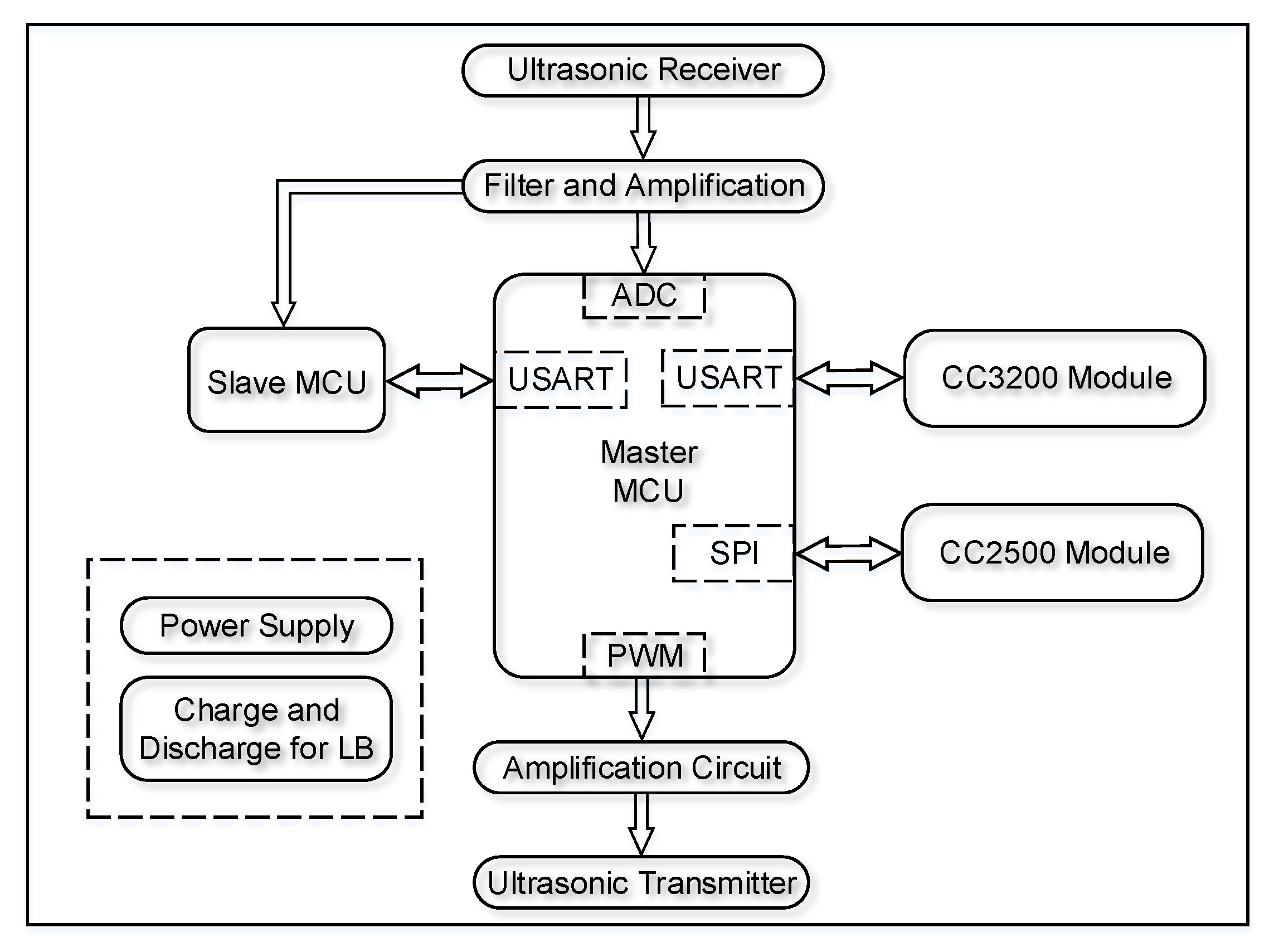
4.1. Hardware
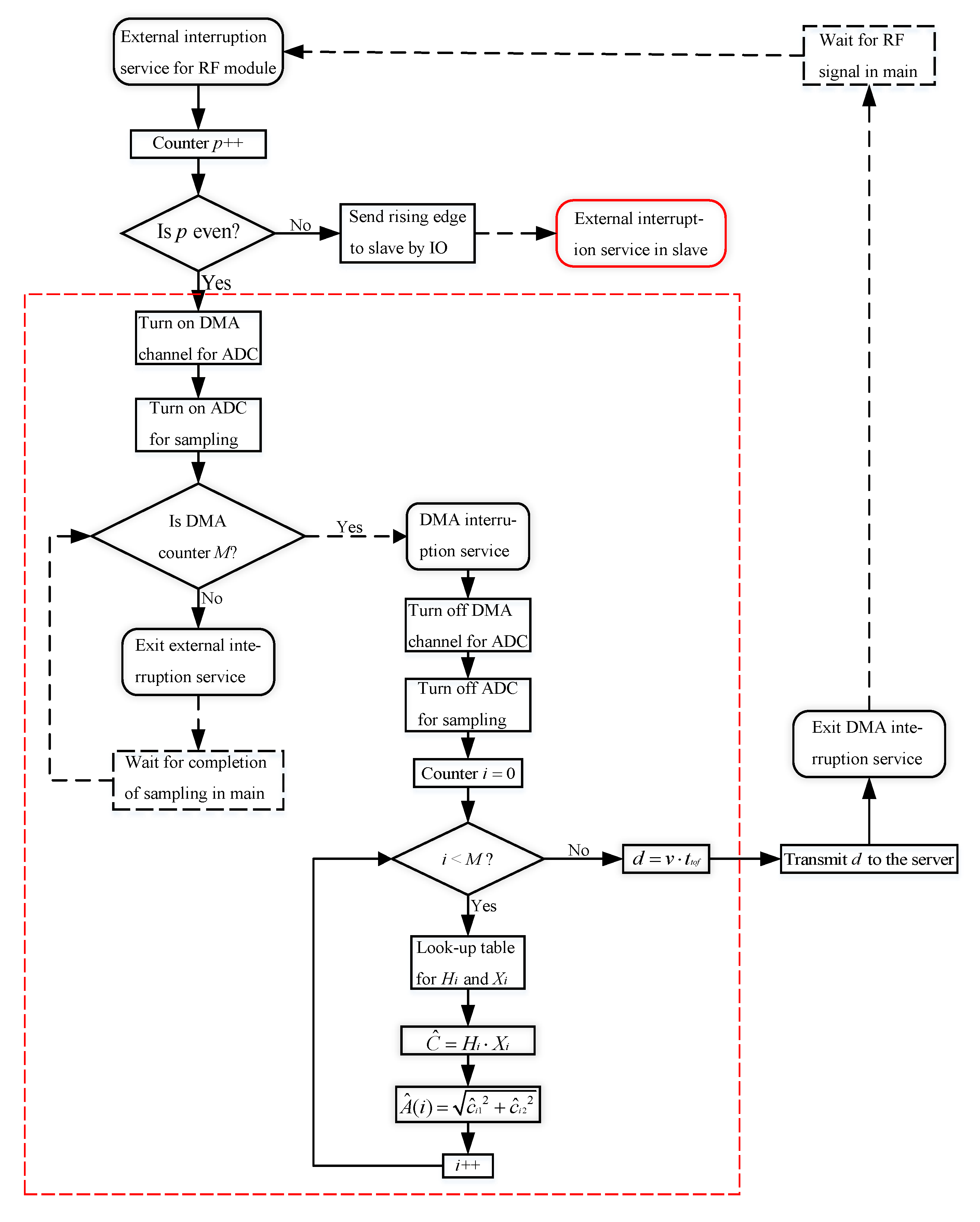
4.2. Software
5. Experiments
5.1. Simulation
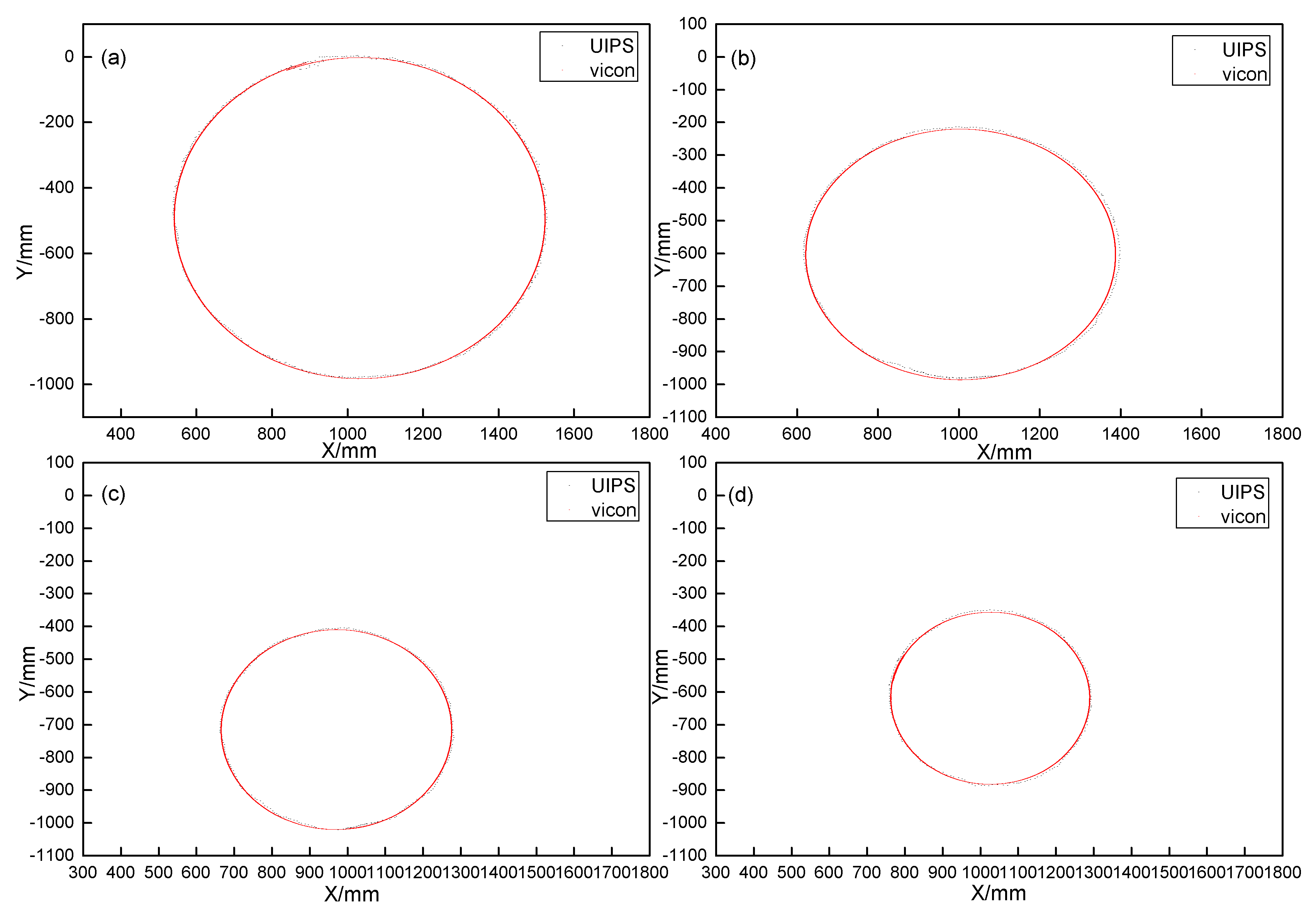
5.2. Applications
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nickitopoulou, A.; Protopsalti, K.; Stiros, S. Monitoring dynamic and quasi-static deformations of large flexible engineering structures with GPS: Accuracy, limitations and promises. Eng. Struct. 2006, 28, 1471–1482. [Google Scholar] [CrossRef]
- Klepeis, N.E.; Nelson, W.C.; Ott, W.R.; Robinson, J.P.; Tsang, A.M.; Switzer, P.; Behar, J.V.; Hern, S.C.; Engelmann, W.H. The National Human Activity Pattern Survey (NHAPS): A resource for assessing exposure to environmental pollutants. J. Expo. Sci. Environ. Epidemiol. 2001, 11, 231–252. [Google Scholar] [CrossRef] [PubMed]
- Kang-Wook, K.; Jihye, K.; Chang-Gun, L.; Junghee, H. Accurate Indoor Location Tracking Exploiting Ultrasonic Reflections. IEEE Sens. J. 2016, 16, 9075–9088. [Google Scholar]
- Liu, H.; Darabi, H.; Banerjee, P.; Liu, J. Survey of wireless indoor positioning techniques and systems. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2007, 37, 1067–1080. [Google Scholar] [CrossRef]
- Brena, R.F.; García-Vázquez, J.P.; Galván-Tejada, C.E.; Muñoz-Rodriguez, D.; Vargas-Rosales, C.; Fangmeyer, J. Evolution of Indoor Positioning Technologies: A Survey. J. Sens. 2017. [Google Scholar] [CrossRef]
- Mainetti, L.; Patrono, L.; Sergi, I. A survey on indoor positioning systems. In Proceedings of the 2014 22nd International Conference on Software, Telecommunications and Computer Networks (SoftCOM), Split, Croatia, 17–19 September 2014; pp. 111–120. [Google Scholar]
- Sayeef, S.; Madawala, U.K.; Handley, P.G.; Santoso, D. Indoor personnel tracking using infrared beam scanning. In Proceedings of the 2004 Position Location and Navigation Symposium, Monterey, CA, USA, 26–29 April 2004; pp. 698–705. [Google Scholar]
- Xiaohan, L.; Makino, H.; Maeda, Y. Basic study on indoor location estimation using visible light communication platform. In Proceedings of the 2008 30th Annual International Conference of Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 20–25 August 2008; pp. 2377–2380. [Google Scholar]
- Ingram, S.J.; Harmer, D.; Quinlan, M. Ultrawideband indoor positioning systems and their use in emergencies. In Proceedings of the 2004 Position Location and Navigation Symposium, Monterey, CA, USA, 26–29 April 2004; pp. 706–715. [Google Scholar]
- Mulloni, A.; Wagner, D.; Barakonyi, I.; Schmalstieg, D. Indoor positioning and navigation with camera phones. IEEE Pervasive Comput. 2009, 8. [Google Scholar] [CrossRef]
- Sanpechuda, T.; Kovavisaruch, L. A review of RFID localization: Applications and techniques. In Proceedings of the 2008 Fifth International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology, Krabi, Thailand, 14–17 May 2008; pp. 769–772. [Google Scholar]
- Rai, A.; Chintalapudi, K.K.; Padmanabhan, V.N.; Sen, R. Zee: Zero-effort crowdsourcing for indoor localization. In Proceedings of the 18th annual international conference on Mobile computing and networking, Istanbul, Turkey, 22–26 August 2012; pp. 293–304. [Google Scholar]
- Goncalo, G.; Helena, S. Indoor location system using ZigBee technology. In Proceedings of the 2009 Third International Conference on Sensor Technologies and Applications, Athens, Greece, 18–23 June 2009; pp. 152–157. [Google Scholar]
- Gualda, D.; Perez, M.C.; Urena, J.; Garcia, J.C.; Ruiz, D.; Garcia, E.; Lindo, A. Ultrasonic LPS adaptation for smartphones. In Proceedings of the 2013 International Conference on Indoor Positioning and Indoor Navigation, Montbéliard, France, 28–31 October 2013; pp. 1–8. [Google Scholar]
- Gueuning, F.E.; Varlan, M.; Eugne, C.E.; Dupuis, P. Accurate distance measurement by an autonomous ultrasonic system combining time-of-flight and phase-shift methods. In Proceedings of the Instrumentation and Measurement Technology Conference, Brussels, Belgium, 4–6 June 1996; pp. 399–404. [Google Scholar]
- Fritsch, C.; Ibanez, A.; Parrilla, M. A digital envelope detection filter for real-time operation. IEEE Trans. Instrum. Meas. 1999, 48, 1287–1293. [Google Scholar] [CrossRef]
- Priyantha, N.B.; Chakraborty, A.; Balakrishnan, H. The cricket location-support system. In Proceedings of the 6th Annual International Conference on Mobile Computing and Networking, Boston, MA, USA, 6–11 August 2000; pp. 32–43. [Google Scholar]
- Lu, Z.; Yang, C.; Qin, D.; Luo, Y.; Momayez, M. Estimating ultrasonic time-of-flight through echo signal envelope and modified Gauss Newton method. Measurement 2016, 94, 355–363. [Google Scholar] [CrossRef]
- Zhao, Y.; Fan, X.; Xu, C.Z.; Li, X. ER-CRLB: An Extended Recursive Cramér–Rao Lower Bound Fundamental Analysis Method for Indoor Localization Systems. IEEE Trans. Veh. Technol. 2017, 66, 1605–1618. [Google Scholar] [CrossRef]
- Huang, S.S.; Huang, C.F.; Huang, K.N.; Young, M.S. A high accuracy ultrasonic distance measurement system using binary frequency shift-keyed signal and phase detection. Rev. Sci. Instrum. 2002, 73, 3671–3677. [Google Scholar] [CrossRef]
- Urena, J.; Hernandez, A.; Jimenez, A.; Villadangos, J.M.; Mazo, M.; Carcia, J.C.; Alvarez, F.J.; Marziani, C.D.; Perez, M.C.; Jiménez, J.A.; et al. Advanced sensorial system for an acoustic LPS. Microproces. Microsyst. 2007, 31, 393–401. [Google Scholar] [CrossRef]
- Seco, F.; Prieto, J.C.; Ruiz, A.R.J.; Guevara, J. Compensation of multiple access interference effects in CDMA-based acoustic positioning systems. IEEE Trans. Instrum. Meas. 2014, 63, 2368–2378. [Google Scholar] [CrossRef]
- Álvarez, F.J.; Aguilera, T.; López-Valcarce, R. CDMA-based acoustic local positioning system for portable devices with multipath cancellation. Dig. Signal Process. 2017, 62, 38–51. [Google Scholar] [CrossRef]
- Khyam, M.O.; Xinde, L.; Ge, S.S.; Pickering, M.R. Multiple Access Chirp-Based Ultrasonic Positioning. IEEE Trans. Instrum. Meas. 2017, 99, 1–12. [Google Scholar] [CrossRef]
- Saad, M.M.; Bleakley, C.J.; Dobson, S. Robust high-accuracy ultrasonic range measurement system. IEEE Trans. Instrum. Meas. 2011, 60, 3334–3341. [Google Scholar] [CrossRef]
- Gonzalez, J.R.; Bleakley, C.J. High-precision robust broadband ultrasonic location and orientation estimation. IEEE J. Sel. Top. Signal Process. 2009, 3, 832–844. [Google Scholar] [CrossRef]
- Medina, C.; Segura, J.C.; De la Torre, A. Ultrasound indoor positioning system based on a low-power wireless sensor network providing sub-centimeter accuracy. Sensors 2013, 13, 3501–3526. [Google Scholar] [CrossRef] [PubMed]
- Demirli, R.; Saniie, J. Model-based estimation of ultrasonic echoes. Part I: Analysis and algorithms. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2001, 48, 787–802. [Google Scholar] [CrossRef] [PubMed]
- Elson, J.; Girod, L.; Estrin, D. Fine-grained network time synchronization using reference broadcasts. ACM SIGOPS Oper. Syst. Rev. 2002, 36, 147–163. [Google Scholar] [CrossRef]
- Cena, G.; Scanzio, S.; Valenzano, A.; Zunino, C. Implementation and evaluation of the reference broadcast infrastructure synchronization protocol. IEEE Trans. Ind. Inform. 2015, 11, 801–811. [Google Scholar] [CrossRef]
- Texas Instruments Incorporated. CC2500. Available online: http://www.ti.com/lit/ds/symlink/cc2500.pdf (accessed on 2 October 2017).
- Gueuning, F.; Varlan, M.; Eugene, C.; Dupuis, P. Accurate distance measurement by an autonomous ultrasonic system combining time-of-flight and phase-shift methods. IEEE Trans. Instrum. Meas. 1997, 46, 1236–1240. [Google Scholar] [CrossRef]
- Khyam, M.O.; Ge, S.S.; Li, X.; Pickering, M.R. Highly Accurate Time-of-Flight Measurement Technique Based on Phase-Correlation for Ultrasonic Ranging. IEEE Sens. J. 2017, 17, 434–443. [Google Scholar] [CrossRef]
- ST Semiconductor Company. STM32F722RC. Available online: http://www.st.com/zh/microcontrollers/stm32f722rc.html (accessed on 1 October 2017).
- Texas Instruments Incorporated. CC3200. Available online: http://www.ti.com/lit/ds/symlink/cc3220.pdf (accessed on 1 October 2017).
- Luo, H.; Fang, X.; Ertas, B. Hilbert transform and its engineering applications. AIAA J. 2009, 47, 923–927. [Google Scholar] [CrossRef]
- Ens, A.; Reindl, L.M.; Bordoy, J.; Wendeberg, J.; Schindelhauer, C. Unsynchronized ultrasound system for TDOA localization. In Proceedings of the 2014 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Busan, Kore, 27–30 October 2014; pp. 601–610. [Google Scholar]
- Angrisani, L.; Schiano Lo Moriello, R. Estimating ultrasonic time-of-flight through quadrature demodulation. IEEE Trans. Instrum. Meas. 2006, 55, 54–62. [Google Scholar] [CrossRef]






| Data Communication Rate | 5 kb/s | 10 kb/s | 20 kb/s | 50 kb/s | 100 kb/s | 150 kb/s |
|---|---|---|---|---|---|---|
| Maximum of (s) | 33,200 | 17,059 | 8986 | 4242 | 2528 | 1991 |
| Minimum of (s) | 33,185 | 17,052 | 8982 | 4140 | 2527 | 1990 |
| Difference (s) | 15 | 7 | 4 | 2 | 1 | 1 |
| Ref (mm) | 1195.16 | 1454.86 | 1666.49 | 1977.27 | 2277.89 | 2605.79 | 2877.75 | 3150.92 | |
|---|---|---|---|---|---|---|---|---|---|
| LSM | 1195.83 | 1453.77 | 1667.61 | 1977.58 | 2278.46 | 2606.49 | 2878.31 | 3151.36 | |
| QS | 1194.34 | 1453.04 | 1666.91 | 1976.38 | 2277.25 | 2506.37 | 2878.09 | 3150.61 | |
| LSM | 0.61 | 0.68 | 0.75 | 0.96 | 1.14 | 1.21 | 1.33 | 1.42 | |
| QS | 1.34 | 1.67 | 1.69 | 2.30 | 1.90 | 1.82 | 3.06 | 2.84 | |
| LSM | 0.23 | 0.26 | 0.27 | 0.34 | 0.21 | 0.22 | 0.37 | 0.40 | |
| QS | 0.41 | 0.60 | 0.38 | 0.70 | 0.76 | 1.02 | 1.14 | 1.13 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, J.; Liu, G.-P. A Robust High-Accuracy Ultrasound Indoor Positioning System Based on a Wireless Sensor Network. Sensors 2017, 17, 2554. https://doi.org/10.3390/s17112554
Qi J, Liu G-P. A Robust High-Accuracy Ultrasound Indoor Positioning System Based on a Wireless Sensor Network. Sensors. 2017; 17(11):2554. https://doi.org/10.3390/s17112554
Chicago/Turabian StyleQi, Jun, and Guo-Ping Liu. 2017. "A Robust High-Accuracy Ultrasound Indoor Positioning System Based on a Wireless Sensor Network" Sensors 17, no. 11: 2554. https://doi.org/10.3390/s17112554
APA StyleQi, J., & Liu, G.-P. (2017). A Robust High-Accuracy Ultrasound Indoor Positioning System Based on a Wireless Sensor Network. Sensors, 17(11), 2554. https://doi.org/10.3390/s17112554





