MEMS Tunable Diffraction Grating for Spaceborne Imaging Spectroscopic Applications
Abstract
:1. Introduction
2. Pitch Tunable Diffraction Grating (PTG)
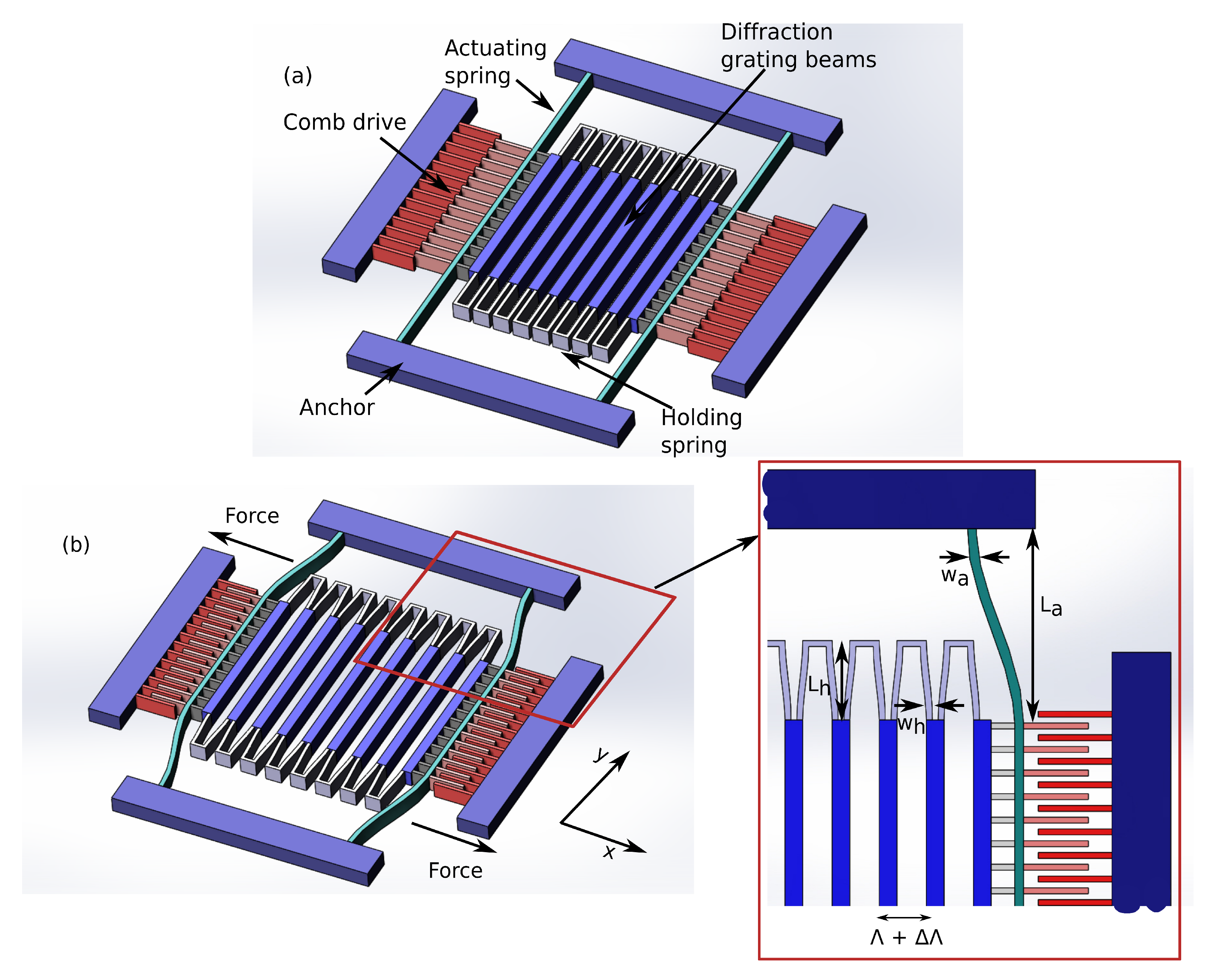
2.1. Micromechanical Implementation
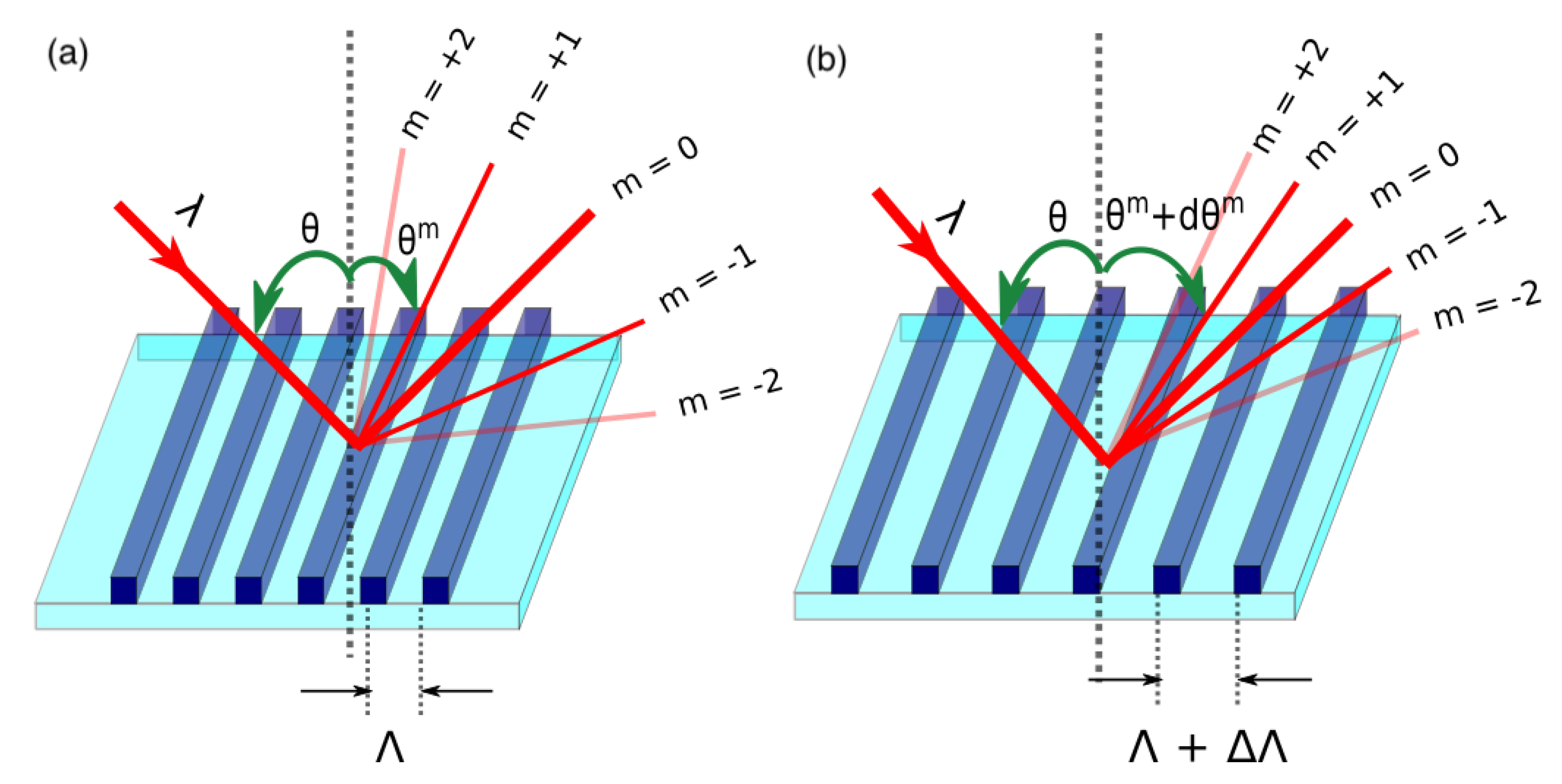
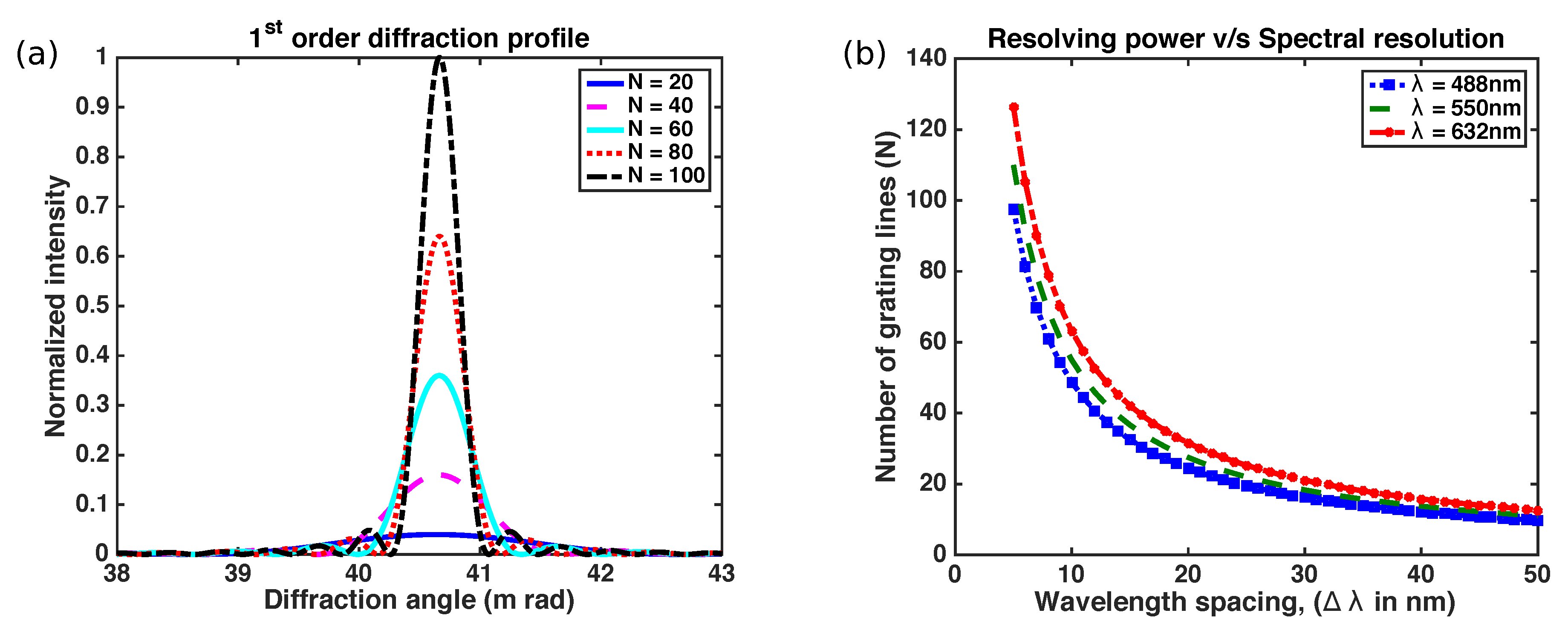
2.2. Optical Design
2.3. Micromechanical Design
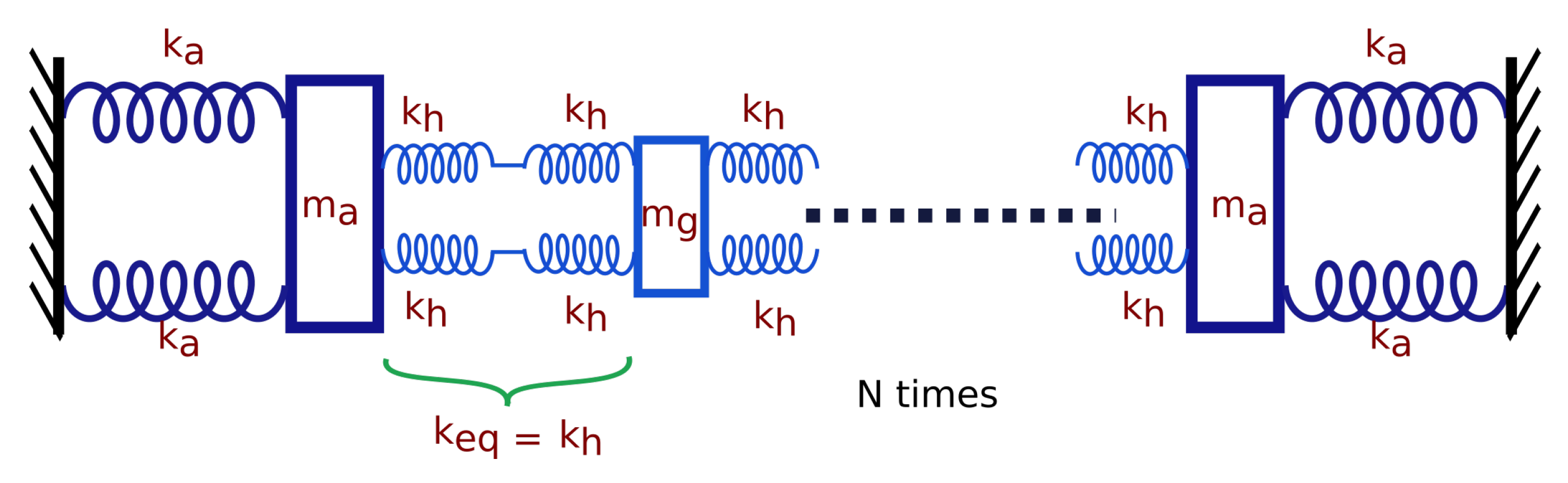
2.3.1. Mass-Spring Model
2.3.2. In-Plane Modal Analysis
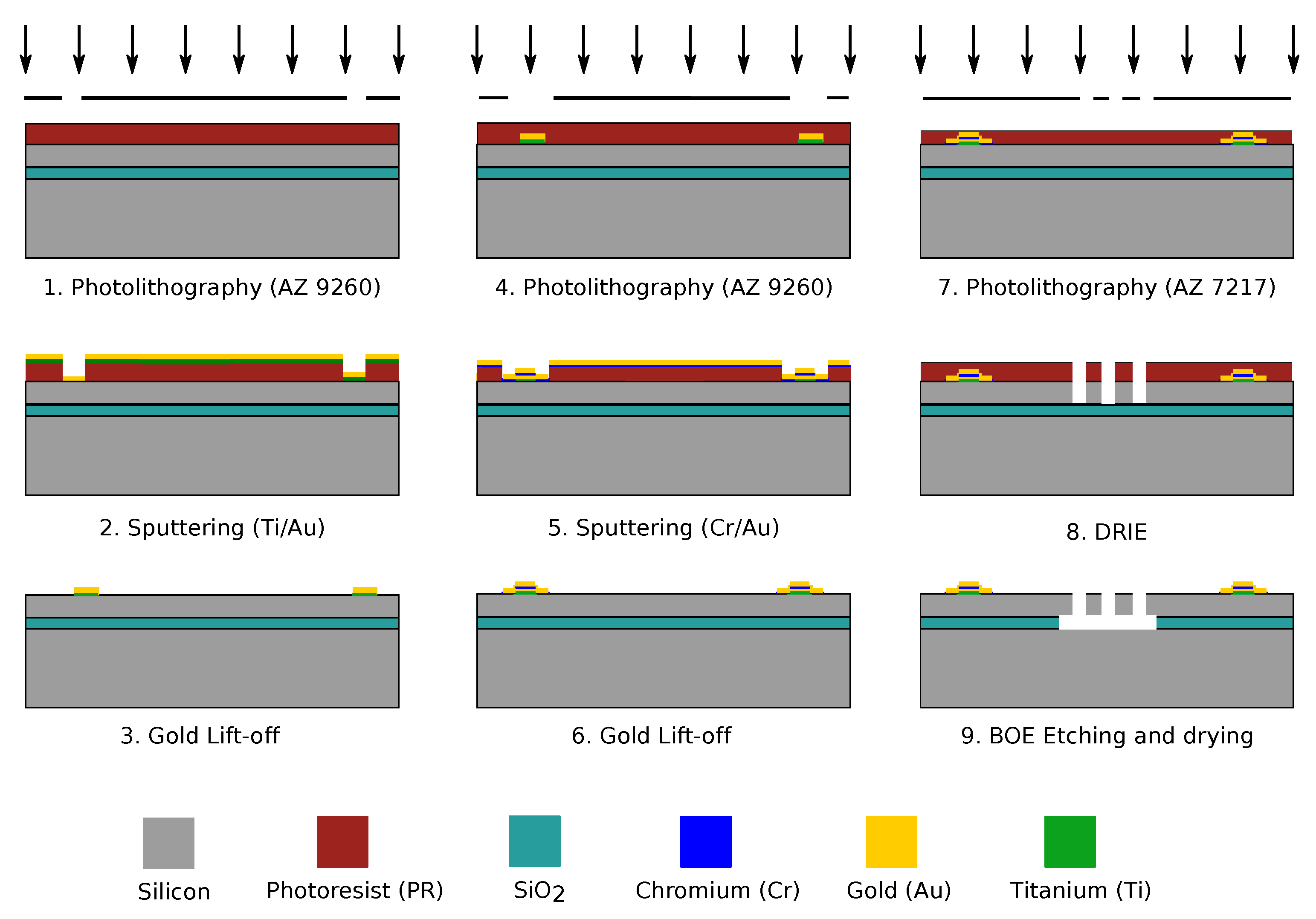
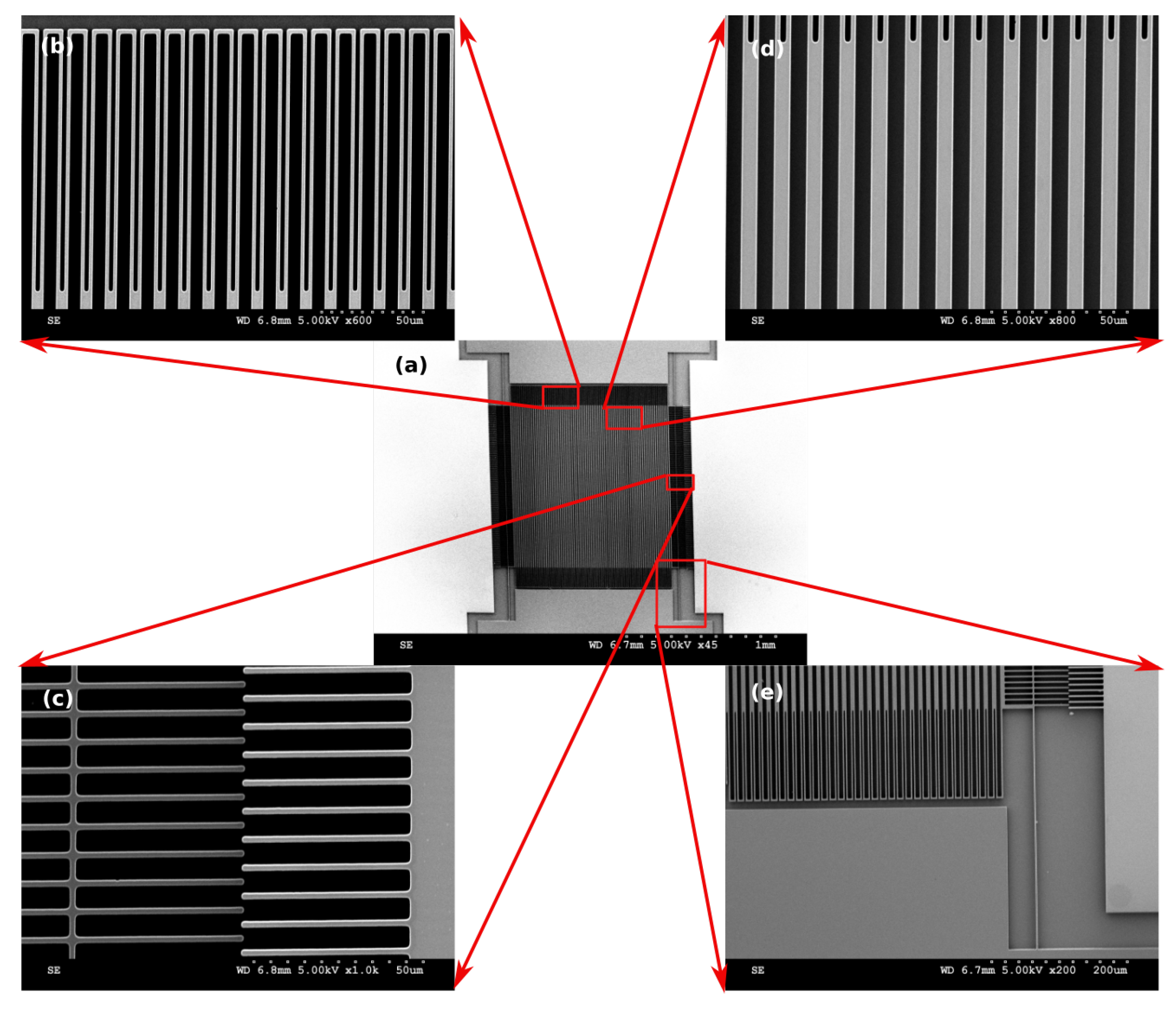
3. Microfabrication
4. Device Characterization and Testing
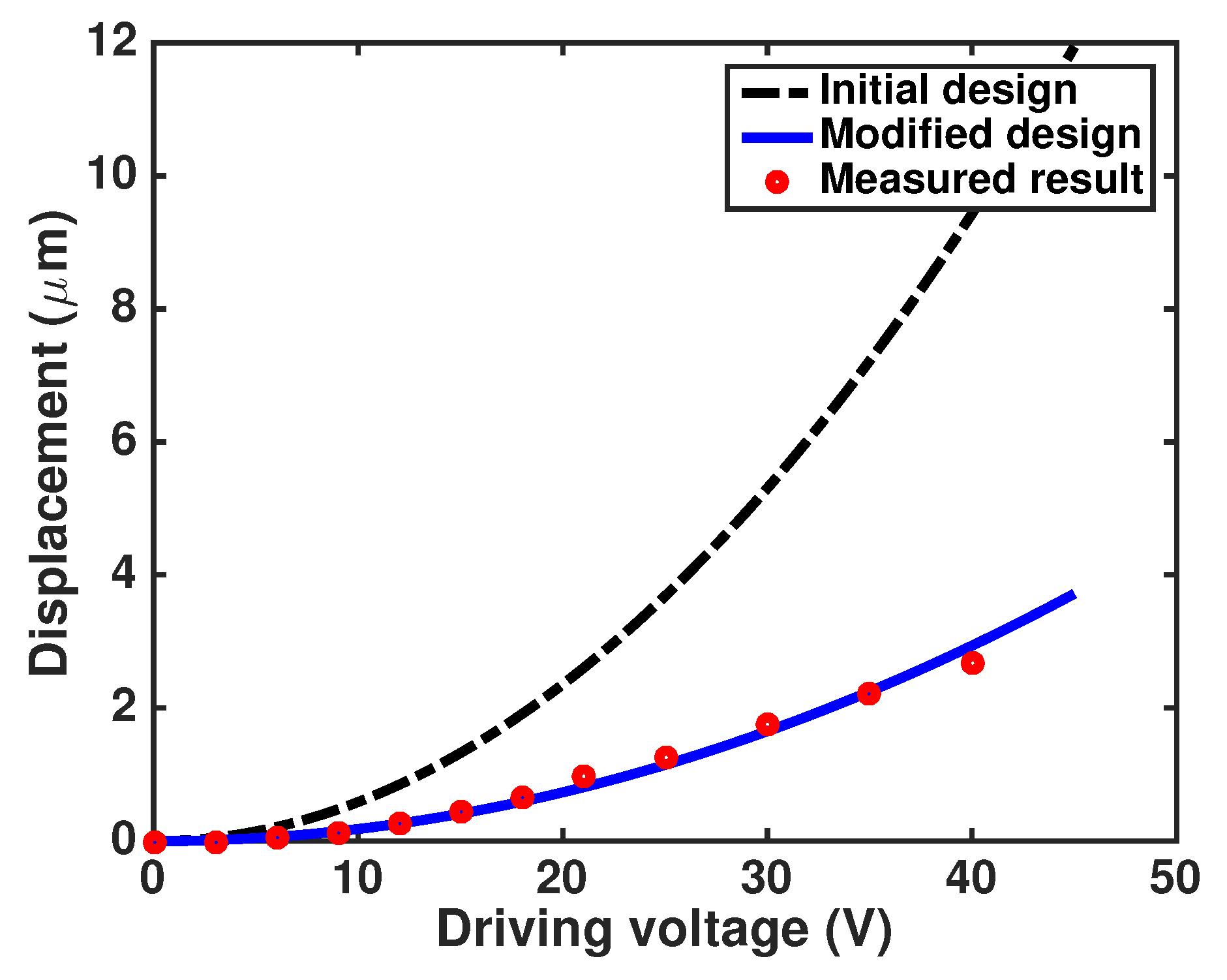
4.1. Static Measurements
4.2. Optical Characterization
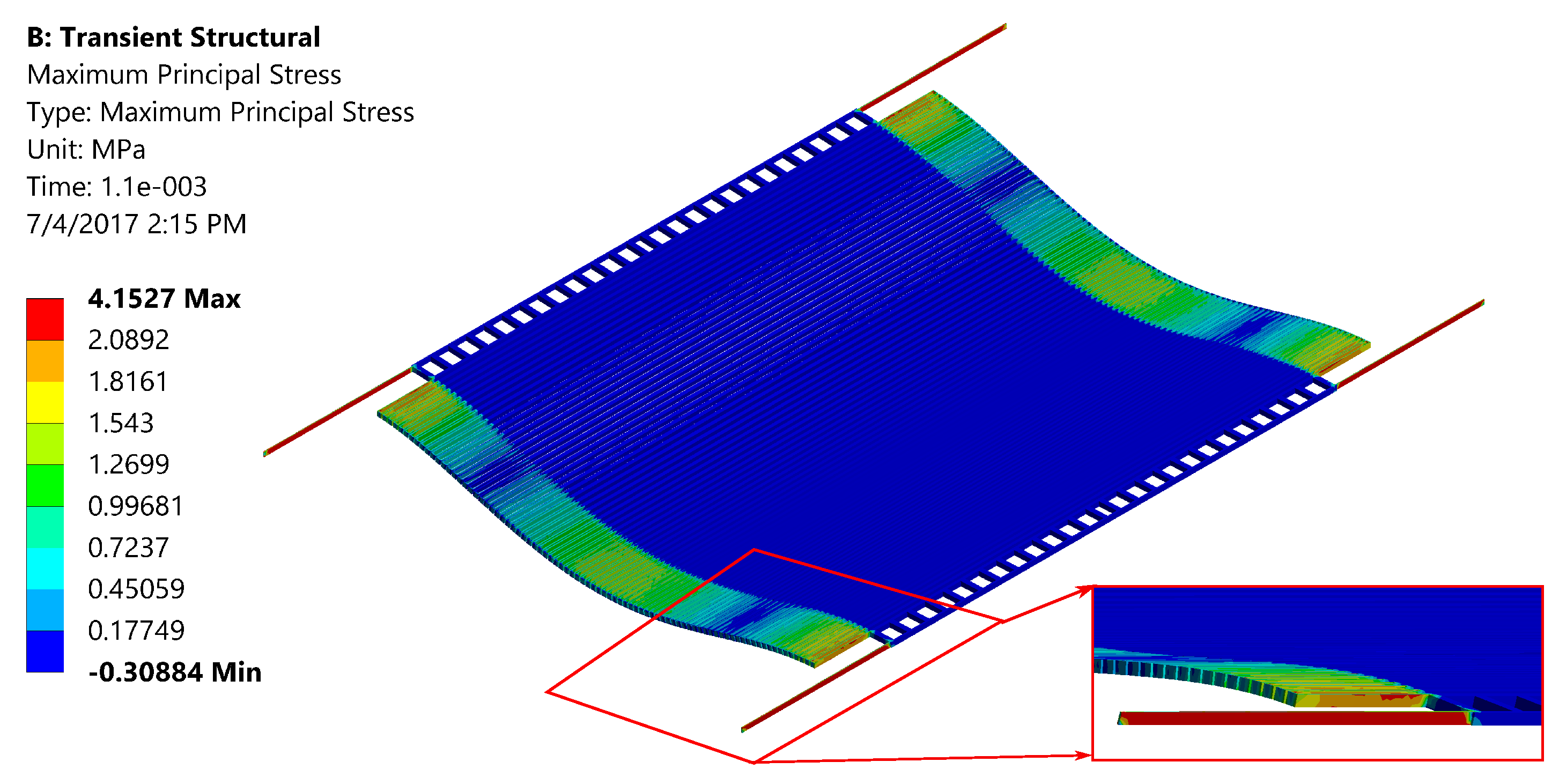
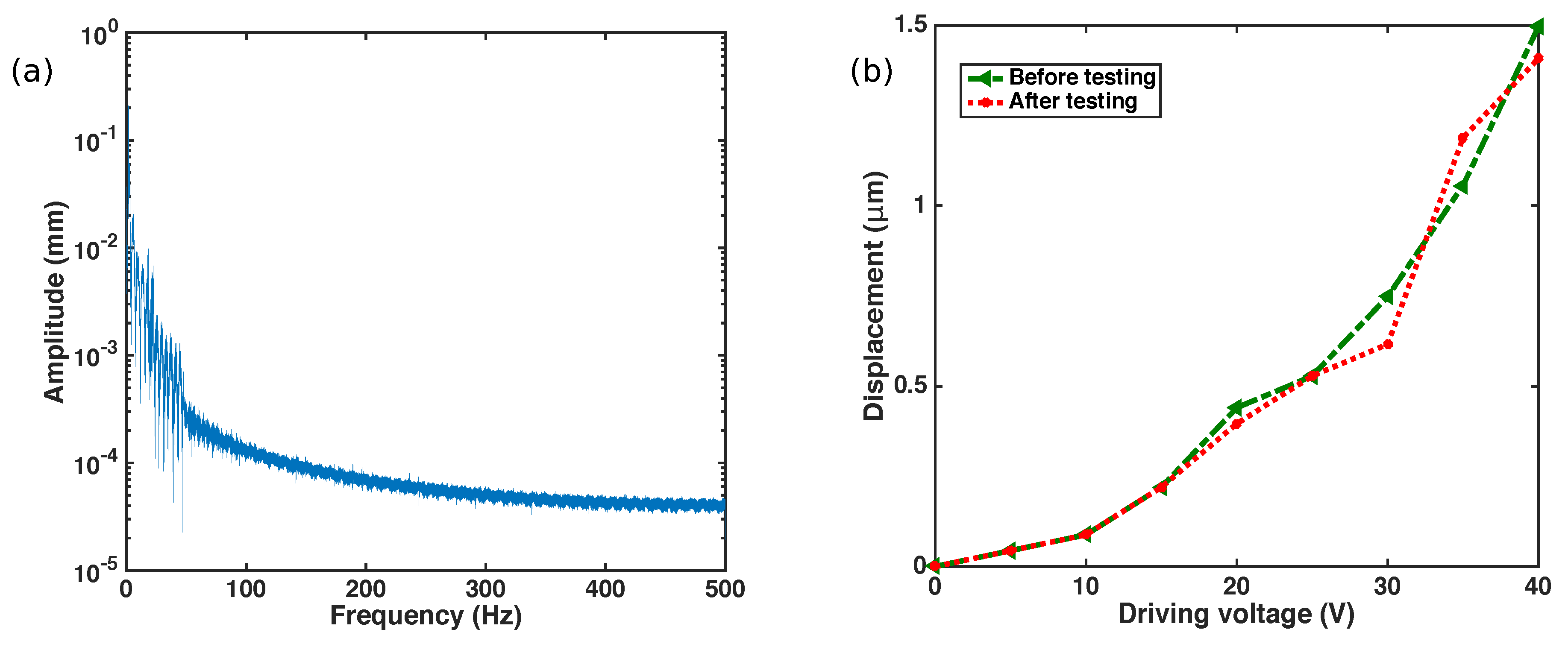
4.3. Mechanical Vibration Test
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kramer, H.J.; Cracknell, A.P. An overview of small satellites in remote sensing*. Int. J. Remote Sens. 2008, 29, 4285–4337. [Google Scholar] [CrossRef]
- Guelman, M.; Ortenberg, F. Small satellite’s role in future hyperspectral Earth observation missions. Acta Astronaut. 2009, 64, 1252–1263. [Google Scholar] [CrossRef]
- De Rooij, N.; Gautsch, S.; Briand, D.; Marxer, C.; Mileti, G.; Noell, W.; Shea, H.; Staufer, U.; Van Der Schoot, B. MEMS for space. In Proceedings of the TRANSDUCERS 2009–2009 International Solid-State Sensors, Actuators and Microsystems Conference, Denver, CO, USA, 21–25 June 2009; pp. 17–24. [Google Scholar]
- Shea, H. MEMS for pico-to micro-satellites. In SPIE MOEMS-MEMS: Micro- and Nanofabrication; International Society for Optics and Photonics: Bellingham, WA, USA, 2009; p. 72080M. [Google Scholar]
- Truxal, S.C.; Kurabayashi, K.; Tung, Y.C. Design of a MEMS tunable polymer grating for single detector spectroscopy. Int. J. Optomechatron. 2008, 2, 75–87. [Google Scholar] [CrossRef]
- Brazas, J.C.; Kowarz, M.W. High-resolution laser-projection display system using a grating electromechanical system (GEMS). In Micromachining and Microfabrication; International Society for Optics and Photonics: Bellingham, WA, USA, 2004; pp. 65–75. [Google Scholar]
- Tohmori, Y.; Yoshikuni, Y.; Ishii, H.; Kano, F.; Tamamura, T.; Kondo, Y.; Yamamoto, M. Broad-range wavelength-tunable superstructure grating (SSG) DBR lasers. IEEE J. Quantum Electron. 1993, 29, 1817–1823. [Google Scholar] [CrossRef]
- Jayaraman, V.; Chuang, Z.M.; Coldren, L.A. Theory, design, and performance of extended tuning range semiconductor lasers with sampled gratings. IEEE J. Quantum Electron. 1993, 29, 1824–1834. [Google Scholar] [CrossRef]
- Mason, B.; Fish, G.A.; DenBaars, S.P.; Coldren, L.A. Widely tunable sampled grating DBR laser with integrated electroabsorption modulator. IEEE Photonics Technol. Lett. 1999, 11, 638–640. [Google Scholar] [CrossRef]
- Senturia, S.D.; Day, D.R.; Butler, M.A.; Smith, M.C. Programmable diffraction gratings and their uses in displays, spectroscopy, and communications. J. Microlithogr. Microfabr. Microsyst. 2005, 4, 041401. [Google Scholar]
- Schueller, O.J.A.; Duffy, D.C.; Rogers, J.A.; Brittain, S.T.; Whitesides, G.M. Reconfigurable diffraction gratings based on elastomeric microfluidic devices. Sens. Actuators A Phys. 1999, 78, 149–159. [Google Scholar] [CrossRef]
- Wong, C.W.; Jeon, Y.; Barbastathis, G.; Kim, S.G. Analog piezoelectric-driven tunable gratings with nanometer resolution. J. Microelectromech. Syst. 2004, 13, 998–1005. [Google Scholar] [CrossRef]
- Shih, W.C.; Kim, S.G.; Barbastathis, G. High-resolution electrostatic analog tunable grating with a single-mask fabrication process. J. Microelectromech. Syst. 2006, 15, 763–769. [Google Scholar] [CrossRef]
- Yu, Y.T.; Yuan, W.Z.; Li, T.P.; Yan, B. Development of a micromechanical pitch-tunable grating with reflective/transmissive dual working modes. J. Micromech. Microeng. 2010, 20, 065002. [Google Scholar] [CrossRef]
- Tormen, M.; Peter, Y.A.; Niedermann, P.; Hoogerwerf, A.; Shea, H.; Stanley, R. Deformable MEMS grating for wide tunability and high operating speed. In MOEMS-MEMS 2006 Micro and Nanofabrication; International Society for Optics and Photonics: Bellingham, WA, USA, 2006; p. 61140C. [Google Scholar]
- Yang, Y.S.; Lin, Y.H.; Hu, Y.C.; Liu, C.H. A large-displacement thermal actuator designed for MEMS pitch-tunable grating. J. Micromech. Microeng. 2008, 19, 015001. [Google Scholar] [CrossRef]
- Aschwanden, M.; Beck, M.; Stemmer, A. Diffractive transmission grating tuned by dielectric elastomer actuator. IEEE Photonics Technol. Lett. 2007, 19, 1090–1092. [Google Scholar] [CrossRef]
- Zhang, W.M.; Yan, H.; Peng, Z.K.; Meng, G. Electrostatic pull-in instability in MEMS/NEMS: A review. Sens. Actuators A Phys. 2014, 214, 187–218. [Google Scholar] [CrossRef]
- Shih, W.C.; Hidrovo, C.; Kim, S.G.; Barbastathis, G. Optical diversity by nanoscale actuation. In Proceedings of the 2003 Third IEEE Conference on Nanotechnology (IEEE-NANO 2003), San Francisco, CA, USA, 12–14 August 2003; Volume 2, pp. 892–895. [Google Scholar]
- Elad, M.; Feuer, A. Restoration of a single superresolution image from several blurred, noisy, and undersampled measured images. IEEE Trans. Image Process. 1997, 6, 1646–1658. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.W.; Gustafson, S.C. Introduction to fourier optics. Opt. Eng. 1996, 35, 1513. [Google Scholar] [CrossRef]
- Wu, J.; Wang, S.; Miao, J. A MEMS Device for Studying the Friction Behavior of Micromachined Sidewall Surfaces. J. Microelectromech. Syst. 2008, 17, 921–933. [Google Scholar]
- Wu, J.; Wang, S.; Miao, J. Friction characteristics of the curved sidewall surfaces of a rotary MEMS device in oscillating motion. J. Micromech. Microeng. 2009, 19, 065020. [Google Scholar] [CrossRef]
- Bell, D.J.; Lu, T.; Fleck, N.A.; Spearing, S.M. MEMS actuators and sensors: observations on their performance and selection for purpose. J. Micromech. Microeng. 2005, 15, S153–S164. [Google Scholar] [CrossRef]
- Legtenberg, R.; Groeneveld, A.; Elwenspoek, M. Comb-drive actuators for large displacements. J. Micromech. Microeng. 1996, 6, 320–329. [Google Scholar] [CrossRef]
- Yu, Y.; Yuan, W.; Sun, R.; Qiao, D.; Yan, B. A strategy to efficiently extend the change rate of period for comb-drive micromechanical pitch-tunable gratings. J. Microelectromech. Syst. 2010, 19, 1180–1185. [Google Scholar] [CrossRef]
- Gao, J.; Yeo, L.; Chan-Park, M.B.; Miao, J.; Yan, Y.; Sun, J.; Lam, Y.; Yue, C. Antistick postpassivation of high-aspect ratio silicon molds fabricated by deep-reactive ion etching. J. Microelectromech. Syst. 2006, 15, 84–93. [Google Scholar] [CrossRef]
- Fu, L.; Miao, J.; Li, X.; Lin, R. Study of deep silicon etching for micro-gyroscope fabrication. Appl. Surface Sci. 2001, 177, 78–84. [Google Scholar] [CrossRef]
- Iliescu, C.; Miao, J. One-mask process for silicon accelerometers on Pyrex glass utilising notching effect in inductively coupled plasma DRIE. Electron. Lett. 2003, 39, 658–659. [Google Scholar] [CrossRef]
- Chen, B.; Miao, J. Influence of deep RIE tolerances on comb-drive actuator performance. J. Phys. D Appl. Phys. 2007, 40, 970–976. [Google Scholar] [CrossRef]
- Wong, C.W.; Jeon, Y.; Barbastathis, G.; Kim, S.G. Analog tunable gratings driven by thin-film piezoelectric microelectromechanical actuators. Appl. Opt. 2003, 42, 621–626. [Google Scholar] [CrossRef] [PubMed]
- Yi, S.; Kim, S.; Song, J. Analysis of the effect of space radiations on the nematode, Caenorhabditis elegans, through the simulated space radiation. Int. J. Astron. Astrophys. 2013, 2013. [Google Scholar] [CrossRef]
- Shaw, T.; Corliss, J.; Gundo, D.; Mulenburg, G.; Breit, G.; Griffith, J. Simulation of shuttle launch G forces and acoustic loads using the NASA Ames Research Center 20G centrifuge. In Proceedings of the 18th Space Simulation Conference on Space Mission Success Through Testing, Baltimore, MD, USA, 31 October–3 November 1994. [Google Scholar]
- Shea, H.R. Reliability of MEMS for space applications. In MOEMS-MEMS 2006 Micro and Nanofabrication; International Society for Optics and Photonics: Bellingham, WA, USA, 2006; p. 61110A. [Google Scholar]


| Device Parameters | Symbol | Designed | Measured |
| grating beam length | 1000 | 1000 | |
| grating beam width | 6 | 5.9 | |
| grating pitch | 12 | 12 | |
| device thickness | t | 10 | 10 |
| holding spring width | 2 | 1.9 | |
| holding spring length | 122 | 122 | |
| actuating spring width | 2 | 2.7 | |
| actuating spring length | 333 | 333 | |
| comb finger length | 50 | 50 | |
| comb finger width | 2 | 0.7 | |
| initial overlap distance | 2 | 1.8 | |
| Device Parameters | Symbol | Designed | |
| No. of grating beams | N | 84 | |
| No. of comb fingers | n | 125 |
| Reference | Actuation Mechanism | Resolving Power | Fill Factor | Actuation Voltage | Displacement |
|---|---|---|---|---|---|
| Author (Year) | (Effective Area/Total Area) (%) | (V) | |||
| Wei et al. (2006) [13] | Electrostatic | 17 | 20 | 10 | 0.46 |
| Yu et al. (2010) [14] | Electrostatic | 30 | 22 | 70 | 10.4 |
| Yu et al. (2010) [26] | Electrostatic | 29 | ≈10 | 100 | 21 |
| Tormen et al. (2006) [15] | Electrostatic | 33 | ≈30 | 100 | 2 |
| Yang et al. (2008) [16] | Thermal | 54 | ≈21 | 19 | 300 |
| Wong et al. (2003) [31] | Piezoelectric | - | - | 10 | ≈0.28 |
| this work | Electrostatic | 84 | 52 | 40 | 2.7 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muttikulangara, S.S.; Baranski, M.; Rehman, S.; Hu, L.; Miao, J. MEMS Tunable Diffraction Grating for Spaceborne Imaging Spectroscopic Applications. Sensors 2017, 17, 2372. https://doi.org/10.3390/s17102372
Muttikulangara SS, Baranski M, Rehman S, Hu L, Miao J. MEMS Tunable Diffraction Grating for Spaceborne Imaging Spectroscopic Applications. Sensors. 2017; 17(10):2372. https://doi.org/10.3390/s17102372
Chicago/Turabian StyleMuttikulangara, Sanathanan S., Maciej Baranski, Shakil Rehman, Liangxing Hu, and Jianmin Miao. 2017. "MEMS Tunable Diffraction Grating for Spaceborne Imaging Spectroscopic Applications" Sensors 17, no. 10: 2372. https://doi.org/10.3390/s17102372
APA StyleMuttikulangara, S. S., Baranski, M., Rehman, S., Hu, L., & Miao, J. (2017). MEMS Tunable Diffraction Grating for Spaceborne Imaging Spectroscopic Applications. Sensors, 17(10), 2372. https://doi.org/10.3390/s17102372





