A LQR-Based Controller with Estimation of Road Bank for Improving Vehicle Lateral and Rollover Stability via Active Suspension
Abstract
:1. Introduction
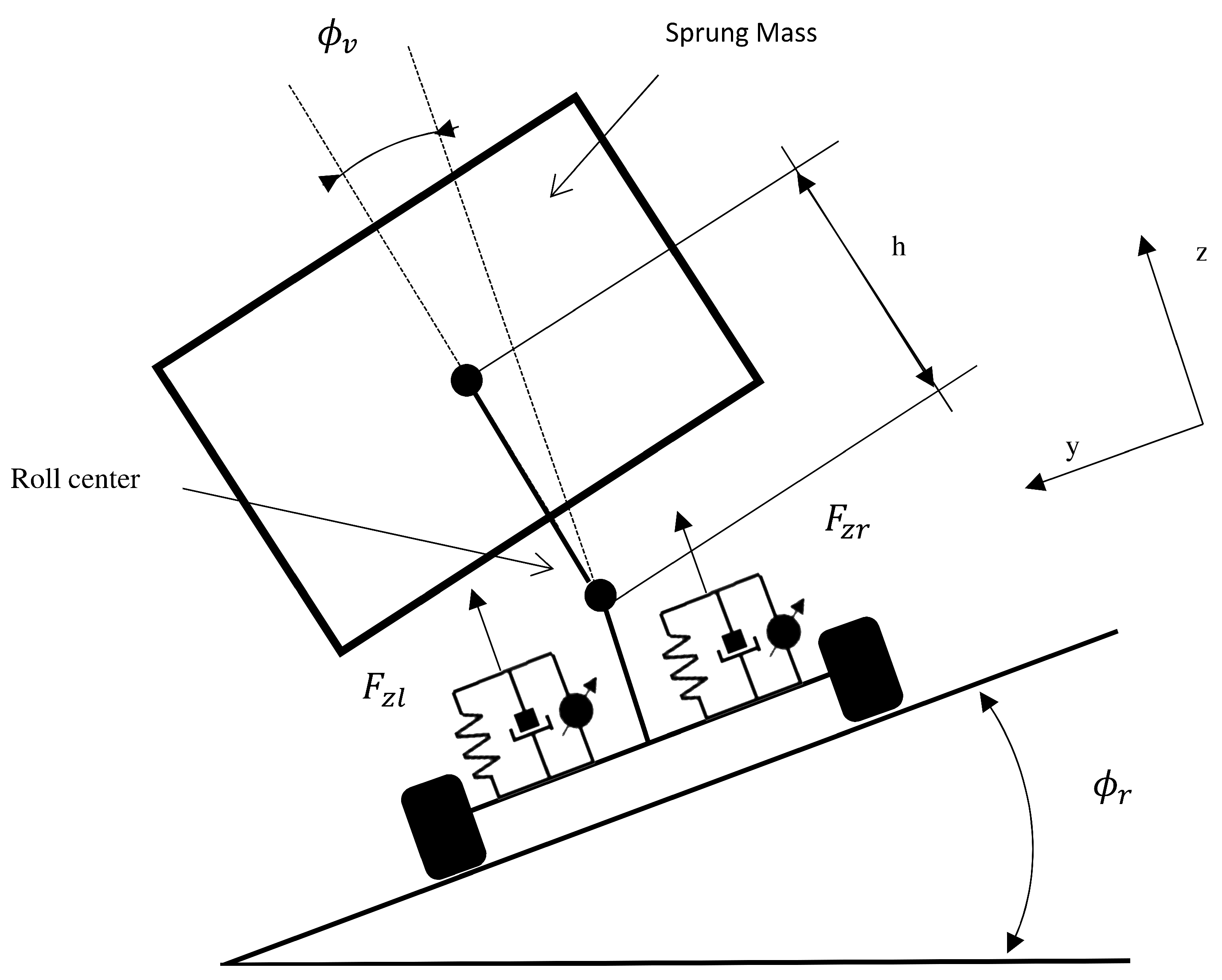
2. Vehicle Model
3. Kalman Filter Estimation
- A is the discrete matrix A for estimation and is calculated as follows, with :
- B is the discrete matrix B for estimation, which is equal to B.
- x represents the state vector for instance k.
- w is the process noise vector for instance k, calculated assuming the normal Gaussian normal distribution as:
- v is the output noise vector for instance k, calculated assuming the normal Gaussian normal distribution as:
- y is the output vector for instance k.
- (1)
- The prediction of the state is given by:
- (2)
- The predicted error covariance is calculated by means of:where:
- (3)
- Therefore, the Kalman Gain is:where:
- (4)
- The state estimation is updated with measurement :
- (5)
- The error covariance is updated:
4. LQR Controller
- v is the input vector:
- u is the control vector:
- , with i = 1–5, are the factors indicating the influence of each variable;
- The subindex d indicates the desired value for that state variable;
- is the moment performed around the x axis to control the vehicle, which can be expressed as:with:
- x is the desired response of the state vector in sample k:with the desired yaw rate as described in [25].
- Q is the positive semi-definite state weighting matrix:
- R is the positive semi-definite control weighting matrix:
- P is the Lagrange multipliers vector seen in Equation (25):
- S is a 4 × 4 matrix calculated solving the second Equation in (32):
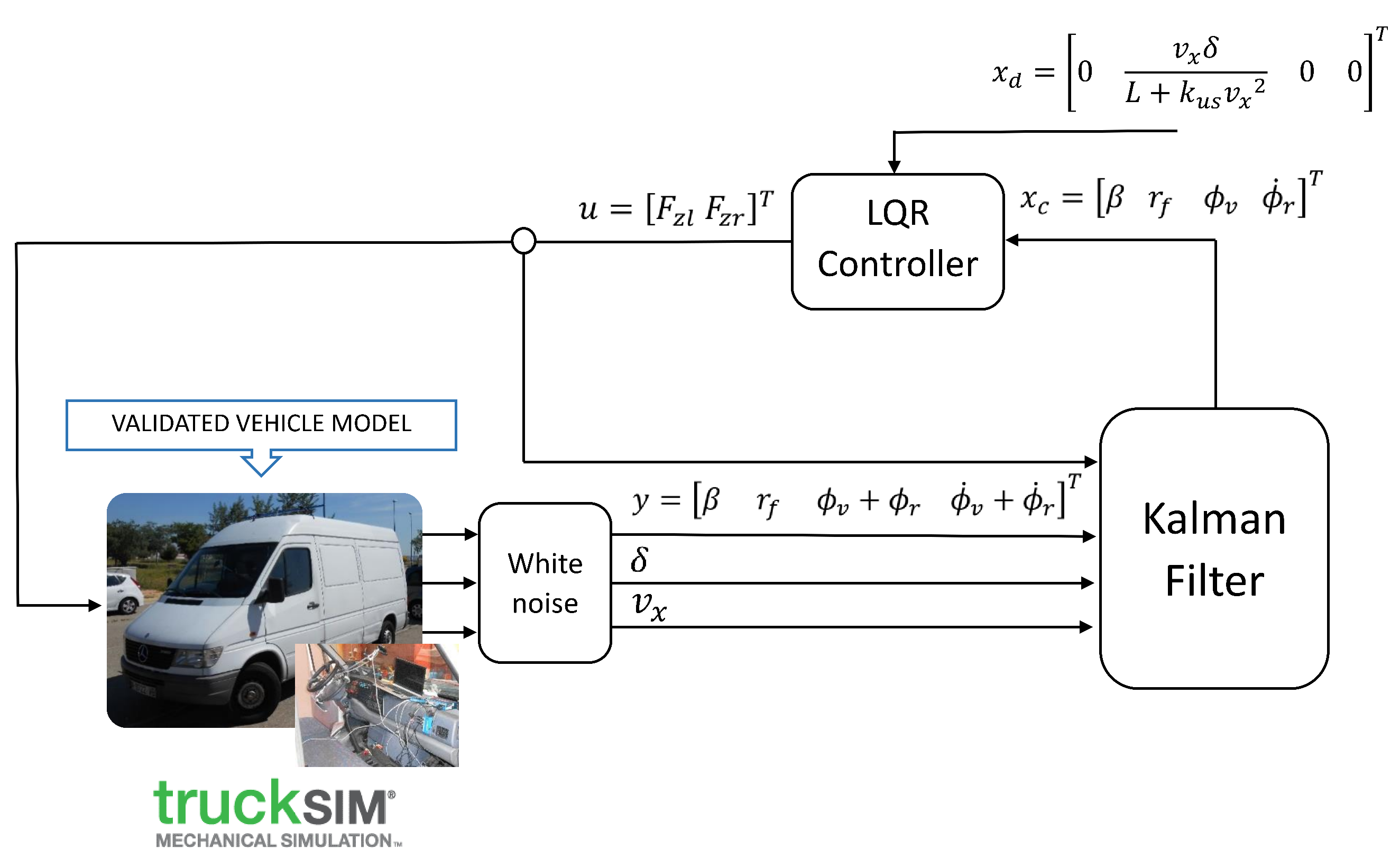
5. Architecture of the Controller
6. Results
- is the approximation error.
- is the standard deviation.
- represents the measured variable.
- is the desired value for each variable.
- u is the average value for each variable
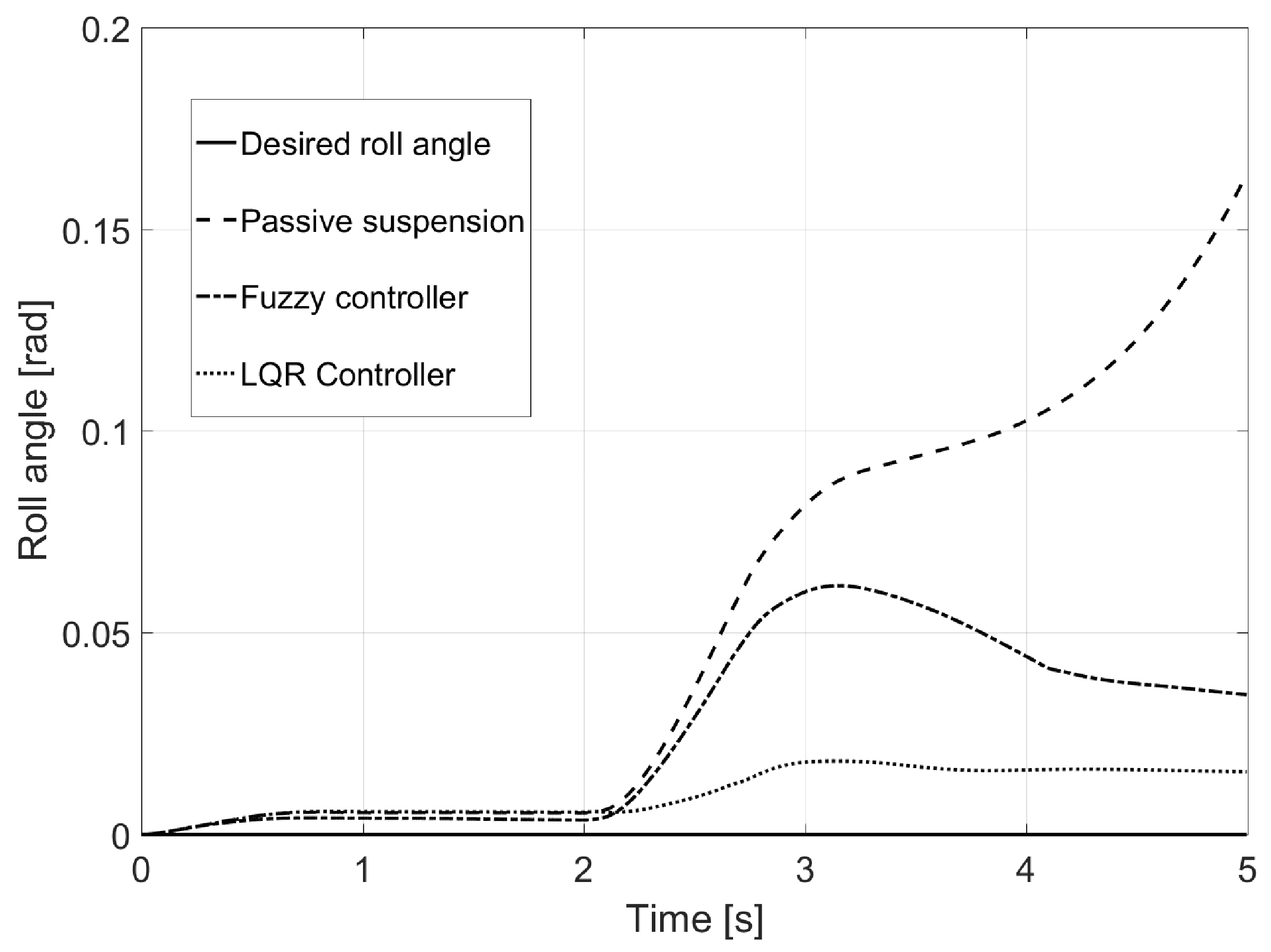
6.1. Test 1: 180-Degree Steering Wheel Turn
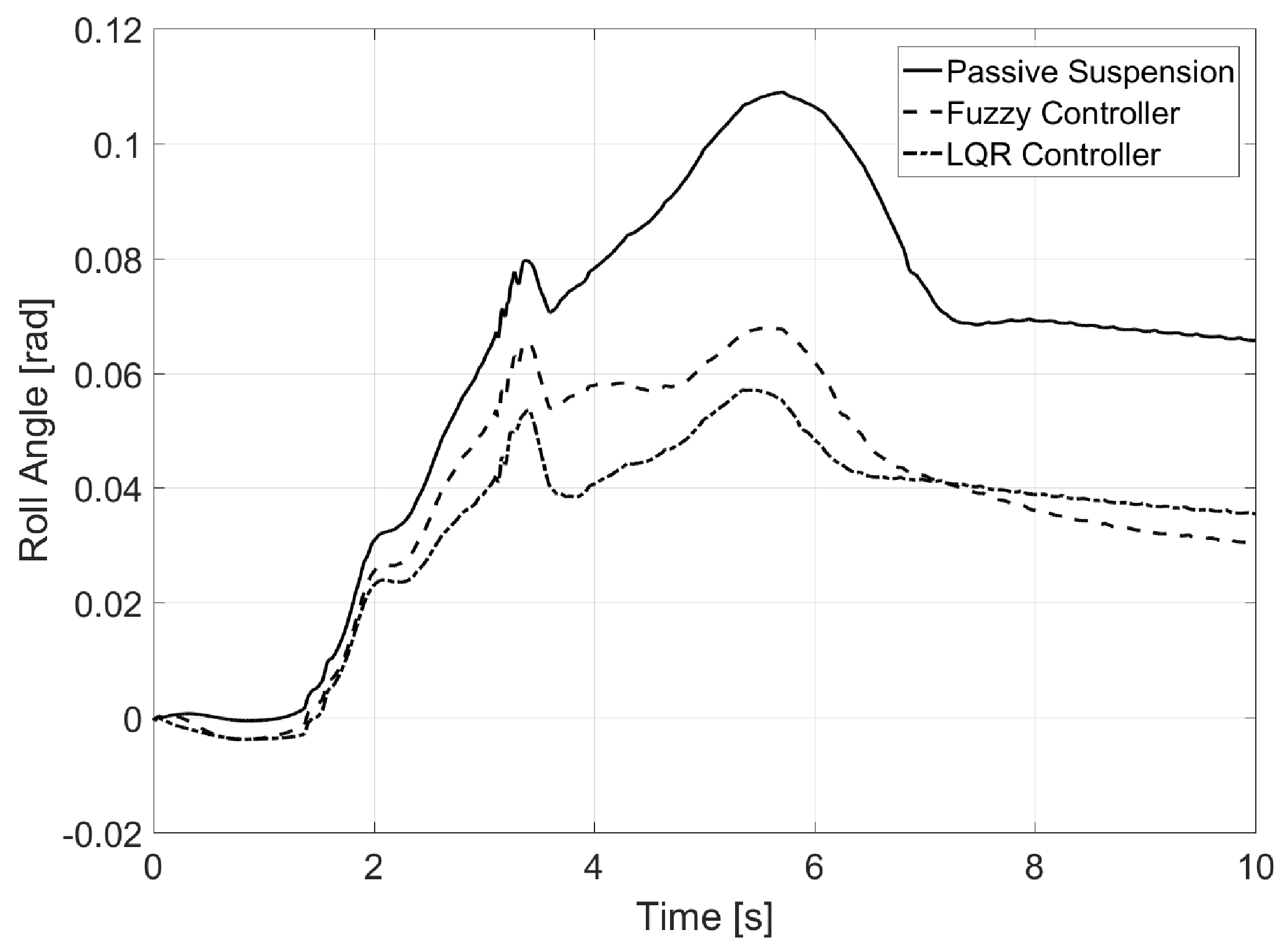
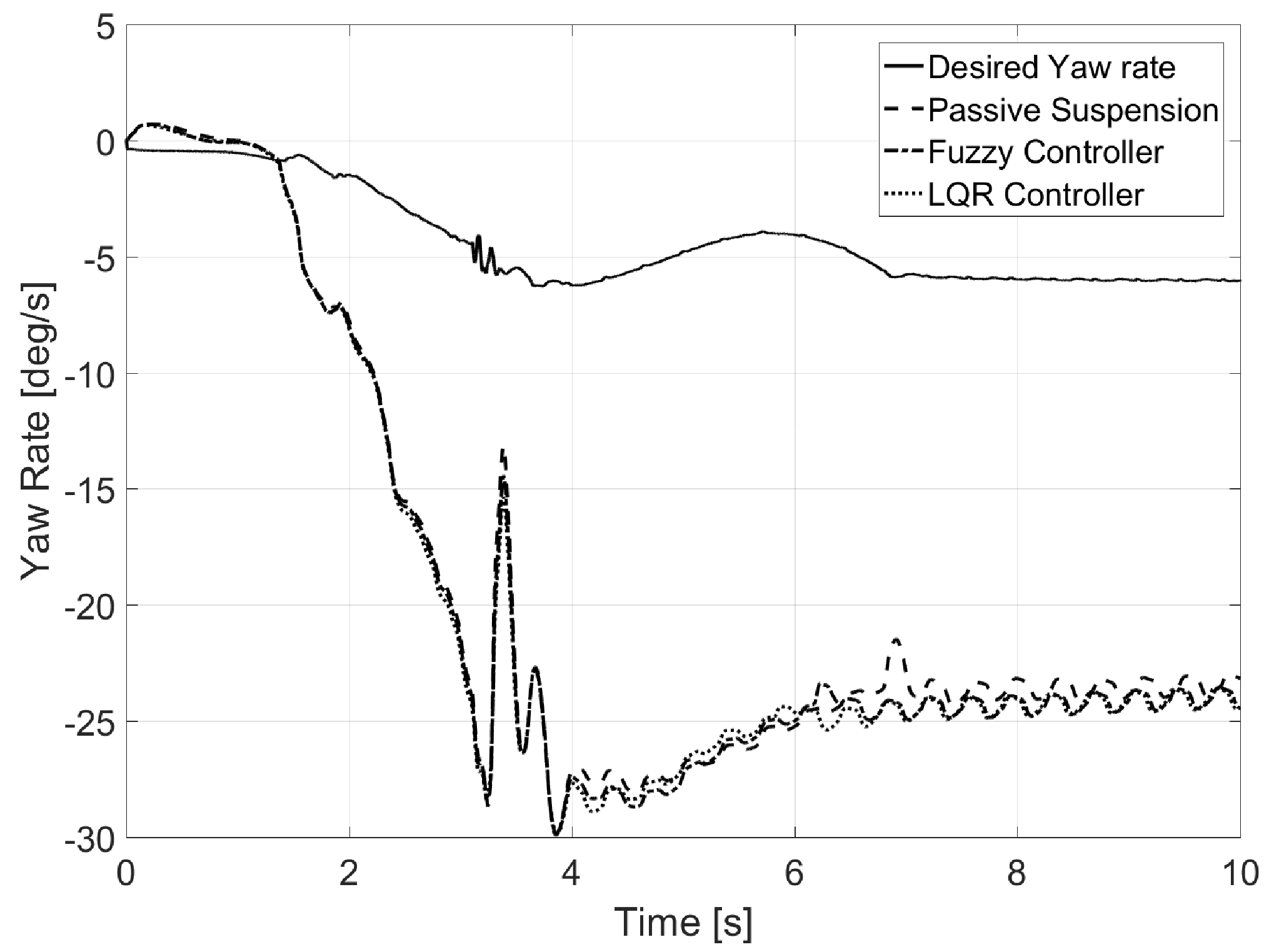
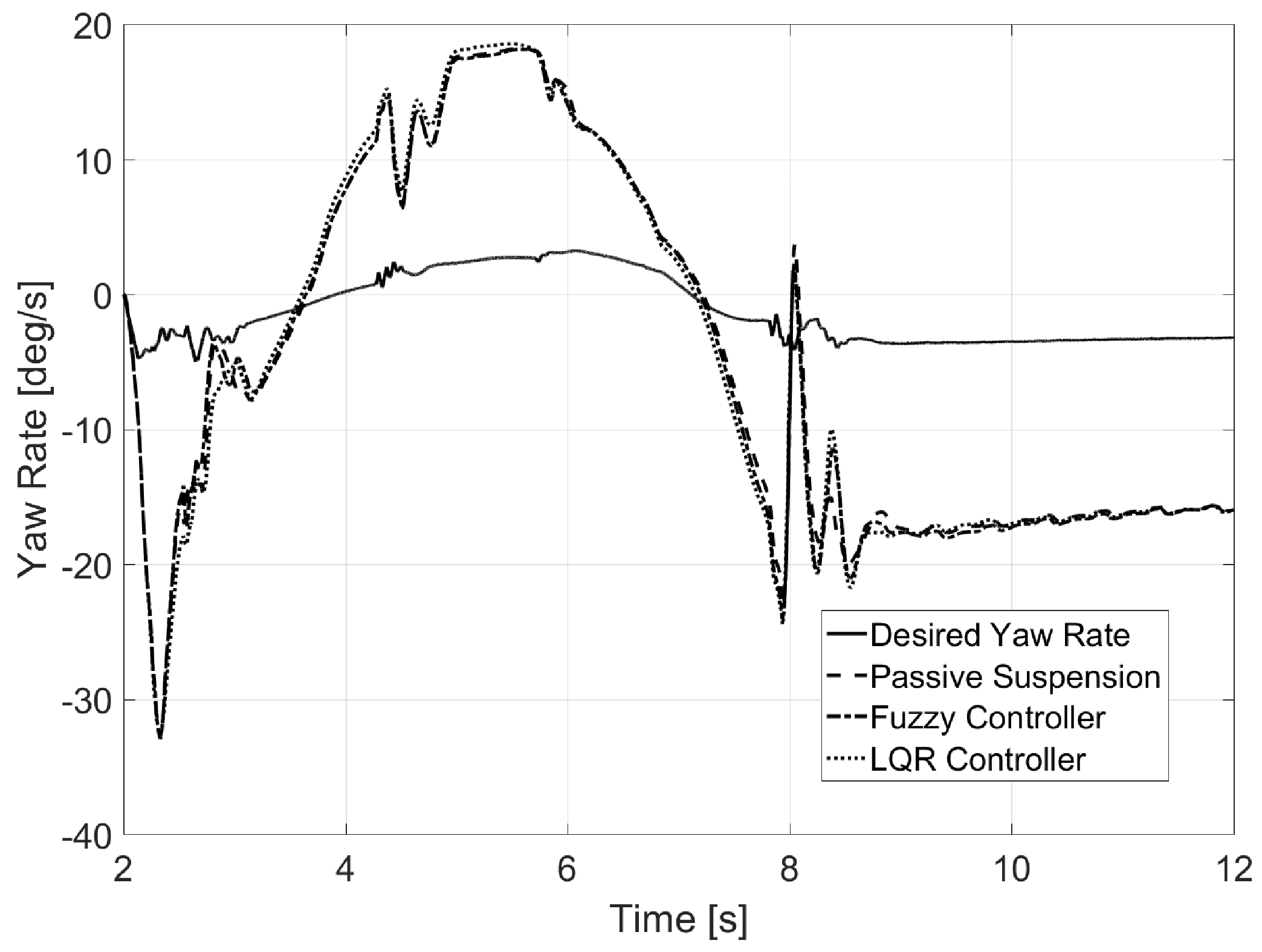
6.2. Test 2: Eight-Shaped Circuit
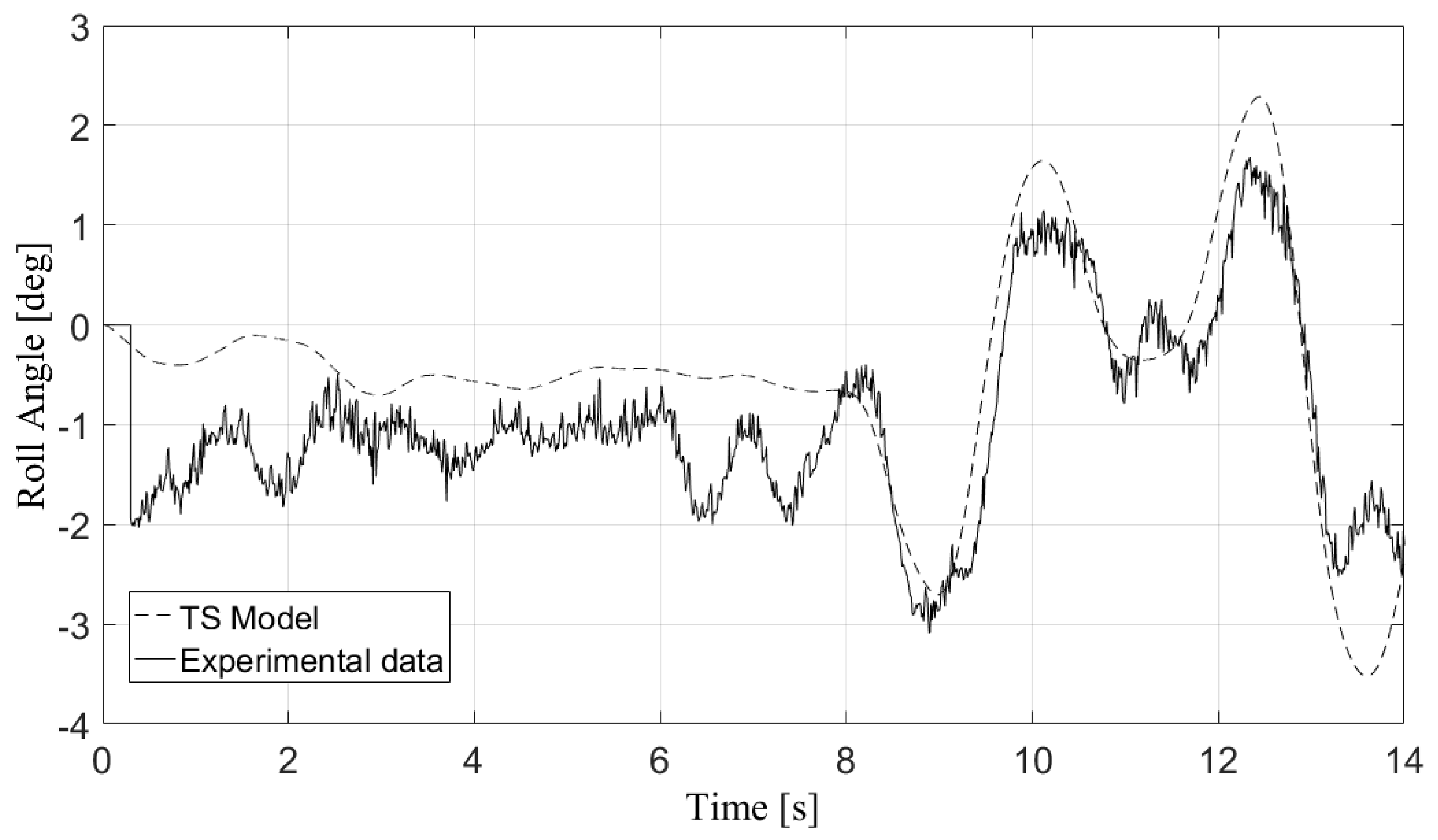
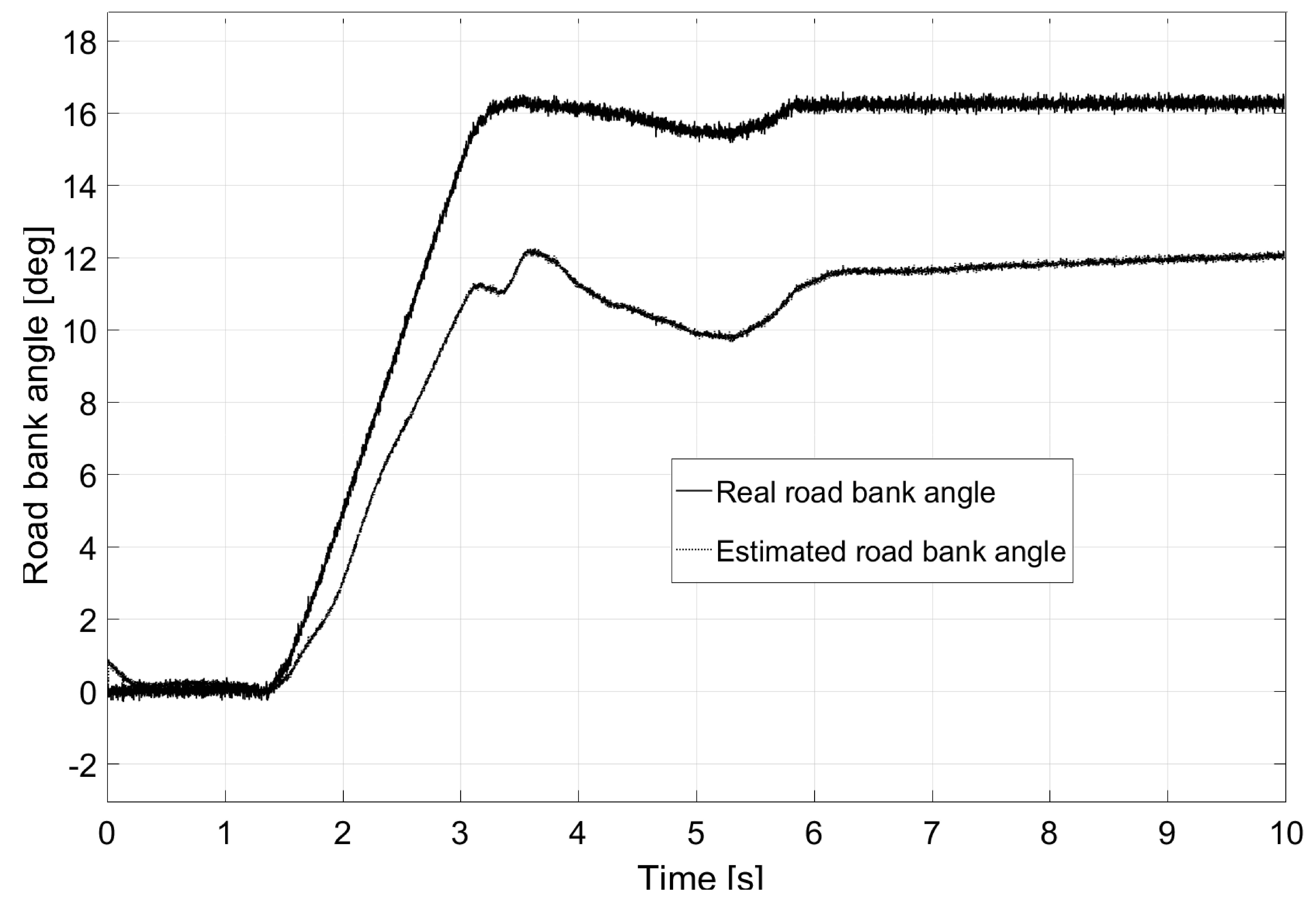
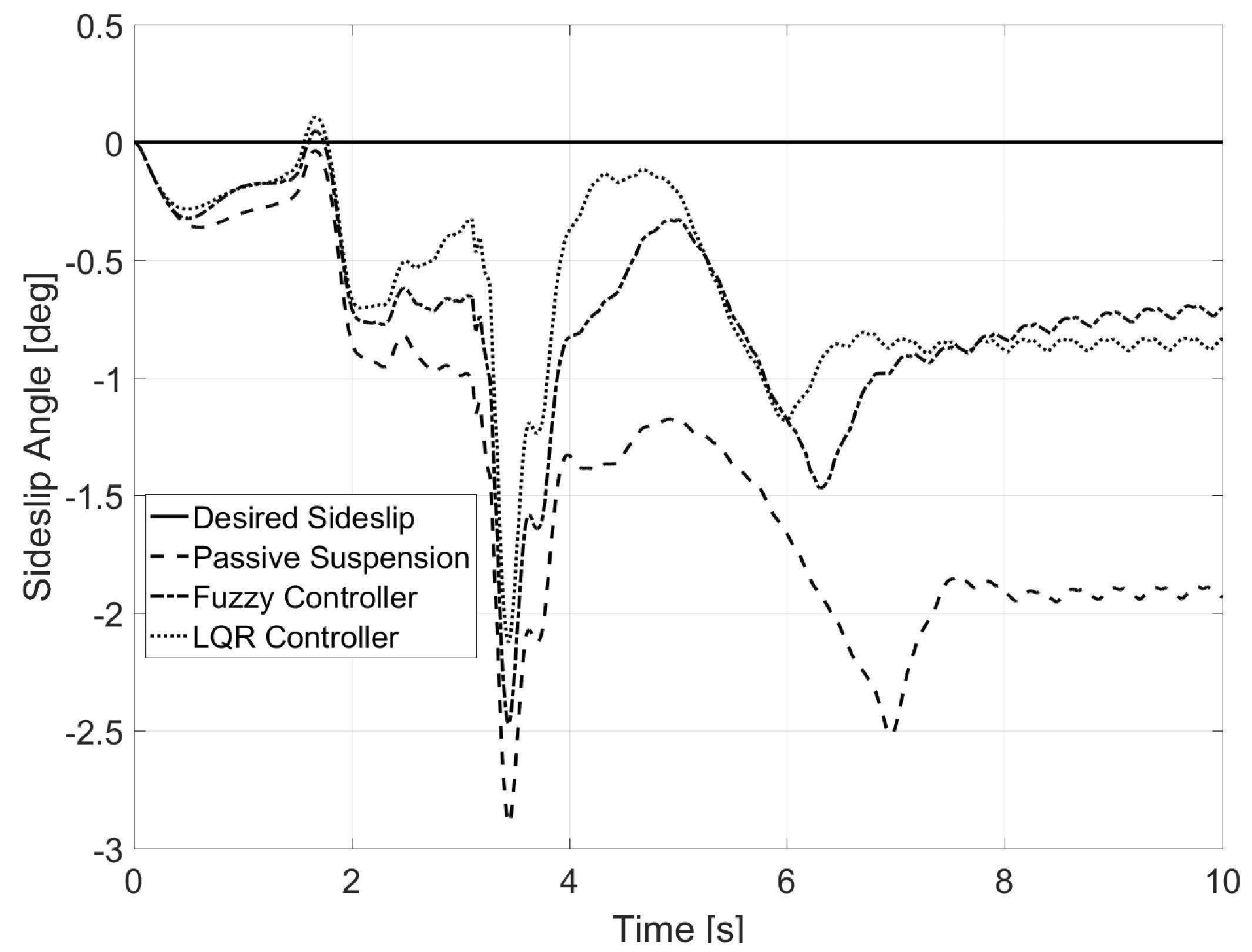
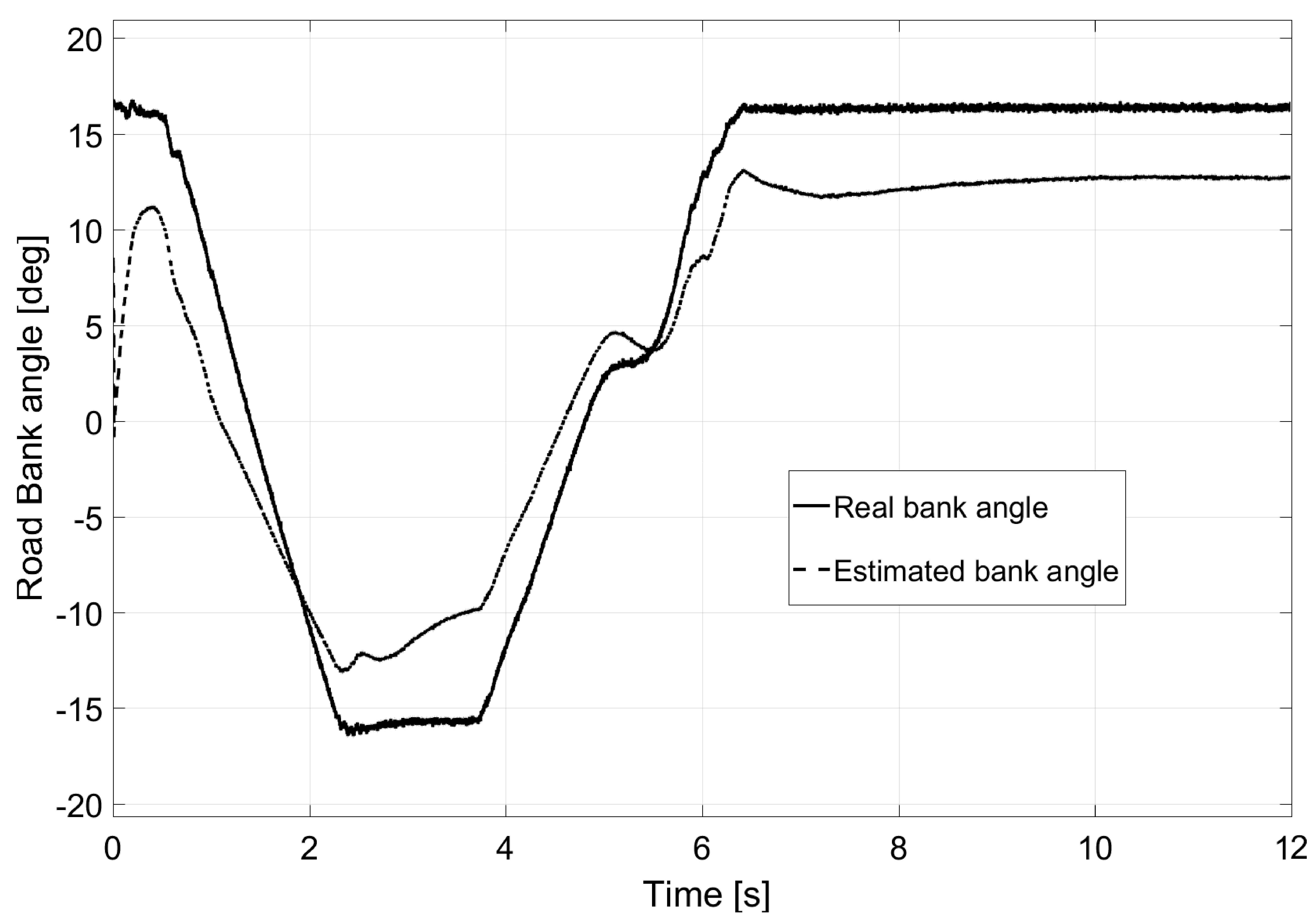
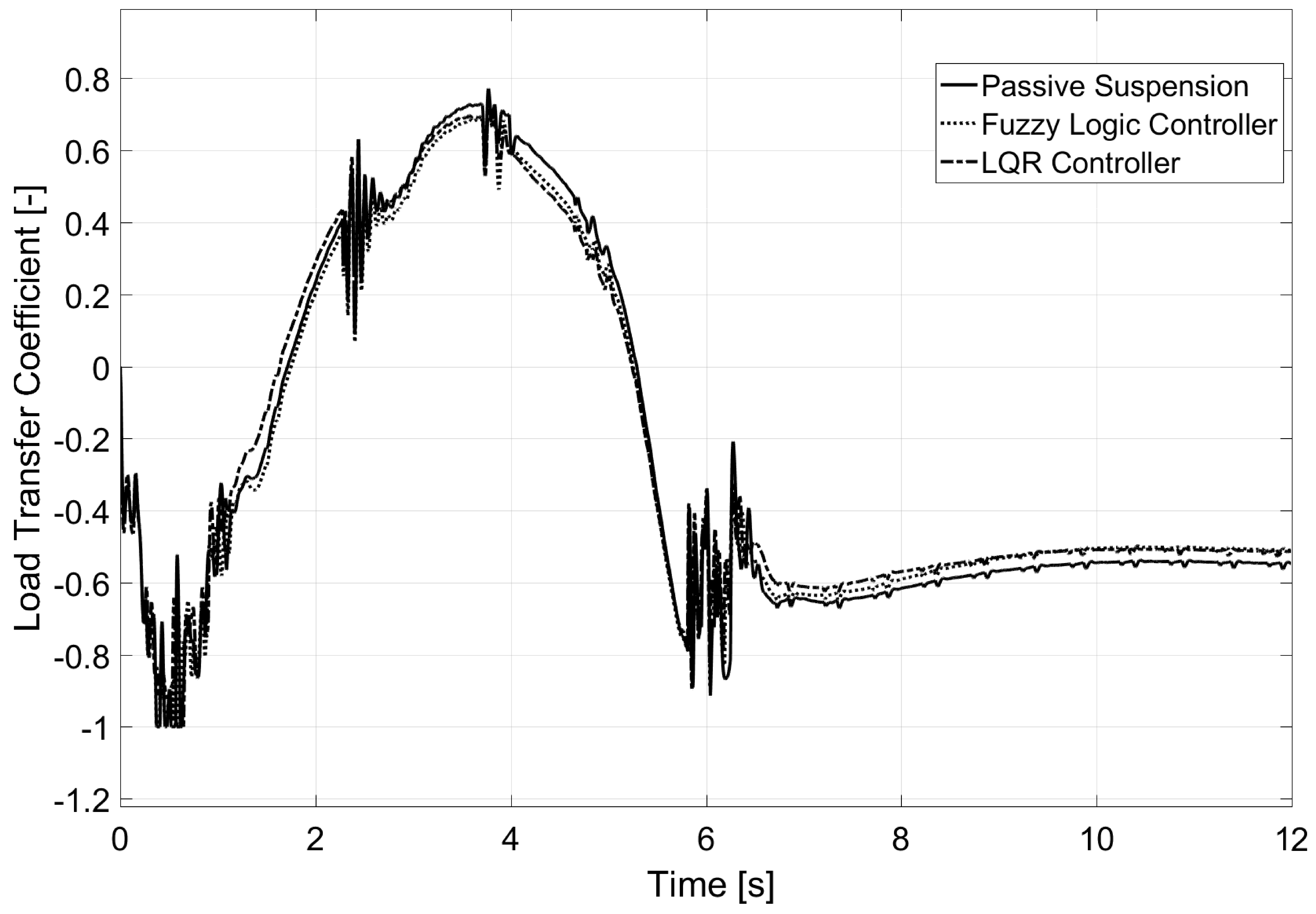
6.3. Test 3: Banked Road
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Symbol | Description | Value | Units |
| a | Distance COG-front axle | 1.51 | (m) |
| b | Distance COG-rear axle | 2.04 | (m) |
| Roll damping coefficient | 4.87 × 10 | (Nms/rad) | |
| Front cornering stiffness | 4.57 × 10 | (rad) | |
| Rear cornering stiffness | 8.14 × 10 | (rad) | |
| Vertical force on the left side | — | (N) | |
| Vertical force on the right side | — | (N) | |
| h | Height From COG to the roll center | 0.18 | (m) |
| Equivalent moment of inertia | 1.38 × 10 | (kgm) | |
| Moment of inertia around the x axis | 1.31 × 10 | (kgm) | |
| Moment of inertia around the z axis | 4.33 × 10 | (kgm) | |
| Roll stiffness | 3.71 × 10 | (Nm/rad) | |
| L | Distance between the front and rear axle | 3.55 | (m) |
| m | Sprung mass | 2150 | (kg) |
| Roll rate of the vehicle frame | — | (rad/s) | |
| Yaw rate of the vehicle frame | — | (rad/s) | |
| Wheel track | 1.63 | (m) | |
| Vehicle’s traveling speed | (m/s) | ||
| Sideslip angle | — | (rad) | |
| Steering wheel angle | — | (rad) | |
| Measurement error for yaw rate | — | (rad/s) | |
| Road bank angle | — | (rad) | |
| Vehicle roll angle | — | (rad) |
References
- Deutermann, W. Characteristics of Fatal Rollover Crashes; Technical Report DOT HS 809 438; NCSA: Chicago, IL, USA, 2002. [Google Scholar]
- Kahane, C.J. Relationships between Fatality Risk, Mass, and Footprint in Model Year 2000–2007 Passenger Cars and LTVs—Final Report; Thecnical Report Report no. DOT HS-811-665; National Highway Traffic Safety Administration: Washington, DC, USA, 2012.
- Furleigh, D.; Vanderploeg, M.; Oh, C. Multiple Steered Axles for Reducing the Rollover Risks of Heavy Articulated Trucks; SAE International: Warrendale, PA, USA; Troy, MI, USA, 1988. [Google Scholar] [CrossRef]
- Yim, S. Design of a robust controller for rollover prevention with active suspension and differential braking. J. Mech. Sci. Technol. 2012, 26, 213–222. [Google Scholar] [CrossRef]
- Zhu, B.; Piao, Q.; Zhao, J.; Guo, L. Integrated chassis control for vehicle rollover prevention with neural network time-to-rollover warning metrics. Adv. Mech. Eng. 2016, 8, 1–13. [Google Scholar] [CrossRef]
- Boada, B.L.; Boada, M.J.L.; Diaz, V.; Babe, A.G.; Ramos, J.A.C.; Diaz, V. Active Roll Control Using Reinforcement Learning for a Single Unit Heavy Vehicle. Int. J. Heavy Veh. Syst. 2009, 16, 412–430. [Google Scholar] [CrossRef]
- Yoon, J.; Cho, W.; Yi, K.; Koo, B. Unified Chassis Control for Vehicle Rollover Prevention. IFAC Proc. Vol. 2008, 41, 5682–5687. [Google Scholar] [CrossRef]
- Yoon, J.; Cho, W.; Koo, B.; Yi, K. Unified Chassis Control for Rollover Prevention and Lateral Stability. IEEE Trans. Veh. Technol. 2009, 58, 596–609. [Google Scholar] [CrossRef]
- Lu, S.; Cen, S.; Hu, X.; Lim, C.; Zhang, J. Integrated Control of Braking and Steering Subsystems for Autonomous Vehicle based on an Efficient Yaw Moment Distribution. IEEE Trans. Ind. Electron. 2017, PP. [Google Scholar] [CrossRef]
- Ohara, H.; Murakami, T. A Stability Control by Active Angle Control of Front-Wheel in a Vehicle System. IEEE Trans. Ind. Electron. 2008, 55, 1277–1285. [Google Scholar] [CrossRef]
- Hu, J.S.; Wang, Y.; Fujimoto, H.; Hori, Y. Robust Yaw Stability Control for In-wheel Motor Electric Vehicles. IEEE/ASME Trans. Mechatron. 2017, 22. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, J. Vehicle Lateral Dynamics Control through AFS/DYC and Robust Gain-Scheduling Approach. IEEE Trans. Veh. Technol. 2016, 65, 489–494. [Google Scholar] [CrossRef]
- Zhai, L.; Sun, T.; Wang, J. Electronic Stability Control Based on Motor Driving and Braking Torque Distribution for a Four In-Wheel Motor Drive Electric Vehicle. IEEE Trans. Veh. Technol. 2016, 65, 4726–4739. [Google Scholar] [CrossRef]
- Li, L.; Lu, Y.; Wang, R.; Chen, J. A Three-Dimensional Dynamics Control Framework of Vehicle Lateral Stability and Rollover Prevention via Active Braking with MPC. IEEE Trans. Ind. Electron. 2017, 64, 3389–3401. [Google Scholar] [CrossRef]
- Tang, X.; Du, H.; Sun, S.; Ning, D.; Xing, Z.; Li, W. Takagi–Sugeno Fuzzy Control for Semi-Active Vehicle Suspension with a Magnetorheological Damper and Experimental Validation. IEEE/ASME Trans. Mechatron. 2017, 22, 291–300. [Google Scholar] [CrossRef]
- Tseng, H.E. Dynamic Estimation of Road Bank Angle. Veh. Syst. Dyn. 2001, 36, 307–328. [Google Scholar] [CrossRef]
- Ryu, J.; Gerdes, J.C. Estimation of vehicle roll and road bank angle. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004; Volume 3, pp. 2110–2115. [Google Scholar]
- Nam, K.; Oh, S.; Fujimoto, H.; Hori, Y. Estimation of Sideslip and Roll Angles of Electric Vehicles Using Lateral Tire Force Sensors Through RLS and Kalman Filter Approaches. IEEE Trans. Ind. Electron. 2013, 60, 988–1000. [Google Scholar] [CrossRef]
- Yoon, J.H.; Peng, H. Robust Vehicle Sideslip Angle Estimation through a Disturbance Rejection Filter That Integrates a Magnetometer with GPS. IEEE Trans. Intell. Transp. Syst. 2014, 15, 191–204. [Google Scholar] [CrossRef]
- Yu, G.; Li, H.; Wang, P.; Wu, X.; Wang, Y. Real-time bus rollover prediction algorithm with road bank angle estimation. Chaos Solitons Fractals 2016, 89, 270–283. [Google Scholar] [CrossRef]
- Menhour, L.; Lechner, D.; Charara, A. Embedded unknown input sliding mode observer to estimate the vehicle roll and road bank angles: Experimental evaluation. IFAC Proc. Vol. 2010, 43, 623–628. [Google Scholar] [CrossRef]
- Boada, B.L.; Garcia-Pozuelo, D.; Boada, M.J.L.; Diaz, V. A Constrained Dual Kalman Filter Based on pdf Truncation for Estimation of Vehicle Parameters and Road Bank Angle: Analysis and Experimental Validation. IEEE Trans. Intell. Transp. Syst. 2017, 18, 1006–1016. [Google Scholar] [CrossRef]
- Boada, B.L.; Boada, M.J.L.; Diaz, V. Vehicle sideslip angle measurement based on sensor data fusion using an integrated ANFIS and an Unscented Kalman Filter algorithm. Mech. Syst. Signal Process. 2016, 72–73, 832–845. [Google Scholar] [CrossRef]
- Tavan, N.; Tavan, M.; Hosseini, R. An optimal integrated longitudinal and lateral dynamic controller development for vehicle path tracking. Latin Am. J. Solids Struct. 2015, 12, 1006–1023. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X.; Wang, J. Robust gain-scheduling energy-to-peak control of vehicle lateral dynamics stabilisation. Veh. Syst. Dyn. 2014, 52, 309–340. [Google Scholar] [CrossRef]
- Vargas-Meléndez, L.; Boada, B.L.; Boada, M.J.L.; Gauchía, A.; Díaz, V. A Sensor Fusion Method Based on an Integrated Neural Network and Kalman Filter for Vehicle Roll Angle Estimation. Sensors 2016, 16, 1400. [Google Scholar] [CrossRef] [PubMed]
- Boada, M.J.L.; Boada, B.L.; Gauchia, A.; Diaz, V. Fuzzy-Based Roll Control for a Single Unit Heavy Vehicle. In Proceedings of the ASME 8th Biennial Conference on Engineering Systems Design and Analysis, Torino, Italy, 4–7 July 2006; Volume 2, pp. 93–99. [Google Scholar] [CrossRef]
- Riofrio, A.; Boada, B.L.; Boada, M.J.L.; Garcia-Pozuelo, D.; Diaz, V. Fuzzy-based anti-rollover controller for a heavy duty vehicle using active suspension. In Proceedings of the FISITA 2016 World Automotive Congress, Busan, Korea, 26–30 September 2016. [Google Scholar]


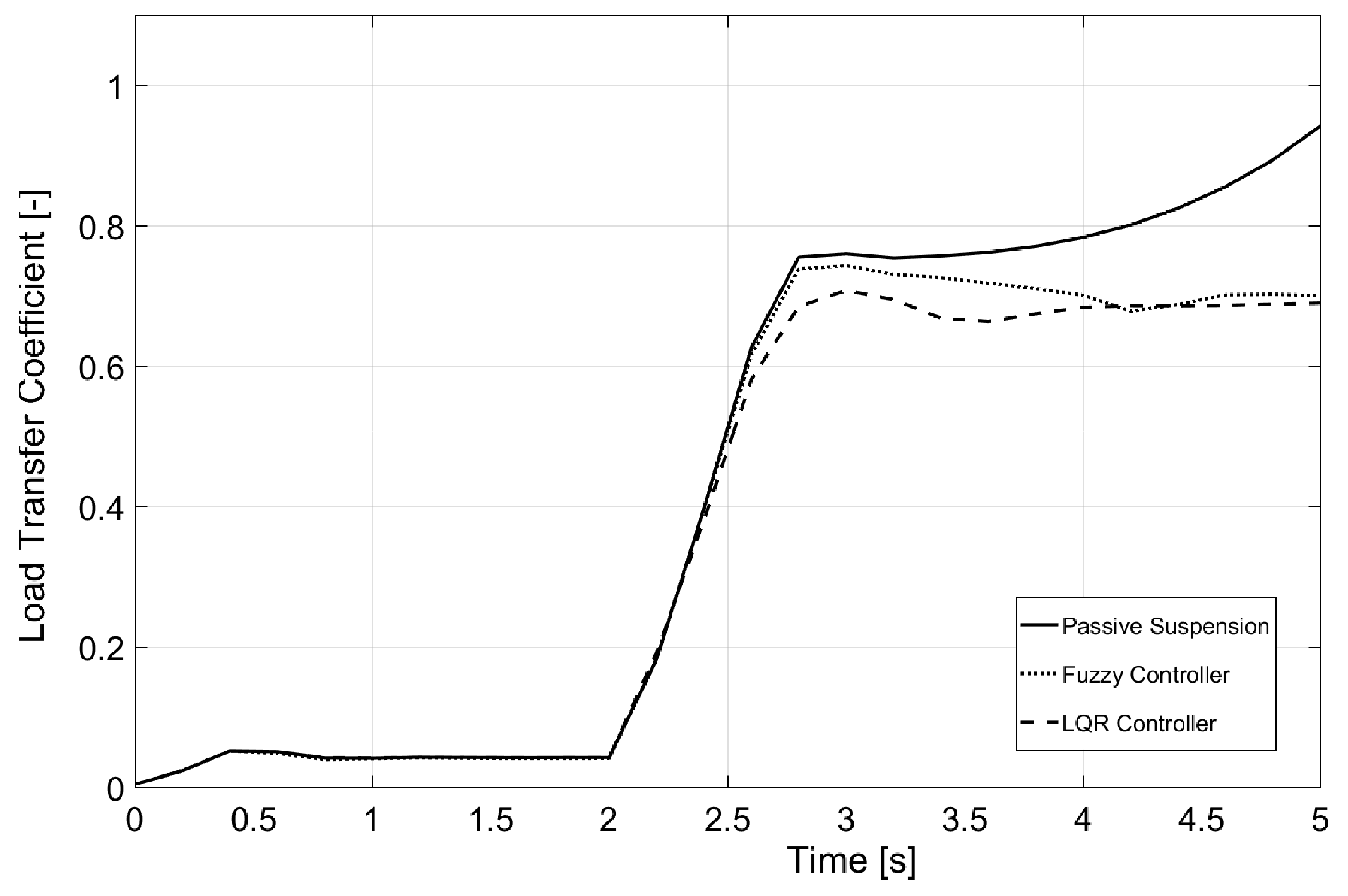







| Test 1 | Test 2 | Test 3 | |
|---|---|---|---|
| Passive Suspension | 1 | 0.85 | 0.75 |
| Fuzzy Controller | 0.75 | 0.8 | 0.65 |
| LQR controller | 0.7 | 0.78 | 0.65 |
| Test 1 | Test 2 | Test 3 | |
|---|---|---|---|
| Roll Angle, | |||
| Passive Suspension | 1.38 | 4.59 | 1.35 |
| Fuzzy Controller | 1.21 | 3.20 | 1.38 |
| LQR Controller | 1.14 | 3.82 | 1.09 |
| Yaw Rate, | |||
| Passive Suspension | 3.04 | 0.60 | 0.63 |
| Fuzzy Controller | 3.04 | 0.60 | 0.64 |
| LQR Controller | 2.91 | 0.60 | 0.64 |
| Sideslip Angle, | |||
| Passive Suspension | 0.99 | 1.10 | 1.00 |
| Fuzzy Controller | 0.56 | 1.11 | 1.03 |
| LQR Controller | 0.49 | 1.08 | 0.99 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riofrio, A.; Sanz, S.; Boada, M.J.L.; Boada, B.L. A LQR-Based Controller with Estimation of Road Bank for Improving Vehicle Lateral and Rollover Stability via Active Suspension. Sensors 2017, 17, 2318. https://doi.org/10.3390/s17102318
Riofrio A, Sanz S, Boada MJL, Boada BL. A LQR-Based Controller with Estimation of Road Bank for Improving Vehicle Lateral and Rollover Stability via Active Suspension. Sensors. 2017; 17(10):2318. https://doi.org/10.3390/s17102318
Chicago/Turabian StyleRiofrio, Andres, Susana Sanz, Maria Jesus L. Boada, and Beatriz L. Boada. 2017. "A LQR-Based Controller with Estimation of Road Bank for Improving Vehicle Lateral and Rollover Stability via Active Suspension" Sensors 17, no. 10: 2318. https://doi.org/10.3390/s17102318
APA StyleRiofrio, A., Sanz, S., Boada, M. J. L., & Boada, B. L. (2017). A LQR-Based Controller with Estimation of Road Bank for Improving Vehicle Lateral and Rollover Stability via Active Suspension. Sensors, 17(10), 2318. https://doi.org/10.3390/s17102318






