Joint Power Charging and Routing in Wireless Rechargeable Sensor Networks
Abstract
1. Introduction
- We present a novel joint optimization model including both charging efficiency and routing, rather than the typical charging optimization problem considering only the predefined data-gathering route.
- We propose a genetic algorithm (GA)-based optimization framework to find the optimal routing tree, in which the specific many-to-one routing tree is coded as an individual for evolution. We design an efficient individual encoding scheme and effective constraints handling mechanisms to achieve quick convergence.
- We then propose a heuristic algorithm to find the optimal resident locations with the given routing tree. By calculating the minimum moving distance and total charging time to evaluate the fitness of each individual, the evolution process of the GA is thus guided.
- We evaluate the proposed algorithms with extensive simulations and study the impact of multiple environmental factors, including the number of sensors and the types of routing tree. Our simulation results have showed that our proposed algorithm achieves a substantial improvement compared with the predefined route.
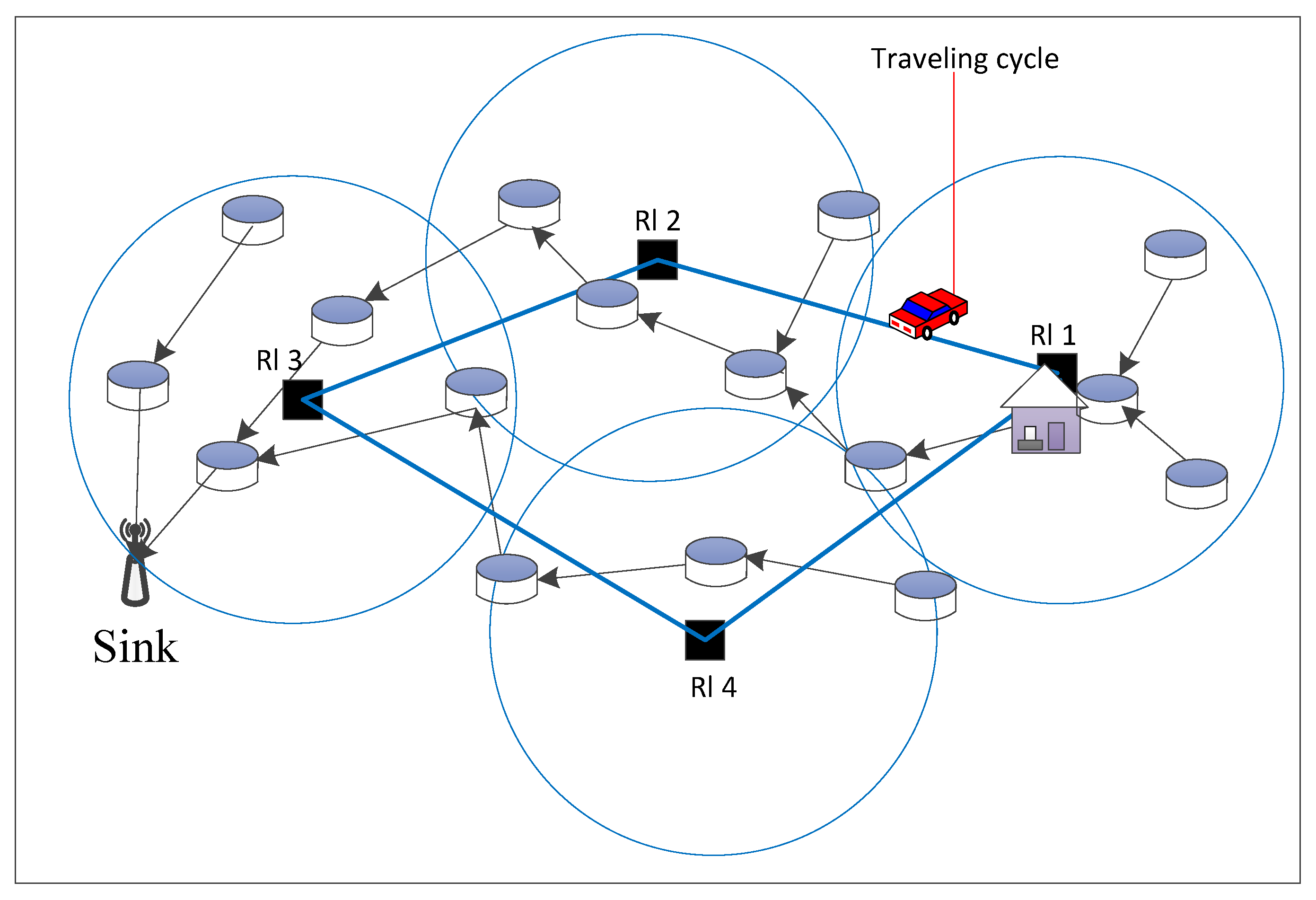
2. System Model and Problem Formulation
2.1. System Model
2.2. Routing Constraints
2.3. Energy Charging Cycle
2.4. Problem Formulation
3. Optimization Algorithms
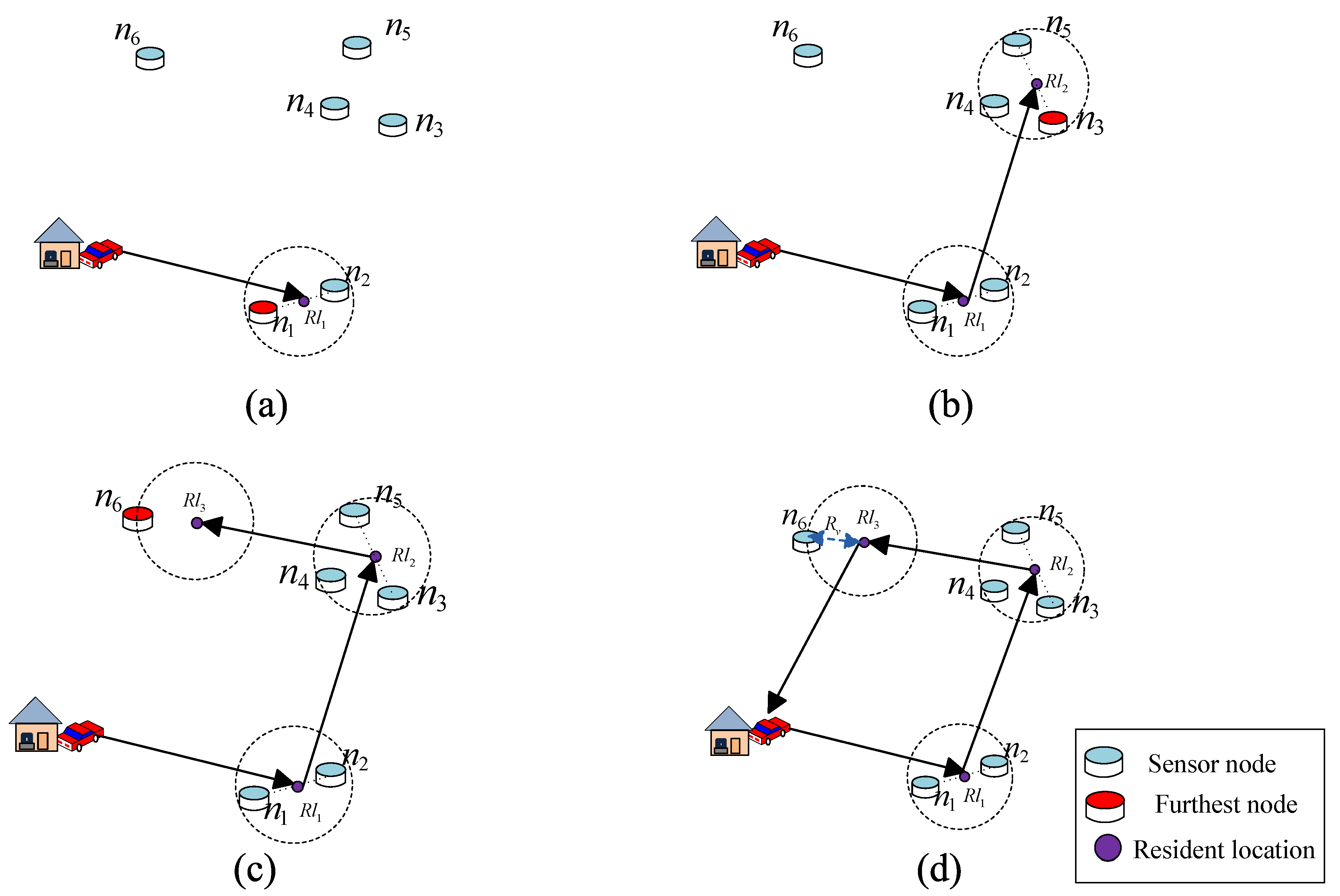
3.1. Heuristic Algorithm for Optimal Charging
| Algorithm 1: Heuristic algorithm for resident location selection |
 |
3.2. Joint Optimization of Routing and Charging
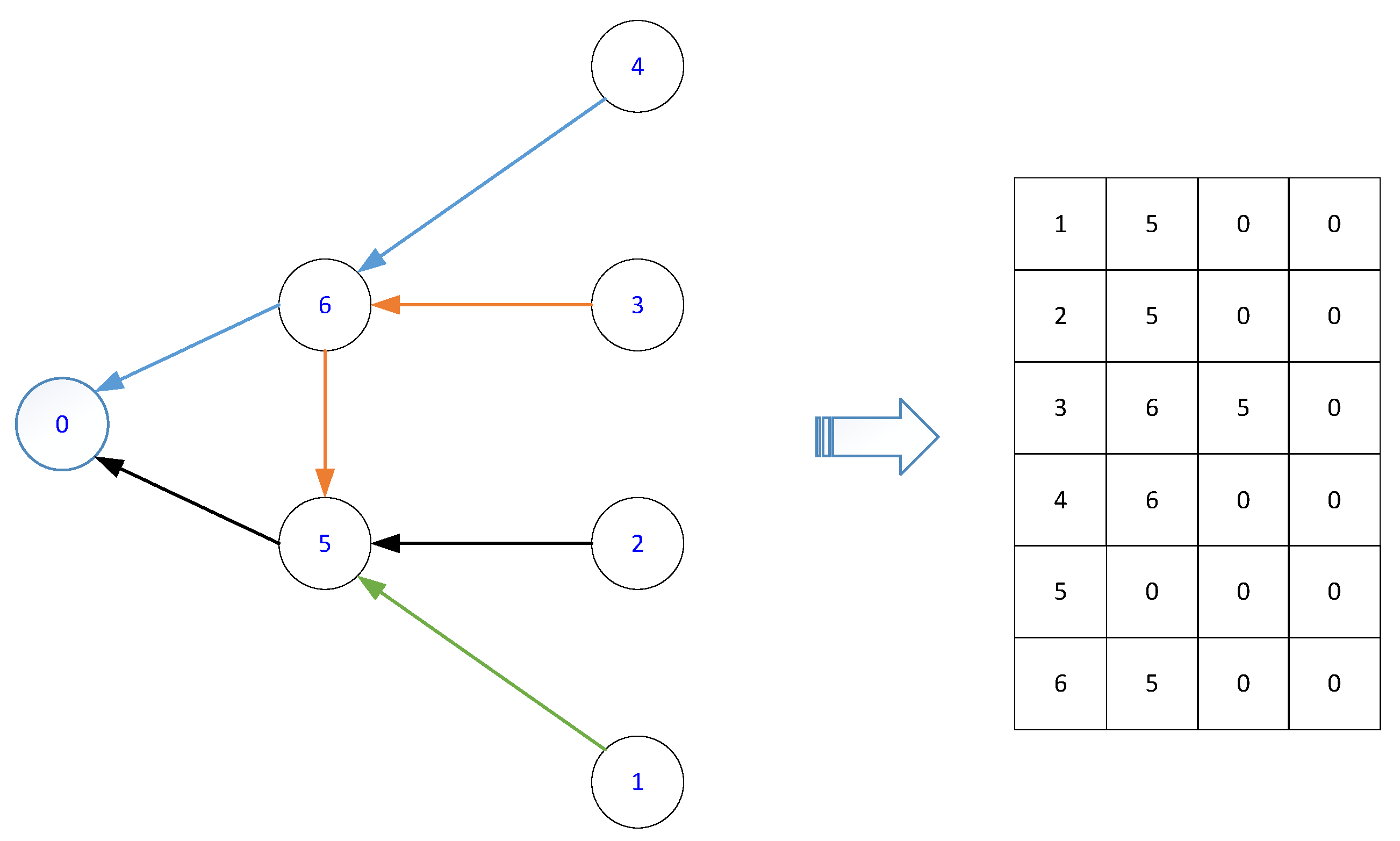
3.2.1. Individual Encoding
| Algorithm 2: Population initialization |
 |
3.2.2. Fitness Functions and Natural Selection
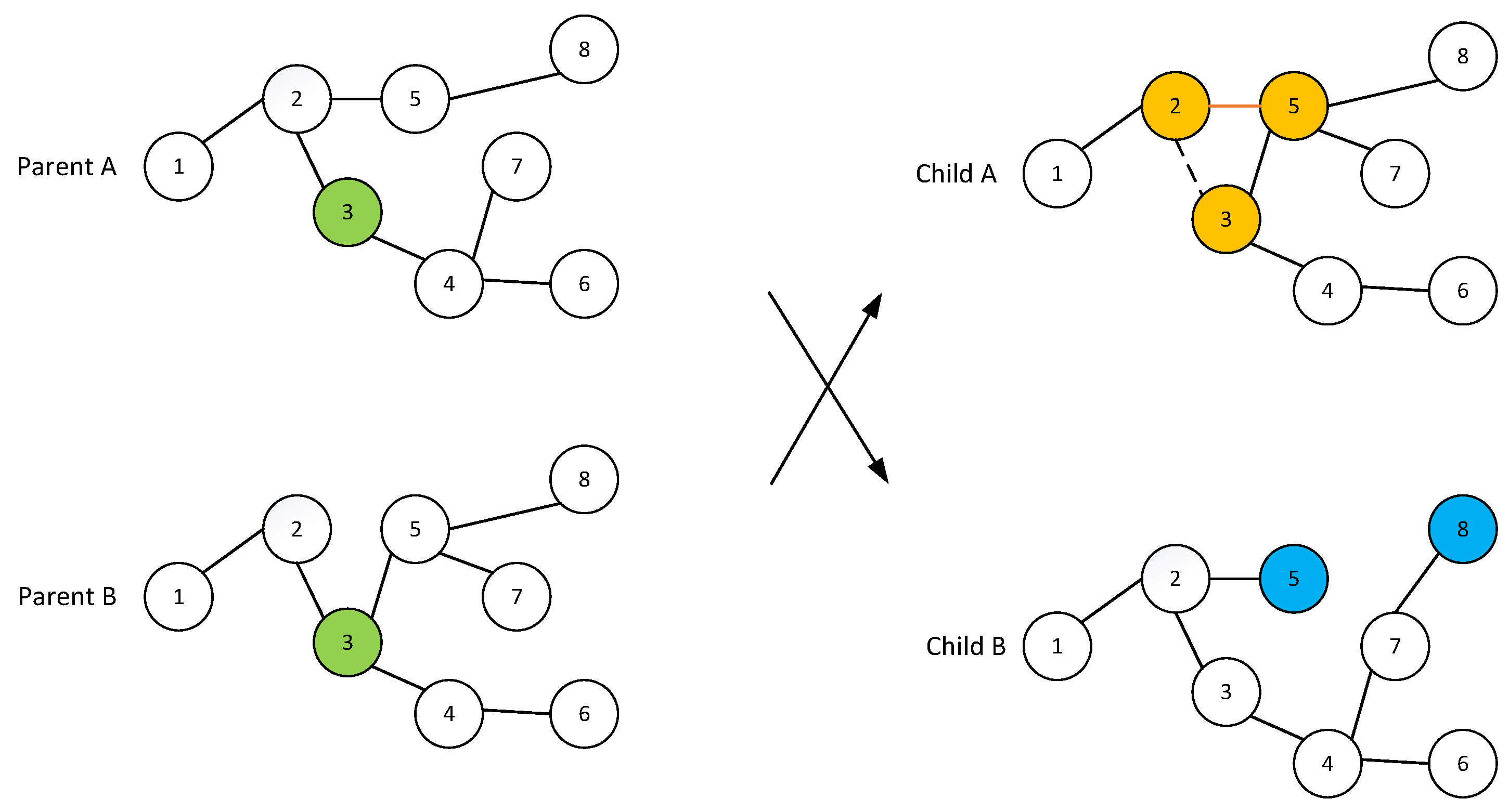
3.2.3. Crossover and Mutation
3.2.4. Replacement
| Algorithm 3: Joint optimization based on genetic algorithm |
 |
4. Numerical Results
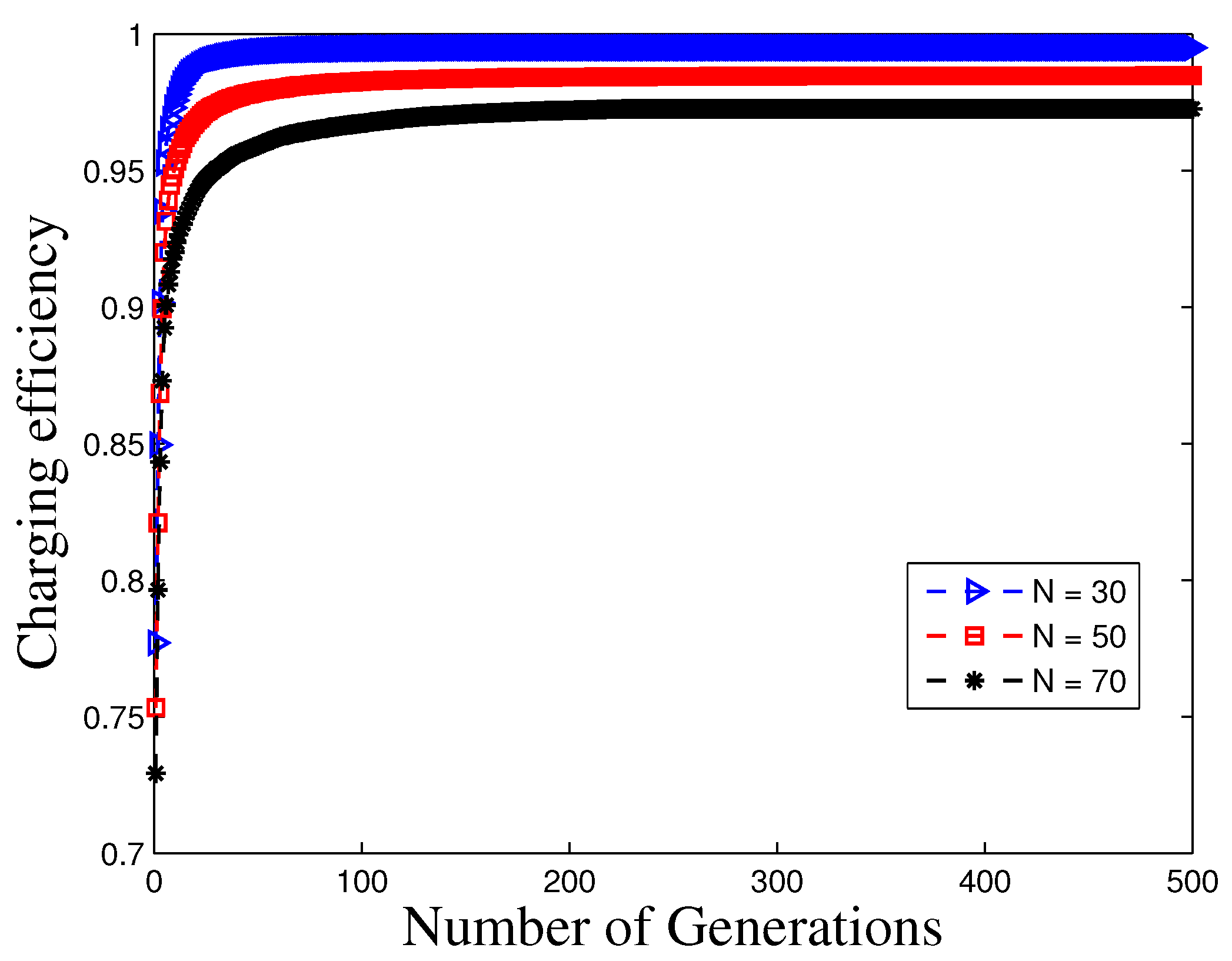
4.1. Convergence Behavior
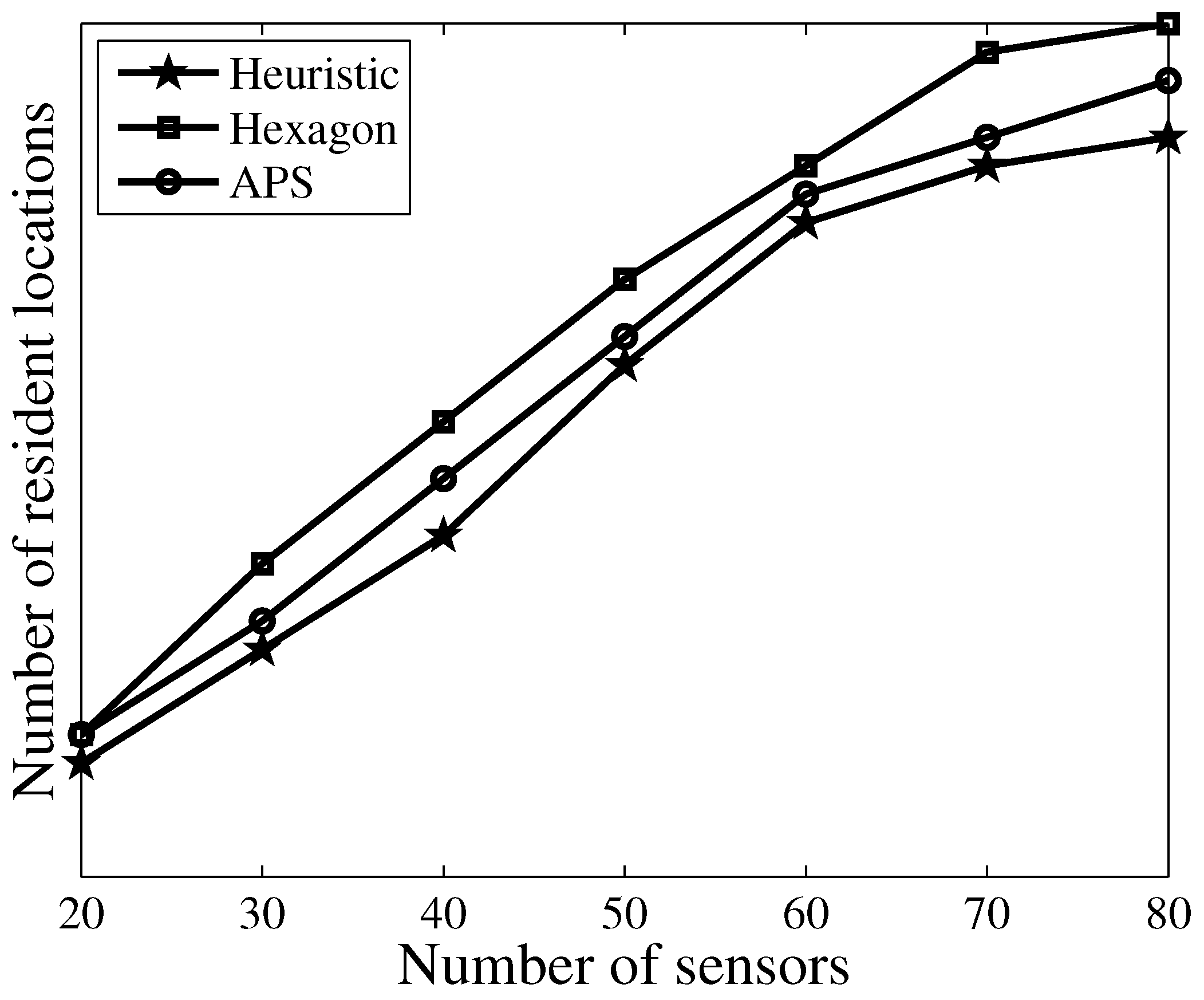
4.2. Total Traveling Distance
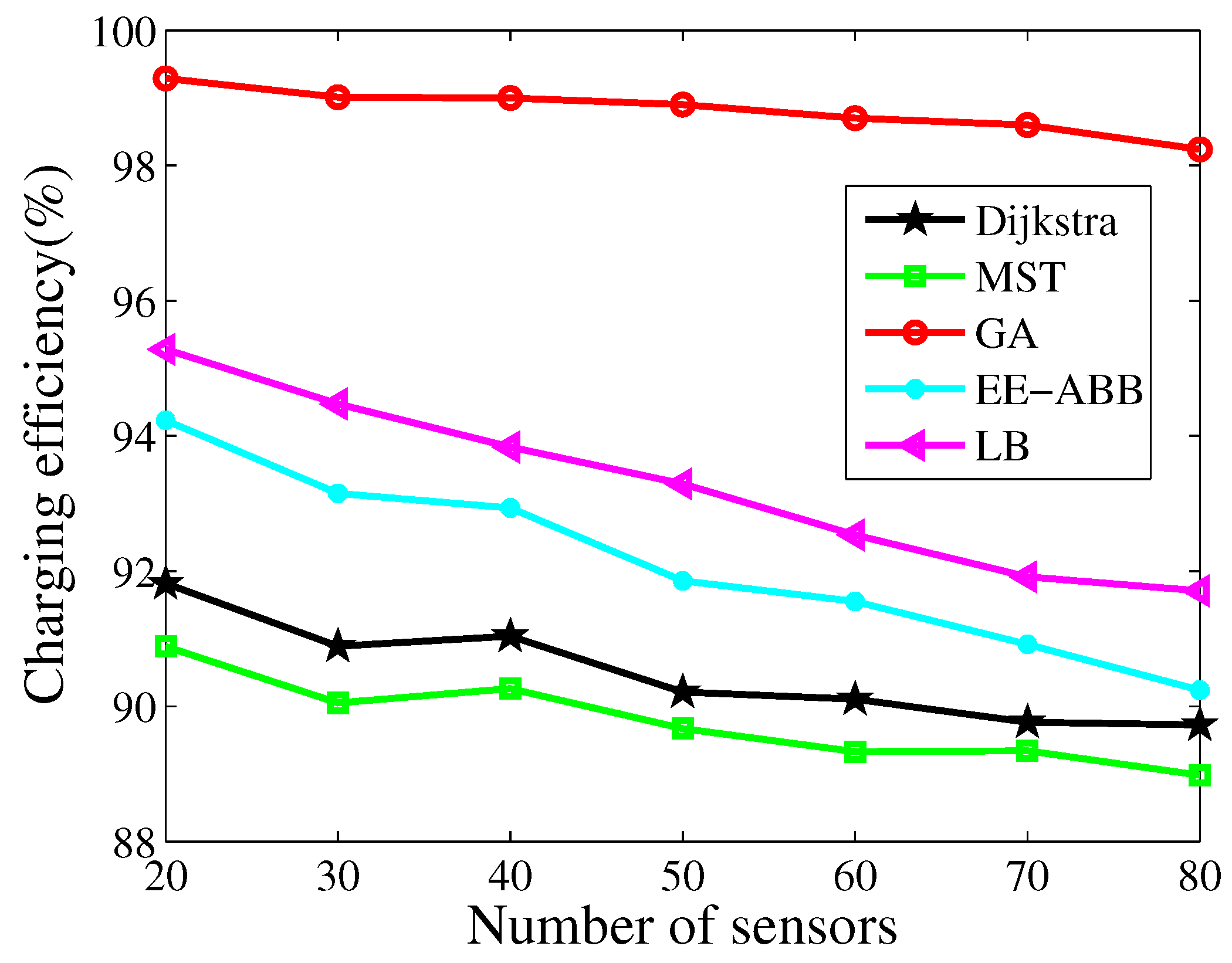
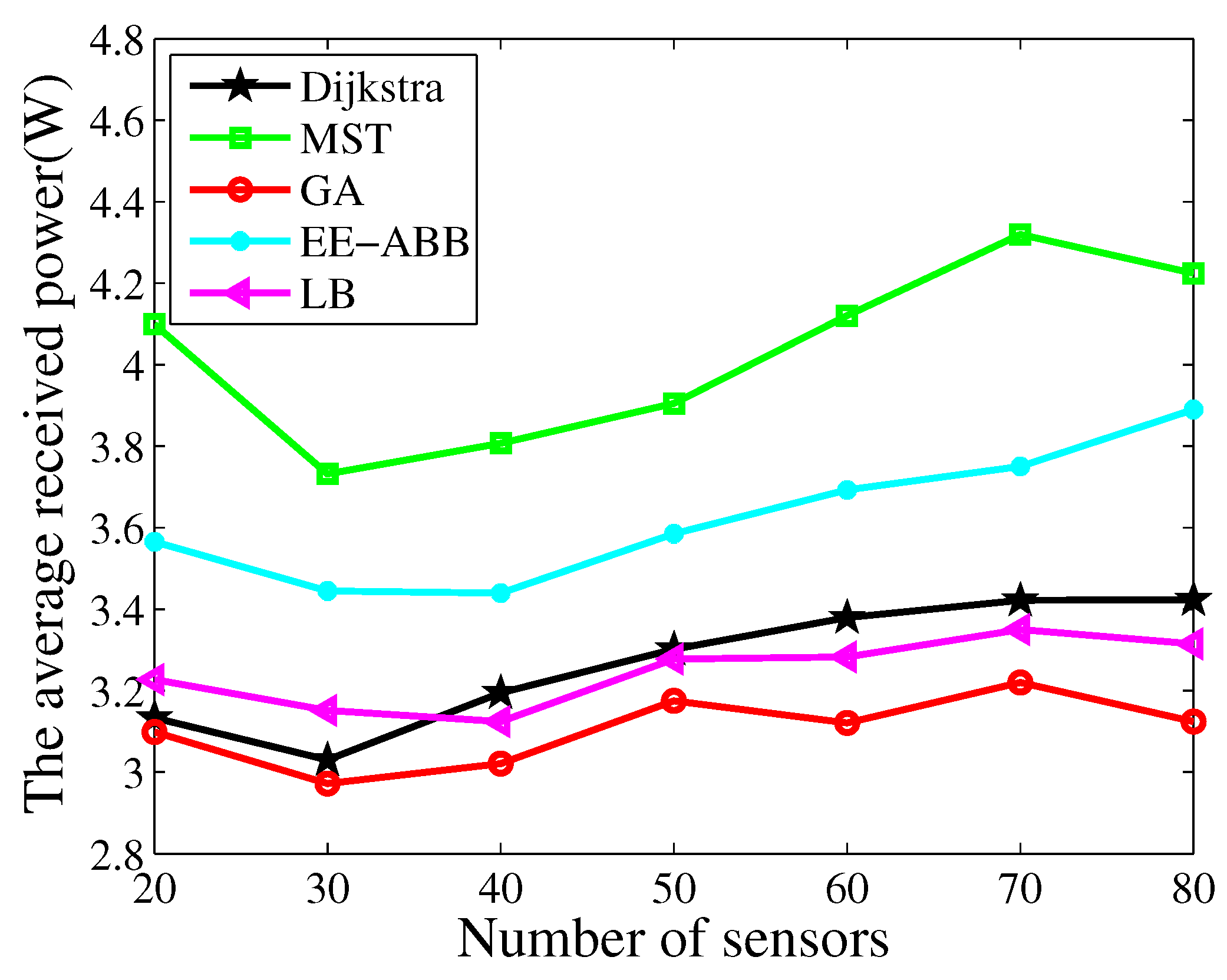
4.3. Routing
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lee, J.; Kao, T. An Improved Three-Layer Low-Energy Adaptive Clustering Hierarchy for Wireless Sensor Networks. IEEE Int. Things J. 2016, 3, 951–958. [Google Scholar] [CrossRef]
- Aguirre, E.; Lopeziturri, P.; Azpilicueta, L.; Redondo, A.; Astrain, J.J.; Villadangos, J.; Bahillo, A.; Perallos, A.; Falcone, F. Design and Implementation of Context Aware Applications with Wireless Sensor Network Support in Urban Train Transportation Environments. IEEE Sens. J. 2016, 17, 169–178. [Google Scholar] [CrossRef]
- Haghighat, J.; Hamouda, W. A Power-Efficient Scheme for Wireless Sensor Networks Based on Transmission of Good Bits and Threshold Optimization. IEEE Trans. Commun. 2016, 64, 3520–3533. [Google Scholar] [CrossRef]
- Jia, J.; Chen, J. An energy-balanced self-deployment algorithm based on virtual force for mobile sensor networks. Int. J. Sens. Netw. 2015, 19, 150–160. [Google Scholar] [CrossRef]
- Lin, D.; Wang, Q. A game theory based energy efficient clustering routing protocol for WSNs. Wirel. Netw. 2016, 23, 1101–1111. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, L.; Elkashlan, M.; Nallanathan, A.; Mallik, R.K. Physical Layer Security in Three-Tier Wireless Sensor Networks: A Stochastic Geometry Approach. IEEE Trans. Inf. Forensics Secur. 2016, 11, 1128–1138. [Google Scholar] [CrossRef]
- Shen, X.; Bo, C.; Zhang, J.; Tang, S.; Mao, X.; Dai, G. EFCon: Energy flow control for sustainable wireless sensor networks. Ad Hoc Netw. 2013, 11, 1421–1431. [Google Scholar] [CrossRef]
- Intel. Wireless Resonant Energy Link (Wrel) Demo. Available online: http://www.thefullwiki.org/WREL_(technology) (accessed on 17 November 2009).
- Product Specifications. TX91501. Available online: http://www.powercastco.com (accessed on 20 February 2017).
- Fu, L.; Cheng, P.; Gu, Y.; Chen, J.; He, T. Optimal Charging in Wireless Rechargeable Sensor Networks. IEEE Trans. Veh. Technol. 2015, 65, 278–291. [Google Scholar] [CrossRef]
- Bi, S.; Zhang, R. Distributed charging control in broadband wireless power transfer networks. IEEE J. Sel. Areas Commun. 2016, 34, 3380–3393. [Google Scholar] [CrossRef]
- Xie, L.; Shi, Y.; Hou, Y.T.; Sherali, H.D. Making sensor networks immortal: An energy-renewal approach with wireless power transfer. IEEE/ACM Trans. Netw. 2012, 20, 1748–1761. [Google Scholar] [CrossRef]
- Shu, Y.; Yousefi, H.; Cheng, P.; Chen, J.; Gu, Y.J.; He, T.; Shin, K.G. Near-Optimal Velocity Control for Mobile Charging in Wireless Rechargeable Sensor Networks. IEEE Trans. Mob. Comput. 2016, 15, 1699–1713. [Google Scholar] [CrossRef]
- Shu, Y.; Shin, K.G.; Chen, J.; Sun, Y. Joint Energy Replenishment and Operation Scheduling in Wireless Rechargeable Sensor Networks. IEEE Trans. Ind. Inform. 2016, 13, 125–134. [Google Scholar] [CrossRef]
- Li, Z.; Peng, Y.; Zhang, W.; Qiao, D. J-RoC: A Joint Routing and Charging scheme to prolong sensor network lifetime. In Proceedings of the IEEE International Conference on Network Protocols, Vancouver, AB, Canada, 17–20 October 2011; pp. 373–382. [Google Scholar]
- Guo, S.; Wang, F.; Yang, Y.; Xiao, B. Energy-Efficient Cooperative Transmission for Simultaneous Wireless Information and Power Transfer in Clustered Wireless Sensor Networks. IEEE Trans. Commun. 2015, 63, 4405–4417. [Google Scholar] [CrossRef]
- Guo, S.; Wang, C.; Yang, Y. Joint Mobile Data Gathering and Energy Provisioning in Wireless Rechargeable Sensor Networks. IEEE Trans. Mob. Comput. 2014, 13, 2836–2852. [Google Scholar] [CrossRef]
- Zhao, M.; Li, J.; Yang, Y. A Framework of Joint Mobile Energy Replenishment and Data Gathering in Wireless Rechargeable Sensor Networks. IEEE Trans. Mob. Comput. 2014, 13, 2689–2705. [Google Scholar] [CrossRef]
- Wang, C.; Guo, S.; Yang, Y. An Optimization Framework for Mobile Data Collection in Energy-Harvesting Wireless Sensor Networks. IEEE Trans. Mob. Comput. 2016, 15, 2969–2986. [Google Scholar] [CrossRef]
- Bi, S.; Zhang, R. Placement optimization of energy and information access points in wireless powered communication networks. IEEE Trans. Wirel. Commun. 2016, 15, 2351–2364. [Google Scholar] [CrossRef]
- Huang, K.; Lau, V.K. Enabling wireless power transfer in cellular networks: Architecture, modeling and deployment. IEEE Trans. Wirel. Commun. 2014, 13, 902–912. [Google Scholar] [CrossRef]
- Che, Y.L.; Duan, L.; Zhang, R. Spatial throughput maximization of wireless powered communication networks. IEEE J. Sel. Areas Commun. 2015, 33, 1534–1548. [Google Scholar] [CrossRef]
- Wu, X.; Chen, G.; Das, S.K. Avoiding Energy Holes in Wireless Sensor Networks with Nonuniform Node Distribution. IEEE Trans. Parallel Distrib. Syst. 2008, 19, 710–720. [Google Scholar]
- Ren, J.; Zhang, Y.; Zhang, K.; Liu, A.; Chen, J.; Shen, X.S. Lifetime and Energy Hole Evolution Analysis in Data-Gathering Wireless Sensor Networks. IEEE Trans. Ind. Inform. 2016, 12, 788–800. [Google Scholar] [CrossRef]
- Jia, J.; Zhang, G.; Wu, X.; Chen, J.; Wang, X.; Yan, X. On the Problem of Energy Balanced Relay Sensor Placement in Wireless Sensor Networks. Int. J. Distrib. Sens. Netw. 2013, 2013, 342904. [Google Scholar] [CrossRef]
- Jia, J.; Chen, J.; Wang, X.; Zhao, L. Energy-Balanced Density Control to Avoid Energy Hole for Wireless Sensor Networks. Int. J. Distrib. Sens. Netw. 2012, 2012, 812013. [Google Scholar] [CrossRef]
- Shahzad, F.; Sheltami, T.R.; Shakshuki, E.M. DV-maxHop: A fast and accurate range-free localization algorithm for anisotropic wireless networks. IEEE Trans. Mob. Comput. 2017, 16, 2494–2505. [Google Scholar] [CrossRef]
- Jia, J.; Zhang, G.; Wang, X.; Chen, J. On distributed localization for road sensor networks: A game theoretic approach. Math. Probl. Eng. 2013, 2013, 640391. [Google Scholar] [CrossRef]
- Shi, Y.; Xie, L.; Hou, Y.T.; Sherali, H.D. On renewable sensor networks with wireless energy transfer. In Proceedings of the IEEE INFOCOM 2011—IEEE Conference on Computer Communications, Shanghai, China, 10–15 Apirl 2011; pp. 1350–1358. [Google Scholar]
- Sun, X.; Wang, S. Resource Allocation Scheme for Energy Saving in Heterogeneous Networks. IEEE Trans. Wirel. Commun. 2015, 14, 4407–4416. [Google Scholar] [CrossRef]
- Lee, S.; Lee, S.; Kim, K.; Kim, Y.H. Base Station Placement Algorithm for Large-Scale LTE Heterogeneous Networks. PLoS ONE 2015, 10, 0139190. [Google Scholar] [CrossRef] [PubMed]
- Liao, C.C.; Ting, C.K. A Novel Integer-Coded Memetic Algorithm for the Set k-Cover Problem in Wireless Sensor Networks. IEEE Trans. Cybern. 2017. [Google Scholar] [CrossRef] [PubMed]
- Jiang, P.; Xu, Y.; Liu, J. A Distributed and Energy-Efficient Algorithm for Event K-Coverage in Underwater Sensor Networks. Sensors 2017, 17, 186. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, K.; Tashiro, T.; Yamamoto, K.; Ohno, K. Transmit power control and channel assignment for femto cells in HetNet systems using genetic algorithm. In Proceedings of the 2015 IEEE 26th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Hong Kong, China, 30 August–2 September 2015; pp. 1669–1674. [Google Scholar]
- Guo, P.; Liu, X.; Tang, S.; Cao, J. Concurrently Wireless Charging Sensor Networks with Efficient Scheduling. IEEE Trans. Mob. Comput. 2017, 16, 2450–2463. [Google Scholar] [CrossRef]
- Vilela, J.; Kashino, Z.; Ly, R.; Nejat, G.; Benhabib, B. A Dynamic Approach to Sensor Network Deployment for Mobile-Target Detection in Unstructured, Expanding Search Areas. IEEE Sens. J. 2016, 16, 4405–4417. [Google Scholar] [CrossRef]
- Liu, N.; Cao, W.; Zhu, Y.; Zhang, J.; Pang, F.; Ni, J. Node Deployment with k-Connectivity in Sensor Networks for Crop Information Full Coverage Monitoring. Sensors 2016, 16, 2096. [Google Scholar] [CrossRef] [PubMed]
- Gharaei, N.; Abu Bakar, K.; Mohd Hashim, S.Z.; Hosseingholi Pourasl, A.; Siraj, M.; Darwish, T. An Energy- Efficient Mobile Sink-Based Unequal Clustering Mechanism for WSNs. Sensors 2017, 17, 1858. [Google Scholar] [CrossRef] [PubMed]
- Goldberg, D.E. Genetic Algorithms; Pearson Education India: Bangalore, India, 2006. [Google Scholar]
- Ngo, D.T.; Tellambura, C.; Nguyen, H.H. Efficient resource allocation for OFDMA multicast systems with spectrum-sharing control. IEEE Trans. Veh. Technol. 2009, 58, 4878–4889. [Google Scholar] [CrossRef]
- Wang, C.; Li, J.; Ye, F.; Yang, Y. NETWRAP: An NDN Based Real-TimeWireless Recharging Framework for Wireless Sensor Networks. IEEE Trans. Mob. Comput. 2014, 13, 1283–1297. [Google Scholar]
- Suzuki, J. A Markov chain analysis on simple genetic algorithms. IEEE Trans. Syst. Man Cybern. 1995, 25, 655–659. [Google Scholar] [CrossRef]
- Sheen, W.; Lin, S.; Huang, C. Downlink Optimization and Performance of Relay-Assisted Cellular Networks in Multicell Environments. IEEE Trans. Veh. Commun. 2010, 59, 2529–2542. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Y.; Dong, S. Research on efficient-efficient routing protocol for WSNs based on improved artificial bee colony algorithm. IET Wirel. Sens. Syst. 2017, 7, 15–20. [Google Scholar] [CrossRef]
- Heinzelman, W.R.; Chandrakasan, A.; Balakrishnan, H. Energy-Efficient Communication Protocol for Wireless Microsensor Networks. In Proceedings of the Hawaii International Conference on System Sciences, Maui, HI, USA, 4–7 January 2000; p. 8020. [Google Scholar]

| Parameters | Value |
|---|---|
| The initial energy of sensor n, | 10,800 J |
| The minimum energy for working, | 540 J |
| The mobile speed, V | 5 m/s |
| The full charging ratio, | 5 W |
| The minimum charging ratio, | 1 J |
| The charging radius, | 2.7 m |
| The sensing ratio of node, n | 1∼10 kbps |
| The number of sensors, N | 20∼80 |
| Distance-independent constant term, | J/b |
| Coefficient of distance-dependent constant term, | J/(bm) |
| Pass-loss index , | 4 |
| Energy consumption for receiving per data rate, | J/b |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, J.; Chen, J.; Deng, Y.; Wang, X.; Aghvami, A.-H. Joint Power Charging and Routing in Wireless Rechargeable Sensor Networks. Sensors 2017, 17, 2290. https://doi.org/10.3390/s17102290
Jia J, Chen J, Deng Y, Wang X, Aghvami A-H. Joint Power Charging and Routing in Wireless Rechargeable Sensor Networks. Sensors. 2017; 17(10):2290. https://doi.org/10.3390/s17102290
Chicago/Turabian StyleJia, Jie, Jian Chen, Yansha Deng, Xingwei Wang, and Abdol-Hamid Aghvami. 2017. "Joint Power Charging and Routing in Wireless Rechargeable Sensor Networks" Sensors 17, no. 10: 2290. https://doi.org/10.3390/s17102290
APA StyleJia, J., Chen, J., Deng, Y., Wang, X., & Aghvami, A.-H. (2017). Joint Power Charging and Routing in Wireless Rechargeable Sensor Networks. Sensors, 17(10), 2290. https://doi.org/10.3390/s17102290





