On-Board Detection of Pedestrian Intentions
Abstract
:1. Introduction
2. Related Work
3. Detecting Pedestrian Intentions
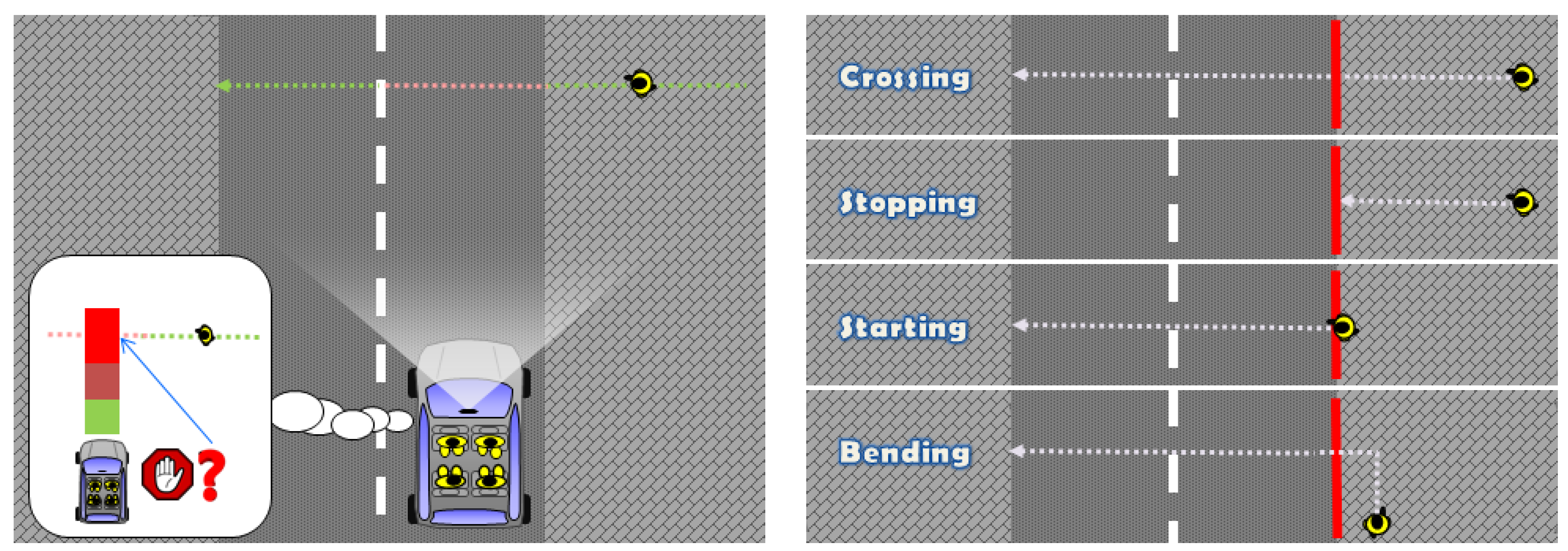
3.1. Our Proposal in a Nutshell
3.2. Skeleton Features
3.3. Classifier
- : Continue walking perpendicularly to the camera (∼crossing) vs. stopping.
- : Continue walking parallel to the camera vs. bending.
- : Continue stopped vs. starting to walk perpendicular to the camera.
4. Experimental Results
4.1. Dataset
4.2. Evaluation Protocol
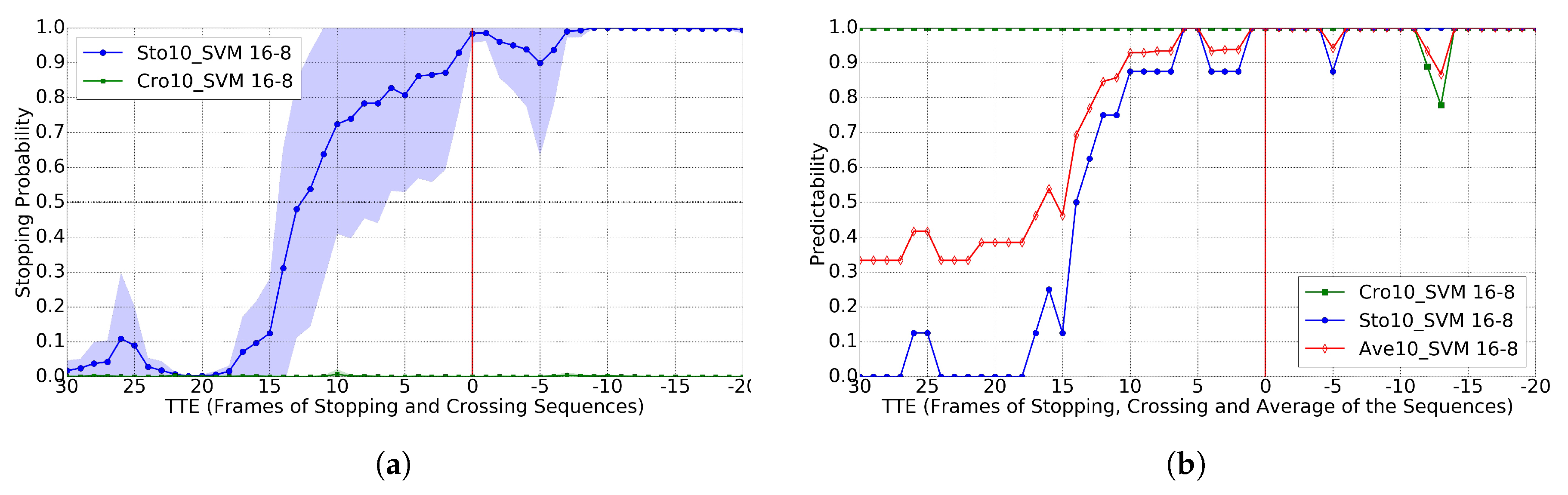
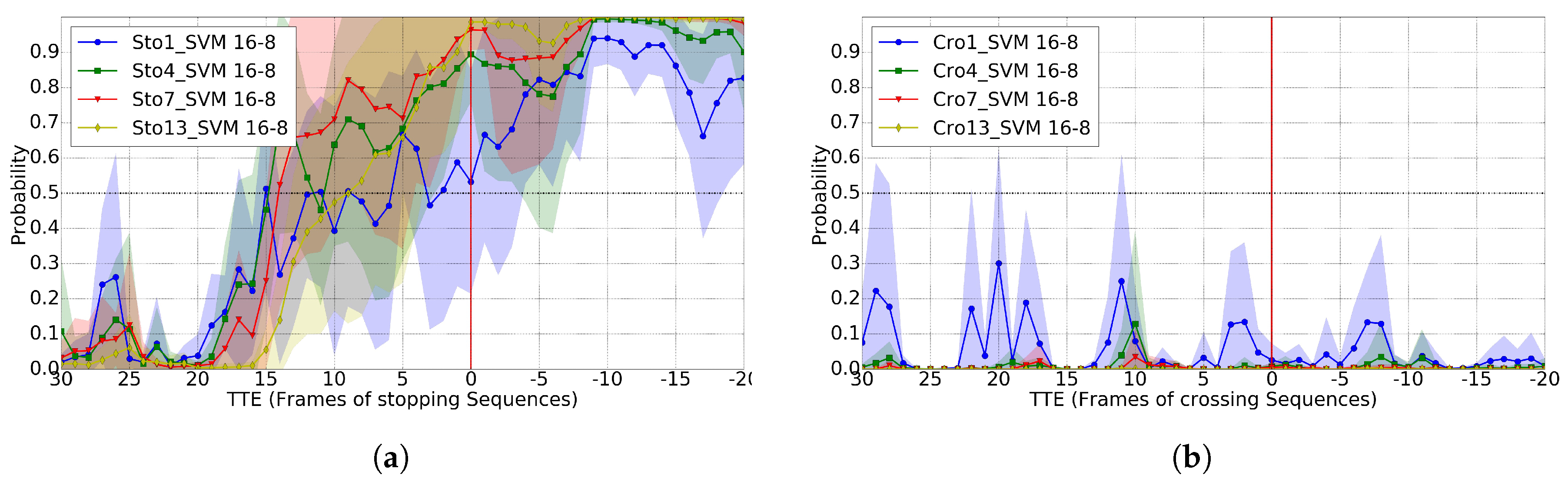
4.3. Crossing vs. Stopping
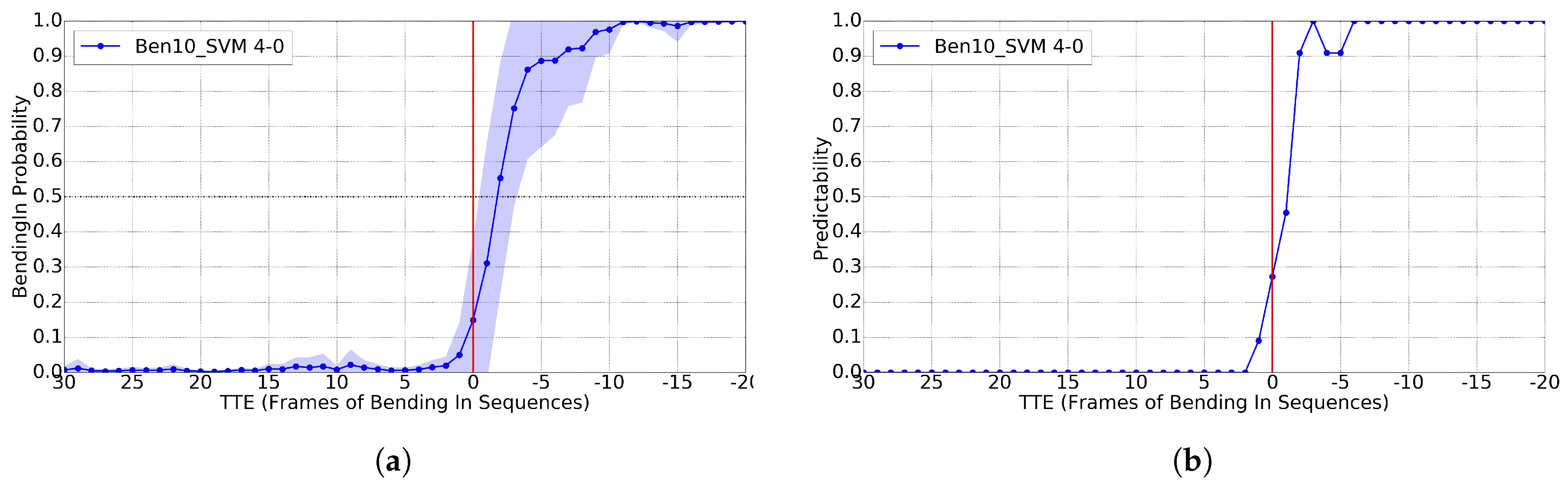
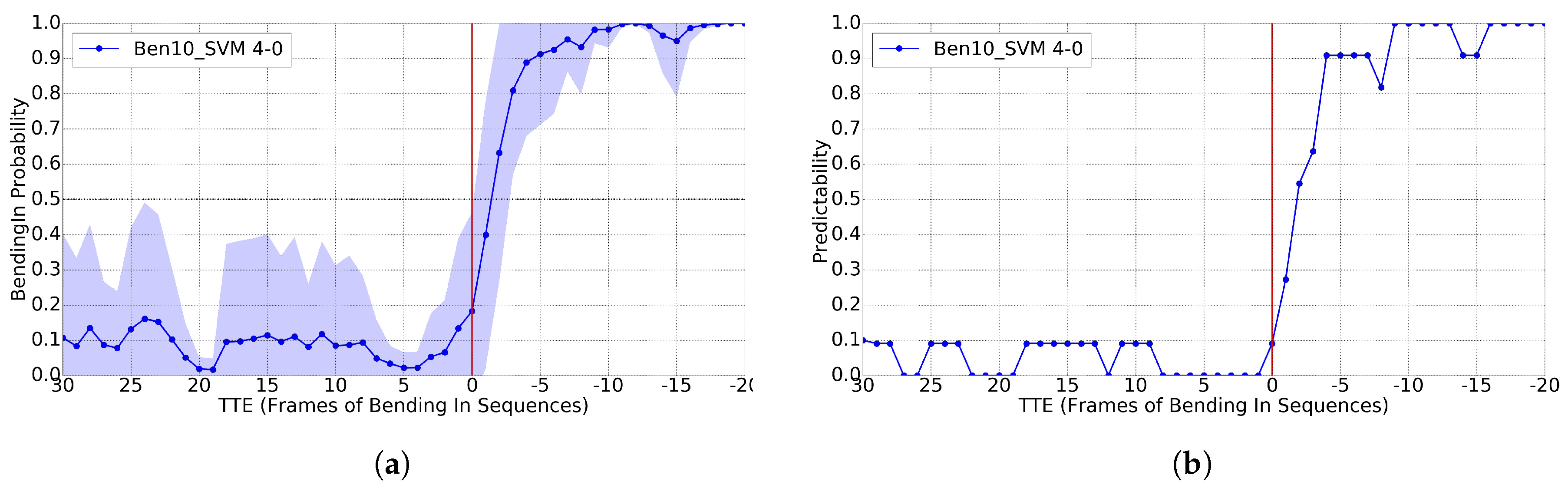
4.4. Bending
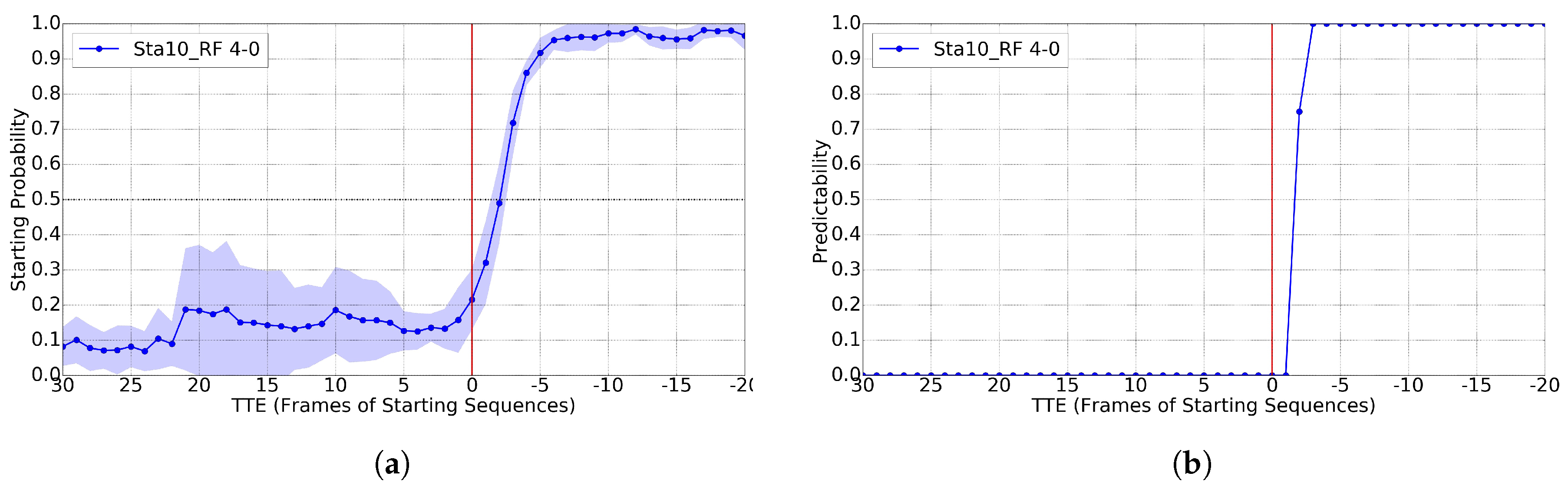
4.5. Starting
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gerónimo, D.; López, A. Vision-Based Pedestrian Protection Systems for Intelligent Vehicles; Springer: New York, NY, USA, 2014. [Google Scholar]
- Ren, J.; Chen, X.; Liu, J.; Sun, W.; Pang, J.; Yan, Q.; Tai, Y.; Xu, L. Accurate Single Stage Detector Using Recurrent Rolling Convolution. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Franke, U. Chapter Autonomous Driving. In Computer Vision in Vehicle Technology: Land, Sea, and Air; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar]
- Enzweiler, M.; Gavrila, D. Monocular Pedestrian Detection: Survey and Experiments. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 2179–2195. [Google Scholar] [CrossRef] [PubMed]
- Dollár, P.; Wojek, C.; Schiele, B.; Perona, P. Pedestrian Detection: An Evaluation of the State of the Art. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 743–761. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Benenson, R.; Omran, M.; Hosang, J.; Schiele, B. Towards Reaching Human Performance in Pedestrian Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2017. [Google Scholar] [CrossRef] [PubMed]
- Schneider, N.; Gavrila, D. Pedestrian Path Prediction with Recursive Bayesian Filters: A comparative Study. In Proceedings of the German Conference on Pattern Recognition (GCPR), Münster, Germany, 2–5 September 2013. [Google Scholar]
- Köhler, S.; Goldhammer, M.; Bauer, S.; Zecha, S.; Doll, K.; Brunsmann, U.; Dietmayer, K. Stationary Detection of the Pedestrian’s Intention at Intersections. IEEE Intell. Transp. Syst. Mag. 2013, 5, 87–99. [Google Scholar] [CrossRef]
- Keller, C.; Gavrila, D. Will the Pedestrian Cross? A Study on Pedestrian Path Prediction. IEEE Trans. Intell. Transp. Syst. 2014, 15, 494–506. [Google Scholar] [CrossRef]
- Rehder, E.; Kloeden, H.; Stiller, C. Head Detection and Orientation Estimation for Pedestrian Safety. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Qingdao, China, 8–11 October 2014. [Google Scholar]
- Köhler, S.; Goldhammer, M.; Zindler, K.; Doll, K.; Dietmeyer, K. Stereo-Vision-Based Pedestrian’s Intention Detection in a Moving Vehicle. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems (ITSC), Las Palmas, Spain, 15–18 September 2015. [Google Scholar]
- Schulz, A.; Stiefelhagen, R. Pedestrian Intention Recognition using Latent-dynamic Conditional Random Fields. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Seoul, Korea, 28 June–1 July 2015. [Google Scholar]
- Flohr, F.; Dumitru-Guzu, M.; Kooij, J.; Gavrila, D. A Probabilistic Framework for Joint Pedestrian Head and Body Orientation Estimation. IEEE Trans. Intell. Transp. Syst. 2015, 16, 1872–1882. [Google Scholar] [CrossRef]
- Schneemann, F.; Heinemann, P. Context-based Detection of Pedestrian Crossing Intention for Autonomous Driving in Urban Environments. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016. [Google Scholar]
- Völz, B.; Behrendt, K.; Mielenz, H.; Gilitschenski, I.; Siegwart, R.; Nieto, J. A Data-driven Approach for Pedestrian Intention Estimation. In Proceedings of the IEEE International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016. [Google Scholar]
- Kwak, J.; Lee, E.; Ko, B.; Jeong, M. Pedestrian’s Intention Prediction Based on Fuzzy Finite Automata and Spatial-temporal Features. In Proceedings of the International Symposium on Electronic Imaging—Video Surveillance and Transportation Imaging Applications, San Francisco, CA, USA, 14–18 February 2016. [Google Scholar]
- Rasouli, A.; Kotseruba, I.; Tsotsos, J. Agreeing to Cross: How Drivers and Pedestrians Communicate. arXiv, 2017; arXiv:1702.03555v1. [Google Scholar]
- Cao, Z.; Simon, T.; Wei, S.; Sheikh, Y. Realtime Multi-Person 2D Pose Estimation using Part Affinity Fields. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Jhuang, H.; Gall, J.; Zuffi, S.; Schmid, C.; Black, M. Towards Understanding Action Recognition. In Proceedings of the International Conference on Computer Vision (ICCV), Sydney, Australia, 1–8 December 2013. [Google Scholar]
- Meinecke, M.; Obojski, M.; Gavrila, D.; Marc, E.; Morris, R.; Töns, M.; Lettelier, L. Strategies in Terms of Vulnerable Road Users. EU Project SAVE-U, Deliverable D6. 2003. Available online: http://www.save-u.org (accessed on 1 December 2005).
- Dalal, N.; Triggs, B. Histograms of Oriented Gradients for Human Detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005. [Google Scholar]
- Lin, T.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollar, P.; Zitnick, C. Microsoft COCO: Common Objects in Context. In Proceedings of the European Conference on Computer Vision (ECCV), Zurich, Switzerland, 6–12 September 2014. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]






| Stopping | Crossing | Bending | Starting | |
|---|---|---|---|---|
| Training | 9 | 9 | 12 | 5 |
| Testing | 8 | 9 | 11 | 4 |
| Total | 17 | 18 | 23 | 9 |
| Vehicle Moving | 12 | 15 | 18 | 9 |
| Vehicle Standing | 5 | 3 | 5 | 0 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Z.; Vázquez, D.; López, A.M. On-Board Detection of Pedestrian Intentions. Sensors 2017, 17, 2193. https://doi.org/10.3390/s17102193
Fang Z, Vázquez D, López AM. On-Board Detection of Pedestrian Intentions. Sensors. 2017; 17(10):2193. https://doi.org/10.3390/s17102193
Chicago/Turabian StyleFang, Zhijie, David Vázquez, and Antonio M. López. 2017. "On-Board Detection of Pedestrian Intentions" Sensors 17, no. 10: 2193. https://doi.org/10.3390/s17102193
APA StyleFang, Z., Vázquez, D., & López, A. M. (2017). On-Board Detection of Pedestrian Intentions. Sensors, 17(10), 2193. https://doi.org/10.3390/s17102193






