RFID Ownership Transfer with Positive Secrecy Capacity Channels
Abstract
:1. Introduction
- (1)
- Define a communication model for ownership transfer that addresses spatiotemporal connectivity (Section 3). Many OTPs do not specify the communication setup and assume channels that are impractical for RFID settings.
- (2)
- Provide a theoretical analysis of wiretaps with noisy tags (Section 4), show how these could be implemented and prove that perfect secrecy is achievable.
- (3)
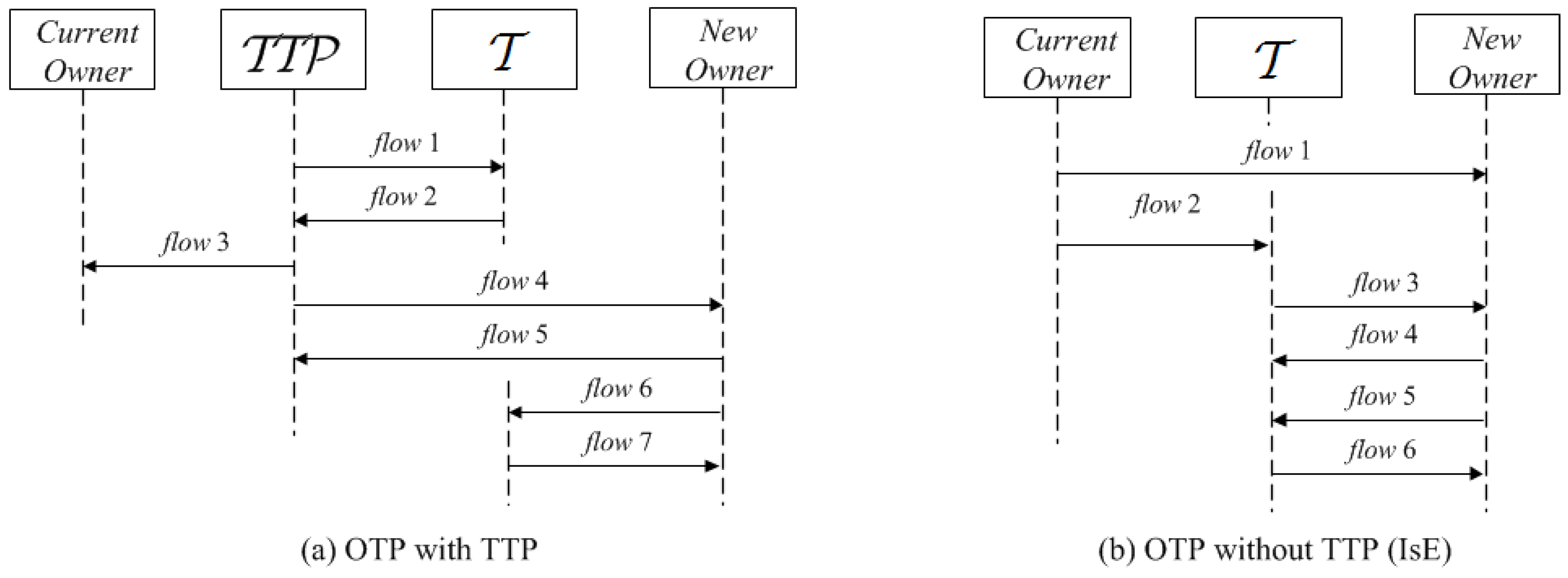
- Present an OTP that is provably secure in this communication model and that uses a wiretap channel with noisy tags to achieve privacy (Section 5). This is the first example of symmetric-key-based OTP that does not require TTPs or an ISE. GNYlogic and strand spaces [12,13,14,15] are used in the Appendix A for the security analysis.
2. Background
2.1. Definition and Security Requirements
2.2. Related Work
Motivation: Comparison with Previous Works
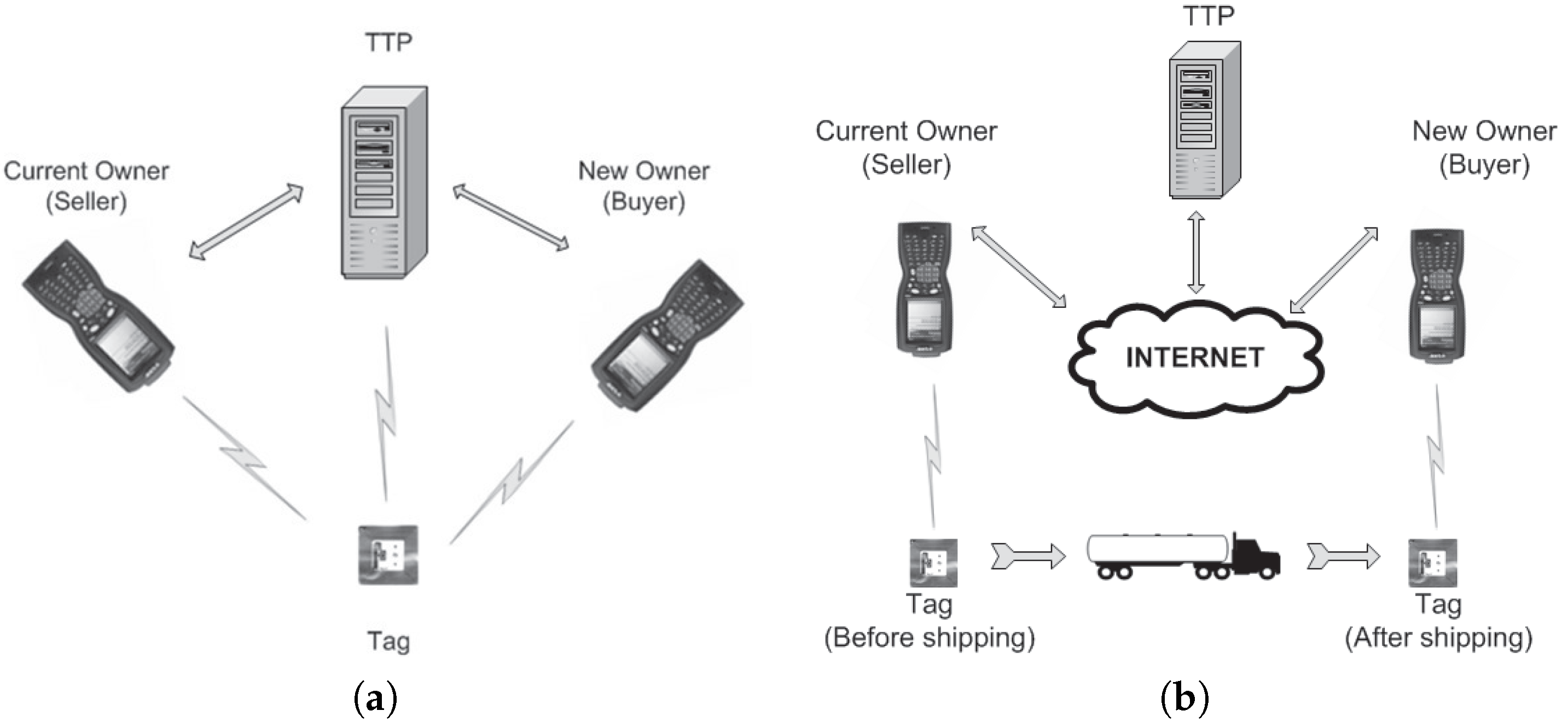
3. A Communication Model for RFID Ownership Transfer
3.1. Entity Capabilities
3.2. Communication Model
3.2.1. Privacy/Integrity Channels
3.2.2. Connectivity
- ,
- .
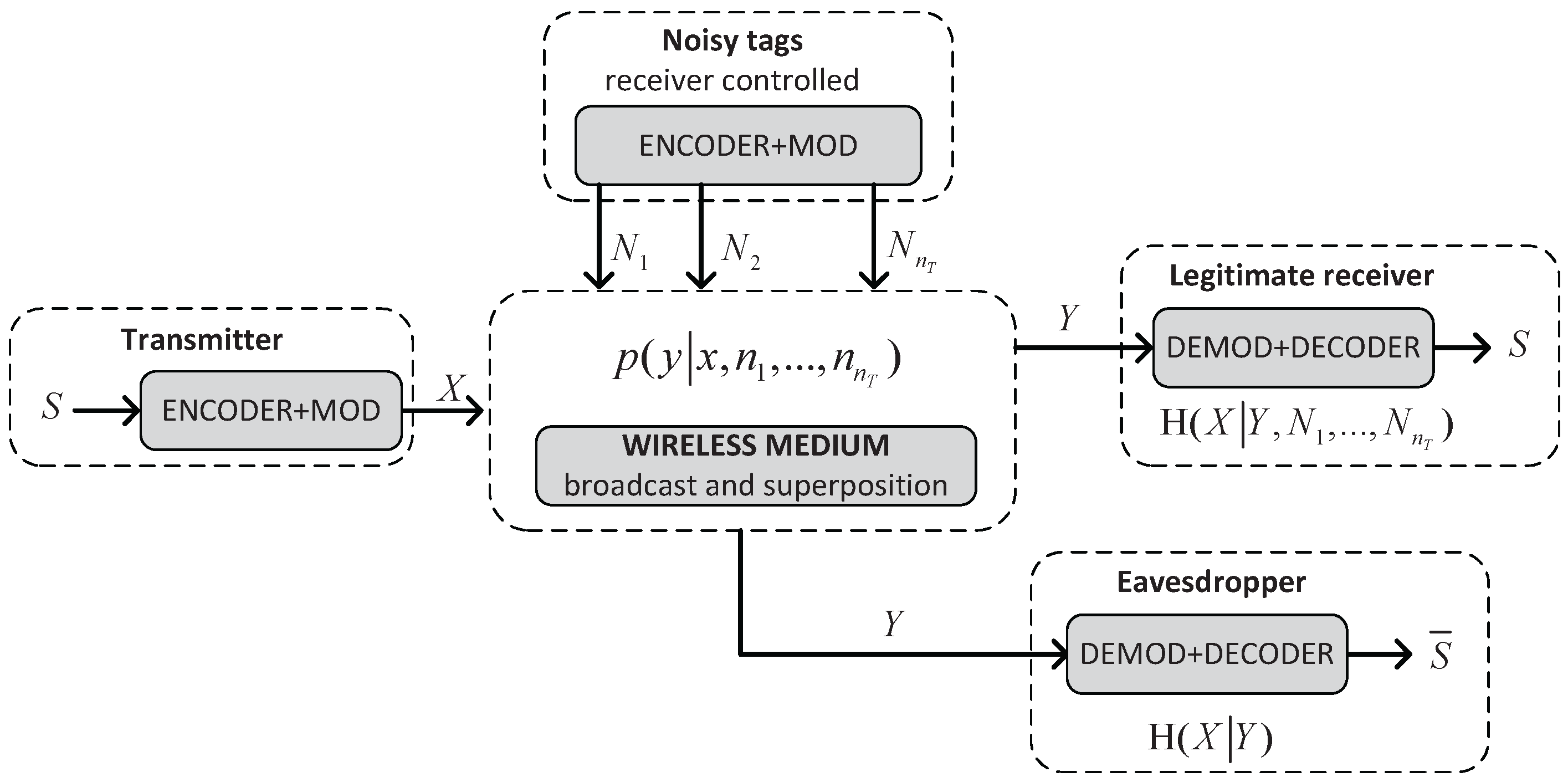
4. A Wiretap Channel with Positive Secrecy Capacity
5. An Ownership Transfer Protocol
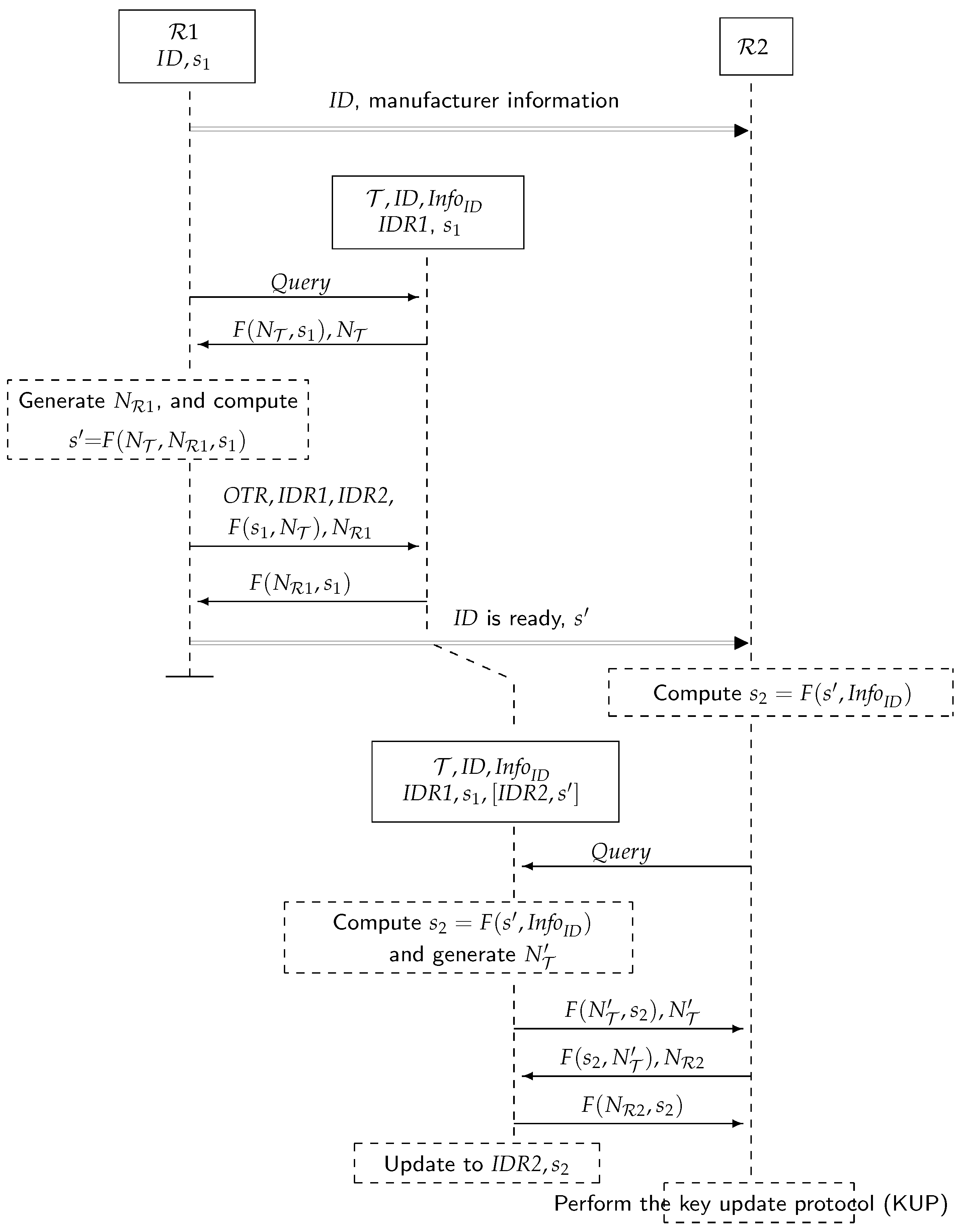
5.1. The Ownership Transfer Protocol, Figure 6
- 1.
- Initially, each owner knows for each tag its information and private key . Likewise, each tag stores, along with its identifier and , the identifier of its owner and the private key. agree to transfer ownership of tag with identifier . sends (secure channel) manufacturer information about the tag ( when hashed).
- 2.
- regularly broadcasts messages to detect the presence of tags.
- 3.
- When receives a (presumably because it is within the range of ), it selects a random nonce and sends:
- 4.
- searches for a pair in its database to get a match. If there is no match, then the process is repeated from Step 2. Otherwise, is singulated: selects a random nonce and a request OTR and sends:
- 5.
- checks to authenticate . does not reply if there is no match. Otherwise, it computes , saves , , until the protocol completes or a new command from is received and replies with:
- 6.
- If this message is not received correctly by after a period of time, the protocol is repeated from Step 2 ( will replace the stored values ). Otherwise, computes and confirms (secure channel) to that is ready to be transferred:
- 7.
- If receives ’s confirmation, then it is ready to take ownership of . computes and broadcasts regularly messages.
- 8.
- When receives a , it selects a random nonce and sends:
- 9.
- If is singulated, then selects a fresh random number and sends:
- 10.
- checks this message for , and if not correct, for (and waits for new commands). It does not reply if this is not correct. If is authenticated, updates the stored values to . These values determine tag ownership. acknowledges this by sending:
- 11.
- If the received message is not correct, the protocol is repeated from Step 7. Otherwise, executes the key update protocol in Section 5.2 to prevent from accessing .
5.1.1. Analysis
- 1
- Untraceable singulation: Replies to ’s (Step 2, Step 7) have the same format and include a nonce selected by the tag. This prevents tag tracing, since messages look random to anyone who does not know the secret key.
- 2
- The privacy of is guaranteed because the key remains unknown to the new owner . Indeed, if can compute given the values: , and , then can also find the F-preimage of , which contradicts the assumption that F is one-way.
- 3
- Forward secrecy: Suppose the adversary succeeds in getting the new key of a tag. The privacy of the prior communications is guaranteed, as in the previous case, because to get from , one has to invert F.
- 4
- The privacy of is achieved by using the key update protocol in Section 5.2.
- 5
- Tag assurance: is the hash of manufacturer information about the tag. The collision resistance of hash functions prevents the adversary from finding another message (pre-image) with the same hash to forge the information given by the manufacturer. The use of to compute guarantees that the information provided by to matches with the information stored by . Note, however, that cloned tags and corruptible memories are beyond this security feature (cf. [17]).
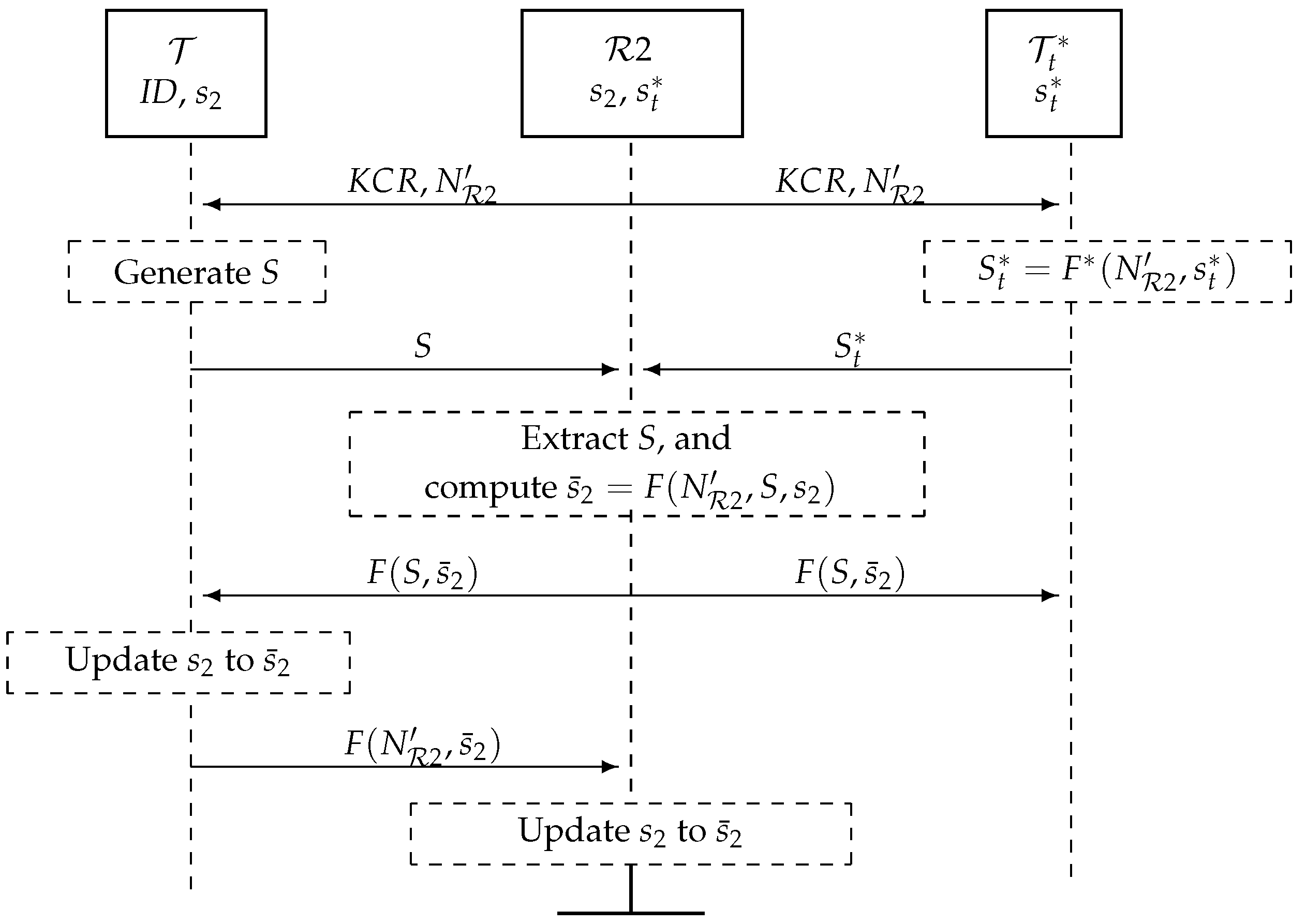
5.2. A Key Update Protocol, Figure 7
- 1
- broadcasts a key change request (KCR) with a random nonce .
- 2
- Upon receiving this, and generate bitstrings S and of length and broadcast these simultaneously (as specified in Section 4): S is a random number, and , where is a cryptographic hash function of length . Note that could be built from F; for example, for , , where denotes concatenation.
- 3
- receives the added signals of S and , extracts S, computes and broadcasts .
- 4
- computes and checks that the message from is correct. If so, updates its private key to .
- 5
- checks the received message. If correct, the key update protocol (KUP) is completed, and informs . Otherwise, sends a new and checks if has updated its key. If not, the KUP is repeated.
5.3. Analysis
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Protocol Analysis
Appendix A.1. GNY Logic
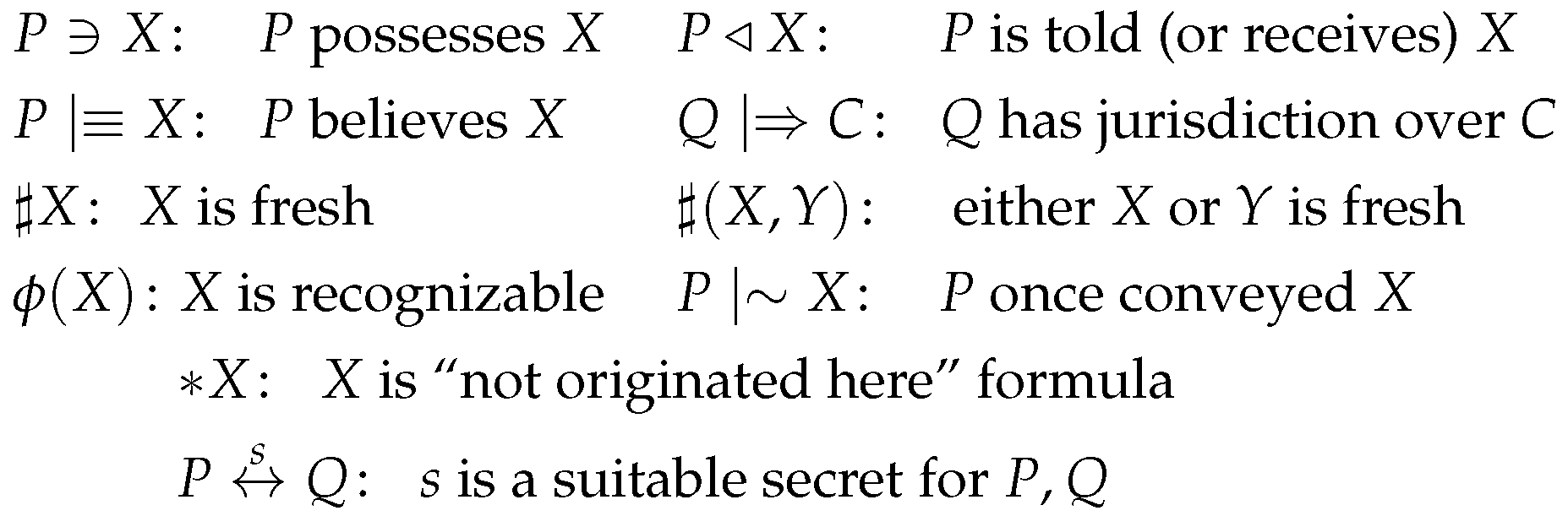
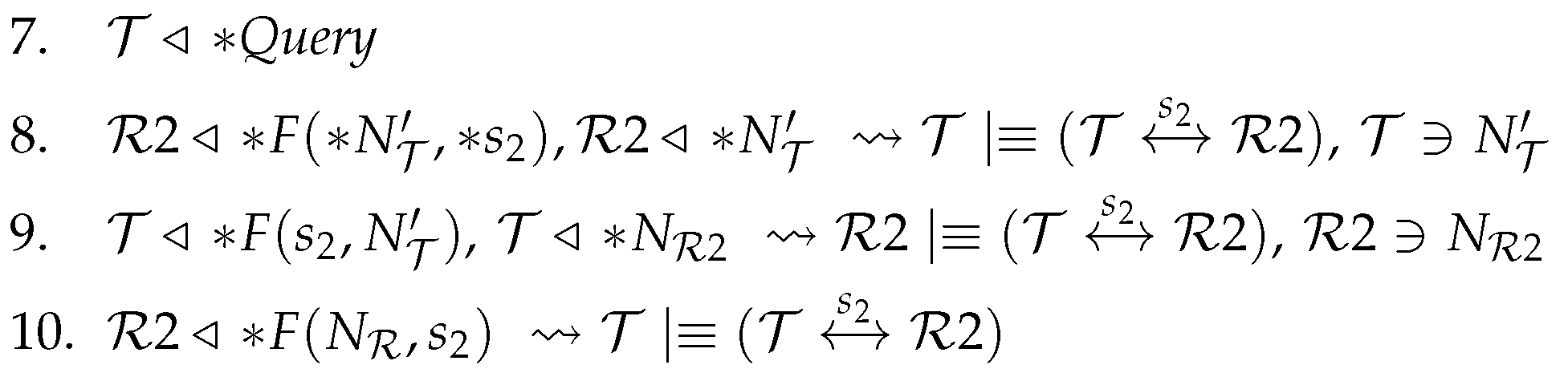
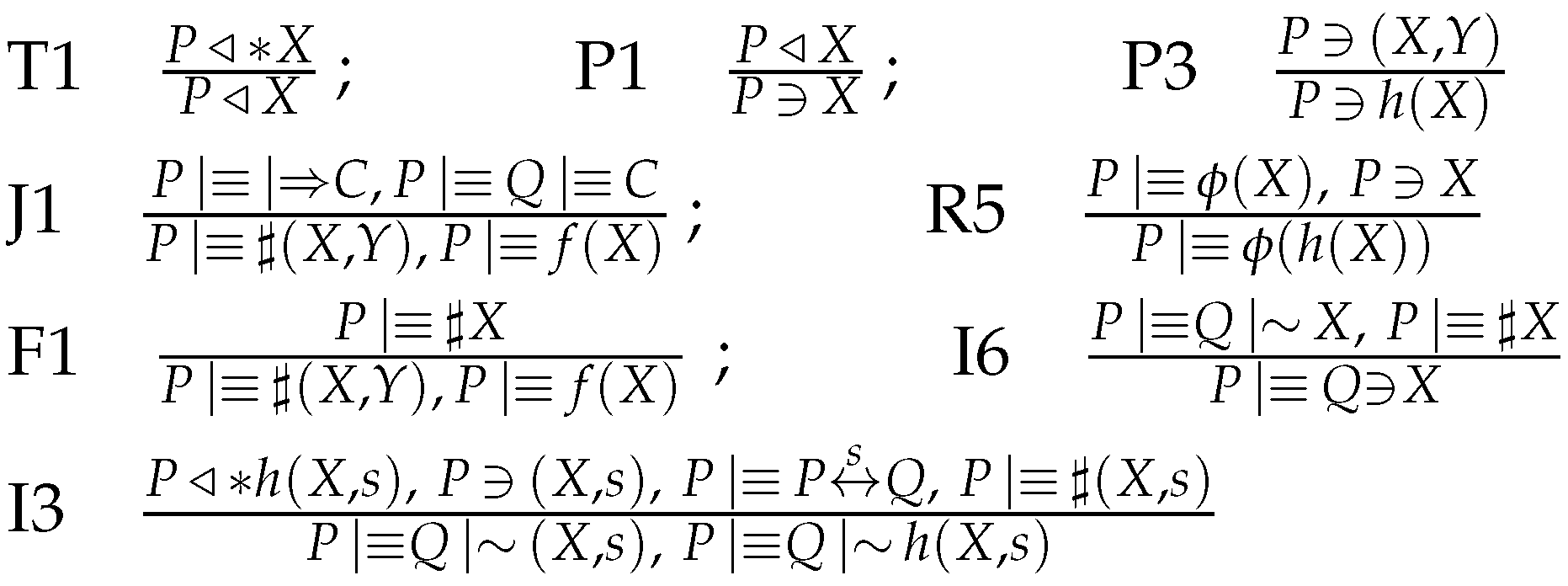
- 7.
- No belief or possession can be derived from this message.
- 8.
- Apply the being-told rule T1 and the possession rule P1 to to get . Apply the recognizability rule R5 to the initial assumptions to get that recognizes . No postulate enables us to further derive new beliefs or possessions from this message. In particular, we cannot derive the freshness of the message.
- 9.
- Apply rules T1 and P1 to to get . Apply the freshness rule F1 to the initial assumptions , to get . Apply the interpretation rule I3 to: the previous result, and the initial assumptions and , to get . Now, apply rule I6 to get Formula (A1): .
- 10.
- Apply the freshness rule F1 to the initial assumptions , to get . Apply rule I3 to: the previous result, and the initial assumptions and , to get . Now, apply rule I6 to get Formula (A2): .
- (a)
- Possession consistency: transmitted messages only include formulae that the sender possesses;
- (b)
- Belief consistency: message extensions include only beliefs held by the sender at the time he/she sends the message.

- Step 1.
- Penetrator strands
- Step 2.
- Initiator strands defined by:with , . is the principal associated with this strand.
- Step 3.
- Responder strands , defined by:with , . is the principal associated with this strand.
- M.
- tr: Then, and originates on t, which is not possible because originates on the regular node (Lemma A1).
- F.
- tr: This has no positive nodes.
- T,C
- tr or : then, the positive nodes are not minimal occurrences.
- K.
- tr with : Since , this case does not apply.
- E.
- tr: Suppose . Then, , . Thus, there is a node m (the first of this strand) with term (. However, , so that this node is regular, but no regular node originates . This contradicts the initial assumption.
- D.
- tr: If the positive node is minimal in S, then and . However, because , if , then , which is a contradiction.
- S.
- tr: Assume term (there is a symmetric case with term ). By the minimality of , . Hence, and . However, then and , contradicting the initial assumption.
References
- Van Deursen, T.; Mauw, S.; Radomirovic, S.; Vullers, P. Secure Ownership and Ownership Transfer in RFID Systems; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5789, pp. 637–654. [Google Scholar]
- Avoine, G. Adversarial Model for Radio Frequency Identification; Technical Report; Swiss Federal Institute of Technology (EPFL); Security and Cryptography Laboratory (LASEC): Lausanne, Switzerland, 2005. [Google Scholar]
- Juels, A.; Weis, S.A. Defining strong privacy for RFID. ACM Trans. Inf. Syst. Secur. 2009, 13, 7:1–7:23. [Google Scholar] [CrossRef]
- Vaudenay, S. On privacy models for RFID. In ASIACRYPT; Kurosawa, K., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4833, pp. 68–87. [Google Scholar]
- Ng, C.Y.; Susilo, W.; Mu, Y.; Safavi-Naini, R. RFID privacy models revisited. In ESORICS; Jajodia, S., Lpez, J., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5283, pp. 251–266. [Google Scholar]
- Vullers, P. Secure Ownership and Ownership Transfer in RFID Systems. Master’s Thesis, Eindhoven University, Eindhoven, The Netherlands, 2009. [Google Scholar]
- Kapoor, G.; Piramuthu, S. Single RFID Tag Ownership Transfer Protocols. IEEE Trans. Syst. Man Cybern. Part C 2012, 42, 164–173. [Google Scholar] [CrossRef]
- Osaka, K.; Takagi, T.; Yamazaki, K.; Takahashi, O. An efficient and secure RFID security method with ownership transfer. In Computational Intelligence and Security; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4456, pp. 778–787. [Google Scholar]
- Sundaresan, S.; Doss, R.; Zhou, W.; Piramuthu, S. Secure ownership transfer for multi-tag multi-owner passive RFID environment with individual-owner privacy. Comput. Commun. 2015, 55, 112–124. [Google Scholar] [CrossRef]
- Song, B. RFID Tag Ownership Transfer. In Proceedings of the Workshop on RFID Security—RFIDSec’08, Budapest, Hungary, 9–11 July 2008.
- Lei, H.; Cao, T. RFID Protocol Enabling Ownership Transfer to Protect against Traceability and DoS Attacks. In Proceedings of the First International Symposium on Data, Privacy, and E-Commerce, ISDPE ’07, Chengdu, China, 1–3 November 2007; IEEE Computer Society Press: Washington, DC, USA, 2007; pp. 508–510. [Google Scholar]
- Gong, L.; Needham, R.; Yahalom, R. Reasoning about belief in cryptographic protocols. In Proceedings of the 1990 IEEE Symposium on Research in Security and Privacy, Oakland, CA, USA, 7–9 May 1990; IEEE Computer Society Press: Washington, DC, USA, 1990; pp. 234–248. [Google Scholar]
- Boyd, C.; Mao, W. On a limitation of BAN logic. In Advances in Cryptology EUROCRYPT 93; Helleseth, T., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1994; Volume 765, pp. 240–247. [Google Scholar]
- Nessett, D. A critique of the Burrows, Abadi, and Needham logic. Oper. Syst. Rev. 1990, 24, 35–38. [Google Scholar] [CrossRef]
- Thayer, F.; Herzog, J.; Guttman, J. Strand Spaces: Proving Security Protocols Correct. J. Comput. Secur. 1999, 7, 191–230. [Google Scholar] [CrossRef]
- Molnar, D.; Soppera, A.; Wagner, D. A Scalable, Delegatable Pseudonym Protocol Enabling Ownership Transfer of RFID Tags. In Proceedings of the Workshop on Selected Areas in Cryptography (SAC 2005), Kingston, ON, Canada, 11–12 August 2005.
- Ng, C.Y.; Susilo, W.; Mu, Y.; Safavi-Naini, R. Practical RFID Ownership Transfer Scheme. J. Comput. Secur. 2011, 19, 319–341. [Google Scholar] [CrossRef]
- Saito, J.; Imamoto, K.; Sakurai, K. Reassignment Scheme of an RFID Tag’s Key for Owner Transfer. In EUC Workshops; Enokido, T., Yan, L., Xiao, B., Kim, D., Dai, Y.-S., Yang, L.T., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3823, pp. 1303–1312. [Google Scholar]
- Avoine, G.; Dysli, E.; Oechslin, P. Reducing time complexity in RFID systems. In Proceedings of the 12th International Conference on Selected Areas in Cryptography (SAC 2005), Kingston, ON, Canada, 11–12 August 2005.
- Soppera, A.; Burbridge, T. Secure by default: The RFID acceptor tag (RAT). In Proceedings of the Workshop on RFID Security—RFIDSec’06, Graz, Austria, 12–14 July 2006.
- Osaka, K.; Takagi, T.; Yamazaki, K.; Takahashi, O. An efficient and secure RFID security method with ownership transfer. In Proceedings of the 2006 International Conference on Computational Intelligence and Security, Guangzhou, China, 3–6 November 2006; pp. 1090–1095.
- Chen, H.-B.; Lee, W.-B.; Zhao, Y.-H.; Chen, Y.-L. Enhancement of the RFID security method with ownership transfer. In Proceedings of the 3rd International Conference on Ubiquitous Information Management and Communication, ICUIMC ’09, Suwon, Korea, 15–16 January 2009.
- Jappinen, P.; Hamalainen, H. Enhanced RFID security method with ownership transfer. In Proceedings of the 2008 International Conference on Computational Intelligence and Security, CIS ’08, Suzhou, China, 13–17 December 2008; pp. 382–385.
- Yoon, E.-J.; Yoo, K.-Y. Two security problems of RFID security method with ownership transfer. In Proceedings of the 2008 IFIP International Conference on Network and Parallel Computing, NPC 2008, Shanghai, China, 18–21 October 2008; pp. 68–73.
- Kapoor, G.; Piramuthu, S. Vulnerabilities in some recently proposed RFID ownership transfer protocols. IEEE Commun. Lett. 2010, 14, 260–262. [Google Scholar] [CrossRef]
- Dimitriou, T. RFIDdot: RFID delegation and ownership transfer made simple. In Proceedings of the 4th International Conference on Security and Privacy in Communication Networks, Istanbul, Turkey, 22–25 September 2008; pp. 1–8.
- Elkhiyaoui, K.; Blass, E.-O.; Molva, R. Rotiv: RFID ownership transfer with issuer verification. In Proceedings of the 7th International Conference on RFID Security and Privacy, RFIDSec’11, Amherst, MA, USA, 26–28 June 2011.
- Song, B.; Mitchell, C.J. Scalable {RFID} security protocols supporting tag ownership transfer. Comput. Commun. 2011, 34, 556–566. [Google Scholar] [CrossRef]
- Kapoor, G.; Zhou, W.; Piramuthu, S. Multi-tag and Multi-owner RFID Ownership Transfer in Supply Chains. Decis. Support Syst. 2011, 52, 258–270. [Google Scholar] [CrossRef]
- EPC Global. EPC Tag Data Standards, vs. 1.3. Available online: http://www.epcglobalinc.org/standards/EPCglobal_Tag_Data_Standard_TDS_Version_1.3.pdf (accessed on 27 December 2016).
- Chen, C.-L.; Lai, Y.-L.; Chen, C.-C.; Deng, Y.-Y.; Hwang, Y.-C. RFID ownership transfer authorization systems conforming epcglobal class-1 generation-2 standards. Int. J. Netw. Secur. 2011, 13, 41–48. [Google Scholar]
- Koralalage, K.H.S.S.; Reza, S.M.; Miura, J.; Goto, Y.; Cheng, J. POP method: An approach to enhance the security and privacy of RFID systems used in product lifecycle with an anonymous ownership transferring mechanism. In Proceedings of the 2007 ACM Symposium on Applied Computing, SAC ’07, Seoul, Korea, 11–15 March 2007.
- Chen, C.-L.; Huang, Y.-C.; Jiang, J.-R. A secure ownership transfer protocol using epcglobal gen-2 RFID. Telecommun. Syst. 2013, 53, 387–399. [Google Scholar] [CrossRef]
- Munilla, J.; Burmester, M.; Peinado, A. Attacks on Ownership Transfer Scheme for Multi-tag Multi-owner Passive RFID Environments. Comput. Commun. 2016, 88, 84–88. [Google Scholar]
- Paret, D. RFID and Contactless Smart Card Applications; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- International Organization for Standardization. ISO/IEC 29192-1: Information Technology—Security Techniques—Lightweight Cryptography—Part 1: General; ISO: Geneva, Switzerland, 2012. [Google Scholar]
- Wyner, A. The Wire-Tap Channel. Bell Syst. Tech. J. 1975, 54, 1355–1387. [Google Scholar] [CrossRef]
- Juels, A.; Rivest, R.; Szydlo, M. The Blocker Tag: Selective Blocking of RFID Tags for Consumer Privacy. In Proceedings of the Conference on Computer and Communications Security, Washington, DC, USA, 27 30 October 2003; Atluri, V., Ed.; ACM Press: New York, NY, USA, 2003; pp. 103–111. [Google Scholar]
- Castelluccia, C.; Avoine, G. Noisy Tags: A Pretty Good Key Exchange Protocol for RFID Tags. In Proceedings of the International Conference on Smart Card Research and Advanced Applications—CARDIS, Tarragona, Spain, 19–21 April 2006; Domingo-Ferrer, J., Posegga, J., Schreckling, D., Eds.; Lecture Notes in Computer Science; Springer: Tarragona, Spain, 2006; Volume 3928, pp. 289–299. [Google Scholar]


© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Munilla, J.; Burmester, M.; Peinado, A.; Yang, G.; Susilo, W. RFID Ownership Transfer with Positive Secrecy Capacity Channels. Sensors 2017, 17, 53. https://doi.org/10.3390/s17010053
Munilla J, Burmester M, Peinado A, Yang G, Susilo W. RFID Ownership Transfer with Positive Secrecy Capacity Channels. Sensors. 2017; 17(1):53. https://doi.org/10.3390/s17010053
Chicago/Turabian StyleMunilla, Jorge, Mike Burmester, Alberto Peinado, Guomin Yang, and Willy Susilo. 2017. "RFID Ownership Transfer with Positive Secrecy Capacity Channels" Sensors 17, no. 1: 53. https://doi.org/10.3390/s17010053
APA StyleMunilla, J., Burmester, M., Peinado, A., Yang, G., & Susilo, W. (2017). RFID Ownership Transfer with Positive Secrecy Capacity Channels. Sensors, 17(1), 53. https://doi.org/10.3390/s17010053








