Node Redeployment Algorithm Based on Stratified Connected Tree for Underwater Sensor Networks
Abstract
:1. Introduction and Related Works
- (1)
- It takes full consideration of node drift with water environment during network operation. At every network adjustment moment, nodes can keep themselves in the monitored space through self-examination and adjustment, which helps to maintain good network monitoring quality.
- (2)
- At every network adjustment moment, the network is converted into a stratified connected tree through level-by-level stratifying, which can achieve full network connectivity and lower the network connectivity decrease speed during network operation.
- (3)
- The sink node performs centralized optimization adjustment on the locations of leaf nodes in the stratified connected tree with synthetically considering the network coverage and connectivity rates, and node movement distance. This can not only maintain excellent network monitoring performances, but also reduce node movement distance during node redeployment, as well as prolong the network lifetime.
2. Model, Definitions and Preliminaries
2.1. Models
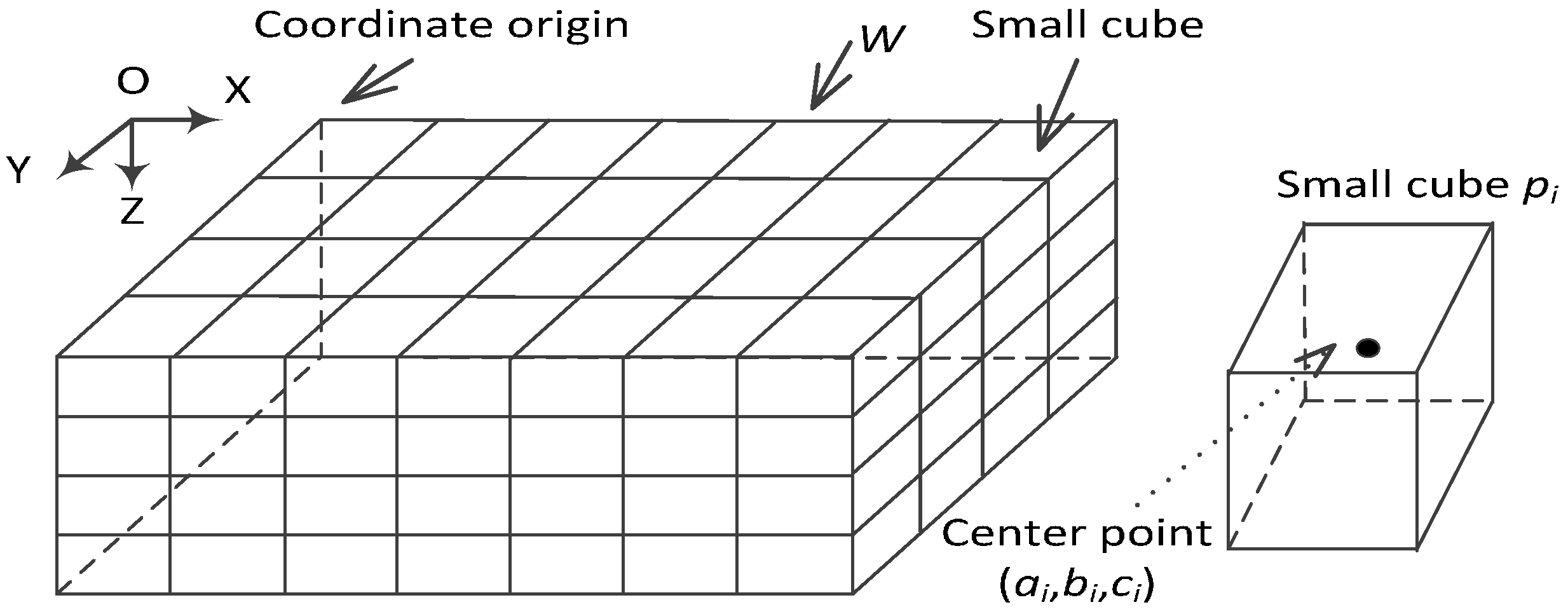
2.1.1. 3D Underwater Space Model
2.1.2. Node Energy Consumption Model
2.1.3. Node Sensing Model
2.1.4. 3D Random Drift Model
2.2. Definitions
2.2.1. Network Coverage Rate
2.2.2. Network Connectivity Rate
2.2.3. Network Adjustment Moment
2.2.4. Energy Threshold
2.2.5. Network Lifetime
2.3. Preliminaries
- (1)
- Inspired by the related assumptions or descriptions in references [18,22], the sink node and all the other nodes can freely move in all directions with the help of related technologies such as AUVs [38] and their real-time locations can be known during network operation with the help of related localization technologies [39].
- (2)
- Before the deployment, the destination location information of the sink node, i.e., the location information of the water surface center, has been stored in the memories of all the other nodes for them to gain information on the destination location of the sink node. Information on the 3D underwater space model and the number of nodes has also been stored in the memory of the sink node.
- (3)
- The communication range of the sink node is Rt and the sink node can be recharged, whereas the sensing capability of the sink node is neglected. All the other nodes are homogeneous, meaning these nodes have the same sensing range Rs, same communication range Rt, and initial energy Ein. Furthermore, each of them has a unique Id number.
3. Problem and Algorithm Description
3.1. Problem Description
3.2. Algorithm Description
3.2.1. Description of Initial Network Distribution
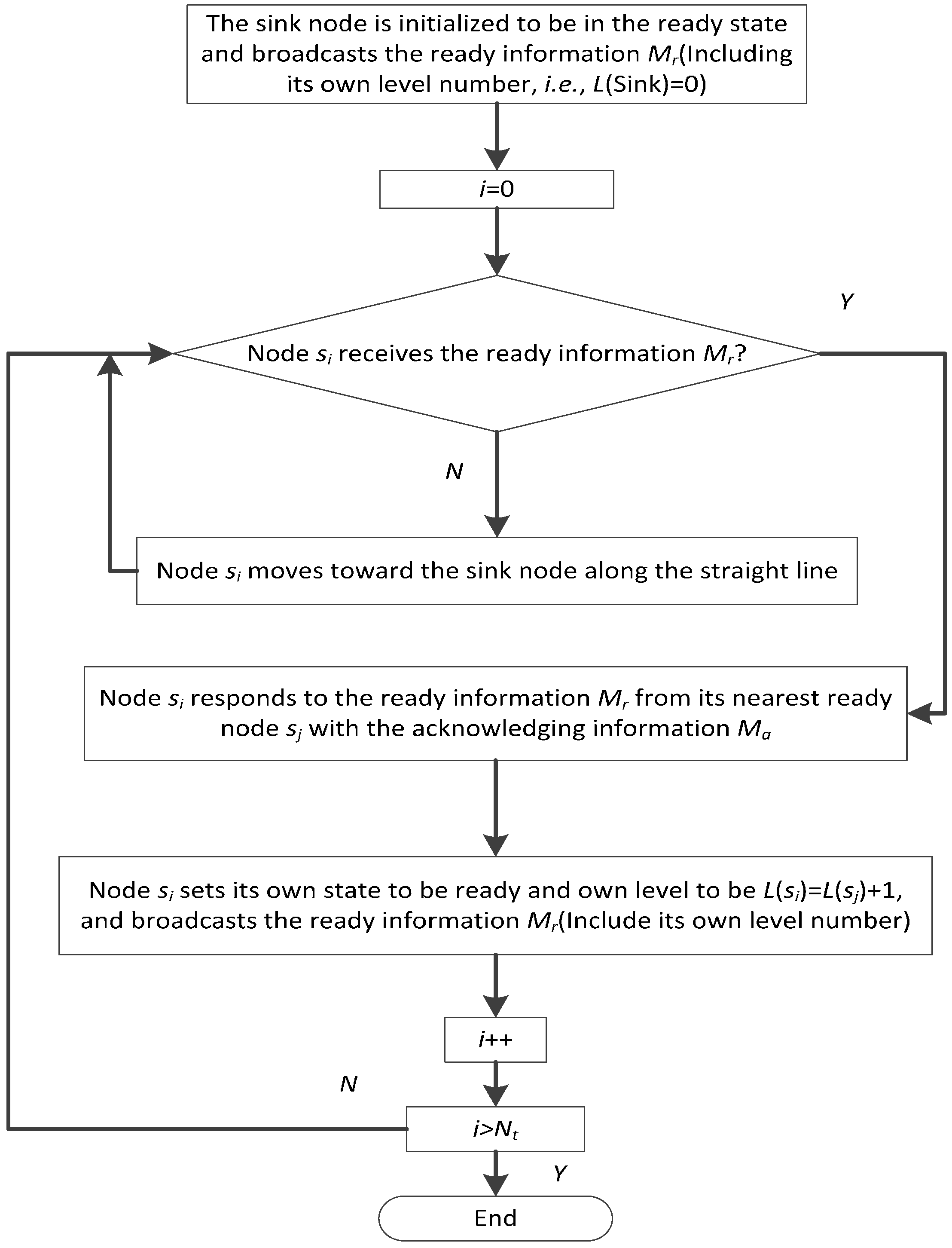
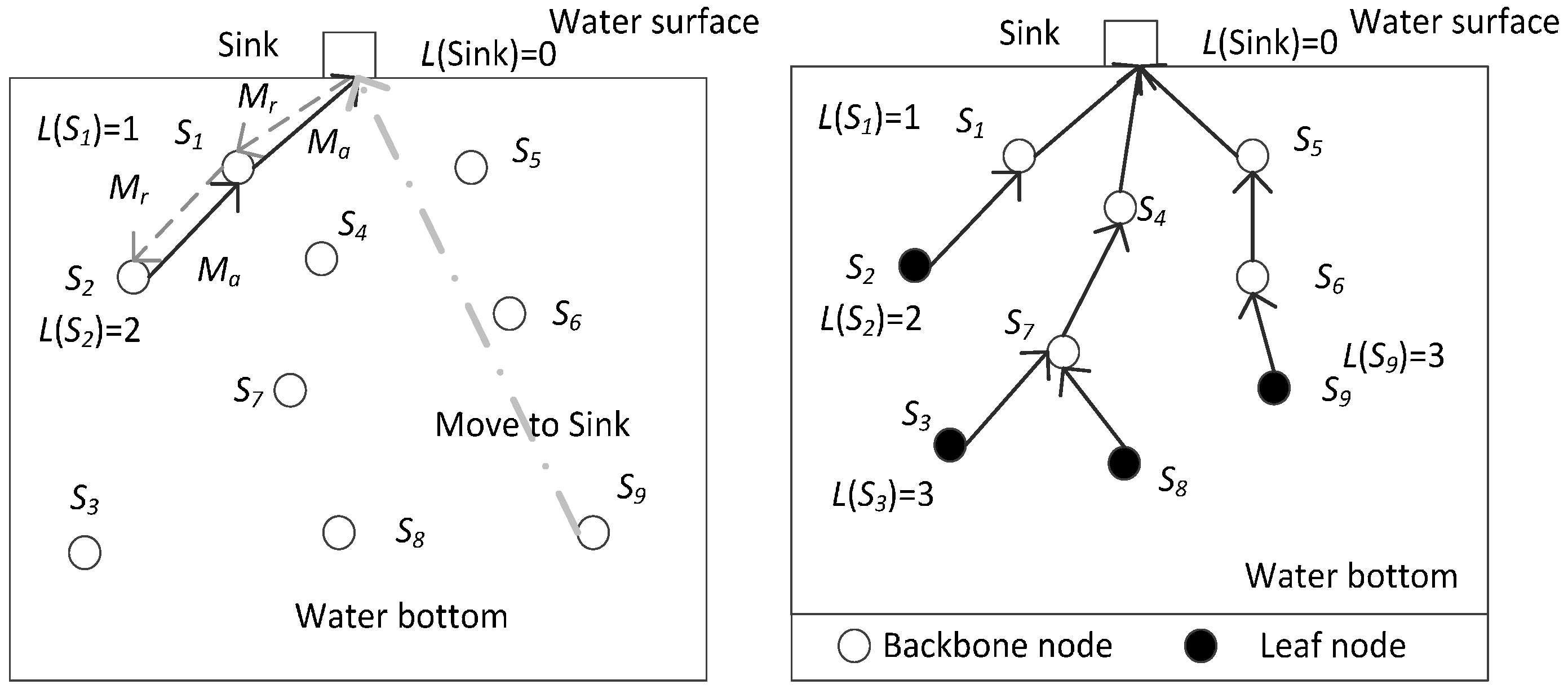
3.2.2. Algorithm Steps
3.2.3. Detailed Description for Algorithm Important Parts
Self-Examination and Adjustment of Nodes Outside the Monitored Space
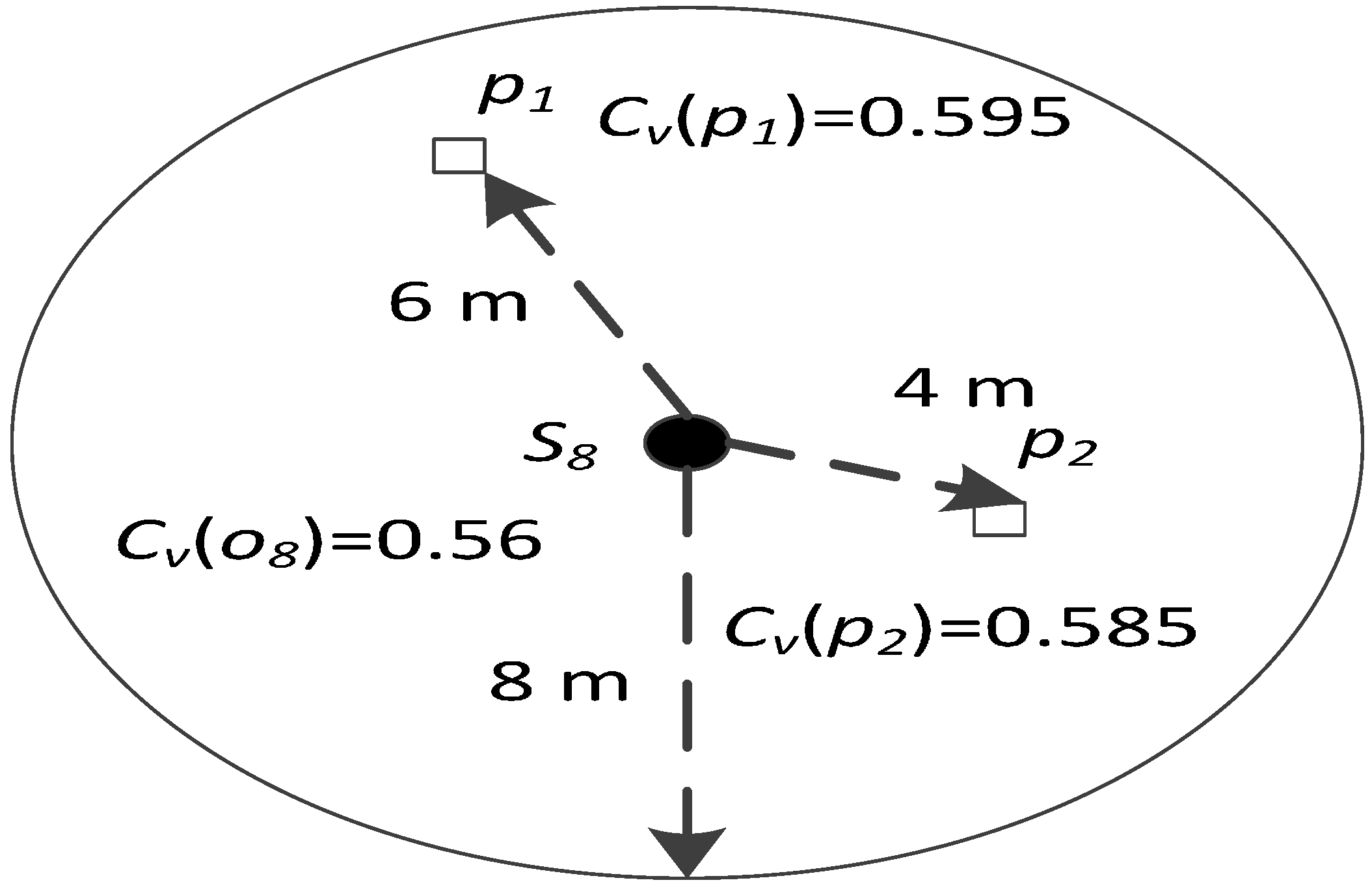
Network Connectivity Rate Improvement
Node Movement Distance Limit
Overall Summarization for Main Mathematical Symbols
3.2.4. Algorithm Analysis
4. Simulation Evaluation
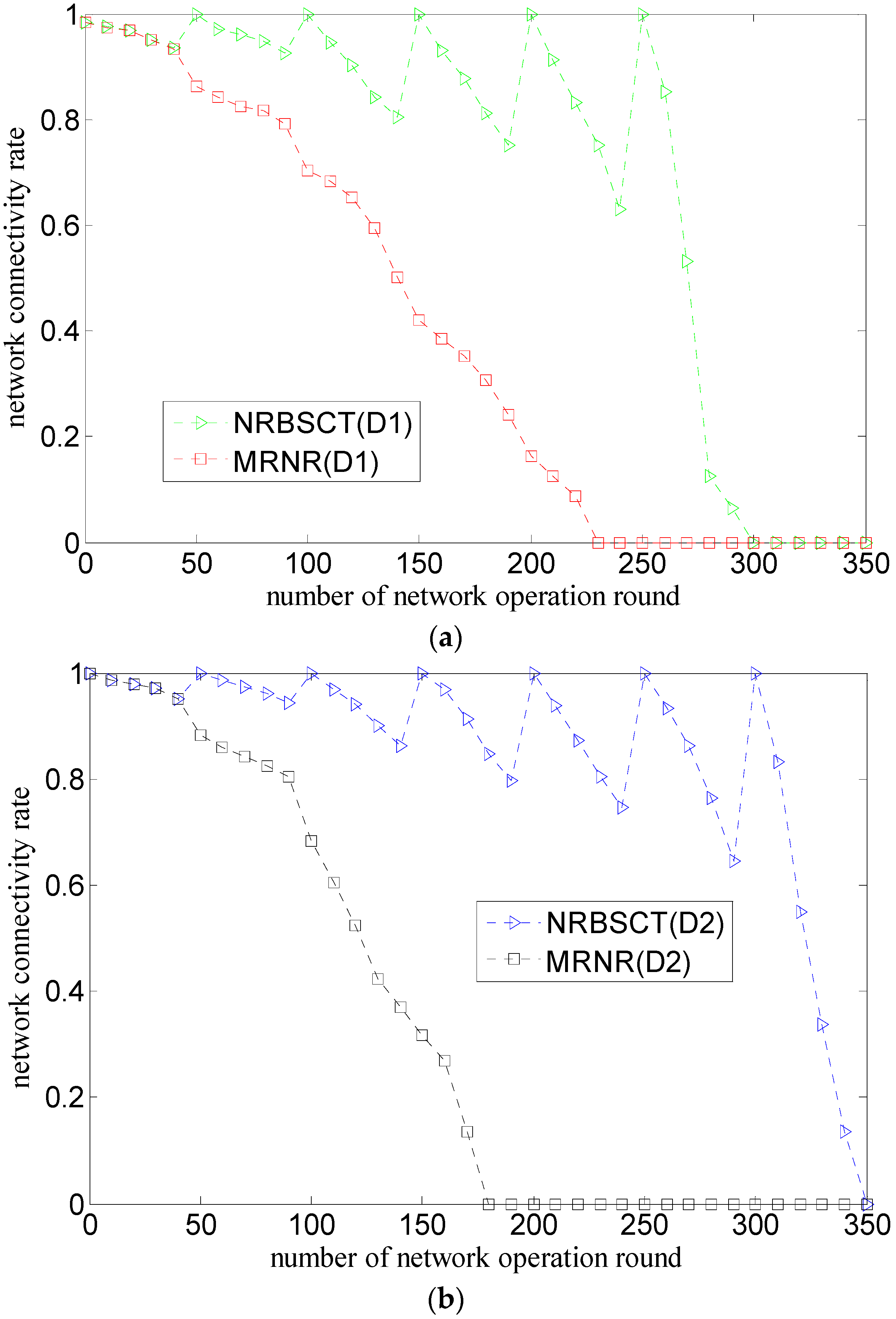
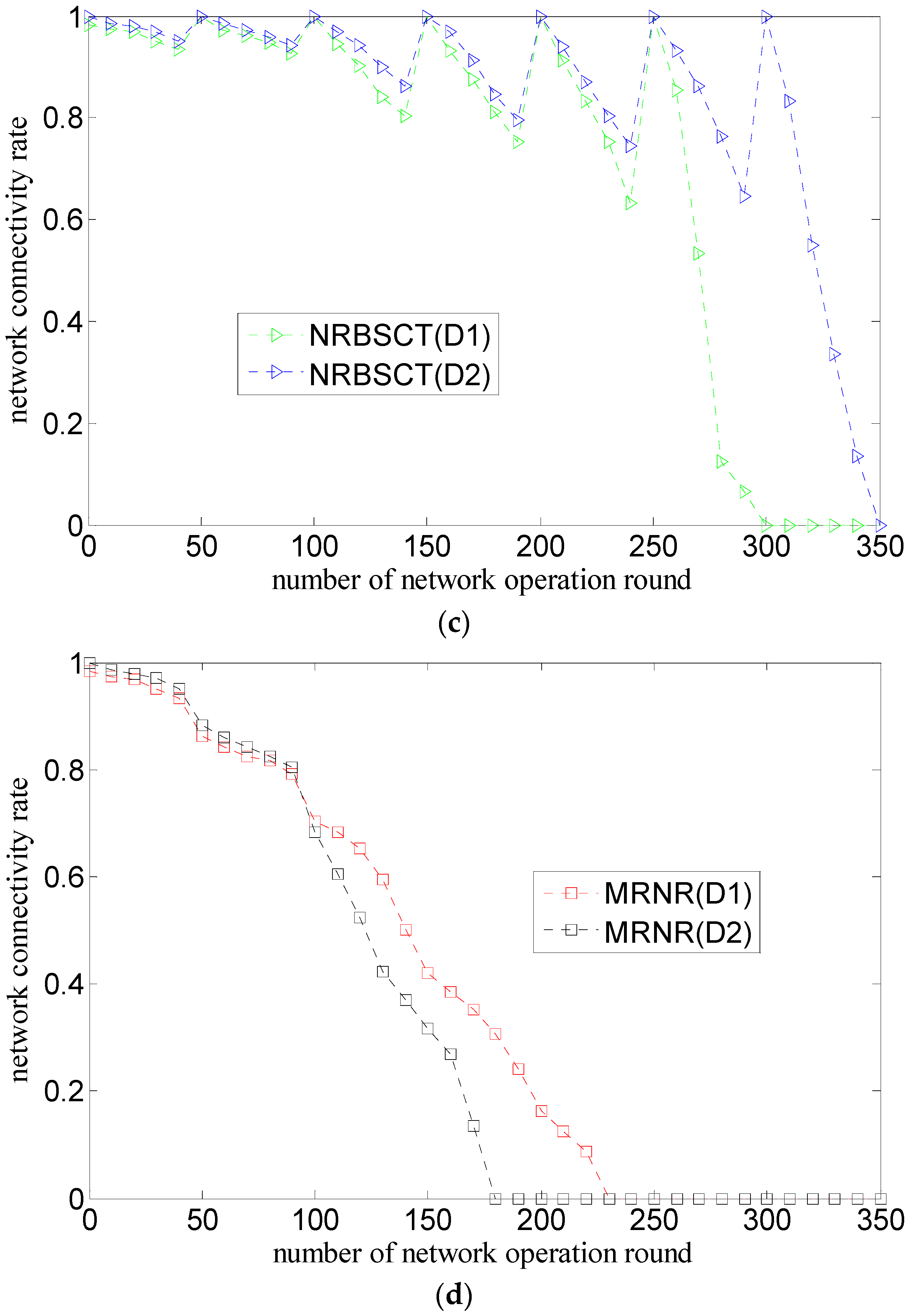
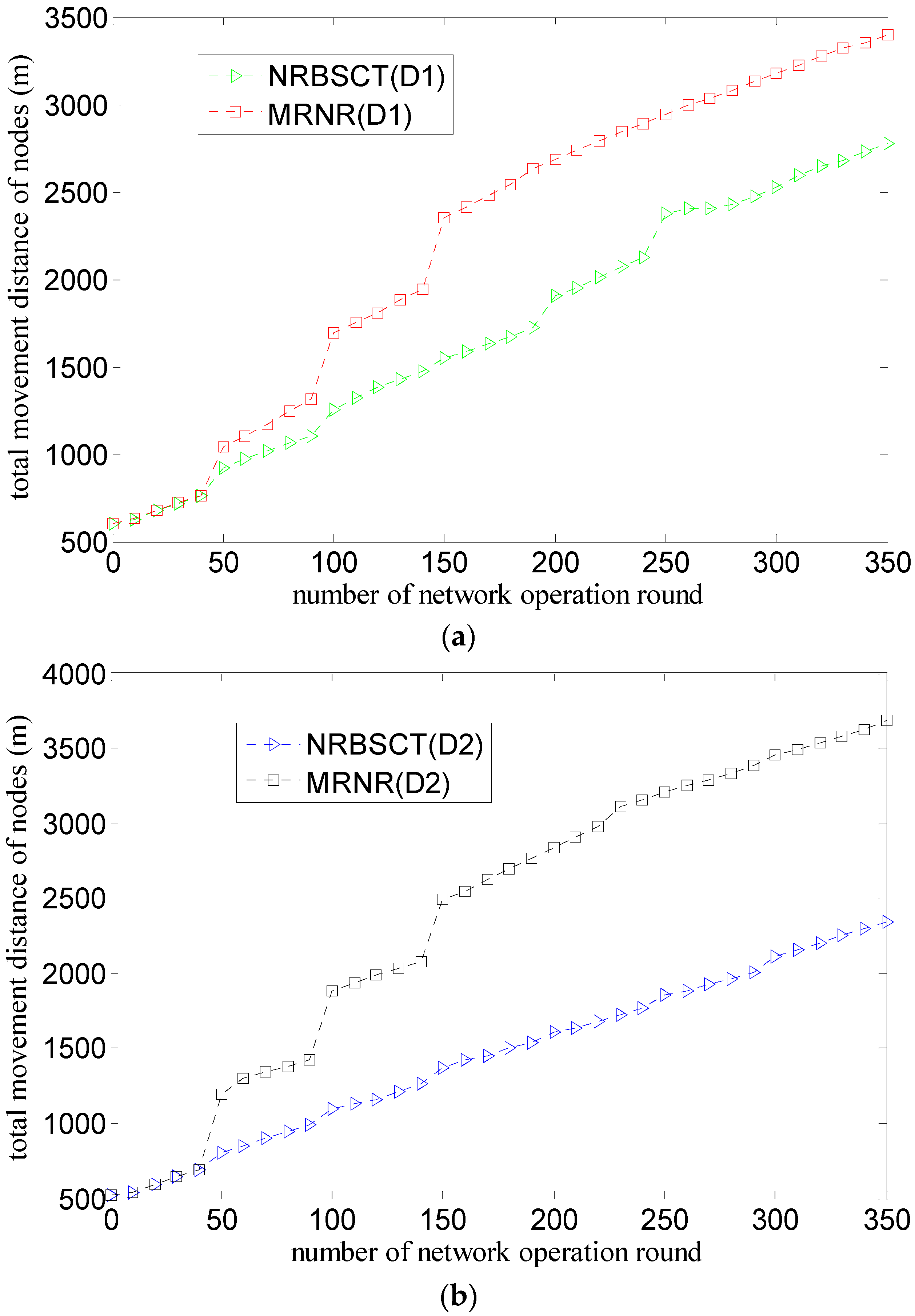
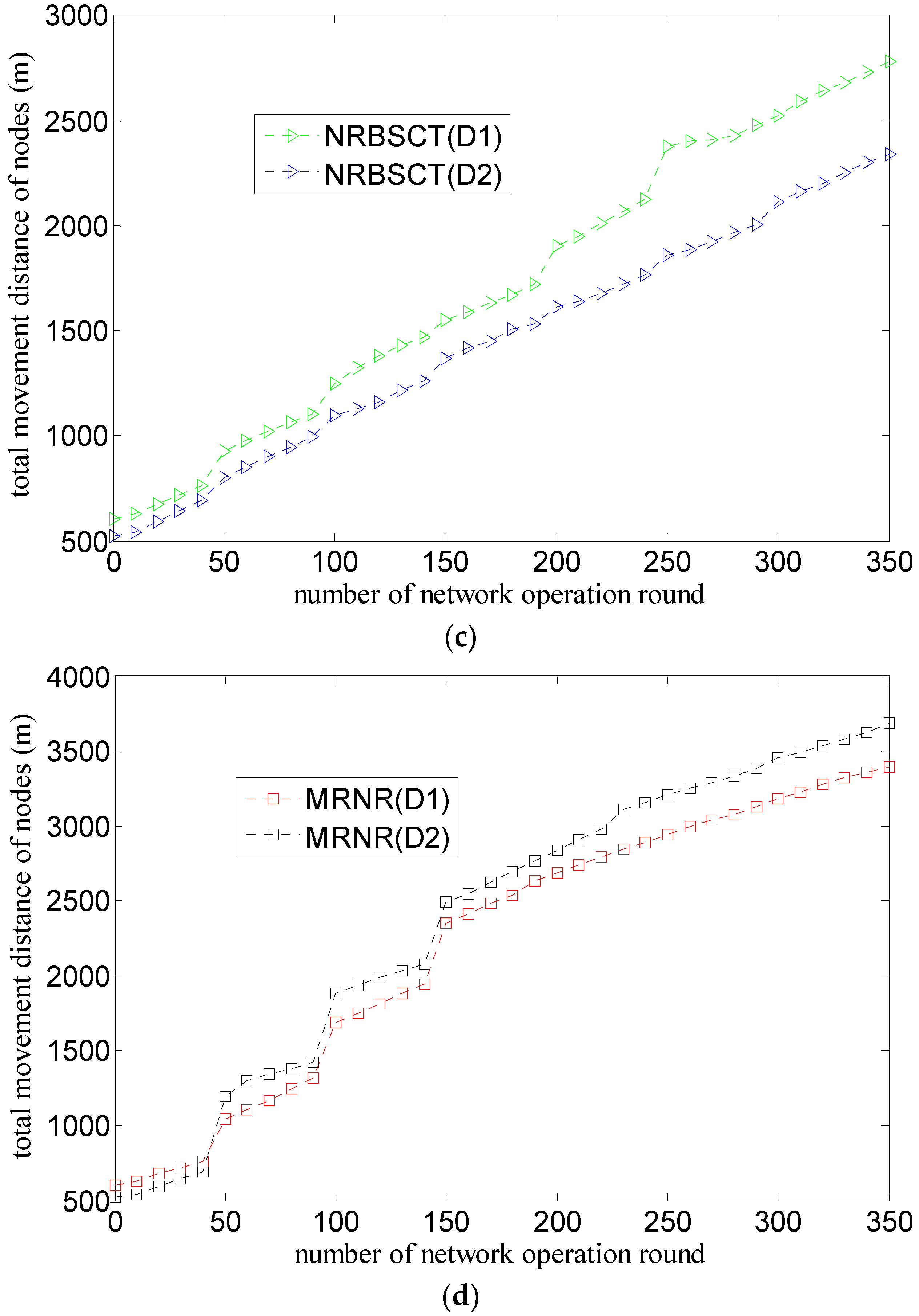
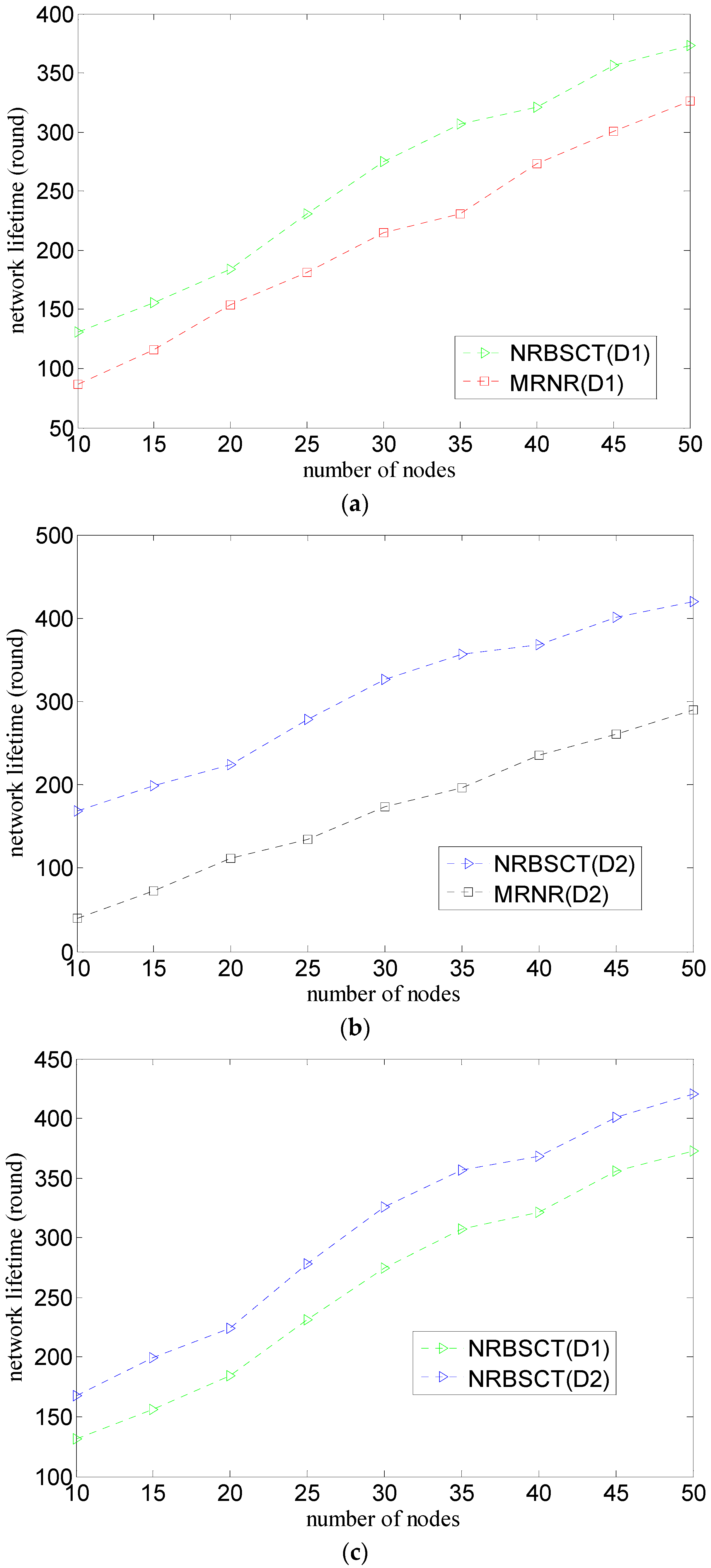
4.1. Algorithm Comparison and Evaluation Metrics
- (1)
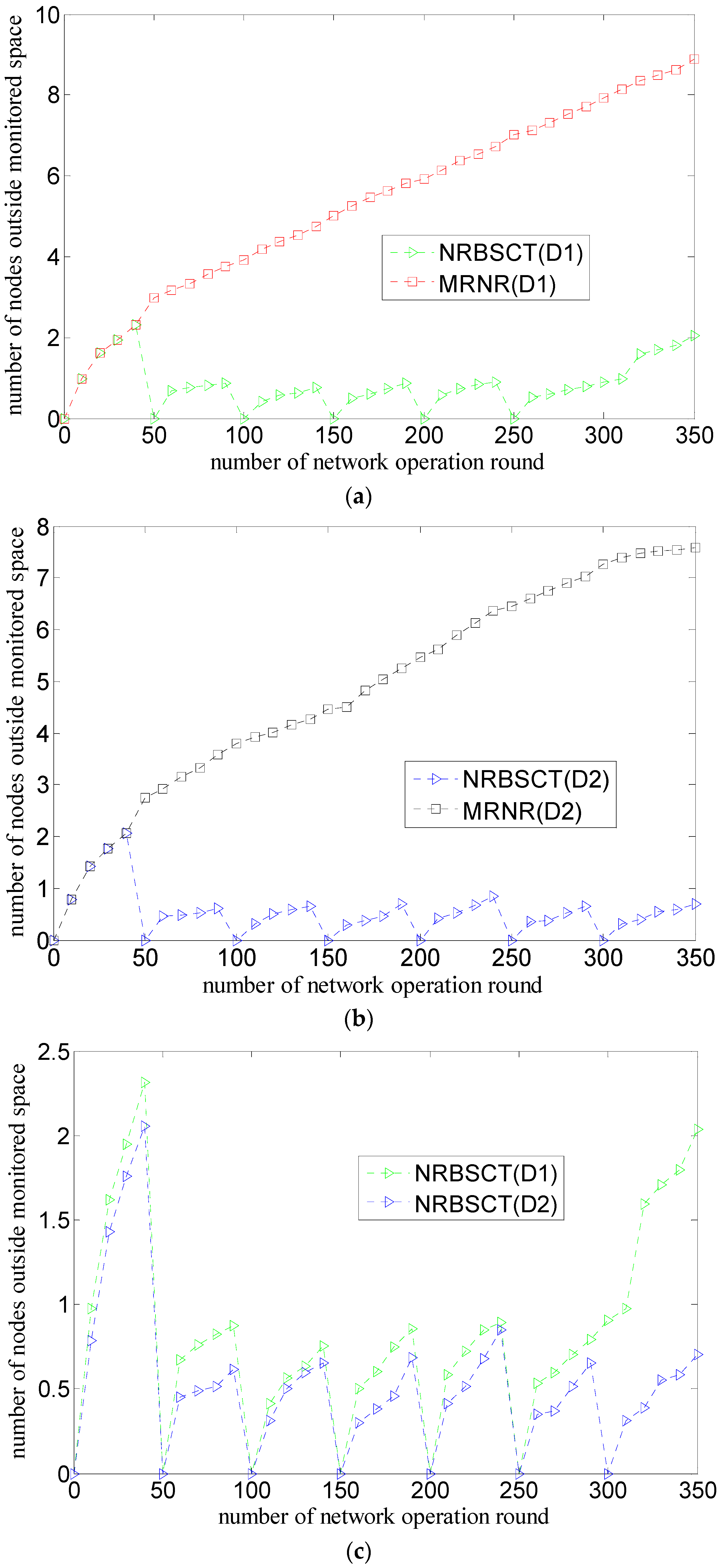
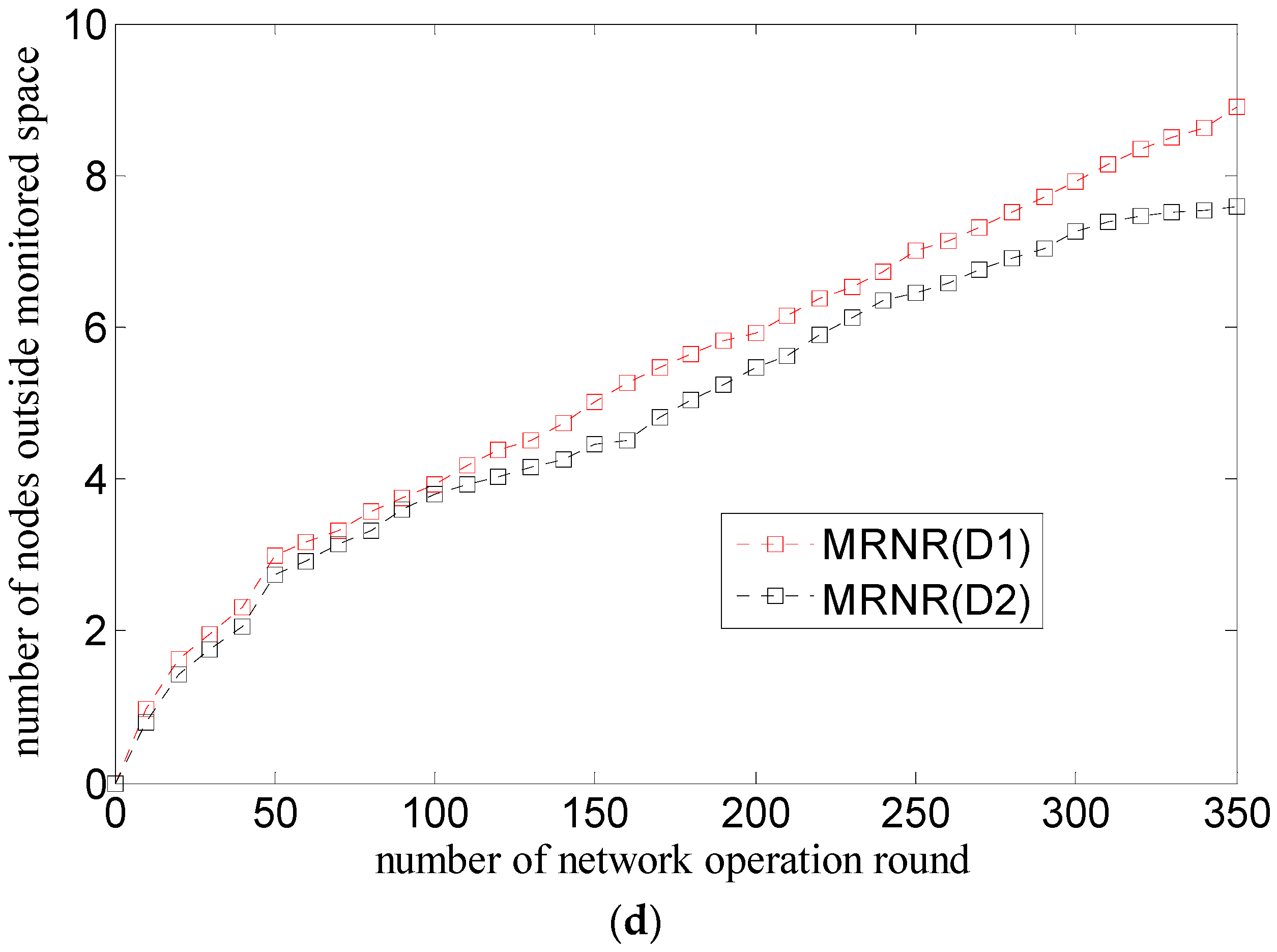
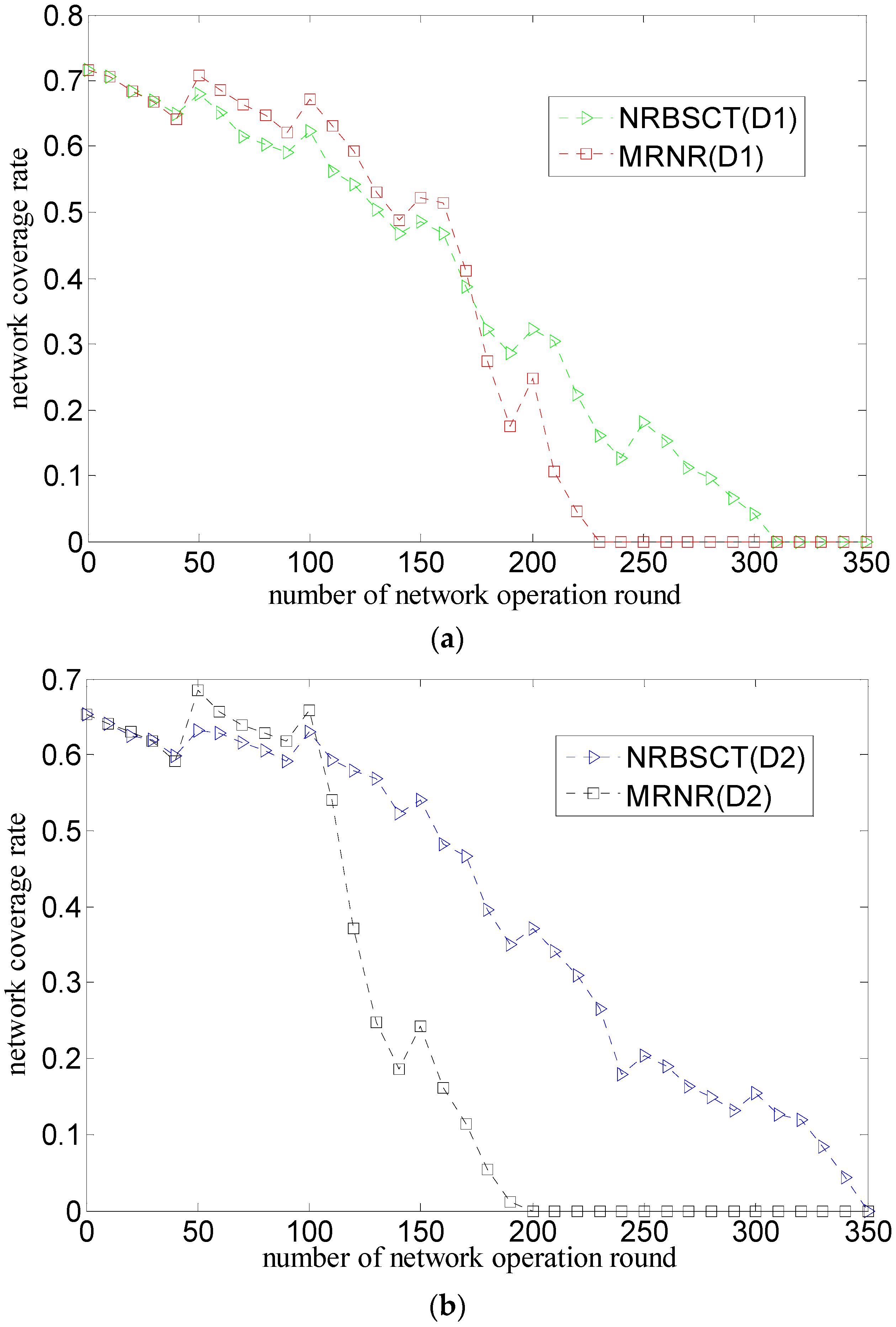
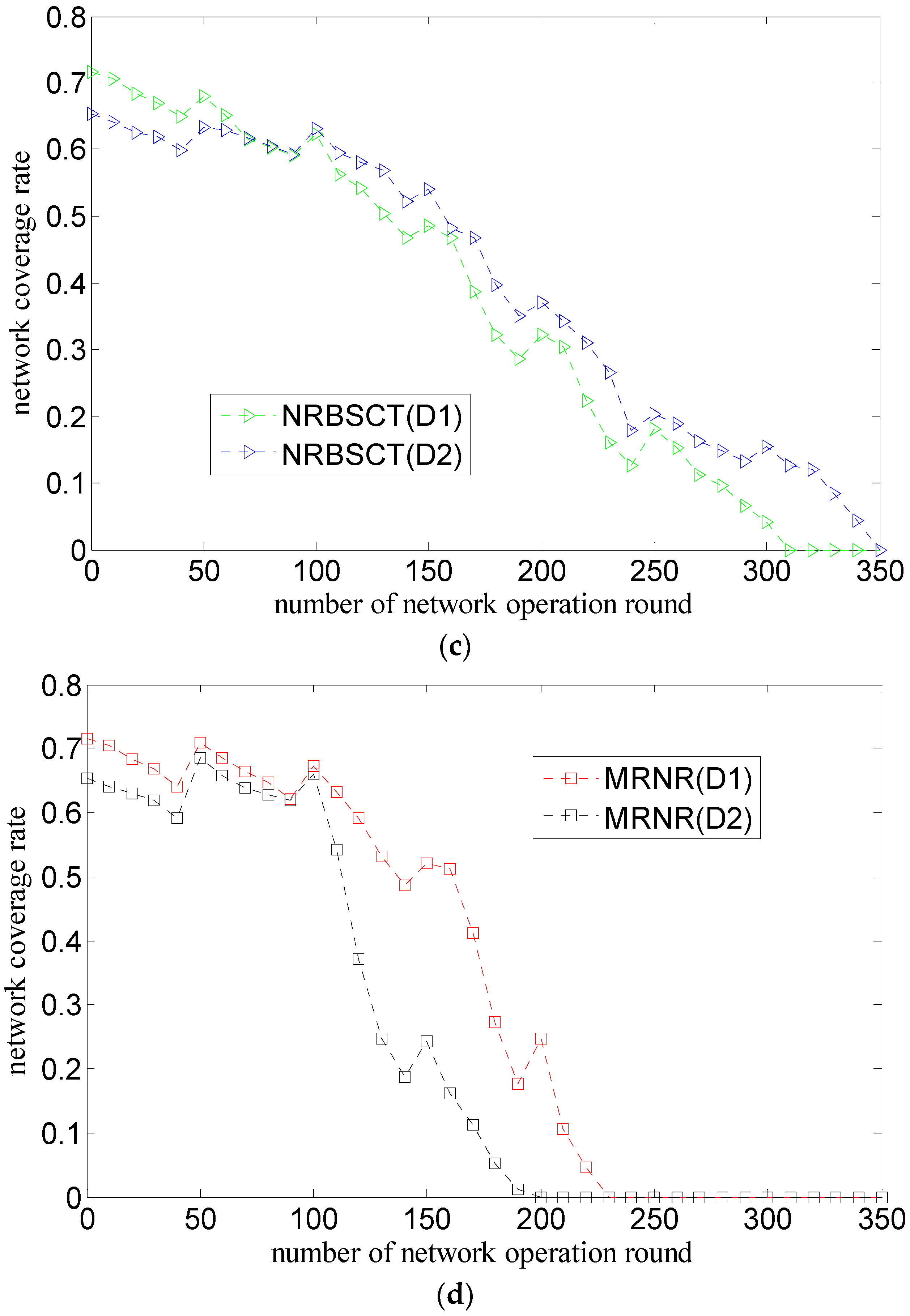
- The MRNR algorithm does not propose effective measures to prevent nodes from drifting out of the monitored space because of water environment. However, the NRBSCT algorithm can make nodes outside the monitored space return back through self-examination and adjustment on node locations, which is goodfor maintaining good network monitoring quality.
- (2)
- The MRNR algorithm only considers how to improve the network coverage rate, but ignores the network connectivity rate improvement. However, at the network adjustment moment, the NRBSCT algorithm can firstly establish a stratified connected tree that takes the sink node as the root node, and then ensure that in the centralized optimization conducted by the sink node, the final destination location of node si will not be Rt away from the backbone nodes, which achieves full network connectivity and also helps to maintain a relatively high network connectivity during network operation.
- (3)
- The MRNR algorithm does not consider how to shorten the movement distance when requiring the least important node to move toward the biggest coverage blind point to improve the network coverage rate. However, the centralized optimization conducted by the sink node in the NRBSCT algorithm considers limiting node movement distance from the left and consumed energy perspectives, which can shorten the total movement distance of nodes during redeployment and prolong the network lifetime.
4.2. Simulation Scenario and Parameter Settings
4.3. Simulation Results and Analysis
5. Conclusions and Future Work
- (1)
- The 3D random drift model adopted to simulate the node drift caused by the water environment is relatively simple, considering the complex flow changes for realistic conditions.
- (2)
- In the description of the energy consumption calculation for transmitting information, the attenuation model of acoustic propagation is relatively rough considering the reasonable uncertainty bounds for realistic conditions.
- (3)
- The movement energy consumption calculation method is also relatively idealized considering the complex current effects for realistic conditions.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Garcia, M.; Bri, D.; Sendra, R.; Lloret, J. Practical deployments of wireless sensor networks: A survey. Int. J. Adv. Netw. Serv. 2010, 3, 170–185. [Google Scholar]
- Bri, D.; Garcia, M.; Lloret, J.; Dini, P. Real Deployments of Wireless Sensor Networks. In Proceedings of the 3rd International Conference on Sensor Technologies and Applications, Athens, Greece, 18–23 June 2009; pp. 415–423.
- Akyildiz, I.F.; Pompili, D.; Melodia, T. Underwater acoustic sensor networks: Research challenges. Ad Hoc Netw. 2005, 3, 257–279. [Google Scholar] [CrossRef]
- Garcia, M.; Sendra, M.; Atenas, M.; Lloret, J. Underwater Wireless Ad-Hoc Networks: A Survey. In Mobile Ad Hoc Networks: Current Status and Future Trends; Jonathan, L., Jaime, L.M., Jesus, H.O., Eds.; CRC Press: Boca Raton, FL, USA, 2011; pp. 379–411. [Google Scholar]
- Heidemann, J.; Stojanovic, M.; Zorzi, M. Underwater sensor networks: Applications, advances and challenges. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2012, 370, 158–175. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.F. A deployment algorithm for underwater sensor networks in ocean environment. J. Circuits Syst. Comput. 2011, 20, 1051–1066. [Google Scholar] [CrossRef]
- Nie, J.; Li, D.; Han, Y. Optimization of multiple gateway deployment for underwater acoustic sensor networks. Comput. Sci. Inf. Syst. 2011, 8, 1073–1095. [Google Scholar] [CrossRef]
- Senel, F. Coverage-aware connectivity-constrained unattended sensor deployment in underwater acoustic sensor networks. Wirel. Commun. Mob. Comput. 2016, 30, 70–77. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Zuba, M.; Peng, Z.; Cui, J.H.; Zhou, S. Da-Sync: A doppler-assisted time-synchronization scheme for mobile underwater sensor networks. IEEE Trans. Mob. Comput. 2014, 13, 582–595. [Google Scholar] [CrossRef]
- Priya, G.; Shobana, P. Time synchronization in mobile underwater sensor network. Adv. Nat. Appl. Sci. 2014, 8, 58–63. [Google Scholar]
- Liu, J.; Wang, Z.; Cui, J.H.; Zhou, S.; Yang, B. A joint time synchronization and localization design for mobile underwater sensor networks. IEEEE Trans. Mob. Comput. 2016, 15, 530–543. [Google Scholar] [CrossRef]
- Misra, S.; Ojha, T.; Mondal, A. Game-theoretic topology control for opportunistic localization in sparse underwater sensor networks. IEEEE Trans. Mob. Comput. 2015, 14, 990–1003. [Google Scholar] [CrossRef]
- Al-Bzoor, M.; Zhu, Y.; Liu, J.; Reda, A.; Cui, J.H.; Rajasekaran, S. Adaptive power controlled routing for underwater sensor networks. Int. J. Sens. Netw. 2015, 18, 549–560. [Google Scholar]
- Yu, H.; Yao, N.; Liu, J. An adaptive routing protocol in underwater sparse acoustic sensor networks. Ad Hoc Netw. 2015, 34, 121–143. [Google Scholar] [CrossRef]
- Luo, H.; Guo, Z.; Wu, K.; Hong, F.; Feng, Y. Energy balanced strategies for maximizing the lifetime of sparsely deployed underwater acoustic sensor networks. Sensors 2009, 9, 6626–6651. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Li, K.; Min, G. Reliable and energy-efficient multipath communications in underwater sensor networks. IEEE Trans. Parallel Distrib. Syst. 2011, 23, 1326–1335. [Google Scholar] [CrossRef]
- Han, G.; Zhang, C.; Shu, L.; Rodrigues, J.J.P.C. Impacts of deployment strategies on localization performance in underwater acoustic sensor networks. IEEE Trans. Ind. Electron. 2015, 62, 1725–1733. [Google Scholar] [CrossRef]
- Han, G.; Zhang, C.; Shu, L.; Sun, L.; Li, Q.W. A survey on deployment algorithms in underwater acoustic sensor networks. Int. J. Distrib. Sens. Netw. 2013, 2013. [Google Scholar] [CrossRef]
- Pompili, D.; Melodia, T.; Akyildiz, I.F. Three-dimensional and two-dimensional deployment analysis for underwater acoustic sensor networks. Ad Hoc Networks 2009, 7, 778–790. [Google Scholar] [CrossRef]
- Alam, S.N.; Haas, Z. Coverage and Connectivity in Three-Dimensional Networks. In Proceedings of the 12th Annual ACM International Conference on Mobile Computing and Networking, Los Angeles, CA, USA, 24–29 Sepember 2006; pp. 346–357.
- Akkaya, K.; Newell, A. Self-deployment of sensors for maximized coverage in underwater acoustic sensor networks. Comput. Commun. 2009, 32, 1233–1244. [Google Scholar] [CrossRef]
- Senel, F.; Akkaya, K.; Erol-Kantarci, M.; Yilmaz, T. Self-deployment of mobile underwater acoustic sensor networks for maximized coverage and guaranteed connectivity. Ad Hoc Netw. 2014, 34, 170–183. [Google Scholar] [CrossRef]
- Li, X.Y.; Ci, L.L.; Yang, M.H.; Tian, C.P.; Li, X. Deploying three-dimensional mobile sensor networks based on virtual forces algorithm. Commun. Comput. Inf. Sci. 2013, 334, 204–216. [Google Scholar]
- Zou, Y.; Chakrabarty, K. Sensor Deployment and Target Localization Based on Virtual Forces. In Proceedings of the 22th Annual Joint Conference of Computer and Communications, San Francisco, CA, USA, 30 March–3 April 2003; pp. 1293–1303.
- Xia, N.; Wang, C.S.; Zheng, R.; Jiang, J.G. Fish swarm inspired underwater sensor deployment. Acta Autom. Sin. 2012, 38, 295–302. [Google Scholar] [CrossRef]
- Du, H.Z.; Xia, N.; Zheng, R. Particle swarm inspired underwater sensor self-deployment. Sensors 2014, 14, 15262–15281. [Google Scholar] [CrossRef] [PubMed]
- Jiang, P.; Wang, X.; Jiang, L. Node deployment algorithm based on connected tree for underwater sensor networks. Sensors 2015, 15, 16763–16785. [Google Scholar] [CrossRef] [PubMed]
- Jiang, P.; Xu, Y.; Wu, F. Node self-deployment algorithm based on an uneven cluster with radius adjusting for underwater sensor networks. Sensors 2016, 16, 98. [Google Scholar] [CrossRef] [PubMed]
- Jiang, P.; Liu, J.; Ruan, B.; Jiang, L.; Wu, F. A new node deployment and location dispatch algorithm for underwater sensor networks. Sensors 2016, 16, 82. [Google Scholar] [CrossRef] [PubMed]
- Jiang, P.; Liu, J.; Wu, F.; Wang, J.; Xue, A. Node deployment algorithm for underwater sensor networks based on connected dominating set. Sensors 2016, 16, 388. [Google Scholar] [CrossRef] [PubMed]
- Jiang, P.; Liu, J.; Wu, F. Node non-uniform deployment based on clustering algorithm for underwater sensor networks. Sensors 2015, 15, 29997–30010. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Ren, F.Y.; Lin, C.; Yang, Y.C.; Zeng, R.F.; Wen, H. The Redeployment Issue in Underwater Sensor Networks. In Proceedings of the Global Telecommunications Conference, New Orleans, LA, USA, 30 November–4 December 2008; pp. 1–6.
- Cayirci, E.; Tezcan, H.; Dogan, Y.; Coskun, V. Wireless sensor networks for underwater surveillance systems. Ad Hoc Networks 2006, 4, 431–446. [Google Scholar] [CrossRef]
- Partan, J.; Kurose, J.; Levine, B.N. A survey of practical issues in underwater networks. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2007, 11, 23–33. [Google Scholar] [CrossRef]
- Sozer, E.M.; Stojanovic, M.; Proakis, J.G. Underwater acoustic networks. IEEE Ocean. Eng. 2000, 25, 72–83. [Google Scholar] [CrossRef]
- Keskin, M.; Altinel, I.K.; Aras, N.; Ersoy, C. Wireless sensor network lifetime maximization by optimal sensor deployment, activity scheduling, data routing and sink mobility. Ad Hoc Netw. 2014, 17, 18–36. [Google Scholar] [CrossRef]
- Bahi, J.; Haddad, M.; Hakem, M.; Kheddouci, H. Efficient distributed lifetime optimization algorithm for sensor networks. Ad Hoc Netw. 2014, 16, 1–12. [Google Scholar] [CrossRef]
- Wynn, R.B.; Huvenne, V.A.I.; Le Bas, T.P.; Murton, B.J.; Connelly, D.P.; Bett, B.J.; Ruhl, H.A.; Morris, K.J.; Peakall, J.; Parsons, D.R.; et al. Autonomous underwater vehicles (auvs): Their past, present and future contributions to the advancement of marine geoscience. Mar. Geol. 2014, 352, 451–468. [Google Scholar] [CrossRef]
- Chandrasekhar, V.; Seah, W.K.; Choo, Y.S.; Ee, H.V. Localization in Underwater Sensor Networks: Survey and Challenges. In Proceedings of the 1st ACM International Workshop on Underwater Networks, Los Angeles, CA, USA, 25 September 2006; pp. 33–40.



| Literature/Algorithm | Node Mobility | Consideration of Node Drift with Water Environment |
|---|---|---|
| [19,20] | Static | No |
| [21,22,27] | limited | Additional |
| [28] | limited | No |
| [23,25,29,30,31] | Free | No |
| [26] | Free | Additional |
| [32], NRBSCT | Free | Full |
| Round | 0 | 40 | 49 | 50 (after Adjustment) |
|---|---|---|---|---|
| Location | (115, 37, 16) | (123, 41, 19) | (125, 43, 21) | (115, 37, 16) |
| Inside/Outside | Inside | Outside | Outside | Inside |
| Node | s2 | s3 | s8 | s9 |
|---|---|---|---|---|
| Left energy (J) | 75 | 61 | 77 | 57 |
| Inside/Outside | Inside | Outside | Outside | Inside |
| Strong leaf node | Yes | No | Yes | No |
| Symbols | Meanings |
|---|---|
| w | cube side length |
| d | transmitting distance of information package |
| Mb | size of information package |
| Tp | transmitting time of information package |
| Sv | transmission speed of information package |
| f | carrier acoustic signal frequency |
| α(f) | water absorption coefficient |
| A(d) | energy attenuation |
| λ | energy spreading factor |
| Etx(d) | energy consumption for transmitting information |
| Pr | power threshold for receiving information package |
| tn | information package transmitting times for a node |
| Rt | communication range |
| Ce | communication energy consumption |
| Me | movement energy consumption |
| md | movement distance |
| mu | energy consumption per movement distance |
| Pe | controlling probability of node drift |
| Cv | network coverage rate |
| Pc | number of cube points covered |
| Pt | total number of all cube points |
| Cn | network connectivity rate |
| nc | number of nodes being able to communicate with sink node |
| n | number of all nodes |
| t | network operation time |
| Tr | network adjustment cycle |
| Tad | network adjust moment |
| Ei | energy of node si |
| Ed | energy threshold judging death of node |
| Ey | energy threshold judging whether leaf node is strong enough |
| Lf | network lifetime |
| Cth | coverage rate threshold |
| Ein | node initial energy |
| Rs | sensing range |
| Tm | node drift cycle |
| Mr | ready information |
| Ma | acknowledging information |
| rg | control coefficient |
| Parameter Names | Parameter Values |
|---|---|
| Initial energy of node (Ei) | 500 J |
| Network coverage rate threshold (Cth) | 0.1 |
| Energy consumption per movement distance (mu) | 1.5 J/m |
| Size of information package (Mb) | 1 Kbit |
| Receiving Power threshold (Pr) | 0.05 w |
| Frequency of carrier acoustic signal (f) | 25 kHz |
| Transmission speed of information package (Sv) | 5 kbps |
| Energy spreading factor (λ) | 1.5 |
| Sensing range of node (Rs) | 15 m |
| Communication range of node (Rt) | 25 m |
| Network adjustment cycle (Tr) | 50 round |
| Node drift cycle (Tm) | 5 round |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Jiang, P.; Wu, F.; Yu, S.; Song, C. Node Redeployment Algorithm Based on Stratified Connected Tree for Underwater Sensor Networks. Sensors 2017, 17, 27. https://doi.org/10.3390/s17010027
Liu J, Jiang P, Wu F, Yu S, Song C. Node Redeployment Algorithm Based on Stratified Connected Tree for Underwater Sensor Networks. Sensors. 2017; 17(1):27. https://doi.org/10.3390/s17010027
Chicago/Turabian StyleLiu, Jun, Peng Jiang, Feng Wu, Shanen Yu, and Chunyue Song. 2017. "Node Redeployment Algorithm Based on Stratified Connected Tree for Underwater Sensor Networks" Sensors 17, no. 1: 27. https://doi.org/10.3390/s17010027
APA StyleLiu, J., Jiang, P., Wu, F., Yu, S., & Song, C. (2017). Node Redeployment Algorithm Based on Stratified Connected Tree for Underwater Sensor Networks. Sensors, 17(1), 27. https://doi.org/10.3390/s17010027





