Compressed Sensing Techniques Applied to Ultrasonic Imaging of Cargo Containers
Abstract
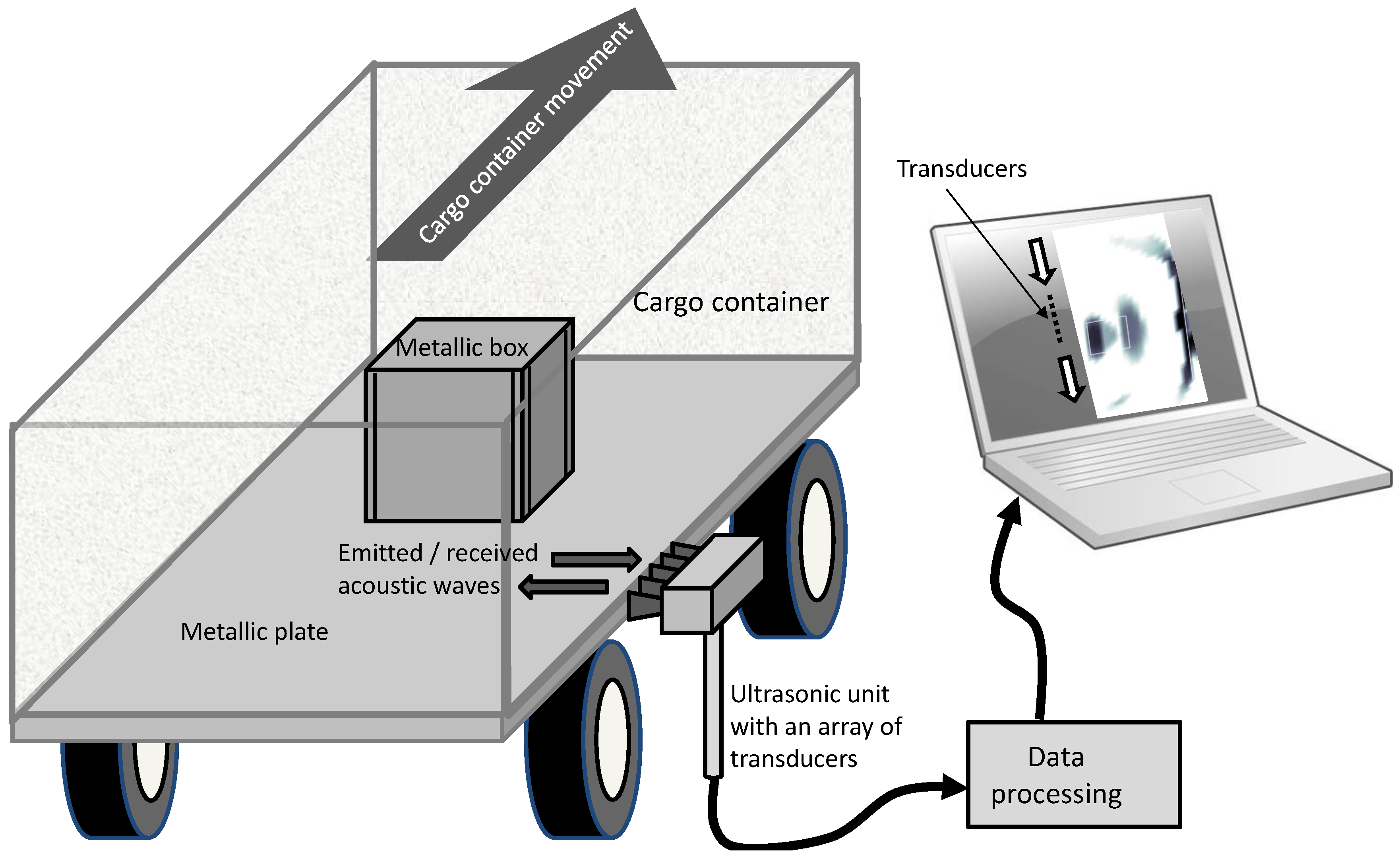
:1. Introduction
2. Backpropagation Imaging Algorithm
3. Compressed Sensing Technique
4. Application Example
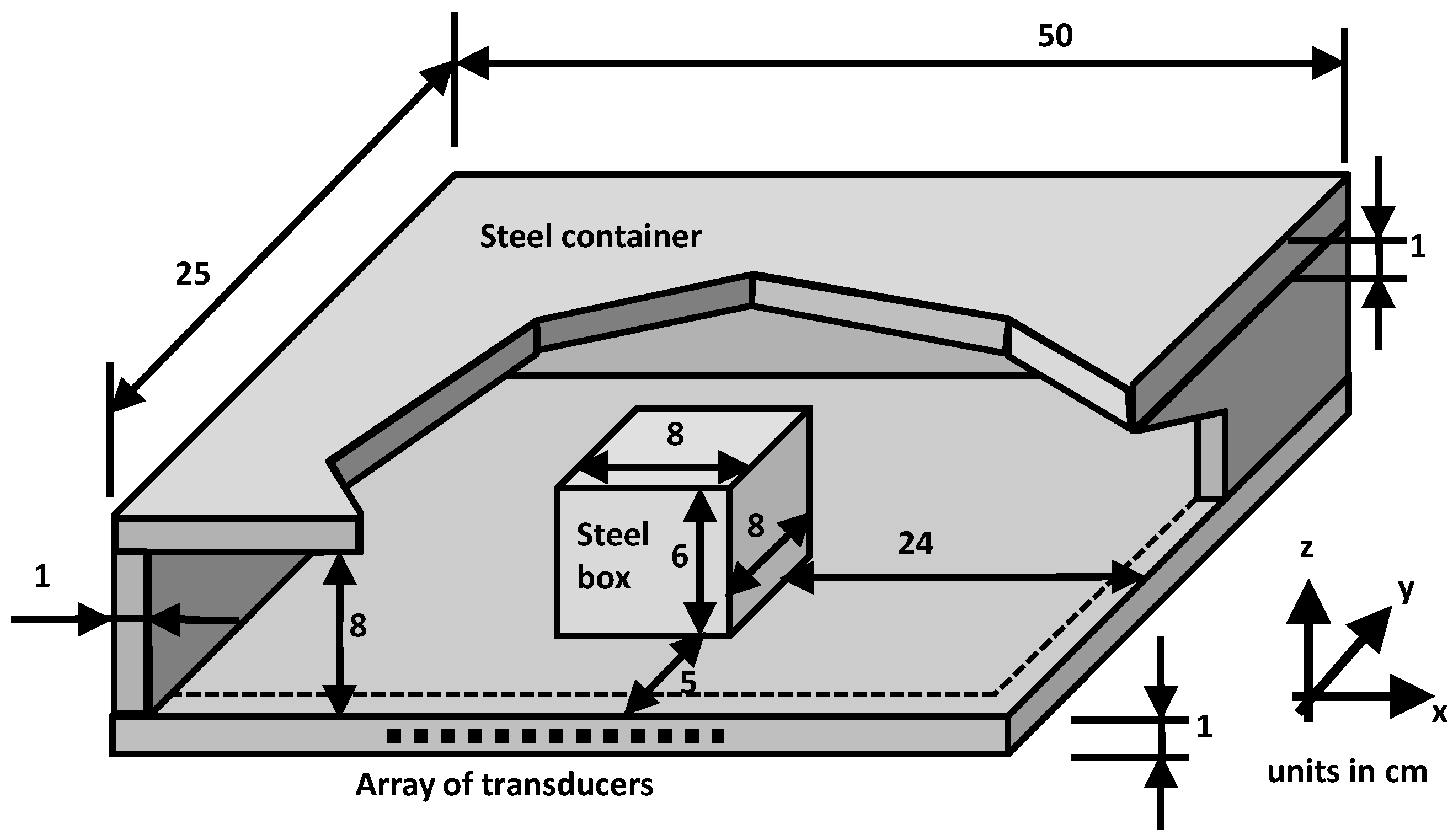
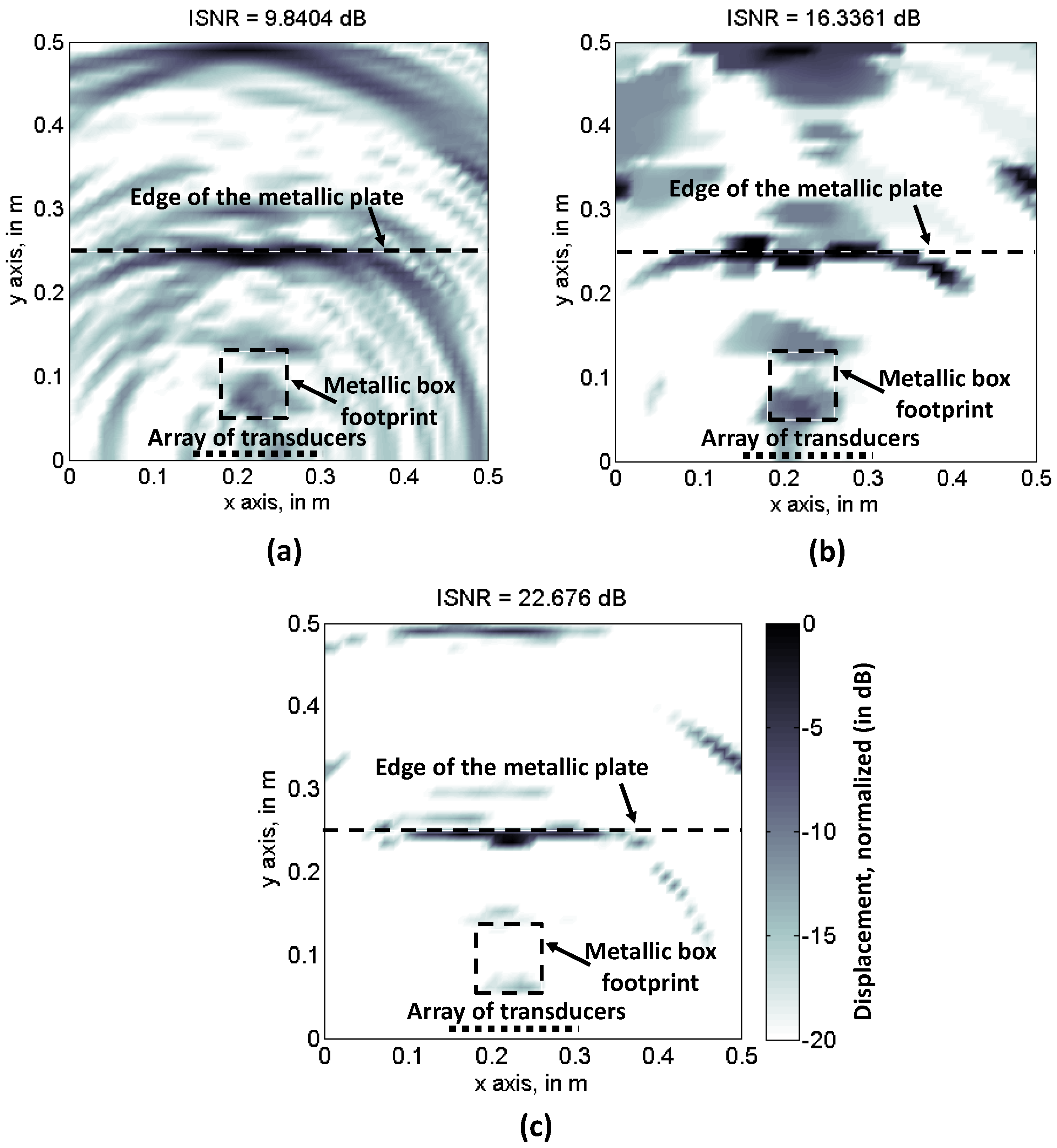
4.1. Description of the Example
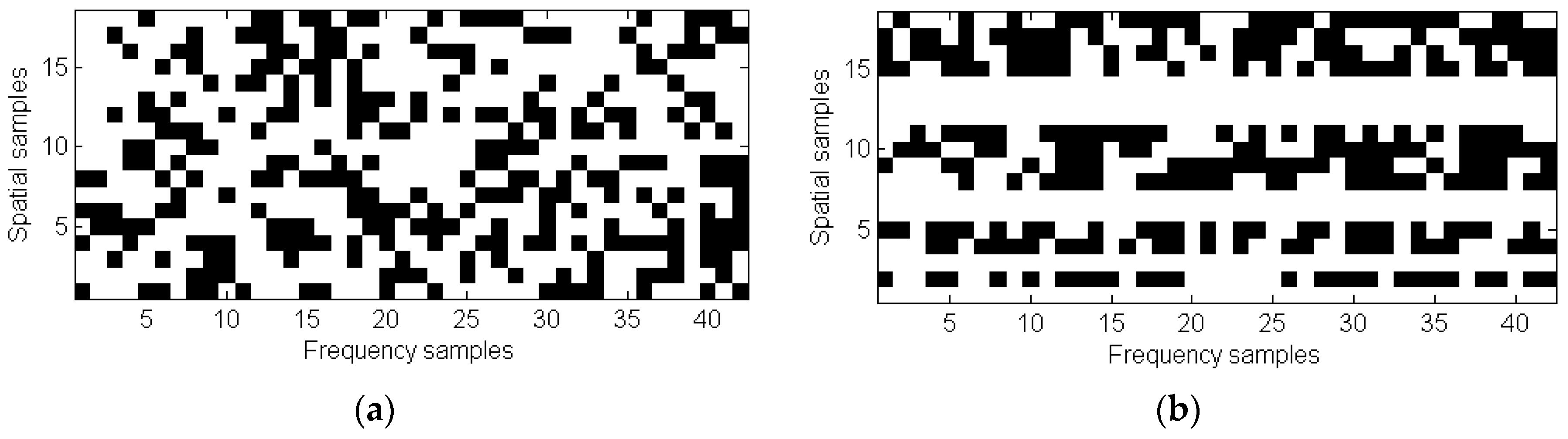
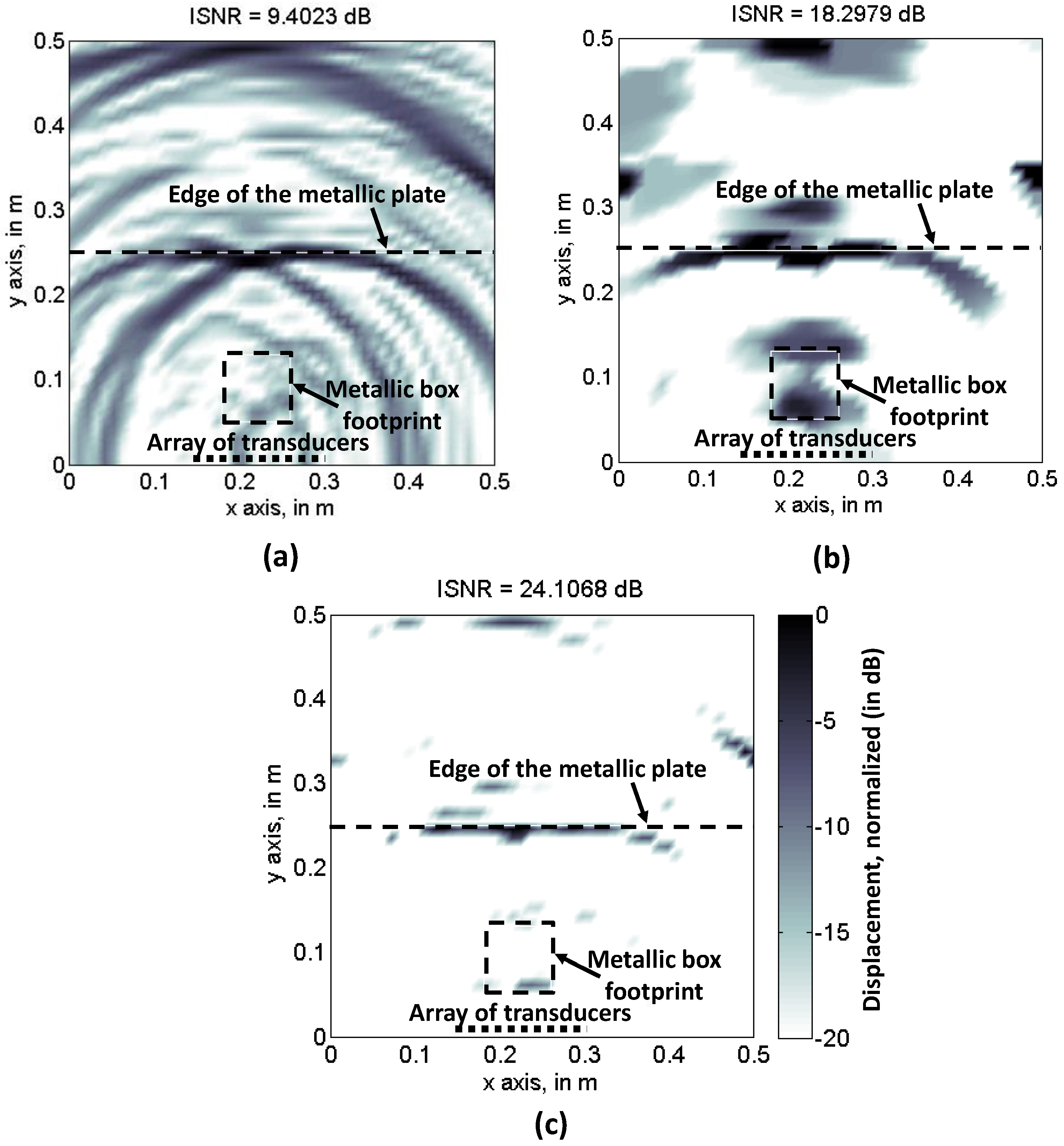
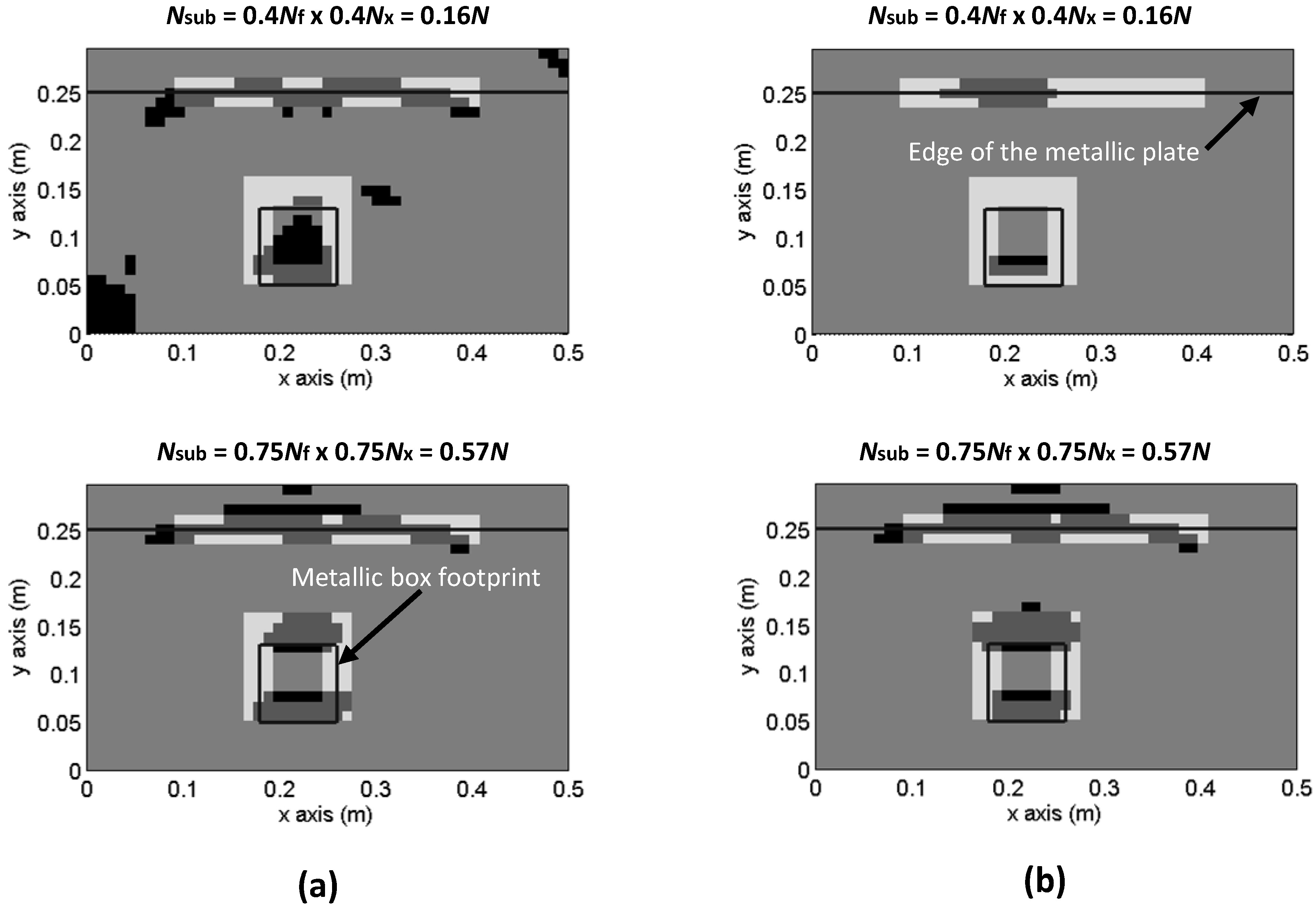
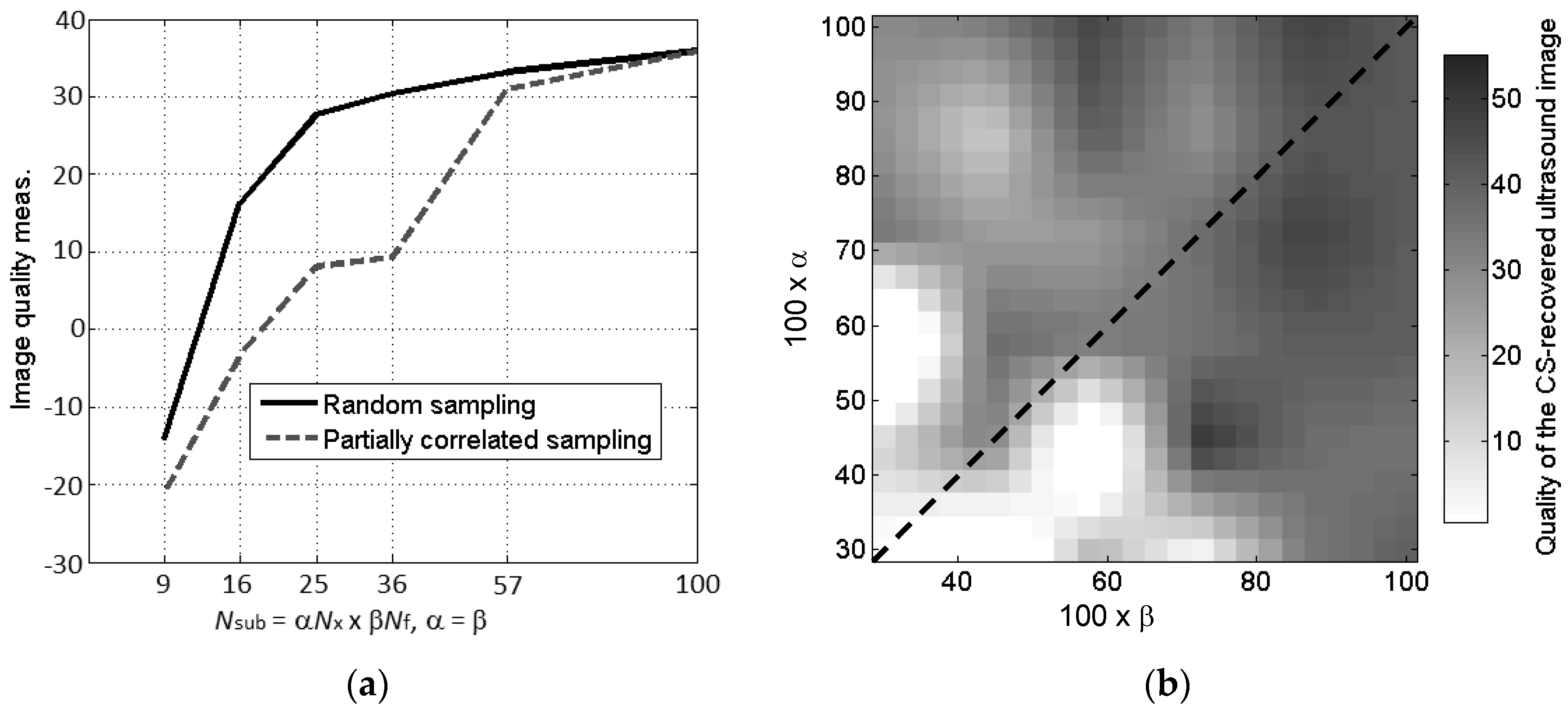
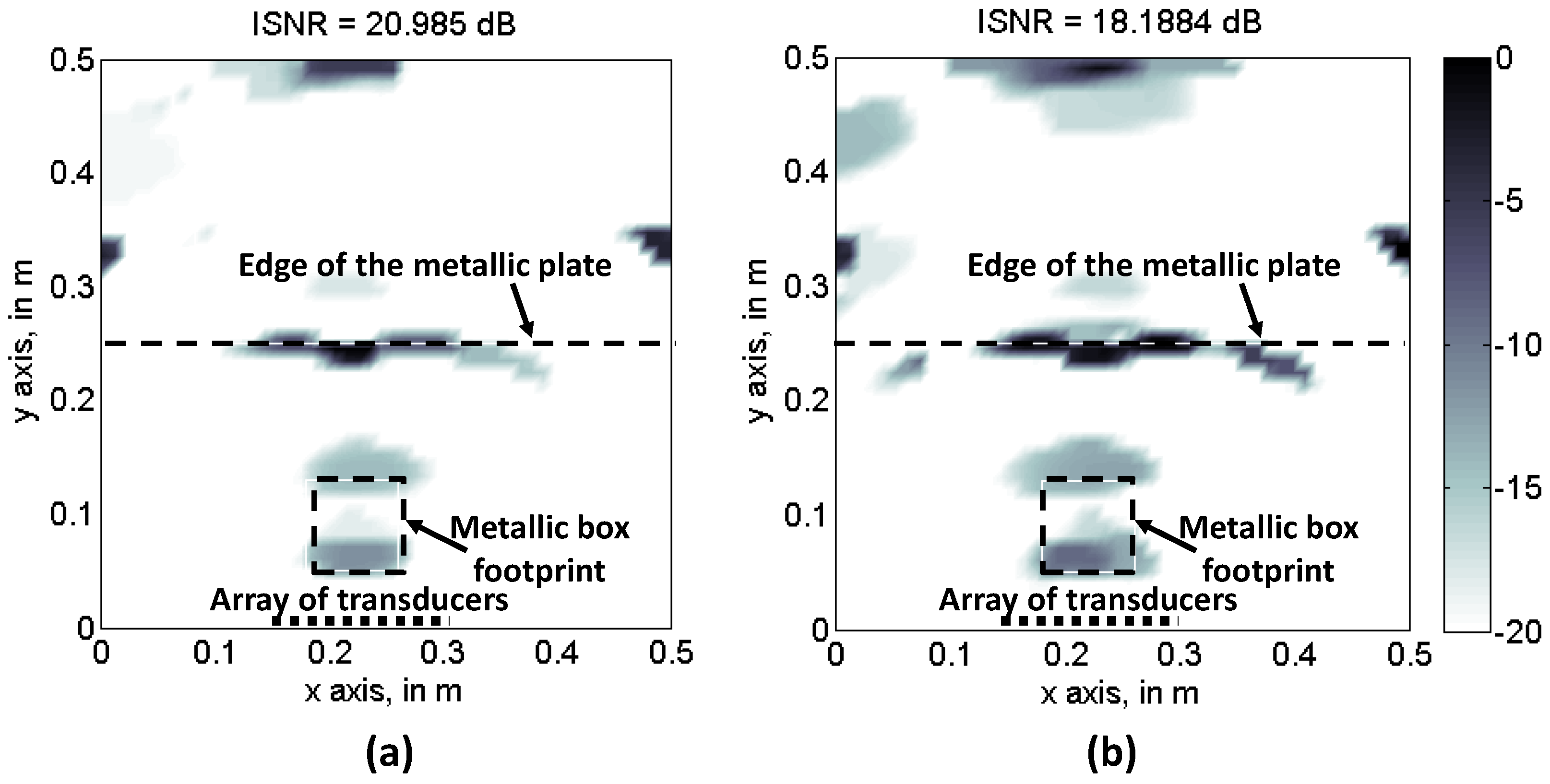
4.2. Analysis of the Sampling Schemes
5. Discussion
- (i)
- (ii)
- The integration of the Fourier-based imaging into the CS algorithm. This study has been undertaken due to the requirement of evenly spaced samples for FFTs. An alternative could be to introduce Non-Uniform FFT (NUFFT), but its capability to filter out non-desired contributions using a reduced set of samples will have to be evaluated.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chang, C.L.; He, M.; Nguyen, M.H. Computational model for automatic cargo container inspection systems. In Proceedings of the 2010 IEEE International Conference on Technologies for Homeland Security (HST 2010), Waltham, MA, USA, 8–10 November 2010; pp. 556–561.
- Brown, B.J.; Minter, A.D. Vehicle Security Inspection System. U.S. Patent US 2004/0232054 A1. Available online: https://goo.gl/Dtq4W5 (accessed on 11 October 2016).
- Medalia, J. Detection of Nuclear Weapons and Materials: Science, Technologies, Observations; DIANE Publishing: Collingdale, PA, USA, 2010. [Google Scholar]
- Duan, X.; Cheng, J.; Zhang, L.; Xing, Y.; Chen, Z.; Zhao, Z. X-ray cargo container inspection system with few-view projection imaging. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2009, 598, 439–444. [Google Scholar] [CrossRef]
- Ahmed, S.S.; Schiessl, A.; Gumbmann, F.; Tiebout, M.; Methfessel, S.; Schmidt, L.P. Advanced microwave imaging. IEEE Microw. Mag. 2012, 13, 26–43. [Google Scholar] [CrossRef]
- Álvarez, Y.; Martínez-Lorenzo, J.Á. On the Use of Ultrasound-based Technology for Cargo Inspection. J. Vib. Acoust. 2016, 138, 1–13. [Google Scholar] [CrossRef]
- Martínez-Lorenzo, J.A.; Álvarez López, Y. Ultrasonic-Based System for Detection of Metallic Security Threats Containers on Cargo. Patent No. WO 2016/065066 A9. Available online: https://goo.gl/OeUPGa (accessed on 18 September 2016).
- Alleyne, D.N.; Cawley, P. The interaction of Lamb waves with defects. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1992, 39, 381–397. [Google Scholar] [CrossRef] [PubMed]
- Michaels, J.E. Detection, localization and characterization of damage in plates with an in situ array of spatially distributed ultrasonic sensors. Smart Mater. Struct. 2008, 17, 035035. [Google Scholar] [CrossRef]
- Norton, S.J.; Linzer, M. Ultrasonic Reflectivity Imaging in Three Dimensions: Exact Inverse Scattering Solutions for Plane, Cylindrical, and Spherical Apertures. IEEE Trans. Biomed. Eng. 1981, 28, 201–220. [Google Scholar] [CrossRef] [PubMed]
- Quinsac, C.; Basarab, A.; Kouamé, D. Frequency domain compressive sampling for ultrasound imaging. Adv. Acoust. Vib. 2012, 2012, 1–16. [Google Scholar] [CrossRef]
- Lorintiu, O.; Liebgott, H.; Alessandrini, M.; Bernard, O.; Friboulet, D. Compressed sensing reconstruction of 3D ultrasound data using dictionary learning and line-wise subsampling. IEEE Trans. Med. Imaging 2015, 34, 2467–2477. [Google Scholar] [CrossRef] [PubMed]
- Liebgott, H.; Prost, R.; Friboulet, D. Pre-beamformed RF signal reconstruction in medical ultrasound using compressive sensing. Ultrasonics 2013, 53, 525–533. [Google Scholar] [CrossRef] [PubMed]
- Wagner, N.; Eldar, Y.C.; Friedman, Z. Compressed beamforming in ultrasound imaging. IEEE Trans. Signal Process. 2012, 60, 4643–4657. [Google Scholar] [CrossRef]
- Harley, J.B.; Moura, J.M. Sparse recovery of the multimodal and dispersive characteristics of lamb waves. J. Acoust. Soc. Am. 2013, 133, 2732–2745. [Google Scholar] [CrossRef] [PubMed]
- Di Ianni, T.; De Marchi, L.; Perelli, A.; Marzani, A. Compressive sensing of full wave field data for structural health monitoring applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2015, 62, 1373–1383. [Google Scholar] [CrossRef] [PubMed]
- Mesnil, O.; Ruzzene, M. Sparse wavefield reconstruction and source detection using compressed sensing. Ultrasonics 2016, 67, 94–104. [Google Scholar] [CrossRef] [PubMed]
- Guarneri, G.A.; Pipa, D.R.; Junior, F.N.; de Arruda, L.V.R.; Zibetti, M.V.W. A sparse reconstruction algorithm for ultrasonic images in nondestructive testing. Sensors 2015, 15, 9324–9343. [Google Scholar] [CrossRef] [PubMed]
- Tang, G.; Hou, W.; Wang, H.; Luo, G.; Ma, J. Compressive sensing of roller bearing faults via harmonic detection from under-sampled vibration signals. Sensors 2015, 15, 25648–25662. [Google Scholar] [CrossRef] [PubMed]
- Rogge, M.D.; Leckey, C.A. Characterization of Impact Damage in Composite Laminates Using Guided Wavefield Imaging and Local Wavenumber Domain Analysis. Ultrasonics 2013, 53, 1217–1226. [Google Scholar] [CrossRef] [PubMed]
- Candès, J.E.; Michael, W.B. An Introduction to Compressive Sensing. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Li, X.; Lan, X.; Yang, M.; Xue, J.; Zheng, N. Efficient Lossy Compression for Compressive Sensing Acquisition of Images in Compressive Sensing Imaging Systems. Sensors 2014, 14, 23398–23418. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Amin, M.G.; Ahmad, F.; Hoorfar, A.; Smith, G.E. Ultrawideband impulse radar through-the-wall imaging with compressive sensing. Int. J. Antennas Propag. 2012, 2012, 1–11. [Google Scholar] [CrossRef]
- Shen, F.; Zhao, G.; Shi, G.; Dong, W.; Wang, C.; Niu, Y. Compressive SAR Imaging with Joint Sparsity and Local Similarity Exploitation. Sensors 2015, 15, 4176–4192. [Google Scholar] [CrossRef] [PubMed]
- Van den Berg, E.; Friedlander, M.P. Probing the Pareto frontier for basis pursuit solutions. SIAM J. Sci. Comput. 2008, 31, 890–912. [Google Scholar] [CrossRef]
- Becker, S.; Bobin, J.; Candès, E.J. NESTA: A Fast and Accurate First-Order Method for Sparse Recovery. SIAM J. Imaging Sci. 2011, 4, 1–39. [Google Scholar] [CrossRef]
- Moghadam, A.; Radha, H. Complex Sparse Projections for Compressed Sensing. In Proceedings of the 44th Annual Conference on Information Sciences and Systems (CISS 2010), Princeton, NJ, USA, 17–19 March 2010; pp. 1–6.
- Anselmi, N.; Oliveri, G.; Massa, A. A Total Variation Compressive Sensing Technique for Imaging Large Scatterers. In Proceedings of the 2015 IEEE European Conference on Antennas and Propagation (EUCAP 2014), The Hague, The Netherlands, 6–12 April 2014; pp. 1514–1518.
- Rodriguez-Vaqueiro, Y.; Alvarez, Y.; Gonzalez-Valdes, B.; Martinez-Lorenzo, J.A.; Las-Heras, F.; Rappaport, C.M. On the Use of Compressed Sensing Techniques for Improving Multistatic Millimeter-Wave Portal-Based Personnel Screening. IEEE Trans. Antennas Propag. 2014, 62, 494–499. [Google Scholar] [CrossRef]
- Comsol Multiphysics. Available online: www.comsol.com (accessed on 2 October 2016).
- Gonzalez-Valdes, B.; Allan, G.; Rodriguez-Vaqueiro, Y.; Alvarez, Y.; Mantzavinos, S.; Nickerson, M.; Berkowitz, B.; Martinez-Lorenzo, J.A.; Las-Heras, F.; Rappaport, C.M. Sparse array optimization using simulated annealing and compressed sensing for near-field millimeter wave imaging. IEEE Trans. Antennas Propag. 2014, 62, 1716–1722. [Google Scholar] [CrossRef]

© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
López, Y.Á.; Lorenzo, J.Á.M. Compressed Sensing Techniques Applied to Ultrasonic Imaging of Cargo Containers. Sensors 2017, 17, 162. https://doi.org/10.3390/s17010162
López YÁ, Lorenzo JÁM. Compressed Sensing Techniques Applied to Ultrasonic Imaging of Cargo Containers. Sensors. 2017; 17(1):162. https://doi.org/10.3390/s17010162
Chicago/Turabian StyleLópez, Yuri Álvarez, and José Ángel Martínez Lorenzo. 2017. "Compressed Sensing Techniques Applied to Ultrasonic Imaging of Cargo Containers" Sensors 17, no. 1: 162. https://doi.org/10.3390/s17010162
APA StyleLópez, Y. Á., & Lorenzo, J. Á. M. (2017). Compressed Sensing Techniques Applied to Ultrasonic Imaging of Cargo Containers. Sensors, 17(1), 162. https://doi.org/10.3390/s17010162





