Optimization of the Coverage and Accuracy of an Indoor Positioning System with a Variable Number of Sensors
Abstract
:1. Introduction
- The multi-objective optimization of different metrics from the CRLB: Most of the related work deals with the determinant of the FIM. This metric is related to the volume of the error ellipsoid. However, an elongated ellipsoid may result in a small volume, whereas the error in the major axis is high.
- We do not constrain the position of the sensors.
- The consideration of obstacles that can cause occlusions to NLOS sensors: we must therefore maximize the coverage of the ROI.
- The number of sensors can vary within an interval. Searching solutions with high accuracy, but a low amount of sensors is also an objective.
- Since we optimize conflicting objectives, we obtain a set of Pareto optimal solutions. We find this to be the greatest advantage of multi-objective optimization, since we obtain every optimal solution and know the values of the objectives. This information can be used by the resource manager according to the current needs and availability. To the best of our knowledge, there are not any other researchers that address the sensor placement problem for localization this way. A comprehensive review of multi-objective optimization applied to sensor networks was recently published [31]. Most of the works referenced in the survey focus on sensor deployment for optimizing coverage and energy management, and those that deal with target tracking just address the sensor scheduling problem [32,33].
2. Problem Statement
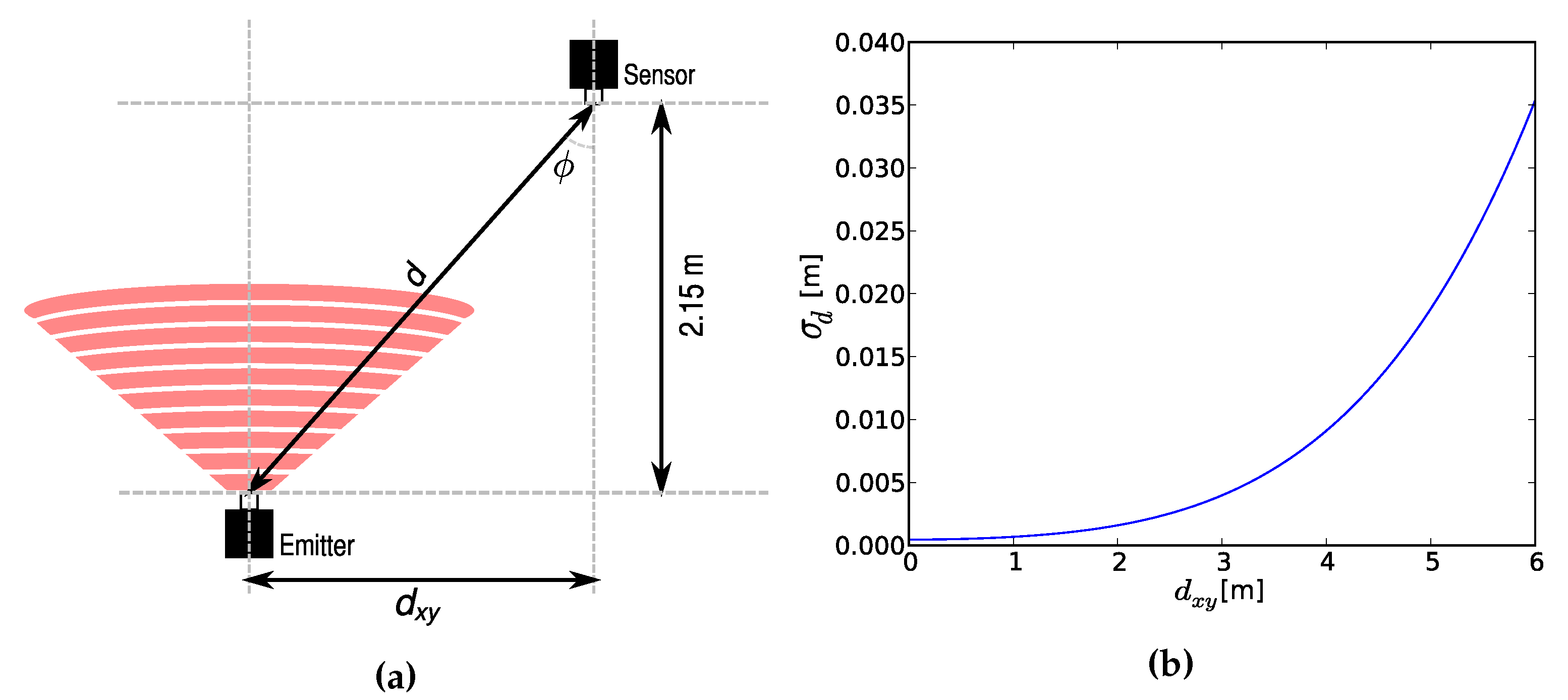
2.1. Position Estimation
2.2. Sensor Placement
2.2.1. Accuracy Objectives
2.2.2. Coverage Objective
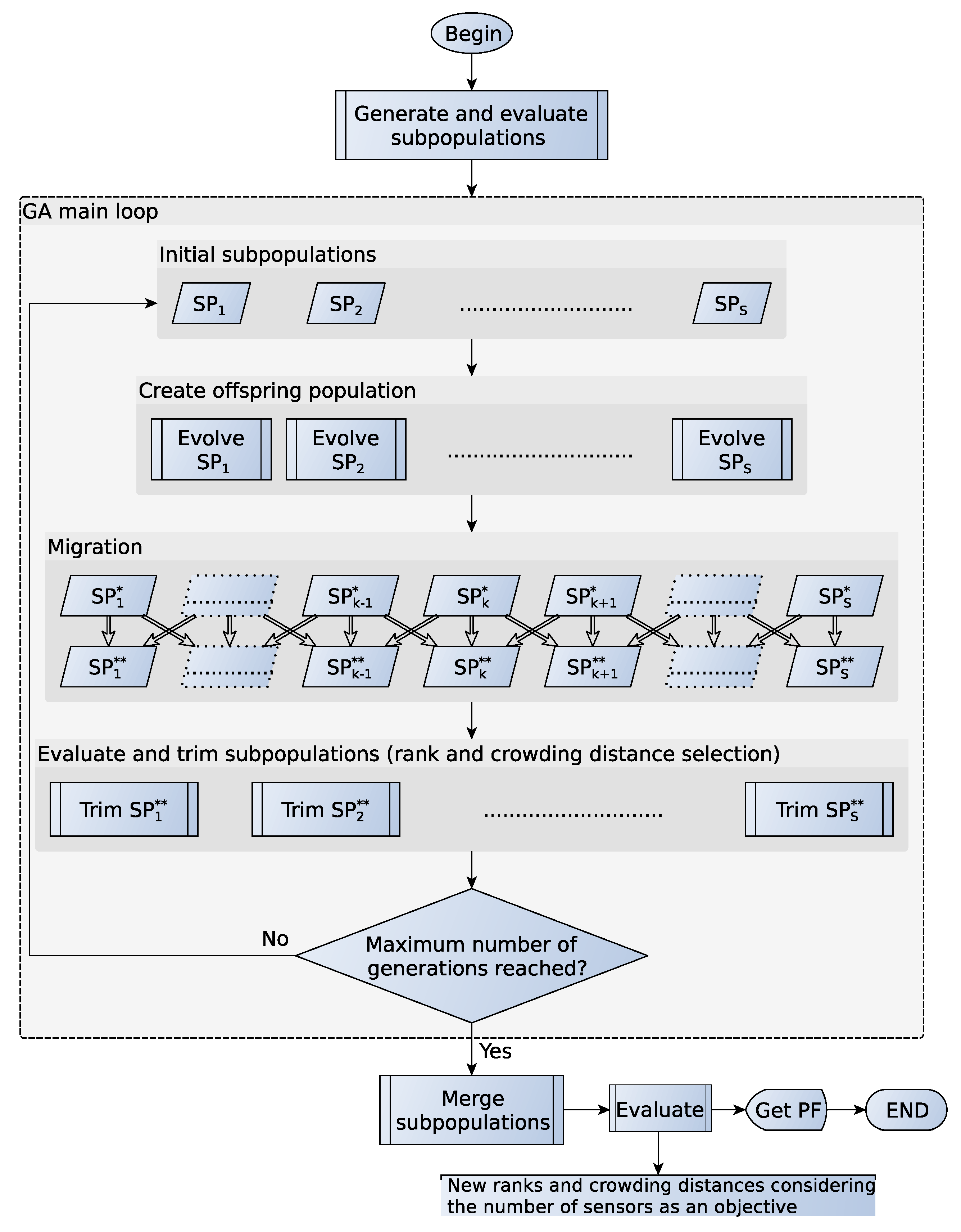
3. Proposed Algorithm
- : initial population. Population size: .
- : evolved population, the initial population and its offspring. It can contain individuals with different number of sensors. Population size: .
- : evolved population without individuals with different numbers of sensors. Population size varies among subpopulations.
- Trimmed : best individuals of according to NSGA-II selection; i.e., non-dominance rank and crowding distance. It becomes the initial population in the next GA iteration. The size of the population is .
- Selection: tournament selection of two individuals. It selects individuals, which will be the parents of the offspring subpopulation. Two individuals are picked randomly among the initial subpopulation. The method checks first the non-dominance rank of each individual and selects the best one; in case they belong to the same front, it chooses the one with the higher crowding distance.
- Crossover: blend crossover. For each consecutive pair of two parents ( and ) of the list given by the previous step, there is an chance of generating two new individuals ( and ) that replace the parents; otherwise, they remain unchanged. Equation (10) gives the new individuals:In our case, and are the coordinates of each sensor of the individual in a consecutive array. The variable α is a vector of random elements with the same length of , and it takes random values in the range . The operator ∘ is the Hadamard (element-wise) product. The offspring can therefore be in the expanded cuboid formed by the parents. In case any sensor falls into any obstacle, the algorithm sends them to the nearer corner, so that they cover a bigger space without altering their position too much.
- Mutation: Gaussian mutation. There is an chance that an individual undergoes mutation. If mutated, a random variable is added to each gene of the individual; i.e., to a coordinate. We perform again the same procedure if the sensor falls into an obstacle.
- Structural mutation: at a given chance , a sensor can be added to or removed from the individual. If the individual belongs to the first or last subpopulation, we can only add or delete a sensor, respectively; otherwise, the operation is randomly selected. When deleting, we compute the number of sensors that are LOS with each other and delete the sensor with the higher value. When there are two or more sensors with the same number of LOS sensors, we compute the sum of the distance from each one of these sensors to its LOS neighbors. The sensor with the lower value is then removed. The sensor that is nearer to the others should be the sensor that adds less information, since very close sensors result in almost overlapping hyperboloids. This deletion mutation allows one to obtain a sensor placement scheme with less sensors without sacrificing a good deal of accuracy and coverage. On the other hand, when adding a new sensor, we compute the k-coverage level for each grid point; as defined in Section 2.2. We place the sensor in the point of the grid with the lowest k-coverage level; in case two or more grid points share the same value, we choose the one with the higher sum of the distances from the grid point to its LOS sensors.
4. Results
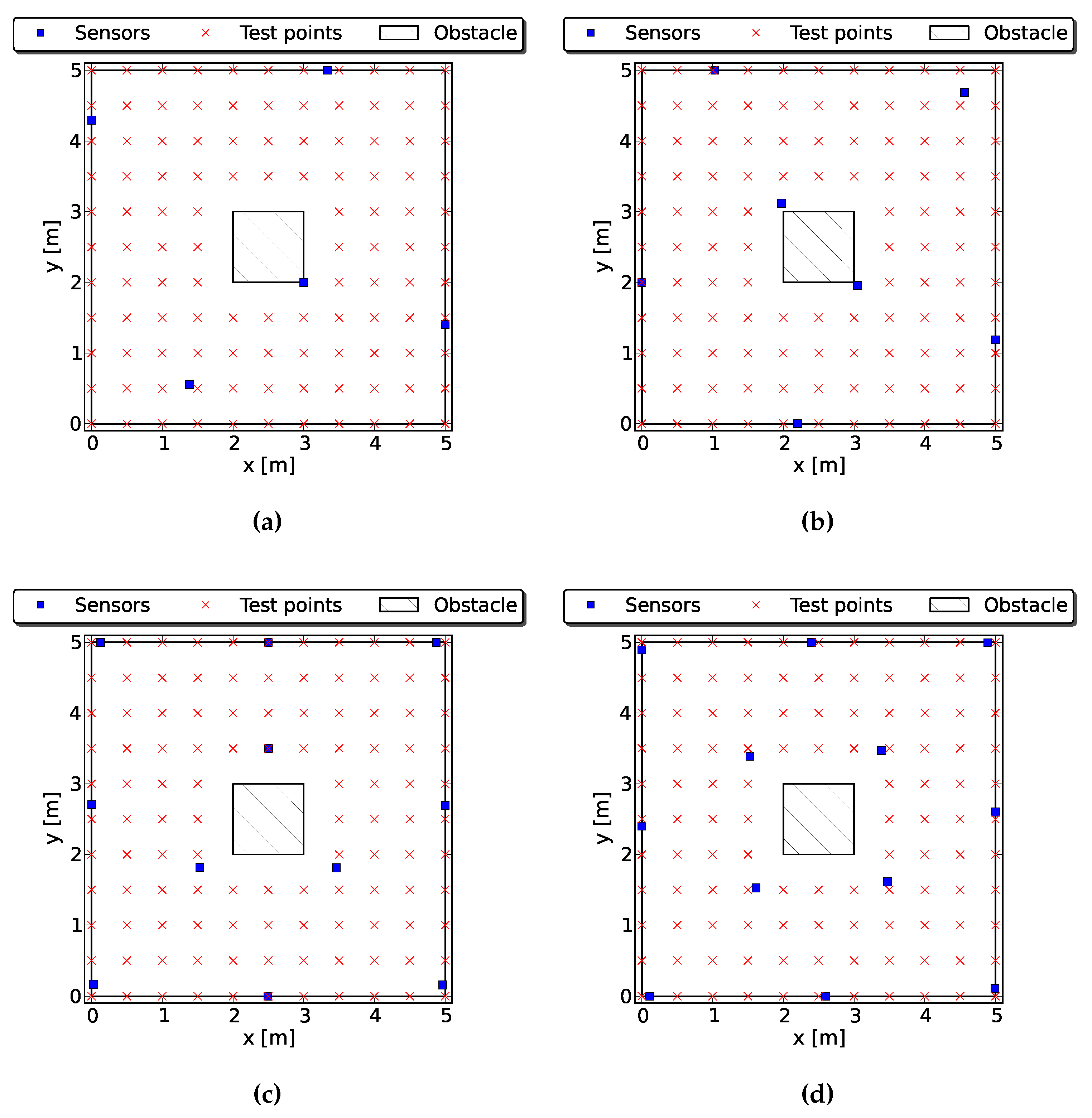
4.1. LOS Sensors
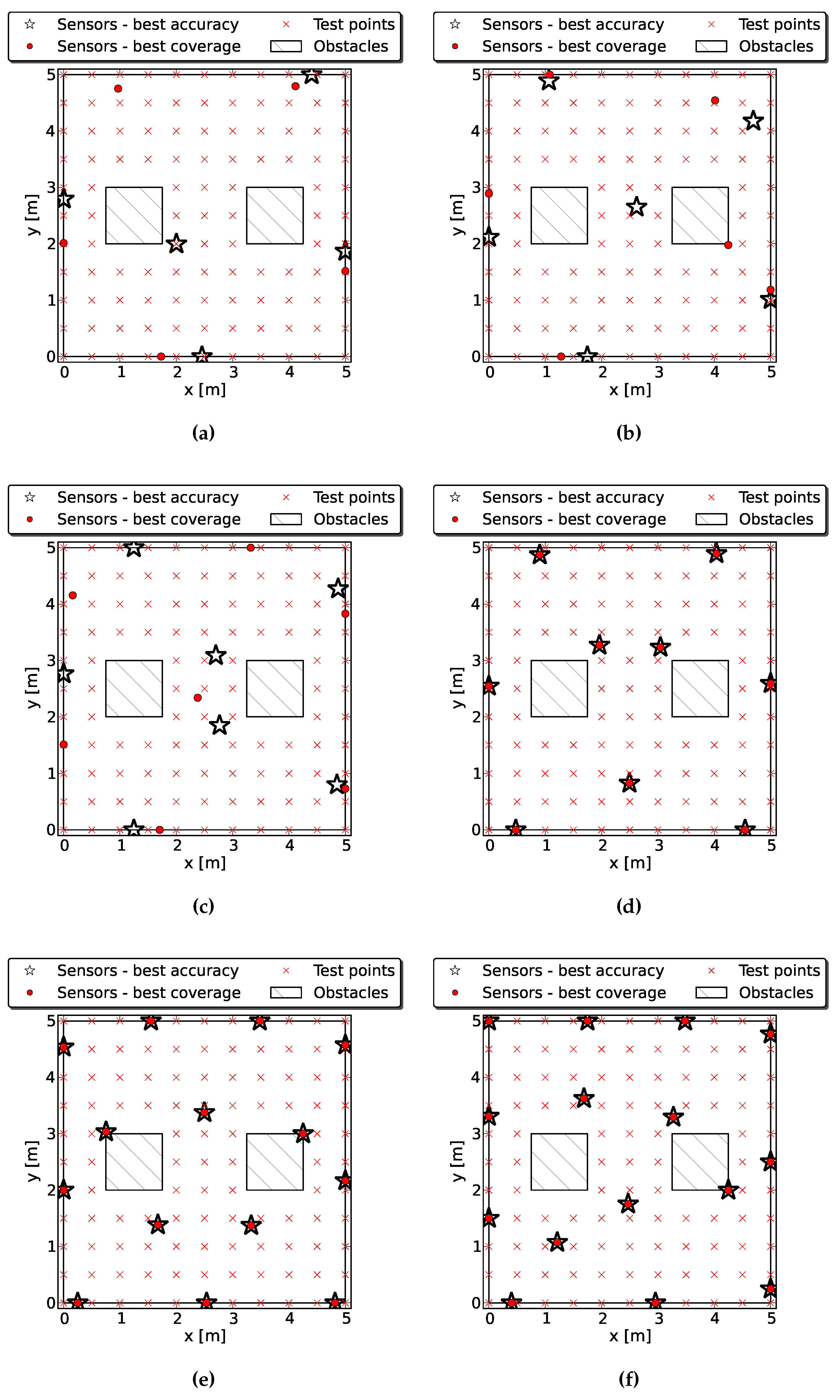
4.2. Occluded Sensors
4.2.1. Case 1: One Obstacle
4.2.2. Case 2: Two Obstacles
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liu, H.; Darabi, H.; Banerjee, P.; Liu, J. Survey of Wireless Indoor Positioning Techniques and Systems. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2007, 37, 1067–1080. [Google Scholar] [CrossRef]
- Kaune, R. Accuracy studies for TDOA and TOA localization. In Proceedings of the 15th International Conference on Information Fusion (FUSION 2012), Maui, HI, USA, 9–12 July 2012; pp. 408–415.
- Chen, Y.; Francisco, J.; Trappe, W.; Martin, R. A Practical Approach to Landmark Deployment for Indoor Localization. In Proceedings of the 3rd Annual IEEE Communications Society on Sensor and Ad Hoc Communications and Networks (SECON 2006), Reston, VA, USA, 25–28 September 2006; pp. 365–373.
- Han, G.; Zhang, C.; Shu, L.; Rodrigues, J.J.P.C. Impacts of Deployment Strategies on Localization Performance in Underwater Acoustic Sensor Networks. IEEE Trans. Ind. Electron. 2015, 62, 1725–1733. [Google Scholar] [CrossRef]
- Abel, J.S. Optimal sensor placement for passive source localization. In Proceedings of the 1990 International Conference on Acoustics, Speech, and Signal Processing (ICASSP 1990), Albuquerque, NM, USA, 3–6 April 1990; Volume 5, pp. 2927–2930.
- Carter, G.C. Variance bounds for passively locating an acoustic source with a symmetric line array. J. Acoust. Soc. Am. 1977, 62, 922. [Google Scholar] [CrossRef]
- Levanon, N. Lowest GDOP in 2-D scenarios. IEE Proc. Radar Sonar Navig. 2000, 147, 149–155. [Google Scholar] [CrossRef]
- Chaffee, J.; Abel, J. GDOP and the Cramer-Rao Bound. In Proceedings of the IEEE Position Location and Navigation Symposium, Las Vegas, NV, USA, 11–15 April 1994; pp. 663–668.
- Yang, B.; Scheuing, J. Cramer-Rao bound and optimum sensor array for source localization from time differences of arrival. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP 2005), Philadelphia, PA, USA, 18–23 March 2005.
- Lui, K.W.; So, H. A study of two-dimensional sensor placement using time-difference-of-arrival measurements. Digit. Signal Process. 2009, 19, 650–659. [Google Scholar] [CrossRef]
- Martínez, S.; Bullo, F. Optimal sensor placement and motion coordination for target tracking. Automatica 2006, 42, 661–668. [Google Scholar] [CrossRef]
- Bishop, A.N.; Fidan, B.; Anderson, B.; Doğançay, K.; Pathirana, P.N. Optimality analysis of sensor-target localization geometries. Automatica 2010, 46, 479–492. [Google Scholar] [CrossRef]
- Dogancay, K.; Hmam, H. On optimal sensor placement for time-difference-of-arrival localization utilizing uncertainty minimization. In Proceedings of the 17th European Signal Processing Conference, Glasgow, UK, 24–28 August 2009; pp. 1136–1140.
- Meng, W.; Xie, L.; Xiao, W. Optimality Analysis of Sensor-Source Geometries in Heterogeneous Sensor Networks. IEEE Trans. Wirel. Commun. 2013, 12, 1958–1967. [Google Scholar] [CrossRef]
- Isaacs, J.T.; Klein, D.J.; Hespanha, J.P. Optimal sensor placement for time difference of arrival localization. In Proceedings of the 48h IEEE Conference on Decision and Control (CDC) Held Jointly with 2009 28th Chinese Control Conference, Shanghai, China, 16–18 December 2009; pp. 7878–7884.
- Ho, K.; Vicente, L. Sensor Allocation for Source Localization with Decoupled Range and Bearing Estimation. IEEE Trans. Signal Process. 2008, 56, 5773–5789. [Google Scholar] [CrossRef]
- Moreno-Salinas, D.; Pascoal, A.; Aranda, J. Optimal Sensor Placement for Multiple Target Positioning with Range-Only Measurements in Two-Dimensional Scenarios. Sensors 2013, 13, 10674–10710. [Google Scholar] [CrossRef] [PubMed]
- Neering, J.; Bordier, M.; Maizi, N. Optimal passive source localization. In Proceedings of the International Conference on Sensor Technologies and Applications (SensorComm 2007), Valencia, Spain, 14–20 October 2007; pp. 295–300.
- Jourdan, D.B.; Roy, N. Optimal sensor placement for agent localization. ACM Trans. Sens. Netw. 2008, 4, 1–40. [Google Scholar] [CrossRef]
- Jourdan, D.B.; Dardari, D.; Win, M.Z. Position error bound for UWB localization in dense cluttered environments. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 613–628. [Google Scholar] [CrossRef]
- Perez-Ramirez, J.; Borah, D.; Voelz, D. Optimal 3-D Landmark Placement for Vehicle Localization Using Heterogeneous Sensors. IEEE Trans. Veh. Technol. 2013, 62, 2987–2999. [Google Scholar] [CrossRef]
- Joshi, S.; Boyd, S. Sensor Selection via Convex Optimization. IEEE Trans. Signal Process. 2009, 57, 451–462. [Google Scholar] [CrossRef]
- Chepuri, S.P.; Leus, G. Sparsity-Promoting Sensor Selection for Non-Linear Measurement Models. IEEE Trans. Signal Process. 2015, 63, 684–698. [Google Scholar] [CrossRef]
- Krause, A.; Singh, A.; Guestrin, C. Near-Optimal Sensor Placements in Gaussian Processes: Theory, Efficient Algorithms and Empirical Studies. J. Mach. Learn. Res. 2008, 9, 235–284. [Google Scholar]
- Shamaiah, M.; Banerjee, S.; Vikalo, H. Greedy sensor selection: Leveraging submodularity. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC 2010), Atlanta, GA, USA, 15–17 December 2010; pp. 2572–2577.
- Rao, S.; Chepuri, S.P.; Leus, G. Greedy sensor selection for non-linear models. In Proceedings of the IEEE 6th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP 2015), Cancun, Mexico, 13–16 December 2015; pp. 241–244.
- Chaudhry, S.B.; Hung, V.C.; Guha, R.K.; Stanley, K.O. Pareto-based evolutionary computational approach for wireless sensor placement. Eng. Appl. Artif. Intell. 2011, 24, 409–425. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Domingo-Perez, F.; Lazaro-Galilea, J.L.; Wieser, A.; Martin-Gorostiza, E.; Salido-Monzu, D.; Llana, A.D.L. Sensor placement determination for range-difference positioning using evolutionary multi-objective optimization. Expert Syst. Appl. 2016, 47, 95–105. [Google Scholar] [CrossRef]
- Domingo-Perez, F.; Lazaro-Galilea, J.L.; Martin-Gorostiza, E.; Salido-Monzu, D.; Wieser, A. Evolutionary optimization of sensor deployment for an indoor positioning system with unknown number of anchors. In Proceedings of the Ubiquitous Positioning Indoor Navigation and Location Based Service (UPINLBS 2014), Corpus Christi, TX, USA, 20–21 November 2014; pp. 195–202.
- Iqbal, M.; Naeem, M.; Anpalagan, A.; Ahmed, A.; Azam, M. Wireless Sensor Network Optimization: Multi-Objective Paradigm. Sensors 2015, 15, 17572–17620. [Google Scholar] [CrossRef] [PubMed]
- Cao, N.; Masazade, E.; Varshney, P.K. A multiobjective optimization based sensor selection method for target tracking in Wireless Sensor Networks. In Proceedings of the 16th International Conference on Information Fusion (FUSION 2013), Istanbul, Turkey, 9–12 July 2013; pp. 974–980.
- Hu, X.; Bao, M.; Hu, Y.H.; Xu, B. Energy Balanced Scheduling for Target Tracking with Distance-Dependent Measurement Noise in a WSN. Int. J. Distrib. Sens. Netw. 2013, 2013, 1–12. [Google Scholar] [CrossRef]
- So, H.C. Source localization: algorithms and analysis. In Handbook of Position Location. Theory, Practice and Advances; Zekavat, R., Buehrer, R.M., Eds.; Wiley-IEEE Press: Piscataway, NJ, USA, 2011; pp. 25–66. [Google Scholar]
- Wieser, A. Reliability checking for GNSS baseline and network processing. GPS Solut. 2004, 8, 55–66. [Google Scholar] [CrossRef]
- Yan, J.; Tiberius, C.C.J.M.; Janssen, G.J.M.; Teunissen, P.J.G.; Bellusci, G. Review of range-based positioning algorithms. IEEE Aerosp. Electron. Syst. Mag. 2013, 28, 2–27. [Google Scholar] [CrossRef]
- Kay, S. Fundamentals of Statistical Signal Processing: Estimation Theory; Prentice-Hall PTR: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Chan, Y.; Ho, K. A simple and efficient estimator for hyperbolic location. IEEE Trans. Signal Process. 1994, 42, 1905–1915. [Google Scholar] [CrossRef]
- Yang, C.; Kaplan, L.; Blasch, E. Performance Measures of Covariance and Information Matrices in Resource Management for Target State Estimation. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2594–2613. [Google Scholar] [CrossRef]
- Fortin, F.A.; De Rainville, F.M.; Gardner, M.A.; Parizeau, M.; Gagné, C. DEAP: Evolutionary Algorithms Made Easy. J. Mach. Learn. Res. 2012, 13, 2171–2175. [Google Scholar]
- Adra, S.F.; Fleming, P.J. Diversity management in evolutionary many-objective optimization. IEEE Trans. Evol. Comput. 2011, 15, 183–195. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Garza-Fabre, M.; Toscano-Pulido, G.; Coello, C.A.C.; Rodriguez-Tello, E. Effective ranking + speciation = many-objective optimization. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC 2011), New Orleans, LA, USA, 5–8 June 2011; pp. 2115–2122.
- Gorostiza, E.M.; Galilea, J.L.L.; Meca, F.J.M.; Monzú, D.S.; Zapata, F.E.; Puerto, L.P. Infrared Sensor System for Mobile-Robot Positioning in Intelligent Spaces. Sensors 2011, 11, 5416–5438. [Google Scholar] [CrossRef] [PubMed]
- Martin-Gorostiza, E.; Meca-Meca, F.; Lazaro-Galilea, J.; Salido-Monzu, D.; Martos-Naya, E.; Wieser, A. Infrared local positioning system using phase differences. In Proceedings of the Ubiquitous Positioning Indoor Navigation and Location Based Service (UPINLBS 2014), Corpus Christi, TX, USA, 20–21 November 2014; pp. 238–247.

| Operator | Symbol | Probability |
|---|---|---|
| Crossover | 0.80 | |
| Mutation | 0.10 | |
| Structural mutation | 0.05 |
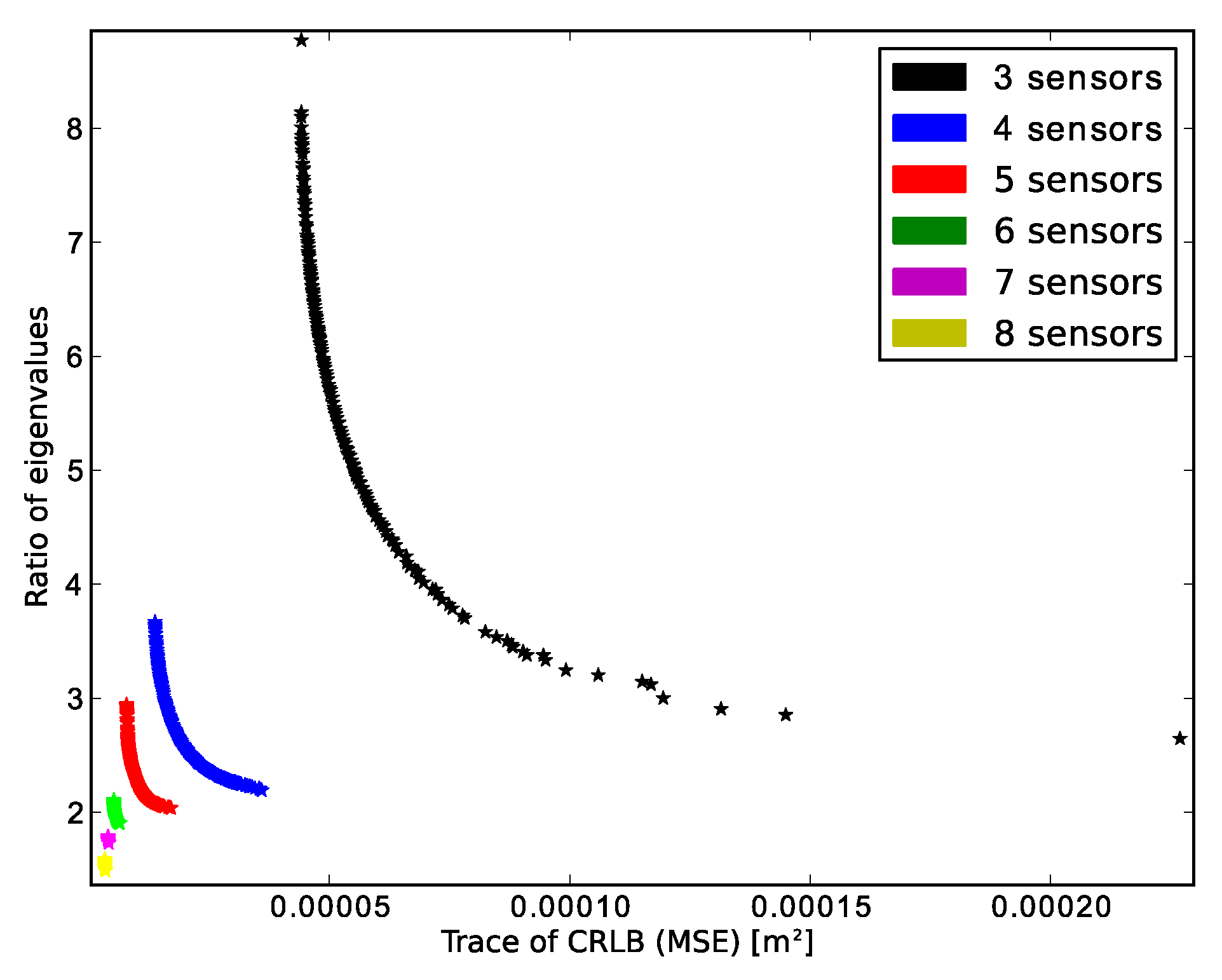
| Algorithm | Amount of Sensors | Amount of Solutions | Lowest CRLB Trace (m2) | Lowest Ratio of Eigenvalues |
|---|---|---|---|---|
| NSGA-II | 3 | 573 | 4.4085e−5 | 2.0723 |
| 4 | 9 | 1.7882e−5 | 2.4111 | |
| 5 | 3 | 8.2704e−6 | 2.6833 | |
| 6 | 7 | 5.2845e−6 | 1.997 | |
| 7 | 4 | 4.117e−6 | 1.8098 | |
| 8 | 4 | 3.3222e−6 | 1.5838 | |
| Proposed algorithm | 3 | 100 | 4.4083e−5 | 2.0397 |
| 4 | 100 | 1.3753e−6 | 2.2331 | |
| 5 | 100 | 7.8631e−6 | 1.9624 | |
| 6 | 100 | 5.2156e−6 | 1.9014 | |
| 7 | 100 | 4.0213e−6 | 1.7361 | |
| 8 | 100 | 3.3117e−6 | 1.5749 |
| Amount of Sensors | Proposed Algorithm | Random Deployment | ||
|---|---|---|---|---|
| CRLB Trace (m2) | Coverage | CRLB Trace (m2) | Coverage | |
| 5 | 9.5475e−5 | 1 | 2.1418 | 0.9116 |
| 6 | 4.1925e−5 | 1 | 0.5002 | 0.9552 |
| 7 | 2.1706e−5 | 1 | 0.5471 | 0.992 |
| 8 | 1.2324e−5 | 1 | 0.0382 | 0.9875 |
| 9 | 9.4244e−6 | 1 | 2.3467e−4 | 0.9989 |
| 10 | 6.9933e−6 | 1 | 1.5574e−4 | 0.9989 |
| 11 | 5.7051e−6 | 1 | 1.1498e−4 | 0.9996 |
| 12 | 4.7841e−6 | 1 | 6.4065e−4 | 0.9998 |
| Amount of Sensors | Worst Pareto Values with Proposed Algorithm | Random Deployment | ||
|---|---|---|---|---|
| CRLB Trace (m2) | Coverage | CRLB Trace (m2) | Coverage | |
| 5 | 2.0486e−4 | 0.7523 | 0.2175 | 0.7593 |
| 6 | 9.2725e−5 | 0.9817 | 0.5072 | 0.8930 |
| 7 | 3.2163e−5 | 0.9817 | 0.0178 | 0.9349 |
| 8 | 1.5879e−5 | 1 | 0.0123 | 0.9624 |
| 9 | 1.2524e−5 | 1 | 0.009 | 0.9679 |
| 10 | 9.4426e−6 | 1 | 2.9721 | 0.9811 |
| 11 | 7.0657e−6 | 1 | 0.3861 | 0.9868 |
| 12 | 5.8686e−6 | 1 | 8.2985e−4 | 0.9910 |
| 13 | 5.1978e−6 | 1 | 6.883e−3 | 0.9901 |
| 14 | 4.4578e−6 | 1 | 0.4218 | 0.9936 |
| 15 | 4.0501e−6 | 1 | 1.508e−4 | 0.9963 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Domingo-Perez, F.; Lazaro-Galilea, J.L.; Bravo, I.; Gardel, A.; Rodriguez, D. Optimization of the Coverage and Accuracy of an Indoor Positioning System with a Variable Number of Sensors. Sensors 2016, 16, 934. https://doi.org/10.3390/s16060934
Domingo-Perez F, Lazaro-Galilea JL, Bravo I, Gardel A, Rodriguez D. Optimization of the Coverage and Accuracy of an Indoor Positioning System with a Variable Number of Sensors. Sensors. 2016; 16(6):934. https://doi.org/10.3390/s16060934
Chicago/Turabian StyleDomingo-Perez, Francisco, Jose Luis Lazaro-Galilea, Ignacio Bravo, Alfredo Gardel, and David Rodriguez. 2016. "Optimization of the Coverage and Accuracy of an Indoor Positioning System with a Variable Number of Sensors" Sensors 16, no. 6: 934. https://doi.org/10.3390/s16060934
APA StyleDomingo-Perez, F., Lazaro-Galilea, J. L., Bravo, I., Gardel, A., & Rodriguez, D. (2016). Optimization of the Coverage and Accuracy of an Indoor Positioning System with a Variable Number of Sensors. Sensors, 16(6), 934. https://doi.org/10.3390/s16060934








