1. Introduction
Fire detection techniques play an important role in various areas by providing assistance to reduce the economic and ecological damage as well as casualties [
1,
2]. To avoid the excessive fire damage, sensor networks composed with cameras, flammable gas detectors, and temperature gauges have been implemented [
2,
3,
4,
5,
6]. Localizing the source is the main concern. Fire intensity and size during the fire also enable forecasting [
7,
8,
9,
10]. Richards
et al. used a zone model and exhaustive search with a black and white video camera to detect, locate and size accidental fires [
7,
8]. Xia
et al. applied a model of a dual-line gas sensor array to collect information on concentrations of gases emitted by the fire and to calculate the time delays of the signals received from various array elements [
3]. However, the localization results are easily affected by any obstructions present in the area of the fire place.
Nowadays, various methods based on temperature measurements have been proposed to locate fires as the temperature change is perhaps the most obvious sign when a fire occurs. The main research direction is that sensor arrays with four detectors are used to locate the fire source based on the time-delay estimation algorithm [
7]. One or two sensor arrays are adopted to calculate the distance between the fire source and the sensor array with far field algorithms [
5,
6], and near field algorithms [
11]. The proposed methods yield good results as long as the fire source is close to the sensor array. However, the reliability of the localization method may suffer in the case of a remote fire. Moreover, a large number of the sensor arrays are needed when the fire has to be monitored in a huge space. Thus it is difficult to overcome the limitations such as high construction costs, difficulty in installing signal-circuits, and difficulty in reducing measurement time when taking into consideration the temperature measurement with discrete sensors.
An optical fiber distributed temperature sensor (DTS) system is a kind of real-time and continuous monitoring space temperature field sensing technology [
12,
13]. The temperature profile can be derived based on the Raman backscattered light and the optical time-domain reflectometry (OTDR). The earliest example of distributed sensing with OTDR we could find is attributable to Dakin
et al. [
14]. A conventional optical fiber was used as the sensing element and the distributed sensor achieved a good spatial resolution of 3 m with sensor lengths up to 1 km. Numerous studies have been performed with the DTS, and a sensing distance >10 km has been achieved based on Raman backscattering [
15]. The DTS has been widely used in many areas due to its unique advantages, such as immunity to electromagnetic fields, easiness of installing wire, remote distributed measurement compared with the conventional temperature sensors [
16,
17,
18,
19,
20]. With an optical fiber as the sensing element, the DTS can realize temperature monitoring with long-distance and wide range, which solves the deficiency of the sensor arrays.
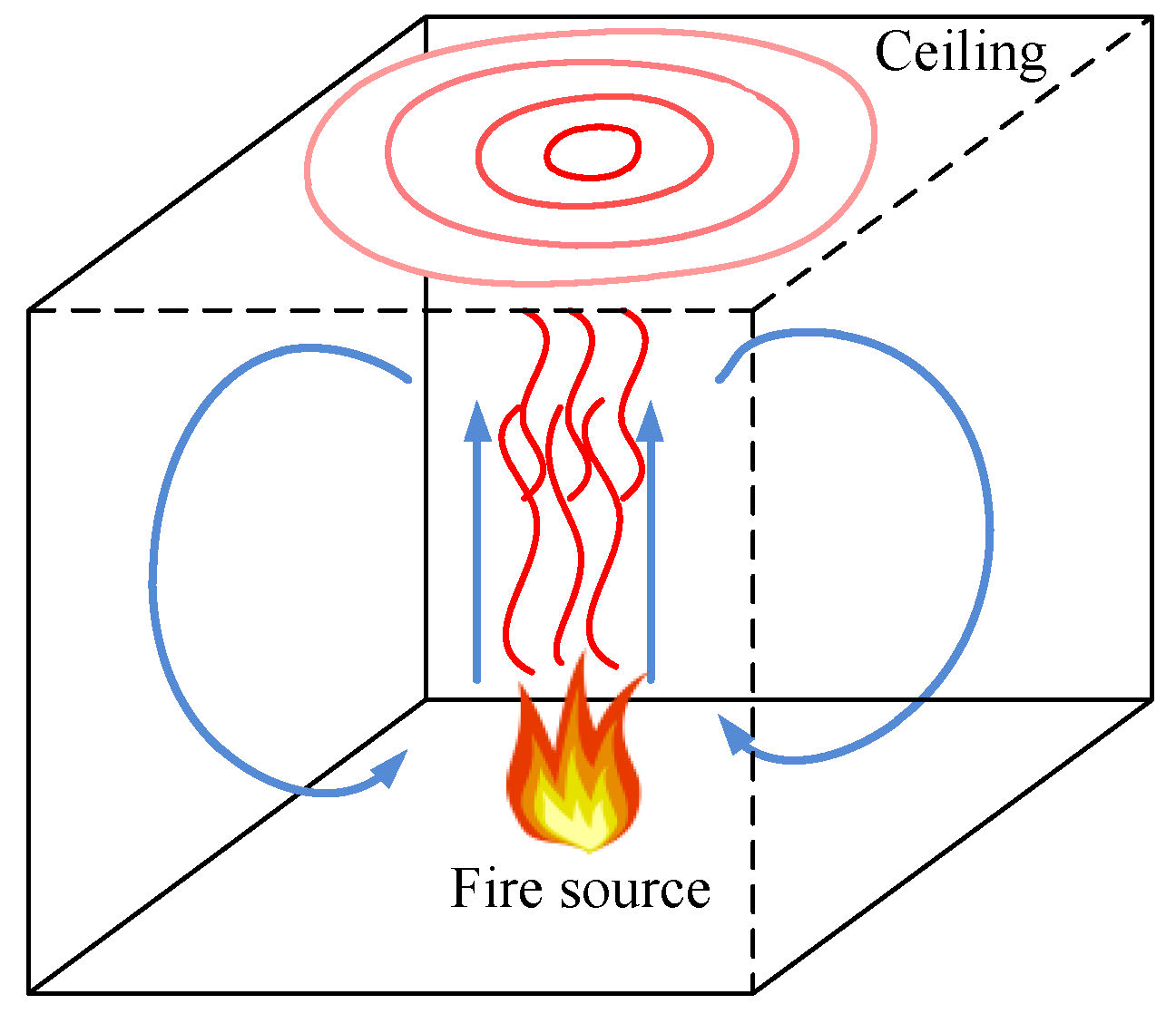
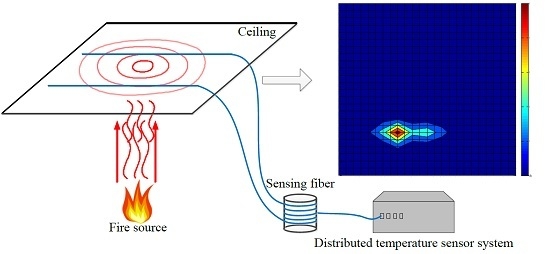
In this study, a novel method of fire source localization based on the DTS system is presented. Two parallel sections of multimode fiber are adopted as the sensing fiber. Hot gases are produced when the fire occurs in a closed room. The hot gases rise and propagate in a circular shape along the ceiling of the room. By analyzing the temperature changes measured with the DTS system, the localization of the fire source is examined theoretically. The experimental results show that the proposed method provides a reliable fire source location for long sensing ranges.
3. Experimental Setup
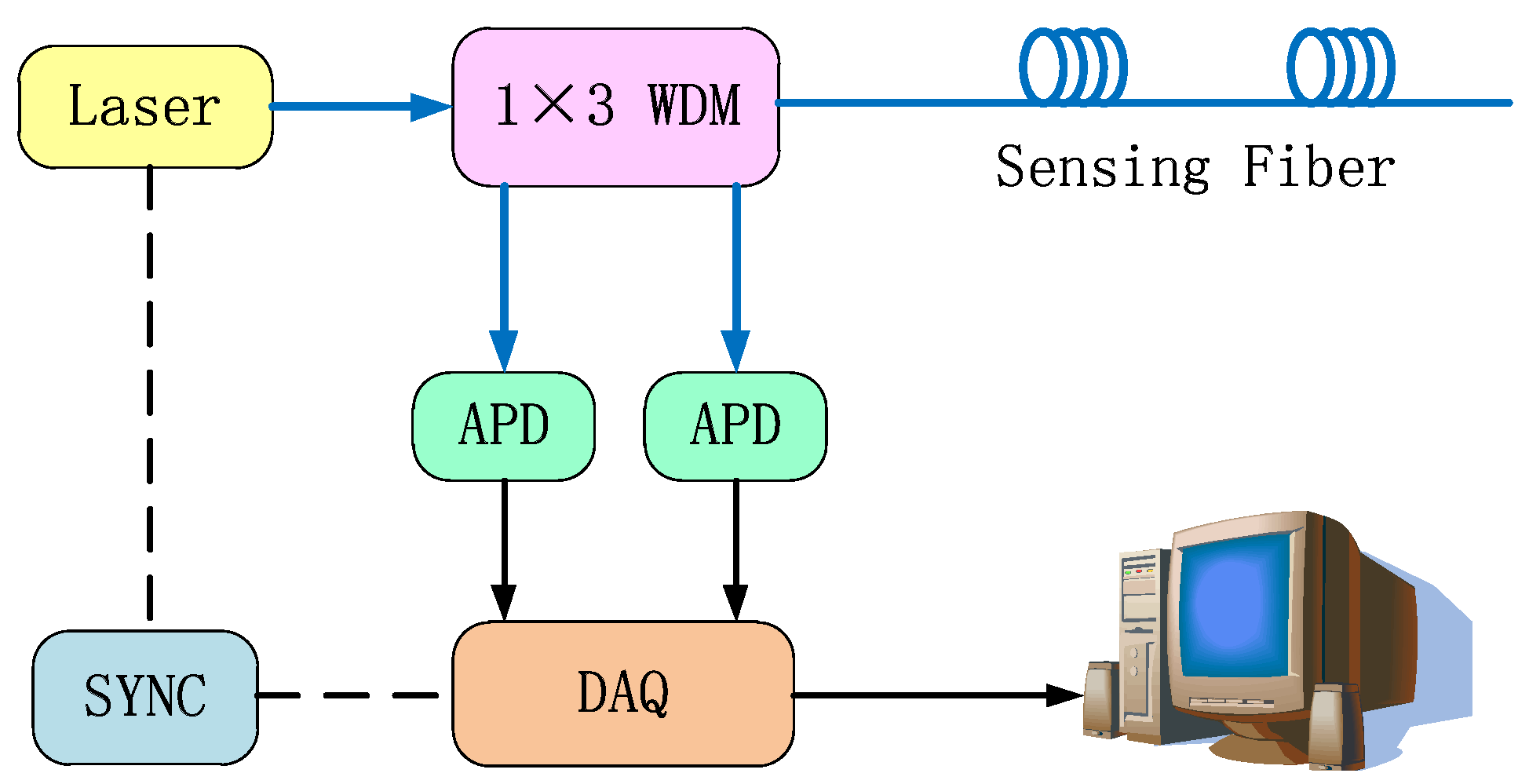
The schematic drawing of the DTS system is presented in
Figure 3. The short pulse of light from a pulsed fiber laser operating at 1550 nm with a maximum peak power of 30 W, 10 ns pulse width and 10 kHz repetition rate is injected into the optical sensing fiber through a 1 × 3 wavelength division multiplexer (WDM). Raman scattering occurs in the optical sensing fiber, and the backscattered Raman Stokes as well as the Raman anti-Stokes light passing through the WDM are injected into a high-performance InGaAs avalanche photodiode (APD). Using the APD, the Raman Stokes and anti-Stokes light are transformed into electrical signals. Then a high speed 100 MHz data acquisition card converts the analog signals to digital signals. Finally, the computer processes the digital signals and calculates the temperature data according to the theoretical analysis presented in
Section 2.1.
To verify the theoretical analysis fire source localization experiments were carried out in a laboratory in a simulated environment. The experimental setup is shown in
Figure 4. A tray of alcohol (11.0 cm × 8.0 cm × 2.1 cm) placed on a table (2.4 m × 1.2 m × 0.8 m) is used as the fire source. In the closed laboratory room, the hot gases rise to the ceiling and propagate under the ceiling. Then the hot gases flow down at the walls and flow back to the fire source origin near floor level. Thus there is a hot flue gas layer with a thickness of 100–300 mm beneath the ceiling if the fire source is located far away from the walls. In order to simplify the experiments, a heat insulation roof (2.4 m × 1.2 m × 0.05 m) supported by four pillars is placed 1 m above the table. This roof is placed parallel to the table and acts as the “ceiling” as discussed above in
Figure 1. The table, the four pillars and the ceiling form an open cabinet in the laboratory. If a fire occurs in the cabinet, the hot gases produced by the fire rise up to the heat insulation roof and propagate under the roof, forming a layer of the hot flue gases beneath the roof. Because the open cabinet is placed far away from the walls of the closed laboratory room, the hot gases propagating to the edge of the roof will continue to flow horizontally instead of flowing down when arriving at the room walls. There is no influence on the inner hot flue gas layer under the roof. As a result, the cabinet is employed to simulate a true situation of a fire with sensors placed far away from the edge of the roof. A standard multimode fiber with an attenuation of <0.3 dB/km at 1550 nm acts as the sensing fiber. The spatial resolution of the DTS system is limited to 2 m by the laser pulse width, APD bandwidth and the DAQ card sampling rate, which is much larger than the diameter of the fire source. An improvement of the spatial resolution is achieved by evenly winding the sensing fiber on bellows; the fiber length wound on every 100 cm bellow is 18 m. As a result, the spatial resolution of the DTS system is improved from 2 m to 11.11 cm. The bellows with the sensing fiber are placed just underneath the heat insulation roof with a distance of 50 mm, where the bellows are totally immersed in the hot flue gas layer. Thus the changes of the temperature can be measured with the DTS system in real-time.
4. Results and Discussion
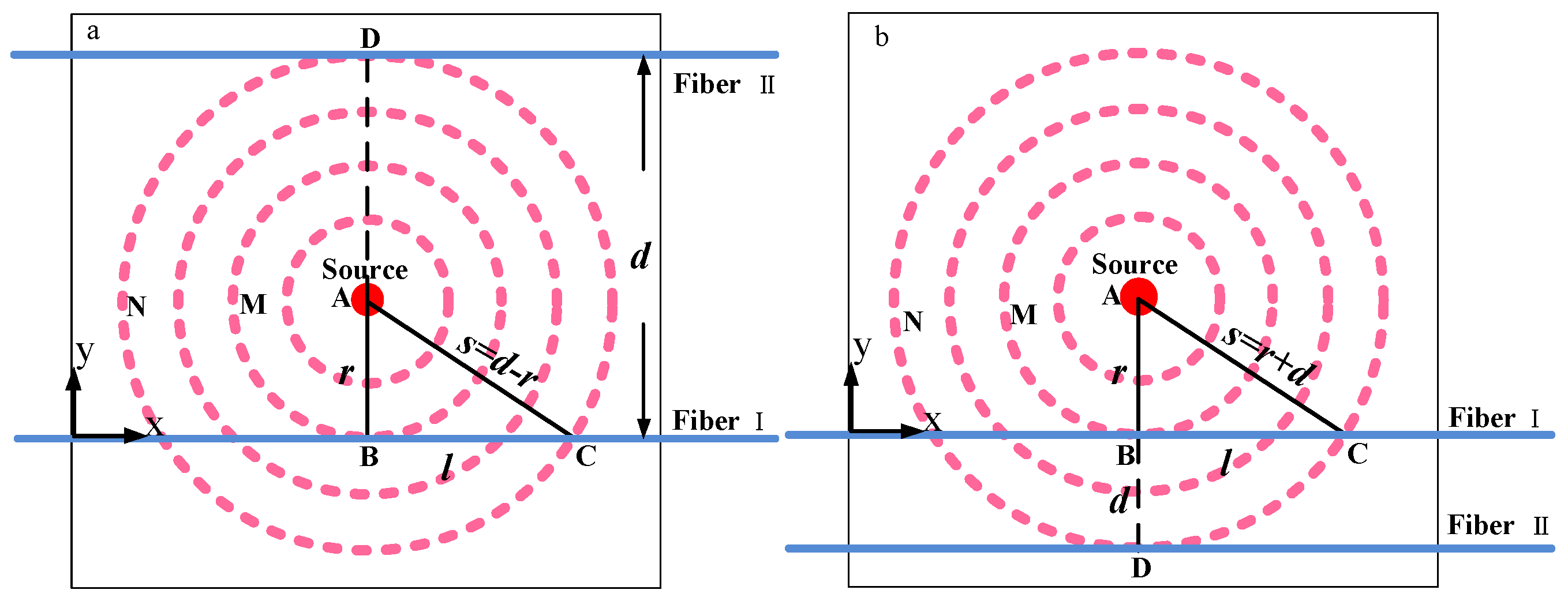
The two-dimensional plane coordinate system is shown in
Figure 4. The left endpoint of bellow I acts as the origin of coordinate system and the direction of bellow I is the horizontal axis while the distance between the fire source and bellow I corresponds to the ordinate y of the fire source. The two parallel fibers are placed on opposite sides of the alcohol tray as shown in
Figure 4a. The distance between the two parallel bellows is 80 cm and the coordinates of the alcohol tray center are (45 cm, 35 cm). On the contrary the two parallel fibers are placed but on the same side of the alcohol tray in
Figure 4b. The distance is 30 cm and the coordinates of the alcohol tray center are (45.5 cm, 32 cm).
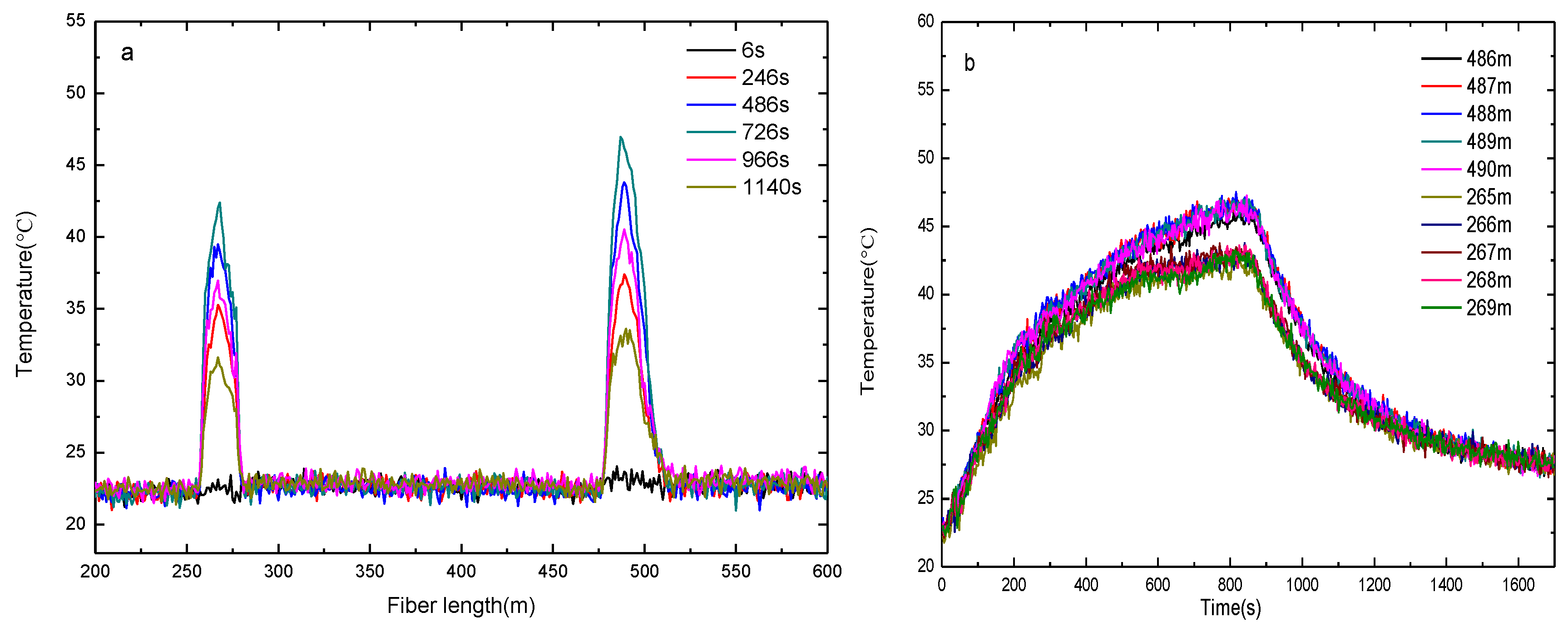
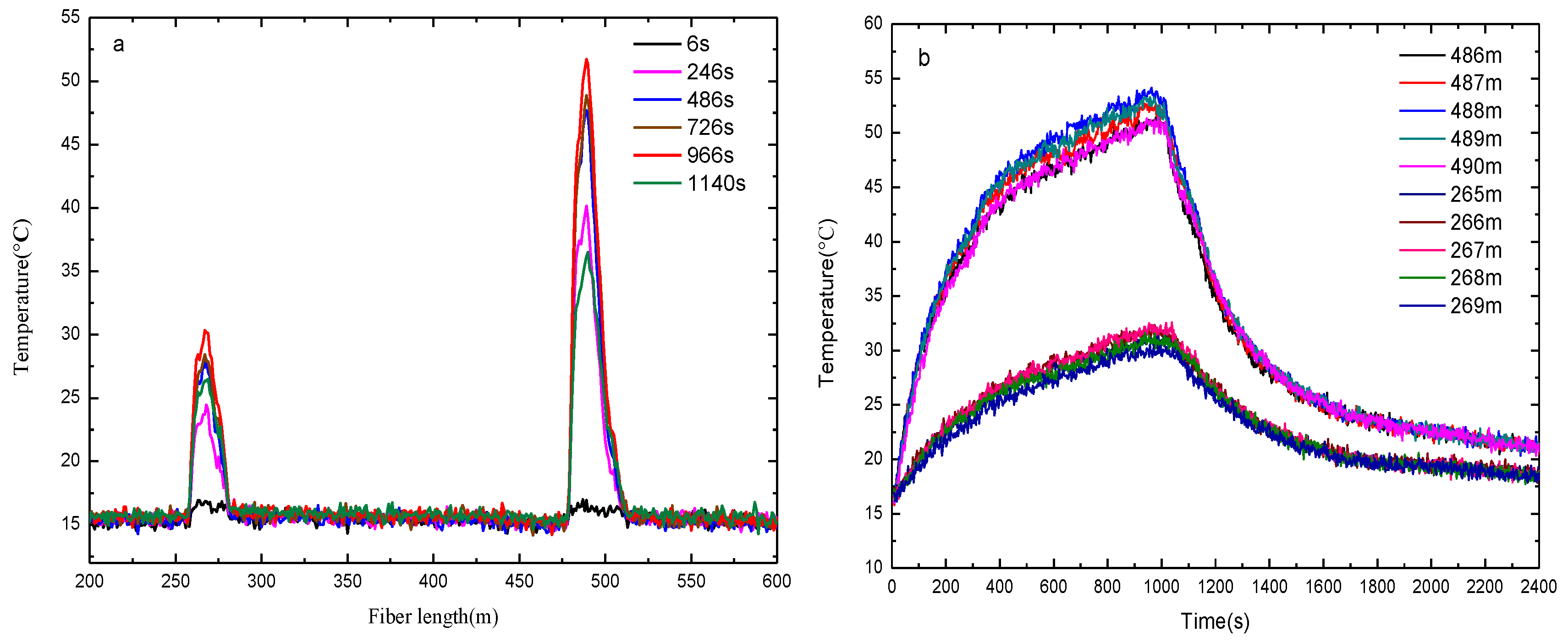
Figure 5 and
Figure 6 show the measured temperature by the DTS system when the alcohol is burning. The temperature measured by the fiber on bellow I is higher than the one recorded on bellow II, which indicates that the bellow I is nearer to the fire source. As shown in
Figure 5a and
Figure 6a, the length range of the sensing fiber winded on bellow I which records an increased temperature is 27 m (from 479 m to 506 m) and the one on the bellow II is 18 m (from 258 m to 276 m). The burning alcohol is a non-uniform heat source, and it cannot be seen as a point heat source. Moreover, some turbulence of the surrounding environment occurs in the process of measuring the temperature when the hot gases are rising to the heat insulation roof. Based on the above reasons, the position of the maximum temperature along the bellows is slightly varying during the measurement.
Figure 5b and
Figure 6b show the measured temperature recorded by the fibers wound on the two bellows with increasing burning time. The measured temperature increases fast at the early stage and the temperature rise rate of the fiber decreases gradually with the time increase. As shown in
Figure 5b and
Figure 6b, the temperature recorded by the fiber at lengths 486–490 m wound on bellow I is displayed. The temperature recorded at a fiber length of 488 m is the highest which corresponds to the closest location to the fire source. The location of the fiber at 488 m length on bellow I corresponds to x = 50 cm, which means that the fire source is located at 50 cm away. In the same way, the temperature curve recorded for fiber lengths of 266 m and 267 m almost coincides with the temperatures measured at 265–269 m. This corresponds to a length of bellow II between 44.4 cm and 50 cm,
i.e., the fire is located between 44.4 cm and 50 cm. Combining the above experimental results, the abscissa of the fire source is obtained as 44.4–50 cm,
i.e., its width is 5.6 cm and the maximum temperature position of the fire source is close to 50 cm.
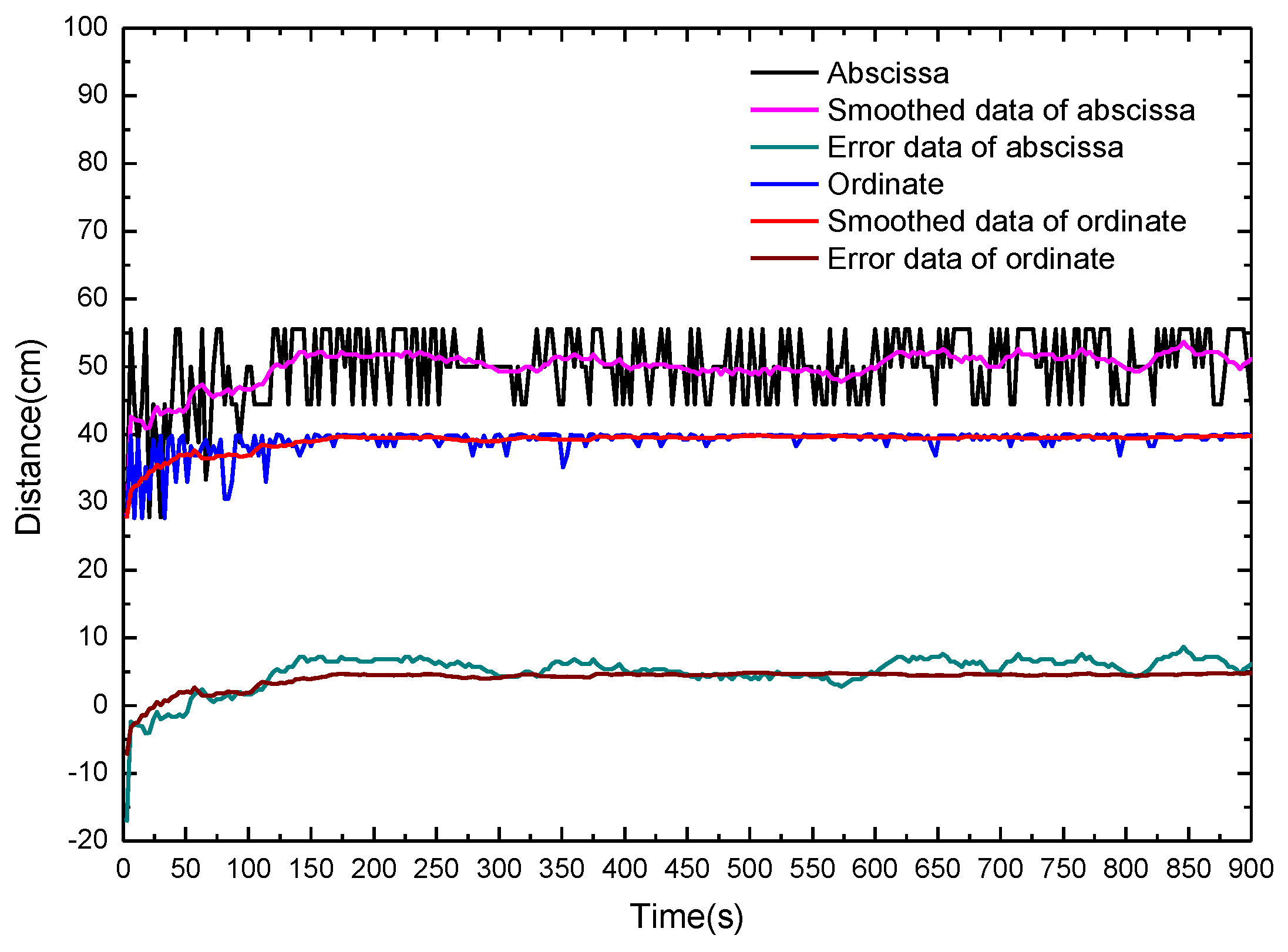
Figure 7 shows the calculated fire source location and the location errors with fibers on opposite sides of the fire source in dependence of the alcohol burning time. With the proposed method and the measured temperature maximum on bellow I, the abscissa x and ordinate y of the fire source can be determined. Obviously, the calculated abscissa x uncertainties are rather large during the whole measurement time. The main reason related to this phenomenon is that the fire source cannot be seen as a point fire source and the surrounding environment turbulence leads to the observed fluctuation of the calculated results. A moving average filter is adopted to overcome this problem. The smoothed distance fluctuations are significantly reduced compared with the original data. The corresponding errors of abscissa and ordinate positions after smoothing the data are shown in
Figure 7. The error ranges of the abscissa and ordinate of the fire source within the burning time 10 s to 60 s are (−4.09 cm, 2.04 cm) and (−2.60 cm, 2.09 cm), respectively. The position of the fire source is determined quickly with an acceptable error range.
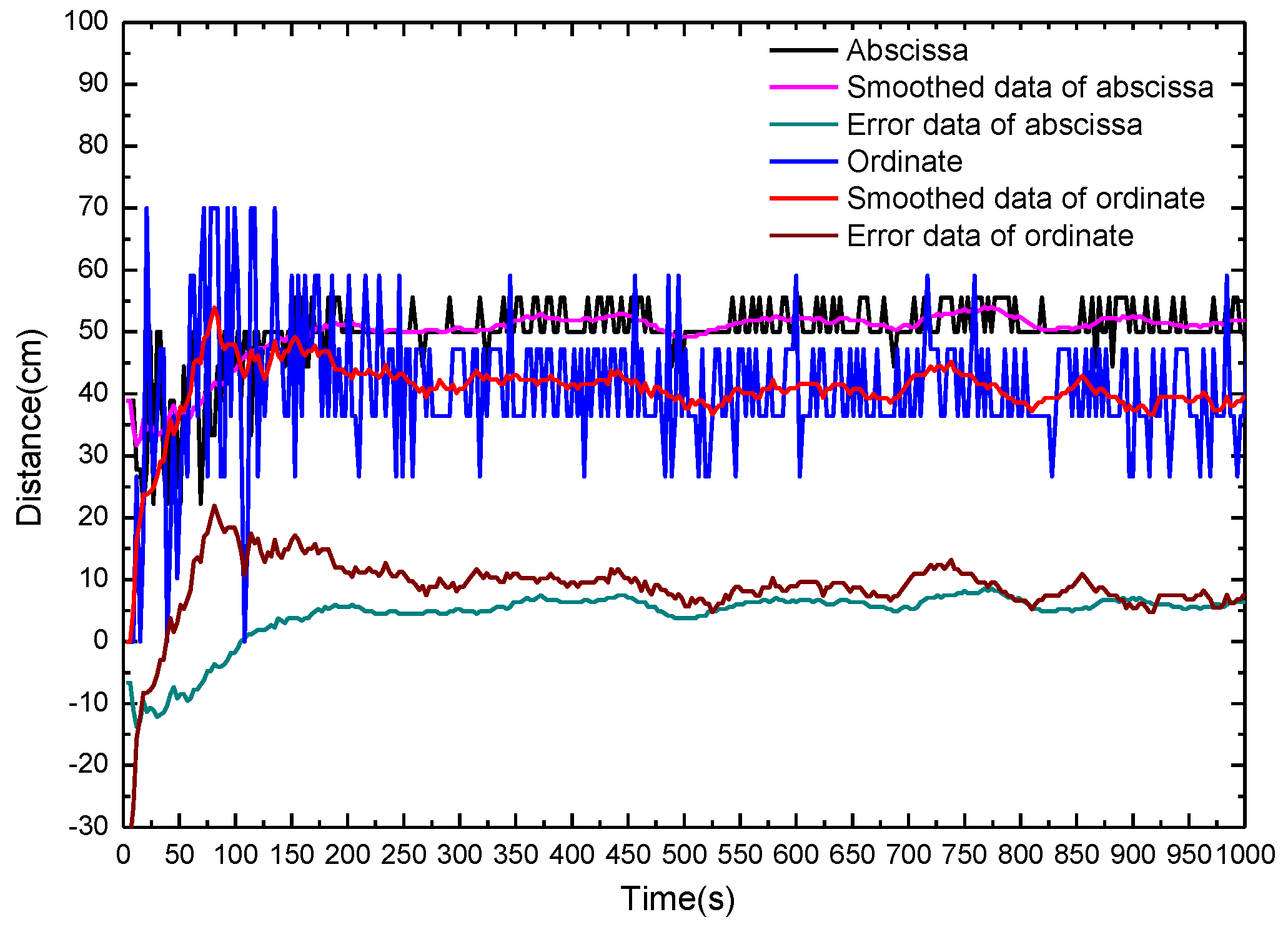
The calculated fire source location and the location errors with fibers on the same side of fire source in dependence of the alcohol burning time is shown in
Figure 8. The calculated ordinate y fluctuates intensely at the beginning of the fire, and gradually stabilizes after 3 min. According to the experimental conditions, thresholds of abscissa and ordinate are set as (0, 100) and (0, 70), respectively. If the calculated values are beyond the scope of the threshold value, the threshold value of minimum and maximum are used instead of the values below or above the threshold, respectively. The fluctuations are reduced evidently after the data are smoothed.
For fire burning times longer than 3 min, the errors of the calculated data are stable, and the maximum errors of the abscissa and ordinate of the fire source are 8.57 cm and 12.43 cm, respectively. Fire source localization determination with fibers on the same side of the fire source takes longer than that with fibers on opposite sides because that the area and flame of burning alcohol is so small that the heat generated at the early stage of alcohol burning stage is small. In addition, the heat flow of transmission can be blocked partly by bellow I. Since the wavefront of the hot gases has no longer a regular circular shape, the calculated position data fluctuate intensely. The measurement errors can be significantly reduced by improving the method of fire source localization and the DTS system such as employing an appropriate data processing method, optimizing thermal capacity of the sensing fiber, and so on. A further possibility for improvement of the accuracy and precision could consist in inserting a third sensing fiber orthogonal to the other two but on the cost of complexity and at higher cost of the whole system.
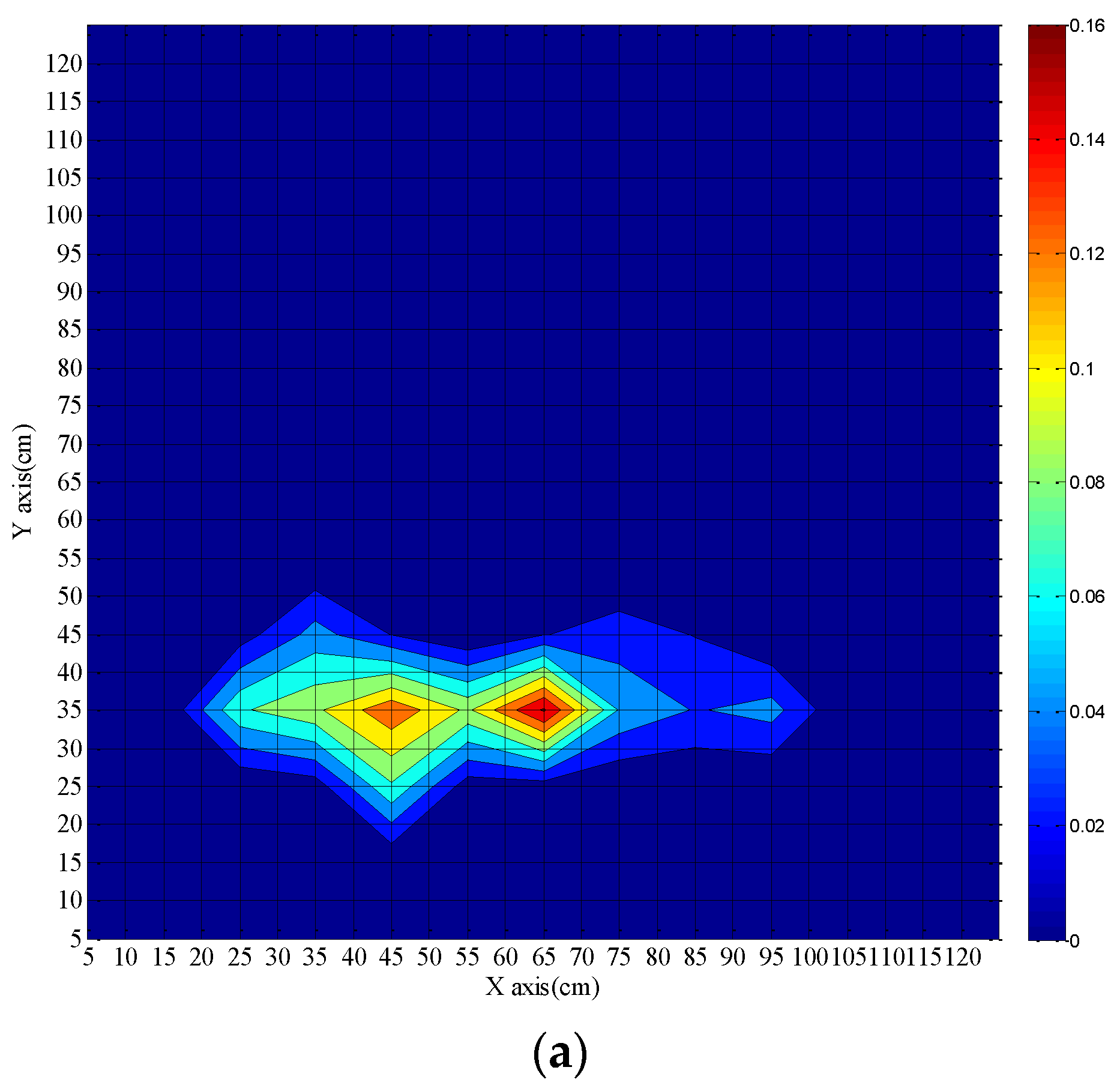
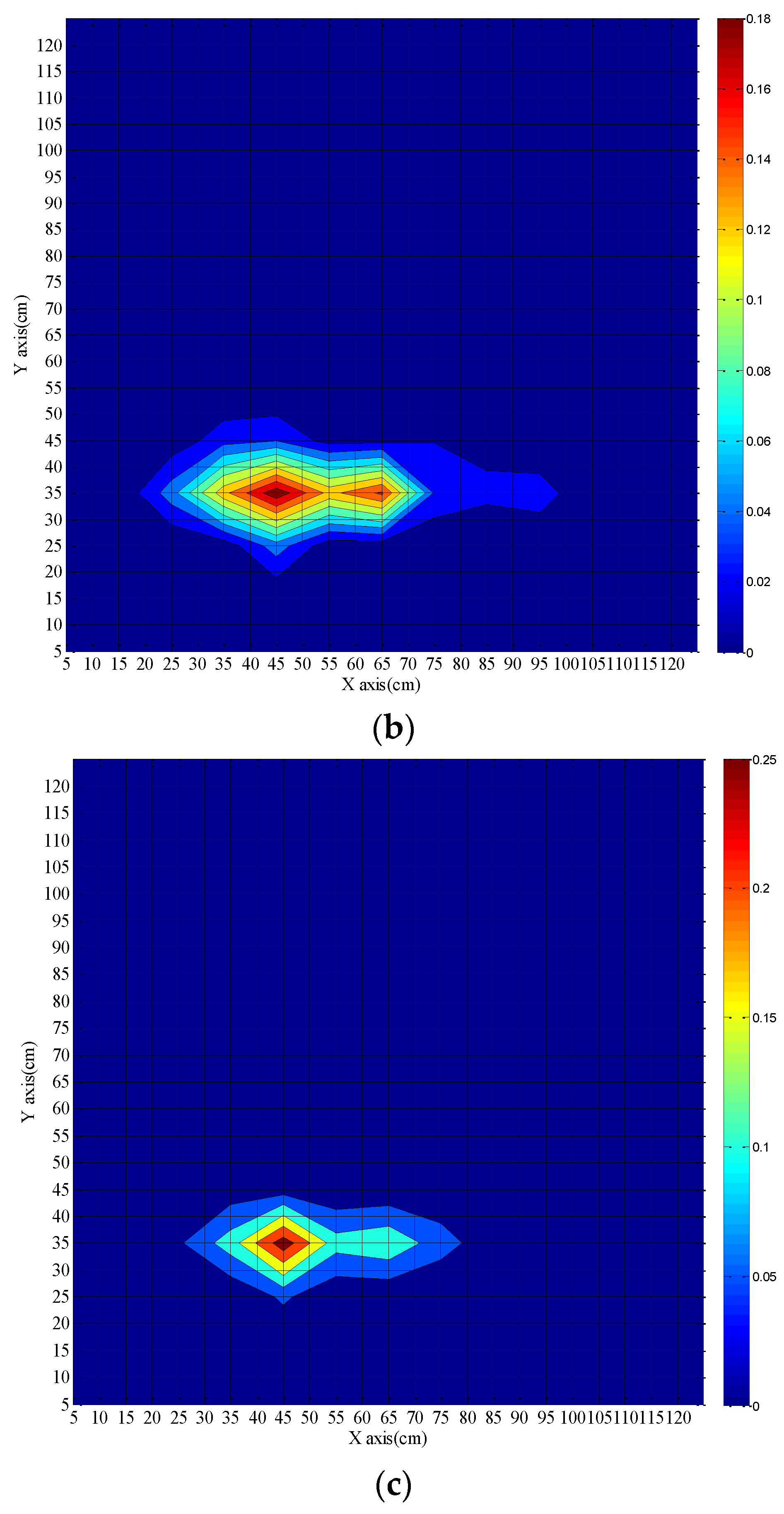
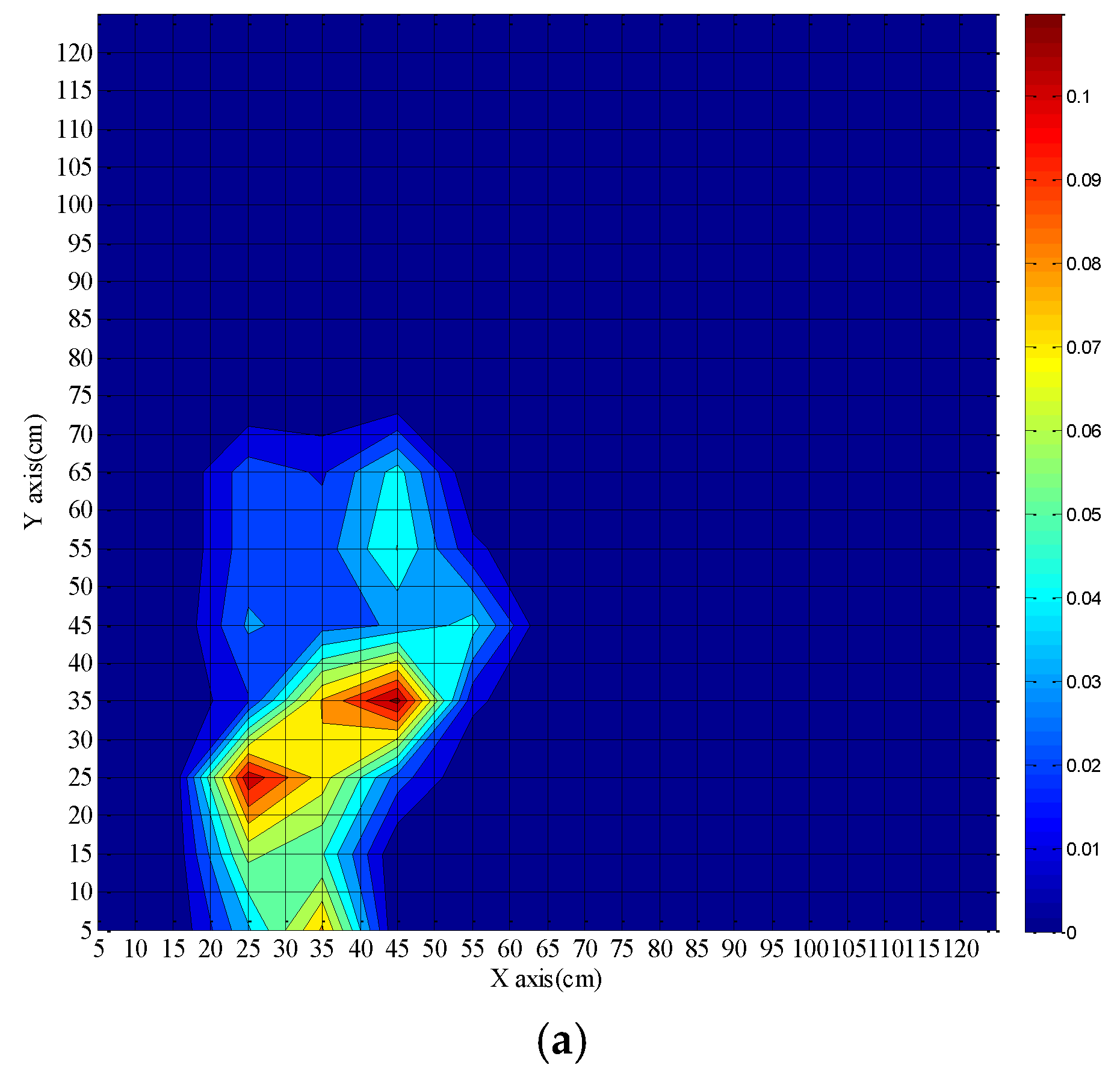
The ability of the DTS system for fire source localization has been discussed above. Due to the real-time nature of the DTS measurement, we get more coordinate data with increasing time. During the measurement, the coordinate data slightly vary around the real position of the fire source and some of them are overlapping. The possible area of the fire source (here is 1.2 m × 1.2 m) is partitioned with a grid (5 cm × 5 cm) spacing, and the coordinate data falling into each grid square are counted. The counting number finally corresponds to a probability. Hence the real fire source is located in the square grid with the highest probability. As a result the position of the fire source is determined. The results are depicted in
Figure 9 and
Figure 10. The color bar represents the probability of the calculated position of the fire source. The calculated coordinates of the fire source location are plotted for different times.
Figure 9 shows results after 40 s, 60 s, and 90 s fire burning time when the fibers are placed on opposite sides of the fire source. The extent of the actual fire source is 11.0 cm × 8.0 cm and the center position is (45 cm, 35 cm). For a fire burning time of 40 s, the shape of the fire source looks irregular almost like two independent fire sources. The coordinates of the two fire centers are (45 cm, 35 cm) and (65 cm, 35 cm), and the coordinate of the most possible position is (65 cm, 35 cm). When the burning time is 60 s, the coordinate of the most possible position changes to (45 cm, 35 cm). The shape of the fire source becomes more regular. When the fire burning time is ≥90 s the coordinate of the fire source is determined at (45 cm, 35 cm). Although there are two centers of fire sources when the burning time is 40 s, the calculated fire source location can cover the actual fire source well and the fire source location becomes more accurate with increasing burning time. As a result, the fire source position can be calculated roughly for 40 s and the accurate position can be achieved for 90 s burning time, which is very helpful for extinguishing the fire.
Figure 10 shows results after 70 s, 80 s, and 180 s fire burning time when the fibers are placed on the same side of the fire source. The center position of the actual fire source is (45.5 cm, 32 cm). As mentioned above, the fluctuations of the calculated fire source location in
Figure 7 are different from those in
Figure 8, thus the shape and range of the fire source in
Figure 9 are quite different from that in
Figure 10.
The fire source location is preliminarily confirmed when the burning time is 70 s, and the actual fire source is covered completely within the calculated fire source. The position of the fire source is finally determined at a burning time of 180 s, which is consistent with the previous discussions. The time of 40 s for a rough determination of a fire source position is considerably shorter than the 90 s reported in [
5] and the location error of the proposed method is much smaller than that achieved with sensor arrays [
5,
6,
11].