A Synergy-Based Optimally Designed Sensing Glove for Functional Grasp Recognition
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theoretical Background
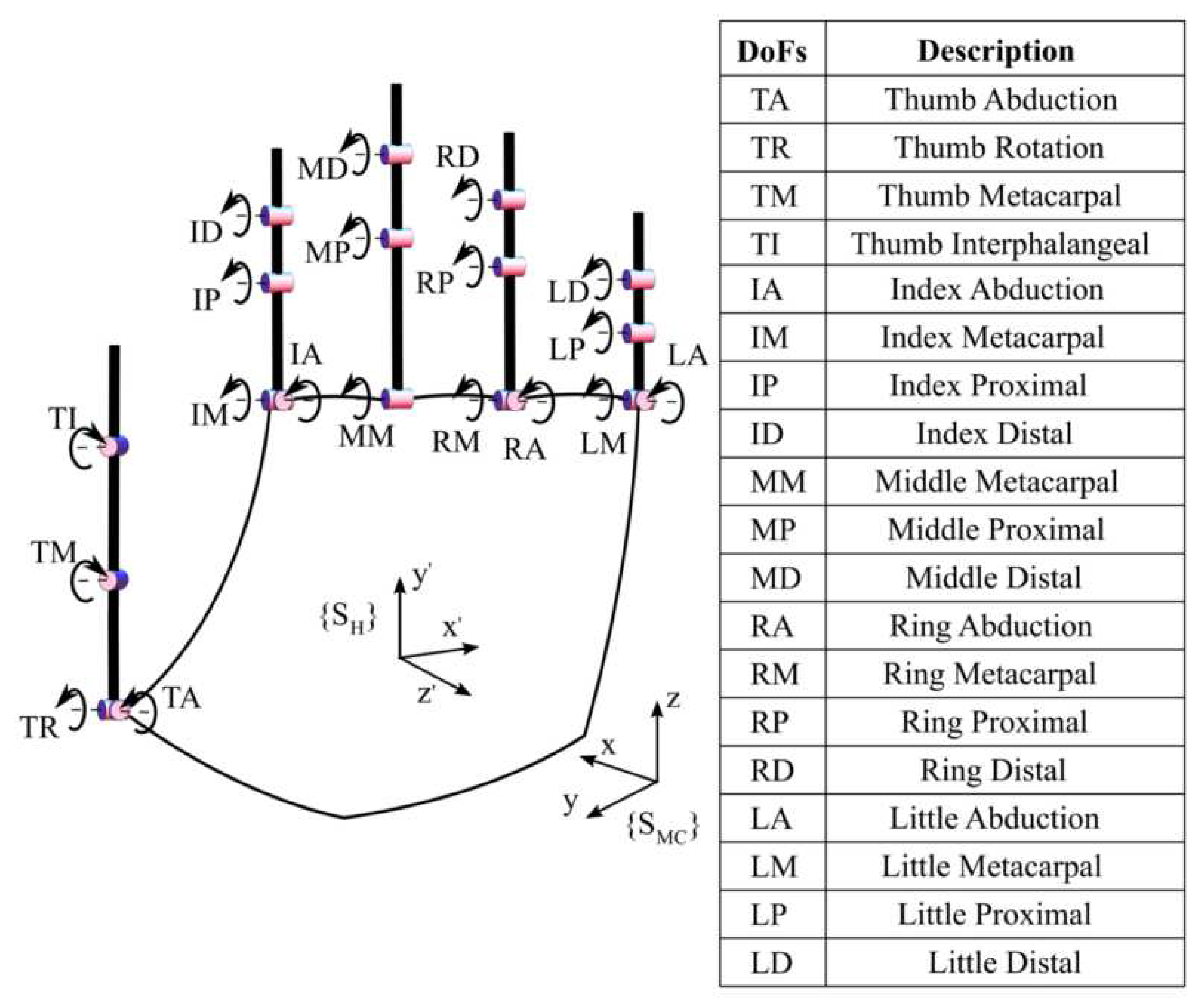
2.1.1. Synergy-Based Hand Pose Reconstruction
2.1.2. Synergy-Based Optimal HPR System Design
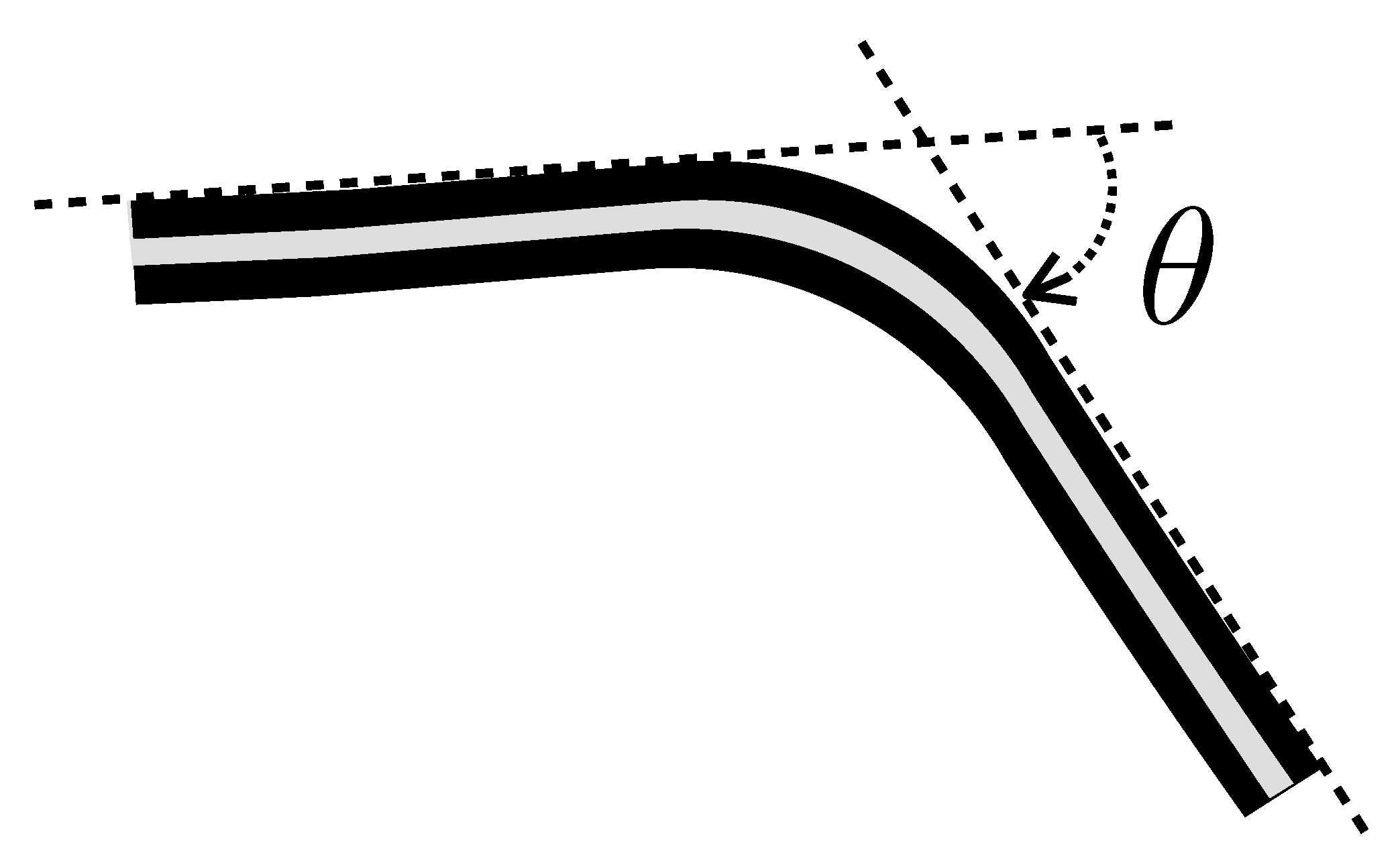
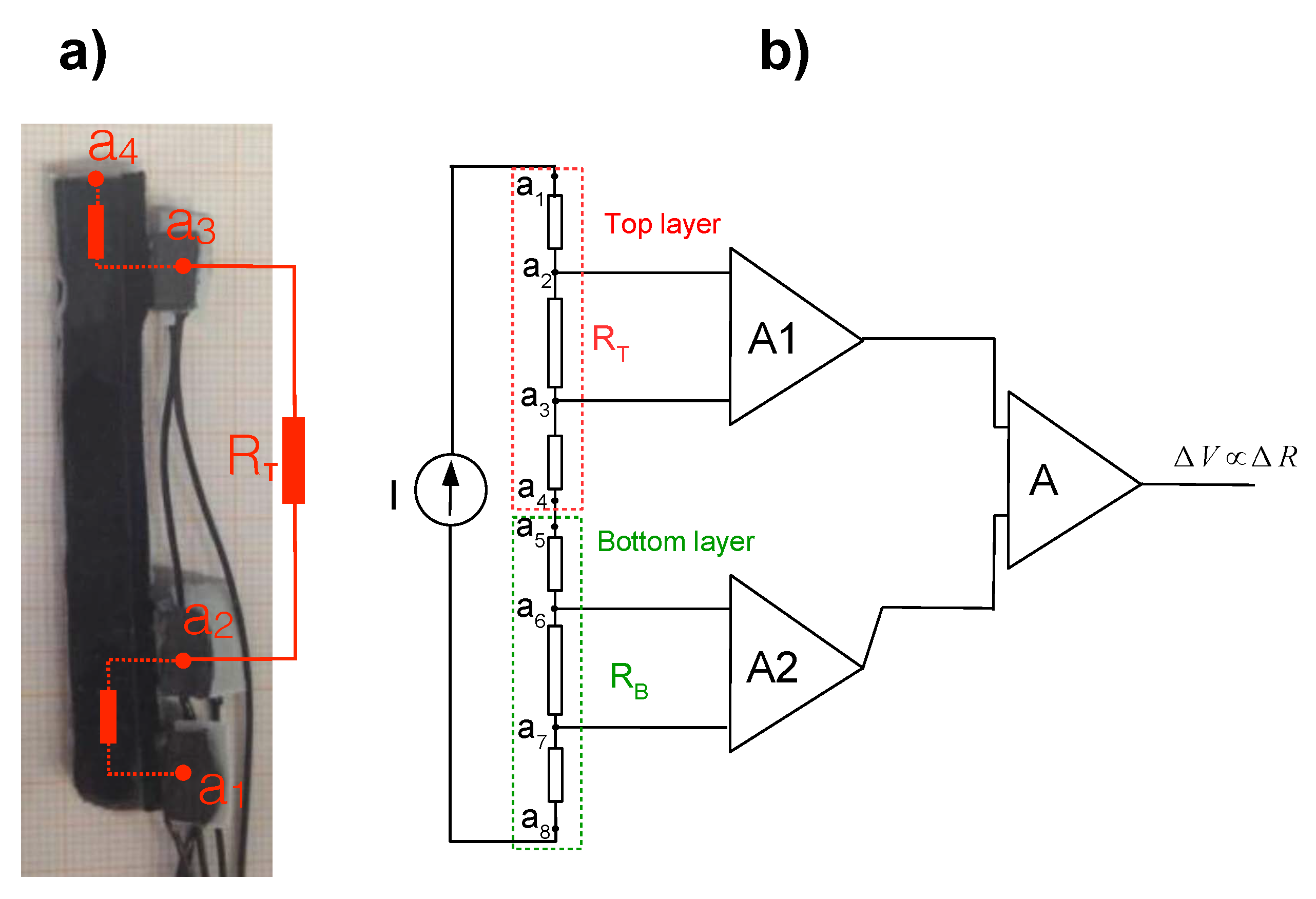
2.2. Sensors: KPF Goniometers
2.3. The Sensing Glove
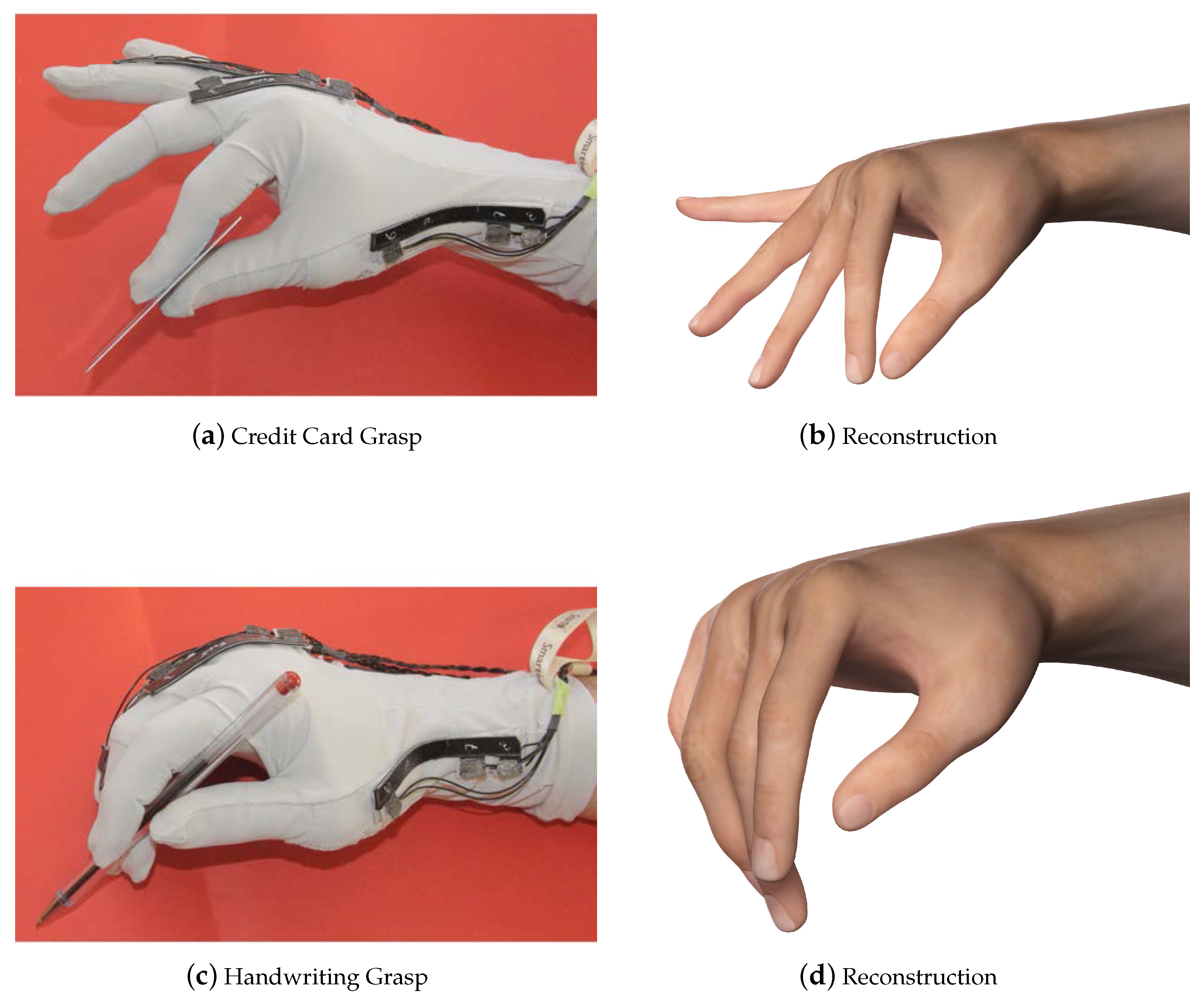
2.4. Data Acquisition
2.5. Experiments and K-Means Algorithm
- Choose k (one for each target pose, i.e., 8, in our case) cluster centroids starting locations;
- Assign each sample to the closest cluster centroid;
- Recompute the cluster centroid using the current cluster memberships;
- If the convergence criterion is not satisfied, go to Step 2.
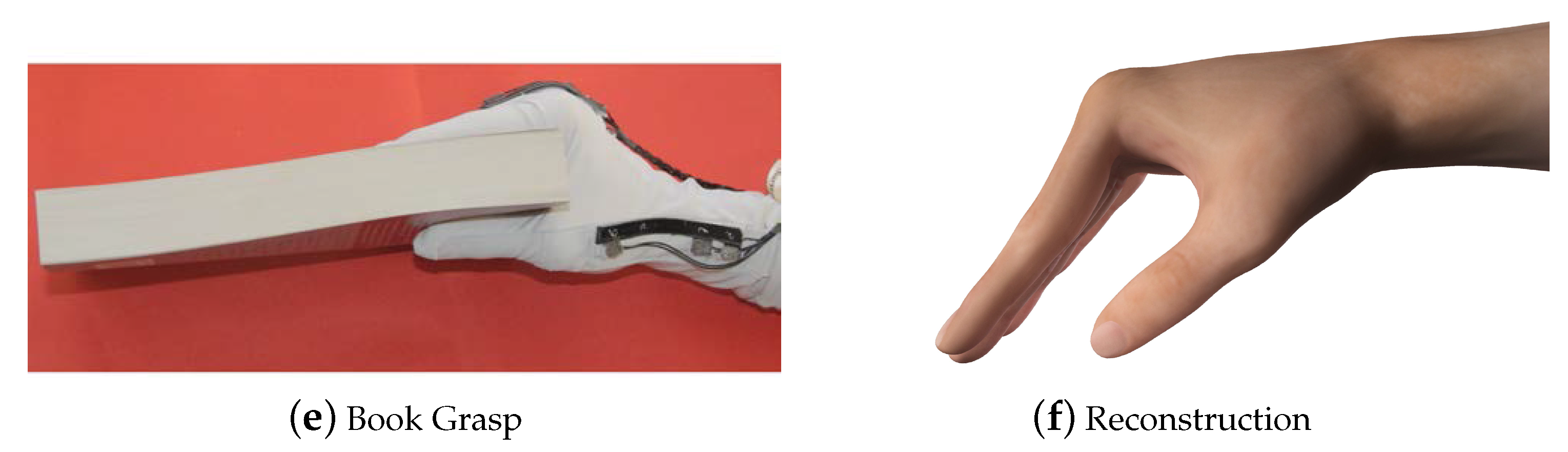
3. Results
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sturman, D.J.; Zeltzer, D. A survey of glove-based input. IEEE Comput. Graph. Appl. 1994, 14, 30–39. [Google Scholar] [CrossRef]
- Liarokapis, M.V.; Artemiadis, P.K.; Kyriakopoulos, K.J. Telemanipulation with the DLR/HIT II robot hand using a dataglove and a low cost force feedback device. In Proceedings of the 21st Mediterranean Conference on Control Automation (MED), Chania, Greece, 25–28 June 2013; pp. 431–436.
- Dipietro, L.; Sabatini, A.; Dario, P. A survey of glove-based systems and their applications. IEEE Trans. Syst. Man Cybern. C Appl. Rev. 2008, 38, 461–482. [Google Scholar] [CrossRef]
- Santello, M.; Flanders, M.; Soechting, J.F. Postural hand synergies for tool use. J. Neurosci. 1998, 18, 10105–10115. [Google Scholar] [PubMed]
- Tognetti, A.; Lorussi, F.; Carbonaro, N.; De Rossi, D.; De Toma, G.; Mancuso, C.; Paradiso, R.; Luinge, H.; Reenalda, J.; Droog, E.; et al. Daily-life monitoring of stroke survivors motor performance: The interaction sensing system. In Proceedings of the 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Chicago, IL, USA, 26–30 August 2014; pp. 4099–4102.
- Klaassen, B.; van Beijnum, B.J.; Weusthof, M.; Hofs, D.; van Meulen, F.; Droog, E.; Luinge, H.; Slot, L.; Tognetti, A.; Lorussi, F.; et al. A full body sensing system for monitoring stroke patients in a home environment. In Biomedical Engineering Systems and Technologies; Springer: Berlin/Heidelberg, Germany, 2015; pp. 378–393. [Google Scholar]
- Lorussi, F.; Carbonaro, N.; De Rossi, D.E.; Paradiso, R.; Veltink, P.H.; Tognetti, A. Wearable textile platform for assessing stroke patient treatment in daily life conditions. Front. Bioeng. Biotechnol. 2016, 4. [Google Scholar] [CrossRef] [PubMed]
- Lister, G. The Hand: Diagnosis and Surgical Indications; Churchill Livingstone: London, UK, 1993. [Google Scholar]
- Dalle Mura, G.; Lorussi, F.; Tognetti, A.; Anania, G.; Carbonaro, N.; Pacelli, M.; Paradiso, R.; De Rossi, D. Piezoresistive goniometer network for sensing gloves. In XIII Mediterranean Conference on Medical and Biological Engineering and Computing; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; Volume 41, pp. 1547–1550. [Google Scholar]
- Carbonaro, N.; Dalle Mura, G.; Lorussi, F.; Paradiso, R.; De Rossi, D.; Tognetti, A. Exploiting wearable goniometer technology for motion sensing gloves. IEEE J. Biomed. Health Inform. 2014, 18, 1788–1795. [Google Scholar] [CrossRef] [PubMed]
- Tognetti, A.; Lorussi, F.; Dalle Mura, G.; Carbonaro, N.; Pacelli, M.; Paradiso, R.; De Rossi, D. New generation of wearable goniometers for motion capture systems. J. Neuroeng. Rehabil. 2014, 11. [Google Scholar] [CrossRef] [PubMed]
- Bianchi, M.; Salaris, P.; Bicchi, A. Synergy-based hand pose sensing: Reconstruction enhancement. Int. J. Robot. Res. 2013, 32, 396–406. [Google Scholar] [CrossRef]
- Bianchi, M.; Salaris, P.; Bicchi, A. Synergy-based hand pose sensing: Optimal glove design. Int. J. Robot. Res. 2013, 32, 407–424. [Google Scholar] [CrossRef]
- Mulatto, S.; Formaglio, A.; Malvezzi, M.; Prattichizzo, D. Using postural synergies to animate a low-dimensional hand avatar in haptic simulation. IEEE Trans. Haptics 2013, 6, 106–116. [Google Scholar] [CrossRef] [PubMed]
- Bianchi, M.; Carbonaro, N.; Battaglia, E.; Lorussi, F.; Bicchi, A.; De Rossi, D.; Tognetti, A. Exploiting hand kinematic synergies and wearable under-sensing for hand functional grasp recognition. In Proceedings of the EAI 4th International Conference on Wireless Mobile Communication and Healthcare (Mobihealth), Athens, Greece, 3–5 November 2014; pp. 168–171.
- Bianchi, M.; Salaris, P.; Turco, A.; Carbonaro, N.; Bicchi, A. On the use of postural synergies to improve human hand pose reconstruction. In Proceedings of the Haptics Symposium (HAPTICS), Vancouver, BC, Canada, 4–7 March 2012; pp. 91–98.
- Bianchi, M.; Salaris, P.; Bicchi, A. Synergy-based optimal design of hand pose sensing. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura, Portugal, 7–12 October 2012; pp. 3929–3935.
- Santello, M.; Baud-Bovy, G.; Jörntell, H. Neural bases of hand synergies. Front. Comput. Neurosci. 2013, 7. [Google Scholar] [CrossRef] [PubMed]
- Catalano, M.G.; Grioli, G.; Farnioli, E.; Serio, A.; Piazza, C.; Bicchi, A. Adaptive synergies for the design and control of the Pisa/IIT SoftHand. Int. J. Robot. Res. 2014, 33, 768–782. [Google Scholar] [CrossRef]
- Bicchi, A.; Gabiccini, M.; Santello, M. Modelling natural and artificial hands with synergies. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2011, 366, 3153–3161. [Google Scholar] [CrossRef] [PubMed]
- Santello, M.; Flanders, M.; Soechting, J.F. Patterns of hand motion during grasping and the influence of sensory guidance. J. Neurosci. 2002, 22, 1426–1435. [Google Scholar] [PubMed]
- Tognetti, A.; Lorussi, F.; Carbonaro, N.; de Rossi, D. Wearable goniometer and accelerometer sensory fusion for knee joint angle measurement in daily life. Sensors 2015, 15, 28435–28455. [Google Scholar] [CrossRef] [PubMed]
- Pacelli, M.; Caldani, L.; Paradiso, R. Textile piezoresistive sensors for biomechanical variables monitoring. In Proceedings of the 28th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, New York, NY, USA, 30 August–3 September 2006; pp. 5358–5361.
- Pacelli, M.; Caldani, L.; Paradiso, R. Performances evaluation of piezoresistive fabric sensors as function of yarn structure. In Proceedings of the 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Osaka, Japan, 3–7 July 2013; pp. 6502–6505.
- Lin, J.; Wu, Y.; Huang, T.S. Modeling the constraints of human hand motion. In Proceedings of the Workshop on Human Motion, Los Alamitos, CA, USA, 7–8 December 2000; pp. 121–126.
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 21 June 1967; University of California Press: Berkeley, CA, USA, 1967; Volume 1, pp. 281–297. [Google Scholar]
- Jain, A.K.; Murty, M.N.; Flynn, P.J. Data Clustering: A Review. ACM Comput. Surv. 1999, 31, 264–323. [Google Scholar]
- Kohavi, R. A Study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20 August 1995; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1995; Volume 2, pp. 1137–1145. [Google Scholar]
- Simone, L.K.; Kamper, D.G. Design considerations for a wearable monitor to measure finger posture. J. Neuroeng. Rehabil. 2005, 2. [Google Scholar] [CrossRef] [PubMed]
- Oess, N.P.; Wanek, J.; Curt, A. Design and evaluation of a low-cost instrumented glove for hand function assessment. J. Neuroeng. Rehabil. 2012, 9. [Google Scholar] [CrossRef] [PubMed]
- Borghetti, M.; Sardini, E.; Serpelloni, M. Sensorized glove for measuring hand finger flexion for rehabilitation purposes. IEEE Trans. Instrum. Meas. 2013, 62, 3308–3314. [Google Scholar] [CrossRef]
- Yu, L.; Xiong, D.; Guo, L.; Wang, J. A remote quantitative Fugl-Meyer assessment framework for stroke patients based on wearable sensor networks. Comput. Methods Progr. Biomed. 2016, 128, 100–110. [Google Scholar] [CrossRef] [PubMed]
- Yuen, A.C.; Bakir, A.A.; Rajdi, N.N.Z.M.; Lam, C.L.; Saleh, S.M.; Wicaksono, D.H. Proprioceptive sensing system for therapy assessment using cotton fabric-based biomedical microelectromechanical system. IEEE Sens. J. 2014, 14, 2872–2880. [Google Scholar] [CrossRef]
- Leigh, S.J.; Bradley, R.J.; Purssell, C.P.; Billson, D.R.; Hutchins, D.A. A simple, low-cost conductive composite material for 3D printing of electronic sensors. PLoS ONE 2012, 7, e49365. [Google Scholar] [CrossRef] [PubMed]
- Muth, J.T.; Vogt, D.M.; Truby, R.L.; Mengüç, Y.; Kolesky, D.B.; Wood, R.J.; Lewis, J.A. Embedded 3D printing of strain sensors within highly stretchable elastomers. Adv. Mater. 2014, 26, 6307–6312. [Google Scholar] [CrossRef] [PubMed]
- Kortier, H.G.; Sluiter, V.I.; Roetenberg, D.; Veltink, P.H. Assessment of hand kinematics using inertial and magnetic sensors. J. Neuroeng. Rehabil. 2014, 11. [Google Scholar] [CrossRef] [PubMed]
- Lin, B.S.; Lee, I.J.; Hsiao, P.C.; Yang, S.Y.; Chou, W. Data glove embedded with 6-DOF inertial sensors for hand rehabilitation. In Proceedings of the Tenth International Conference on Intelligent Information Hiding and Multimedia Signal Processing (IIH-MSP), Kitakyushu, Japan, 27–29 August 2014; pp. 25–28.
- Hsiao, P.C.; Yang, S.Y.; Lin, B.S.; Lee, I.J.; Chou, W. Data glove embedded with 9-axis IMU and force sensing sensors for evaluation of hand function. In Proceedings of the 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 4631–4634.
- Thakur, P.H.; Bastian, A.J.; Hsiao, S.S. Multidigit movement synergies of the human hand in an unconstrained haptic exploration task. J. Neurosci. 2008, 28, 1271–1281. [Google Scholar] [CrossRef] [PubMed]
- Santello, M.; Lang, C.E. Are movement disorders and sensorimotor injuries pathologic synergies? When normal multi-joint movement synergies become pathologic. Front. Hum. Neurosci. 2015, 8, 1050. [Google Scholar] [CrossRef] [PubMed]





| Recognized Grasp | Relative Accuracy | Absolute Accuracy | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||
| Grasp Type | 1 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 100% | 100% |
| 2 | 0 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 100% | ||
| 3 | 0 | 0 | 12 | 0 | 0 | 0 | 0 | 0 | 100% | ||
| 4 | 0 | 0 | 0 | 12 | 0 | 0 | 0 | 0 | 100% | ||
| 5 | 0 | 0 | 0 | 0 | 12 | 0 | 0 | 0 | 100% | ||
| 6 | 0 | 0 | 0 | 0 | 0 | 12 | 0 | 0 | 100% | ||
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 0 | 100% | ||
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 100% | ||
| Recognized Grasp | Relative Accuracy | Absolute Accuracy | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||
| Grasp Type | 1 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 100% | 100% |
| 2 | 0 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 100% | ||
| 3 | 0 | 0 | 12 | 0 | 0 | 0 | 0 | 0 | 100% | ||
| 4 | 0 | 0 | 0 | 12 | 0 | 0 | 0 | 0 | 100% | ||
| 5 | 0 | 0 | 0 | 0 | 12 | 0 | 0 | 0 | 100% | ||
| 6 | 0 | 0 | 0 | 0 | 0 | 12 | 0 | 0 | 100% | ||
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 0 | 100% | ||
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 100% | ||
| Recognized Grasp | Relative Accuracy | Absolute Accuracy | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||
| Grasp Type | 1 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 100% | 95.83% |
| 2 | 0 | 10 | 0 | 0 | 0 | 2 | 0 | 0 | 83.33% | ||
| 3 | 1 | 0 | 11 | 0 | 0 | 0 | 0 | 0 | 91.67% | ||
| 4 | 0 | 0 | 0 | 12 | 0 | 0 | 0 | 0 | 100% | ||
| 5 | 0 | 0 | 0 | 0 | 12 | 0 | 0 | 0 | 100% | ||
| 6 | 0 | 0 | 0 | 1 | 0 | 11 | 0 | 0 | 91.67% | ||
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 0 | 100% | ||
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 100% | ||
| Recognized Grasp | Relative Accuracy | Absolute Accuracy | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||
| Grasp Type | 1 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 100% | 95.83% |
| 2 | 0 | 9 | 0 | 0 | 0 | 3 | 0 | 0 | 75% | ||
| 3 | 0 | 0 | 12 | 0 | 0 | 0 | 0 | 0 | 100% | ||
| 4 | 0 | 0 | 0 | 12 | 0 | 0 | 0 | 0 | 100% | ||
| 5 | 0 | 0 | 0 | 0 | 12 | 0 | 0 | 0 | 100% | ||
| 6 | 0 | 0 | 0 | 1 | 0 | 11 | 0 | 0 | 91.67% | ||
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 0 | 100% | ||
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 100% | ||
| Recognized Grasp | Relative Accuracy | Absolute Accuracy | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||
| Grasp Type | 1 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 100% | 98.96% |
| 2 | 0 | 11 | 0 | 0 | 0 | 1 | 0 | 0 | 91.67% | ||
| 3 | 0 | 0 | 12 | 0 | 0 | 0 | 0 | 0 | 100% | ||
| 4 | 0 | 0 | 0 | 12 | 0 | 0 | 0 | 0 | 100% | ||
| 5 | 0 | 0 | 0 | 0 | 12 | 0 | 0 | 0 | 100% | ||
| 6 | 0 | 0 | 0 | 0 | 0 | 12 | 0 | 0 | 100% | ||
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 0 | 100% | ||
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 100% | ||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciotti, S.; Battaglia, E.; Carbonaro, N.; Bicchi, A.; Tognetti, A.; Bianchi, M. A Synergy-Based Optimally Designed Sensing Glove for Functional Grasp Recognition. Sensors 2016, 16, 811. https://doi.org/10.3390/s16060811
Ciotti S, Battaglia E, Carbonaro N, Bicchi A, Tognetti A, Bianchi M. A Synergy-Based Optimally Designed Sensing Glove for Functional Grasp Recognition. Sensors. 2016; 16(6):811. https://doi.org/10.3390/s16060811
Chicago/Turabian StyleCiotti, Simone, Edoardo Battaglia, Nicola Carbonaro, Antonio Bicchi, Alessandro Tognetti, and Matteo Bianchi. 2016. "A Synergy-Based Optimally Designed Sensing Glove for Functional Grasp Recognition" Sensors 16, no. 6: 811. https://doi.org/10.3390/s16060811
APA StyleCiotti, S., Battaglia, E., Carbonaro, N., Bicchi, A., Tognetti, A., & Bianchi, M. (2016). A Synergy-Based Optimally Designed Sensing Glove for Functional Grasp Recognition. Sensors, 16(6), 811. https://doi.org/10.3390/s16060811







