Wireless Sensor Array Network DoA Estimation from Compressed Array Data via Joint Sparse Representation
Abstract
:1. Introduction
- A joint sparse representation-based DoA estimation approach is proposed, that exposes the joint spatial and spectral domain sparse structure of array signals and incorporates the multiple measurement vector [26] approach to solve the DoA estimation problem;
- A theoretical mutual coherence bound of a uniform linear sensor array is provided, which defines the minimum angular separation of the sources that are required for the CSJSR-DoA approach to yield a reliable solution with a high probability;
- The Cramr–Rao bound of the CSJSR-DoA estimator is derived to quantify the theoretical DoA estimation performance;
- A prototype acoustic WSAN platform is developed to validate the effectiveness of the proposed CSJSR-DoA approach.
2. Background
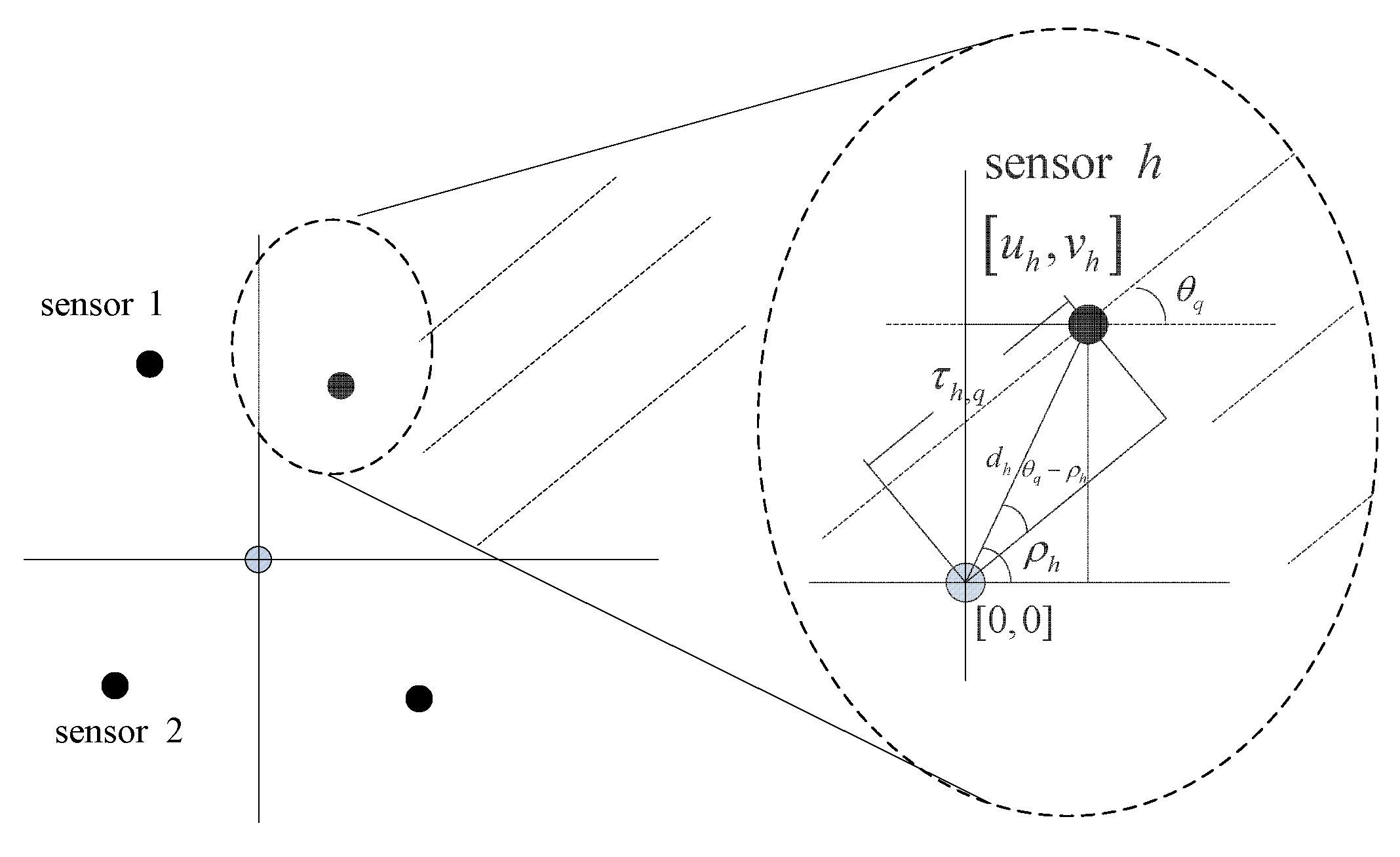
2.1. Signal Model and Joint Spatial-Spectral Sparse Structure
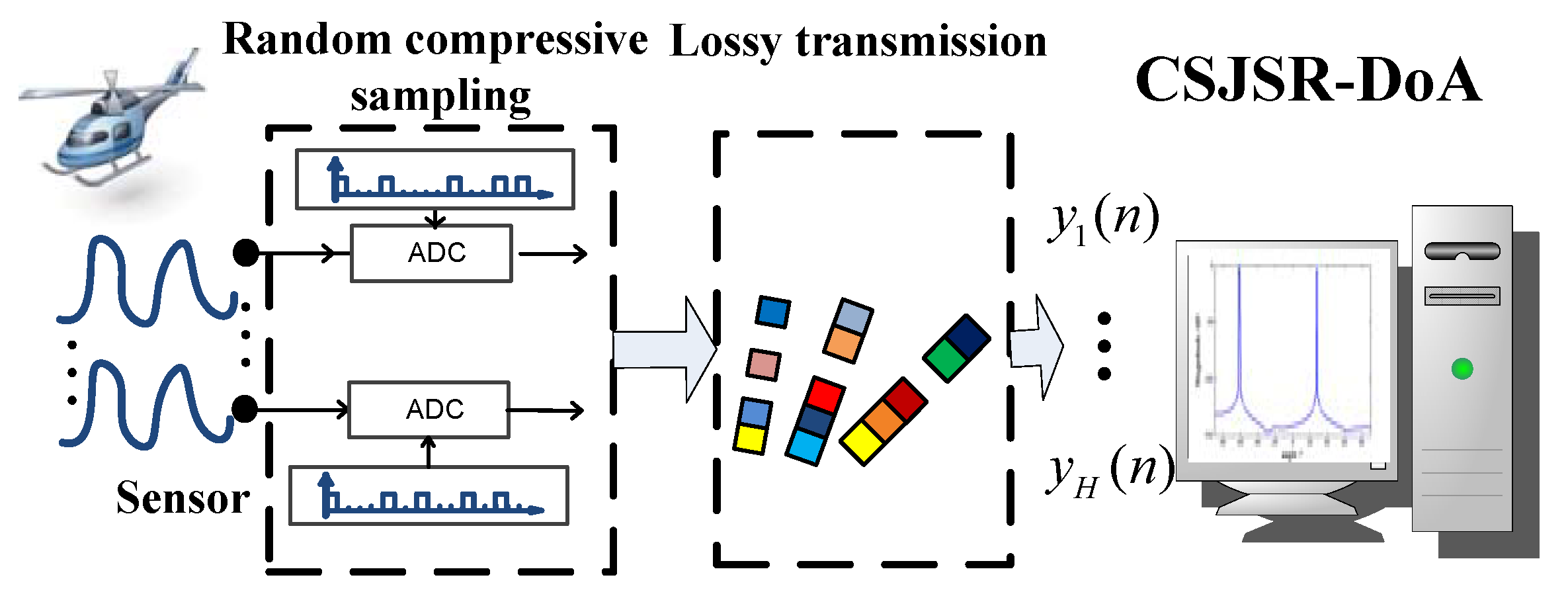
2.2. Compressive Sensing and Random Sub-Sampled Measurements
3. CSJSR-DoA Formulation
- Estimate the frequency domain support of array signals by reconstructing the spectral sparse indicative vector from the joint measurements and prune the joint reconstruction matrix Υ by selecting with non-zero frequency bins;
- reconstruct the DoA indicative vector directly from the joint measurements using the pruned joint reconstruction matrix.
| Algorithm 1 Decoupled joint sparse reconstruction. |
| Input: Received joint random measurement vector ; |
| Equivalent random measurement matrix ; |
| Output: DoA indicating vector ; |
| 1. Estimate the noise level by random sampling in source free scenario, ; |
| 2. Estimate the common support by solving: |
| 3. Construct the pruned joint reconstruction matrix ; |
| ; |
| 4. Solve the pruned reconstruction problem: |
4. Performance Analysis
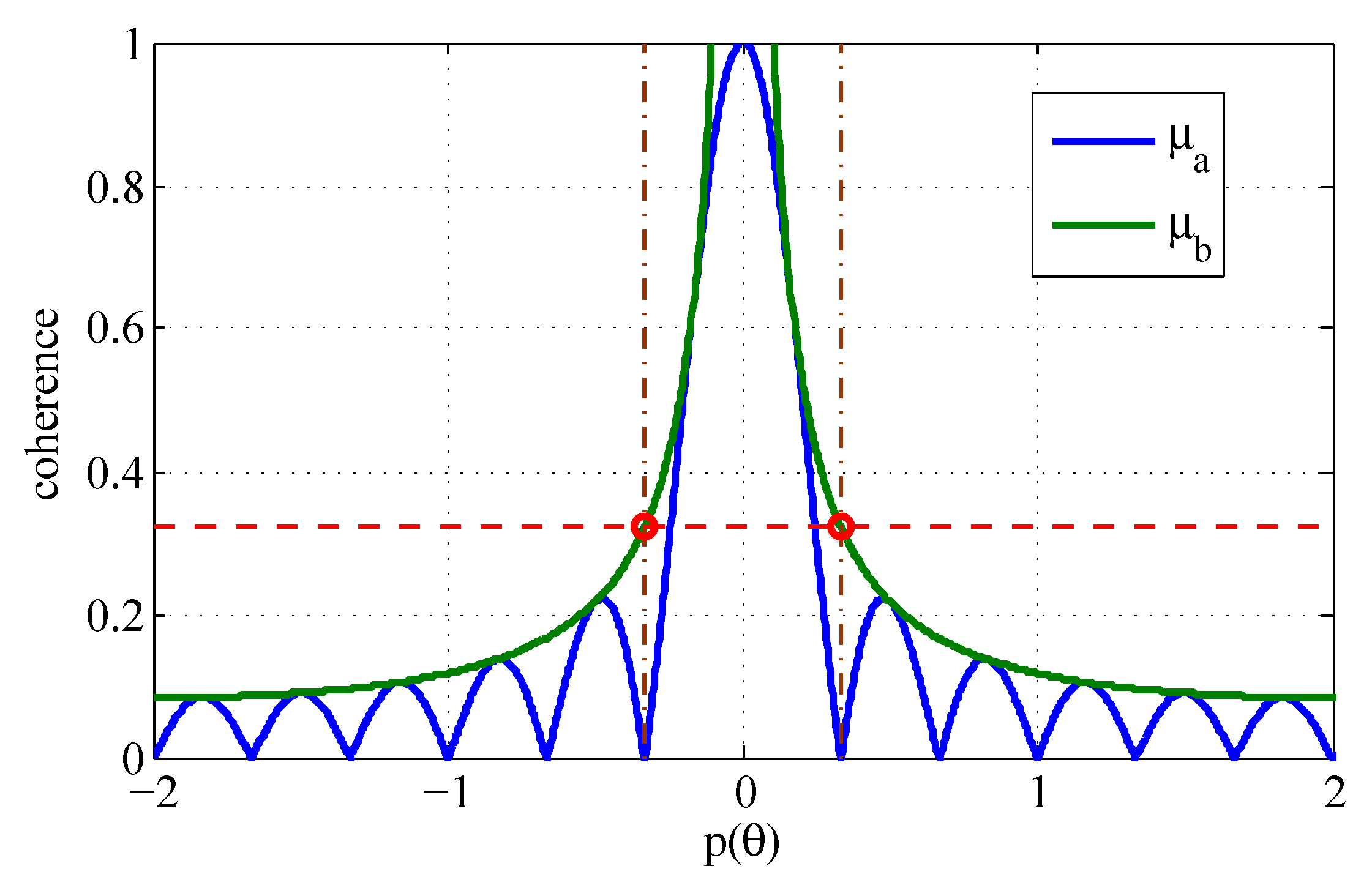
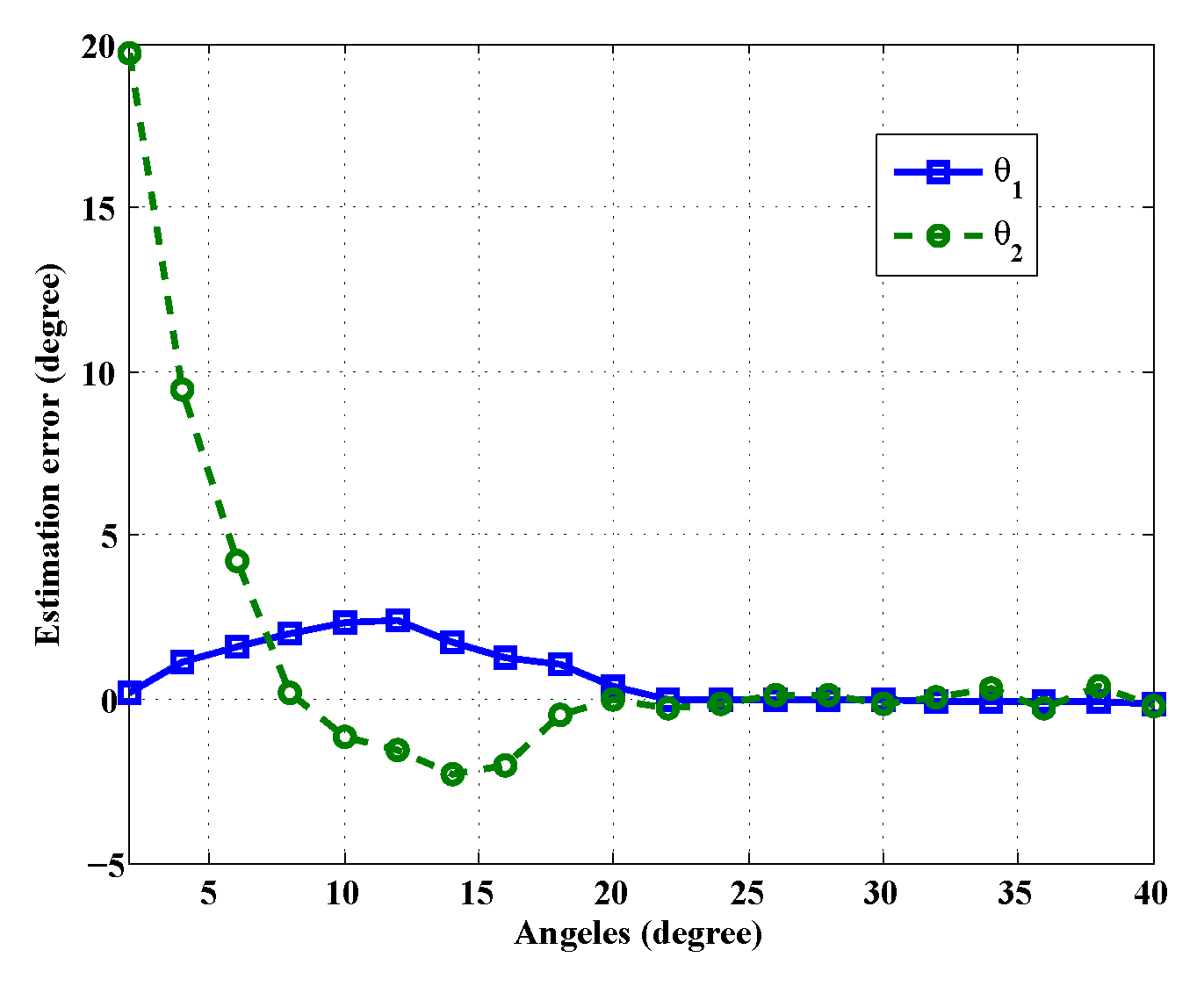
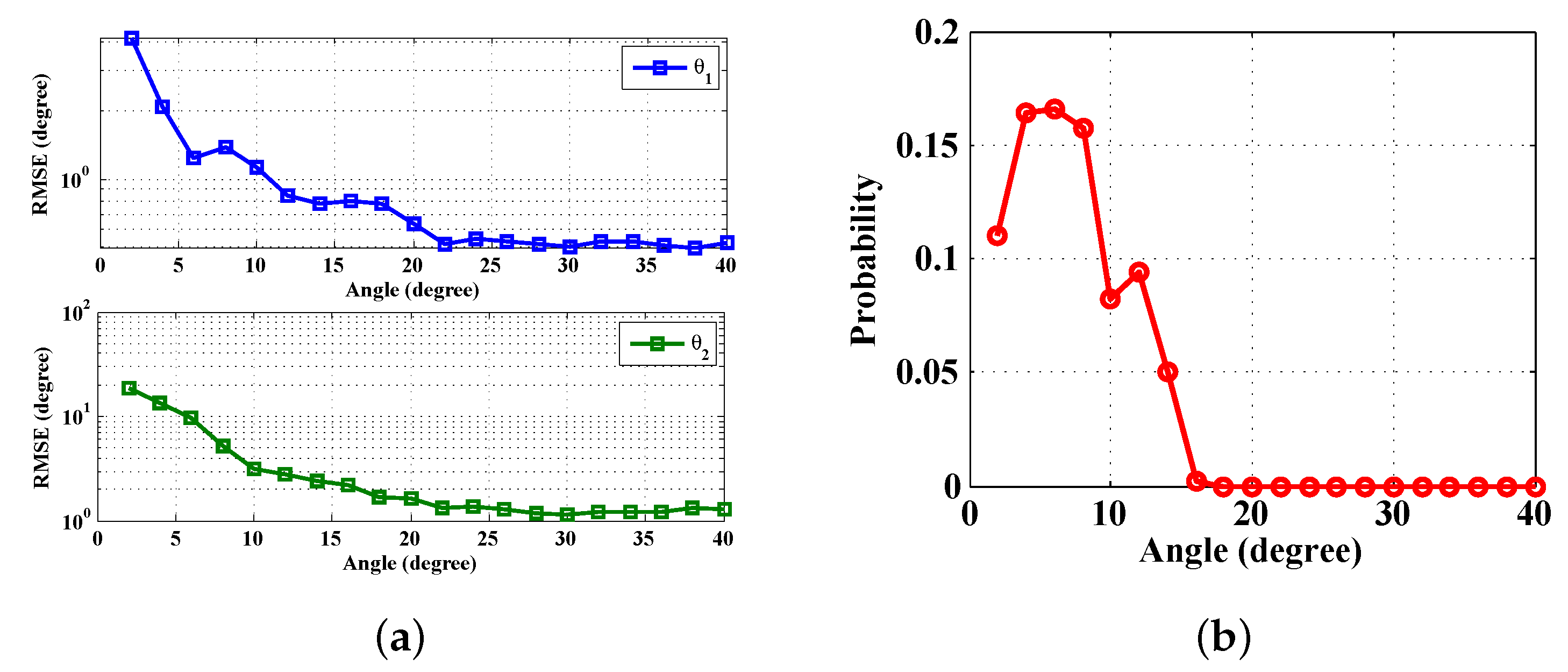
4.1. Sparse Reconstruction Analysis and Angle Separation
4.2. Cramr–Rao Bound of CSJSR-DoA
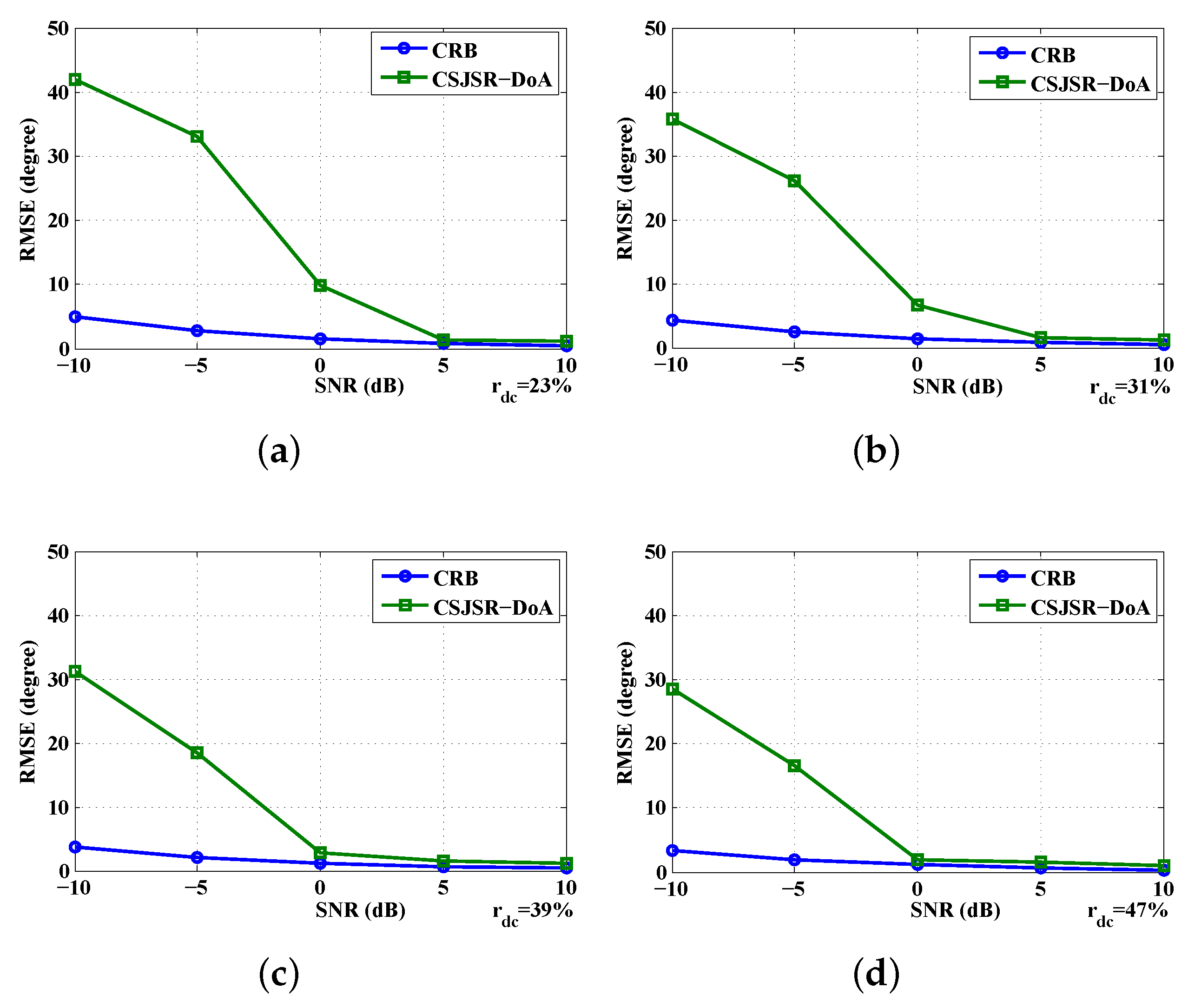
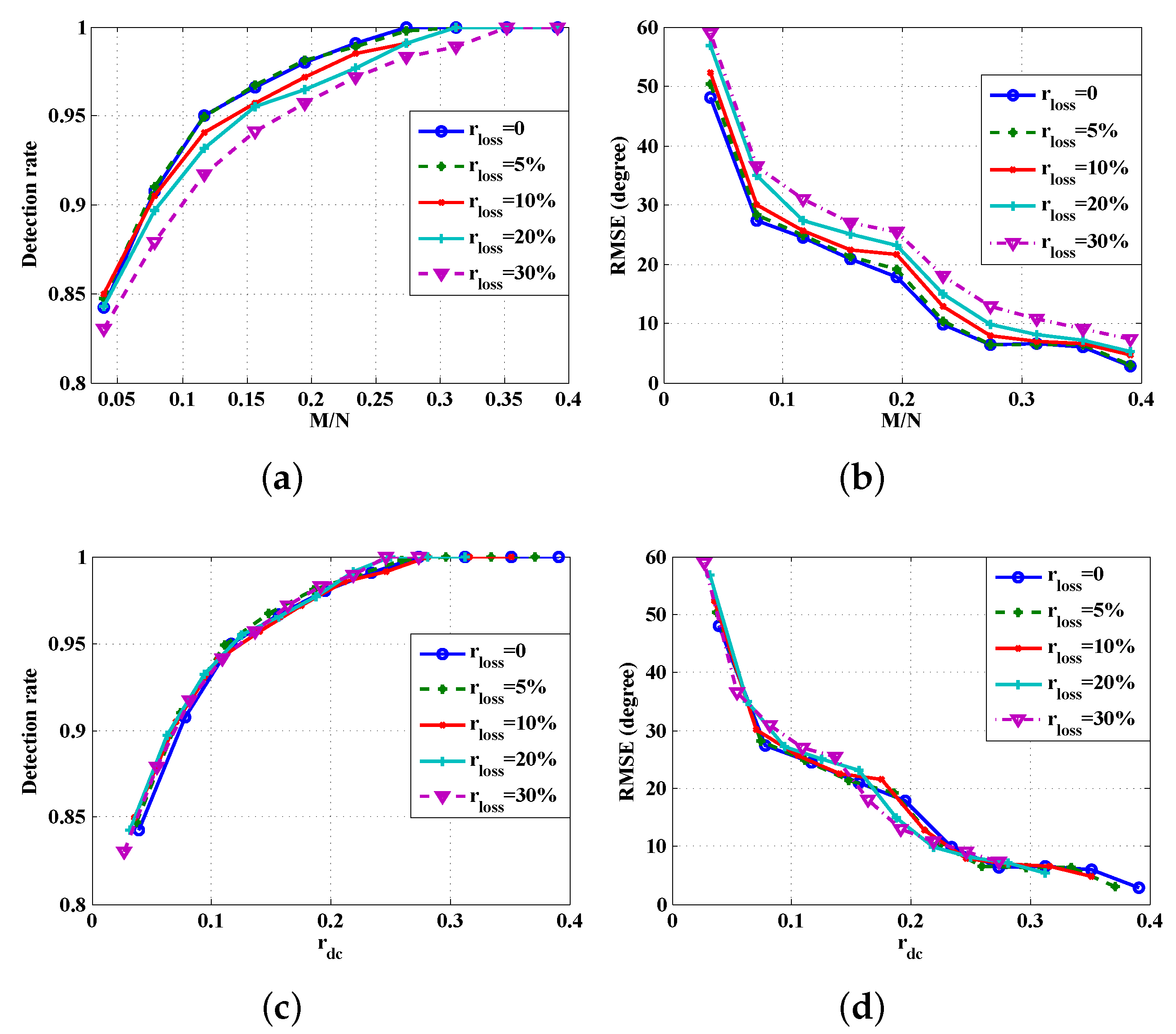
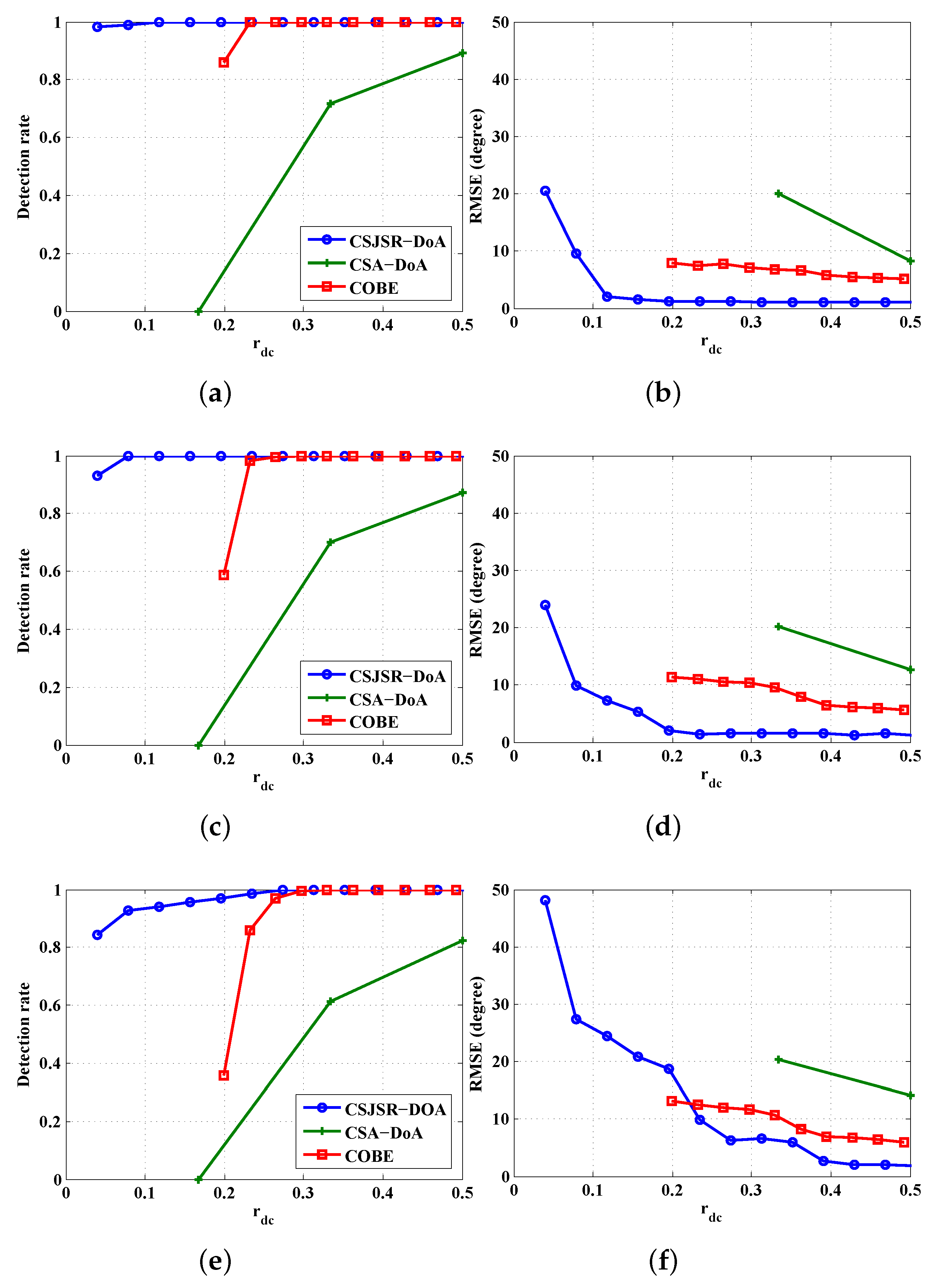
5. Performance Evaluation
5.1. Simulation Settings
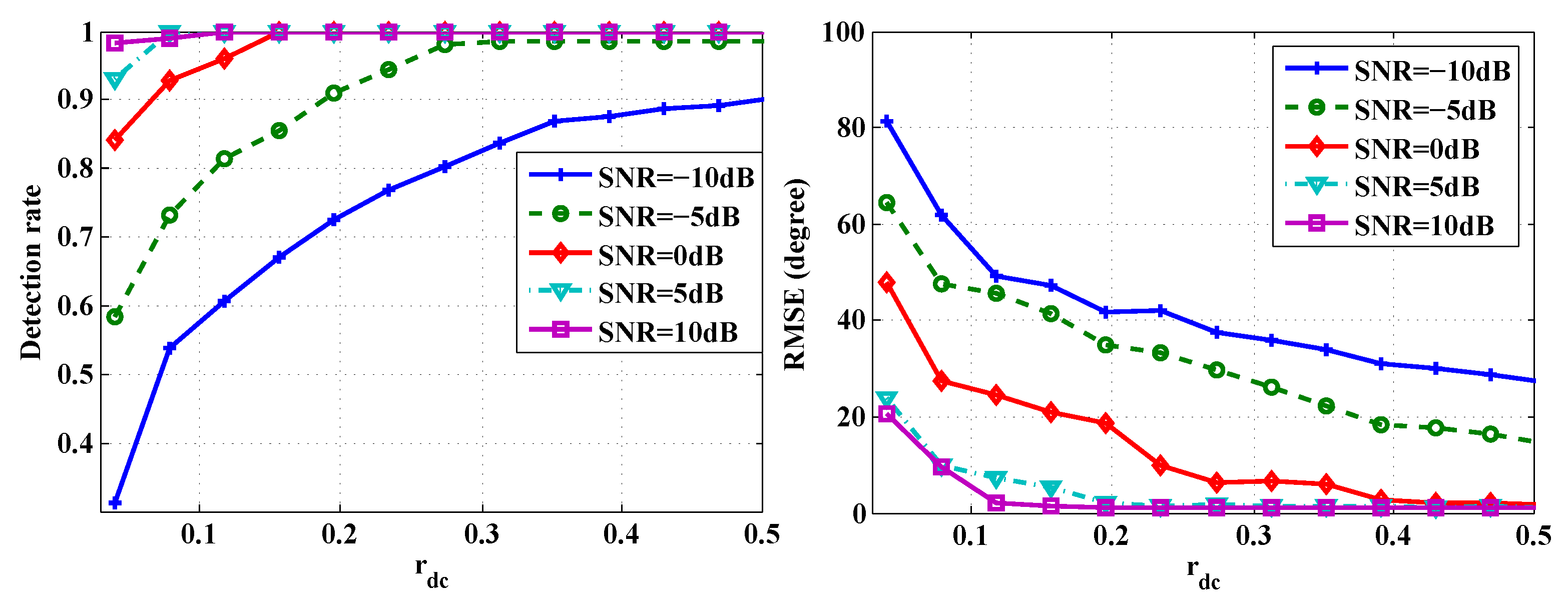
5.2. CSJSR-DoA Performance Evaluation
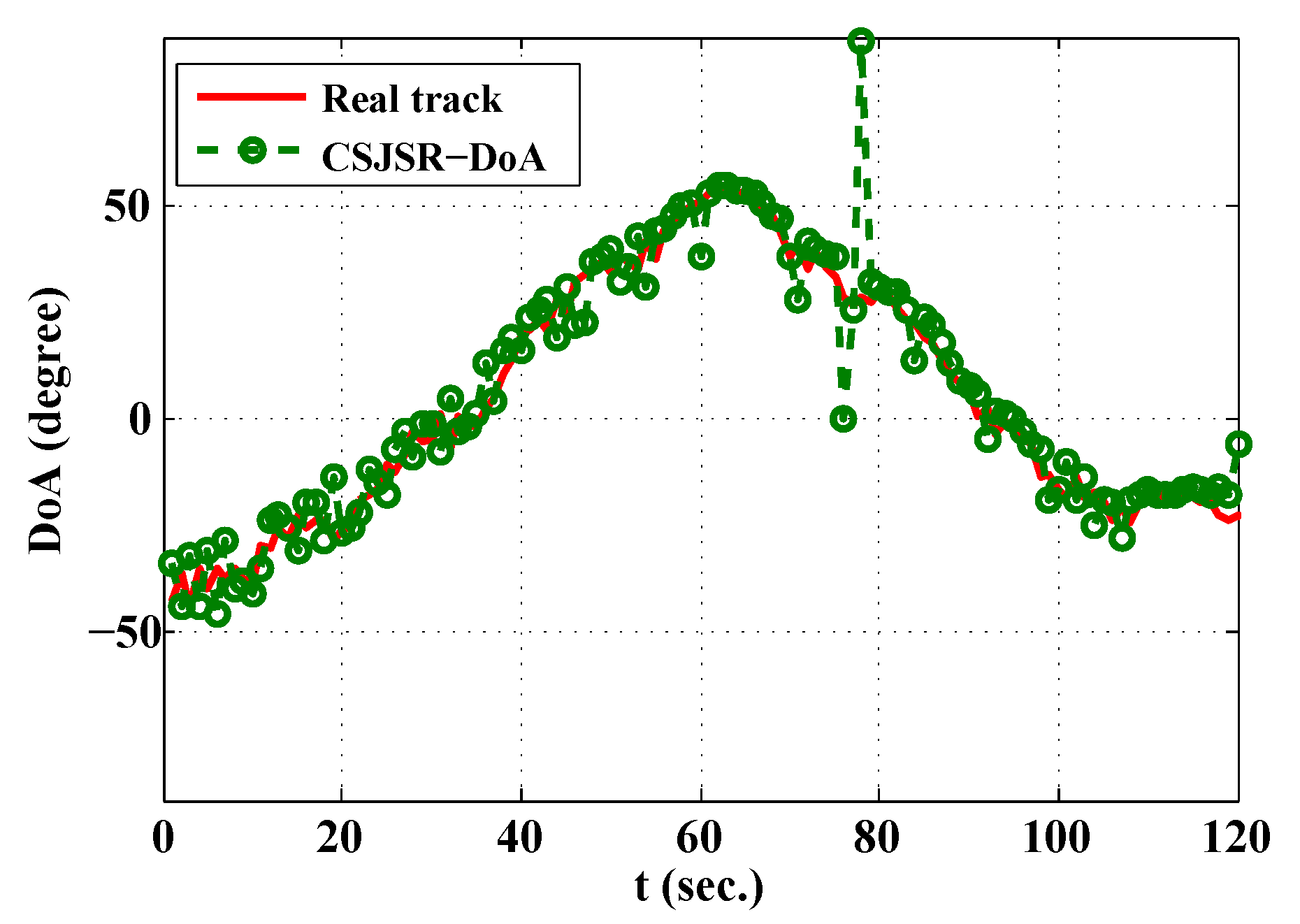
5.3. Prototype WSAN Platform and Field Experiment
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A.
Appendix B.
Appendix C.
References
- Ilyas, P.; Chen, H.; Tremoulis, G. Tracking of multiple moving speakers with multiple microphone arrays. IEEE Trans. Speech Audio Process. 2004, 12, 520–529. [Google Scholar]
- Wang, Z.; Luo, J.; Zhang, X. A noval location-penalized maximum likelihood estimator for bearing-only target localization. IEEE Trans. Speech Audio Process. 2012, 60, 6166–6181. [Google Scholar]
- Wang, Z.; Liao, J.; Cao, Q.; Qi, H.; Wang, Z. Achieving k-barrier Coverage in Hybrid Directional Sensor Networks. IEEE Transactions on Mob. Comput. 2014, 13, 1443–1455. [Google Scholar] [CrossRef]
- Krim, H.; Viberg, M. Two decades of array signal processing research: the parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Winder, A. Sonar system technology. IEEE Trans. Sonics Ultrason. 1975, 22, 291–332. [Google Scholar] [CrossRef]
- Chen, J.C.; Yao, K.; Hudson, R.E.; Tung, T.; Reed, C.; Chen, D. Source localization and tracking of a wideband source using a randomly distributed beam-forming sensor array. Int. J. High Perform. Comput. Appl. 2002, 16, 259–272. [Google Scholar] [CrossRef]
- Chen, J.C.; Yip, L.; Elson, J.; Wang, H.; Maniezzo, D.; Hudson, R.E.; Yao, K.; Estrin, D. Coherent acoustic array processing and localization on wireless sensor networks. IEEE Process. 2003, 91, 1154–1162. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressive sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Baraniuk, R. Compressive sensing. IEEE Signal Process. Mag. 2007, 2007, 118–120. [Google Scholar] [CrossRef]
- Candés, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar]
- Gurbuz, A.C.; Mcclellan, J.H.; Cevher, V. A compressive beamforming method. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Las Vegas, NV, USA, 31 March–4 April 2008; pp. 2617–2620.
- Cevher, V.; Gurbuz, A.C.; Mcclellan, J.H.; Chellappa, R. Compressive wireless arrays for bearing estimation. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Las Vegas, NV, USA, 31 March–4 April 2008; pp. 2497–2500.
- Gurbuz, A.C.; Cevher, V.; Mcclellan, J.H. Bearing estimation via spatial sparsity using compressive sensing. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 1358–1369. [Google Scholar] [CrossRef]
- Wang, Y.; Leus, G.; Pandharipande, A. Direction estimation using compressive sampling array processing. In Proceedings of the 15th IEEE Workshop on Statistical Signal Process, Cardiff, UK, 31 August–3 September 2009; pp. 626–629.
- Li, B.; Zou, Y.; Zhu, Y. Direction estimation under compressive sensing framework: A review and experimental results. In Proceedings of the International Conference on Information and Automation (ICIA), Shenzhen, China, 6–8 June 2011; pp. 63–68.
- Zhang, J.; Bao, M.; Li, X. Wideband DOA estimation of frequency sparse sources with one receiver. In Proceedings of the International Conference on Mobile Ad-hoc and Sensor System (IEEE MASS), Hangzhou, China, 14–16 October 2013; pp. 609–613.
- Gu, J.; Zhu, W.; Swamy, M. Compressed sensing for DOA estimation with fewer receivers than sensors. In Proceedings of the International Symposium on Circuits and Systems (ISCAS), Rio de Janeiro, Brazil, 15–18 May 2011; pp. 1752–1755.
- Duarte, M.F.; Davenport, M.A.; Takhar, D.; Laska, J.N.; Kelly, K.F.; Sun, T.; Baraniuk, R.G. Single-pixel imaging via compressive sampling. IEEE Signal Process. Mag. 2007, 24, 83–91. [Google Scholar] [CrossRef]
- Luo, J.; Zhang, X.; Wang, Z. Direction-of-arrival estimation using sparse variable projection optimization. In Proceedings of the International Symposium on Circuits and Systems (ISCAS), Seoul, Korea, 20–23 May 2012; pp. 3106–3109.
- Luo, J.; Zhang, X.; Wang, Z. A new subband information fusion method for wideband DOA estimation using sparse signal representation. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 4016–4020.
- Carlin, M.; Rocca, P.; Oliveri, G.; Viani, F. Directions-of-Arrival Estimation Through Bayesian Compressive Sensing Strategies. IEEE Trans. Antennas Propag. 2013, 61, 3828–3838. [Google Scholar] [CrossRef]
- Ji, S.; Xue, Y.; Carin, L. Bayesian Compressive Sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef]
- Yu, L.; Sun, H.; Barbot, J.P.; Zheng, G. Bayesian compressive sensing for cluster structured sparse signals. Signal Process. 2012, 92, 259–269. [Google Scholar]
- Zhang, J.; Kossan, G.; Hedley, R.W.; Hudson, R.E.; Taylor, C.E.; Yao, K.; Bao, M. Fast 3D AML-based bird song estimation. Unmanned Syst. 2014, 2, 249–259. [Google Scholar] [CrossRef]
- Duarte, M.F.; Davenport, M.A.; Wakin, M.B.; Baraniuk, R.G. Sparse signal detection from incoherent projections. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toulouse, France, 14–19 May 2006; pp. 305–308.
- Malioutov, D.; Cetin, M.; Willsky, A.S. A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Trans. Signal Process. 2005, 53, 3010–3022. [Google Scholar] [CrossRef]
- Candés, E.J. The restricted isometry property and its implications for compressed sensing. Comptes Rendus Math. 2008, 346, 589–592. [Google Scholar]
- Yu, K.; Yin, M.; Hu, Y.-H.; Wang, Z. CoSCoR framework for DoA estimation in wireless array sensor network. In Proceedings of the IEEE China Summit and International Conference on Signal and Information Processing (ChinaSIP), Beijing, China, 6–10 July 2013; pp. 215–219.
- Candés, E.J.; Romberg, J.K.; Tao, T. Stable signal recovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math. 2005, 19, 410–412. [Google Scholar]
- Viswanathan, R. Signal-to-noise ratio comparison of amplify-forward and direct link in wireless sensor networks. In Proceedings of the Communication Systems Software and Middleware, Bangalore, Indian, 7–12 January 2007; pp. 1–4.
- Alirezaei, G. Optimizing Power Allocation in Sensor Networks with Application in Target Classification; Shaker Verlag: Aachen, Germany, 2014. [Google Scholar]
- Wu, L.; Yu, K.; Cao, D.; Hu, Y.-H.; Wang, Z. Efficient sparse signal transmission over lossy link using compressive sensing. Sensors 2015, 15, 880–911. [Google Scholar] [CrossRef] [PubMed]
- Lv, X.; Bi, G.; Chen, W. The group lasso for stable recovery of block-sparse signal representations. IEEE Trans. Signal Process. 2011, 59, 1371–1382. [Google Scholar] [CrossRef]
- Jie, C.; Huo, X. Theoretical results on sparse representations of multiple-measurement vectors. IEEE Trans. Signal Process. 2006, 54, 4634–4643. [Google Scholar]
- Cotter, S.F.; Rao, B.D.; Engan, K.; Kreutz-Delgado, K. Sparse solutions to linear inverse problems with multiple measurement vectors. IEEE Trans. Signal Process. 2005, 53, 2477–2488. [Google Scholar] [CrossRef]
- Lobo, M.S.; Vandenberghe, L.; Boyd, S.; Lebret, H. Applications of second-order cone programming. Linear Algebra Its Appl. 1998, 284, 193–228. [Google Scholar] [CrossRef]
- Shen, Q.; Liu, W.; Cui, W.; Wu, S.; Zhang, Y.D.; Amin, M.G. Low complexity direction of arrival estimation based on wideband co-prime arrays. IEEE Trans. Audio Speech Lang. Process. 2015, 23, 1445–1456. [Google Scholar] [CrossRef]
- Wang, H.; Kaveh, M. Coherent signal-subspace processing for the detection and estimation of angles of arrival of multiple wide-band sources. IEEE Trans. Acoust. Speech Signal Process. 1985, 33, 823–831. [Google Scholar] [CrossRef]
- Sun, L.; Liu, J.; Chen, J.; Ye, J. Efficient recovery of jointly sparse vectors. In Proceedings of the 2009 Conference on Advances in Neural Information Processing System, Vancouver, BC, Canada, 7–10 December 2009; pp. 1812–1820.
- Davenport, M.; Duarte, M.F.; Eldar, Y.C.; Kutyniok, G. Introduction to Compressed Sensing, Chapter in Compressed Sensing: Theory and Applications; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Eldar, Y.; Kuppinger, P.; Bolcskei, H. Block-sparse signals: Uncertainty relations and efficient recovery. IEEE Trans. Signal Process. 2010, 58, 3042–3054. [Google Scholar] [CrossRef]
- Hansen, R. Array pattern control and synthesis. IEEE Proc. 1992, 80, 141–151. [Google Scholar] [CrossRef]
- Sengijpta, S.K. Fundamentals of statistical signal processing: Estimation theory. Technometrics 1995, 37, 465–466. [Google Scholar] [CrossRef]
- Sedumi. Available online: http://sedumi.ie.lehigh.edu/ (accessed on 9 May 2016).
- Likar, A.; Vidmar, T. A peak-search method based on spectrum convolution. J. Phys. D Appl. Phys. 2003, 36, 1903–1909. [Google Scholar] [CrossRef]
- Guo, Q.; Liao, G. Fast music spectrum peak search via metropolis-hastings sampler. J. Electron. 2005, 22, 599–604. [Google Scholar] [CrossRef]
- Yu, K.; Yin, M.; Du, T.; Wu, L.; Wang, Z. Demo: AWSAN: A realtime wireless sensor array platform. In Proceedings of the International Conference on Mobile Ad-hoc and Sensor System (IEEE MASS), Hangzhou, China, 14–16 October 2013; pp. 441–442.
- ZigBee Specifications. Available online: http://www.zigbee.org (accessed on 9 May 2016).
- Xia, P.; Zhou, S.; Giannakis, G.B. Achieving the welch bound with difference set. IEEE Trans. Inf. Theory 2005, 51, 1900–1907. [Google Scholar] [CrossRef]
- Tang, Z.; Blacquiere, G.; Leus, G. Aliasing-free wideband beamforming using sparse signal representation. IEEE Trans. Signal Process. 2011, 59, 3464–3469. [Google Scholar] [CrossRef]


| Symbol | Explanation |
|---|---|
| H | number of sensors within an array |
| Q | number of sources |
| sparsity of the q-th source signal | |
| the q-th source signal in the time domain | |
| dominant sparse vector in the frequency domain with -sparsity | |
| less prominent components of in the frequency domain | |
| time delay of the q-th source between the h-th sensor and the array centroid | |
| received time domain signal in the h-th array | |
| Ψ | inverse DFT matrix |
| received time domain signal at the h-th sensor, | |
| signal spectrum of , | |
| array data spectrum at the k-th frequency, | |
| steering vector of at the k-th frequency, | |
| source signal vector of L directions, | |
| steering matrix of L directions at the k-th frequency | |
| array data spectrum matrix | |
| permutation matrix | |
| wideband array data spectrum, | |
| array spectrum of H sensors, | |
| sample intervals, | |
| rounding operation | |
| Φ | random sub-sampling matrix |
| channel loss matrix | |
| received measurement of the h-th sensor in the fusion center | |
| joint measurement vector of H sensors, | |
| joint noise vector of N frequencies, | |
| Θ | joint measurement matrix of H sensors, |
| block diagonal matrix operation | |
| Υ | joint sparse matrix |
| direction indicative vector, | |
| nonzero index of a vector, | |
| pruned joint sparse matrix, | |
| Fisher information matrix of parameter Λ | |
| Cramr–Rao bound of the CSJSR algorithm |
| L1-SVD | CSJSR-DoA | CSA-DoA | COBE | |
|---|---|---|---|---|
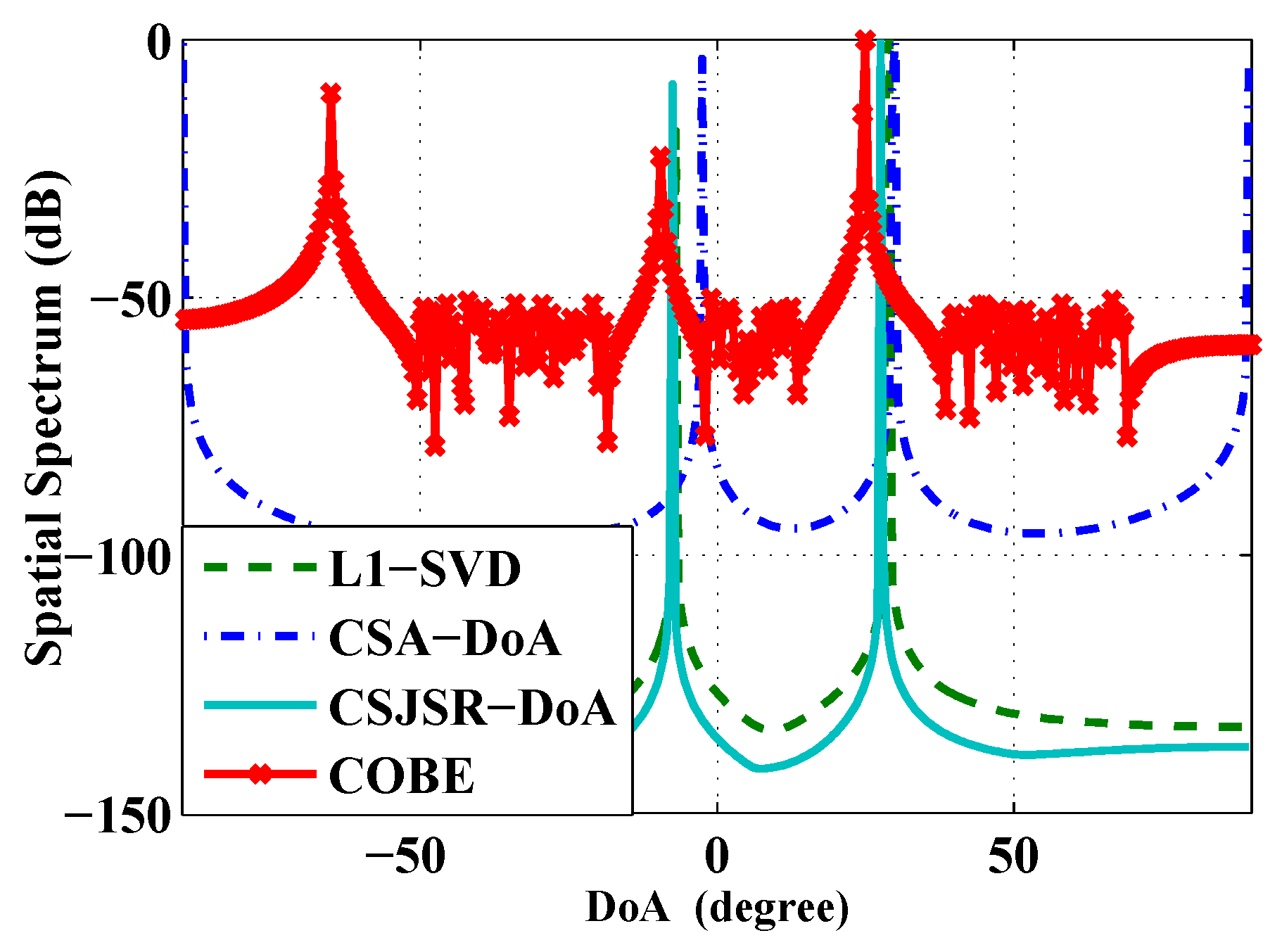
| DoA () | [,29] | [,27.5] | [,30] | [,25] |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, K.; Yin, M.; Luo, J.-A.; Wang, Y.; Bao, M.; Hu, Y.-H.; Wang, Z. Wireless Sensor Array Network DoA Estimation from Compressed Array Data via Joint Sparse Representation. Sensors 2016, 16, 686. https://doi.org/10.3390/s16050686
Yu K, Yin M, Luo J-A, Wang Y, Bao M, Hu Y-H, Wang Z. Wireless Sensor Array Network DoA Estimation from Compressed Array Data via Joint Sparse Representation. Sensors. 2016; 16(5):686. https://doi.org/10.3390/s16050686
Chicago/Turabian StyleYu, Kai, Ming Yin, Ji-An Luo, Yingguan Wang, Ming Bao, Yu-Hen Hu, and Zhi Wang. 2016. "Wireless Sensor Array Network DoA Estimation from Compressed Array Data via Joint Sparse Representation" Sensors 16, no. 5: 686. https://doi.org/10.3390/s16050686
APA StyleYu, K., Yin, M., Luo, J.-A., Wang, Y., Bao, M., Hu, Y.-H., & Wang, Z. (2016). Wireless Sensor Array Network DoA Estimation from Compressed Array Data via Joint Sparse Representation. Sensors, 16(5), 686. https://doi.org/10.3390/s16050686






