Review of the Usefulness of Various Rotational Seismometers with Laboratory Results of Fibre-Optic Ones Tested for Engineering Applications
Abstract
:1. Introduction
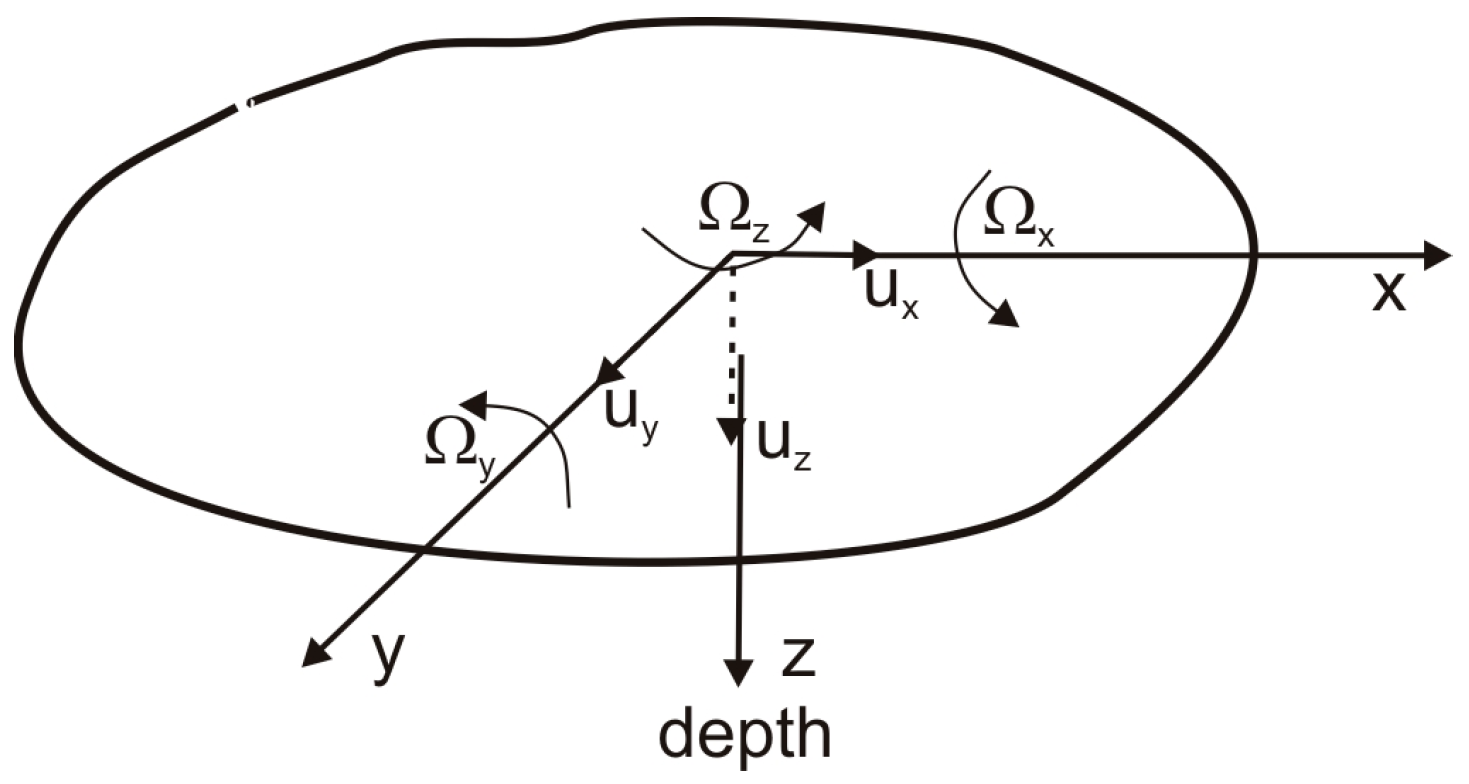
2. Fundamental Requirements for Rotational Seismometers Depending on Area of Interest
3. Rotational Seismometers for Indirect Measurement of Rotation
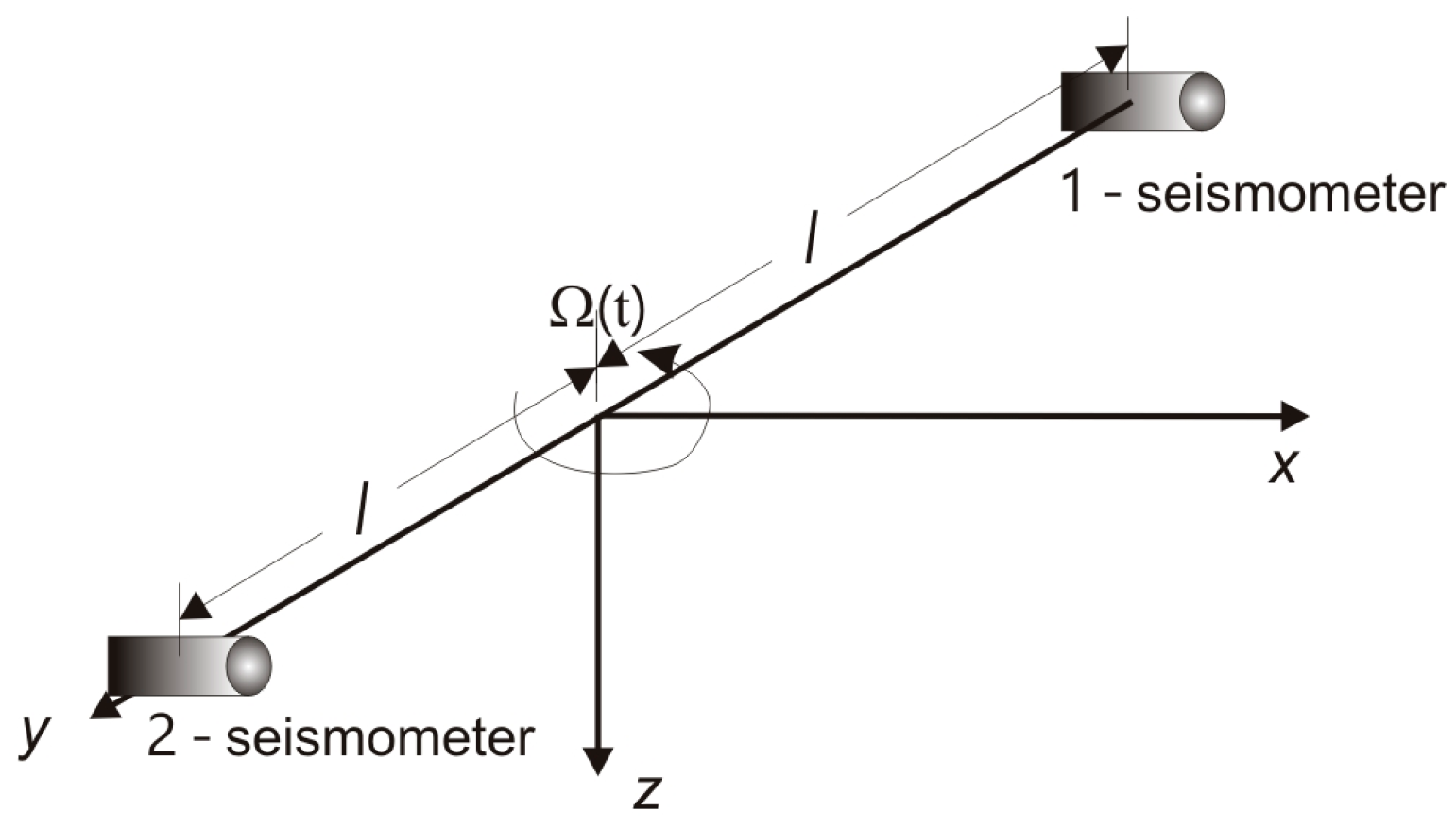
3.1. Rotational Seismometer Using a Pair of Classical Pendulum Seismometers
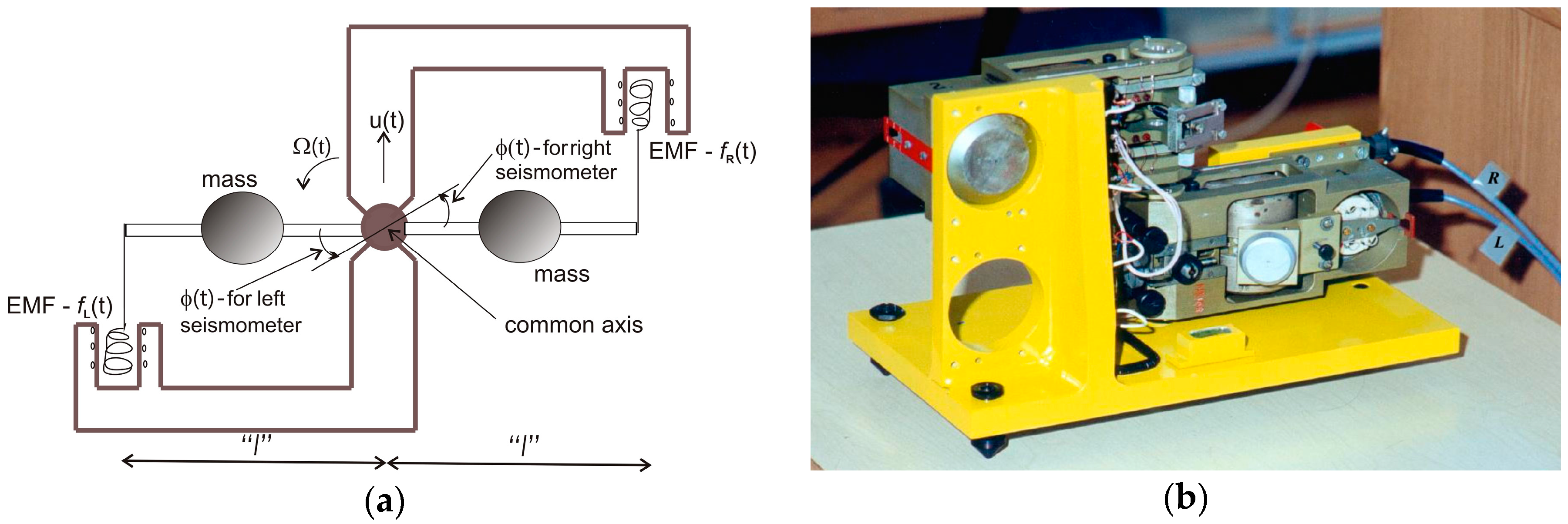
3.2. Rotational Seismometers Using Pairs of Classical Geophones
4. Rotational Seismometers for Direct Measurement of Rotation
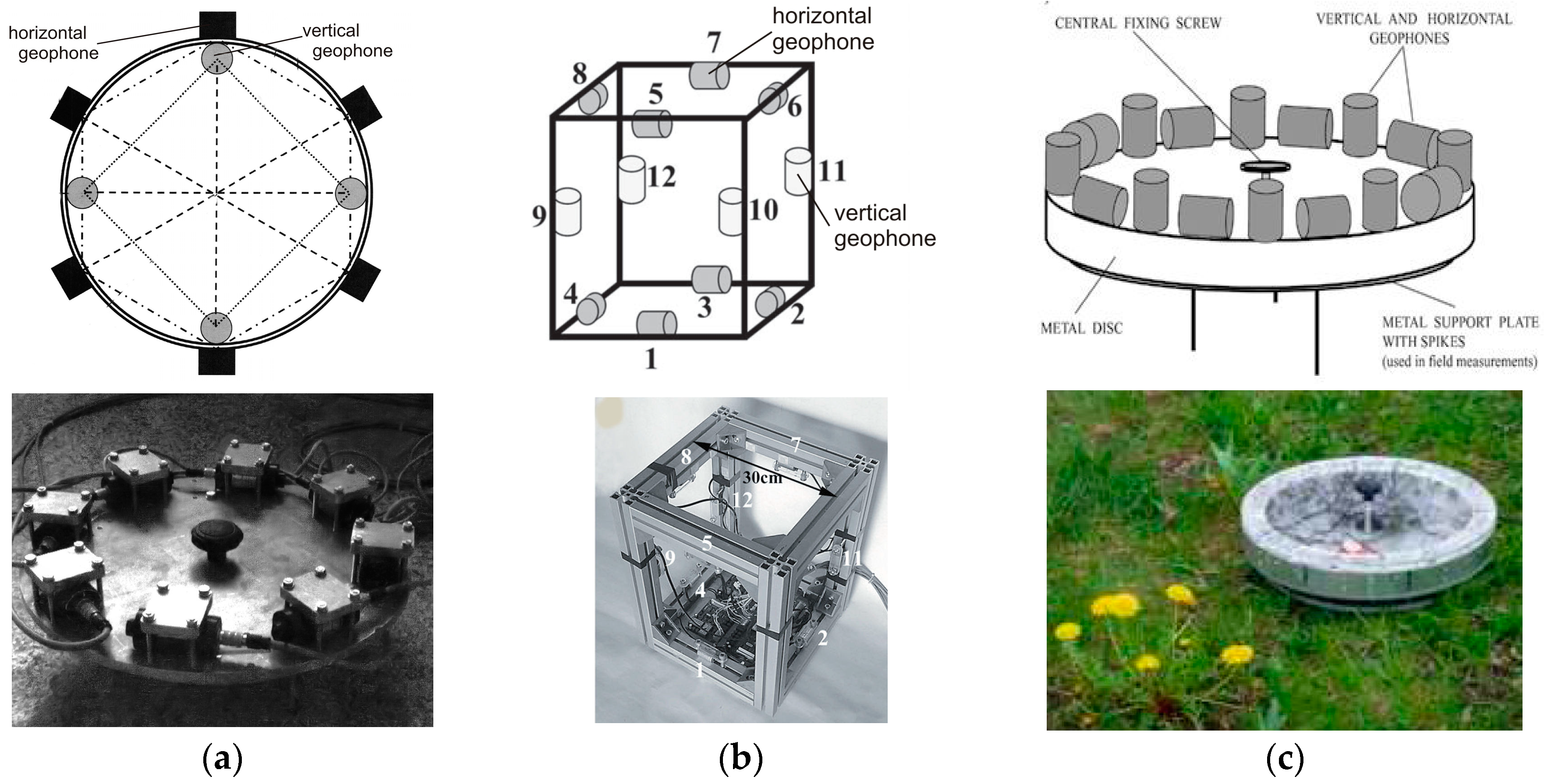
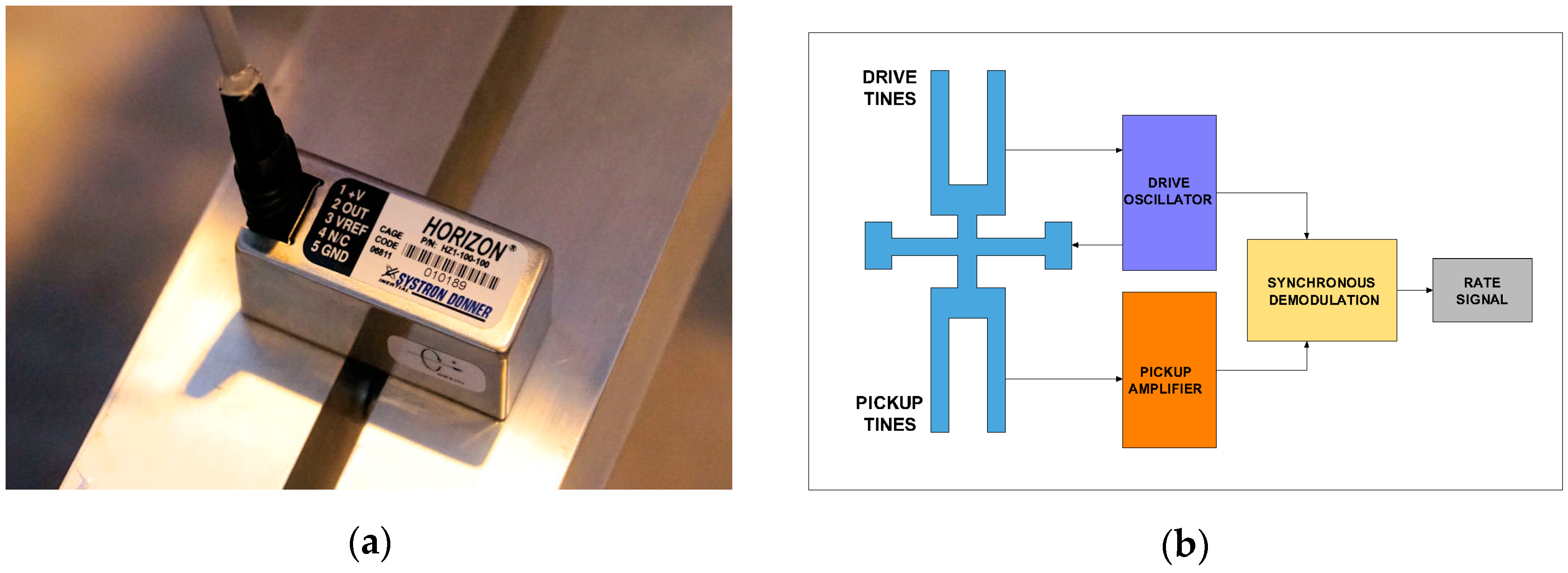
4.1. Rotational Seismometer Using Mechanical Sensor Technology
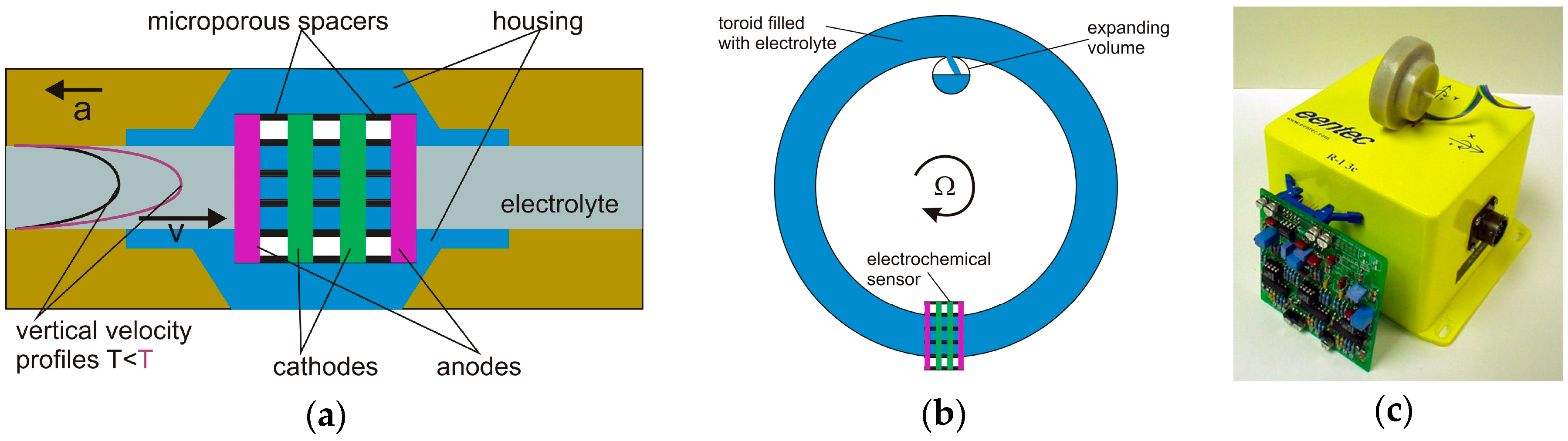
4.2. Rotational Seismometers Using Electrochemical Sensor Technology
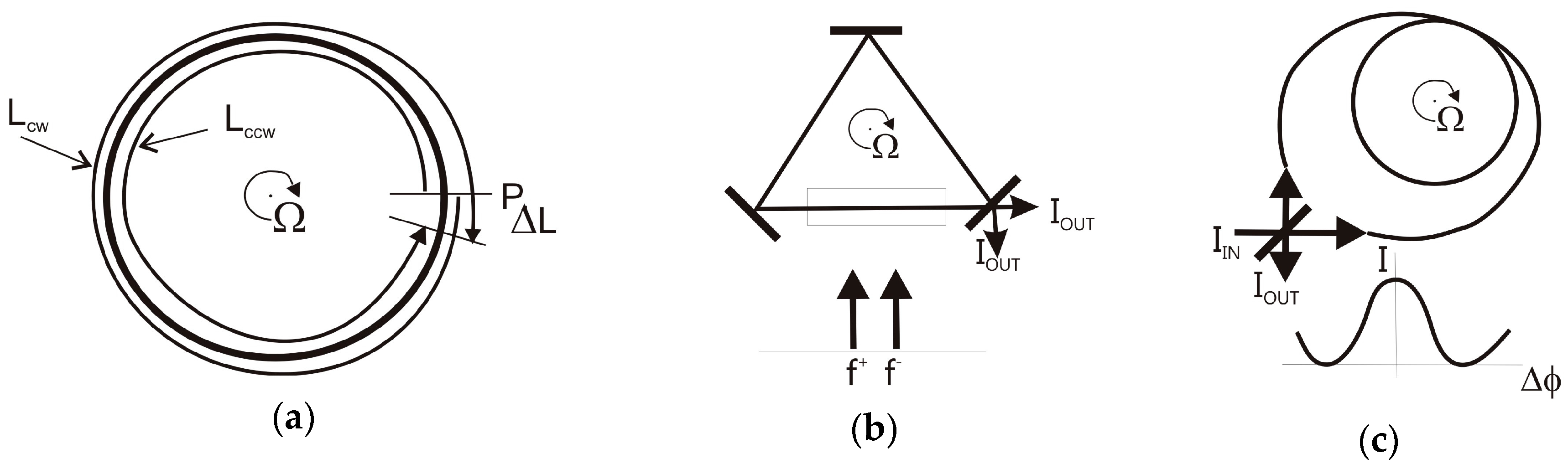
4.3. Rotational Seismometers Using Optical Sensor Technology
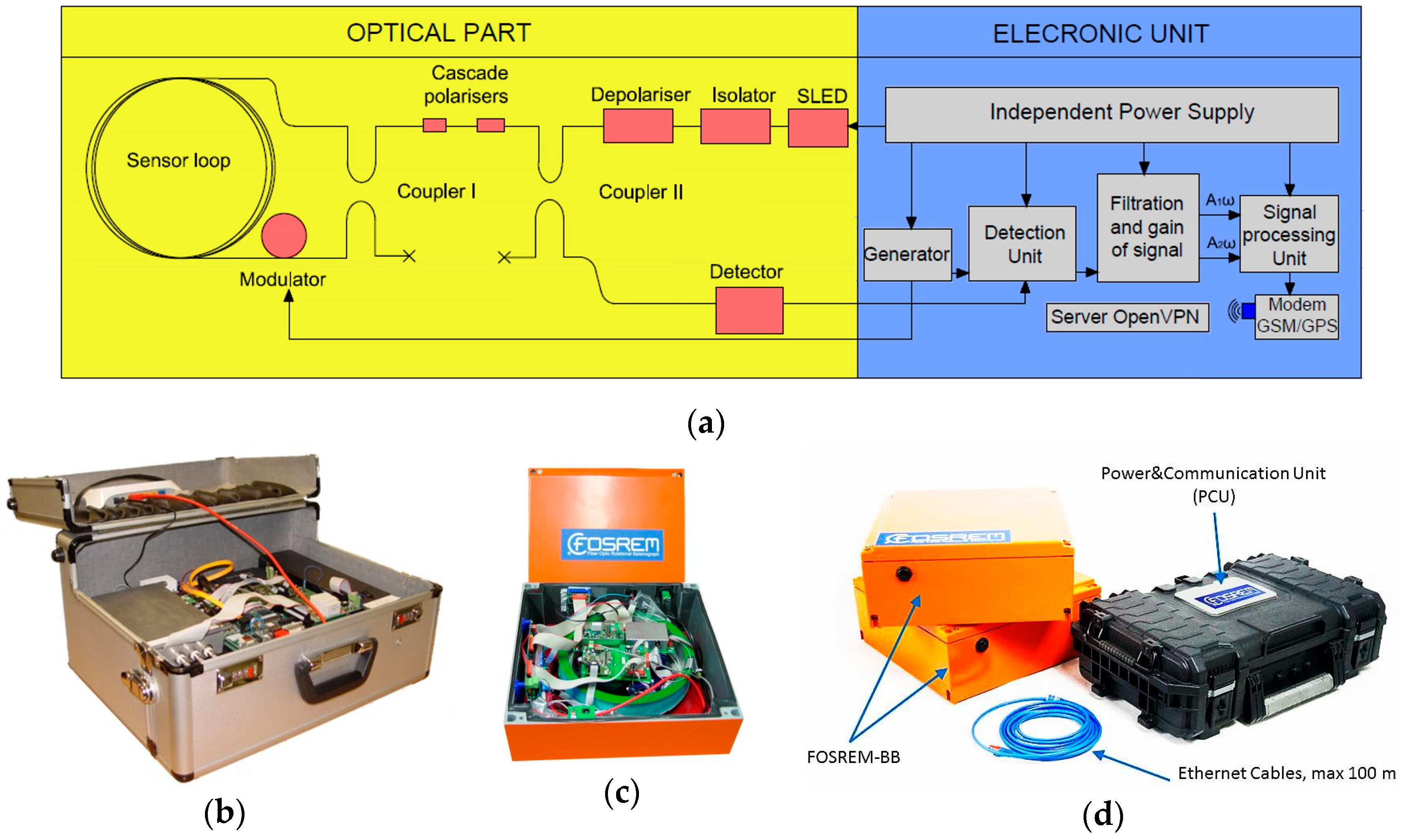
5. FOSREM as a System for Seismological as Well as Engineering Applications
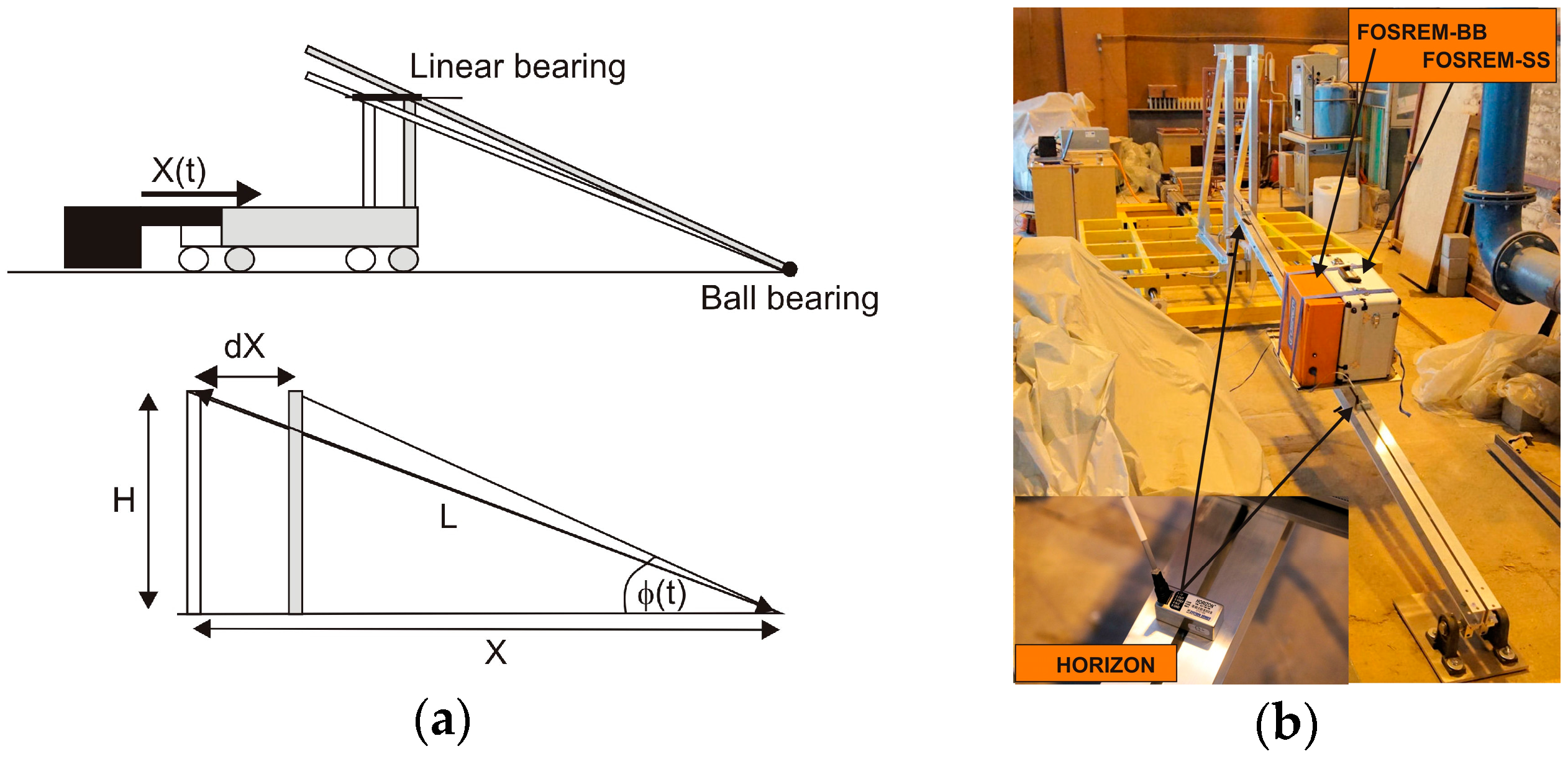
5.1. Construction, Operation and Main Parameters of FOSREM
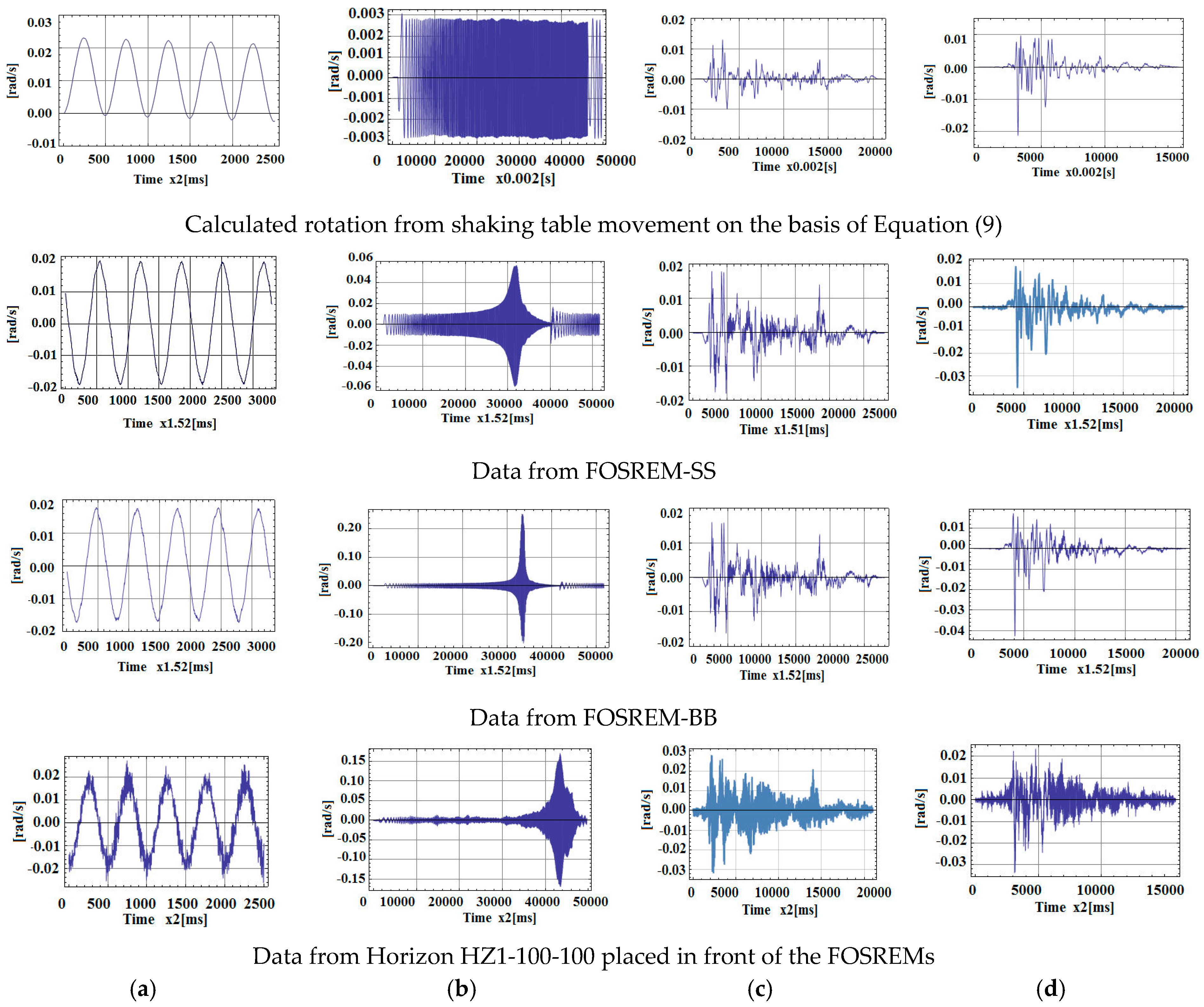
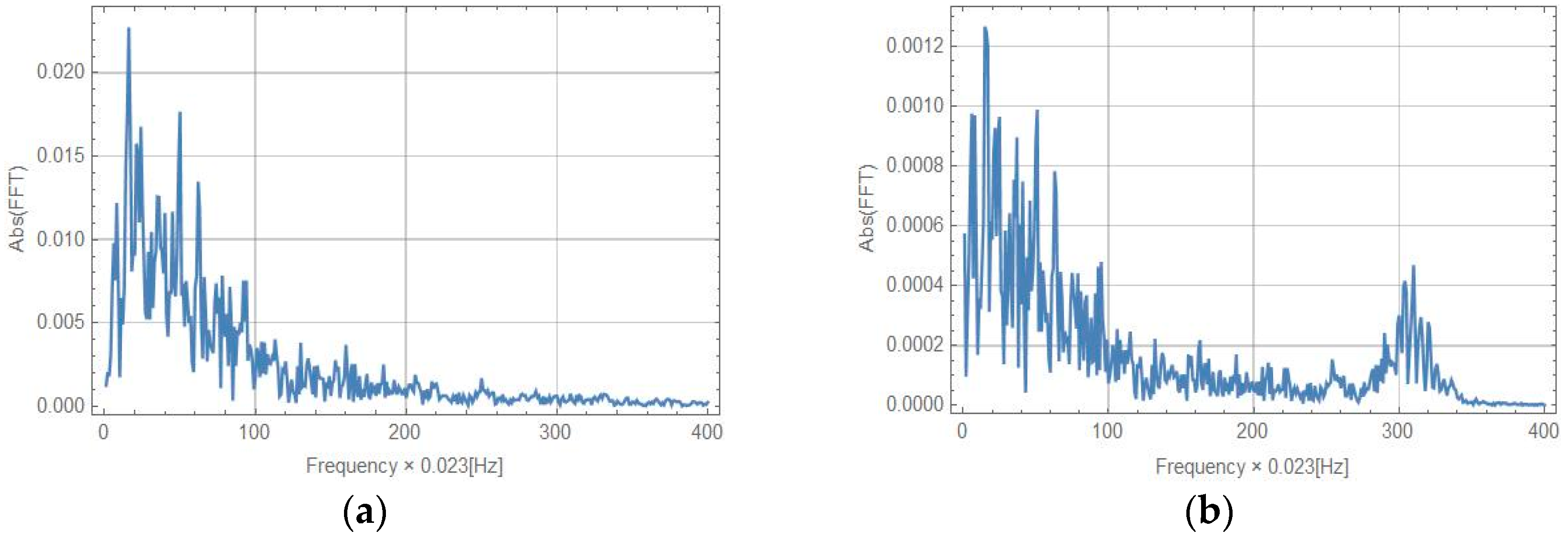
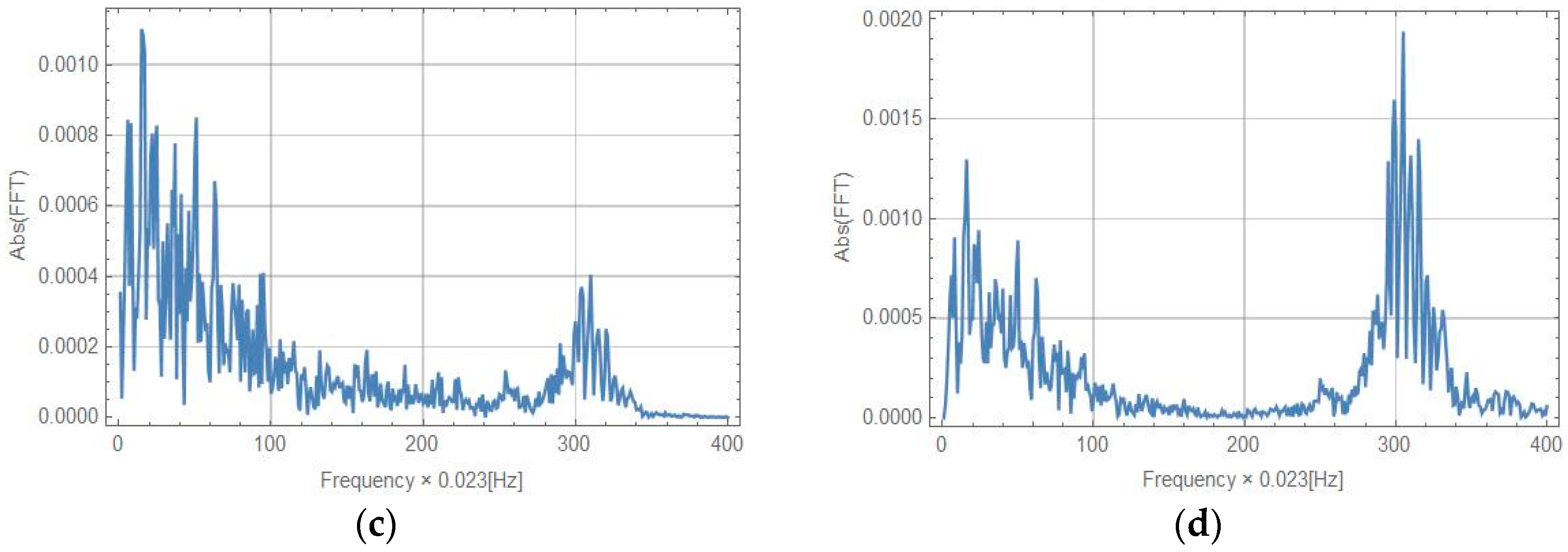
5.2. Recording Strong Rotational Motion with a New Set-Up Using Earthquake Simulations
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lee, W.H.K.; Celebi, M.; Todorovska, M.; Igel, H. Introduction to the Special Issue on Rotational Seismology and Engineering Applications. Bull. Seismol. Soc. Am. 2009, 99, 945–957. [Google Scholar] [CrossRef]
- Anderson, J.G. Strong-motion seismology. In The International Handbook of Earthquake and Engineering Seismology, Part B, 1st ed.; Lee, W.H.K., Kanamori, H., Jennings, P.C., Kisslinger, C., Eds.; Academic Press: Amsterdam, The Netherlands, 2003; Chapter 57; pp. 937–965. [Google Scholar]
- Trifunac, M.D. Review: Rotations in Structural Response. Bull. Seismol. Soc. Am. 2009, 99, 968–979. [Google Scholar] [CrossRef]
- Mustafa, A. Earthquake Engineering—From Engineering Seismology to Optimal Seismic Design of Engineering Structures, 1st ed.; InTech: Rijeka, Croatia, 2015. [Google Scholar]
- Teisseyre, R.; Takeo, M.; Majewski, E. Earthquake Source Asymmetry, Structural Media and Rotation Effects, 1st ed.; Springer: Heidelberg, Germany, 2006. [Google Scholar]
- Teisseyre, R.; Nagahama, H.; Majewski, E. Physics of Asymmetric Continuum: Extreme and Fracture Process Earthquake Source Asymmetry, Structural Media and Rotation Effects, 1st ed.; Springer: Heidelberg, Germany, 2008. [Google Scholar]
- Havskov, J.; Alguacil, G. Instrumentation in Earthquake Seismology, 2nd ed.; Springer: Cham, Switzerland, 2016. [Google Scholar]
- McGuire, R. Probabilistic seismic hazard analysis: Early history. Earthq. Eng. Struct. D 2008, 37, 329–338. [Google Scholar] [CrossRef]
- Presentation on Seismotectonics from the Department of Geophysics, University of Munich. Available online: http://www.geophysik.uni-muenchen.de/~igel/Lectures/Sedi/sedi_tectonics.ppt (accessed on 10 August 2016).
- Carey, S.W. Earth expansion and the null Universe. In Expanding Earth Symposium, Sydney, 1981; Carey, S.W., Ed.; University of Tasmania: Hobart, Australia, 1983; pp. 365–372. [Google Scholar]
- Ju, L.; Blair, D.G.; Zhao, C. Detection of gravitational waves. Rep. Prog. Phys. 2000, 63, 1317–1427. [Google Scholar] [CrossRef]
- Lantz, B.; Schofield, R.; O’Reilly, B.; Clark, D.E.; DeBra, D. Review: Requirements for a ground rotation sensor to improve advanced LIGO. Bull. Seismol. Soc. Am. 2009, 99, 980–989. [Google Scholar] [CrossRef]
- Kozák, J.T. Tutorial on earthquake rotational effects: Historical examples. Bull. Seismol. Soc. Am. 2009, 99, 998–1010. [Google Scholar] [CrossRef]
- Kozák, J.T. Development of earthquake rotational effect study. In Earthquake Source Asymmetry, Structural Media and Rotation Effects, 1st ed.; Teisseyre, R., Takeo, M., Majewski, E., Eds.; Springer: Heidelberg, Germany, 2006; Chapter 1; pp. 3–10. [Google Scholar]
- Igel, H.; Brokesova, J.; Evans, J.; Zembaty, Z. Preface to the special issue on advances in rotational seismology: Instrumentation, theory, observations and engineering. J. Seismol. 2012, 16, 571–572. [Google Scholar] [CrossRef]
- Mallet, R. Great Neapolitan Earthquake of 1857: The First Principles of Observational Seismology as Developed in the Report to the Royal Society of London of the Expedition Made by Command of the Society into the Interior of the Kingdom of Naples to Investigate the Circumstances of the Great Earthquake of December 1857; Chapman and Hall: London, UK, 1862; Volume 2. [Google Scholar]
- Teisseyre, R.; Suchcicki, J.; Teisseyre, K.P.; Wiszniowski, J.; Palangio, P. Seismic rotation waves: Basic elements of the theory and recordings. Ann. Geophys. 2003, 46, 671–685. [Google Scholar]
- Majewski, E. Spinors and twistors in the description of rotational seismic waves and spin and twist solitons. Bull. Seismol. Soc. Am. 2009, 99, 1137–1146. [Google Scholar] [CrossRef]
- Merkel, A.; Tournat, V.; Gusev, V. Experimental evidence of rotational elastic waves in granular photonic crystals. Phys. Rev. Lett. 2011, 107, 225502. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Igel, H.; Gallovič, F.; Cochard, A. Source and basin effects on rotational ground motions: Comparison with translations. Bull. Seismol. Soc. Am. 2009, 99, 1162–1173. [Google Scholar] [CrossRef]
- Newmark, N.M.; Hall, H.J. Seismic design criteria for nuclear reactor facilities. In B4 Proceedings of the 4th World Conference on Earthquake Engineering, Santiago, Chile, 13–18 January 1969; pp. 37–50.
- Newmark, N.M.; Rosenblueth, E. Fundamentals of Earthquake Engineering, 1st ed.; Prentice Hall: New York, NY, USA, 1971. [Google Scholar]
- Zembaty, Z.B. Tutorial on surface rotations from the wave passage effects—Stochastic approach. Bull. Seismol. Soc. Am. 2009, 99, 1040–1049. [Google Scholar] [CrossRef]
- Trifunac, M.D. Effects of torsional and rocking excitations on the response of structures. In Earthquake Source Asymmetry, Structural Media and Rotation Effects, 1st ed.; Teisseyre, R., Takeo, M., Majewski, E., Eds.; Springer: Heidelberg, Germany, 2006; Chapter 39; pp. 569–582. [Google Scholar]
- Kalakan, E.; Graizer, V. Coupled tilt and translational ground motion response spectra. J. Struct. Eng. 2007, 133, 609–619. [Google Scholar] [CrossRef]
- Galitzin, B.B. Lectures on Seismometry; Russian Academy of Sciences: St. Petersburg, Russia, 1912. (In Russian) [Google Scholar]
- Kharin, D.A.; Simonov, L.I. VBPP seismometer for separate registration of translational motion and rotations. Seism. Instrum. 1969, 5, 51–66. (In Russian) [Google Scholar]
- Droste, Z.; Teisseyre, R. Rotational and displacemental components of ground motion as deduced from data of the azimuth system of seismographs. Pub. Inst. Geophys. Pol. Acad. Sci. 1976, 97, 157–167. [Google Scholar]
- Farrell, W.E. A gyroscope seismometer: Measurements during the Borrego earthquake. Bull. Seismol. Soc. Am. 1969, 59, 1239–1245. [Google Scholar]
- Graizer, V.M. Inertial seismometry methods. Izv. USSR Acad. Sci. Phys. Solid Earth 1991, 27, 51–61. [Google Scholar]
- Nigbor, R.L. Six-degree-of-freedom ground motion measurement. Bull. Seismol. Soc. Am. 1994, 84, 1665–1669. [Google Scholar]
- Trifunac, M.D. A note on surface strains associated with incident body waves. Bull. Eur. Assoc. Earthq. Eng. 1979, 5, 85–95. [Google Scholar]
- Trifunac, M.D. A note on rotational components of earthquake motions on ground surface for incident body waves. Soil Dyn. Earthq. Eng. 1982, 1, 11–19. [Google Scholar] [CrossRef]
- Olivera, C.S.; Bolt, B.A. Rotational components of surface strong ground motion. Earthq. Eng. Struct. Dyn. 1989, 18, 517–526. [Google Scholar] [CrossRef]
- Spudich, P.; Steck, L.K.; Hellweg, M.; Fletcher, J.B.; Baker, L.M. Transient stress at Parkfield, California produced by the M 7.4 Landers earthquake of June 28, 1992: Observations from the UPSAR dense seismograph array. J. Geophys. Res. 1995, 100, 675–690. [Google Scholar] [CrossRef]
- Bodin, P.; Gomberg, J.; Singha, S.K.; Santoyo, M. Dynamic deformations of shallow sediments in the Valley of Mexico, part 1: Three dimensional strains and rotations recorded on a seismic array. Bull. Seismol. Soc. Am. 1997, 87, 528–539. [Google Scholar]
- Huang, B.S. Ground rotational motions of the 1991 Chi-Chi, Taiwan earthquake as inferred from dense array observations. Geophys. Res. Lett. 2003, 30, 1307–1310. [Google Scholar]
- Suryanto, W.; Igel, H.; Wassermann, J.; Cochard, A.; Schuberth, B.; Vollmer, D.; Scherbaum, F.; Schreiber, U.; Velikoseltsev, A. First comparison of array-derived rotational ground motions with direct ring laser measurements. Bull. Seismol. Soc. Am. 2006, 96, 2059–2071. [Google Scholar] [CrossRef]
- Wassermann, J.; Lehndorfer, S.; Igel, H.; Schreiber, U. Performance test of a commercial rotational motions sensor. Bull. Seismol. Soc. Am. 2009, 99, 1449–1456. [Google Scholar] [CrossRef]
- Bernauer, F.; Wassermann, J.; Igel, H. Rotational sensors—A comparison of different sensor types. J. Seismol. 2012, 16, 595–602. [Google Scholar] [CrossRef]
- Takeo, M. Rotation motion observed during an earthquake swarm in April, 1998 at offshore Ito, Japan. Bull. Seismol. Soc. Am. 2009, 99, 1457–1467. [Google Scholar] [CrossRef]
- Moriya, T.; Teisseyre, R. Design of rotation seismometer and non-linear behaviour of rotation components of earthquakes. In Earthquake Source Asymmetry, Structural Media and Rotation Effects, 1st ed.; Teisseyre, R., Takeo, M., Majewski, E., Eds.; Springer: Heidelberg, Germany, 2006; Chapter 32; pp. 439–450. [Google Scholar]
- Zembaty, Z.; Mutke, G.; Nawrocki, D.; Bobra, P. Rotational ground motion records from induced seismic events. Seismol. Res. Lett. 2016. [CrossRef]
- Evans, J.R.; Igel, H.I.; Knopftt, L.; Teng, T.I.; Trifunac, M.D. Rotational seismology and engineering—Online proceedings for the first international workshop. US Geol. Surv. Open-File Rep. 2007, 1144, 36–37. [Google Scholar]
- Lee, W.H.K. A glossary of rotational seismology. Bull. Seismol. Soc. Am. 2009, 99, 1082–1090. [Google Scholar] [CrossRef]
- Teisseyre, R.; Nagahama, H. Micro-inertia continuum: Rotations and semi-waves. Acta Geophys. Pol. 1999, 47, 259–272. [Google Scholar]
- Nowożyński, K.; Teisseyre, K.P. Time-domain filtering of seismic rotation waves. Acta Geophys. Pol. 2002, 51, 51–61. [Google Scholar]
- Jaroszewicz, L.R.; Krajewski, Z.; Solarz, L.; Marć, P.; Kostrzyński, T. A new area of the fiber-optic Sagnac interferometer application. In Proceedings of the International Microwave and Optoelectronics Conference IMOC-2003, Iguazu Falls, Brazil, 20–23 September 2003; pp. 661–666.
- Teisseyre, R.; Suchcicki, J.; Teisseyre, K.P. Recording of seismic rotation waves: Reliability analysis. Acta Geophys. Pol. 2003, 51, 37–50. [Google Scholar]
- Solarz, L.; Krajewski, Z.; Jaroszewicz, L.R. Analysis of seismic rotations detected by two antiparallel seismometers: Spine function approximation of rotation and displacement velocities. Acta Geophys. Pol. 2004, 52, 198–217. [Google Scholar]
- Teisseyre, R. Continuum with defect and self-rotation fields. Acta Geophys. Pol. 2002, 50, 51–68. [Google Scholar]
- Teisseyre, R.; Boratyński, W. Continuum with self-rotation nuclei: Evolution of defect fields and equation of motion. Acta Geophys. Pol. 2002, 50, 223–230. [Google Scholar]
- Jaroszewicz, L.R.; Krajewski, Z.; Solarz, L.; Teisseyre, R. Application of the FORS-II for investigation of the seismic rotation waves. Proc. SPIE 2005, 5776, 385–393. [Google Scholar]
- Wiszniowski, J. Rotation and twist motion recording—couple pendulum and rigid seismometer system. In Earthquake Source Asymmetry, Structural Media and Rotation Effects, 1st ed.; Teisseyre, R., Takeo, M., Majewski, E., Eds.; Springer: Heidelberg, Germany, 2006; Chapter 33; pp. 451–470. [Google Scholar]
- Skrzyński, A.; (Institute of Geophysics PAS, Warsaw, Poland); Krajewski, Z.; (Military University of Technology, Warsaw, Poland). The main parameters of the Two Antiparallel Pendulum Seismometers. Personal communication, Poland, 2016. [Google Scholar]
- Brokešová, J.; Málek, J.; Štrunc, J. Rotational Seismic Sensor System, Seismic Measuring Set Containing that System, and Seismic Survey Method. Patent CZ301217 B6, 8 December 2009. [Google Scholar]
- Brokešová, J.; Málek, J. New portable sensor system for rotational seismic motion measurements. Rev. Sci. Instrum. 2010, 81, 084501. [Google Scholar] [CrossRef] [PubMed]
- Brokešová, J.; Málek, J.; Kolínský, P. Rotaphone, a mechanical seismic sensor system for field rotation rate measurements and its in situ calibration. J. Sesimol. 2012, 16, 603–621. [Google Scholar] [CrossRef]
- Brokešová, J.; Málek, J.; Evans, J.R. Rotaphone, a new self-calibrated six-degree-of-freedom seismic sensor. Rev. Sci. Instrum. 2012, 83, 086108. [Google Scholar] [CrossRef] [PubMed]
- Brokešová, J.; Málek, J. Rotaphone, a self-calibrated six-degree-of-freedom seismic sensor and its strong-motion records. Seismol. Res. Lett. 2013, 84, 737–744. [Google Scholar] [CrossRef]
- Brokešová, J.; Málek, J.; Evans, J.R. Rotaphone-D—A new six-degree-of freedom short-period seismic sensor: Features, parameters, field records. In Proceedings of the 4th International Working Group on Rotational Seismology Meeting, Tutzing, Germany, 20–23 June 2016; Available online: http://www.rotational-seismology.org/events/workshops/Presentations_2016/presentations/Brokesova_talk (accessed on 10 August 2016).
- Brokešová, J. Short-Period Seismic Rotations and Translations Recorded by Rotaphone. Habilitation Thesis, Department of Geophysics, Faculty of Mathematics and Physics, Charles University, Prague, Czech Republic, 2014. [Google Scholar]
- Brokešová, J.; Málek, J. Six-degree-of-freedom near-source seismic motions II: Examples of real seismogram analysis and S-wave velocity retrieval. J. Seismol. 2015, 19, 511–539. [Google Scholar]
- Horizon™ MEMS Quartz Angular Rate Sensor. Available online: http://www.systron.com/sites/default/files/964120_n-hz1.pdf (accessed on 10 August 2016).
- Quartz MEMS Technology. Available online: http://www.systron.com/support/technology (accessed on 17 September 2016).
- Zembaty, Z.; Kokot, S.; Bobra, P. Application of rotation rate sensors in an experiment of stiffness ‘reconstruction’. Smart Mater. Struct. 2013, 22, 077001. [Google Scholar] [CrossRef]
- Horizon User’s Guide. Available online: http://www.systron.com/sites/default/files/964013-rev._d_horizon_user_guide.pdf (accessed on 20 August 2016).
- High Resolution Rotational Seismometer Model R-1. Available online: http://www.eentec.com/R-1_data_new.htm (accessed on 7 July 2016).
- Rotational Seismometers R-2, R3. Data sheet from AST LLC Distributed. In Proceedings of the 4th International Working Group on Rotational Seismology Meeting, Tutzing, Germany, 20–23 June 2016.
- Abramovich, J.A.; Kharlamov, A.V. Electrochemical transducer and a method for fabricating the same. Electrochemical Sensors Transducer. Patent US6576103 B2, 8 August 2001. [Google Scholar]
- Wraszczatelnyie Seismiczeskie Datcziki i MGD Obratnaia Swiaz. Available online: http://www.сейсмометр.рф/mhd.html (accessed on 1 October 2016).
- Nighor, R.L.; Evans, J.R.; Hutt, Ch.R. Laboratory and field testing of commercial rotational seismometers. Bull. Seismol. Soc. Am. 2009, 99, 1215–1227. [Google Scholar]
- Lee, W.H.K.; Evans, J.R.; Huang, B.-S.; Hut, C.R.; Lin, C.-J.; Liu, C.C.; Nigbor, R.L. Measuring rotational ground motions in seismological practice. In New Manual of Seismological Observatory Practice 2 (NMSOP-2), 1st ed.; Bormann, P., Ed.; Deutsches GeoForschungsZentrum GFZ: Potsdam, Germany, 2012; pp. 1–27. [Google Scholar]
- Lee, W.H.K.; Huang, B.S.; Langston, C.A.; Lin, C.J.; Liu, C.C.; Shin, T.C.; Teng, T.L.; Wu, C.F. Review: Progress in rotational ground-motion observations from explosions and local earthquakes in Taiwan. Bull. Seismol. Soc. Am. 2009, 99, 958–967. [Google Scholar] [CrossRef]
- Sagnac, G. L’ether lumineux demontre par l’effet du vent relatif d’Etherdanus un interferometre en rotation uniforme. C. R. Acad. Sci. 1913, 95, 708–710. (In French) [Google Scholar]
- Post, E.J. Sagnac effect. Rev Mod. Phys. 1967, 39, 475–494. [Google Scholar] [CrossRef]
- Jaroszewicz, L.R.; Krajewski, Z.; Solarz, L. Absolute rotation measurement based on the Sagnac effect. In Earthquake Source Asymmetry, Structural Media and Rotation Effects, 1st ed.; Teisseyre, R., Takeo, M., Majewski, E., Eds.; Springer: Heidelberg, Germany, 2006; Chapter 31; pp. 413–438. [Google Scholar]
- Rosenthal, A.H. Regenerative circulatory multiple-beam interferometry for the study of light propagation effect. J. Opt. Soc. Am. 1962, 52, 1143–1148. [Google Scholar] [CrossRef]
- Aronowitz, F. The laser gyro. In Laser Applications; Ross, M., Ed.; Academic Press: New York, NY, USA, 1971; Volume 1, pp. 133–200. [Google Scholar]
- Stedman, G.E. Ring laser tests of fundamental physics and geophysics. Rep. Progr. Phys. 1997, 60, 615–688. [Google Scholar] [CrossRef]
- Rowe, C.H.; Schreiber, K.U.; Cooper, S.J.; King, B.T.; Poulten, M.; Stedman, G.E. Design and operation of a very large ring laser gyroscope. Appl. Opt. 1999, 38, 2516–2523. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, K.U.; Schneider, M.; Rowe, C.H.; Stedman, G.E.; Schlüter, W. Aspects of ring lasers as local earth rotation sensors. Surv. Geophys. 2001, 22, 603–611. [Google Scholar] [CrossRef]
- Cochard, A.; Igel, H.; Schuberth, B.; Suryanto, W.; Velikoseltsev, A.; Schreiber, K.U.; Wassermann, J.; Scherbaum, F.; Vollmer, D. Rotation motions in seismology, theory, observation, simulation. In Earthquake Source Asymmetry, Structural Media and Rotation Effects, 1st ed.; Teisseyre, R., Takeo, M., Majewski, E., Eds.; Springer: Heidelberg, Germany, 2006; Chapter 30; pp. 391–412. [Google Scholar]
- Wells, J.-P.; Schreiber, K.U. Rotation sensing with lasers. In Proceedings of the 4th International Working Group on Rotational Seismology Meeting, Tutzing, Germany, 20–23 June 2016; Available online: http://www.rotational-seismology.org/events/workshops/Presentations_2016/presentations/Wells_talk (accessed on 10 August 2016).
- Schreiber, K.U.; Stedman, G.E.; Igel, H.; Flaws, A. Ring Laser Gyroscopes as rotation sensors for seismic wave studies. In Earthquake Source Asymmetry, Structural Media and Rotation Effects, 1st ed.; Teisseyre, R., Takeo, M., Majewski, E., Eds.; Springer: Heidelberg, Germany, 2006; Chapter 29; pp. 377–390. [Google Scholar]
- Schreiber, K.U.; Hautmann, J.N.; Velikoseltsev, A.; Wassermann, J.; Igel, H.; Otero, J.; Vernon, F.; Wells, J.-P.R. Ring laser measurements of ground rotations for seismology. Bull. Seismol. Soc. Am. 2009, 99, 1190–1198. [Google Scholar] [CrossRef]
- Widmer-Schnidrig, R.; Zurm, W. Perspectives for Ring Laser Gyroscopes in low-frequency seismology. Bull. Seismol. Soc. Am. 2009, 99, 1199–1206. [Google Scholar] [CrossRef]
- Schreiber, K.U.; Velikoseltsev, A.; Carr, A.J.; Franco-Anaya, R. The application of Fiber Optic Gyroscope for measurement of rotations in structural engineering. Bull. Seismol. Soc. Am. 2009, 99, 1207–1214. [Google Scholar] [CrossRef]
- μFORS-36m/-1 Fiber Optic Rate Sensors. Available online: http://www.northropgrumman.litef.com/fileadmin/downloads/Datenblaetter/Datenblatt_uFors-36_-1.pdf (accessed on 2 October 2016).
- Jaroszewicz, L.R.; Krajewski, Z.; Kowalski, H.; Mazur, G.; Zinówko, P.; Kowalski, J. AFORS Autonomous Fibre-Optic Rotational Seismograph: Design and application. Acta Geophys. 2011, 59, 578–596. [Google Scholar] [CrossRef]
- Jaroszewicz, L.R.; Krajewski, Z.; Teisseyre, K.P. Usefulness of AFORS—Autonomous Fibre-Optic Rotational Seismograph for investigation of rotational phenomena. J. Seismol. 2012, 16, 573–586. [Google Scholar] [CrossRef]
- Bernauer, F.; Wassermann, J.; Guattari, F.; Igel, H. Testing a prototype broadband fiber-optic gyro. In Proceedings of the 4th International Working Group on Rotational Seismology Meeting, Tutzing, Germany, 20–23 June 2016; Available online: http://www.rotational-seismology.org/events/workshops/Presentations_2016/presentations/Bernauer_talk (accessed on 10 August 2016).
- BlueSeis-3A Rotational Seismometer. In Proceedings of the 4th International Working Group on Rotational Seismology Meeting, Tutzing, Germany, 20–23 June 2016; Available online: http://www.rotational-seismology.org/events/workshops/Presentations_2016/Posters/Blueseis-3a (accessed on 10 August 2016).
- LeFevre, H.C. The Fiber Optic Gyroscope, 2nd ed.; Artech House: Norwood, MA, USA, 2014. [Google Scholar]
- Vali, V.; Shorthill, R.W. Fiber ring interferometer. Appl. Opt. 1976, 15, 1099–1100. [Google Scholar] [CrossRef] [PubMed]
- Takeo, M.; Ueda, H.; Matzuzawa, T. Development of High-Gain Rotational-Motion Seismograph; Research grant 11354004; Earthquake Research Institute, University of Tokyo: Tokyo, Japan, 2002; pp. 5–29. [Google Scholar]
- Jaroszewicz, L.R.; Krajewski, Z.; Solarz, L.; Teisseyre, R. Application of the fibre-optic Sagnac interferometer in the investigation of seismic rotational waves. Meas. Sci. Technol. 2006, 17, 1186–1193. [Google Scholar] [CrossRef]
- Kurzych, A.; Jaroszewicz, L.R.; Krajewski, Z.; Teisseyre, K.P.; Kowalski, J.K. Fibre optic system for monitoring rotational seismic phenomena. Sensors 2014, 14, 5459–5469. [Google Scholar] [CrossRef] [PubMed]
- Jaroszewicz, L.R.; Krajewski, Z.; Teisseyre, K.P. Fibre-Optic Sagnac Interferometer as Seismograph for Direct Monitoring of Rotation Events. In Earthquake Research and Analysis: Statistical Studies, Observations and Planning; D’Amico, S., Ed.; InTech Open Access Pub.: Rijeka, Croatia, 2012; Chapter 16; pp. 335–354. [Google Scholar]
- Jaroszewicz, L.R.; Kurzych, A.; Krajewski, Z.; Kowalski, J.K.; Teisseyre, K.P. FOSREM—Fibre-Optic System for Rotational Events & Phenomena Monitoring: Construction, investigation and area of application. In Seismic Behaviour and Design of Irregular and Complex Civil Structures II; Zembaty, Z., De Stefano, M., Eds.; Springer: Berlin, Germany, 2015; Chapter 5; pp. 49–64. [Google Scholar]
- Kurzych, A.; Kowalski, J.K.; Sakowicz, B.; Krajewski, Z.; Jaroszewicz, L.R. The laboratory investigation of the innovative sensor for torsional effects in engineering structures’ monitoring. Opto-Electron. Rev. 2016, 24, 134–143. [Google Scholar] [CrossRef]
- Kowalski, J.K.; Jaroszewicz, L.R.; Krajewski, Z.; Kurzych, A.; Marć, P. Measurement Method and System for Measuring Amplitude of First Two Harmonics of Signal Derived from SAGNAC System. Patent PCT/IB2015/059521, 10 December 2015. [Google Scholar]


| Parameter | Unit | TAPS [55] | Rotaphone | ||
|---|---|---|---|---|---|
| 3DOF [62] | 6DOF [62] | D [61] | |||
| Frequency range | Hz | 7 × 10−1–50 (1),(2) | 1–100 (2) | 2–60 (2) | 2–80 (2) |
| Sampling frequency | Hz | 100 | 250 | 250 | 250 |
| Sensitivity (3) | rad/s | 1 × 10−7 | 1.67 ×10−8 | 2.16 × 10−9 | 3.77 × 10−9 |
| Maximum rate | rad/s | 1 × 10−1 | 1 × 10−2 | 2.87 × 10−1 | 3.17 × 10−2 |
| Dynamic range | dB | 120 | 100 | 120 | 120 |
| Paired sensor spacing | m | 0.28 | 0.30 | 0.30 | 0.40 |
| Operating temperature | °C | −10–45 | −20–40 | −20–40 | −40–100 (4) |
| Weight | kg | 15 | 4.5 | 9.5 | 15.3 |
| Dimensions [L × W × H] | mm | 450 × 180 × 350 | 250 (5) × 10 | 350 × 350 × 430 | 445 (5) × 112 |
| Sensors: [pcs × type] | 2 × SM-3 | 8 × LF-24 | 12 × SM-6 | 16 × SM-6 | |
| Natural frequency | Hz | 4.5 | 1 | 4.5 | 4.5 |
| A/D converter: | type | Sigma-Delta | 2 × AD16021 | 4 × Tedia | 1 × EE & S |
| dynamic | Bit | 26 | 21 | 28 | 24 |
| range | V | ±10 | ±5 | ±2.5 | ±1 or ±2.5 |
| GPS receiver and antenna | Stationary system | Garmin GPS 18 (mobile) | |||
| Software: | type | Own | Own | Own | Own |
| output format | miniSEED | RotaCal | RotaCal | RotaCal | |
| Parameter | Unit | HZ1-200-100 [67] | R-1 [68] | R-2 [69] |
|---|---|---|---|---|
| Axial | uniaxial | triaxial | triaxial | |
| Sensitivity (1) | rad/s/√Hz | 4.4 × 10−4 | 1.2 × 10−7 | 0.6 × 10−7 |
| Clip level (2) | rad/s | 3.49 | 0.10 | 0.40 |
| Dynamic range | dB | 78 | 110 | 117 |
| Frequency band | Hz | >60 | 0.05–20 | 0.03–50 |
| optional extended | n/a | 0.03–50 | 0.01–100 | |
| Scale factor (3) | V/rad/s | 0.57(±2%) | 50 | 50 |
| optional | n/a | 2 × 102 | 5–2 × 102 | |
| Operating temperature | °C | −40 to +71 | −15 to +55 (extended −45 to +55) | |
| Output signal | V | +0.5 to +4.5 | ±5, ±2.5 | ±20 differential |
| Calibration (S.F. deviation from 20/22 °C) | %/°C | <0.08 | <0.03 | Internal calibration electronics |
| Shock survival | g | 200 | 200 | 200 |
| Power supply | VDC | 8–12 | 9–14 | 9–18 |
| Supply current | mA | <20 | 20 | 30 |
| Power consumption | W | 0.24 | 0.28 | 0.54 |
| Weight | kg | <0.06 | 1.0 | 1.5 |
| Dimensions [L × W × H] | mm | 58.3 × 25.3 × 25.3 | 120 × 120 × 90 | 120 × 120 × 100 |
| NEMA rating | 4 | 4 | Waterproof (submersible) | |
| Software | type | Own | Own | Own |
| Parameter | Unit | G-Ring [85] | μFORS-1 [88,89] | LCG (1) [40] | AFORS-1 [90,91] | BlueSeis-3A [92,93] |
|---|---|---|---|---|---|---|
| Axial | uniaxial | uniaxial | triaxial | uniaxial | triaxial | |
| Sensitivity (2) | rad/s/√Hz | 9 × 10−11 | 3 × 10−5 | 6.3 × 10−7 | 4 × 10−9 | 2 × 10−8 |
| Maximum Rate | rad/s | 1 | 17.5 | No data | 6.4 × 10−3 | 0.1 |
| Dyn. Range | dB | 280 | 115 | No data | 124 | 135 |
| Freq. Band | Hz | 0.003–10 | No data | DC–100 | 0.83–106.15 | DC–100 |
| S. F. Error (3) | %/°C | Not observed | ≤0.05(1σ) | Not observed | No data | <0.01 |
| Oper. Temp. | °C | Constant | −40 to 77 | No data | −10 to 50 | −10 to 50 |
| Calibration | Needs | No data | Not needed | Remote | Not needed | |
| Shock Survival | g | No data | 250 | 10 | No data | No data |
| Power Supply | VDC | high | ±5, 3.3 | 24 | 12 | 24 |
| Power Cons. | W | high | 2.5 | 25 | <24 | <20 |
| Weight | kg | No data | 0.137 | 2.7 | 18 | 20 |
| Dimensions [L × W × H] | mm | Area equal to 16 m2 | 22 × 73 × 58 | 278 × 102 × 128 | 700 diameter × 160 | 300 × 300 × 280 |
| Ingress Protection | none | hermetically sealed | none | IP66 | ||
| Sampling rate | Hz | 4 | 5 to 1000 | 200 | 212 | up to 200 |
| Output format | No data | TIL/CMOS | miniSEED | miniSEED | miniSEED | |
| Software | type | No data | No data | UDP Ethernet protocol | Web-based interface for configuration | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaroszewicz, L.R.; Kurzych, A.; Krajewski, Z.; Marć, P.; Kowalski, J.K.; Bobra, P.; Zembaty, Z.; Sakowicz, B.; Jankowski, R. Review of the Usefulness of Various Rotational Seismometers with Laboratory Results of Fibre-Optic Ones Tested for Engineering Applications. Sensors 2016, 16, 2161. https://doi.org/10.3390/s16122161
Jaroszewicz LR, Kurzych A, Krajewski Z, Marć P, Kowalski JK, Bobra P, Zembaty Z, Sakowicz B, Jankowski R. Review of the Usefulness of Various Rotational Seismometers with Laboratory Results of Fibre-Optic Ones Tested for Engineering Applications. Sensors. 2016; 16(12):2161. https://doi.org/10.3390/s16122161
Chicago/Turabian StyleJaroszewicz, Leszek R., Anna Kurzych, Zbigniew Krajewski, Paweł Marć, Jerzy K. Kowalski, Piotr Bobra, Zbigniew Zembaty, Bartosz Sakowicz, and Robert Jankowski. 2016. "Review of the Usefulness of Various Rotational Seismometers with Laboratory Results of Fibre-Optic Ones Tested for Engineering Applications" Sensors 16, no. 12: 2161. https://doi.org/10.3390/s16122161
APA StyleJaroszewicz, L. R., Kurzych, A., Krajewski, Z., Marć, P., Kowalski, J. K., Bobra, P., Zembaty, Z., Sakowicz, B., & Jankowski, R. (2016). Review of the Usefulness of Various Rotational Seismometers with Laboratory Results of Fibre-Optic Ones Tested for Engineering Applications. Sensors, 16(12), 2161. https://doi.org/10.3390/s16122161










