Abstract
Localization of machine type communication (MTC) devices is essential for various types of location-based applications. In this paper, we investigate a distributed localization problem in noisy networks, where an estimated position of blind MTC machines (BMs) is obtained by using noisy measurements of distance between BM and anchor machines (AMs). We allow positioned BMs also to work as anchors that are referred to as virtual AMs (VAMs) in this paper. VAMs usually have greater position errors than (original) AMs, and, if used as anchors, the error propagates through the whole network. However, VAMs are necessary, especially when many BMs are distributed in a large area with an insufficient number of AMs. To overcome the error propagation, we propose a greedy successive anchorization process (GSAP). A round of GSAP consists of consecutive two steps. In the first step, a greedy selection of anchors among AMs and VAMs is done by which GSAP considers only those three anchors that possibly pertain to the localization accuracy. In the second step, each BM that can select three anchors in its neighbor determines its location with a proposed distributed localization algorithm. Iterative rounds of GSAP terminate when every BM in the network finds its location. To examine the performance of GSAP, a root mean square error (RMSE) metric is used and the corresponding Cramér–Rao lower bound (CRLB) is provided. By numerical investigation, RMSE performance of GSAP is shown to be better than existing localization methods with and without an anchor selection method and mostly close to the CRLB.
1. Introduction
Machine type communication (MTC) services with location-based information are becoming popular such as combat zone surveillance, health monitoring, fire detection and wild habitat monitoring [1,2,3]. MTC devices (in this paper, we use the term “devices” and “machines” interchangeably) with which sensors are equipped as a basic component are usually distributed randomly, accessed from far-away and configured automatically. Thus, location information in MTC services is crucial. One way to get position information is to fit each MTC device with global positioning system (GPS) that enables it to get its position by interacting with GPS satellites. However, this method may not be cost-effective for large scale implementation and is not even possible for indoor or space applications, where MTC devices cannot receive GPS signals [4].
When GPS is not available, each MTC device will estimate its location based on its relative distances to some of the other MTC devices that already have acquired their positions, which are so-called anchor machines (AMs). Localization algorithms that are used to determine the unknown location of devices are computationally complicated in radar and sonar systems [5,6]. However, MTC devices are usually small, and, hence, the localization algorithms should be simple and distributed [7,8,9,10,11].
In [7], a distributed and range-free centroid localization (CL) method is proposed on the assumption that every blind machine (BM that needs to determine its location) should be in the neighbor of three or more AMs. The CL is extremely simple but a little bit inaccurate and requires uniformly distributed AMs near BM. Weighted centroid localization (WCL) improves CL by giving different weights to AMs on the basis of noisy distance information between BM and AMs [8]. WCL gives more importance to the nearer AMs. However, giving how much or finding an optimal weight is the underlying difficulty. In [9], computing an optimal weight in WCL is considered with received signal strength (RSS), which is effective only when AMs are densely distributed.
In practice, it is not easy for blind MTC devices to hear from a sufficient number of AMs since the range of MTC communication is usually limited due to the battery capacity. To overcome this problem, we investigate a method of using BMs that have determined their positions as new anchors, referred to as virtual AMs (VAMs) in this paper. Compared with ordinary (original) AMs, VAMs could have relatively high position errors but if no AM is found (for example, in indoor environments), using VAMs to determine the location BM is acceptable. Though AM itself can have position error, most of the works in this field have assumed that the location information is perfectly accurate [12,13]. However, in a few works [14,15], the position error in AMs is modeled as Gaussian noise and a gradual refinement of the localization error is also proposed [16]. In this paper, we assume that every VAM estimates its position error during its localization process and broadcasts the estimation on its beacon. The position error in VAMs is due to the noise in measurement as well as the error in the location of AMs used in determining its location. In the localization method proposed in this paper, BM can change into and be used as VAM after determining its position, which is referred to as a successive anchorization process (SAP). With SAP, the localization errors propagate through the whole network. One of the objectives of this paper is to propose an efficient localization method that minimizes the localization errors over the whole MTC network. To achieve this goal, every BM chooses VAMs (usually three VAMs are enough) with the smallest localization error in the proposed algorithm, which is referred to as a greedy SAP (GSAP).
In order to speed up the computation for GSAP through the network, each BM takes a linearization of its non-linear distance error-function by using the first-order Taylor expansion. The proposed GSAP is essentially distributed in a sense that each BM determines its location only with the location information of AMs or VAMs from its neighbour, starting from an arbitrary initial position. To have fast convergence of distributed GSAP, a decentralized method of finding a good initial position is provided, which is based on a multidimensional scaling (MDS) technique [17]. Using a good initial position is, however, optional in implementing GSAP. We numerically investigate the effect of using this good initial position in GSAP. The Cramér–Rao lower bound (CRLB) of the overall error is also investigated and the performance of the proposed method is numerically compared with CRLB and other existing methods such as CL, WCL, LLS (linear least square) [10] and the subspace technique [11]. The results show that the proposed GSAP significantly improves the BM position accuracy, and it can also attain the performance mostly close to CRLB.
The rest of the paper is organized as follows. In Section 2, a system model used in this paper is provided. Section 3 provides GSAP that consists of a greedy anchor selection, a linearized iterative localization algorithm and (optional) initial position search. In Section 4, CRLB of the overall position error is investigated. In Section 5, numerical investigation is provided for evaluating the proposed GSAP, for which the root mean square error (RMSE) results of existing localization methods are compared with that of GSAP. Section 6 concludes the paper. The main notations used in this paper are listed in Table 1.

Table 1.
Symbols and notations. AMs: anchor machines; BMs: blind machines; VAMs: virtual anchor machines.
2. System Model
We consider an MTC network that consists of n BMs and m AMs or VAMs in a two-dimensional space (this work also can be straightforwardly applied for localization in a three-dimensional space). Let and denote the actual coordinates of machine i, and let , and be index sets of AMs, VAMs and BMs, respectively. We assume that each AM or VAM knows its position as well as its positioning error (). It is reasonable to assume that the positioning error of AM is less than or at least equal to that of VAM.
In the MTC environments, each machine is capable of communication with the other machines if they are in the communication range. We use RSS measurement to determine unknown positions of BMs. We assume that each AM and VAM broadcasts reference signals as well as its coordinates with the positioning error (and sometimes with a value of its transmit power). BMs that can hear the information from three or more anchors first select the anchor nodes and then run a localization algorithm to be provided below. It is noted that the localization algorithm is distributed in nature, that is, each BM independently determines its position without cooperation by the other BMs.
We assume that transmit power (denoted by ) for the broadcast information is known to BMs. Let denote RSS measurement at BM i from anchor j. Then, we can use a path loss model in [18]:
where , β is a distance–power gradient (i.e., a path loss exponent), is the actual distance between machines i and j, and is noisy power due to measurement errors at BM i and unmodeled variability in the fading channel between machines i and j (for example, shadowing). We assume that s are independently distributed zero-mean Gaussian random variables with standard deviation (dB). We also assume that is known to BMs. From the RSS measurements, each BM can compute the expected error in measurement denoted by . If BM i receives L RSS samples from anchor j, since noisy power is assumed to be independent.
3. Greedy Successive Anchorization Process (GSAP)
3.1. Anchor Selection
3.1.1. Greedy Selection
BM i selects anchors to be used in the localization process by comparing
where j is an index of anchors in its communication range, from which the BM successfully receives the broadcast information. Since three anchors are enough to determine the location of BM in two-space, each BM selects anchors up to smallest , which is referred to as greedy selection in this paper.
3.1.2. Removing Collinear Anchors
If anchors selected from Section 3.1.1 are collinear, high localization error is caused mostly due to vertex flipping instead of the position or the measurement error [19,20]. In order to overcome such a problem, we test , where a and γ are the shortest side and the smallest angle of the triangle built by the greedy-selected three anchors, and is a predetermined constant. This test is provided in [19] as a method of constructing a so-called robust triangle. If the three anchors fail to pass the test, we select another anchor that has the next smallest and do the same test for every combination of the selected anchors. If the test fails for all the anchors whose information is available at a BM, the BM detours the localization procedure for the next round in which more anchors are possibly available since new VAMs can be added to the list of anchors.
3.1.3. Other Anchor Selection Methods in the Literature
Though all of the existing anchor selection methods do not consider the position error at an anchor, there are some methods in the literature. In CL [7], BM selects all those anchors that are one-hop neighbors of that BM. In [21], in order to increase the accuracy, a convex-hull anchor selection method is proposed by considering the geometry of anchors, where only those anchors that have the greatest distance from each other are selected. When applying the convex-hull method with RSS measurement, possibly large measurement error is problematic since the increasing distance between anchors usually increases the distance between an anchor and BM, and thus the error [22]. The work of [21] has proposed an advanced convex-hull method where BM selects those AMs that are close to the ordinary convex-hull with the highest virtual location accuracy. The main drawback of this method is that it assumes highly dense anchors. We will numerically compare the performance of proposed greedy selection with that of the existing methods in Section 5.
3.2. Iterative Localization Algorithm
Let be a set of selected anchors and be a column vector of augmented RSS measurement (or observed path loss) at BM i from the selected anchors. BM i determines (or estimates) its position by
where
Furthermore, is a column vector, the element of which is
A general solution of Equations (3) and (4) can be obtained through a nonlinear optimization method [23,24,25], which iterates to get the optimal value in the feasible region. However, its computational complexity is usually very high [26]. In order to make the computational cost low [27], we linearize by using the first-order Taylor series expansion [28]
where
and is any initially estimated position of BM i (finding a good will be shortly discussed in Section 3.3). In the above expression and in the sequel, we assume that 1 to j are indexes of the selected anchors for notational brevity. Putting Equation (6) into Equation (4), we have
In [29], it is shown that the localization accuracy can be increased by inserting a symmetric weighting matrix into Equation (8), and the resulting equation is defined as weighted least square (WLS), which has the form
As a weighting matrix, we use , where s are the metrics used in anchor selection in this paper.
The proposed method stops with a solution if for a given positive termination threshold δ. Otherwise, we update the initial estimate as and find the next solution in Equation (10) again. At the termination, BM i can estimate its position error by , which will be broadcast by BM i as a VAM after finding its position.
3.3. Initial Location Estimation
If BM has received information from a sufficient number of AMs or VAMs and starts to determine its location, it needs a certain initial estimate of its location when the linearization provided in Equation (6) is evoked. Though the proposed algorithm in Section 3.2 works well with any arbitrary initial point, we describe a method of finding a good initial point in the following and will show that it improves the convergence speed significantly in Section 5. The following method is based on MDS in [17] and implemented in a distributed way.
Let be the number of AMs or VAMs, the signals from which BM can hear, and let index 1 denote the current BM that wants to have its initial location. In addition, indicate the AMs and the VAMs for notational simplicity. Let be the distance estimate between machine i and j. Since BM 1 can measure RSS from the anchors, we can have, from Equation (1),
Since the BM can see the position of anchors in the broadcast information, letting be the broadcast coordinate from anchor j, it can estimate the distance between those anchors by
If we further let , then we can construct a so-called proximity information matrix (PIM) = . It is noted that is an square symmetric matrix.
Using PIM , an objective of MDS is to find relative coordinates of the machines in the hearing range of BM 1, such that matches as well as possible. For this purpose, an optimization problem to be solved is
where
is a so-called stress function provided in [30]. A solution is obtained by decomposing a double centered matrix Ω so as to have [31], where each element of Ω is constructed by
It is noted that the rank of Ω is 2. Let be a diagonal matrix of the eigenvalue s of Ω. In addition, let be a matrix of the eigenvectors corresponding to . Then, taking eigendecomposition of Ω gives , and we have a solution
and can use as an initial position of BM.
4. Cramér–Rao Lower Bound
In this section, we derive a CRLB of the localization error for multiple BMs that commonly use m AMs and VAMs. Let denote the position vector of BMs. We assume that AMs have their locations without position error and without loss of generality. Let us denote actual and estimated positions of VAMs by and , respectively. The errors in measurement as well as position are Gaussian-distributed and mutually independent. The log-likelihood function of data vector is then
where represents the unknown vector, is a constant that is independent of the unknowns, and is a covariance matrix of position errors in .
Let denote a position estimator. Then, the error performance can be determined by its bias , its covariance and its mean square error [28,32]. When RSS noise is sufficiently small, an estimator could be unbiased and . In this case, the following inequality also holds
where Γ is the fisher information matrix (FIM) [32]. For multiple BMs, equivalent FIM (EFIM) is developed in [33] and has a form of
where
By using a formula of partitioned matrix inversion similarly in [28], we can obtain
is similar to the CRLB of given in [34] when an exact value of is known. Consequently, the second term in Equation (21) is the cost in CRLB when is not known or known with errors. In [35], CRLB when is provided, which is a special case of Equation (21).
5. Numerical Results
For numerical investigation, we assume 17 AMs, and 120 BMs are randomly distributed inside a square-region: , where unit of length. We use two different configurations of AM distribution: (a) uniformly distributed over the whole area (as shown in Figure 1a) and (b) uniformly distributed in the lower left corner (in Figure 1b). We assume a distance–power gradient of , a standard deviation of measurement of dB and transmit power of dBm for all of the transmitting machines. We also assume that BMs can hear the signals from those AMs or VAMs, the actual distance to which is not greater than R, which is referred to as a communication range.
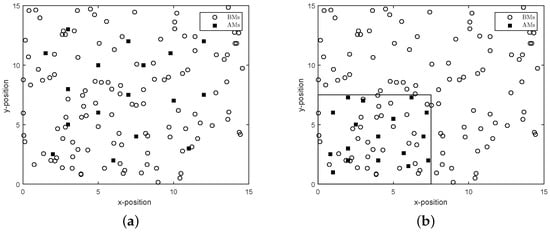
Figure 1.
Distribution of anchor machines (AMs). (a) AMs uniformly distributed over the whole area; (b) AMs distributed uniformly in the lower left corner.
As a performance metric, we use a normalized RMSE
where Q is the number of Monte Carlo runs, is the estimated coordinate of BM j in the i-th run whose actual coordinate is and n is the total number of BMs. For each result in the figures below, runs were done. The performance of proposed GSAP is compared with that of existing methods CL [7], WCL [8], LLS [10], subspace [11], and the CRLB provided in Equation (21). For a termination criterion of the localization algorithm, we have used .
We have suggested an algorithm of determining a good initial position of BMs using MDS. Figure 2 compares convergence speeds of the localization algorithm provided in this paper when a random initial position or a initial position is used. For the test, an actual location of BM is investigated and R is assumed to be 2. A randomly generated initial point is and an initial point obtained from MDS is . From Figure 2, we can see that the convergence is faster if the initial point from MDS is used. When we take for a stopping criterion of the algorithm, a good initial point terminates the localization at nine iterations compared to 20 iterations with the random initial point. Both are convergent at the same position .
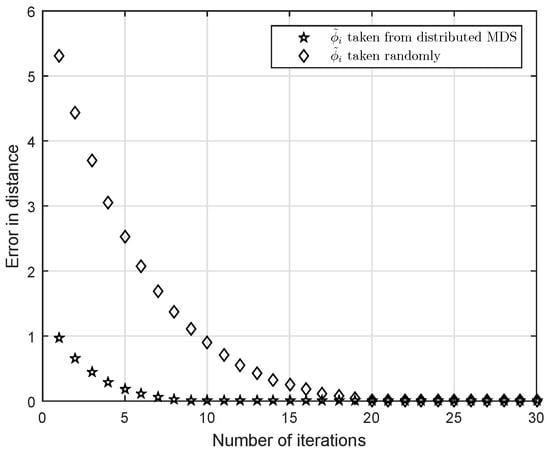
Figure 2.
Estimate of blind machines (BM) vs. number of iterations using Equation (10).
In Figure 3a,b, the effect of AM distributions on the localization speed is investigated. They plot the number of machines marked as anchors (AMs or VAMs) and BMs at the start of each round in GSAP. In Figure 3a, at round 5, all of the 120 BMs can determine their locations when . If , only three rounds are enough. If AMs are located in the lower left corner, seven and four rounds are needed to determine the location of 120 BMs when and , respectively. It is seen that a biased-distribution of AMs can severely degrade the localization speed, especially when the communication range is relatively small.
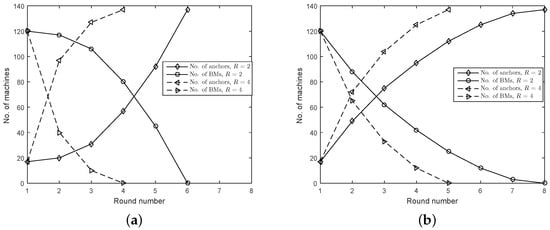
Figure 3.
Number of rounds needed to localize the whole machine type communication (MTC) network. (a) AMs uniformly distributed over the whole area; (b) AMs distributed uniformly in the lower left corner.
Figure 4 shows the effect of on the performance of localization algorithms. is assumed. In the simulation, identical is applied for each transmitter–receiver pair. For CL and WCL, anchor selection methods (ASM) provided in [20] are used, and the greedy anchor selection (GAS) proposed in this paper is used for LLS and Subspace techniques. The RMSE degrades (gets greater) as increases for every algorithm tested. The proposed GSAP, however, provides the best performance regardless of the assumptions on the AM distribution. Comparing the results from the two AM distributions, we can see that if AMs are uniformly distributed over the whole area, RMSE gain is about 4.165 dB compared with the locally distributed case at . In both of the cases, the performance gap between GSAP and CRLB increases according to the increasing uncertainty.
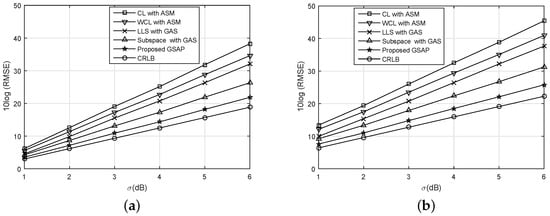
Figure 4.
Root mean square error (RMSE) performance vs. . (a) AMs uniformly distributed over the whole area; (b) AMs distributed uniformly in the lower left corner.
Figure 5 shows the effect of communication range R on the RMSE performance. When the communication range increases, each BM has the reference information from more anchors. However, since the location information from VAMs has some errors, the larger number of anchors is not always helpful. To make the comparison fair, we also have applied similar weight matrices, which are used in WCL, to the LLS and subspace techniques, referred to as weighted LLS and weighted subspace in Figure 5, respectively. It can be seen that, without anchor selection, the RMSE performance degrades though R increases in both Figure 5a,b. However, with anchor selection, it is improved with increasing R. If R is large enough (for example, when ), most of the BMs can communicate with more than two anchors at the first round, and the RMSE can be reduced though anchor selection is not used. Comparing the performances with and without anchor selection, the localization algorithms with certain anchor selection certainly achieve better RMSE than without the anchor selection if the communication range is limited.
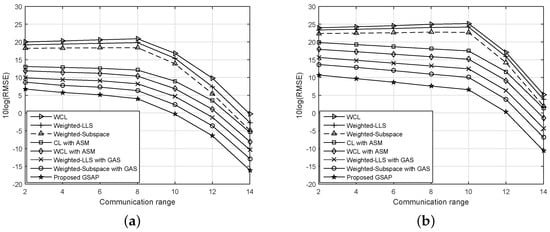
Figure 5.
RMSE performance vs. communication range, R. (a) AMs uniformly distributed over the whole area; (b) AMs distributed uniformly in the lower left corner.
6. Conclusions
In this paper, we have proposed and investigated GSAP. In an MTC network that consists of a certain number of AMs and many BMs, GSAP eventually estimates the location of all the BMs. Though some BMs cannot find enough anchors in their respective neighbors in an initial round of GSAP, they can find anchors in the following rounds by regarding positioned BMs as VAMs. In this procedure, RMSE is, of course, increasing by the positioning error in VAMs, but it is numerically shown that GSAP provides RMSE better than the existing methods (CL, WCL, LLS and subspace techniques). Specifically, the proposed method achieves about 52%–97% improvement in terms of RMSE when AMs are uniformly distributed over the area. If AMs are located in a corner, the improvement increases to about 57%–98%. To reduce the effect of positioning error in VAMs, GSAP selects and uses only the three best anchors in terms of the errors. The RMSE performance of GSAP is also shown to be close to the CRLB. GSAP is a generic procedure in finding the location of BMs in a relatively large area with a limited number of anchors and is promising in determining the location of MTC devices in future Internet of Things applications.
Acknowledgments
This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2015R1D1A1A01059612).
Author Contributions
Mian Imtiaz Ul Haq prepared an initial draft of the paper and performed the simulation in the paper. Dongwoo Kim organized and polished the contents of the paper and provided directions for the simulation.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MTC | Machine type communication |
| AM | Anchor machine |
| BM | Blind machine |
| CRLB | Cramér–Rao lower bound |
| GPS | Global positioning system |
| CL | Centroid localization |
| WCL | Weighted centroid localization |
| RSS | Received signal strength |
| VAM | Virtual anchor machine |
| SAP | Successive anchorization process |
| GSAP | Greedy successive anchorization process |
| MDS | Multidimensional scaling |
| LLS | Linear least square |
| RMSE | Root mean square error |
| PIM | Proximity information matrix |
| FIM | Fisher information matrix |
| ASM | Anchor selection method |
| GAS | Greedy anchor selection |
References
- Verma, P.K.; Verma, R.; Prakash, A.; Agrawal, A.; Naik, K.; Tripathi, R.; Alsabaan, M.; Khalifa, T.; Abdelkader, T.; Abogharaf, A. Machine-to-Machine (M2M) communications: A survey. J. Netw. Comput. Appl. 2016, 66, 83–105. [Google Scholar] [CrossRef]
- Bourgeau, T.; Chaouchi, H.; Kirci, P. Machine-to-Machine Communications. In Next-Generation Wireless Technologies: 4G and Beyond; Chilamkurti, N., Zeadally, S., Chaouchi, H., Eds.; Springer: London, UK, 2013; pp. 221–241. [Google Scholar]
- Karim, L.; Mahmoud, Q.H.; Nasser, N.; Anpalagan, A.; Khan, N. Localization in terrestrial and underwater sensor-based M2M communication networks: Architecture, classification and challenges. Int. J. Commun. Syst. 2015. [Google Scholar] [CrossRef]
- Bal, M.; Liu, M.; Shen, W.; Ghenniwa, H. Localization in Cooperative Wireless Sensor Networks: A Review. In Proceedings of the 13rd International Conference on Computer Supported Cooperative Work in Design, Santiago, Chile, 22–24 April 2009; pp. 438–443.
- Carter, G.C. Time delay estimation for passive sonar signal processing. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 463–470. [Google Scholar] [CrossRef]
- Ehud, W. Optimal source localization and tracking from passive array measurements. IEEE Trans. Acoust. Speech Signal Process. 1982, 30, 69–76. [Google Scholar]
- Karim, L.; Nidal, N.; Mahmoud, Q.H.; Anpalagan, A.; Salti, T.E. Range-free localization approach for M2M communication system using mobile anchor nodes. J. Netw. Comput. Appl. 2015, 47, 137–146. [Google Scholar] [CrossRef]
- Neha, S.; Gazal, C.; Mehak, K. Weighted Centroid Range Free Localization Algorithm based on IoT. Int. J. Comput. Appl. 2013, 83, 27–30. [Google Scholar]
- Hu, L.; Liu, B.; Zhao, K.; Meng, X.; Wang, F. Research and Implementation of the Localization Algorithm Based on RSSI Technology. J. Netw. 2014, 9, 3135–3142. [Google Scholar] [CrossRef]
- Ibrahim, W.M.; Taha, A.E.M.; Hassanein, H.S. Scalability Issues in Localizing Things. In Proceedings of the IEEE International Conference on Local Computer Networks, Bonn, Germany, 4–7 October 2011; pp. 673–680.
- Haq, M.I.U.; Kim, D. A Novel Localization Algorithm for Internet of Things in 3D. In Proceedings of the International Conference on Information and Communication Technology Convergence, Jeju Island, Korea, 28–30 October 2015; pp. 237–241.
- Chan, F.K.W.; So, H.C. Efficient Weighted Multidimensional Scaling for Wireless Sensor Network Localization. IEEE Trans. Signal Process. 2009, 57, 4548–4553. [Google Scholar] [CrossRef]
- Kim, E.; Lee, S.; Kim, C.; Kim, K. Mobile Beacon-Based 3D-Localization with Multidimensional Scaling in Large Sensor Networks. IEEE Commun. Lett. 2010, 14, 647–649. [Google Scholar] [CrossRef]
- Savvides, A.; Garber, W.L.; Moses, R.L.; Srivastava, M.B. An analysis of error inducing parameters in multihop sensor node localization. IEEE Trans. Mob. Comput. 2005, 4, 567–577. [Google Scholar] [CrossRef]
- Rui, L.; HO, K.C. Algebraic Solution for Joint Localization and Synchronization of Multiple Sensor Nodes in the Presence of Beacon Uncertainties. IEEE Trans. Wirel. Commun. 2014, 13, 5196–5210. [Google Scholar] [CrossRef]
- Chiu, W.Y.; Chen, B.S.; Yang, C.Y. Robust Relative Location Estimation in Wireless Sensor Networks with Inexact Position Problems. IEEE Trans. Mob. Comput. 2012, 11, 935–946. [Google Scholar] [CrossRef]
- Borg, I.; Groenen, P.J.F. Modern Multidimensional Scaling: Theory and Applications, 2nd ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Lohrasbipeydeh, H.; Gulliver, T.A.; Amindavar, H. Blind received signal strength difference based source localization with system parameter errors. IEEE Trans. Signal Process. 2014, 62, 4516–4531. [Google Scholar] [CrossRef]
- Moore, D.; Leonard, J.; Rus, D.; Teller, S. Robust Distributed Network Localization with Noisy Range Measurements. In Proceedings of the 2nd International Conference on Embedded Networked Sensor Systems, Baltimore, MD, USA, 3–5 November 2004; pp. 50–61.
- Hendrickson, B. Conditions for unique graph realizations. SIAM J. Comput. 1992, 21, 65–84. [Google Scholar] [CrossRef]
- Ermel, E.; Fladenmuller, A.; Pujolle, G.; Cotton, A. On Selecting Nodes to Improve Estimated Positions. In Proceedings of the IFIP TC6/WG6.8 Conference on Mobile and Wireless Communication Networks, Paris, France, 25–27 October 2004; pp. 449–460.
- Ji, Y.; Biaz, S.; Wu, S.; Qi, B. Optimal sniffers deployment on wireless indoor localization. In Proceedings of the IEEE International Conference Computer Communications and Networks, Honolulu, HI, USA, 13–16 August 2007; pp. 251–256.
- Beck, A. Introduction to Nonlinear Optimization: Theory, Algorithms, and Applications with MATLAB; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2014. [Google Scholar]
- Yu, T.M.; Jian, X.D.; Liang, S.J.; Yan, S. Application of the Newton-Raphson Method in a Voice Localization System. Appl. Mech. Mater. 2014, 513, 4435–4438. [Google Scholar]
- Chepuri, S.P.; Leus, G. Sparsity-Promoting Sensor Selection for Non-Linear Measurement Models. IEEE Trans. Signal Process. 2015, 63, 684–698. [Google Scholar] [CrossRef]
- Rudich, S.; Wigderson, A. Computational Complexity Theory; American Mathematical Society: Providence, RI, USA, 2004. [Google Scholar]
- Hamdi, M.; Boudriga, N.; Obaidat, M.S. Bandwidth-Effective Design of a Satellite-Based Hybrid Wireless Sensor Network for Mobile Target Detection and Tracking. IEEE Syst. J. 2008, 2, 74–82. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation Theory, 1st ed.; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- So, H.C.; Lin, L. Linear Least Squares Approach for Accurate Received Signal Strength Based Source Localization. IEEE Trans. Signal Process. 2011, 59, 4035–4040. [Google Scholar] [CrossRef]
- Kruskal, J.B. On the shortest spanning subtree of a graph and the traveling salesman problem. Proc. Am. Math. Soc. 1956, 7, 48–50. [Google Scholar] [CrossRef]
- Wei, H.W.; Wan, Q.; Chen, Z.X.; Ye, S.F. A Novel Weighted Multidimensional Scaling Analysis for Time-of-Arrival-Based Mobile Location. IEEE Trans. Signal Process. 2008, 56, 3018–3022. [Google Scholar] [CrossRef]
- Trees, H.L.V. Detection, Estimation, and Modulation Theory; John Wiley & Sons: New York, NY, USA, 2004. [Google Scholar]
- Shen, Y.; Win, M.Z. Performance of Localization and Orientation Using Wideband Antenna Arrays. In Proceedings of the IEEE International Conference on Ultra-Wideband, Marina Mandarin, Singapore, 24–26 September 2007; pp. 288–293.
- Patwari, N.; Hero, A.O.; Perkins, M.; Correal, N.S.; O’Dea, R.J. Relative location estimation in wireless sensor networks. IEEE Trans. Signal Process. 2003, 51, 2137–2148. [Google Scholar] [CrossRef]
- Haq, M.I.U.; Kim, D. Improved Localization by Time of Arrival for Internet of Things in 3D. In Proceedings of the International Conference on Applied Electromagnetics and Communications, Dubrovnik, Croatia, 19–21 September 2016.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).