A Geometry-Based Cycle Slip Detection and Repair Method with Time-Differenced Carrier Phase (TDCP) for a Single Frequency Global Position System (GPS) + BeiDou Navigation Satellite System (BDS) Receiver
Abstract
:1. Introduction
2. Methodology
2.1. TDCP Model
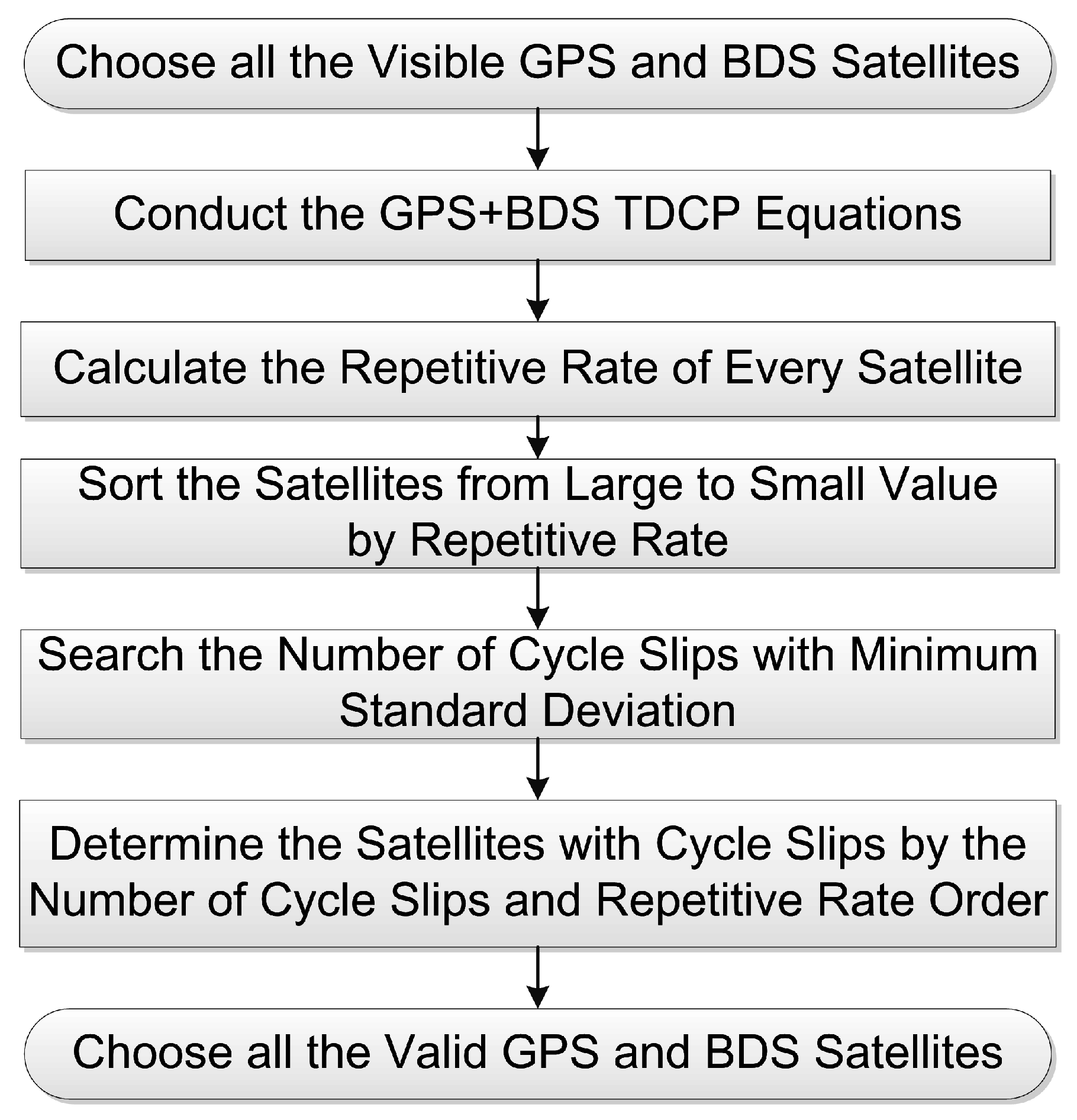
2.2. Cycle Slip Detection with ILAM
2.3. Cycle Slip Repair Method with Success Probability
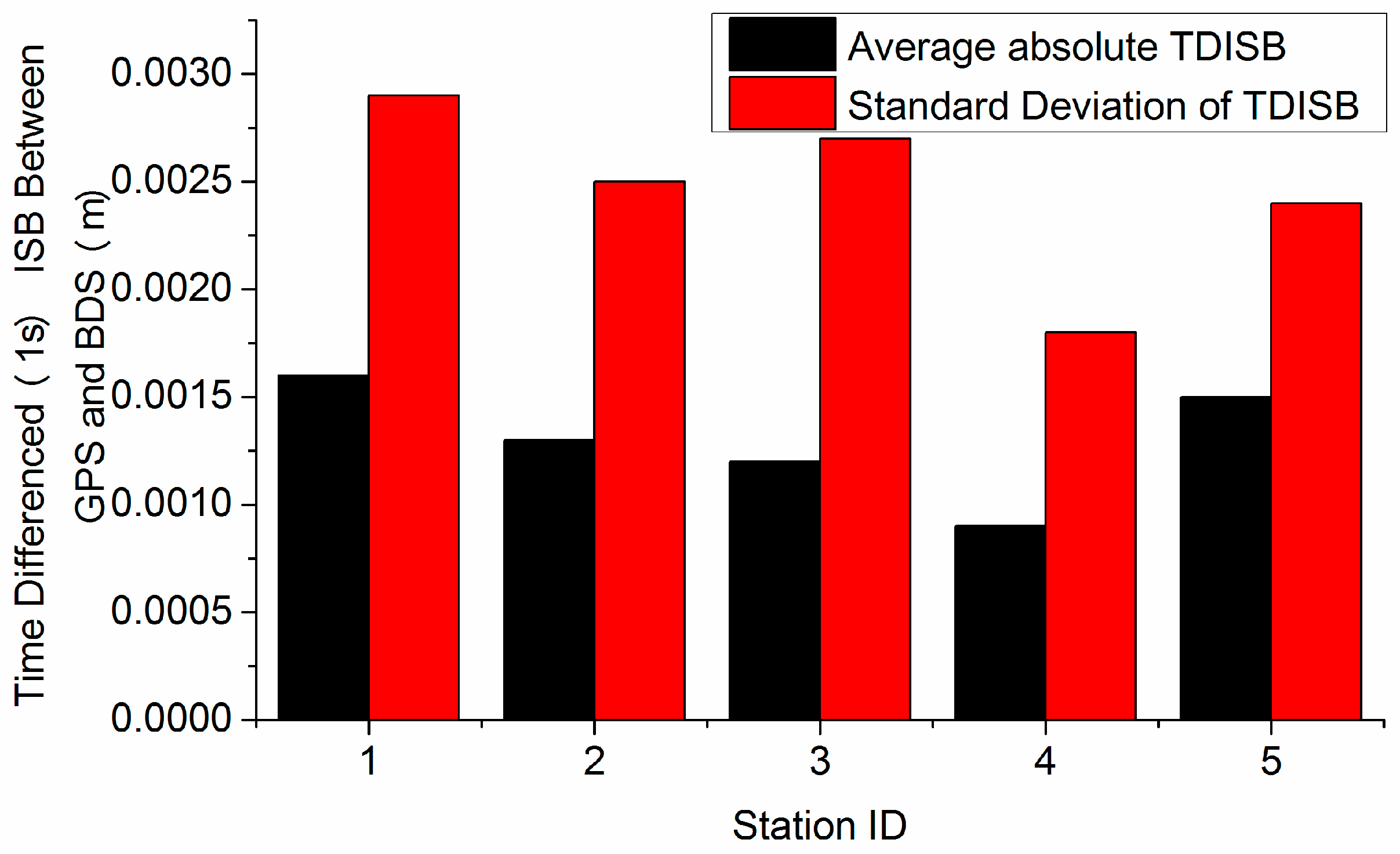
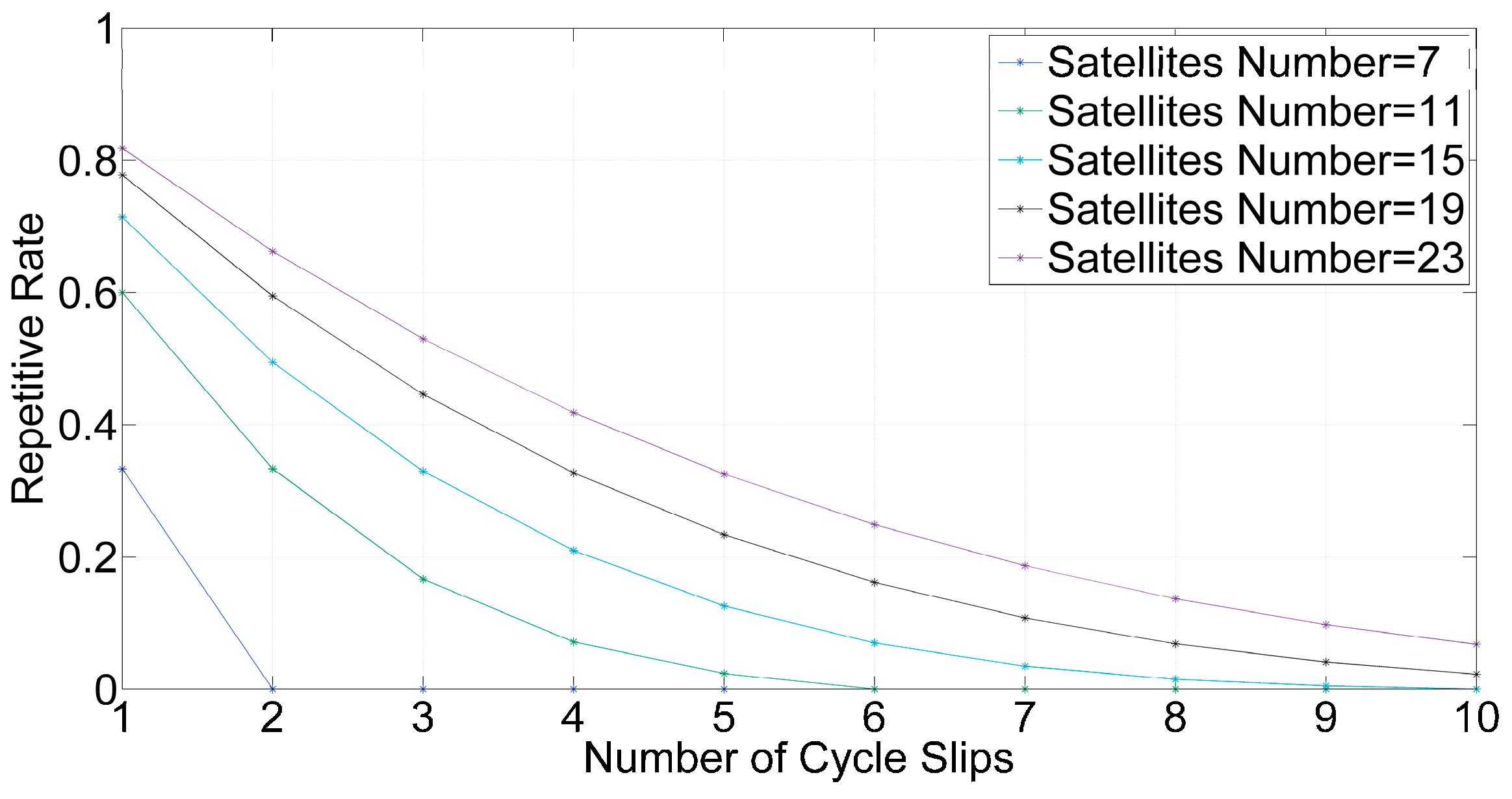
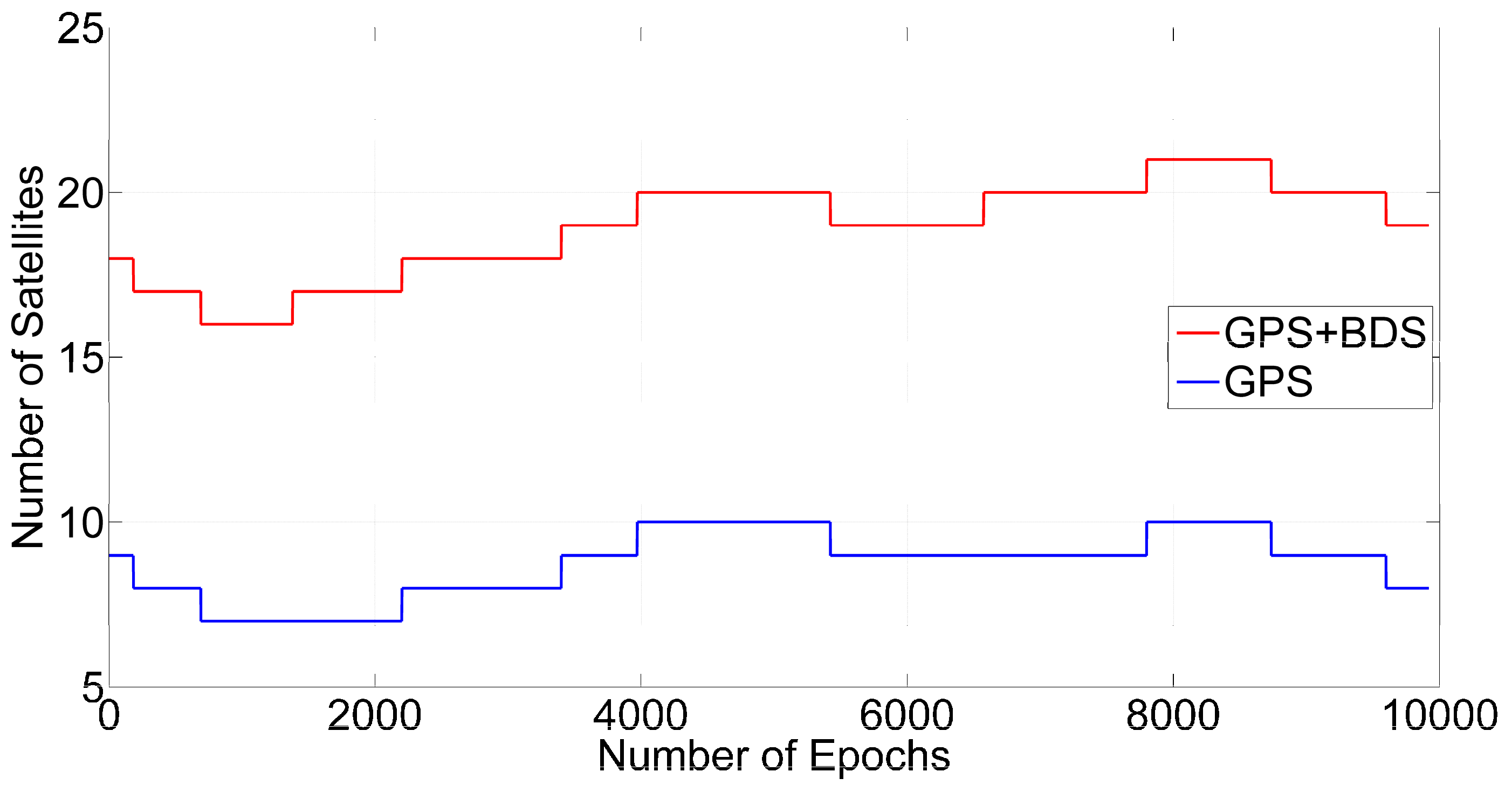
3. Results and Discussion
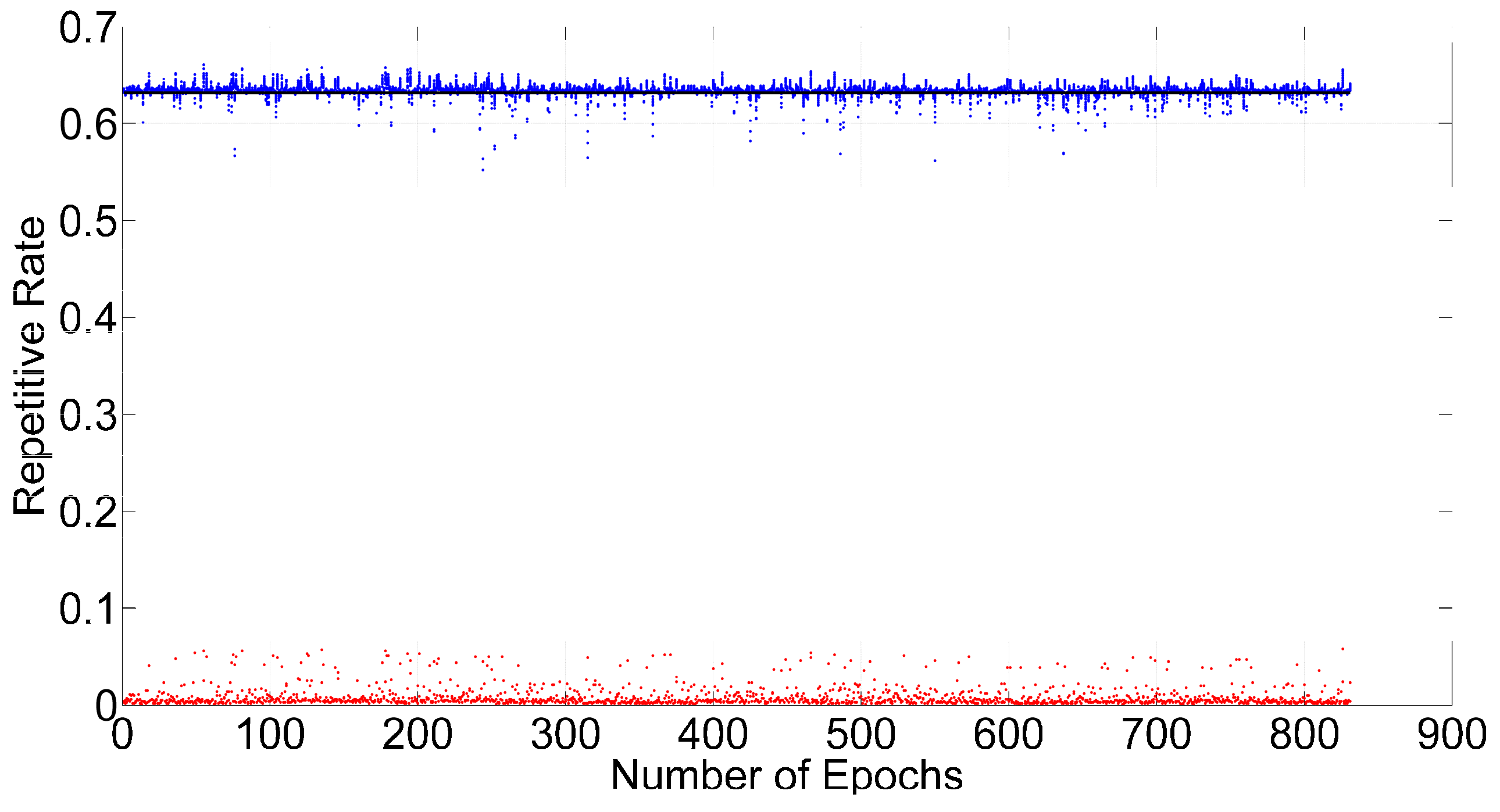
3.1. ILAM for Detecting Cycle Slips
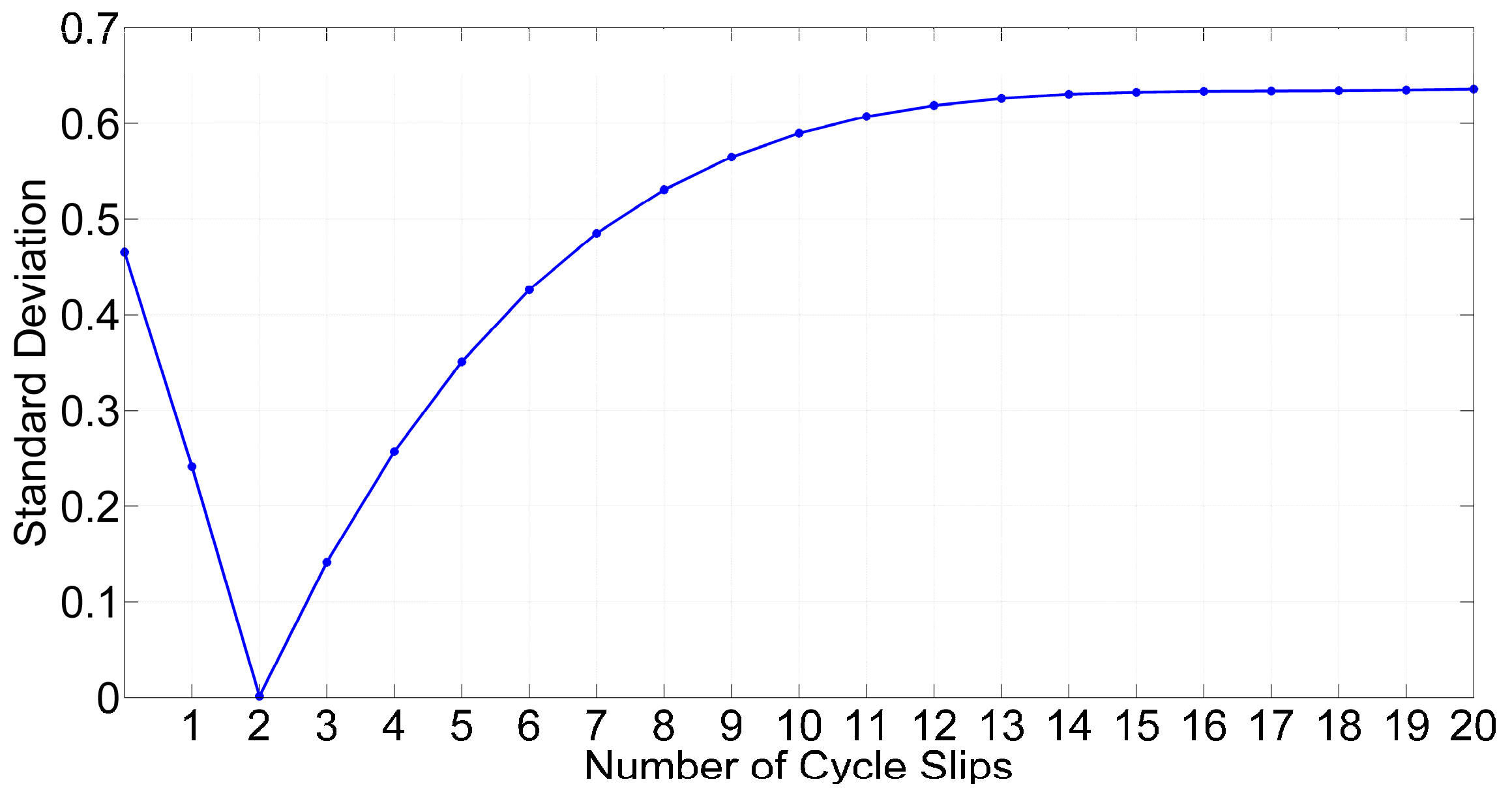
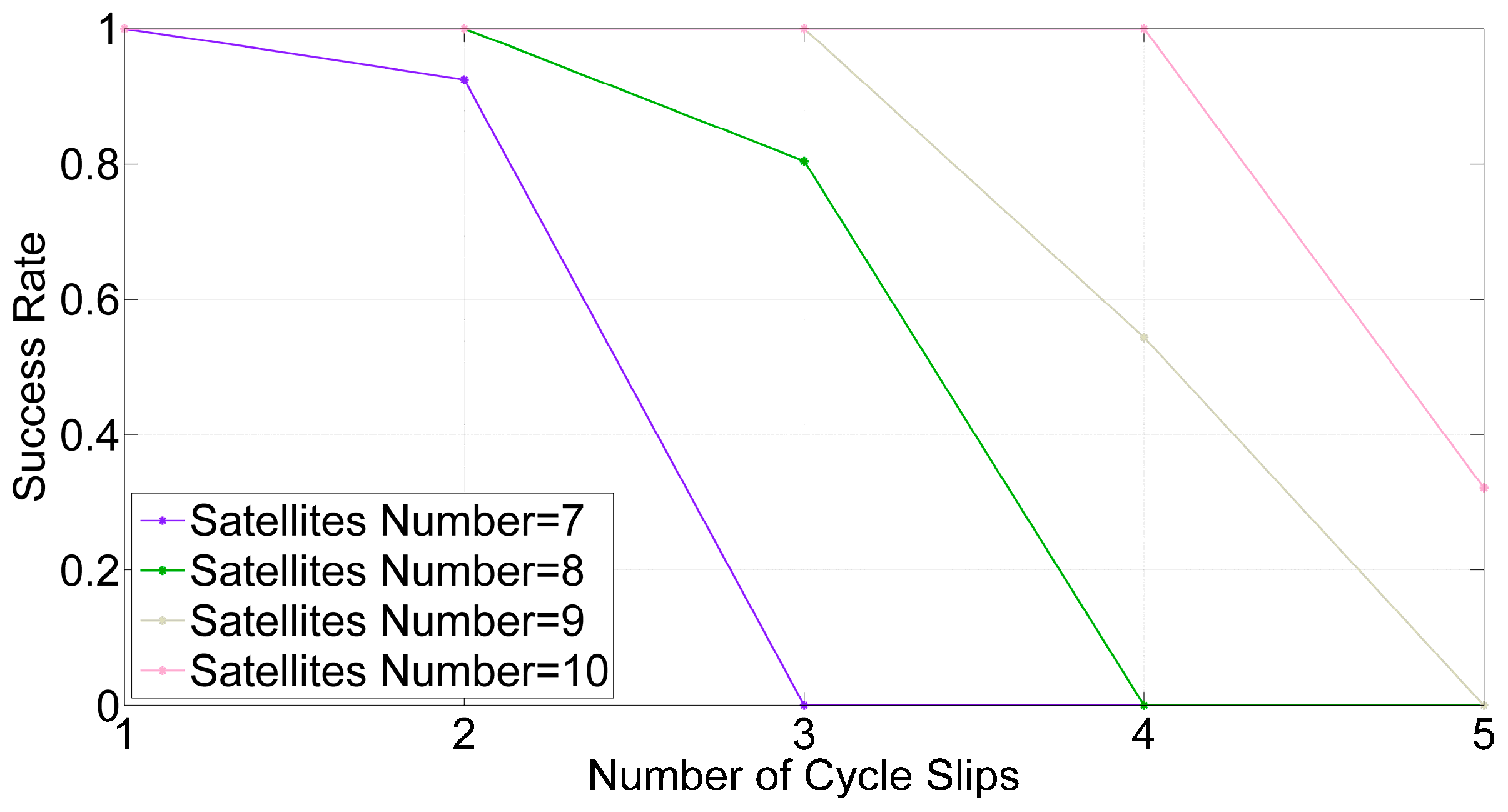
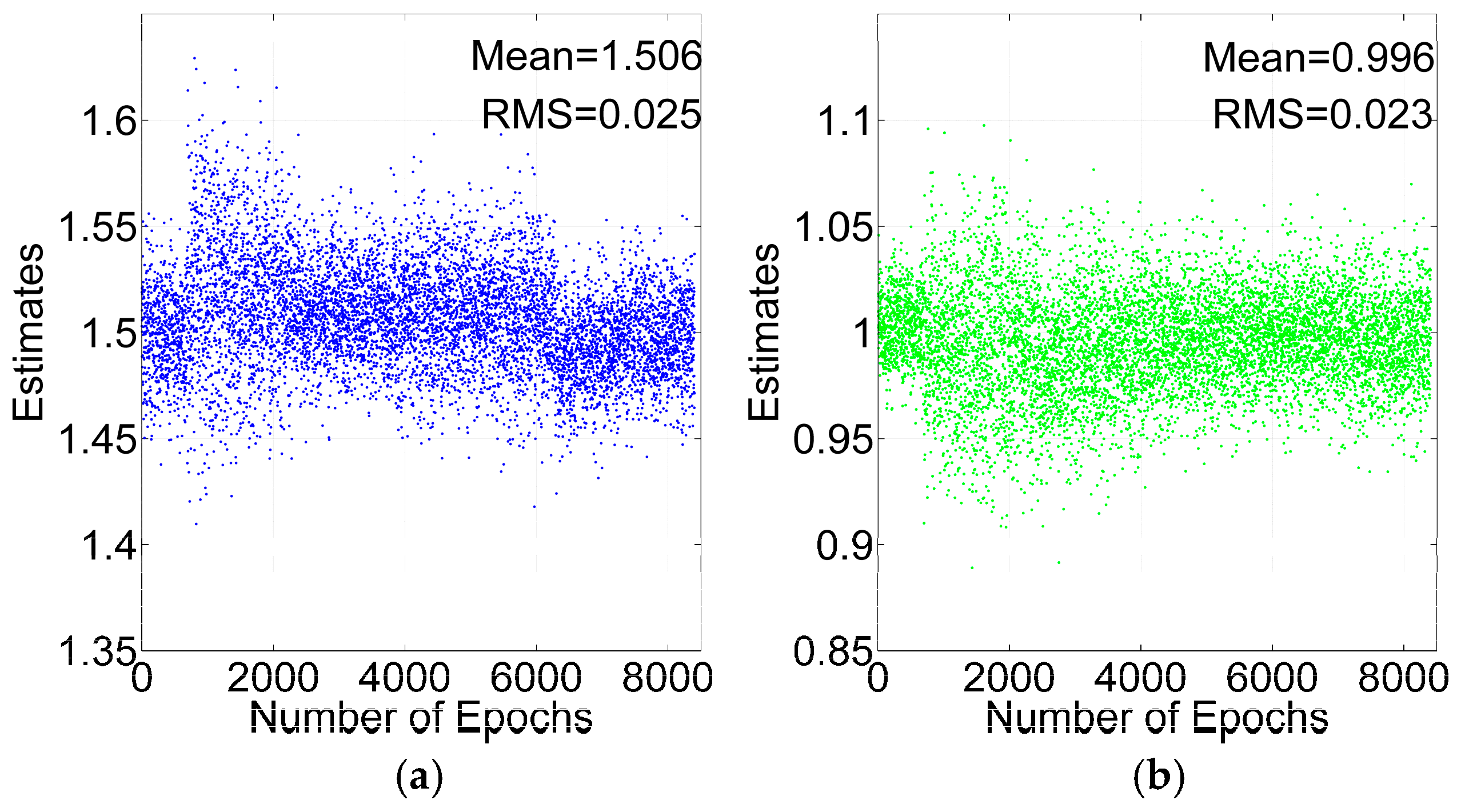
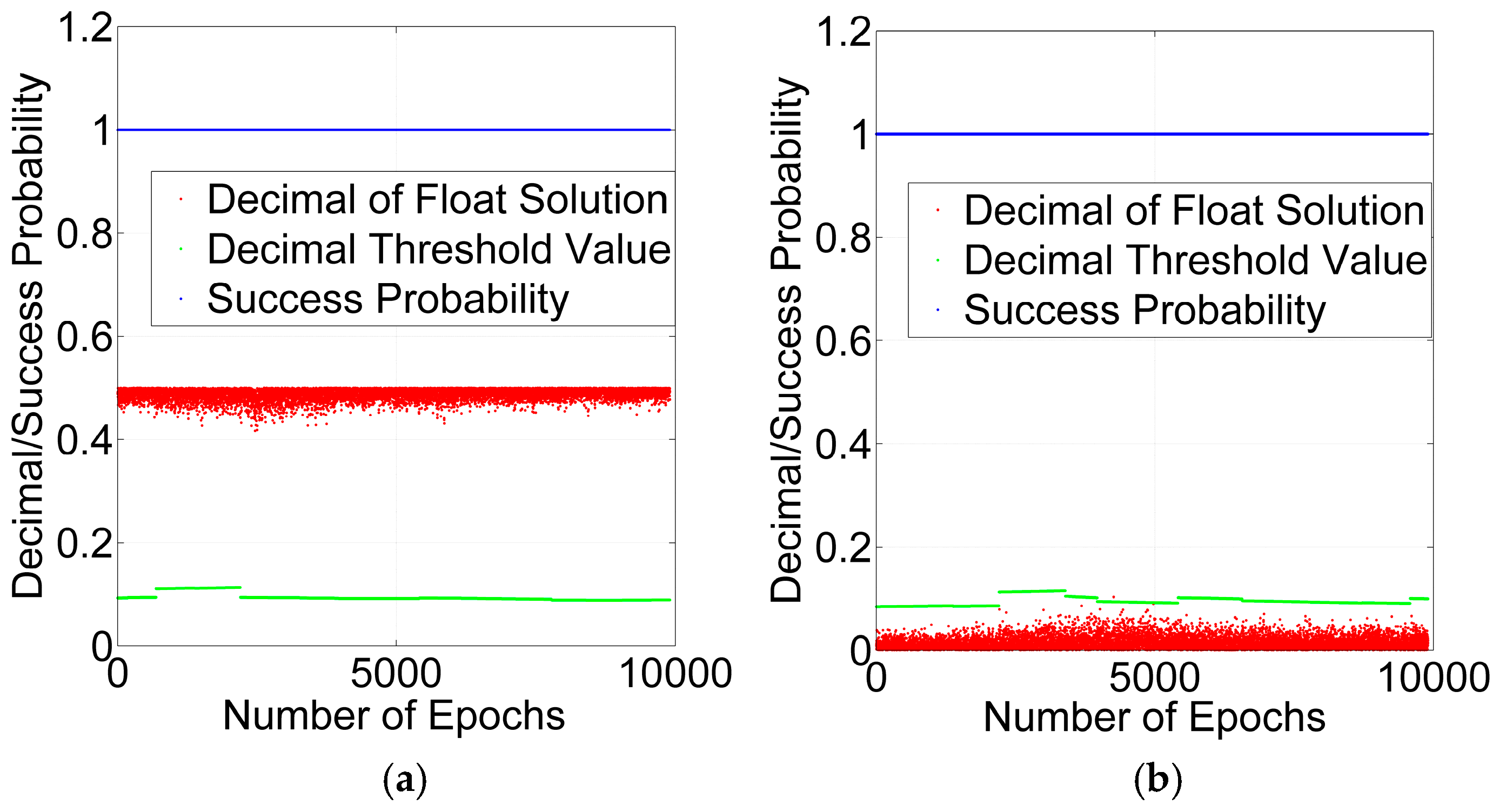
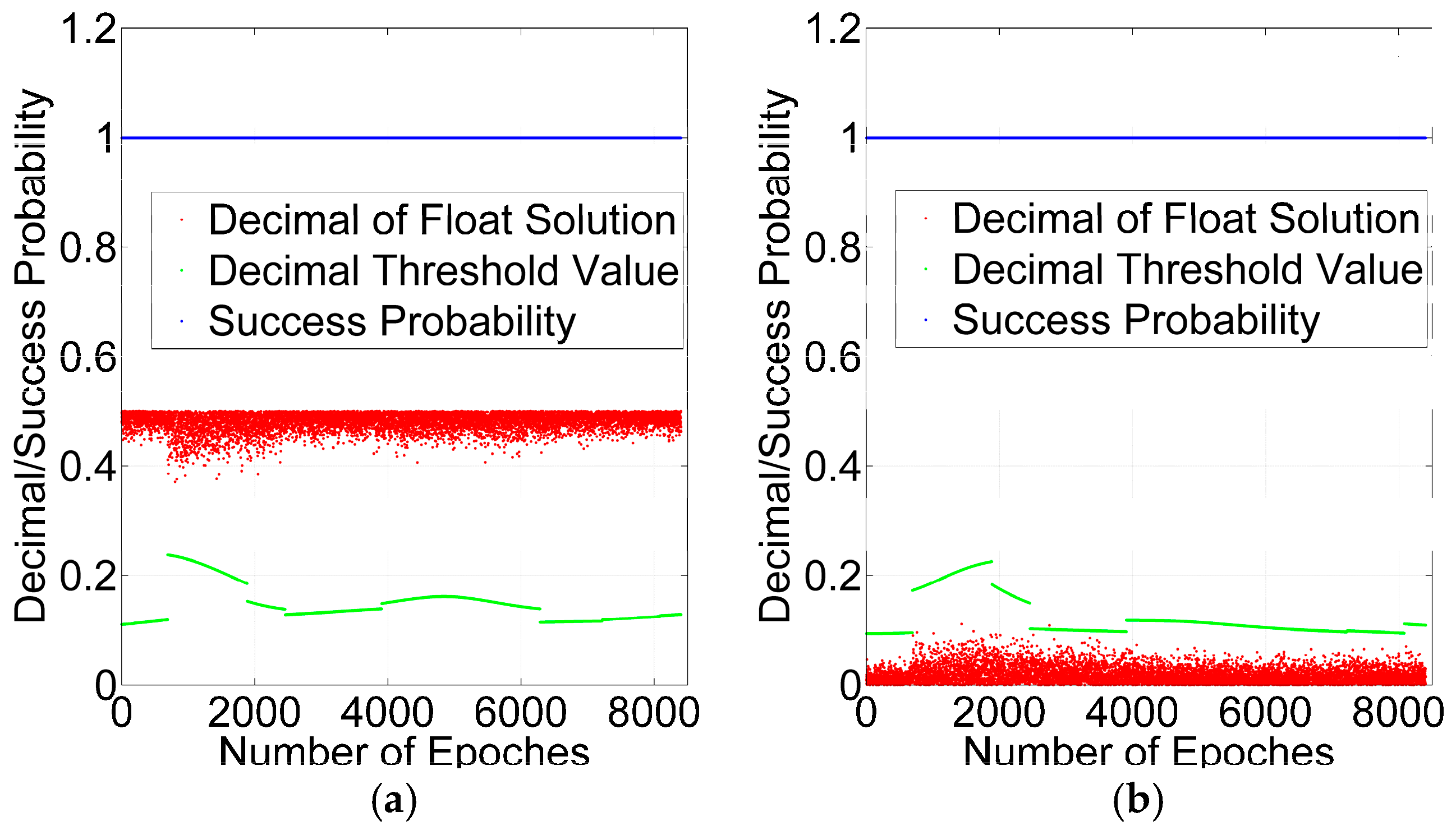
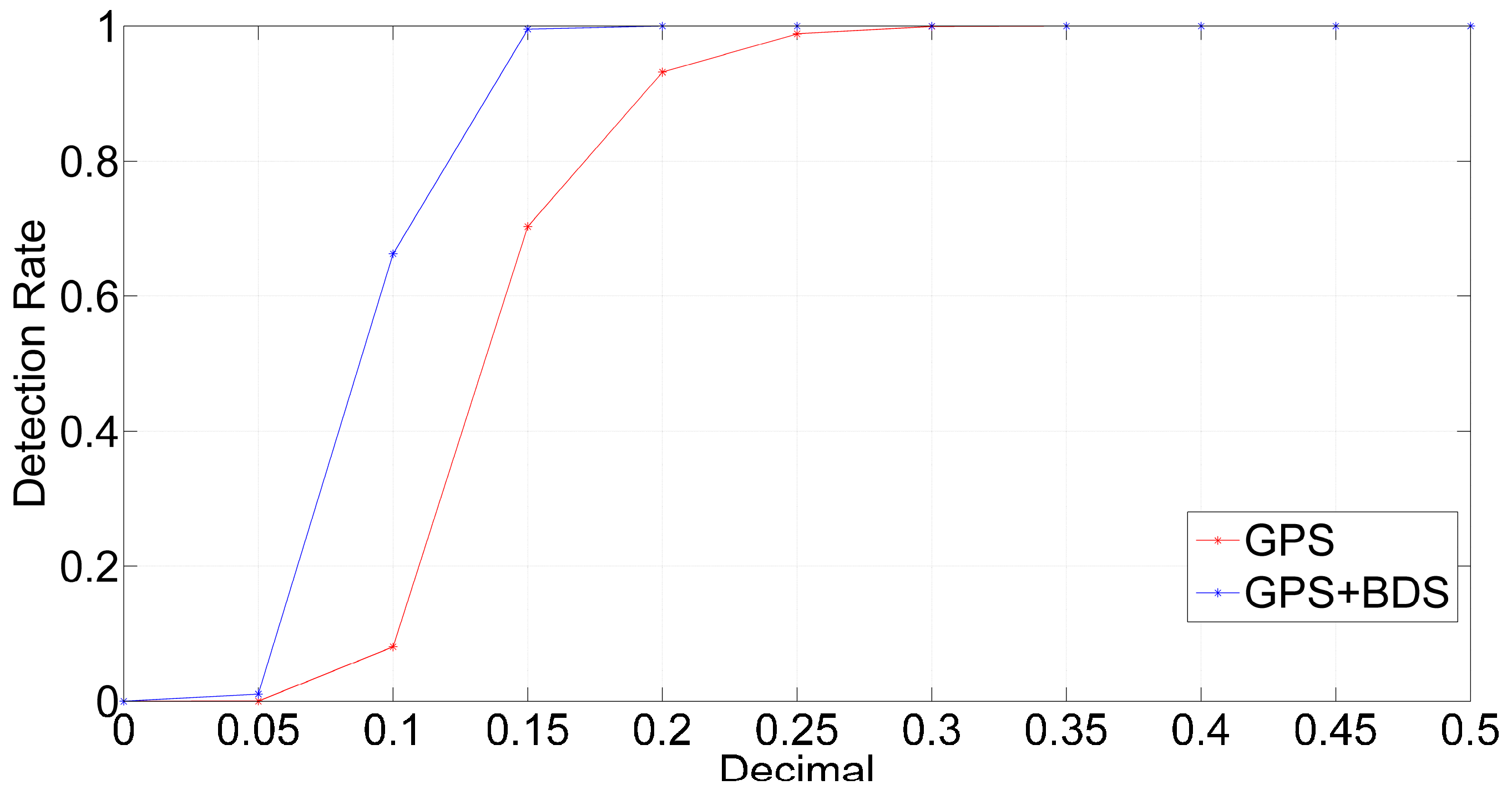
3.2. Success Probability and Decimal Test for Cycle Slip Repair
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Xu, G. GPS: Theory, Algorithms and Applications, 2nd ed.; Springer: Berlin, Germany, 2007. [Google Scholar]
- Bastos, L.; Landau, H. Fixing cycle slips in dual-frequency kinematic GPS-applications using Kalman filtering. Manuscr. Geod. 1988, 13, 249–256. [Google Scholar]
- Chen, D.; Ye, S.; Zhou, W.; Liu, Y.; Jiang, P.; Tang, W.; Yuan, B.; Zhao, L. A double-differenced cycle slip detection and repair method for GNSS CORS network. GPS Solut. 2015, 20, 439–450. [Google Scholar] [CrossRef]
- Gao, Y.; Li, Z. Cycle slip detection and ambiguity resolution algorithms for dual-frequency GPS data processing. Mar. Geod. 1999, 22, 169–181. [Google Scholar]
- Lee, H.K.; Wang, J.; Rizos, C. Effective cycle slip detection and identification for high precision GPS/INS integrated systems. J. Navig. 2003, 56, 475–486. [Google Scholar] [CrossRef]
- Du, S.; Gao, Y. Inertial aided cycle slip detection and identification for integrated PPP GPS and INS. Sensors 2012, 12, 14344–14362. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Song, J.; Kee, C.; Park, B. GPS Cycle Slip Detection Considering Satellite Geometry Based on TDCP/INS Integrated Navigation. Sensors 2015, 15, 25336–25365. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z. A new automated cycle slip detection and repair method for a single dual-frequency GPS receiver. J. Geod. 2011, 85, 171–183. [Google Scholar] [CrossRef]
- Blewitt, G. An Automatic Editing Algorithm for GPS Data. Geophys. Res. Lett. 1990, 17, 199–202. [Google Scholar] [CrossRef]
- Cai, C.; Liu, Z.; Xia, P.; Dai, W. Cycle slip detection and repair for undifferenced GPS observations under high ionospheric activity. GPS Solut. 2013, 17, 247–260. [Google Scholar] [CrossRef]
- De Lacy, M.C.; Reguzzoni, M.; Sansò, F.; Venuti, G. The Bayesian detection of discontinuities in a polynomial regression and its application to the cycle-slip problem. J. Geod. 2008, 82, 527–542. [Google Scholar] [CrossRef]
- Wang, C. Development of a Low-Cost GPS-Based Attitude Determination System. Master’s Thesis, University of Calgary, Calgary, AB, Canada, June 2003. [Google Scholar]
- Karaim, M.; Karamat, T.B.; Noureldin, A.; El-Shafie, A. GPS Cycle Slip Detection and Correction at Measurement Level. Br. J. Appl. Sci. Technol. 2014, 4, 4239–4251. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X. Instantaneous re-initialization in real-time kinematic PPP with cycle slip fixing. GPS Solut. 2012, 16, 315–327. [Google Scholar]
- Ye, S.; Liu, Y.; Song, W.; Lou, Y.; Yi, W.; Zhang, R.; Jiang, P.; Xiang, Y. A cycle slip fixing method with GPS + GLONASS observations in real-time kinematic PPP. GPS Solut. 2016, 20, 101–110. [Google Scholar] [CrossRef]
- Carcanague, S. Real-time geometry-based cycle slip resolution technique for single-frequency PPP and RTK. In Proceedings of the ION GNSS 2012, Nashville, TN, USA, 17–21 September 2012; pp. 1136–1148.
- Liu, T.; Ou, J.; Yuan, Y. An improved algorithm of real-time coseismic velocity extraction with a stand-alone GPS receiver based on QUAD method. Chin. J. Geophys. 2014, 57, 2507–2517. [Google Scholar]
- Fujita, S.; Saito, S.; Yoshihara, T. Cycle Slip Detection and Correction Methods with Time-Differenced Model for Single Frequency GNSS Applications. Trans. Inst. Syst. Control Inf. Eng. 2013, 26, 8–15. [Google Scholar] [CrossRef]
- Kirkko-Jaakkola, M.; Traugott, J.; Odijk, D.; Collin, J.; Sachs, G.; Holzapfel, F. A RAIM approach to GNSS outlier and cycle slip detection using L1 carrier phase time-differences. In Proceedings of the 2009 IEEE Workshop on Signal Processing Systems, Tampere, Finland, 7–9 October 2009; pp. 273–278.
- Song, W.; Yao, Y. Pre-process Strategy in Complex Movement Using Single-frequency GPS Data. Geomat. Inf. Sci. Wuhan Univ. 2009, 34, 1005–1008. [Google Scholar]
- Freda, P.; Angrisano, A.; Gaglione, S.; Troisi, S. Time-differenced carrier phases technique for precise GNSS velocity estimation. GPS Solut. 2015, 19, 335–341. [Google Scholar] [CrossRef]
- Ding, W.; Wang, J. Precise velocity estimation with a stand-alone GPS receiver. J. Navig. 2011, 64, 311–325. [Google Scholar] [CrossRef]
- Torre, A.; Caporali, A. An analysis of intersystem biases for multi-GNSS positioning. GPS Solut. 2015, 19, 297–307. [Google Scholar] [CrossRef]
- Wang, J.; Knight, N.L.; Lu, X. Impact of the GNSS time offsets on positioning reliability. J. Glob. Position. Syst. 2011, 10, 165–172. [Google Scholar] [CrossRef]
- Baarda, W. A Testing Procedure for Use in Geodetic Networks; Netherlands Geodetic Commission: Delft, The Netherlands, 1968. [Google Scholar]
- Knight, N.L.; Wang, J.; Rizos, C. Generalised measures of reliability for multiple outliers. J. Geod. 2010, 84, 625–635. [Google Scholar] [CrossRef]
- Wang, J.; Knight, N.L. New outlier separability test and its application in GNSS positioning. J. Glob. Position. Syst. 2012, 11, 46–57. [Google Scholar] [CrossRef]
- Yang, L.; Wang, J.; Knight, N.L.; Shen, Y. Outlier separability analysis with a multiple alternative hypotheses test. J. Geod. 2013, 87, 591–604. [Google Scholar] [CrossRef]
- Sun, H.; Huang, H.; Wang, X. Local Analysis Method on Gross Error of Multidimensional Adjustment Problem. Acta Geod. Cartogr. Sin. 2012, 41, 54–58. [Google Scholar]
- Teunissen, P.J. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Teunissen, P.J. Success probability of integer GPS ambiguity rounding and bootstrapping. J. Geod. 1998, 72, 606–612. [Google Scholar] [CrossRef]



| System | GPS + BDS | GPS | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Number of Satellites | 16 | 17 | 18 | 19 | 20 | 21 | 7 | 8 | 9 | 10 |
| Detectable Cycle Slips Number | 9 | 9 | 10 | 11 | 11 | 12 | 1 | 2 | 3 | 4 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, C.; Liu, H.; Zhang, M.; Shu, B.; Xu, L.; Zhang, R. A Geometry-Based Cycle Slip Detection and Repair Method with Time-Differenced Carrier Phase (TDCP) for a Single Frequency Global Position System (GPS) + BeiDou Navigation Satellite System (BDS) Receiver. Sensors 2016, 16, 2064. https://doi.org/10.3390/s16122064
Qian C, Liu H, Zhang M, Shu B, Xu L, Zhang R. A Geometry-Based Cycle Slip Detection and Repair Method with Time-Differenced Carrier Phase (TDCP) for a Single Frequency Global Position System (GPS) + BeiDou Navigation Satellite System (BDS) Receiver. Sensors. 2016; 16(12):2064. https://doi.org/10.3390/s16122064
Chicago/Turabian StyleQian, Chuang, Hui Liu, Ming Zhang, Bao Shu, Longwei Xu, and Rufei Zhang. 2016. "A Geometry-Based Cycle Slip Detection and Repair Method with Time-Differenced Carrier Phase (TDCP) for a Single Frequency Global Position System (GPS) + BeiDou Navigation Satellite System (BDS) Receiver" Sensors 16, no. 12: 2064. https://doi.org/10.3390/s16122064
APA StyleQian, C., Liu, H., Zhang, M., Shu, B., Xu, L., & Zhang, R. (2016). A Geometry-Based Cycle Slip Detection and Repair Method with Time-Differenced Carrier Phase (TDCP) for a Single Frequency Global Position System (GPS) + BeiDou Navigation Satellite System (BDS) Receiver. Sensors, 16(12), 2064. https://doi.org/10.3390/s16122064




