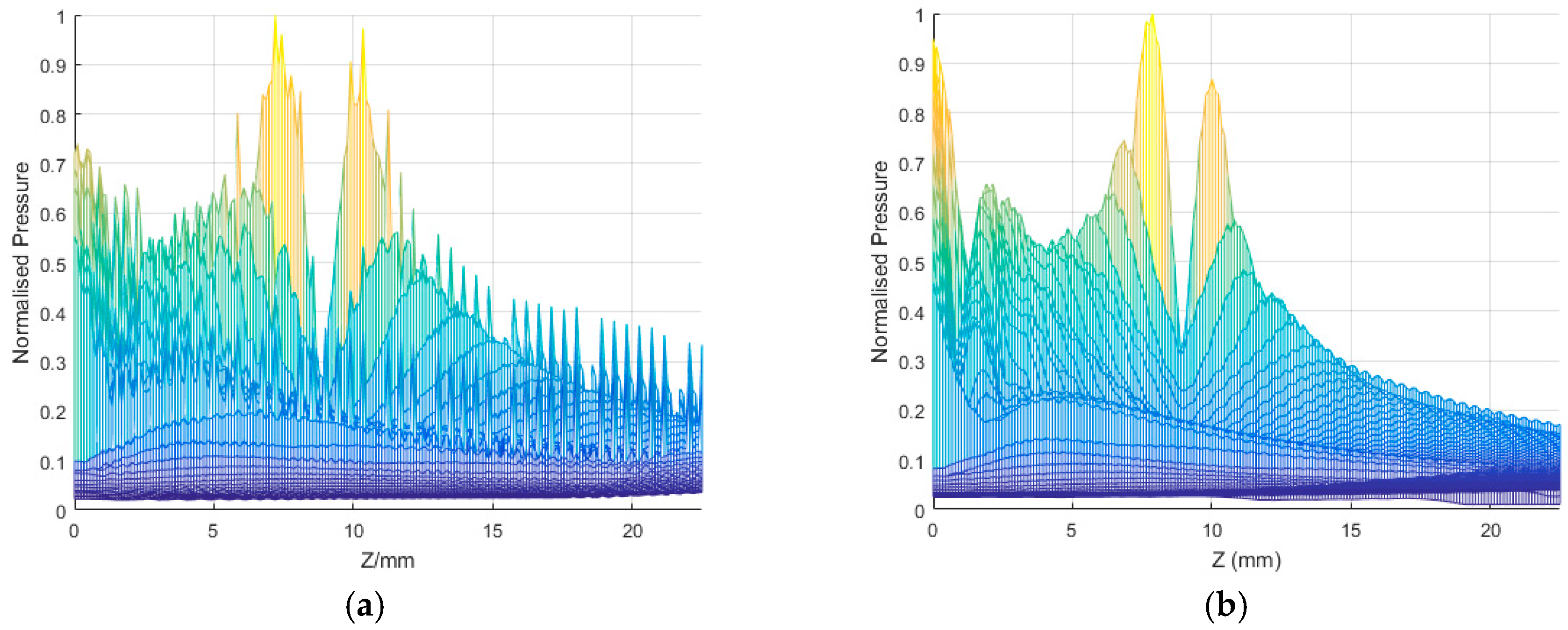
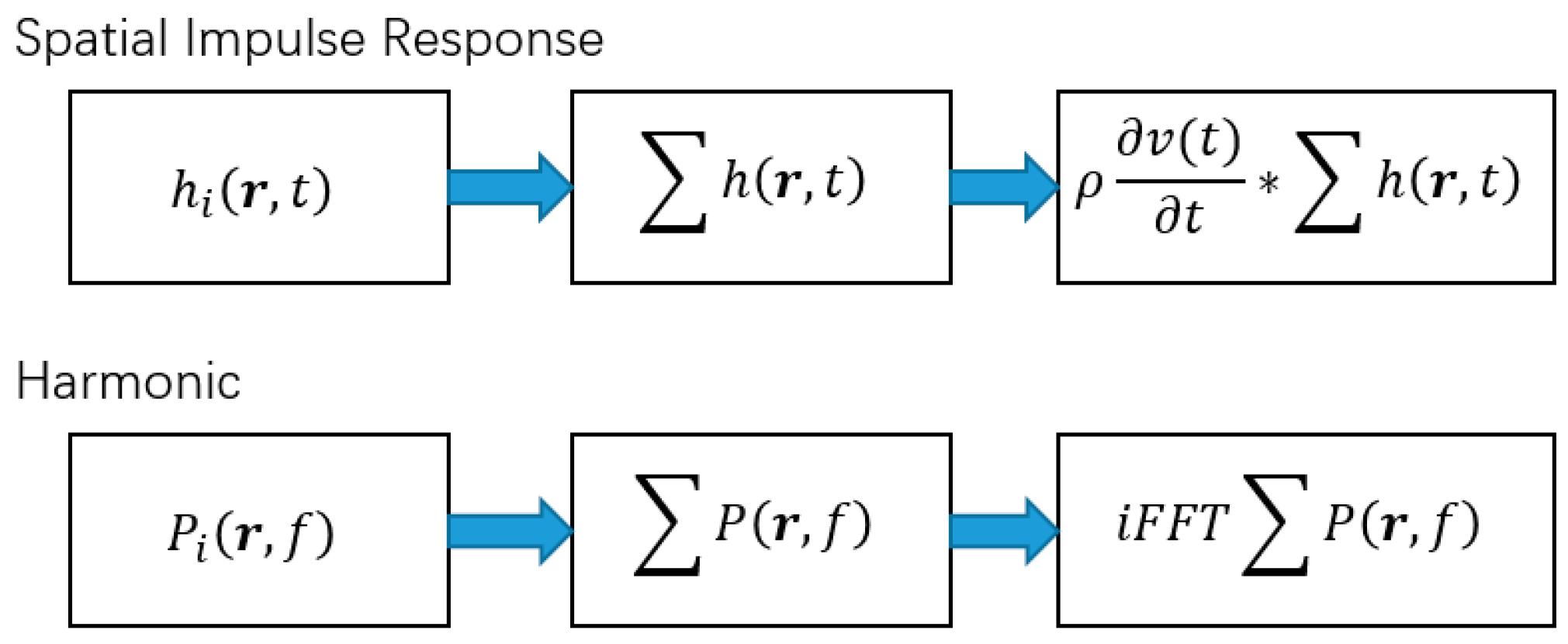
2.1. Spatial Impulse Response Function
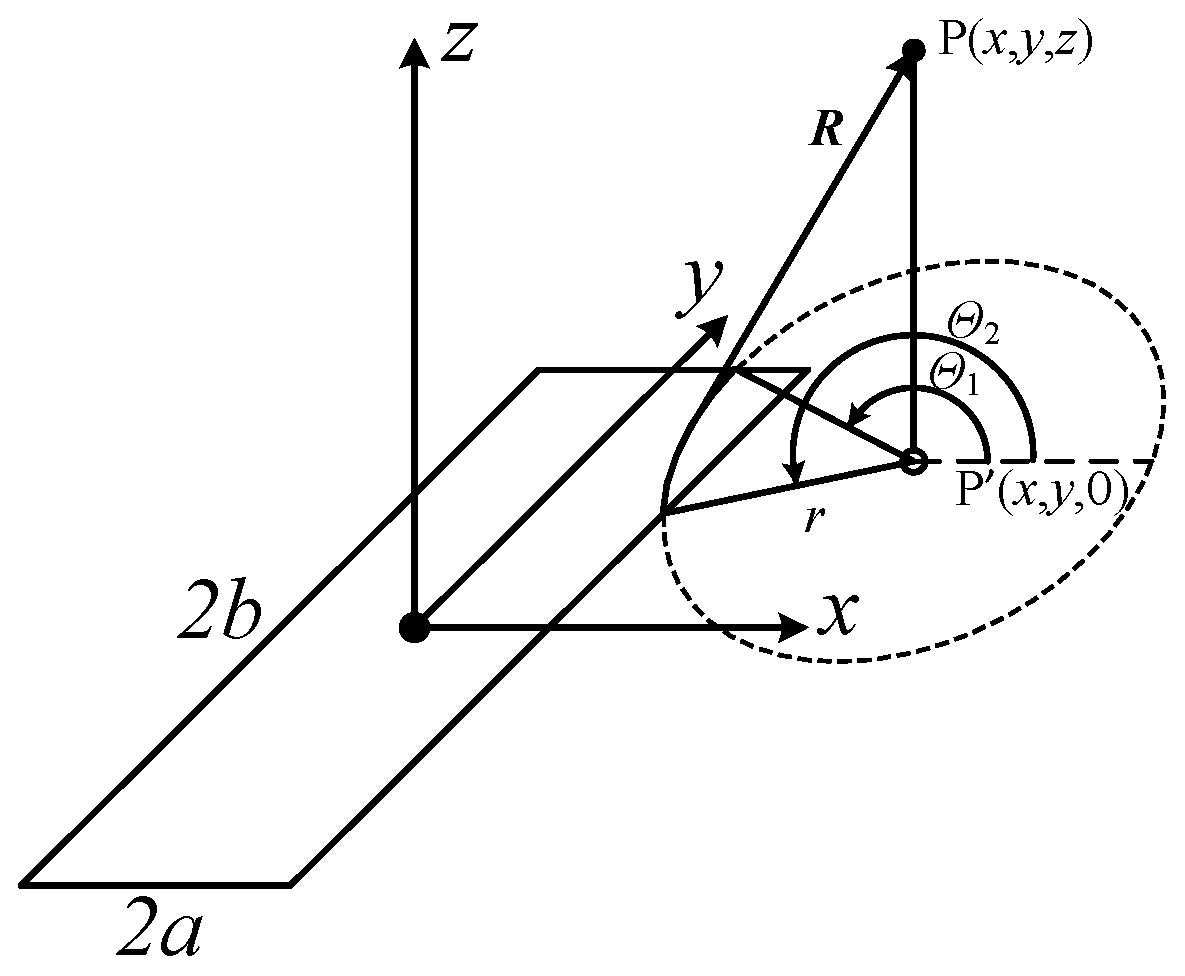
A rectangular transducer, with length 2
b and width 2
a (2
b ≥ 2
a), is located on the plane
z = 0, surrounded by an infinite rigid baffle, as shown in
Figure 1. The radiated space is a homogeneous lossless fluid medium, with density
ρ and speed of sound
c. The center of the aperture is located at the origin of the coordinate system, with length along the
y axis and width along the
x axis. The transient pressure
p(
x,
y,
z;
t) radiated from a planar transducer at point P(
x,
y,
z), and the time instant
t, can be written as the convolution of the first-order derivative of the normal velocity of the aperture surface,
u(
t) with a spatial impulse response function
h(
x,
y,
z;
t):
where the asterisk (*) denotes the convolution operation, and the spatial impulse response function
h(
x,
y,
z;
t) is derived from the Huygens’ principle [
17] as:
where
S denotes the active radiating surface of the aperture,
δ(
t) is the Kronecker function, and
R is the distance between the infinitesimal d
s and the field point P(
x,
y,
z).
From Equation (2), the spatial impulse response at the time instant
t only varies with the position of the field point for a specific aperture. The surface integral in Equation (2) can be expressed instead by using polar coordinates with the origin at the field point projection on the aperture plane P′(
x,
y,0):
where Θ
1 and Θ
2 are the minimum and maximum angle components, and
r2 and
r1 are the minimum and maximum radius components.
Deriving from the relationship
R2 =
r2 +
z2, the equation 2
Rd
R = 2
rd
r can be obtained, and then substituting the equation with
τ =
R/
c into Equation (3), the spatial impulse response function can be simplified as the integral of angle at time instant
t multiplying with a constant term:
where
tmin and
tmax determine the time range of integration, and Θ
1(
t) and Θ
2(
t) are determined by the intersection of the transducer and the projection spherical wave centered at the field projection as shown in
Figure 2 with radius
R =
ct at the time instant
t. The intersection between the spherical wave and the plane
z = 0 is a projection circle centered at P′(
x,
y,0) with radius
, when
t >
z/
c. The integral Equation (4) can be expressed as superimposition of the central angles of the arcs intersected between the projection circle and the transducer aperture. If more than one arc exists, the spatial impulse response can be expressed as the summation of the central angles of all the intersected arcs inside the transducer aperture:
where
k is the index of the intersected arcs, Θ
k1(
x,
y,
z;
t) and Θ
k2(
x,
y,
z;
t) denote the start and the end angle of intersected arc seperately, Θ
k(
x,
y,
z;
t) denotes the central angle of the
k-th arc, and Θ
Σ(
x,
y,
z;
t) denotes the summation of all of the central angles of the intersected arcs.
2.2. Spatial Impulse Response Function of a Rectangular Piston
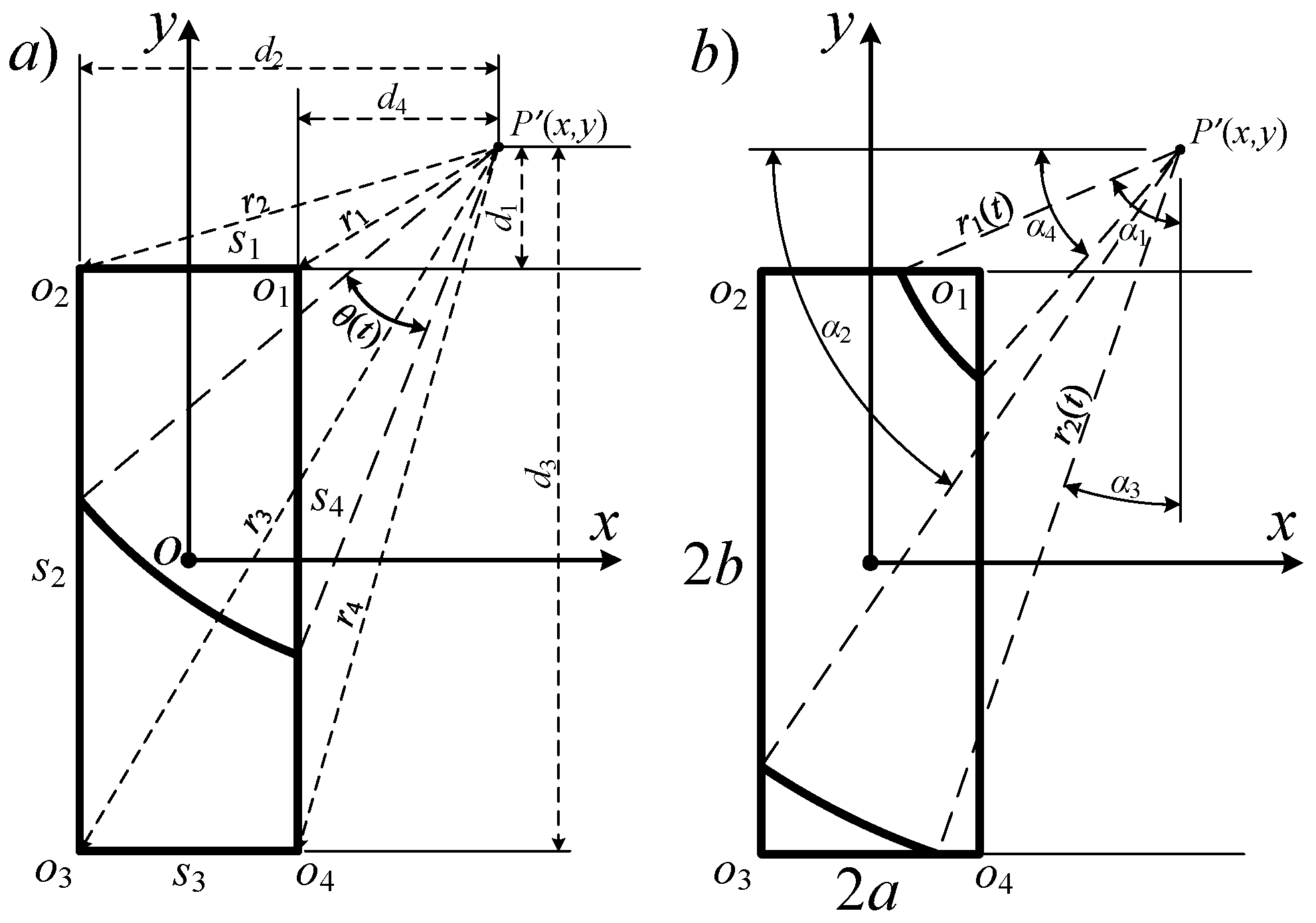
Based on the previous derivation, the spatial impulse response function is expressed as a summation of the central angles of the intersected arcs. The calculation of the central angles become the key point for computing the spatial impulse response. Consider the Cartesian coordinates in the transducer aperture plane, as shown in
Figure 2. Due to the geometrical symmetry of rectangular aperture, the projection points can be transformed to the first quadrant
x ≥ 0,
y ≥ 0:
The points in the first quadrant will be considered. The four vertices are named as
oi (
i = 1–4). The four edges are named as
si (
i = 1–4). The distance between the projection point P′ and the vertices and the edges of the rectangle are defined as
ri (
i = 1–4) and
di (
i = 1–4), separately:
Define
tdi and
tri as the time constants when the projection circle expands encountering edges and the vertices:
Define t0 = z/c as the spherical wave encounter with the aperture plane z = 0.
To reduce the calculation expressions, the angles
αi (
i = 1–4) are defined as critical angles of the intersected arc, with radius
r(
t) intersected with the
i-th edge:
where
r(
t) denotes the radius that varies with
t for the projection point at (
x,
y,
z). The spatial coordinate symbols are omitted here. It should be noted that Equations (7) and (8) hold when
t ≥
t0, and Equation (10) holds when the arc intersects with corresponding edge,
di ≤
r(
t). The complementary angle of
αi is defined as:
Due to the complexity of the rectangular aperture geometry, expression changes may occur when the intersected arcs step over the vertices or the edges of the rectangle. The expression changes then cause discontinuities in the temporal slope of Θ
Σ(
x,
y,
z;
t) and finally affect the temporal slope of
p(
x,
y,
z;
t). San Emeterio and Ullate [
18] presented a detailed solution about this problem, and the methods proposed by them will be implemented as the classical method in the following sections. The calculation procedure varies with the position of the projection points.
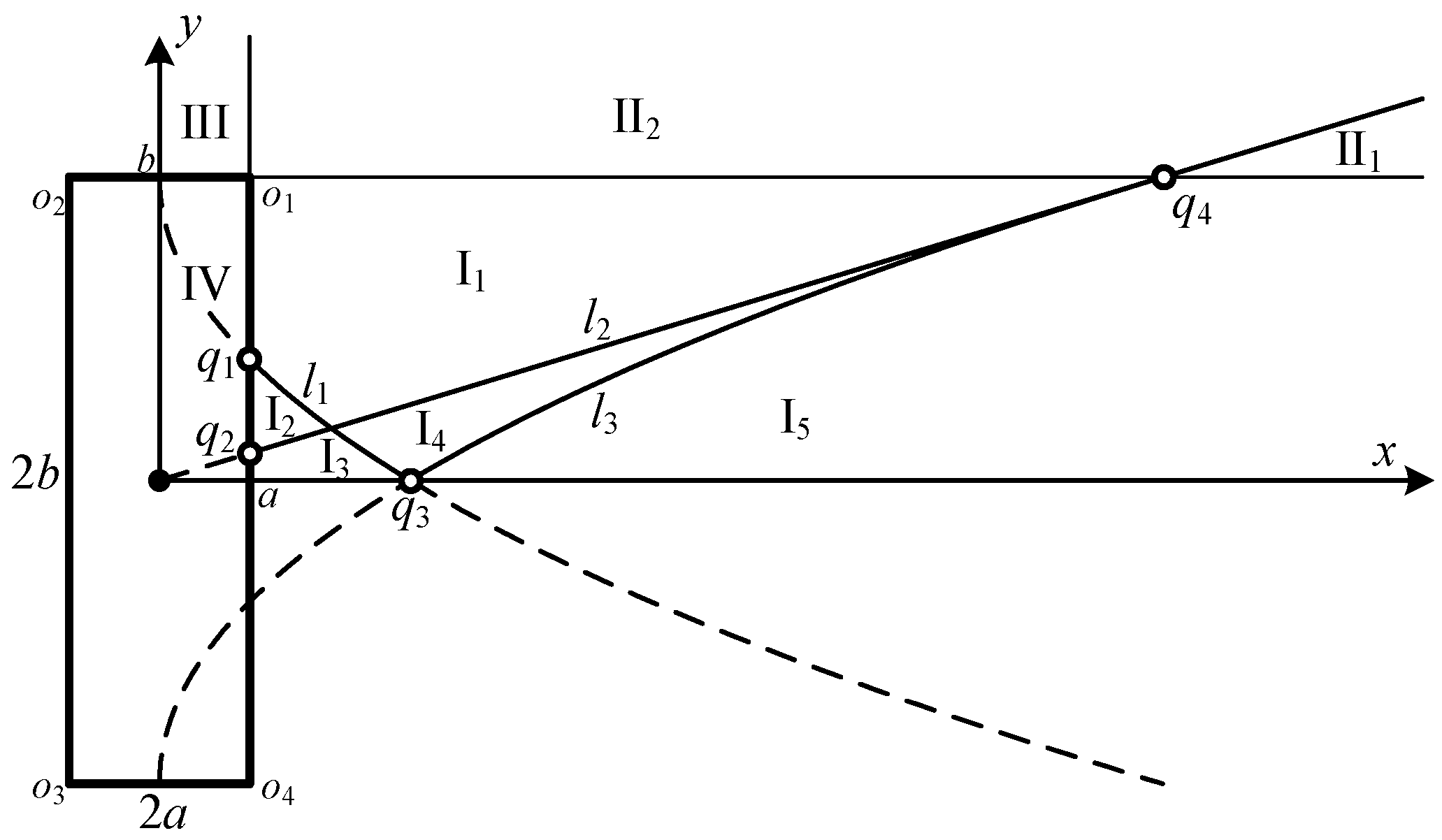
As shown in
Figure 3, the first quadrant of the aperture plane is divided into four regions by the lines
x =
a and
y =
b: I (
x ≥
a,
y ≤
b), II (
x ≥
a,
y ≥
b), III (
x ≤
a,
y ≥
b) and IV (
x ≤
a,
y ≤
b).
The curves
l1,
l2, and
l3 denote
r1 =
d2,
r2 =
r4, and
r4 =
d3 separately, which are expressed as:
The dashed lines are illustrated as the extension of Equation (12). The curves l1 and x = a intersect at the point q1(a,b−2a). The curves l2 and x = a intersect at the point q2(a,a2/b). The curves l1, l3, and y = 0 intersect at the point q3(b2/4a,0). The curves l2 and y = b intersect at the point q4(b2/a,b).
The four regions are then divided into several sub-regions by the curves. The projection points located in the same sub-region share the same calculation procedure for the central angle summation ΘΣ(x,y,z;t).
As presented in
Figure 3, the number of sub-regions in region I relies on the position of the three intersection points
q1,
q2, and
q3, which has direct relation to the calculation procedure of the central angle of intersected arcs. It can be derived that the position of the three intersection points are related to the ratio of the width and height of the rectangle. The relationships between the number of sub-regions in region I and the ratio of the width and height are presented in
Table 1.
The order of time instant precedence and the central angle summation Θ
Σ(
t) for the projection points located in the sub-regions of region I are presented in
Table 2. Typically, 1-D array transducers employ rectangular transducers with
, which means there are five sub-regions in the region I.
Region II is always divided into two sub-regions by the line
l2, which are denoted as II
1 and II
2. The central angle summation calculation expressions for the projection points located in the sub-regions of region II are shown in
Table 3.
Region III maintains itself without sub-regions. There is only one possibility of the discontinuity order of the time instant for the projection points located in region III. The computation procedure for projection points in region III is:
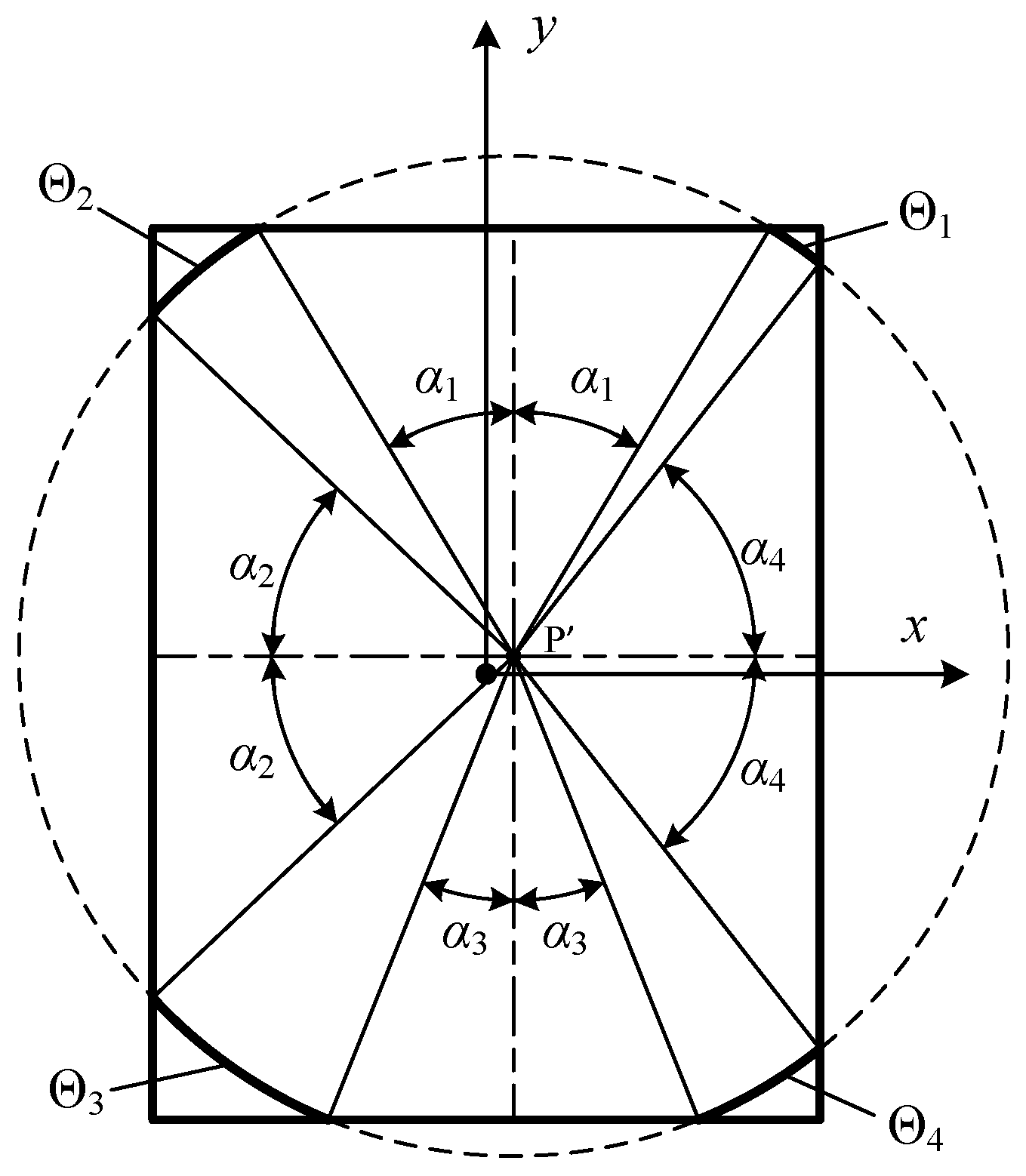
Since the possibilities of the discontinuity order of the time instant are complicated when the projection points are located inside the rectangle, region IV, the calculation procedure is far more complicated when compared to the procedure for points outside the rectangle [
18]. The alternative solution for this condition is implemented in this paper. The projection point P′ is used to divide the rectangle aperture into four sub-rectangles, as shown in
Figure 4. The shape of the rectangle, the position of the projection point P′ and the circle shown in
Figure 4 are selected so as to illustrate the condition that the projection circle intersects with all of the four edges.
The final central angle summation can be expressed as the sum of central angles created by intersection of the projection circle and each sub-rectangle:
where the symbols
x,
y,
z, and
t are omitted for simplicity.
where
αi is defined from Equation (10) when the arc intersects the
i-th edge. In addition,
αi equals 0 and
equals π/2 when
r(
t) ≤
di.
The expressions introduced are direct, although, they are complicated due to the complexity of the rectangular geometry. However, they can be easily implemented.
Moreover, since the intersected arcs only exist when the wave sphere intersects with the rectangular aperture, the spatial impulse response function is continuous nonzero from the first time instant,
tmin, the projection circle intersects the rectangle or is located within the rectangle to the last time instant,
tmax, the radius exceeds
r3. The range of for each region and sub-region is shown in
Table 4. The values beyond this range are zeros and summation procedure of these zero values can be avoided.
2.3. Spatial Impulse Response for Linear Array Transducers
Previously, the classical methodology for computing the transient pressure at field point (
x,
y,
z) radiated from a linear array transducer with
N planar rectangular transducers was a simple summation of the pressure from each single element [
25]:
where
i is the element index number, from 0 to
N − 1,
hi(
x,
y,
z;
t) is the spatial impulse response at field point (
x,
y,
z) radiated from the
i-th element,
ui(
t) is the aperture surface vibration velocity of the
i-th element, and
ai is the weighting level of the
i-th element.
Ti is the delayed time of the
i-th element.
Generally, the aperture surface vibration velocities are the same, so Equation (16) can be expressed as:
where
hΣ(
x,
y,
z;
t) is the total spatial impulse response at field point P:
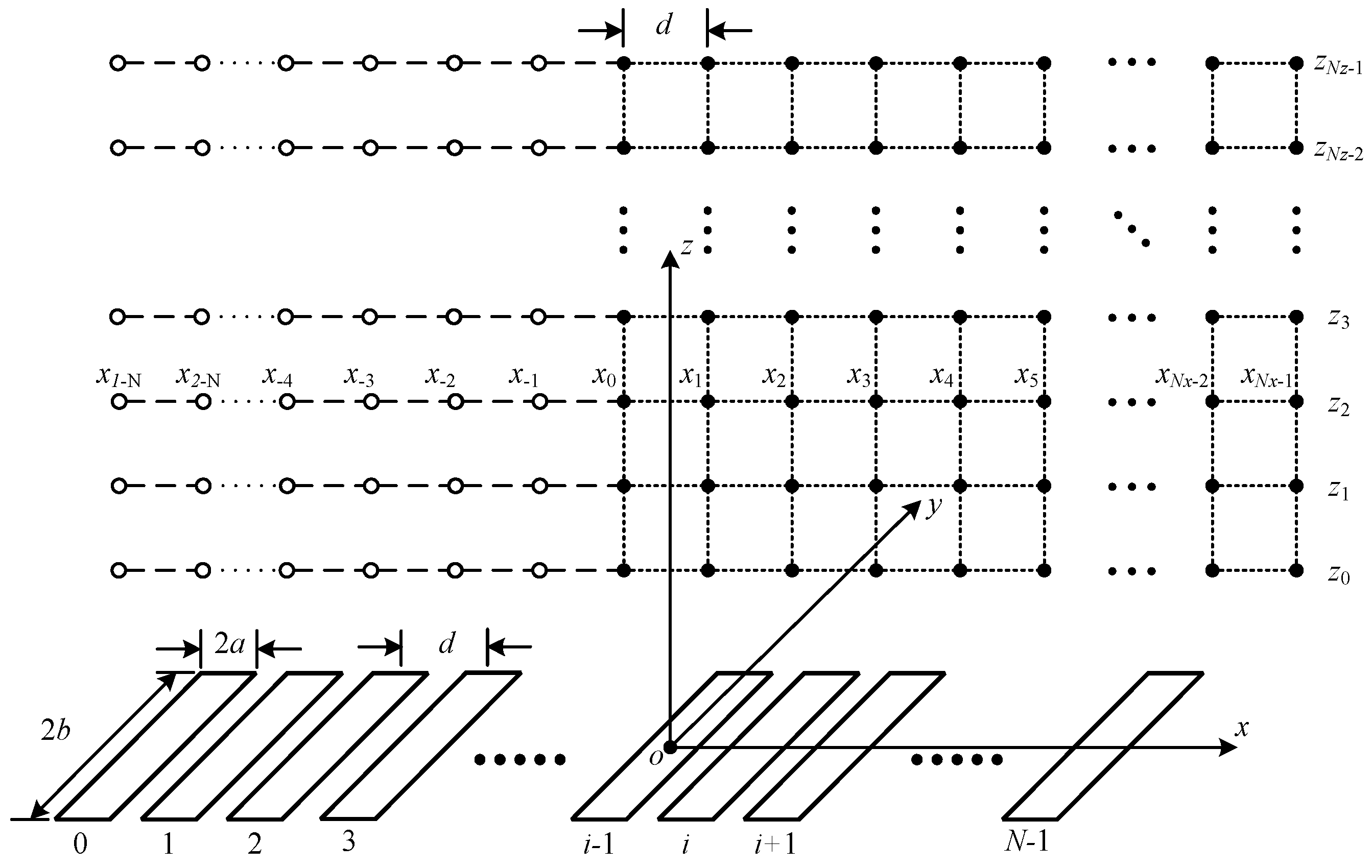
The general geometry of linear phased array transducers and the discretized field points are shown in
Figure 5.
The field points are discretized with
Nx,
Ny, and
Nz along with the
x,
y, and
z axes. The
x component of each point meet the relationship:
where
k is the
x component index, and
d is the pitch between two neighboring transducers. Although the
y and
z components do not have a mandatory rule, they are typically evenly distributed.
The spatial impulse response at field points (
xk+j,
y,
z) and (
xk,
y,
z) will meet the relationship:
where
j is an arbitrary integer.
This can be easily understood under the assumption that the geometry shape and the surface vibration velocity of the transducer elements are identical, because if two different field points have the same relative distance from two different transducers, they share the same spatial impulse response function contributed from the corresponding transducers. This means that repeated computations exist if the traditional summation method is utilized. The calculation process can be optimized for the field points which meet the distribution requirement introduced previously. The spatial impulse response
hi(
xk,
y,
z;
t) at point (
xk,
y,
z) contributed from transducer 1 to
N−1 can be derived from the expression:
which means the final result can be derived only from computing the result contributed from transducer 0. The redundant calculation procedures can be avoided.
From Equation (21), if
k <
N − 1, the condition that
k −
i < 0 may occur, which means that the right part of Equation (21) may not exist since the
x indices of the field points are not less than zero. In order to fix this problem,
N − 1 auxiliary points are created in the
x direction for every
y and
z:
Thus, the total spatial impulse response function at field point (
xk,
y,
z) can be expressed as:
Finally, the pressure at field point (xk,y,z) can be obtained from Equation (17) by only considering the field contributed from transducer 0.
Generally, a field point gap in the
x direction set equal to
d lowers the obtained precision. However, if higher accuracy needs to be obtained, the proposed method can be easily modified. For more accuracy, the field point gap in the
x direction can be set as
d/M, where M > 1, the field points can be divided into M groups:
where
xm,0 is the start field point on direction of
x for group
m. Consequently,
N − 1 auxiliary points are required to be created on direction of
x for each group of field points:
The spatial impulse response at field points (
xm,k+j,
y,
z) and (
xm,k,
y,
z) will meet the relationship:
Correspondingly, Equation (21) can be expressed as:
The spatial impulse response function at field point (
xm,i,
y,
z) can be expressed as:
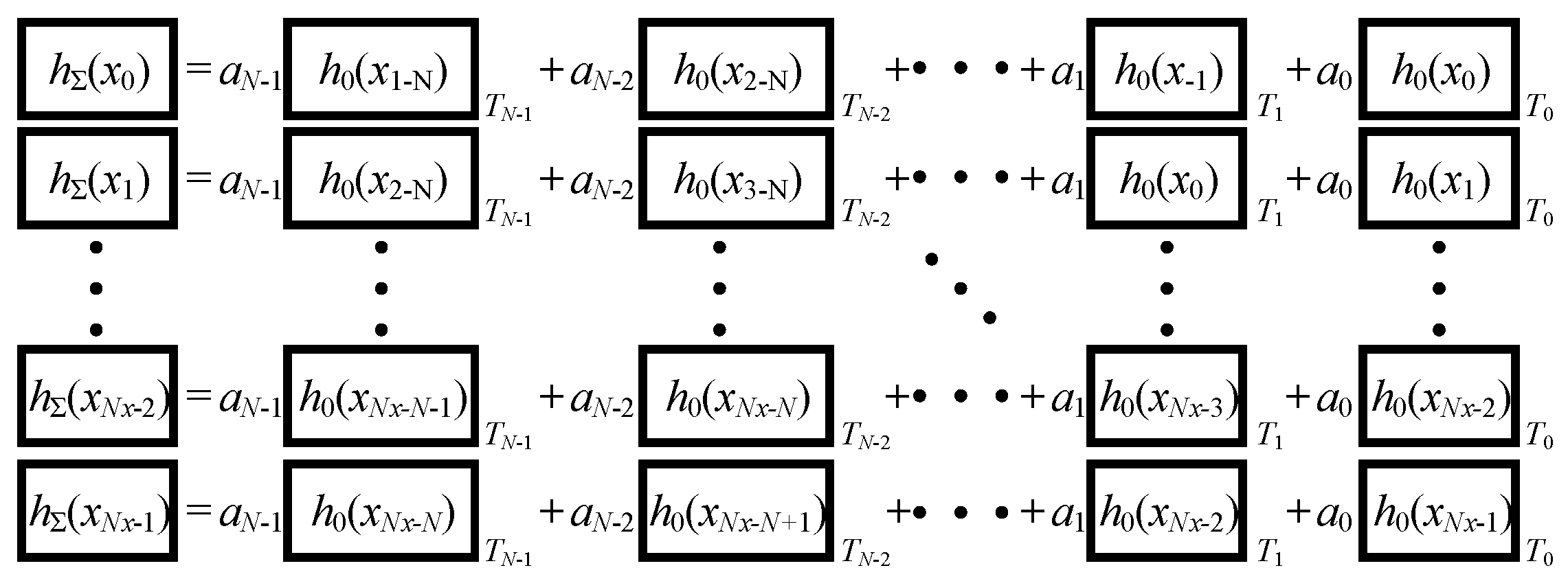
The computation procedure of Equation (28) is illustrated in
Figure 6 for
m = 0,…, M − 1 loops.
The block shown in
Figure 6 denotes one step of the calculation of spatial impulse response function for a field point at the time constant
t contributed from the one single transducer. Since the functions are related to the
x variable, the symbols
y,
z, and
t are omitted and the symbol
xm,k is simplified as
xk for simplicity of illustration.
Ti denotes the time shift index for summation. It can be seen from
Figure 6 that the calculation of the spatial impulse response involves the same transducer, which is called the basic transducer. Moreover, the basic transducer can be any one from the array transducers because the relationship shown in Equation (20) implies that the identical characteristic holds only if the field points are distributed as required.
2.4. Optimization of the Computation Procedure
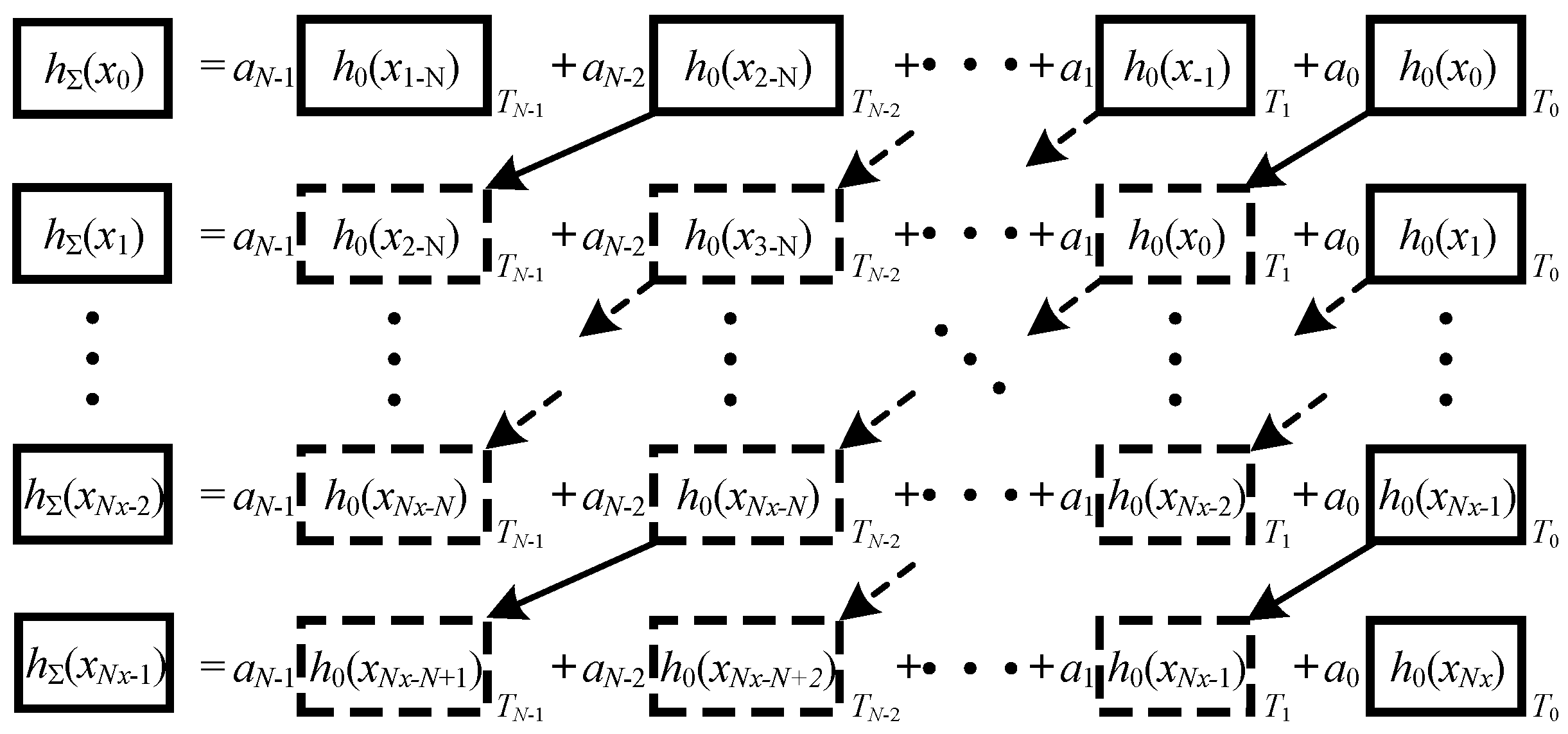
Furthermore, from
Figure 6, the computation procedure contains noteworthy redundancy. For example, the calculation of
h0(
x2−N), …,
h0(
x−1) and
h0(
x0) are used to calculate
hΣ(
x1) again. Only
h0(
x1) needs to be calculated if the results obtained during the last step can be stored in a lookup memory. Consequently, the computational cost can be reduced by reusing the results which have been calculated for the last field point. The procedure of the optimized method is illustrated in
Figure 7.
The classical method for calculating the spatial impulse response for linear phased array transducers implements a simple summation of the radiated field from each transducer and suffers
Nx ×
Ny ×
Nz ×
N times the number of calculations of the spatial impulse response functions and
Nx ×
Ny ×
Nz × (
N − 1) times the number of calculations of summations. The proposed method reduces the calculation to only (
Nx +
N − 1) ×
Ny ×
Nz times the number of calculations of the spatial impulse response functions and
Nx ×
Ny ×
Nz × (
N − 1) times the number of calculations of summations. The estimated speed-up ratio of computation times between the classical method and the proposed method can be expressed as:
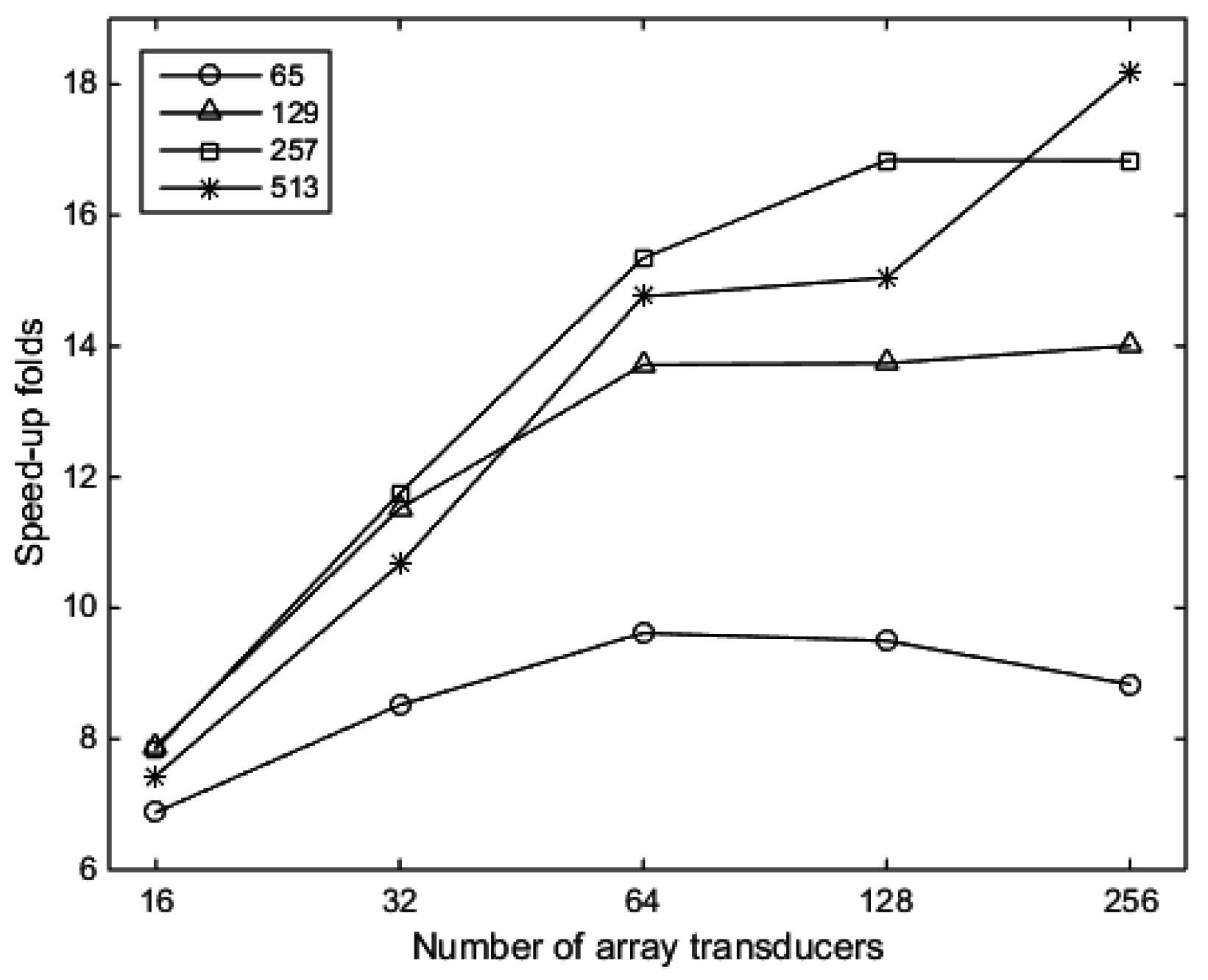
From Equation (29), the speed-up ratio is dependent on two factors: the number of discretized field points in the direction of the x axis and the transducer number. The speed-up ratio also increases along with both of the two factors.
Since the anti-trigonometric calculation process costs much more time than the summation process, this can greatly reduce the impulse response calculation process without any nonlinear approximation. Examples will be given to demonstrate how much the efficiency the proposed method can be improved. It is expected that the efficiency can be improved even more when the transducer number increases.