Signal Conditioning for the Kalman Filter: Application to Satellite Attitude Estimation with Magnetometer and Sun Sensors
Abstract
:1. Introduction
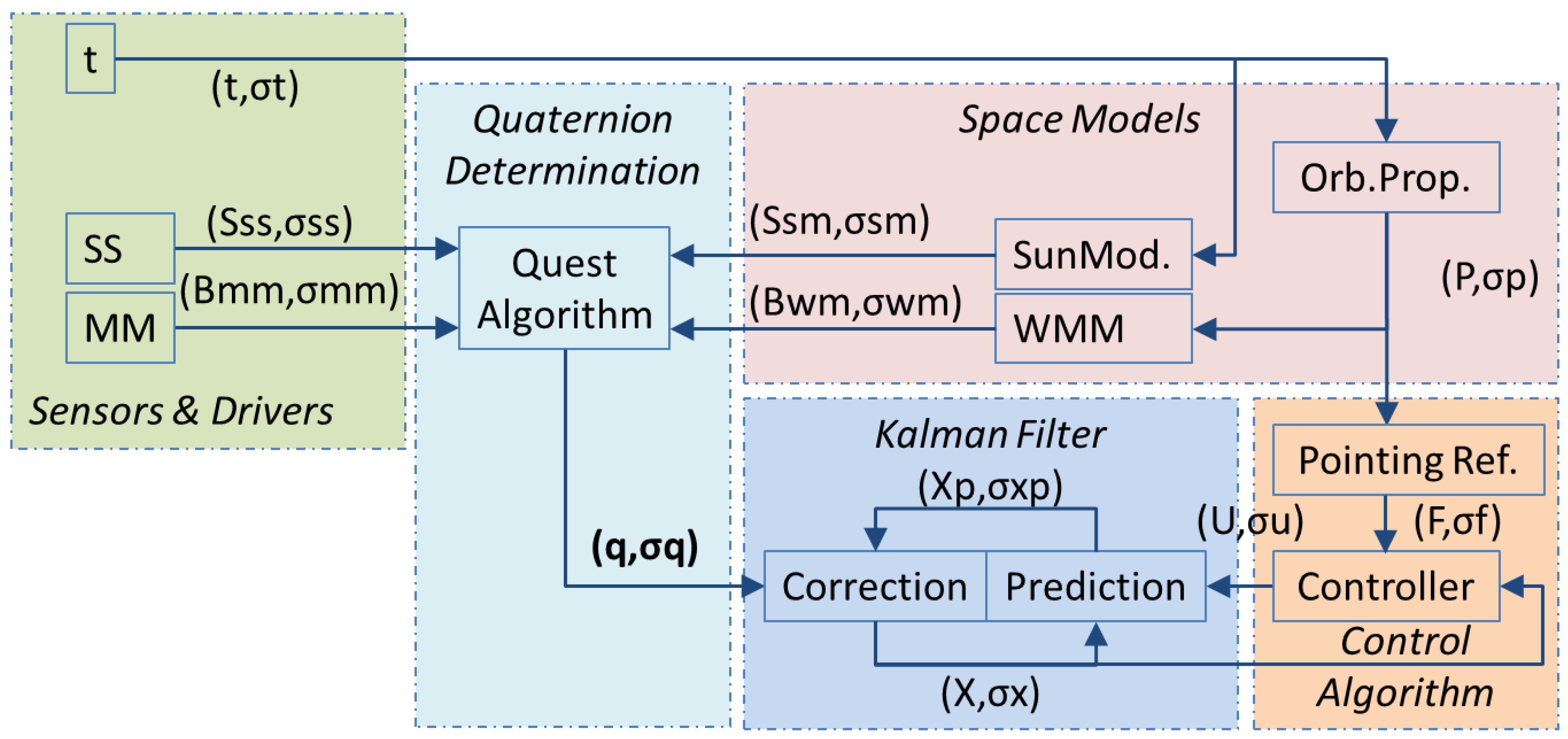
- Sensors & Drivers: It gives the direction vector of the Earth’s magnetic field (Bmm, σmm) and the direction vector of the Sun (Sss, σss). The vectors are measured in Satellite Body Reference Frame (SBF). In addition, the ADCS should know the system time (t, σt).
- Space Models: Based on a set of mathematical models, namely a model of orbital propagation [6], a model of Earth magnetic field [7] and an orbital model of Earth [8], the ADCS calculates the orbital position (P, σp), a direction vector of the Sun (Ssm, σsm) and a direction vector of the Earth’s magnetic field (Bwm, σwm). The vectors Ssm and Bwm should be referenced to the Earth Centered Inertial Frame (ECI) [8].
- Quaternion Determination: The quaternion (q, σq) that describes the satellite orientation would be computed from measured vectors and calculated vectors. It will be shown in this article that ill conditioned problems can appear.
- Kalman Filter: In order to estimate the system state, the Kalman filter proceeds iteratively, with two steps in each iteration. The first step is prediction of state (Xp, σxp), and the second step is correction of that prediction (X, σx). The correction is based on the quaternion just determined at the time of correction.
- Control Algorithm: The attitude controller should generate a control signal (U, σu) for the actuation. The controller takes into account the estimated state (X, σx) and a reference signal (F, σf).
2. Background
2.1. Attitude Representation with Quaternions
2.2. State Variable Models
2.3. Kalman Filter
3. Attitude Estimation with the Kalman Filter
3.1. Attitude Behaviour
- ω is the angular velocity vector of the satellite in body axes;
- J is the tensor of inertia;
- τ is in body axes the vector of torques applied to the satellite: it includes perturbations and control actions;
- .
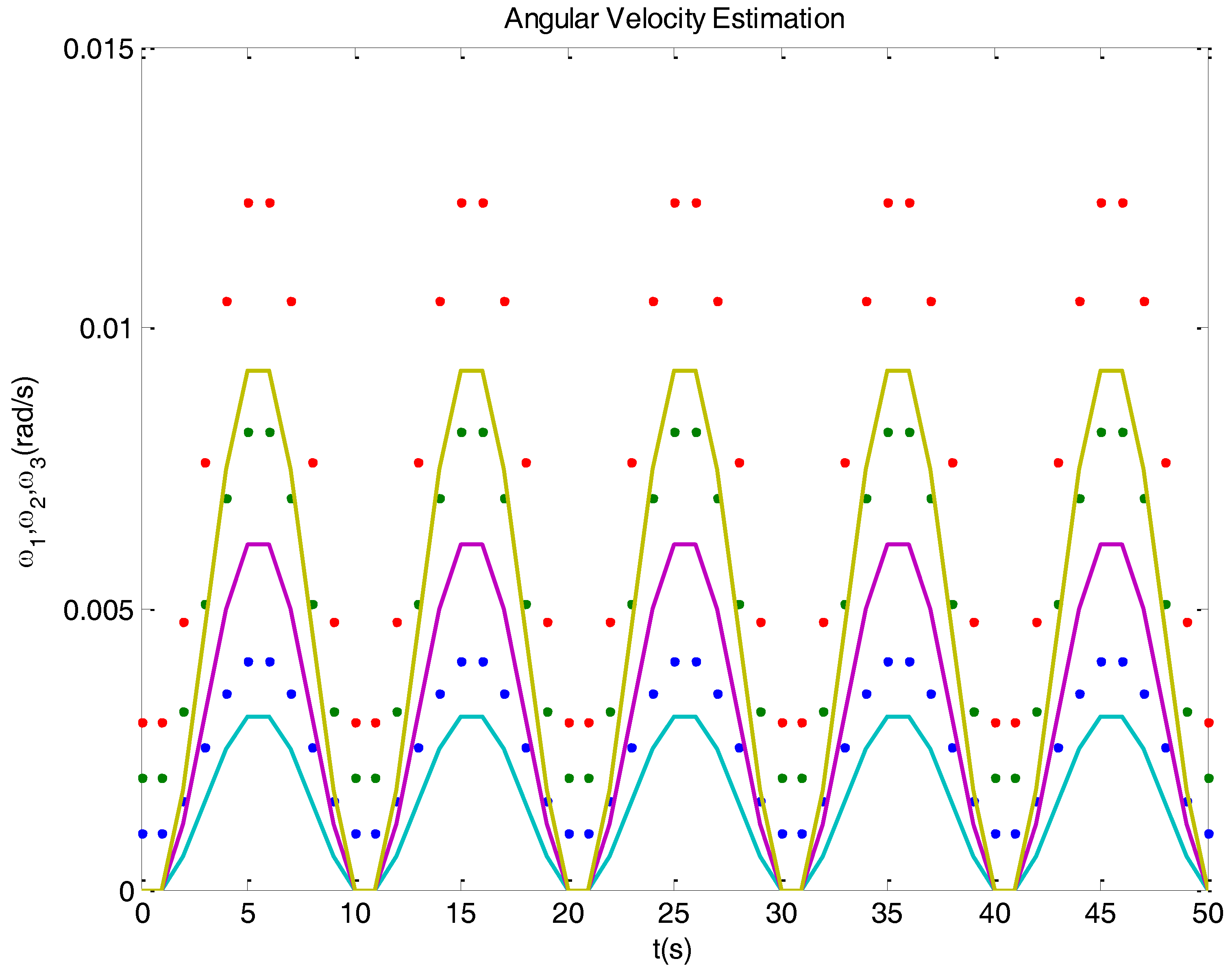
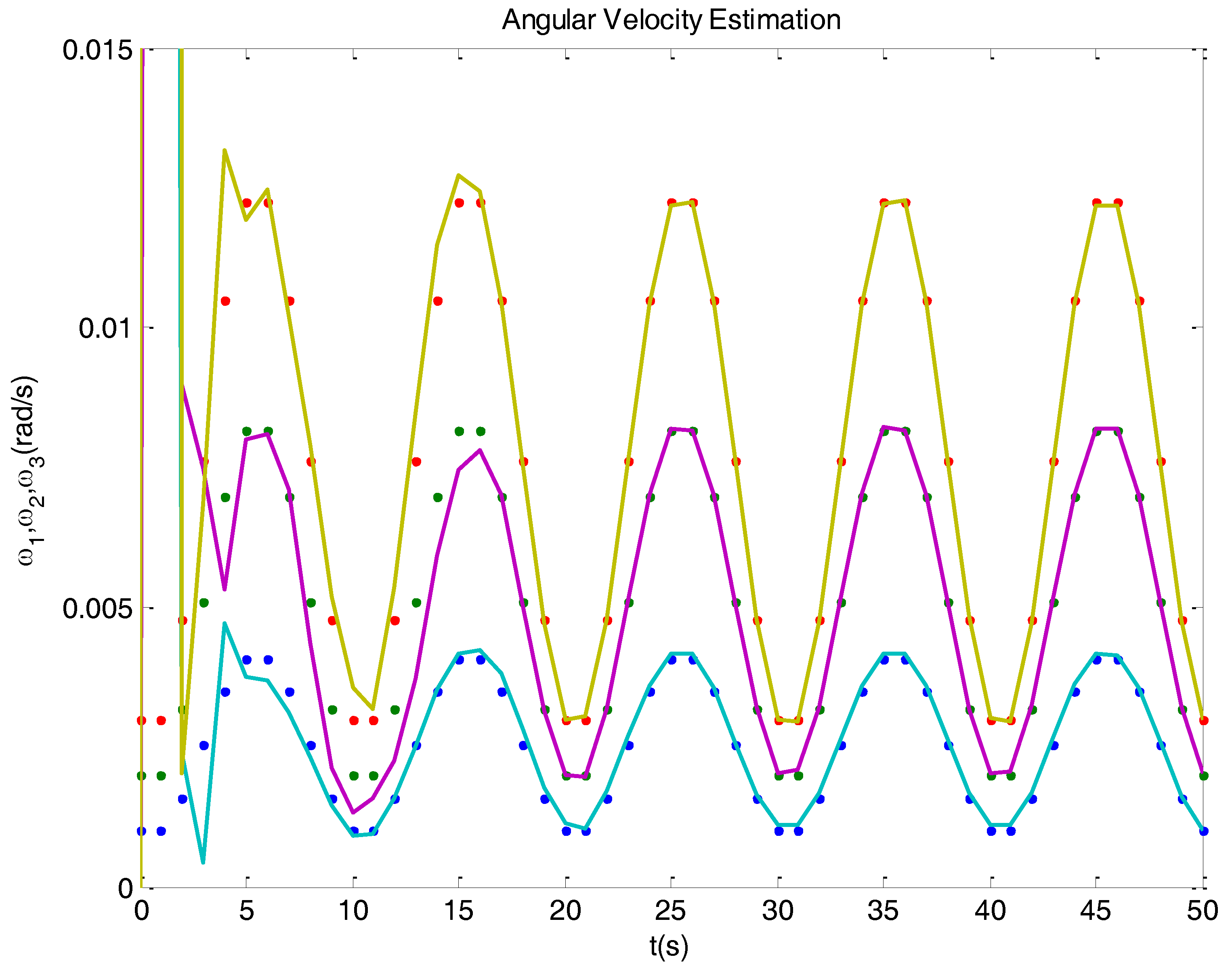
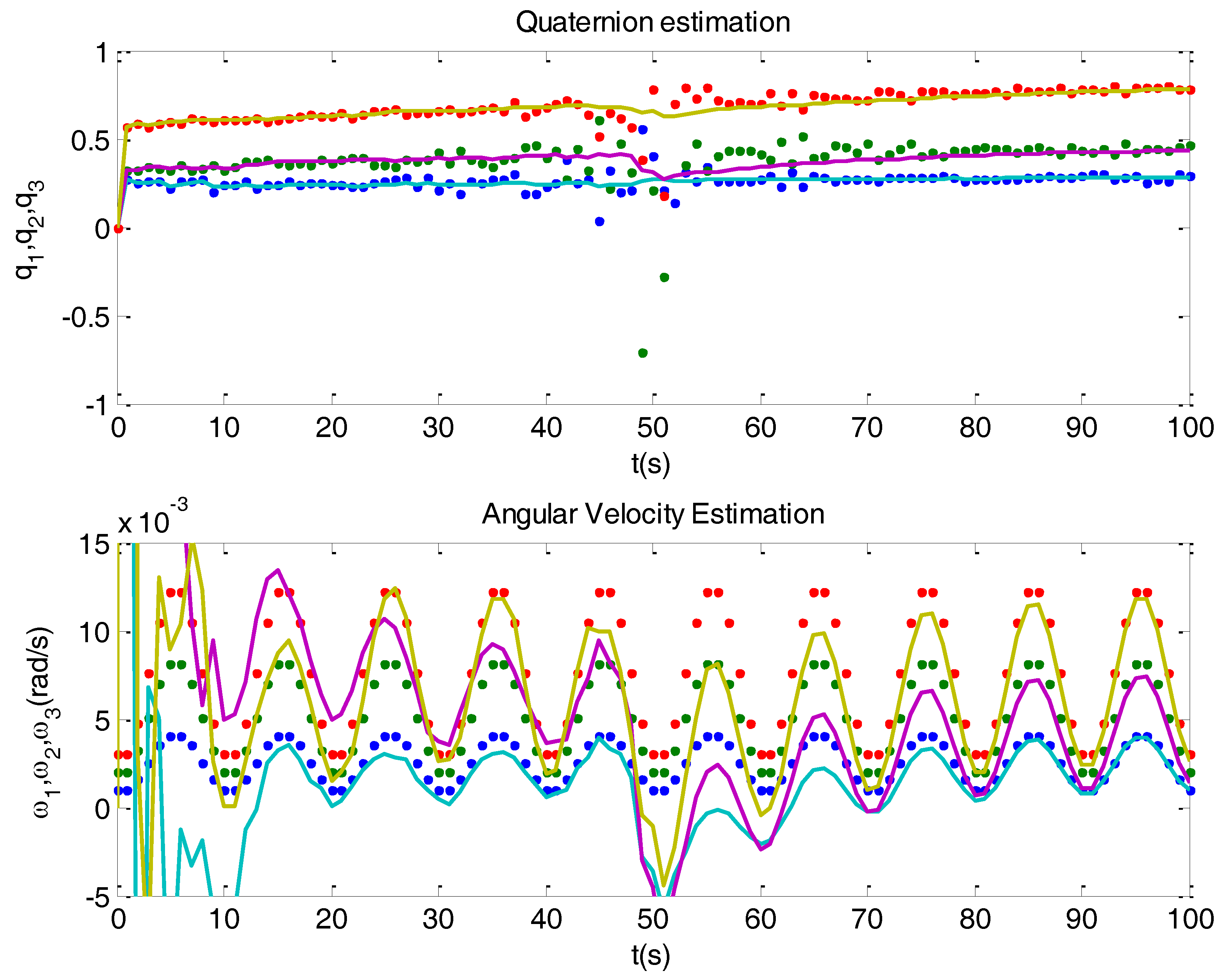
3.2. Observability Issues
3.3. Discretization
4. Quaternion Determination. Conditioning
4.1. Quest
4.2. Problems Related to Singularities
4.3. A Solution Based on Conditioning
5. Aspects of the Application to a Satellite
5.1. INTA Nanosat-1B Satellite
5.2. Measurement Noise and Sensors
5.2.1. Magnetometer
5.2.2. Sun Sensors
5.3. Process Noise
5.3.1. Input and Perturbation Noise
5.3.2. Discretization Noise
5.4. Magentic Dipole Estimation
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wertz, J.R. Spacecraft Attitude Determination and Control; Kluwer Academic Publisher: Dordrecht, The Netherlands, 1978. [Google Scholar]
- Sidi, M.J. Spacecraft Dynamics & Control; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Kalman, R.E.; Bucy, R.S. New results in linear filtering and prediction theory. J. Basic Eng. 1961, 83, 95–108. [Google Scholar] [CrossRef]
- Diebel, J. Representing attitude: Euler angles, unit quaternions, and rotation vectors. Matrix 2006, 58, 1–35. [Google Scholar]
- Hoots, F.R.; Roehrich, R.L. Models for Propagation of NORAD Element Sets. Spacetrack Report No. 3. December 1988. Available online: www.celestrak.com/NORAD/documentation/spacetrk.pdf (accessed on 2 August 2016).
- Maus, S.; Macmillan, S.; McLean, S.; Hamilton, B.; Nair, M.; Thomson, A.; Rollins, C. The US/UK World Magnetic Model for 2010–2015. NOAA Technical Report NESDIS/NGDC 2010. Available online: www.geomag.bgs.ac.uk/documents/WMM2010_Report.pdf (accessed on 2 August 2016).
- Vallado, D.A. Fundamentals of Astrodynamics and Applications; Springer Science & Business Media: Berlin, Germany, 2003. [Google Scholar]
- Wen, J.Y.; Kreutz-Delgado, K. The attitude control problem. IEEE Trans. Autom. Control 1991, 36, 1148–1162. [Google Scholar] [CrossRef]
- Shuster, M.D. A survey of attitude representations. Navigation 1993, 8, 439–517. [Google Scholar]
- Lefferts, E.J.; Markley, F.L.; Shuster, M.D. Kalman filtering for spacecraft attitude estimation. J. Guid. Control Dyn. 1982, 5, 417–429. [Google Scholar] [CrossRef]
- Trawny, N.; Roumeliotis, S.I. Indirect Kalman Filter for 3D Attitude Estimation; Technical Report Number 2005-002; Department of Computer Science & Engineering, University of Minnesota: Minneapolis, MN, USA, 2005; Volume 2. [Google Scholar]
- Crassidis, J.L.; Markley, F.L. Predictive filtering for attitude estimation without rate sensors. Adv. Astronaut. Sci. 1996, 93, 1021–1038. [Google Scholar] [CrossRef]
- Edwan, E.; Knedlik, S.; Loffeld, O. Angular motion estimation using dynamic models in a gyro-free inertial measurement unit. Sensors 2012, 12, 5310–5327. [Google Scholar] [CrossRef] [PubMed]
- Hamzah, N.H.; Yaacob, S.; Muthusamy, H.; Hamzah, N. Comparative Study of Extended Kalman Filter and Particle Filter for Attitude Estimation in Gyroless Low Earth Orbit Spacecraft. In Advanced Computational Methods for Knowledge Engineering; Springer International Publishing: Berlin, Germany, 2015; pp. 95–106. [Google Scholar]
- Crespillo, O.G.; Cuccci, D.A.; Khaghani, M. Unscented Kalman Filter for Angular Rate Estimation in Gyro-Free Inertial System. In Proceedings of the ION GNSS+ 2016, Portland, OR, USA, 12–13 September 2016.
- Yang, Y. Spacecraft attitude determination and control: Quaternion based method. Ann. Rev. Control 2012, 36, 198–219. [Google Scholar] [CrossRef]
- Wahba, G. A least squares estimate of spacecraft attitude. SIAM Rev. 1965, 7, 409. [Google Scholar] [CrossRef]
- Shuster, M.D.; Oh, S.D. Three-Axis attitude determination form vector observations. J. Guid. Control 1981, 4, 70–77. [Google Scholar] [CrossRef]
- INTA NanoSat-1B at eoPortal Directory. Available online: https://directory.eoportal.org/web/eoportal/satellite-missions/n/nanosat-1b (accessed on 2 August 2016).
- Díaz-Michelena, M. Small Magnetic Sensors for Space Applications. Sensors 2009, 9, 2271–2288. [Google Scholar] [CrossRef] [PubMed]
- Pita, L.C.; San Roman, S.E.; Giron-Sierra, J.M.; Barriga, J.R.; de Vicente, P.D.; Jerez, M.A. Getting more performance from INTA NanoSat-1B truncated pyramid Sun sensors. IEEE Sens. J. 2014, 14, 1867–1877. [Google Scholar] [CrossRef]
- Polo, O.R.; Esteban, S.; Cercos, L.; Parra, P.; Angulo, M. End-to-end validation process for the INTA-Nanosat-1B Attitude Control System. Acta Astronaut. 2014, 93, 94–105. [Google Scholar] [CrossRef]

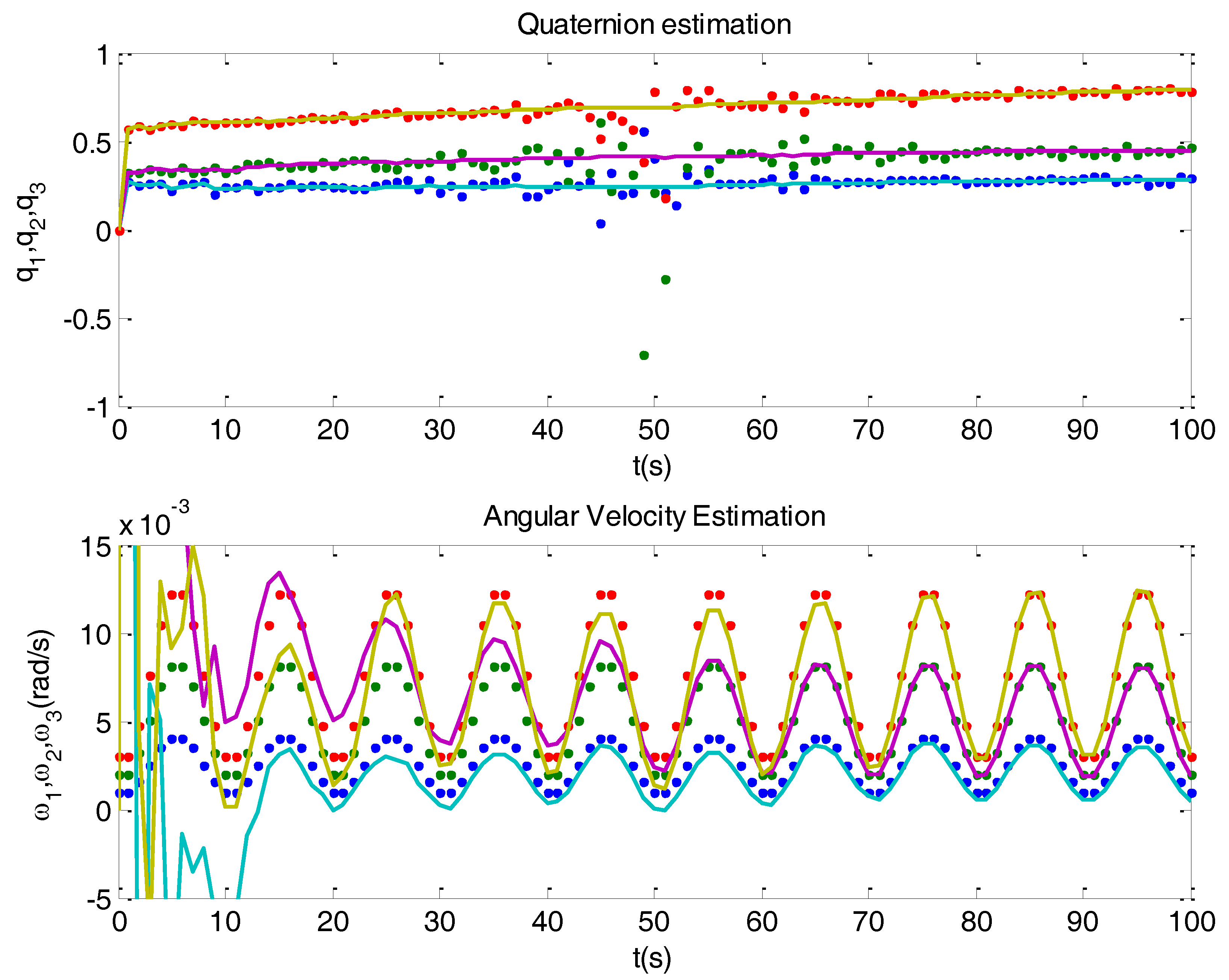
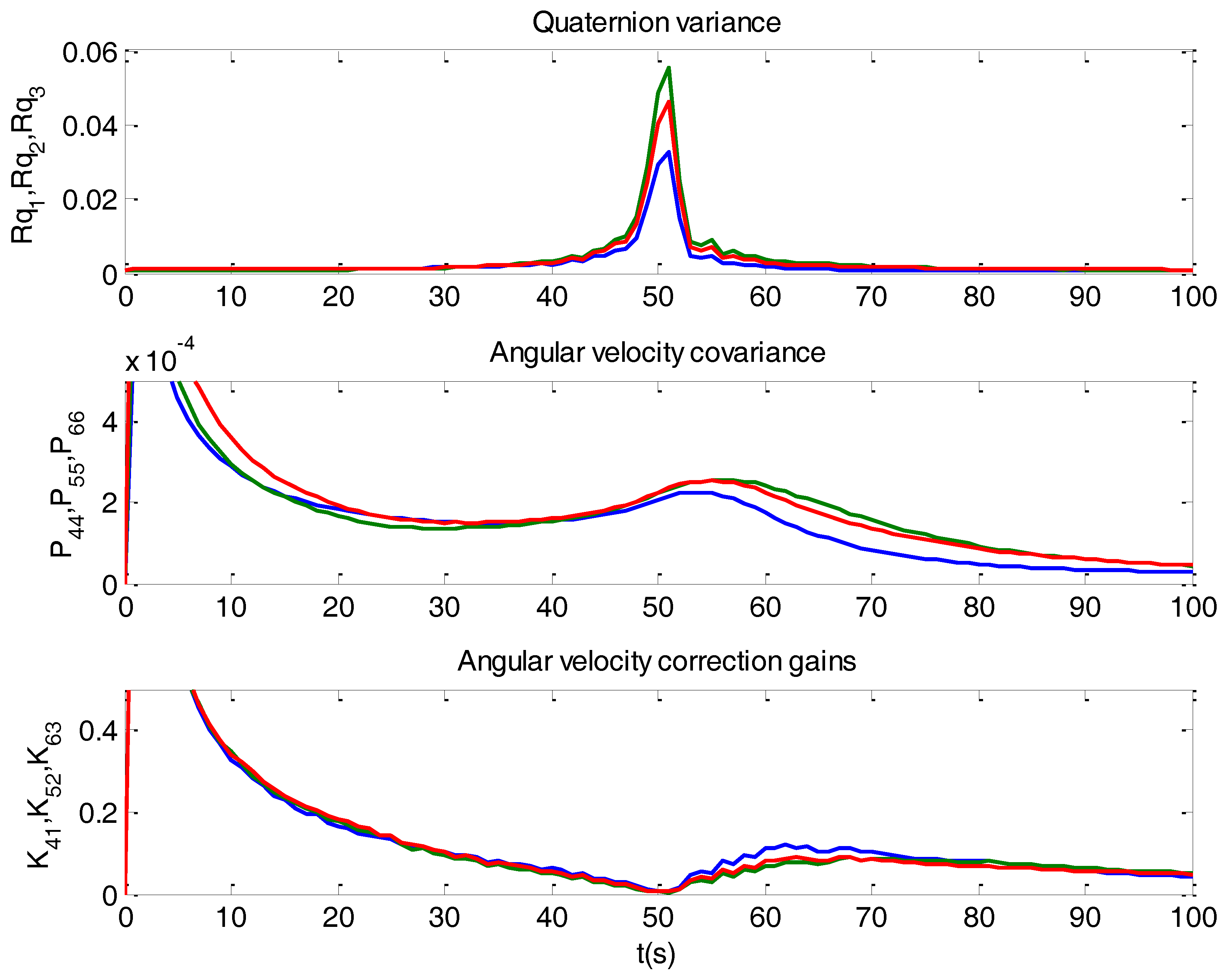



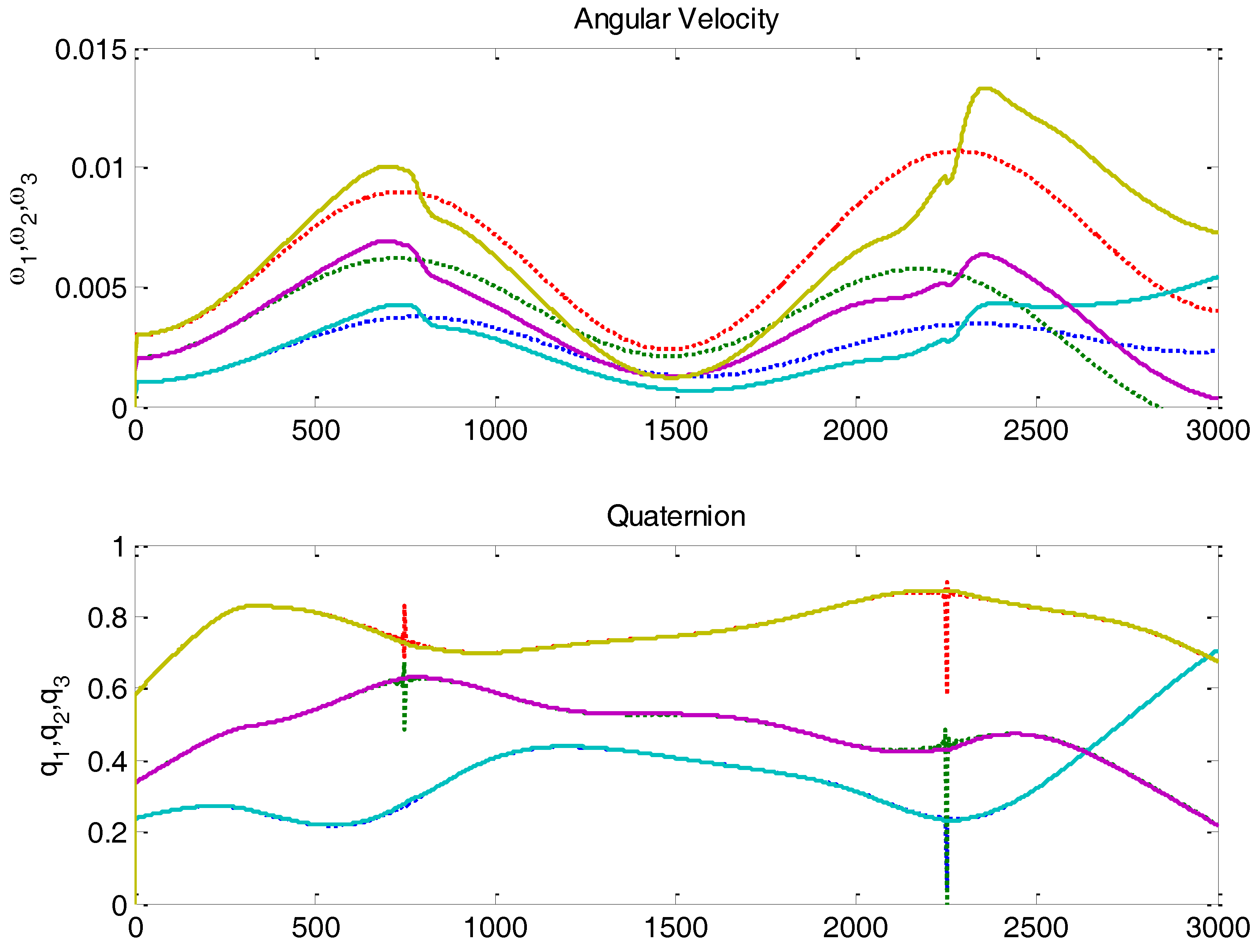
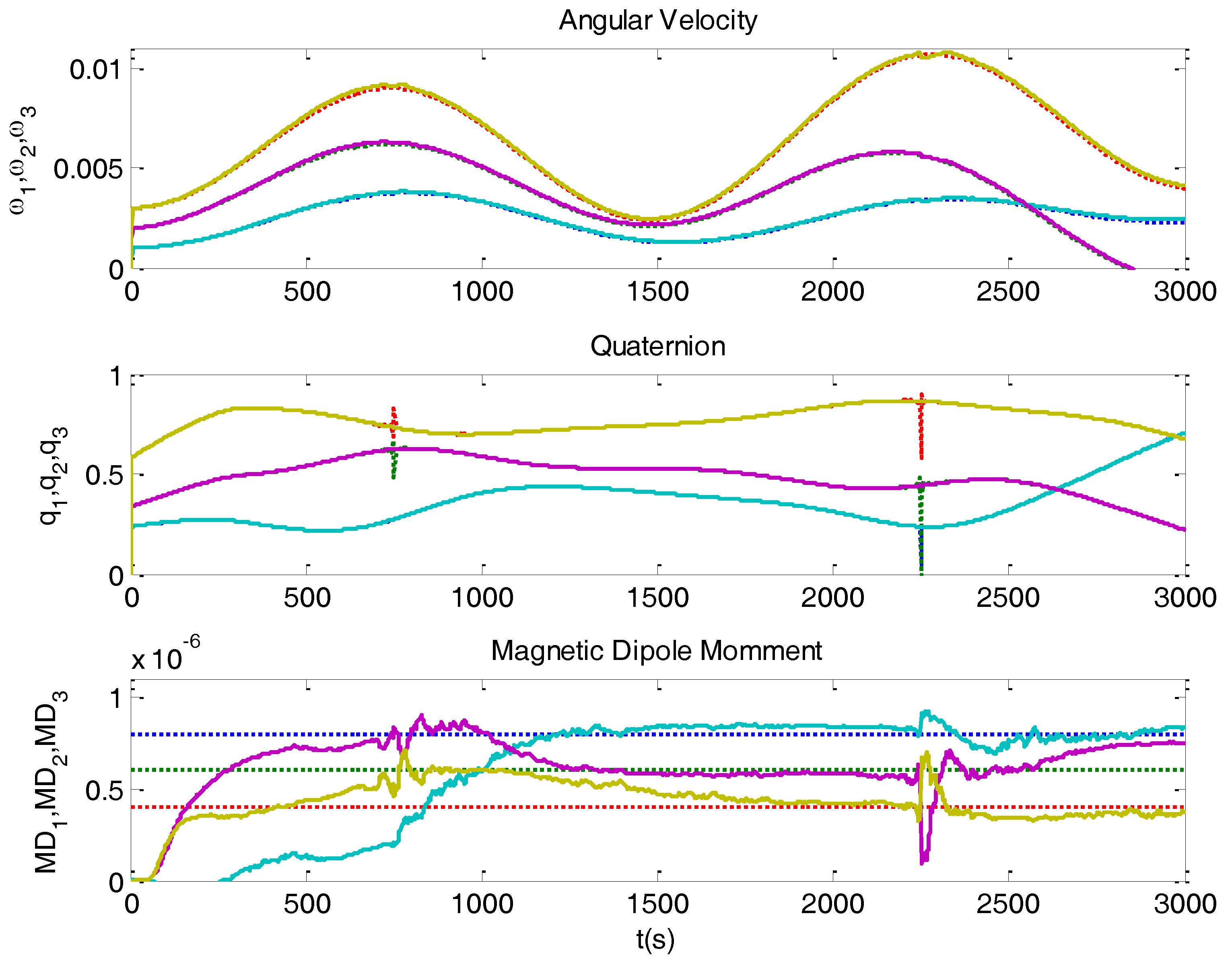
| Variable | Magnitude | Error % | Variance |
|---|---|---|
| |MagDipMT| | 0.5 A·m2 | |
| |MagDipSAT| | 0.02 A·m2 | |
| |Bmax| | 0.5 × 10−4 Teslas | |
| τMT ≤ |Bmax|·|MagDipMT| | 2.5 × 10−5 N·m | 3σ = 1% | QMT = 6.9444 × 10−15 |
| τPER ≤ |Bmax|·||MagDipSAT| | 1 × 10−6 N·m | 3σ = 100% | QPER = 1.1111 × 10−13 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esteban, S.; Girón-Sierra, J.M.; Polo, Ó.R.; Angulo, M. Signal Conditioning for the Kalman Filter: Application to Satellite Attitude Estimation with Magnetometer and Sun Sensors. Sensors 2016, 16, 1817. https://doi.org/10.3390/s16111817
Esteban S, Girón-Sierra JM, Polo ÓR, Angulo M. Signal Conditioning for the Kalman Filter: Application to Satellite Attitude Estimation with Magnetometer and Sun Sensors. Sensors. 2016; 16(11):1817. https://doi.org/10.3390/s16111817
Chicago/Turabian StyleEsteban, Segundo, Jose M. Girón-Sierra, Óscar R. Polo, and Manuel Angulo. 2016. "Signal Conditioning for the Kalman Filter: Application to Satellite Attitude Estimation with Magnetometer and Sun Sensors" Sensors 16, no. 11: 1817. https://doi.org/10.3390/s16111817
APA StyleEsteban, S., Girón-Sierra, J. M., Polo, Ó. R., & Angulo, M. (2016). Signal Conditioning for the Kalman Filter: Application to Satellite Attitude Estimation with Magnetometer and Sun Sensors. Sensors, 16(11), 1817. https://doi.org/10.3390/s16111817






