The core contribution of this work is a novel processing and representation paradigm capable of extracting underlying correlations in incoming sensory streams and integrating their contributions into a coherent percept. In this work we employ a processing principle known to be ubiquitous in the mammalian cortex, namely distributed processing with only local processing and storage. Obeying local dynamics of mutual interaction, the multitude of sensorimotor streams, encoded as processing maps, converge to global consensus. Aiming at obtaining a globally consistent representation, each map tries to minimize the disagreement among connected representations. Globally, this process learns an internal model based on underlying physical properties of cross-sensory interactions via continuous belief update given sensory observations.
In order to validate our framework and its hypotheses, we extend the basic model in [
15] towards perceptual learning for multisensory fusion. Using cortical maps as neural substrate for distributed representations of sensorimotor streams, the system is able to learn its connectivity (i.e., structure) from the long-term evolution of sensory observations. Changing representation, from single point estimates to a sparse encoding of sensorimotor streams, the system exploits the intrinsic correlations in the activity patterns of a network of neural processing units. This process mimics a typical development process where self-construction (connectivity learning), self-organization, and correlation extraction ensure a refined and stable representation and processing substrate, as shown in [
16]. Following these principles, we propose a model based on Self-Organizing Maps (SOM) [
17] and Hebbian Learning (HL) [
18] as main ingredients for extracting underlying correlations in sensory data.
2.1. Basic Correlation Learning Model
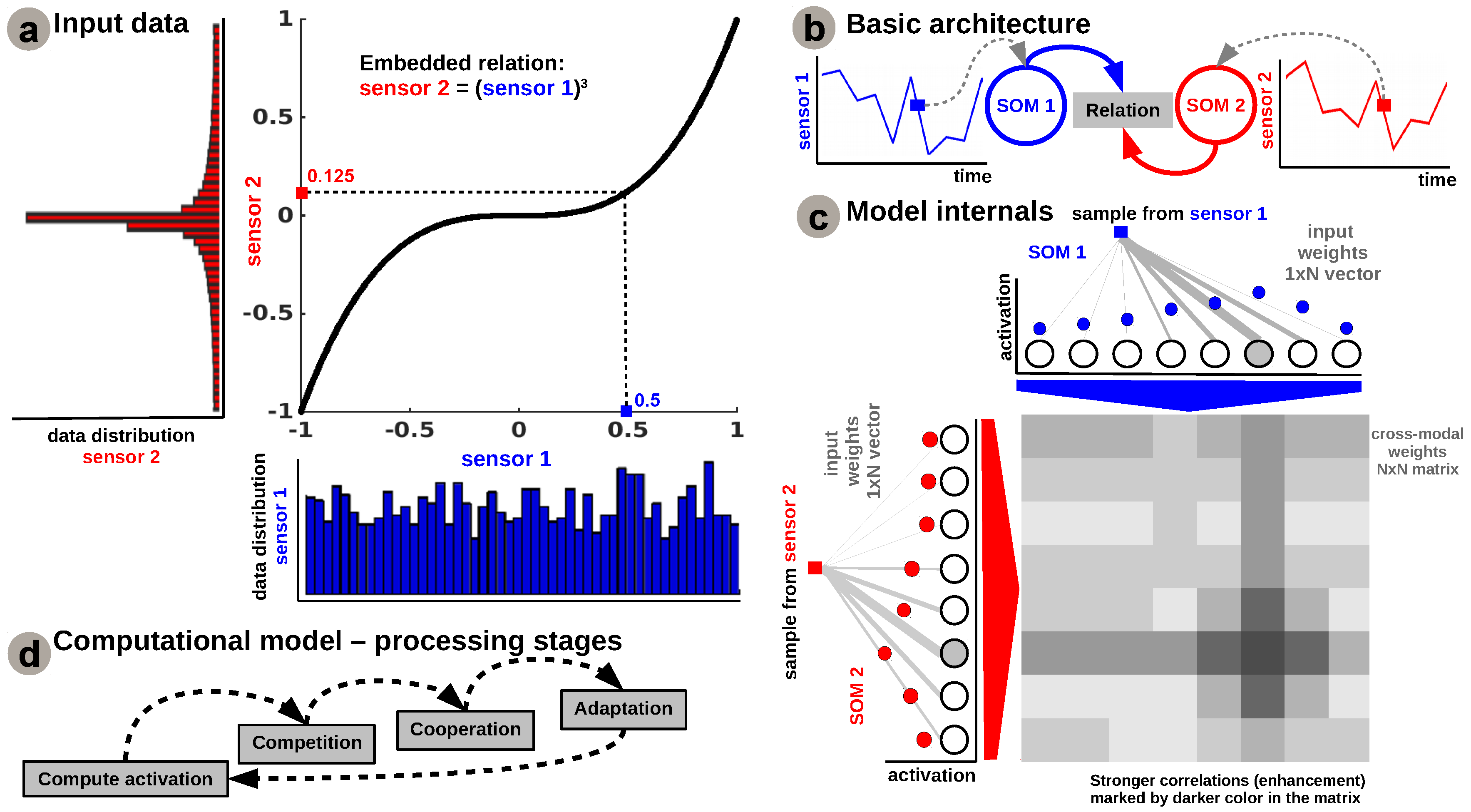
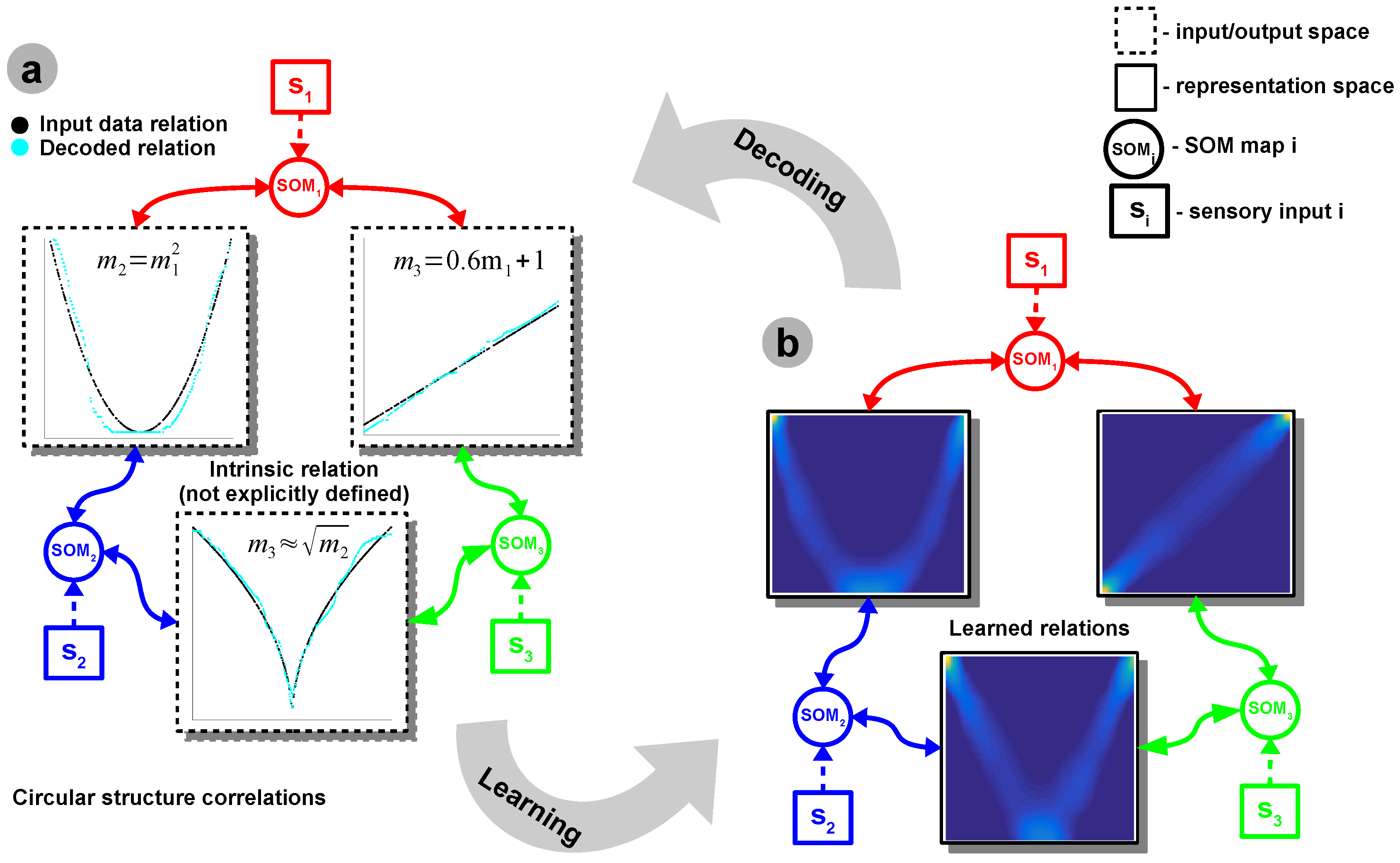
In order to give an intuition on the inner workings of the aforementioned mechanisms, we start with a simple bimodal scenario, depicted in
Figure 1b, in which the correlation among two sensors is represented by a simple nonlinear relation, e.g., power-law, as depicted in
Figure 1a.
The input Self-Organizing Maps (SOMs) are responsible for extracting the statistics of the incoming data and encoding sensory samples in a distributed activity pattern, as shown in
Figure 1a,c, respectively. This activity pattern is generated such that the neuron closest to the input sample, in terms of its preferred value, will be strongly activated. Activation decays as a function of distance between input and preferred value. Using the SOM distributed representation, the model learns the boundaries of the input data, such that, after relaxation, the SOMs provide a topology preserving representation of the input space. We extend the basic SOM, introduced in [
17], in such a way that each neuron not only specialises in representing a certain (preferred) value in the input space, but also learns its own sensitivity (i.e., tuning curve shape). Given an input sample,
at time step
k, the network follows the processing stages depicted in
Figure 1d. For each
i-th neuron in the
p-th input SOM, with the preferred value
and
tuning curve width, the sensory elicited activation is given by
The winner neuron of the
p-th population,
, is the one which elicits the highest activation given the sensory input at time step
kDuring self-organisation, at the input level, competition for highest activation is followed by cooperation in representing the input space (second and third step in
Figure 1d). Similar to the generic SOM model, given the winner neuron,
, the interaction kernel,
allows neighbouring cells (found at position
in the network) to precisely represent the sensory input sample given their location in the neighbourhood
. The interaction kernel in Equation (
3), ensures that specific neurons in the network specialise on different areas in the sensory space, such that the input weights (i.e., preferred values) of the neurons are pulled closer to the input sample with a decaying learning rate
,
This corresponds to the adaptation stage in
Figure 1d and ends with updating the tuning curves. Each neuron’s tuning curve is modulated by the spatial location of the neuron, the (Euclidian) distance to the input sample, the interaction kernel size, and the learning rate,
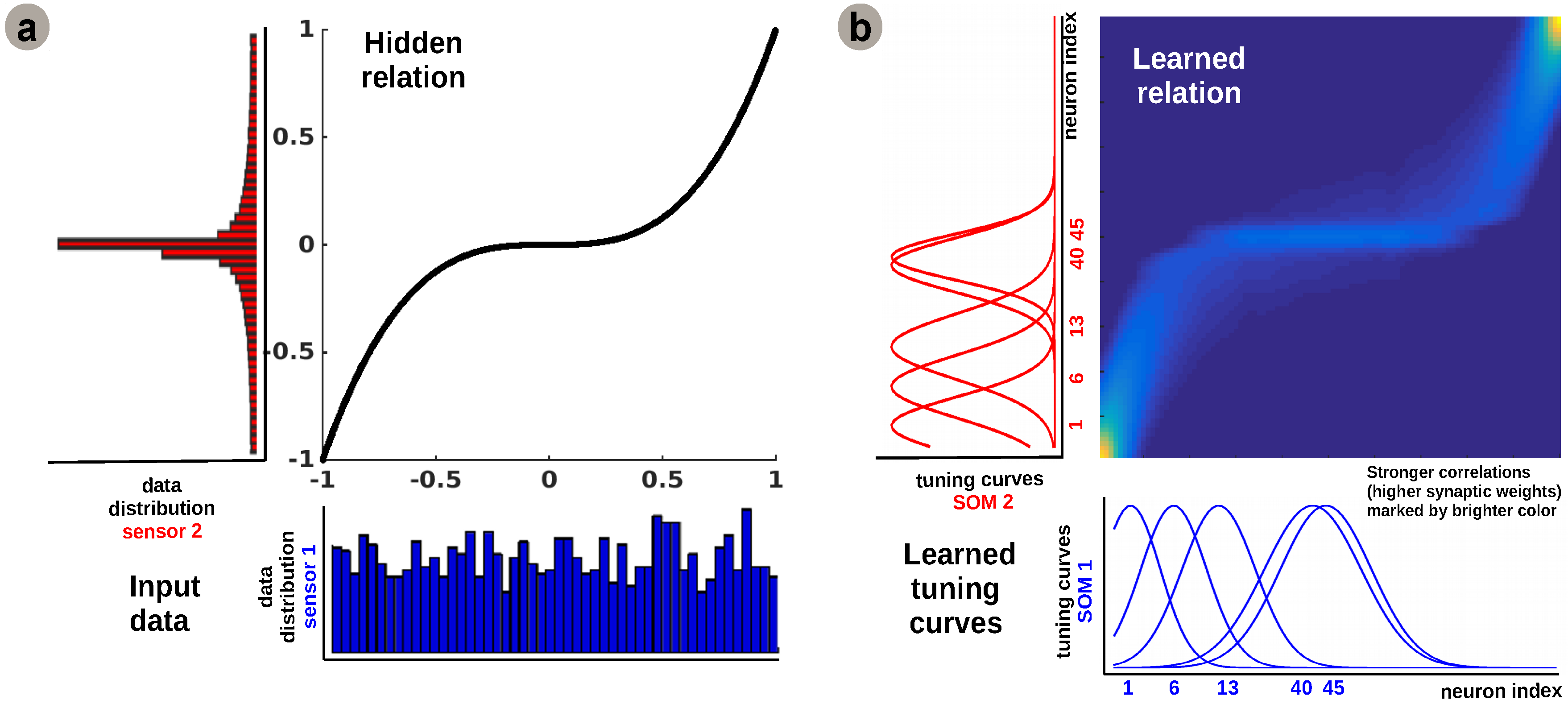
The learned tuning curve shapes for 5 representative neurons in the input SOMs (i.e., neurons 1, 6, 13, 40, 45) are depicted in
Figure 2b. We observe that higher input probability distributions, as shown in
Figure 2a, are represented by a large number of sharp tuning curves, whereas lower or uniform probability distributions are represented by a small number of wide tuning curves.
Using this mechanism, the network optimally allocates resources (i.e., neurons): a higher amount to areas in the input space which need a finer representation; and a lower amount for those areas that don’t. This feature emerging from the model is consistent with recent work on optimal sensory encoding in neural populations [
19]. This claims that, in order to maximise the information extracted from the sensory streams, the prior distribution of sensory data must be embedded in the neural representation.
The second component of our model is the Hebbian linkage, more precisely a covariance learning rule akin to the one introduced in [
18]: a fully connected matrix of synaptic connections between neurons in each input SOM, such that the projections propagate from pre-synaptic units to post-synaptic units in the network. Using an all-to-all connectivity pattern, each SOM unit activation is projected through the Hebbian matrix. The Hebbian learning process is responsible for extracting the co-activation pattern between the input layers (i.e., SOMs), as shown in
Figure 1c, and for eventually encoding the learned relation between the sensors, as shown in
Figure 2b. The central panel of
Figure 2b demonstrates that connections between uncorrelated (or weakly correlated) neurons in each population are suppressed (i.e., darker color-lower value) while correlated neurons’ connections are enhanced (i.e., brighter color-higher value). The boundary effects are not explicitly handled in the network as they don’t disrupt the overall relation learning process. A simple solution will be to consider a distance metric
, with
i,
j-units in the population, that allows wrap-up and a uniform distribution of the activity at the boundaries.
The effective correlation pattern encoded in the
matrix, imposes constraints upon possible sensory values. Moreover, after the network converges, the learned sensory dependency will make sure that values are “pulled” towards the correct (i.e., learned) corresponding values, will neglect outliers, and will allow inferring missing sensory quantities. Formally, Hebbian connection weights,
, between neurons
in each of the input SOM population are updated using
where
and
,
are monotonically decaying functions (i.e., inverse time functions) parametrized as:
where
are the pre-set initial (time
) and final (time
) values of
. Self-organisation and correlation learning processes evolve simultaneously, such that both representation and correlation pattern are continuously refined.
2.2. Structure Learning for the Multisensory Fusion Model
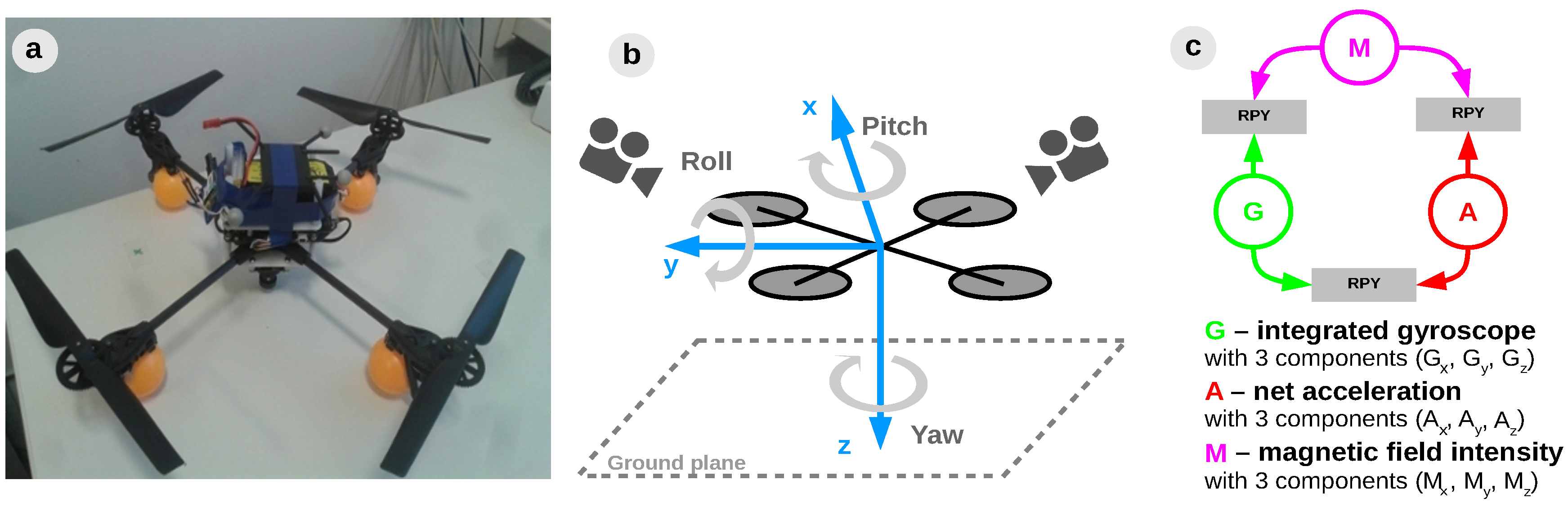
In order to test the proposed model, we apply it for a quadrotor 3D egomotion estimation, as depicted in
Figure 3.
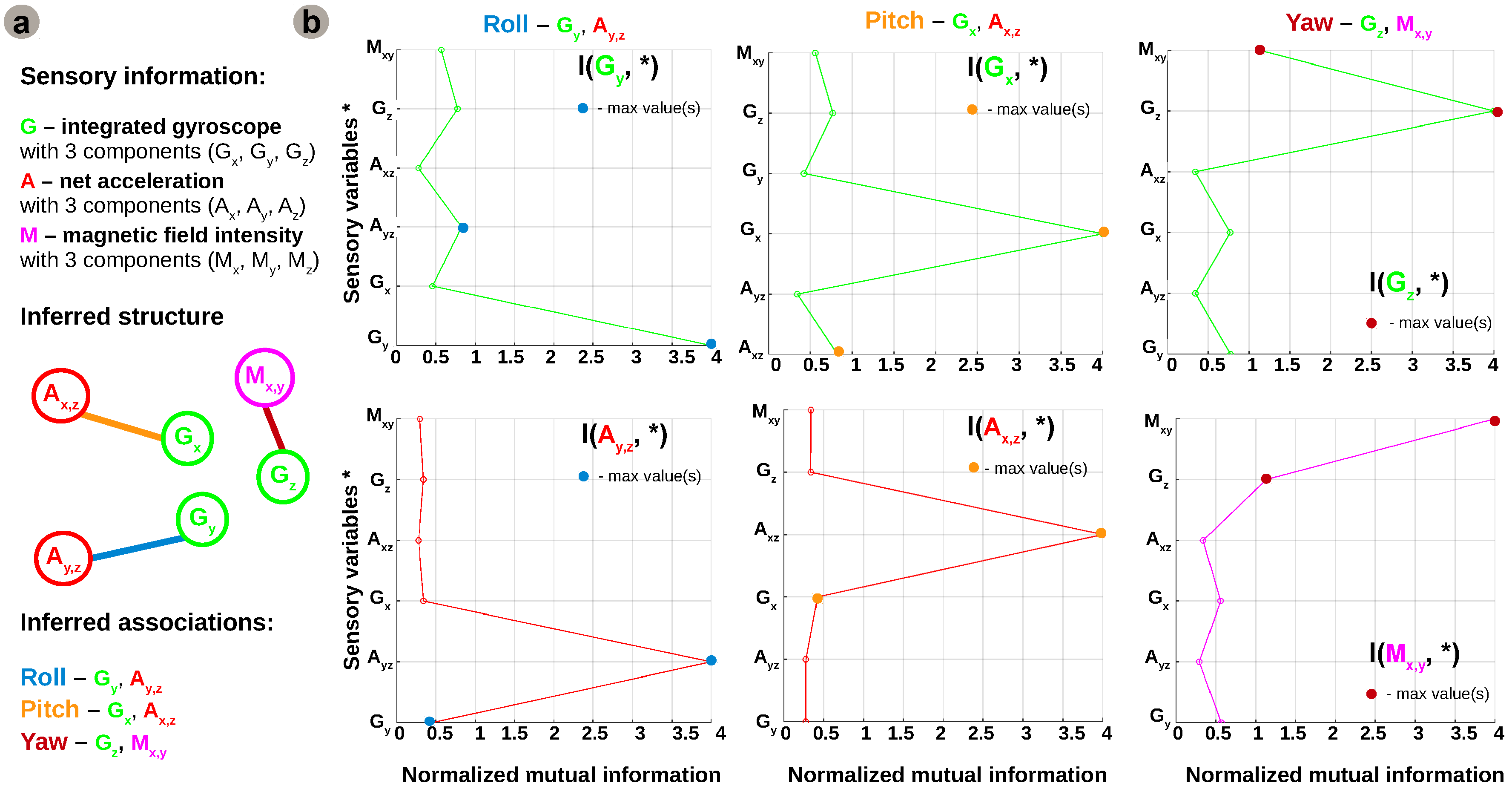
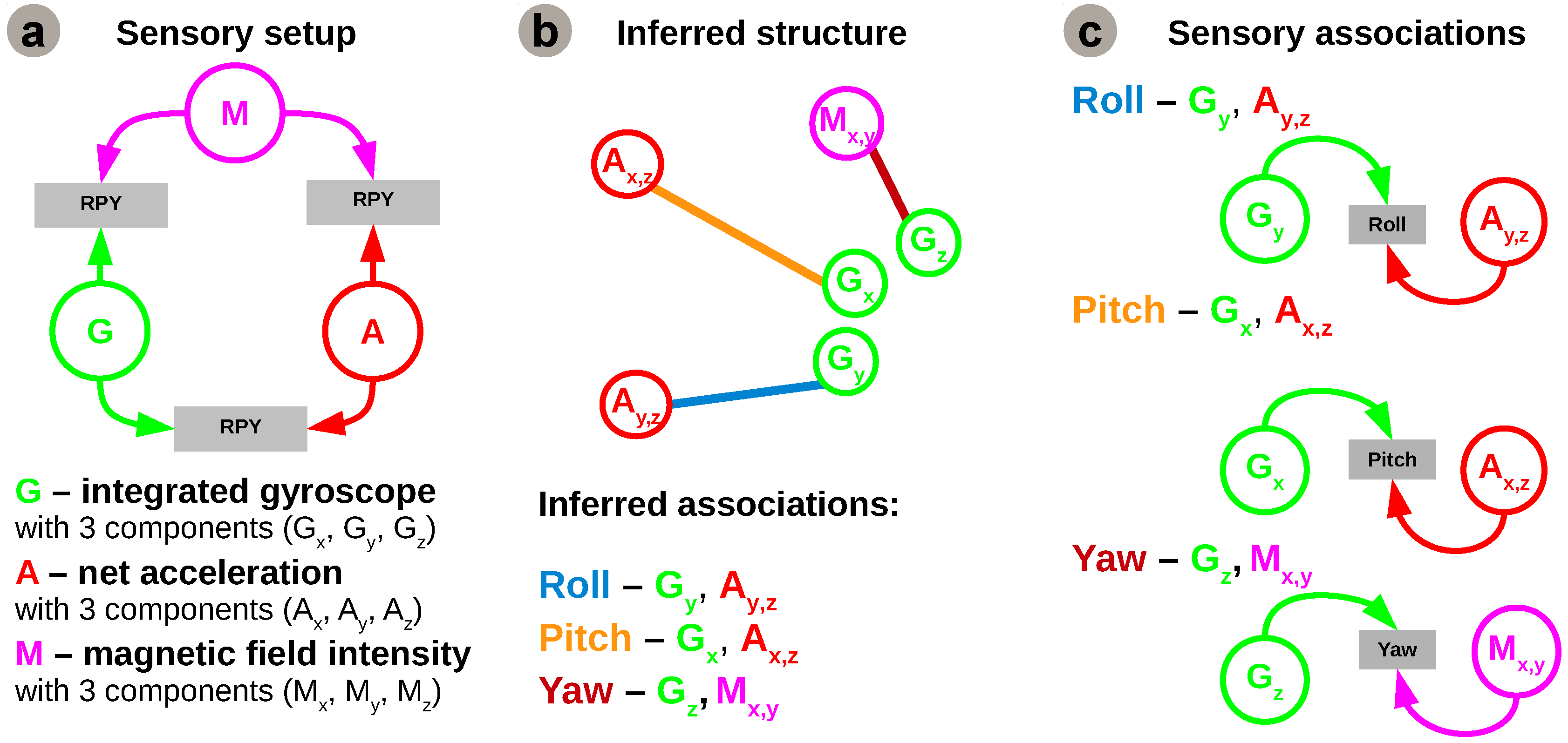
This shall serve as an example to introduce the system structure learning mechanism, namely the process that infers a plausible network structure for multisensory fusion. Envisioning a system capable of self-deployment, our work proposes an autonomous method to learn a system’s structure from sensory associations. Prior to learning multisensory fusion rules, the system must decide which sensors can be associated for coherent estimates of each motion component, using only available on-board sensors. The basic idea is to determine which regularities in the different sensory streams are informative and enforce the connections between correlated sensors to provide a relevant rule for fusion. As the system follows a developmental process (offline), one can only evaluate the system’s real-time capabilities after learning. The sensors used in our instantiation are the 3-dimensional integrated gyroscope readings, 3-dimensional net accelerations, and 3-dimensional magnetic field intensities, as shown in
Figure 3c. In order to obtain informative quantities into the algorithm we combine the 3 components of each sensor in derived cues relevant for each degree of freedom. For example, we combine acceleration on
x-axis and gravity (i.e., acceleration on
y-axis) to extract the pitch contribution of the acceleration, and we combine magnetic field intensities on the x and y axes to extract the yaw contribution of the magnetometer.
Physical systems are continuously and dynamically coupled to their environment. This coupling offers the system the capability to explicitly structure its sensory input and generate statistical regularities in it [
20]. Such regularities in the structure of the incoming multisensory streams are crucial to enabling adaptation, learning, and development. Providing a practical approach to measure statistical regularities, dependencies, or relationships between sensory streams, information theoretic measures can be used to quantify statistical structure in real-world data streams, as shown in [
21,
22].
In our approach we address the problem of recovering the structure of a network from available sensory data in its most general form, namely time-series streams of sensory data. No assumptions about the underlying structure of the sensory data are made and no prior knowledge about the system is taken into account. Furthermore, interactions between the various sensory streams are deduced from the statistical features of the data using information theoretic tools. This approach extends the generality of our framework for learning sensory correlations used for multisensory fusion.
In the simplest bimodal scenario, we assume
X and
Y to denote random sensory variables consisting of the set of possible samples
, with associated probability mass functions
. An important information theoretic metric, relevant for this problem, is the relative entropy between the joint distribution
and the product distribution
of the two sensory variables, which defines the mutual information:
given that we consider the general form of information entropy,
Intuitively, mutual information is high if both sensory quantities have high variance (i.e., high entropy) and are highly correlated (i.e., high covariance) [
23]. In our scenario, if two components of the network of sensory variables interact closely (correlated statistical regularities) their mutual information will be large, whereas if they are not related their mutual information will be near zero.
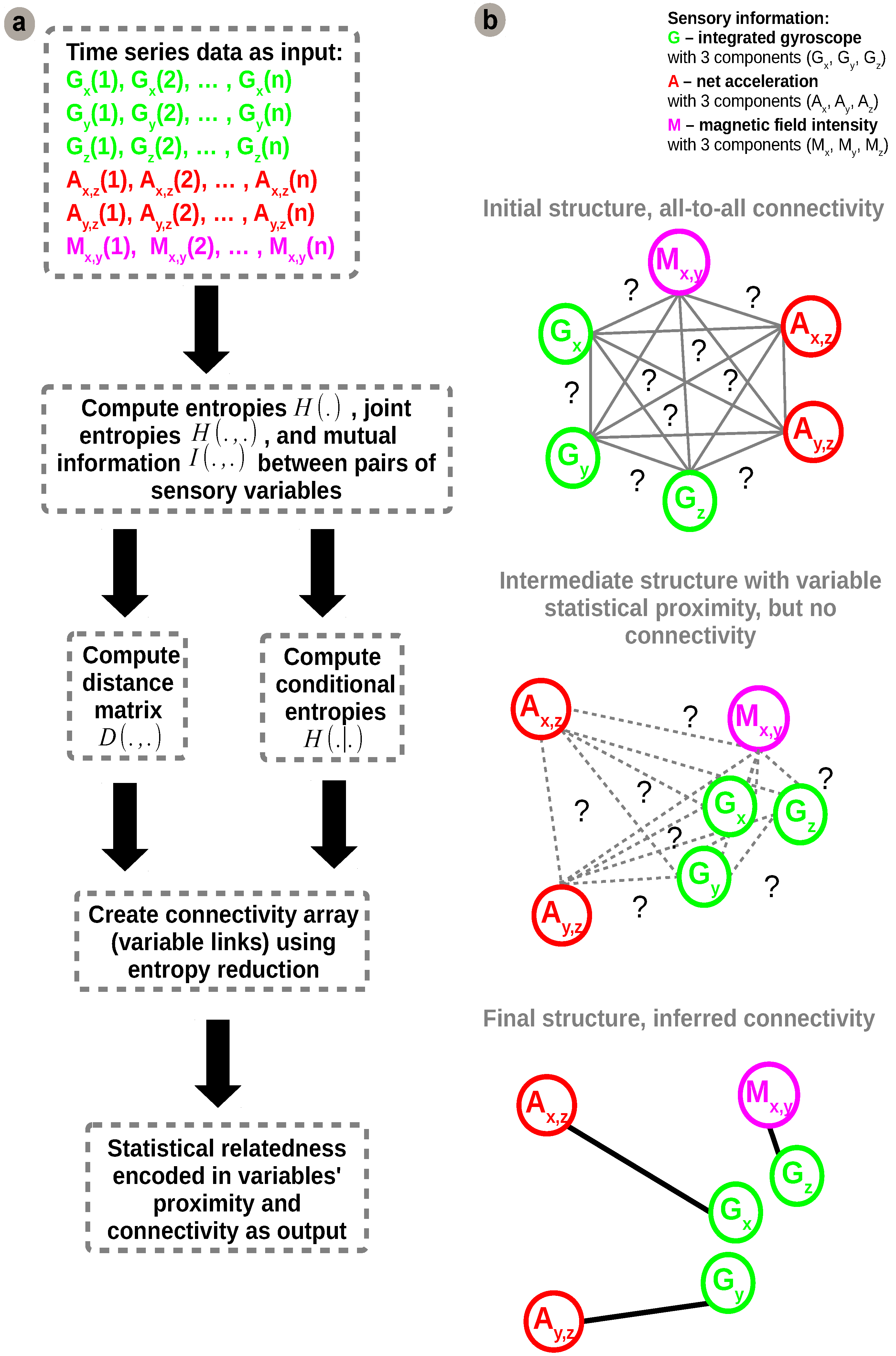
Using this basic formulation of information theoretic metrics, we developed our network inference algorithm which is synthetically depicted in
Figure 4.
Initially, uni-dimensional, multi-dimensional (joint and conditional variables) entropies,
, and mutual information measures are estimated from sensory data, as shown in
Figure 4a. The estimates are subsequently used for calculating distances between variables and build a distance matrix. In order to discriminate between direct and indirect (implicit) connections an entropy reduction (minimisation) step is applied on conditional entropies, similar to [
24].
The distance metric used for constructing the distance matrix is the Entropy Metric Construction (EMC) [
25,
26]. An important feature of this metric is that it takes into account possible time delays
τ in the sensory data time-series:
The sensory readings are coming from different sources but all measure the consequences of the robot motion. Equation (
11) provides a generic formulation in which, for example, one sensor can be a delayed copy of another (i.e., measuring the same quantity but with different principle). In our case
τ is 0, as the sensors are sampled at the same time although, due to physics, they have different reaction time induced by the motion of the robot. It is easy to see that high values of mutual information between variables determine a smaller distance value as shown in
Figure 5b. Due to the fact that we need to infer the network structure from sensory data, knowledge about the underlying system cannot be used. Hence, we need to estimate mutual information from the datasets instead of using the analytical form. In order to refine the interactions among sensory variables we use an entropy reduction process that seeks to determine variation in one sensory variable given variation in another sensory variable. The mechanism assumes that if a sensory variable
is connected to
Y (which has already been predicted to be connected to a subset
of
), its inclusion in the network structure must reduce the entropy by a proportion at least equal to a threshold
T. The threshold
T is computed as a function of overall entropy values, a subunit average of all possible combinations of variables in all network configurations (i.e., circular permutations on all available variables). Hence, a link between
and
Y is predicted if and only if the entropy reduction
, in Equation (
12), exceeds the threshold
T.
In order to obtain reliable estimates of joint entropies of the many sensory variables, the large amount of data observations ( >13,000 samples) provides an advantage. Furthermore, exploiting the rich input space, the proposed algorithm is able to exploit the intrinsic statistical regularities of the sensory data to generate a plausible network configuration. The raw sensory data fed to the system is sampled at 200 Hz. For each degree of freedom there is decoupled data from each sensor axis paired for each degree of freedom (roll—
and
, pitch—
and
, yaw—
and
). Analysing individual statistics, from the perspective of each variable with respect to all the others, the network configuration generated by the algorithm is supported by the pairs of mutual information estimates depicted in
Figure 5.
Although initially the network considers all sensory contributions for the estimation of all motion components it will enforce only those connections providing a coherent correlation for each degree of freedom based on the resulting configuration from the network inference algorithm. Using only the underlying statistical regularities and information content in incoming sensory streams, the algorithm detects, connects, and combines sensory contributions which are informative for estimating the same degree of freedom into motion estimates, as depicted in
Figure 6c.
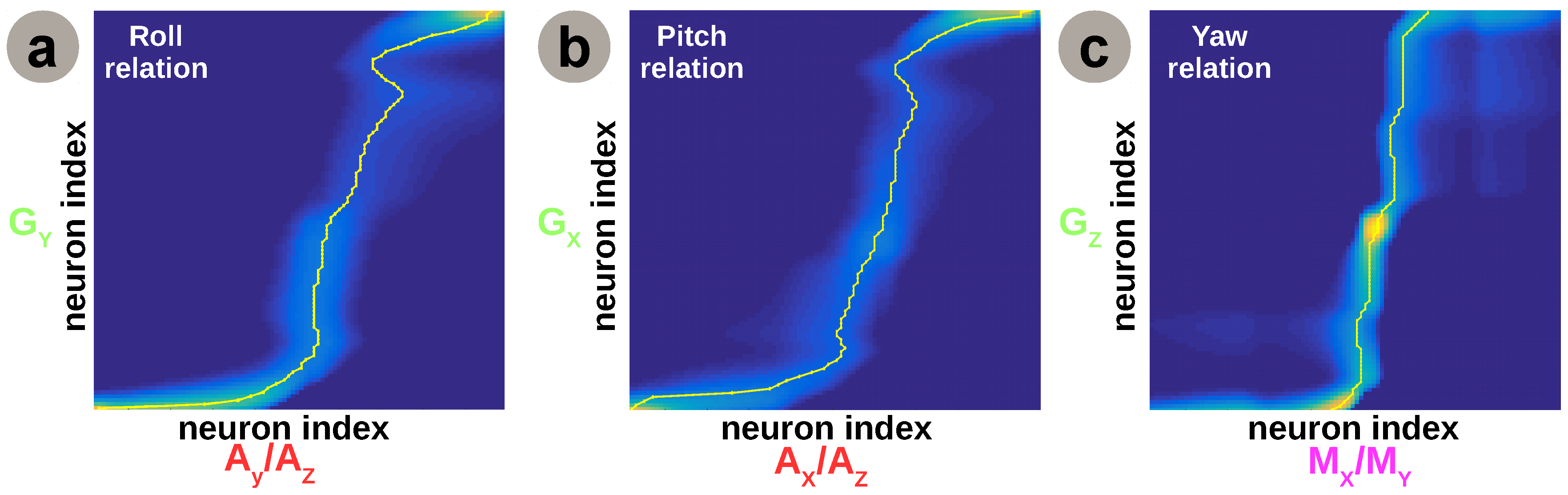
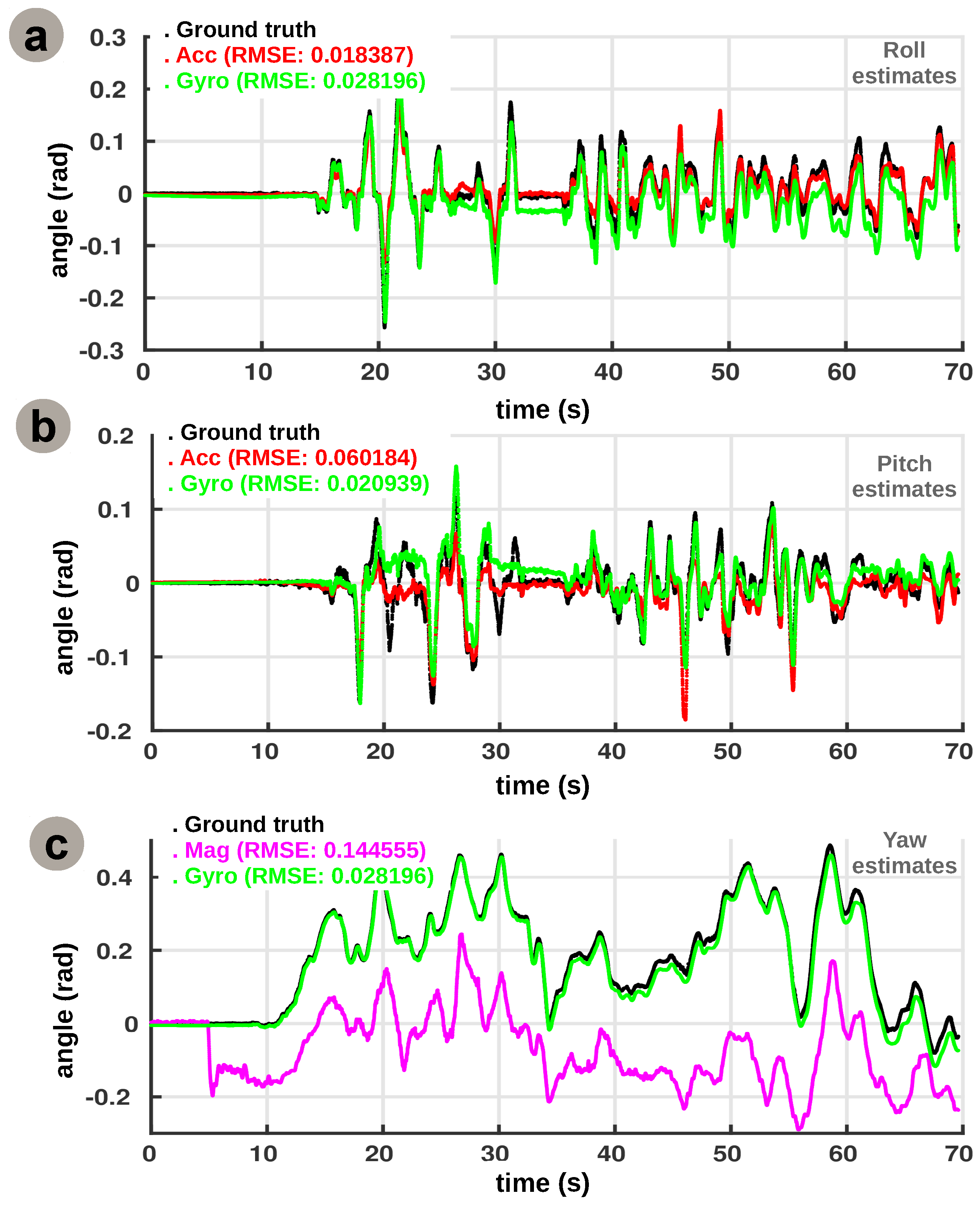
For roll and pitch angles (i.e., rotation around the x and y reference frame axes), the network learns the relation between the roll and pitch angle estimates from gyroscope data and rotational acceleration components (i.e., orthogonal x and y with respect to z reference frame axes). Similarly, the yaw angle is extracted by learning the relation between the yaw angle estimate from integrated gyroscope data (i.e., absolute angle) and aligned magnetic field components from the magnetic sensor (i.e., projected magnetic field vectors on orthogonal x and y reference frame axes). The learned sensory associations are not arbitrary, but rather represent the dynamics of the system and are consistent with recently developed modelling and attitude control approaches for quadrotors [
27,
28].
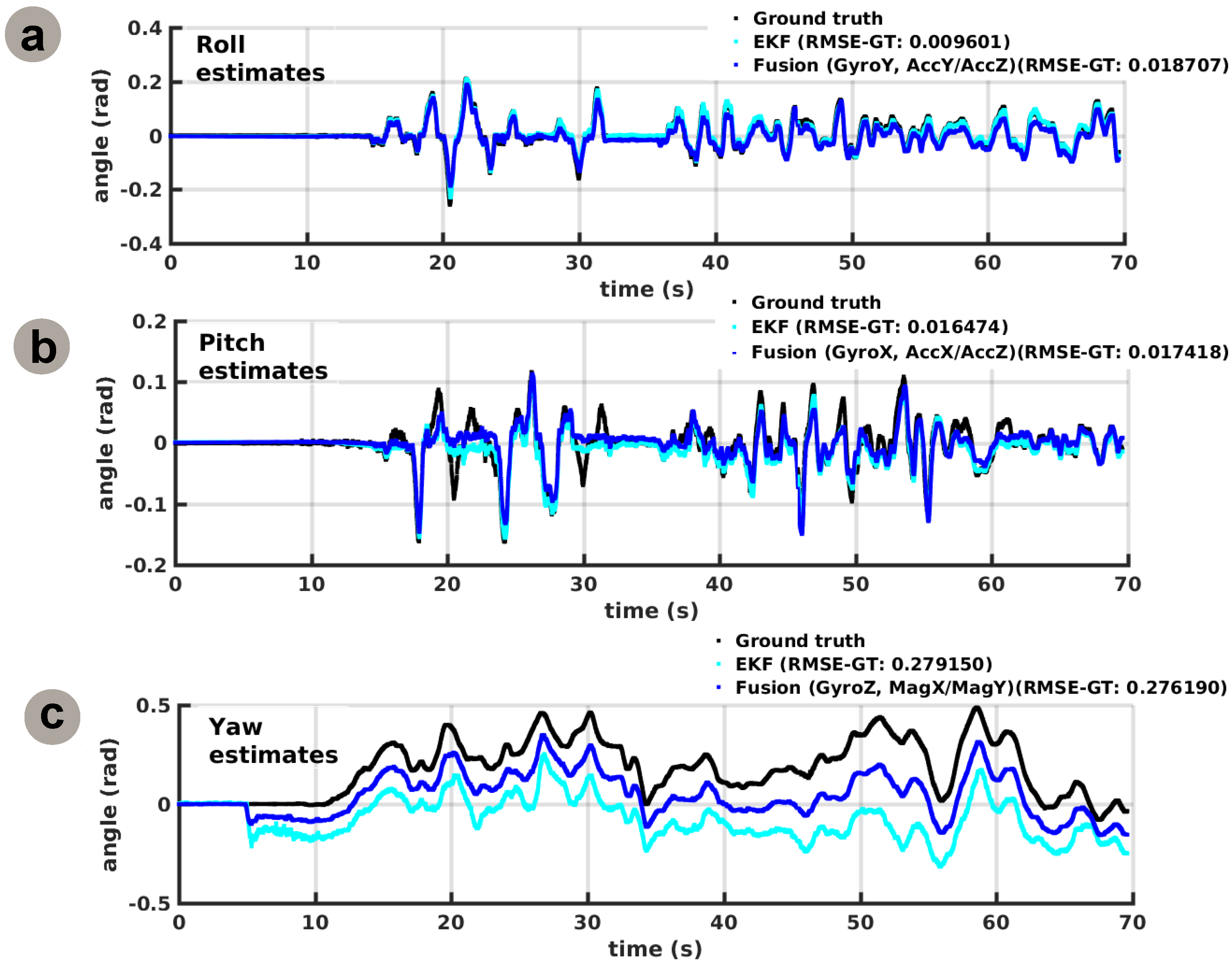
To make use of the learned relations, we decode the Hebbian connectivity matrix using a relatively simple optimisation method [
29]. After learning, we apply sensory data from one source and compute the sensory elicited activation in its corresponding (presynaptic) SOM neural population. Furthermore, using the learned cross-modal Hebbian weights and the presynaptic activation, we can compute the postsynaptic activation. Given that the neural populations encoding the sensory data are topologically organised (i.e., adjacent values coding for adjacent places in the input space), we can precisely extract (through optimisation) the sensory value for the second sensor, given the postsynaptic activation pattern. Without using an explicit function to optimise, but rather the correlation in activation patterns in the input SOMs, the network can extract the relation between the sensors.