Iterative Diffusion-Based Distributed Cubature Gaussian Mixture Filter for Multisensor Estimation
Abstract
:1. Introduction
2. Centralized Cubature Gaussian Mixture Filter
2.1. Cubature Gaussian Mixture Kalman Filter
2.1.1. Prediction Step
2.1.2. Update Step
2.2. Centralized Cubature Gaussian Mixture Filter
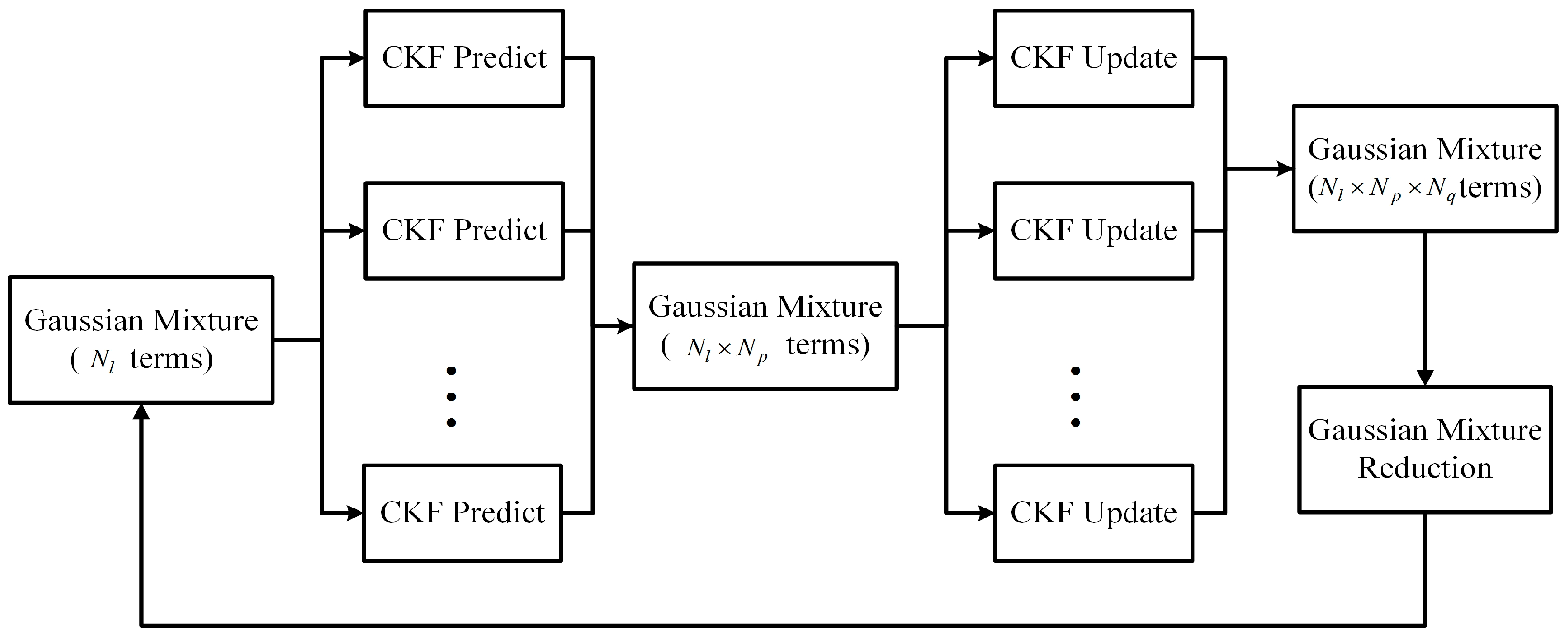
3. Iterative Diffusion-Based Distributed Cubature Gaussian Mixture Filter
3.1. Incremental Update
3.2. Diffusion Update
| Algorithm 1 |
|
- (a)
- for all ;
- (b)
- , ;
- (c)
- for all ;
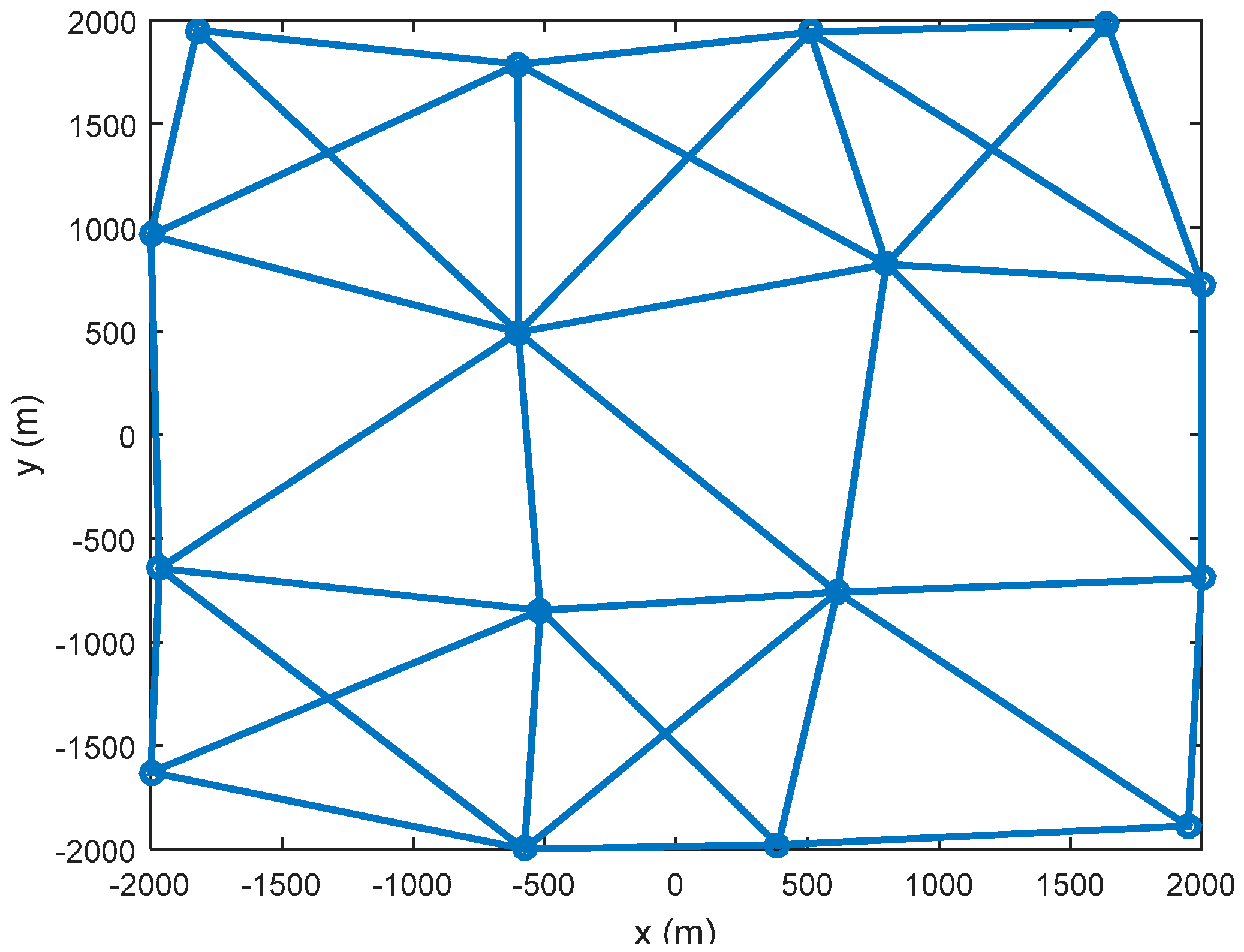
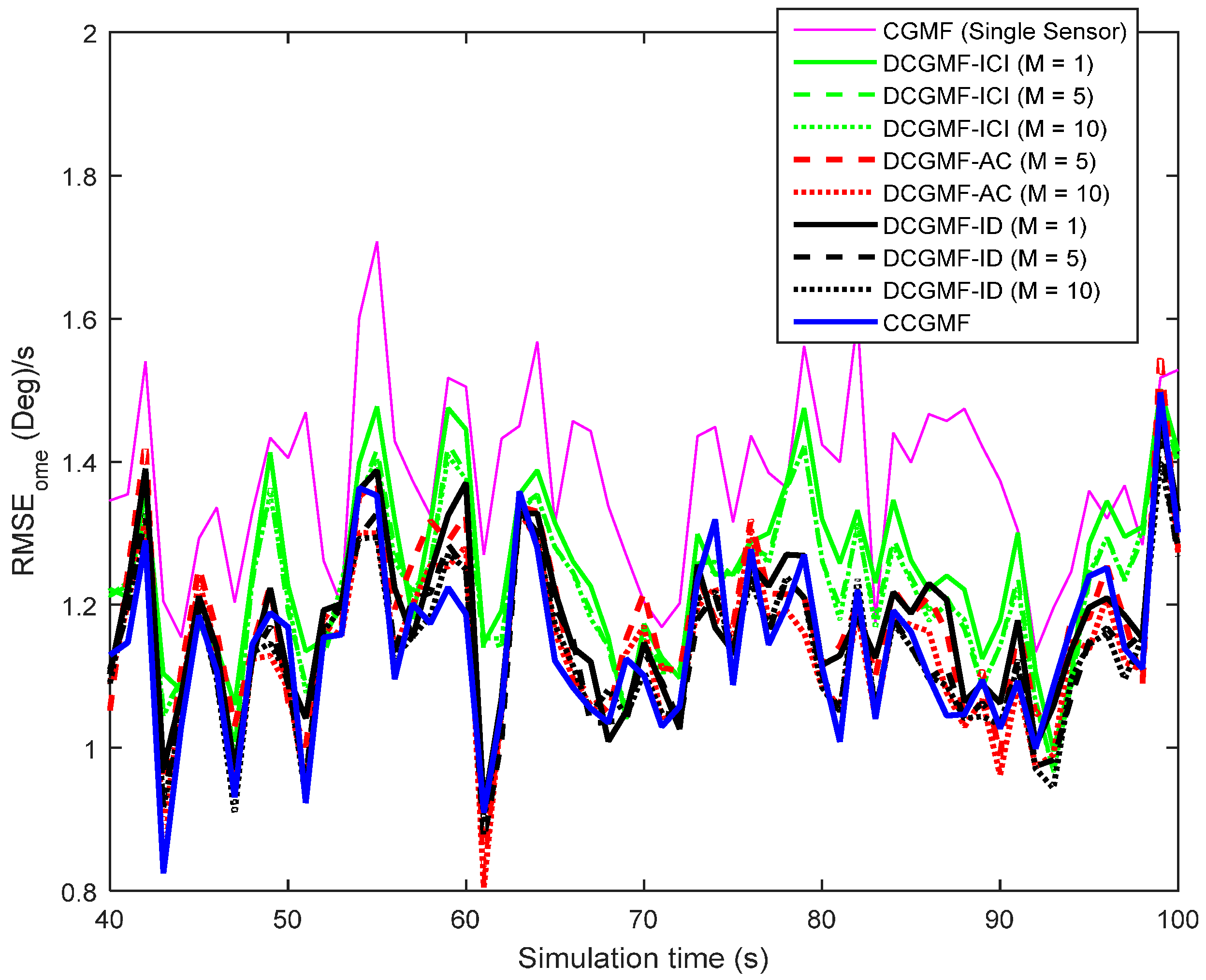
4. Numerical Results and Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Alspach, D.L.; Sorenson, H.W. Nonlinear Bayesian estimation using Gaussian sum approximation. IEEE Trans. Autom. Control 1972, 17, 439–448. [Google Scholar] [CrossRef]
- Arulampalam, M.S.; Maskell, S.; Gordon, N.; Clapp, T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Signal Proc. 2002, 50, 174–188. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S. Cubature Kalman filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef]
- Jia, B.; Xin, M. Multiple sensor estimation using a new fifth-degree cubature information filter. Trans. Inst. Meas. Control 2015, 37, 15–24. [Google Scholar] [CrossRef]
- Gelb, A. Applied Optimal Estimation; MIT Press: Cambridge, MA, USA, 1974; pp. 182–202. [Google Scholar]
- Juier, S.J.; Uhlmann, J.K.; Durrant-Whyte, H.F. A new method for the nonlinear transformation of means and covariances in filters and estimators. IEEE Trans. Autom. Control 2000, 45, 477–482. [Google Scholar]
- Olfati-Saber, R. Distributed Kalman filter with embedded consensus filters. In Proceedings of the 44th IEEE Conference on Decision and Control, and 2005 European Control Conference, Seville, Spain, 15 December 2005; pp. 8179–8184.
- Olfati-Saber, R. Distributed Kalman filter for sensor networks. In Proceedings of the 46th IEEE on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 5492–5498.
- Kamal, A.T.; Farrell, J.A.; Roy-Chodhury, A.K. Information weighted consensus. In Proceedings of the 51st IEEE on Decision and Control, Maui, HI, USA, 10–13 December 2012; pp. 2732–2737.
- Kamal, A.T.; Farrell, J.A.; Roy-Chodhury, A.K. Information weighted consensus filters and their application in distributed camera networks. IEEE Trans. Autom. Control 2013, 58, 3112–3125. [Google Scholar] [CrossRef]
- Sun, T.; Xin, M.; Jia, B. Distributed estimation in general directed sensor networks based on batch covariance intersection. In Proceedings of the 2016 American Control Conference, Boston, MA, USA, 6–8 July 2016; pp. 5492–5497.
- Cattivelli, F.S.; Sayed, A.H. Diffusion strategies for distributed Kalman filtering and smoothing. IEEE Trans. Autom. Control 2010, 55, 2069–2084. [Google Scholar] [CrossRef]
- Cattivelli, F.S.; Lopes, C.G.; Sayed, A.H. Diffusion recursive least-squares for distributed estimation over adaptive networks. IEEE Trans. Autom. Control 2008, 56, 1865–1877. [Google Scholar] [CrossRef]
- Cattivelli, F.S.; Sayed, A.H. Diffusion LMS strategies for distributed estimation. IEEE Trans. Autom. Control 2010, 55, 1035–1048. [Google Scholar] [CrossRef]
- Hu, J.; Xie, L.; Zhang, C. Diffusion Kalman filtering based on covariance intersection. IEEE Trans. Signal Proc. 2012, 60, 891–902. [Google Scholar] [CrossRef]
- Hlinka, O.; Sluciak, O.; Hlawatsch, F.; Rupp, M. Distributed data fusion using iterative covariance intersection. In Proceedings of the 2014 IEEE on Acoustics, Speech, and Signal Processing, Florence, Italy, 4–9 May 2014; pp. 1880–1884.
- Li, W.; Jia, Y. Distributed consensus filtering for discrete-time nonlinear systems with non-Gaussian noise. Signal Proc. 2012, 92, 2464–2470. [Google Scholar] [CrossRef]
- Runnalls, A.R. Kullback-Leibler approach to Gaussian mixture reduction. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 989–999. [Google Scholar] [CrossRef]
- Salmond, D. Mixture reduction algorithms for target tracking in clutter. In Proceedings of the SPIE 1305 Signal and Data Processing of Small Targets, Los Angeles, CA, USA, 16–18 April 1990; pp. 434–445.
- Williams, J.L. Gaussian Mixture Reduction for Tracking Multiple Maneuvering Targets in Clutter. Master’s Thesis, Air Force Institute of Technology, Dayton, OH, USA, 2003. [Google Scholar]
- Jia, B.; Xin, M.; Cheng, Y. Multiple sensor estimation using the sparse Gauss-Hermite quadrature information filter. In Proceedings of the 2012 American Control Conference, Montreal, QC, Canada, 27–29 June 2012; pp. 5544–5549.
- Niehsen, W. Information fusion based on fast covariance intersection. In Proceedings of the 2002 5th International Conference on Information Fusion, Annapolis, MD, USA, 8–11 July 2002.
- Julier, S.; Uhlmann, J. General decentralized data fusion with covariance intersection (CI). In Handbook of Multisensor Data Fusion; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Battistelli, G.; Chisci, L. Consensus-based linear and nonlinear filtering. IEEE Trans. Autom. Control 2015, 60, 1410–1415. [Google Scholar] [CrossRef]
- Alex, O.; Tsitsiklis, J.N. Convergence speed in distributed consensus and averaging. SIAM Rev. 2011, 53, 747–772. [Google Scholar]
- Horn, R.; Johnson, C. Matrix Analysis; Cambridge University Press: New York, NY, USA, 1985. [Google Scholar]
- Seneta, E. Nonnegative Matrices and Markov Chains; Springer: New York, NY, USA, 2006. [Google Scholar]
- Battistelli, G.; Chisci, L. Kullback-Leibler average, consensus on probability densities, and distributed state estimation with guaranteed stability. Automatica 2014, 50, 707–718. [Google Scholar] [CrossRef]
- Hurley, M.B. An information theoretic justification for covariance intersection and its generalization. In Proceedings of the 5th International Conference on Information Fusion, Annapolis, MD, USA, 8–11 July 2002.
- Jia, B.; Xin, M.; Cheng, Y. High degree cubature Kalman filter. Automatica 2013, 49, 510–518. [Google Scholar] [CrossRef]
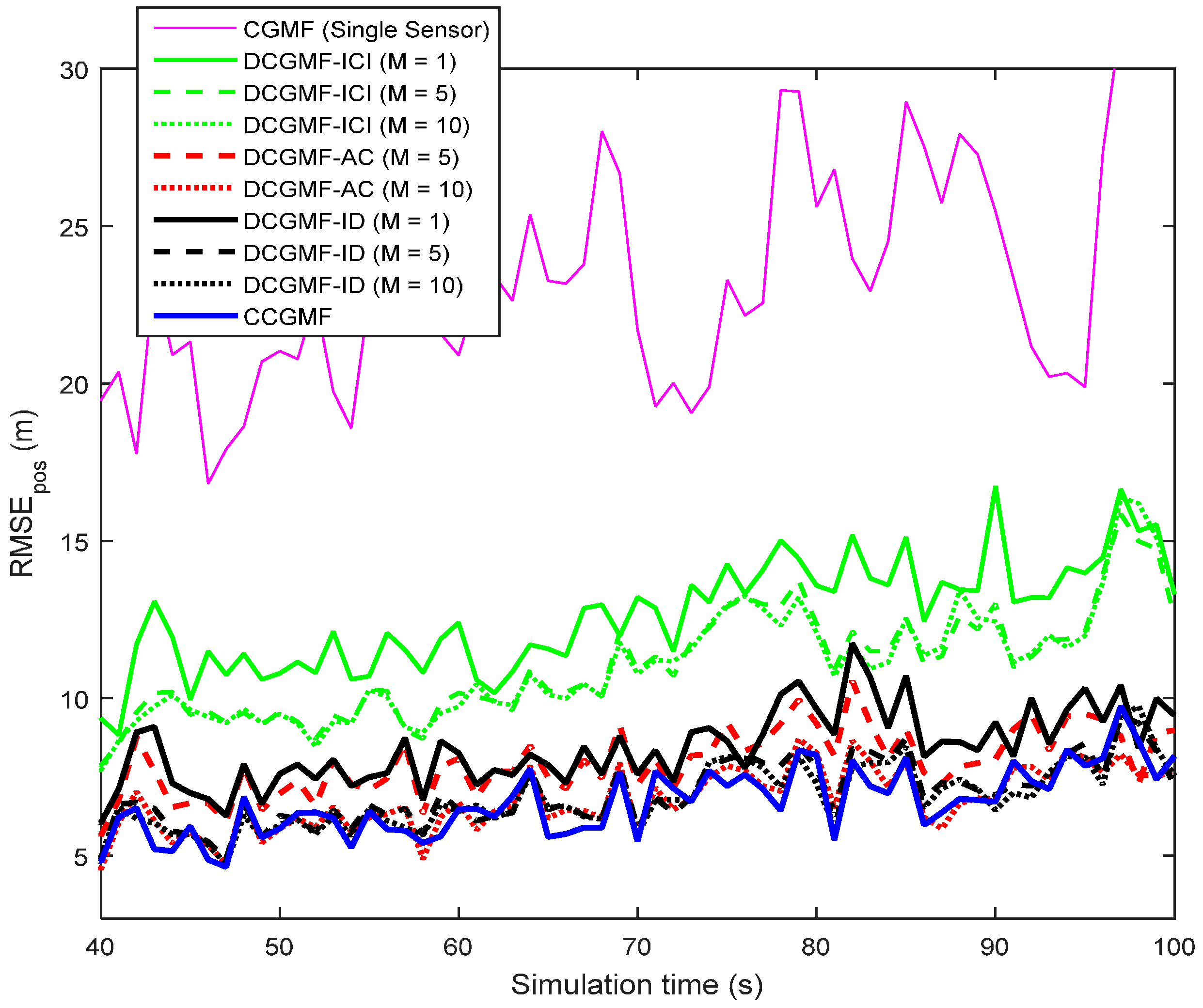
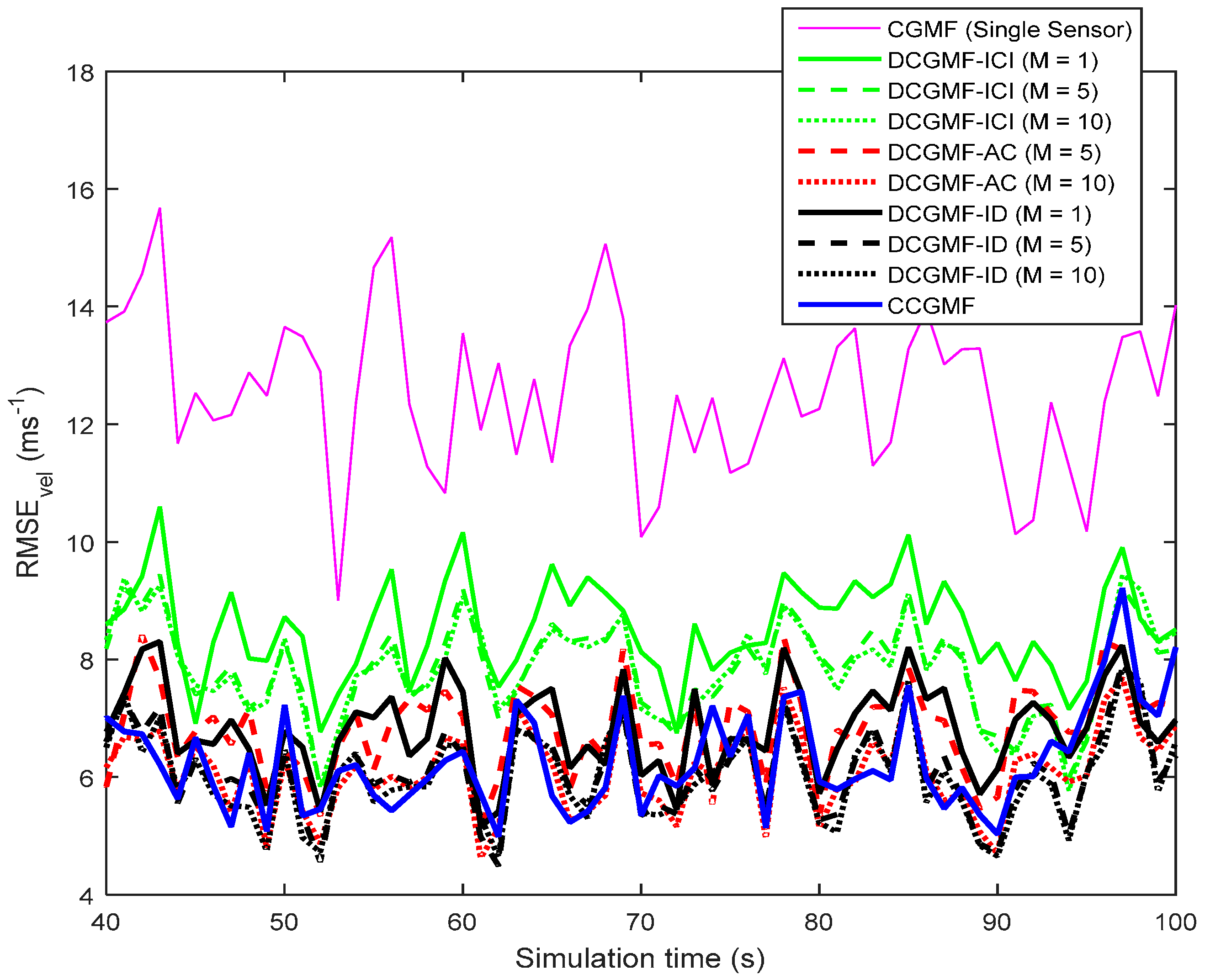
| Filters | CRMSE (Position) | CRMSE (Velocity) | CRMSE (Turn Rate) |
|---|---|---|---|
| DCGMF-ID (third-degree, M = 20) | 5.85892 | 5.60166 | 0.019392 |
| DCGMF-ID (fifth-degree, M = 20) | 5.78748 | 5.57730 | 0.019375 |
| DCGMF-ICI (third-degree, M = 20) | 8.81274 | 7.22025 | 0.020837 |
| DCGMF-ICI (fifth-degree, M = 20) | 8.02142 | 7.11939 | 0.020804 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, B.; Sun, T.; Xin, M. Iterative Diffusion-Based Distributed Cubature Gaussian Mixture Filter for Multisensor Estimation. Sensors 2016, 16, 1741. https://doi.org/10.3390/s16101741
Jia B, Sun T, Xin M. Iterative Diffusion-Based Distributed Cubature Gaussian Mixture Filter for Multisensor Estimation. Sensors. 2016; 16(10):1741. https://doi.org/10.3390/s16101741
Chicago/Turabian StyleJia, Bin, Tao Sun, and Ming Xin. 2016. "Iterative Diffusion-Based Distributed Cubature Gaussian Mixture Filter for Multisensor Estimation" Sensors 16, no. 10: 1741. https://doi.org/10.3390/s16101741
APA StyleJia, B., Sun, T., & Xin, M. (2016). Iterative Diffusion-Based Distributed Cubature Gaussian Mixture Filter for Multisensor Estimation. Sensors, 16(10), 1741. https://doi.org/10.3390/s16101741






