Toward Epileptic Brain Region Detection Based on Magnetic Nanoparticle Patterning
Abstract
:1. Introduction
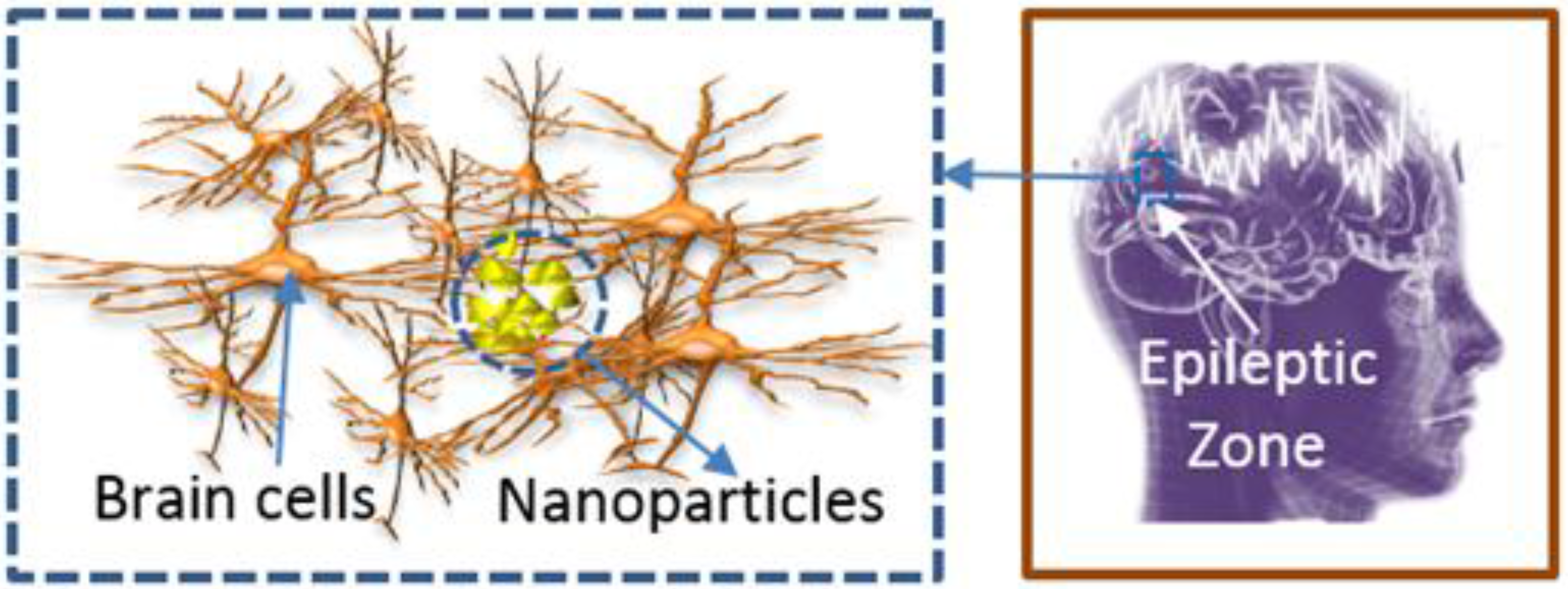
2. Mathematical Models
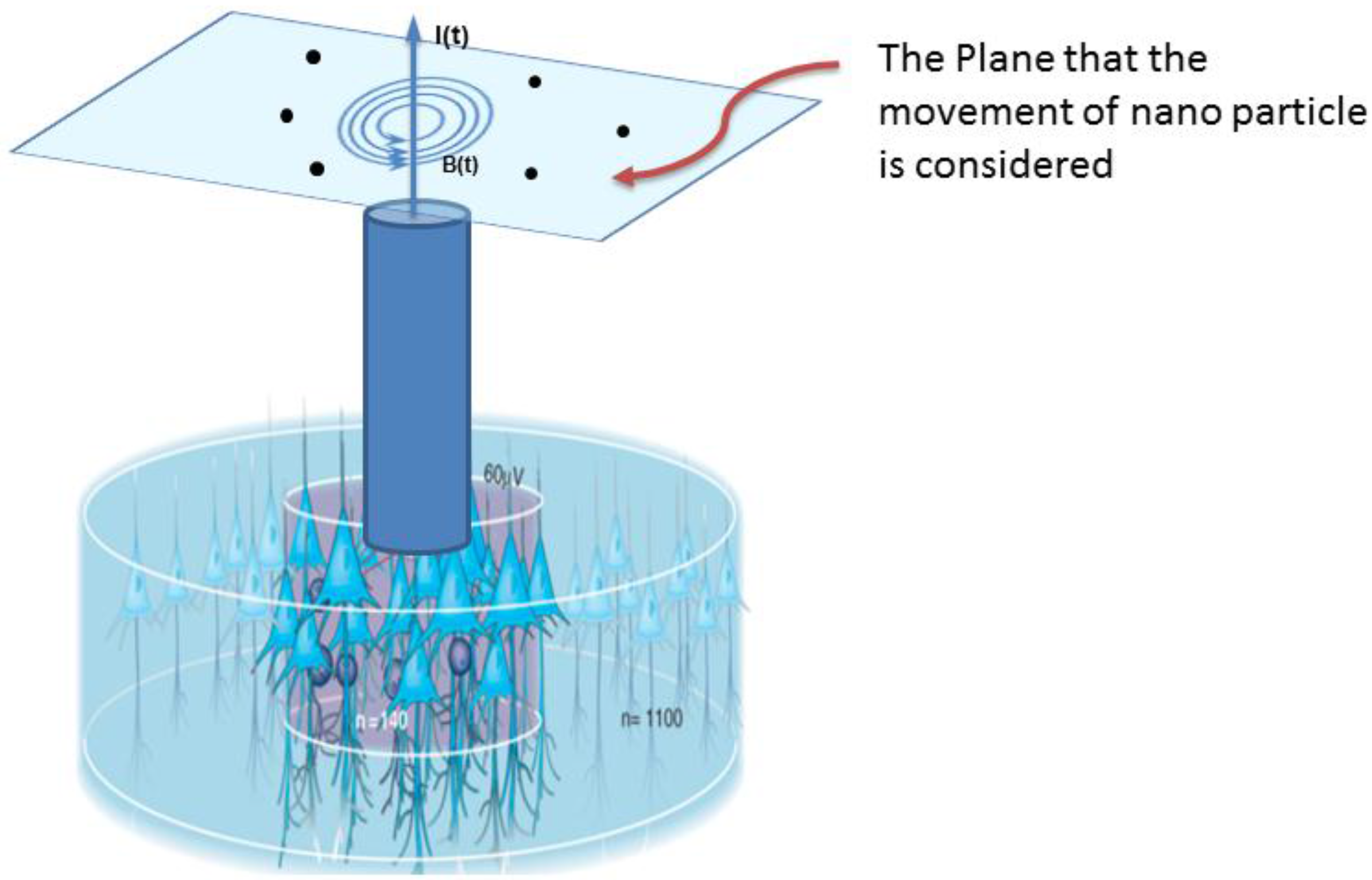
2.1. Creation of Magnetic Field on Neurons
2.2. Effect of Magnetic Field and Brain Fluid on Superparamagnetic Nanoparticles (SPMNs)
2.3. Aggregation of Nanoparticles
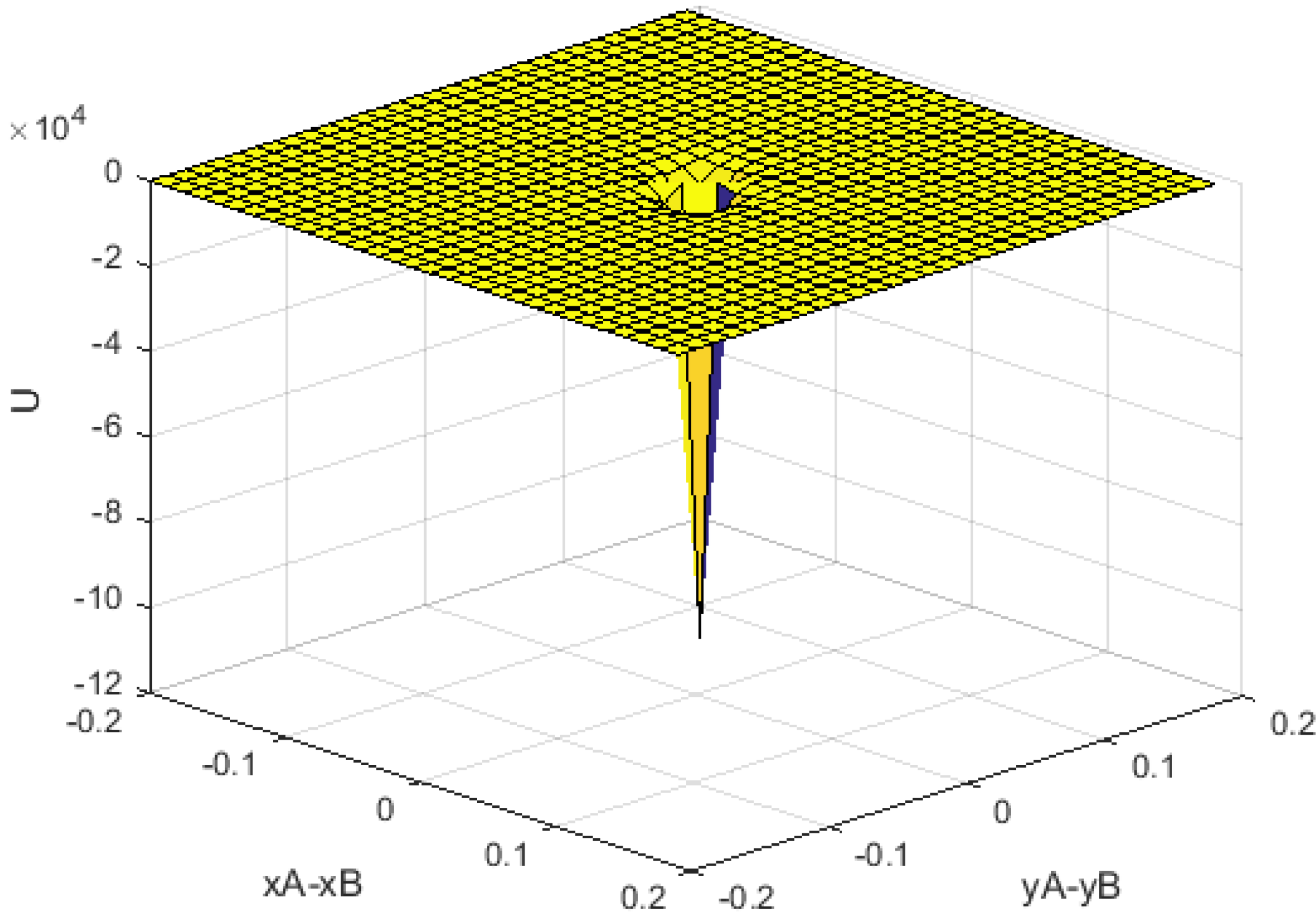
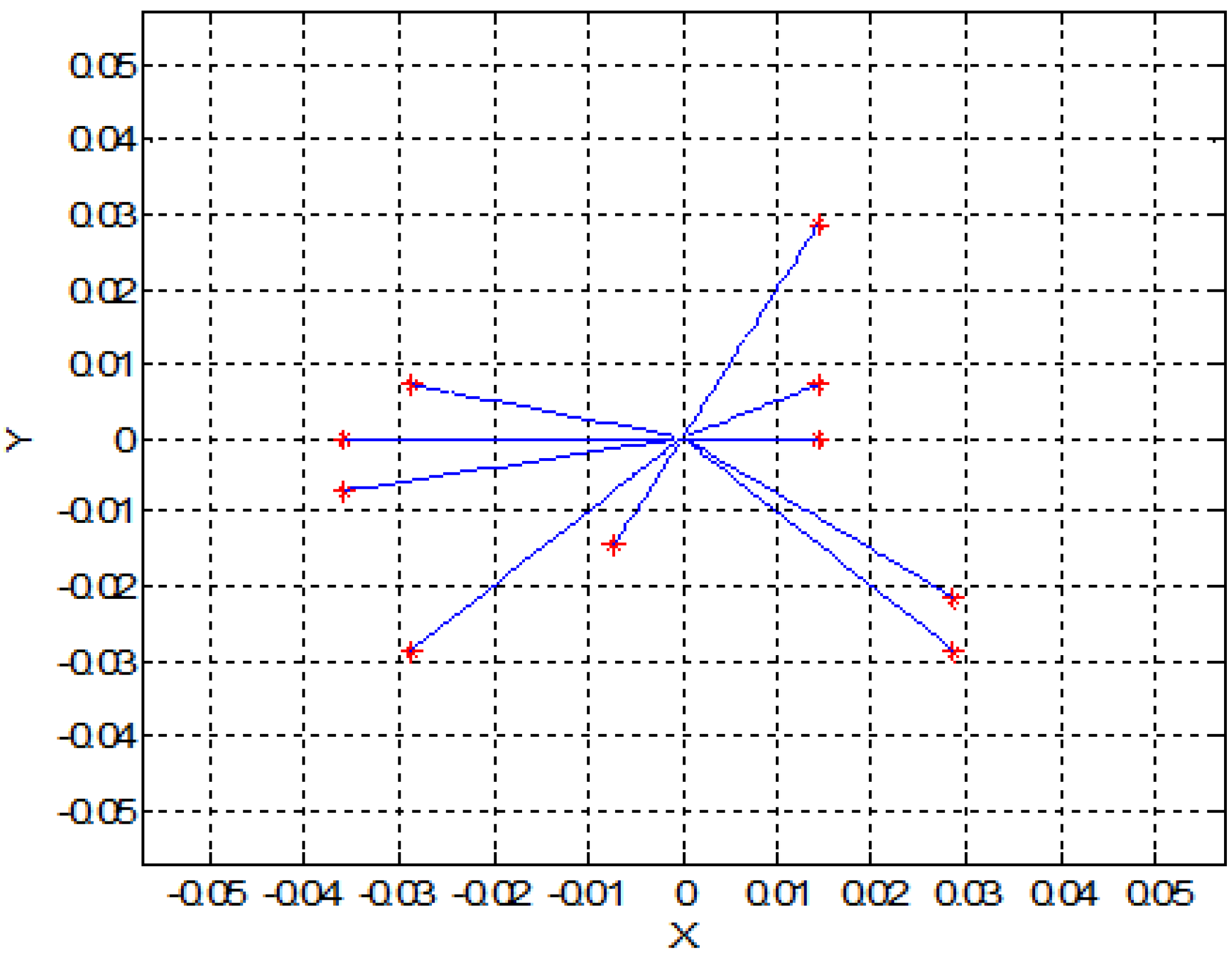
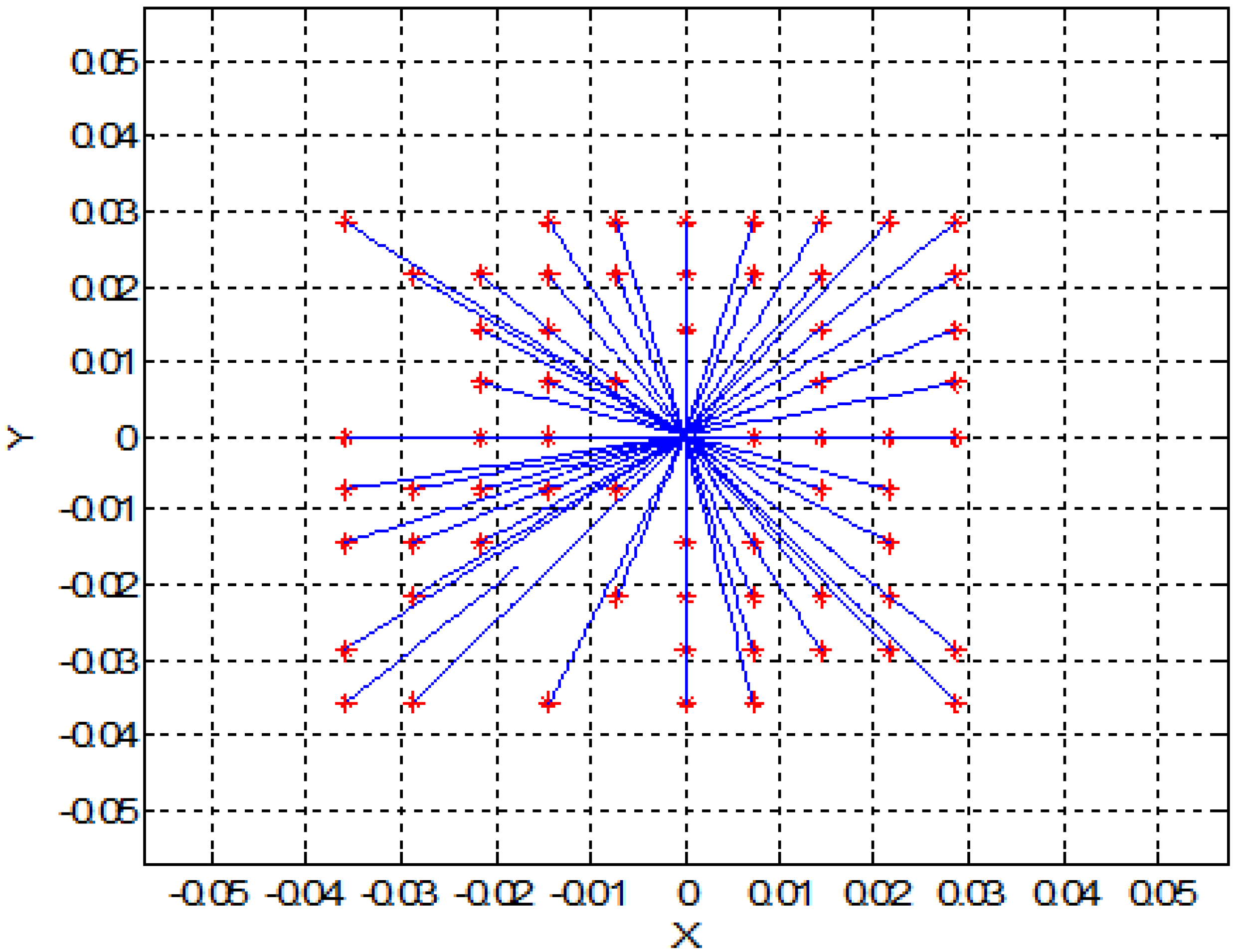
3. Two-Dimensional (2D) Simulation Results

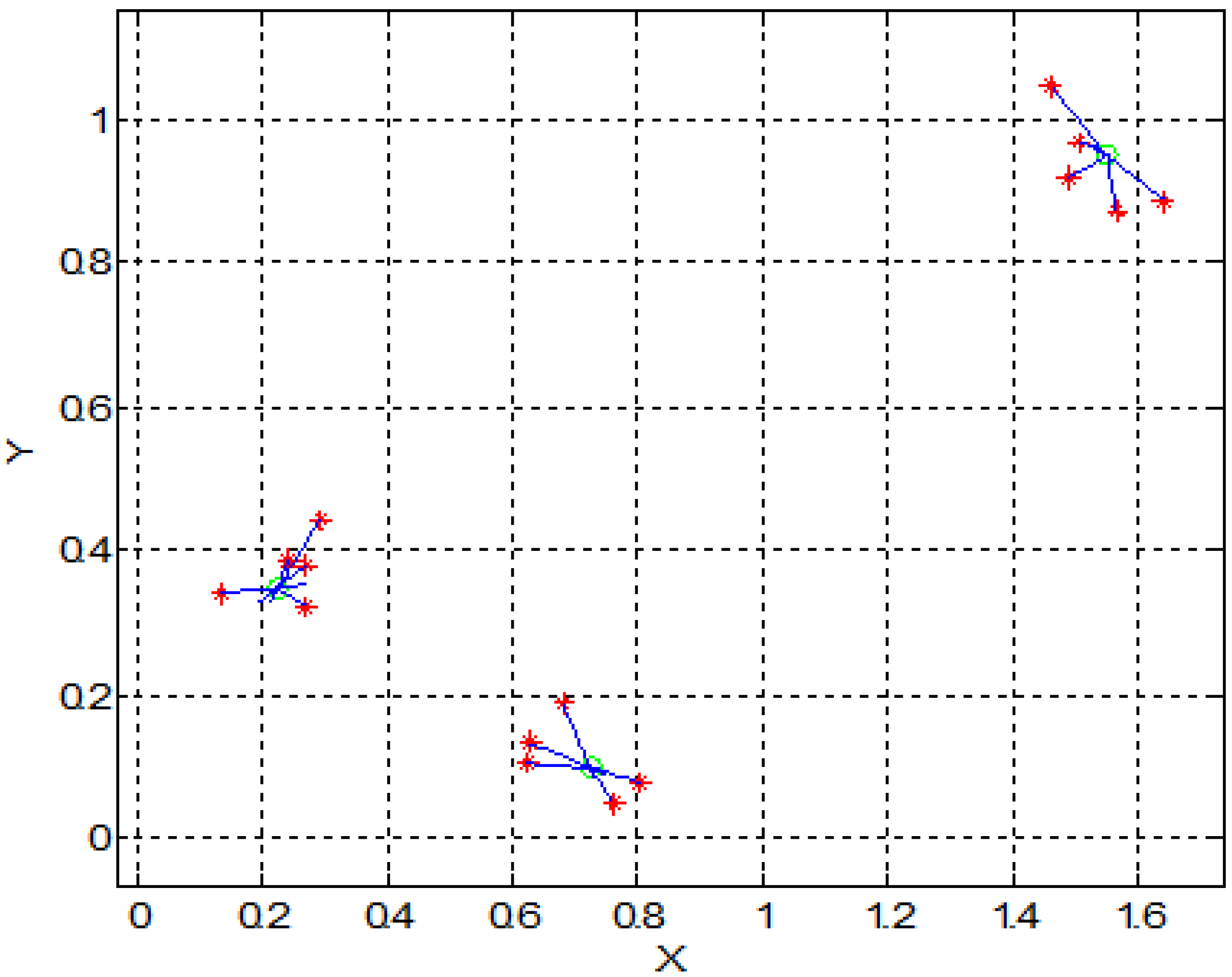

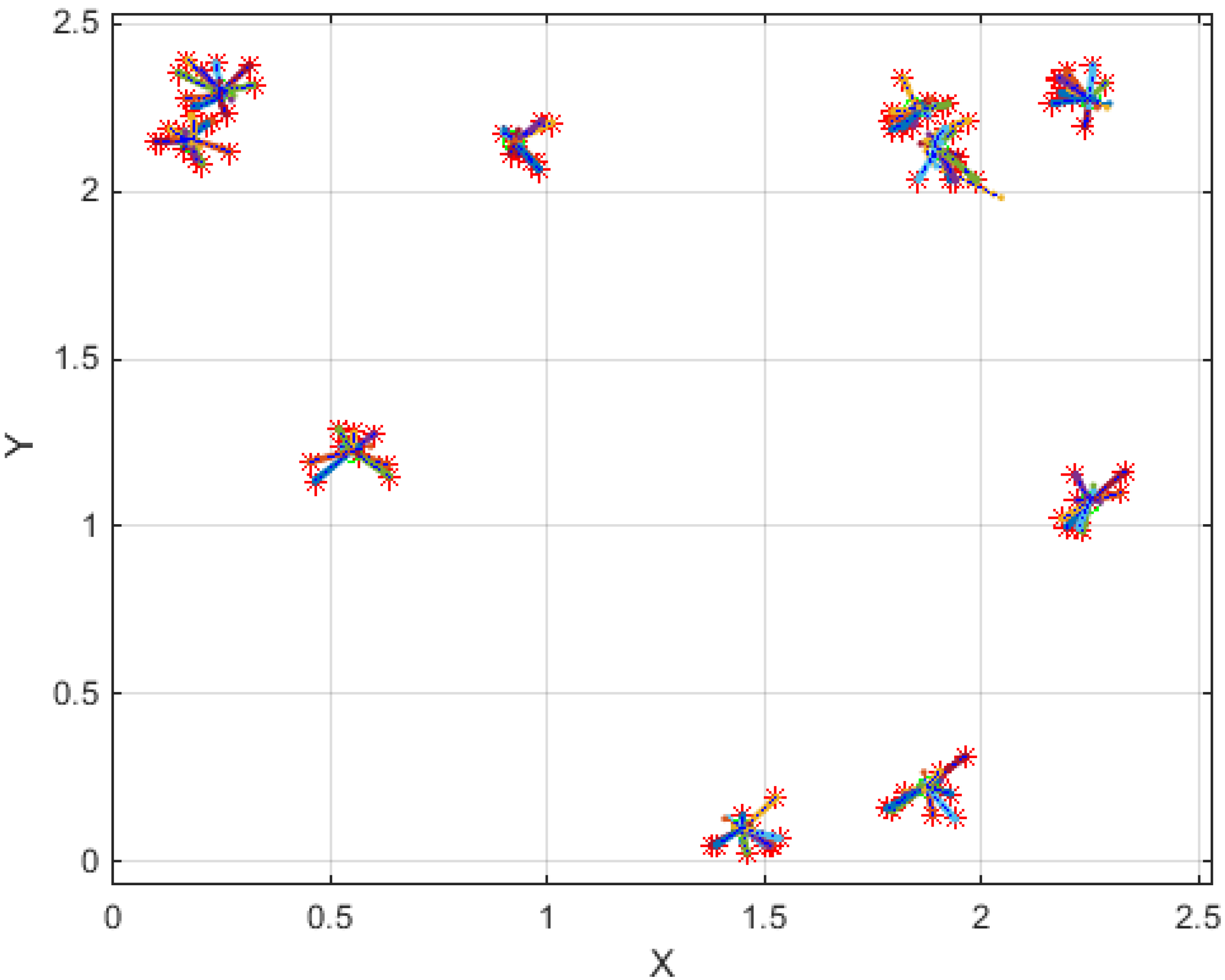
4. Experimental Model and Results
4.1. Experimental Setup
4.2. COMSOL Simulation Results of Micro Coils
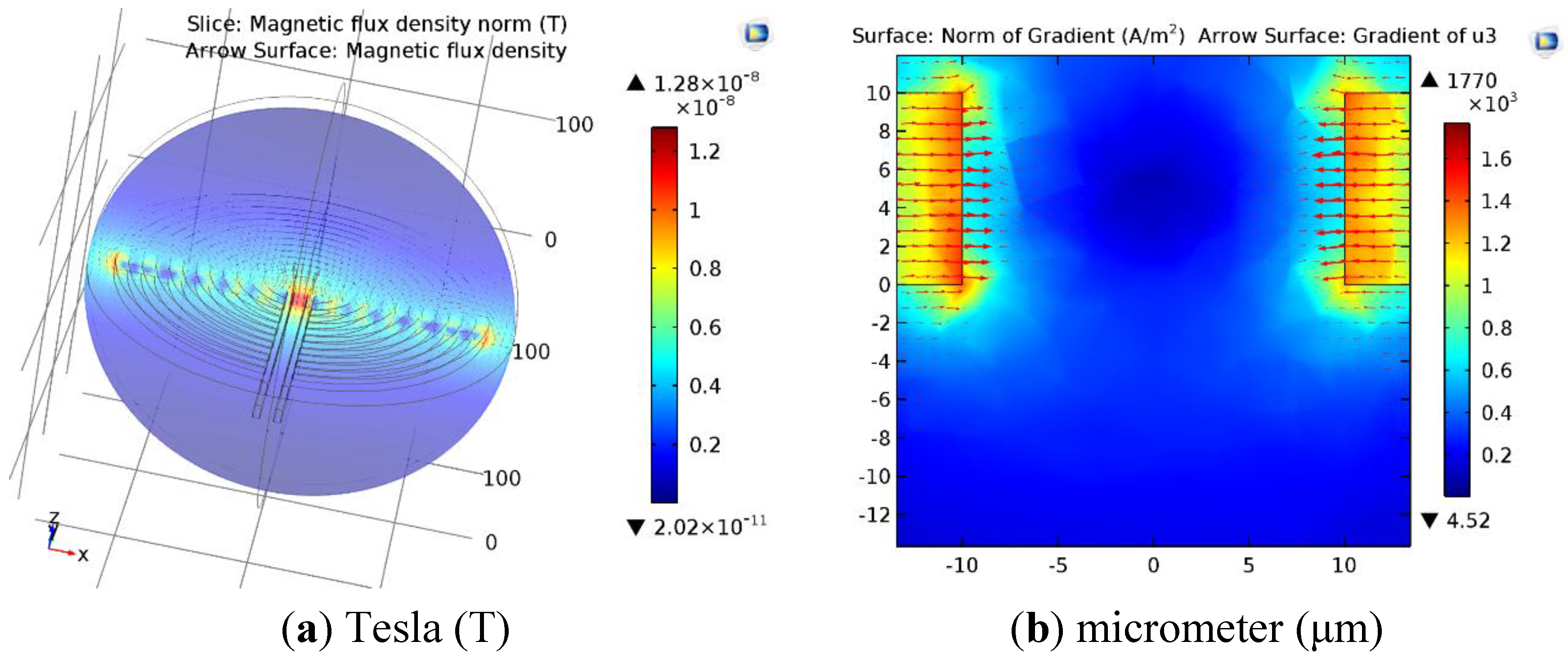
4.3. Experimental Results


5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
A. Electromagnetic Activities of Brain
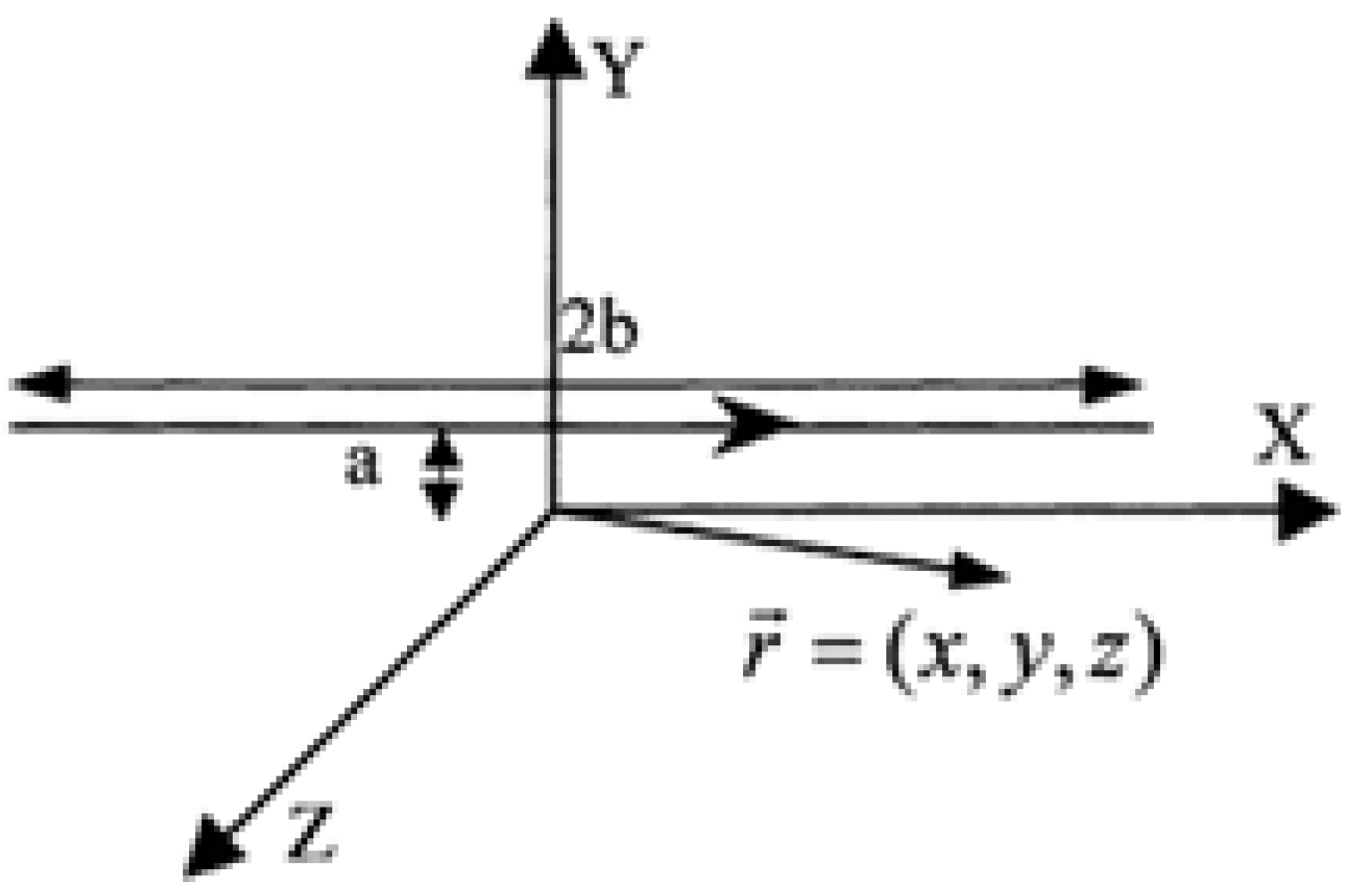
B. Electromagnetic Field of Finite Length Wires
C. U Function
References
- Ben-Menachem, E.; Henriksen, O.; Dam, M.; Mikkelsen, M.; Schmidt, D.; Reid, S.; Reife, R.; Kramer, L.; Pledger, G.; Karim, R. Double-Blind, Placebo-Controlled Trial of Topiramate as Add-on Therapy in Patients with Refractory Partial Seizures. Epilepsia 1996, 37, 539–543. [Google Scholar] [CrossRef] [PubMed]
- Rosenow, F.; Lüders, H. Presurgical evaluation of epilepsy. Brain 2001, 124, 1683–1700. [Google Scholar] [CrossRef] [PubMed]
- Woermann, F.; Free, S.L.; Koepp, M.J.; Sisodiya, S.M.; Duncan, J.S. Abnormal cerebral structure in juvenile myoclonic epilepsy demonstrated with voxel-based analysis of MRI. Brain 1999, 122, 2101–2108. [Google Scholar] [CrossRef] [PubMed]
- Iwasaki, M.; Pestana, E.; Burgess, R.C.; Lüders, H.O.; Shamoto, H.; Nakasato, N. Detection of epileptiform activity by human interpreters: Blinded comparison between electroencephalography and magnetoencephalography. Epilepsia 2005, 46, 59–68. [Google Scholar] [CrossRef] [PubMed]
- Halama, J.; Henkin, R. Single photon emission computed tomography (SPECT). In Freeman and Johnson’s Clinical Radionuclide Imaging; Grune and Stratton Inc.: Orlando, FL, USA, 1986; Volume 3. [Google Scholar]
- Ter-Pogossian, M.M. Positron emission tomography (PET). In Diagnostic Imaging in Medicine; Springer: Berlin/Heidelberg, Germany, 1983; pp. 273–277. [Google Scholar]
- Claassen, J.; Mayer, S.A.; Kowalski, R.G.; Emerson, R.G.; Hirsch, L.J. Detection of electrographic seizures with continuous EEG monitoring in critically ill patients. Neurology 2004, 62, 1743–1748. [Google Scholar] [CrossRef] [PubMed]
- Georganopoulou, D.G.; Chang, L.; Nam, J.M.; Thaxton, C.S.; Mufson, E.J.; Klein, W.L.; Mirkin, C.A. Nanoparticle-based detection in cerebral spinal fluid of a soluble pathogenic biomarker for Alzheimer’s disease. Proc. Natl. Acad. Sci. USA 2005, 102, 2273–2276. [Google Scholar] [CrossRef] [PubMed]
- Jordan, A.; Scholz, R.; Wust, P.; Fähling, H.; Felix, R. Magnetic fluid hyperthermia (MFH): Cancer treatment with AC magnetic field induced excitation of biocompatible superparamagnetic nanoparticles. J. Magn. Magn. Mater. 1999, 201, 413–419. [Google Scholar] [CrossRef]
- Brigger, I.; Dubernet, C.; Couvreur, P. Nanoparticles in cancer therapy and diagnosis. Adv. Drug Deliv. Rev. 2002, 54, 631–651. [Google Scholar] [CrossRef]
- Akhtari, M.; Bragin, A.; Cohen, M.; Moats, R.; Brenker, F.; Lynch, M.D.; Vinters, H.V.; Engel, J., Jr. Functionalized magnetonanoparticles for MRI diagnosis and localization in epilepsy. Epilepsia 2008, 49, 1419–1430. [Google Scholar] [CrossRef] [PubMed]
- Brown, R.W.; Haacke, E.M.; Thompson, M.R.; Venkatesan, R. Magnetic Resonance Imaging: Physical Principles and Sequence Design; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Flynn, E.; Bryant, H. A biomagnetic system for in vivo cancer imaging. Phys. Med. Biol. 2005, 50, 1273–1293. [Google Scholar] [CrossRef] [PubMed]
- Wallace, E.; Benayoun, M.; van Drongelen, W.; Cowan, J.D. Emergent oscillations in networks of stochastic spiking neurons. PLoS ONE 2011, 6. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Hereld, M.; Stevens, R.; van Drongelen, W. Epileptiform Activity Patterns in Coupled Neuronal Networks. Int. J. Bioelectromag. 2005, 7, 42–43. [Google Scholar]
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500–544. [Google Scholar] [CrossRef] [PubMed]
- Brzychczy, S.; Poznanski, R.R. Mathematical Neuroscience; Academic Press: Waltham, MA, USA, 2013. [Google Scholar]
- Terman, D. Mathematical Neuroscience. Am. Math. Mon. 2014, 121, 824–839. [Google Scholar]
- Ferguson, A.S. Theoretical Calculation of Magnetic Fields Generated by Neural Currents; Case Western Reserve University: Cleveland, OH, USA, 1991. [Google Scholar]
- Jolesz, F.A. Science to Practice: Opening the Blood-Brain Barrier with Focused Ultrasound—A Potential Treatment for Alzheimer Disease? Radiology 2014, 273, 631–633. [Google Scholar] [CrossRef] [PubMed]
- Kinoshita, M.; McDannold, N.; Jolesz, F.A.; Hynynen, K. Noninvasive localized delivery of Herceptin to the mouse brain by MRI-guided focused ultrasound-induced blood–brain barrier disruption. Proc. Natl. Acad. Sci. USA 2006, 103, 11719–11723. [Google Scholar] [CrossRef] [PubMed]
- Kinoshita, M.; McDannold, N.; Jolesz, F.A.; Hynynen, K. Targeted delivery of antibodies through the blood–brain barrier by MRI-guided focused ultrasound. Biochem. Biophys. Res. Commun. 2006, 340, 1085–1090. [Google Scholar] [CrossRef] [PubMed]
- Lampropoulos, N.; Karvelas, E.; Sarris, I. Computational Modeling of an MRI Guided Drug Delivery System Based on Magnetic Nanoparticle Aggregations for the Navigation of Paramagnetic Nanocapsules. 2015; arXiv:1504.03490. [Google Scholar]
- Latulippe, M.; Martel, S. Dipole Field Navigation for targeted drug delivery. In Proceedings of the 2014 5th IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics, São Paulo, Brazil, 12–15 August 2014.
- Liu, X.; Tu, M.; Kelly, R.S.; Chen, C.; Smith, B.J. Development of a computational approach to predict blood-brain barrier permeability. Drug Metab. Dispos. 2004, 32, 132–139. [Google Scholar] [CrossRef] [PubMed]
- Sonavane, G.; Tomoda, K.; Makino, K. Biodistribution of colloidal gold nanoparticles after intravenous administration: Effect of particle size. Colloids Surf. B 2008, 66, 274–280. [Google Scholar] [CrossRef] [PubMed]
- Masserini, M. Nanoparticles for brain drug delivery. ISRN Biochem. 2013, 2013. [Google Scholar] [CrossRef] [PubMed]
- Nunez, P.L.; Srinivasan, R. Electric Fields of the Brain: The Neurophysics of EEG; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Hämäläinen, M.; Hari, R.; Ilmoniemi, R.J.; Knuutila, J.; Lounasmaa, O.V. Magnetoencephalography—Theory, instrumentation, and applications to noninvasive studies of the working human brain. Rev. Modern Phys. 1993, 65. [Google Scholar] [CrossRef]
- Barkley, G.L.; Baumgartner, C. MEG and EEG in epilepsy. J. Clin. Neurophysiol. 2003, 20, 163–178. [Google Scholar] [CrossRef] [PubMed]
- Iida, K.; Hashizume, A.; Otsubo, H. MEG and Magnetic Source Imaging in MRI-Negative Refractory Focal Epilepsy. In MRI-Negative Epilepsy: Evaluation and Surgical Management; Cambridge University Press: Cambridge, UK, 2015; p. 47. [Google Scholar]
- Cao, Q.; Han, X.; Li, L. Numerical analysis of magnetic nanoparticle transport in microfluidic systems under the influence of permanent magnets. J. Phys. D 2012, 45. [Google Scholar] [CrossRef]
- Guo, S.; Deng, Y.L.; Zhao, L.B.; Chan, H.L.W.; Zhao, X.Z. Effect of patterned micro-magnets on superparamagnetic beads in microchannels. J. Phys. D 2008, 41. [Google Scholar] [CrossRef]
- Pankhurst, Q.A.; Connolly, J.; Jones, S.K.; Dobson, J.J. Applications of magnetic nanoparticles in biomedicine. J. Phys. D 2003, 36. [Google Scholar] [CrossRef]
- Haverkort, J.; Kenjereš, S.; Kleijn, C. Magnetic particle motion in a Poiseuille flow. Phys. Rev. E 2009, 80. [Google Scholar] [CrossRef]
- Griffiths, D.J.; College, R. Introduction to Electrodynamics; Prentice Hall Upper: Saddle River, NJ, USA, 1999; Volume 3. [Google Scholar]
- Izhikevich, E.M.; Moehlis, J. Dynamical Systems in Neuroscience: The geometry of excitability and bursting. SIAM Rev. 2008, 50, 397. [Google Scholar]
- Corson, D.R.; Lorrain, P. Introduction to Electromagnetic Fields and Waves; WH Freeman: San Francisco, CA, USA, 1962. [Google Scholar]
- Yee, K.S. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pedram, M.Z.; Shamloo, A.; Alasty, A.; Ghafar-Zadeh, E. Toward Epileptic Brain Region Detection Based on Magnetic Nanoparticle Patterning. Sensors 2015, 15, 24409-24427. https://doi.org/10.3390/s150924409
Pedram MZ, Shamloo A, Alasty A, Ghafar-Zadeh E. Toward Epileptic Brain Region Detection Based on Magnetic Nanoparticle Patterning. Sensors. 2015; 15(9):24409-24427. https://doi.org/10.3390/s150924409
Chicago/Turabian StylePedram, Maysam Z., Amir Shamloo, Aria Alasty, and Ebrahim Ghafar-Zadeh. 2015. "Toward Epileptic Brain Region Detection Based on Magnetic Nanoparticle Patterning" Sensors 15, no. 9: 24409-24427. https://doi.org/10.3390/s150924409
APA StylePedram, M. Z., Shamloo, A., Alasty, A., & Ghafar-Zadeh, E. (2015). Toward Epileptic Brain Region Detection Based on Magnetic Nanoparticle Patterning. Sensors, 15(9), 24409-24427. https://doi.org/10.3390/s150924409






