A Self-Adaptive Dynamic Recognition Model for Fatigue Driving Based on Multi-Source Information and Two Levels of Fusion
Abstract
:1. Introduction
2. Preliminaries
2.1. Facial Feature Based Measurements
2.2. Vehicle Behavior Feature Based Measurements
3. Self-Adaptive Dynamic Fatigue Recognition Model
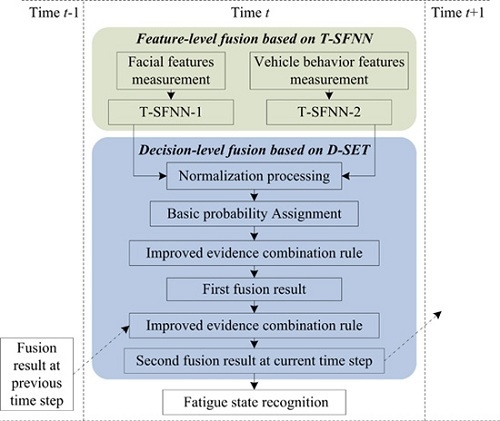
3.1. General Recognition Framework
- (i)
- Feature-level fusion based on T-SFNN: First, the most effective fatigue features are measured in real-time, and provide two types of information: driver’s facial expression and vehicle behavior. Second, facial features and vehicle behavior features are inputs to two T-SFNN models: T-SFNN-1 and T-SFNN-2, respectively. The outputs of T-SFNN-1 and T-SFNN-2 at time t are considered as the inputs to the decision-level fusion based on D-SET, which can realize dynamic BPA assignments in the proposed model as shown in Figure 1.
- (ii)
- Decision-level fusion based on D-SET: First, the outputs of T-SFNN-1 and T-SFNN-2 are normalized. Second, as shown in Figure 1, the normalized results are regarded as two pieces of evidence for decision-level fusion. Third, the two pieces of evidence are fused by an improved evidence combination rule. The first fusion result is regarded as an intermediate result which is used as input to the second fusion. Fourth, the first fusion result is fused with the fusion result at the previous time step t − 1. The second fusion result is regarded as the final decision-level fusion result at time step t. Fifth, the decision-level fusion result at time step t is recorded to be used as a piece of evidence in the decision-level fusion at next time step t + 1, as illustrated in Figure 1.
- (iii)
- Output recognition result: The driver’s fatigue state at time step t is determined based on the decision-level fusion result and the fatigue decision rule.
3.2. Feature-Level Fusion
3.2.1. Structure of T-SFNN
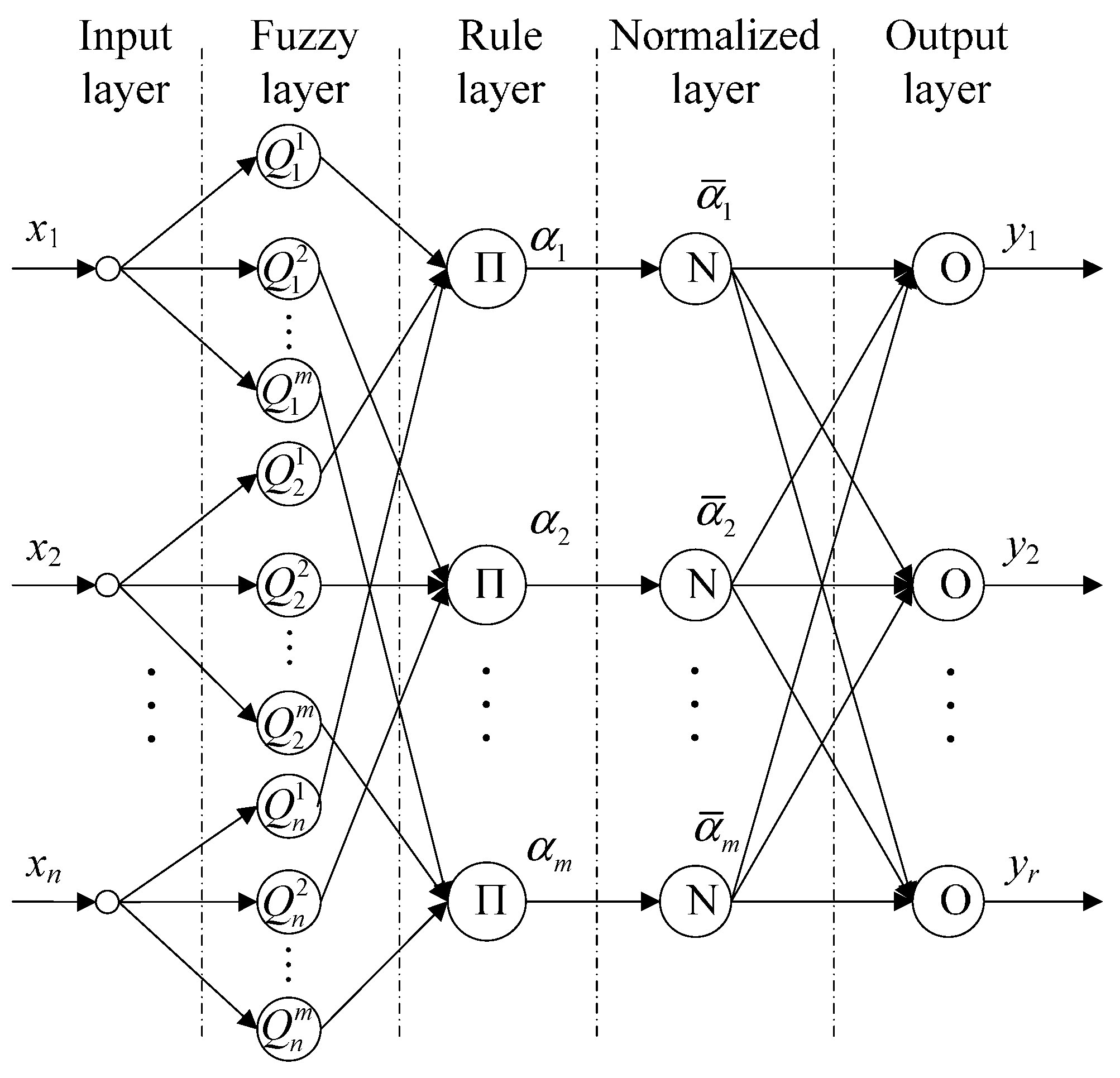
3.2.2. Learning Algorithm
3.3. Decision-Level Fusion
3.3.1. Dynamic BPA Calculation
3.3.2. The Improved Evidence Combination
3.3.3. Fatigue State Decision
4. Experiment Results and Analysis
4.1. Experiment Design

4.2. Fatigue State Assessment
- (i)
- Observer Assessment: Fatigue states of participants are evaluated by three observers according to the video of facial expression and driving behavior captured by three cameras. Of the three cameras, one is placed towards the driver’s face, another towards the steering-wheel, brake pedal, and gearshift, and the third one towards the front lane. Every video is evaluated by the three observers according to the fatigue state characteristics described in Table 1. If the fatigue state of the participant is evaluated as “Non-Fatigue (NF)”, then let si,j = 0, where si,j indicates the score of the jth video evaluated by the observer; if the fatigue state is determined as “Moderate Fatigue (MF)” or “Severe Fatigue (SF)”, then let si,j = 1 or si,j = 2, respectively. To reduce subjectivity of assessment, the average of the scores given by three observers is regarded as the final score, i.e., , where, is a rounding operator. The fatigue state of the participant in the jth video is evaluated according to the average . If , then the fatigue state is “NF”; if , then fatigue state is “MF”; if , then fatigue state is “SF”.
| Fatigue State | State Description | Score |
|---|---|---|
| NF | Eyes are active and concentrated; sits straight, operation of hands and feet is agile, keeps focusing on the front, and stable vehicle speeds. | 1 |
| MF | Eyes, mouth and hands move slightly unconsciously, yawns, head swings, adjusts the sitting position discontinuously, consistent operation of hands and feet; eye movement declines, eyelids sometimes close, frequently yawns, operations of hands and feet are not agile, not too stable vehicle speeds. | 2 |
| SF | Eyelids always closed, eyes are dull, nods, winks and shakes the head to resist fatigue, uncoordinated operation of hands and feet; eyes suddenly open after closing for a period, head droop and body incline begin to occur, hands and feet operate unconsciously, unstable speeds and zigzag routing occur. | 3 |
- (ii)
- EEG Assessment: The objective assessment based on EEG is conducted to evaluate the fatigue state of the participants. The value of rα,θ,β is considered as an index to reflect the fatigue state, which is defined as [38]:where, Pα, Pθ and Pβ are the power spectra of the three wave bands of α, θ and β, respectively, and the frequency ranges of α, θ and β bands are (4–8 Hz), (8–13 Hz), and (13–22 Hz), respectively. The fatigue state is categorized into three levels according to the value of rα,θ,β defined in Table 2.
- (iii)
- Self-Assessment: Let the participant make a self-assessment of fatigue state according to his/her current physical, physiological and psychological situations. Based on the scores gained and the 7-point Stanford Sleepiness Scale (SSS) table [39], fatigue is then rated into one of three states: “NF” (1–2 points), “MF” (3–5 points), and “SF” (6–7 points).
| Fatigue State | |
|---|---|
| NF | |
| MF | |
| SF |
- (iv)
- Comprehensive Assessment: The participant’s fatigue state is determined according to the results from steps (i)–(iii). If the fatigue state results from all three methods are consistent, then the assessment result obtained is considered valid and correct, which will be regarded as the actual fatigue state of the participant. Otherwise, it is removed from the ground truth set.
4.3. Data Collection
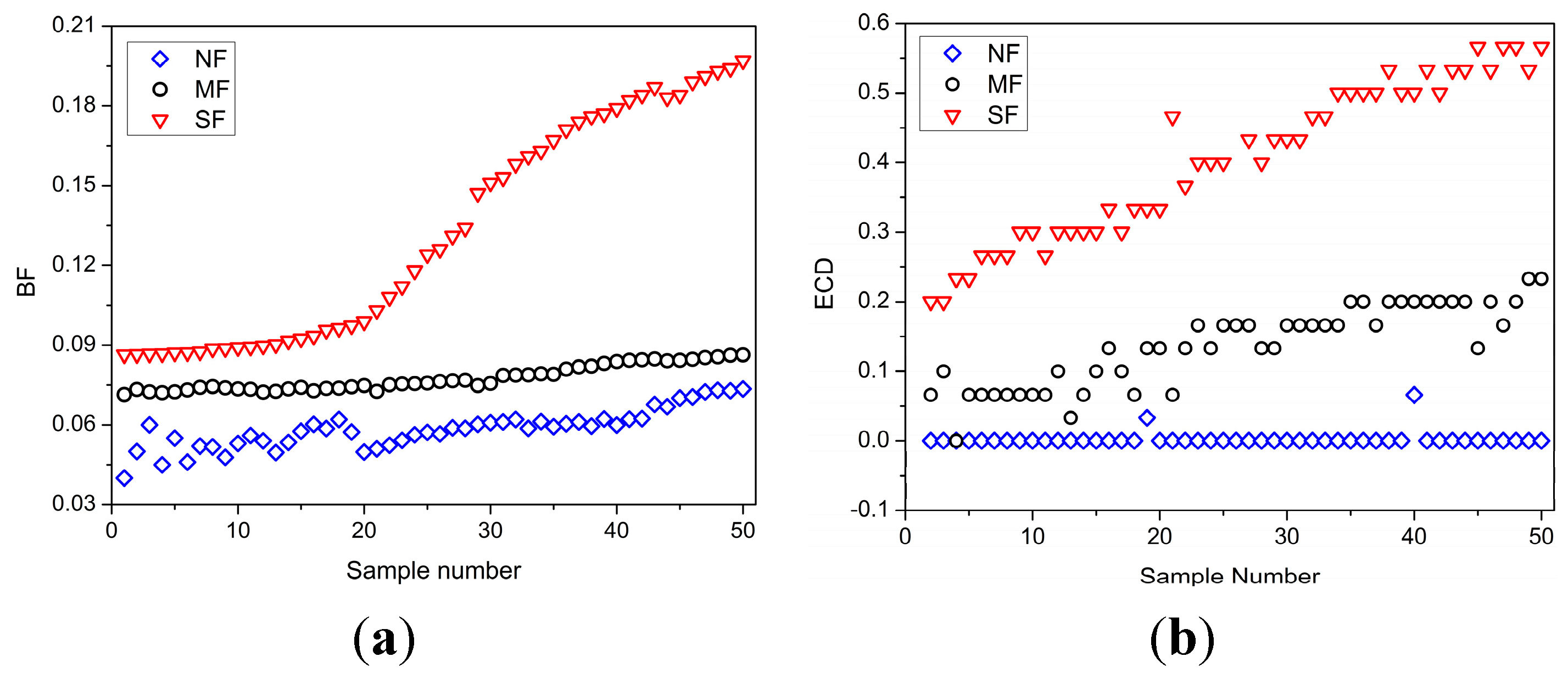

4.4. Fatigue Feature Identification
- (i)
- The Kolmogorov-Smirnov test [40]: It is used to estimate whether every fatigue feature follows a normal distribution. For the features not normally distributed, they will be normalized through logarithmic transformation.
- (ii)
- Pearson test [40]: It is used to verify the correlation between a fatigue feature and fatigue.
- (iii)
- Feature selection: The most effective fatigue features are selected according to the correlation calculated by Pearson test. If the statistic value of a fatigue feature is smaller than the quantile value, it is considered uncorrelated to fatigue driving and removed from the candidate set of fatigue features.
| Fatigue Feature Parameters | Kolmogorov-Smirnov Testing | ||||
|---|---|---|---|---|---|
| Mean | Standard Deviation | Statistic Value | Significance Level | Statistic Quantile Value | |
| BF | 0.1237 | 0.0214 | 0.0576 | 0.05 | 0.1297 |
| ECD | 0.3178 | 0.0414 | 0.0742 | 0.05 | 0.1297 |
| MEOL | 10.194 | 2.347 | 0.069 | 0.05 | 0.1297 |
| YF | 0.2074 | 0.0213 | 0.0703 | 0.05 | 0.1297 |
| PNS | 0.2857 | 0.0278 | 0.0583 | 0.05 | 0.1297 |
| SDSA | 12.69 | 2.4157 | 0.0623 | 0.05 | 0.1297 |
| FALD | 0.6138 | 0.0872 | 0.0718 | 0.05 | 0.1297 |
| SDVS | 7.315 | 1.0773 | 0.0715 | 0.05 | 0.1297 |
| Fatigue Features | Fatigue | |||
|---|---|---|---|---|
| Correlation Coefficient | Significance Level | Statistic Value | Statistic Quantile Value | |
| BF | 0.787 | 0.05 | 6.362 | 1.982 |
| ECD | 0.389 | 0.05 | 3.137 | 1.982 |
| MEOL | −0.034 | 0.05 | 1.107 | 1.982 |
| YF | 0.613 | 0.05 | 4.814 | 1.982 |
| PNS | 0.713 | 0.05 | 6.324 | 1.982 |
| SDSA | −0.622 | 0.05 | 4.896 | 1.982 |
| FALD | 0.562 | 0.05 | 4.528 | 1.982 |
| SDVS | 0.675 | 0.05 | 5.968 | 1.982 |
4.5. Feature-Level Fusion Results
| Parameters of T-SFNN | T-SFNN-1 | T-SFNN-2 | ||
|---|---|---|---|---|
| Without SCA | With SCA | Without SCA | With SCA | |
| Input-output space | 3 inputs, 3 output | 3 inputs, 3 output | 4 inputs, 3 output | 4 inputs, 3 output |
| Shape of membership function | Gaussian | Gaussian | Gaussian | Gaussian |
| Number of linguistic values | 3 | 3 | 3 | 3 |
| Number of fuzzy rules | 27 | 3 | 81 | 3 |
| Number of parameters for training | 99 | 27 | 267 | 33 |
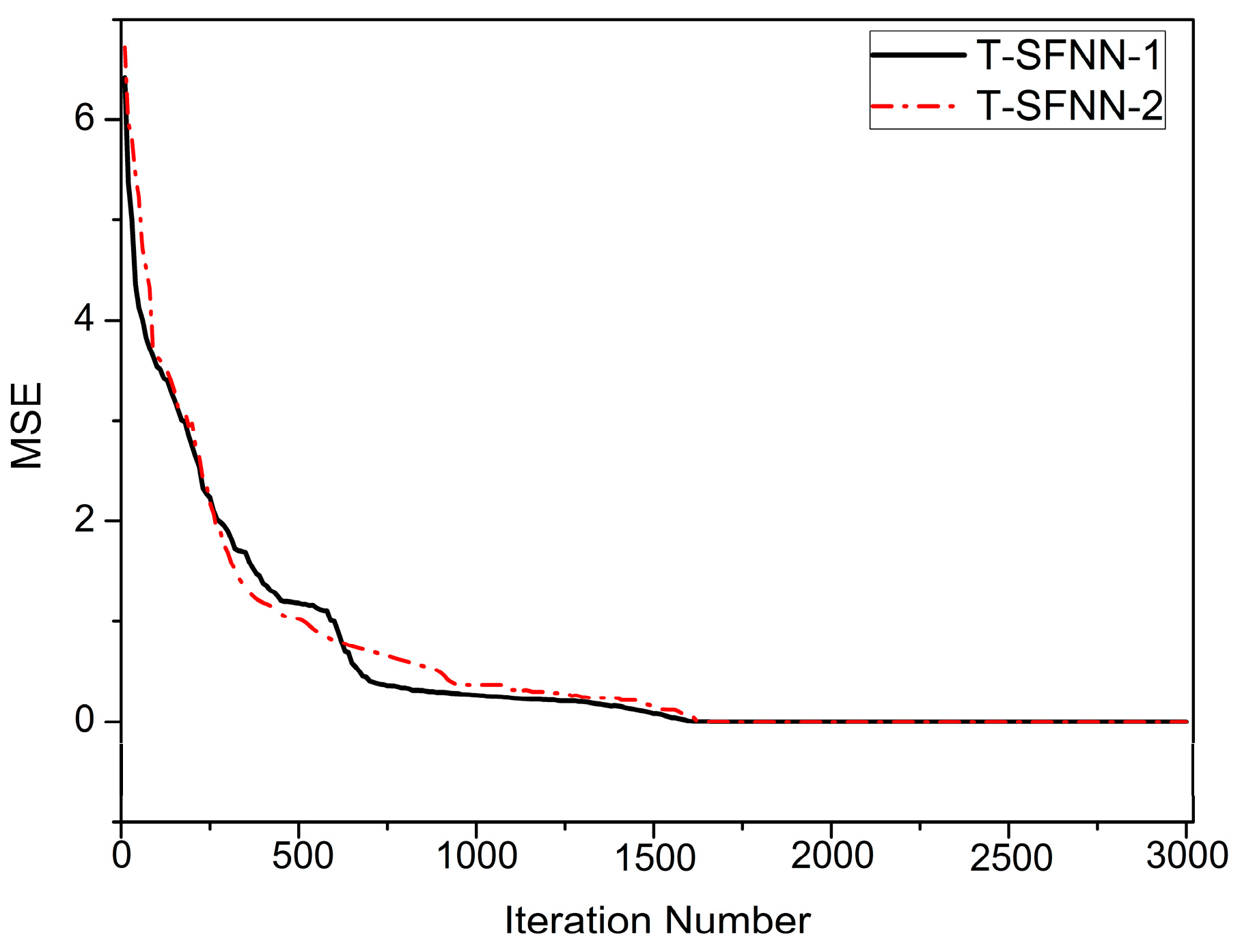
| Index | ||
|---|---|---|
| 1 | {0.812, 0.087, 0.103} | {0.782, 0.311, 0.074} |
| 2 | {0.203, 0.763, 0.052} | {0.402, 0.432, 0.207} |
| 3 | {0.237, 0.624, 0.178} | {0.383, 0.552, 0.134} |
| 4 | {0.412, 0.488, 0.106} | {0.721, 0.234, 0.071} |
| 5 | {0.127, 0.073, 0.811} | {0.442, 0.551, 0.107} |
| 6 | {0.292, 0.457, 0.393} | {0.112, 0.476, 0.389} |
4.6. Decision-Level Fusion Results
| Index | {ṁt(A1), ṁt(A2), ṁt(A3)} | sEEG | ||||
|---|---|---|---|---|---|---|
| 1 | {0.810, 0.087, 0.103} | {0.670, 0.266, 0.064} | 0.441 | {0.971, 0.476, 0.012} | NF | NF |
| 2 | {0.199, 0.750, 0.051} | {0.386, 0.415, 0.199} | 0.603 | {0.193, 0.784, 0.026} | MF | MF |
| 3 | {0.228, 0.601, 0.171} | {0.359, 0.516, 0.125} | 0.587 | {0.198, 0.751, 0.052} | MF | MF |
| 4 | {0.410, 0.485, 0.105} | {0.703, 0.228, 0.069} | 0.593 | {0.708, 0.272, 0.018} | NF | NF |
| 5 | {0.126, 0.072, 0.802} | {0.402, 0.501, 0.097} | 0.835 | {0.307, 0.219, 0.471} | SF | SF |
| 6 | {0.256, 0.400, 0.344} | {0.115, 0.487, 0.398} | 0.640 | {0.082, 0.541, 0.380} | MF | SF |
| Index | K | {mt(A1), mt(A2), mt(A3)} | sF | ||
|---|---|---|---|---|---|
| 1 | {0.793, 0.102, 0.105} | {0.665, 0.326, 0.009} | 0.44 | {0.942, 0.059, 0.002} | NF |
| 2 | {0.192, 0.713, 0.095} | {0.192, 0.782, 0.026} | 0.304 | {0.053, 0.801, 0.004} | MF |
| 3 | {0.179, 0.599, 0.222} | {0.198, 0.75, 0.052} | 0.503 | {0.071, 0.904, 0.023} | MF |
| 4 | {0.647, 0.285, 0.068} | {0.709, 0.273, 0.018} | 0.463 | {0.854, 0.145, 0.002} | NF |
| 5 | {0.186, 0.127, 0.687} | {0.308, 0.220, 0.472} | 0.591 | {0.140, 0.068, 0.793} | SF |
| 6 | {0.135, 0.079, 0.786} | {0.082, 0.539, 0.379} | 0.608 | {0.028, 0.109, 0.760} | SF |
| Models | AR | MR | FAR |
|---|---|---|---|
| Single feature based (BF) | 88.7% | 4.2% | 3.9% |
| Single-source fusion based (Vehicle behavior features and T-SFNN) | 90.8% | 3.6% | 4.1% |
| Single-source fusion based (Facial features and T-SFNN) | 91.6% | 3.4% | 3.7% |
| The proposed model (Using all fatigue features) | 92.1% | 3.1% | 3.5% |
| The proposed model (Based on the most effective features) | 93.8% | 2.3% | 2.8% |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sahayadhas, A.; Sundaraj, K.; Murugappan, M. Detecting driver drowsiness based on sensors: A review. Sensors 2012, 12, 16937–16953. [Google Scholar] [PubMed]
- Sandberg, D.; Åkerstedt, T.; Anund, A.; Kecklund, G.; Wahde, M. Detecting driver sleepiness using optimized nonlinear combinations of sleepiness indicators. IEEE Trans. Intell. Transp. Syst. 2011, 12, 97–108. [Google Scholar] [CrossRef]
- Patel, M.; Lal, S.K.L.; Kavanagh, D.; Rossiter, P. Applying neural network analysis on heart rate variability data to assess driver fatigue. Expert Syst. Appl. 2011, 38, 7235–7242. [Google Scholar] [CrossRef]
- Correa, A.G.; Orosco, L.; Laciar, E. Automatic detection of drowsiness in EEG records based on multimodal analysis. Med. Eng. Phys. 2014, 36, 244–249. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Chung, W.Y. Detection of driver drowsiness using wavelet analysis of heart rate variability and a support vector machine classifier. Sensors 2013, 13, 16494–16511. [Google Scholar] [CrossRef] [PubMed]
- Khushaba, R.N.; Kodagoda, S.; Lal, S.; Dissanayake, G. Driver drowsiness classification using fuzzy wavelet-packet-based feature-extraction algorithm. IEEE Trans. Biomed. Eng. 2011, 58, 121–131. [Google Scholar] [PubMed]
- Sahayadhas, A.; Sundaraj, K.; Murugappan, M. Drowsiness detection during different times of day using multiple features. Australas. Phys. Eng. Sci. Med. 2013, 36, 243–250. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.G.; Lee, B.L.; Chung, W.Y. Mobile healthcare for automatic driving sleep-onset detection using wavelet-based EEG and respiration signals. Sensors 2014, 14, 17915–17936. [Google Scholar] [PubMed]
- Liang, W.; Yuan, J.; Sun, D.; Lin, M. Changes in physiological parameters induced by indoor simulated driving: Effect of lower body exercise at mid-term break. Sensors 2009, 9, 6913–6933. [Google Scholar] [CrossRef] [PubMed]
- Jo, J.; Lee, S.J.; Park, K.R.; Kim, I.; Kim, J. Detecting driver drowsiness using feature-level fusion and user-specific classification. Expert Syst. Appl. 2014, 41, 1139–1152. [Google Scholar] [CrossRef]
- Eriksson, M.; Papanikolopoulos, N.P. Driver fatigue: a vision-based approach to automatic diagnosis. Transp. Res. Part C Emerg. Technol. 2001, 9, 399–413. [Google Scholar] [CrossRef]
- D’Orazio, T.; Leo, M.; Guaragnella, C.; Distante, A. A visual approach for driver inattention detection. Pattern Recognit. 2007, 40, 2341–2355. [Google Scholar] [CrossRef]
- Du, Y.; Hu, Q.; Chen, D.; Ma, P. Kernelized fuzzy rough sets based yawn detection for driver fatigue monitoring. Fundam. Inf. 2011, 111, 65–79. [Google Scholar]
- Sun, R.; Ochieng, W.Y.; Feng, S. An integrated solution for lane level irregular driving detection on highways. Transp. Res. Part C Emerg. Technol. 2015, 56, 61–79. [Google Scholar] [CrossRef]
- Wang, J.G.; Lin, C.J.; Chen, S.M. Applying fuzzy method to vision-based lane detection and departure warning system. Expert Syst. Appl. 2010, 37, 113–126. [Google Scholar] [CrossRef]
- Wu, C.F.; Lin, C.J.; Lee, C.Y. Applying a functional neurofuzzy network to real-time lane detection and front-vehicle distance measurement. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2012, 42, 577–589. [Google Scholar]
- McDonald, A.D.; Lee, J.D.; Schwarz, C.; Brown, T.L. Steering in a random forest: Ensemble learning for detecting drowsiness-related lane departures. Hum. Factors 2014, 56, 986–998. [Google Scholar] [CrossRef] [PubMed]
- Sayed, R.; Eskandarian, A. Unobtrusive drowsiness detection by neural network learning of driver steering. J. Automob. Eng. 2001, 215, 969–75. [Google Scholar] [CrossRef]
- Boyraz, P.; Acar, M.; Kerr, D. Multi-sensor driver drowsiness monitoring. J. Automob. Eng. 2008, 222, 2041–2062. [Google Scholar] [CrossRef]
- Yang, G.; Lin, Y.; Bhattacharya, P. A driver fatigue recognition model using fusion of multiple features. In Proceedings of 2005 IEEE International Conference on Systems, Man and Cybernetics, Waikoloa, HA, USA, 10–12 October 2005; pp. 1777–1784.
- Cheng, B.; Zhang, W.; Lin, Y.; Feng, R.; Zhang, X. Driver drowsiness detection based on multisource information. Hum. Factors Ergon. Manuf. Serv. Ind. 2012, 22, 450–467. [Google Scholar] [CrossRef]
- Lee, B.G.; Chung, W.Y. Driver alertness monitoring using fusion of facial features and bio-signals. IEEE Sens. J. 2012, 12, 2416–2422. [Google Scholar] [CrossRef]
- Yang, G.; Lin, Y.; Bhattacharya, P. A driver fatigue recognition model based on information fusion and dynamic Bayesian network. Inf. Sci. 2010, 180, 1942–1954. [Google Scholar] [CrossRef]
- Wong, W.K.; Zeng, X.H.; Au, W.M.R. A decision support tool for apparel coordination through integrating the knowledge-based attribute evaluation expert system and the T-S fuzzy neural network. Expert Syst. Appl. 2009, 36, 2377–2390. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, X.; Zhuang, W.; Tang, H. Driver fatigue driving detection based on eye state. Int. J. Digit. Content Technol. Appl. 2011, 5, 307–314. [Google Scholar]
- Sun, W.; Zhang, X.; Sun, Y.; Tang, H.; Song, A. Color space lip segmentation for drivers’ fatigue detection. High Technol. Lett. 2012, 18, 416–422. [Google Scholar]
- Lee, J.W. A machine vision system for lane-departure detection. Comput. Vision Image Underst. 2002, 86, 52–78. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, W.; Li, X.; Chen, G. Driving fatigue fusion detection based on T-S fuzzy neural network evolved by subtractive clustering and particle swarm optimization. J. Southeast Univ. 2009, 25, 356–361. [Google Scholar]
- Wang, D.; Song, X.; Yin, W.; Yuan, J. Forecasting core business transformation risk using the optimal rough set and the neural network. J. Forecast. 2015, 34, 478–491. [Google Scholar] [CrossRef]
- Aziz, K.; Rai, S.; Rahman, A. Design flood estimation in ungauged catchments using genetic algorithm-based artificial neural network (GAANN) technique for Australia. Nat. Hazard. 2015, 77, 805–821. [Google Scholar] [CrossRef]
- Cai, B.; Liu, Y.; Fan, Q.; Zhang, Y.; Liu, Z.; Yu, S.; Ji, R. Multi-source information fusion based fault diagnosis of ground-source heat pump using Bayesian network. Appl. Energ. 2014, 114, 1–9. [Google Scholar] [CrossRef]
- Ai, L.; Wang, J.; Wang, X. Multi-features fusion diagnosis of tremor based on artificial neural network and D-S evidence theory. Signal Process. 2008, 88, 2927–2935. [Google Scholar] [CrossRef]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976; pp. 60–134. [Google Scholar]
- Fan, X.F.; Zuo, M.J. Fault diagnosis of machines based on D-S evidence theory. Part 1: D-S evidence theory and its improvement. Pattern Recognit. Lett. 2006, 27, 366–376. [Google Scholar] [CrossRef]
- Fan, X.F.; Zuo, M.J. Fault diagnosis of machines based on D-S evidence theory. Part 2: Application of the improved D-S evidence theory in gearbox fault diagnosis. Pattern Recognit. Lett. 2006, 27, 377–385. [Google Scholar] [CrossRef]
- Guo, K.; Li, W. Combination rule of D-S evidence theory based on the strategy of cross merging between evidences. Expert Syst. Appl. 2011, 38, 13360–13366. [Google Scholar] [CrossRef]
- Fu, R.; Wang, H. Detection of driving fatigue by using noncontact EMG and ECG signals measurement system. Int. J. Neural Syst. 2014. [Google Scholar] [CrossRef] [PubMed]
- He, Q.; Li, W.; Fan, X. Estimation of driver’s fatigue based on steering wheel angle. In Proceedings of the 14th International Conference on Human-Computer Interaction, Orlando, FL, USA, 9–14 July 2011; pp. 145–155.
- Stanford Sleepiness Scale. Available online: http://web.stanford.edu/~dement/sss.html (accessed on 8 July 2015).
- Taeger, D.; Kuhnt, S. Statistical Hypothesis Testing with SAS and R; Wiley: Chichester, UK, 2014. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Zhang, X.; Peeta, S.; He, X.; Li, Y.; Zhu, S. A Self-Adaptive Dynamic Recognition Model for Fatigue Driving Based on Multi-Source Information and Two Levels of Fusion. Sensors 2015, 15, 24191-24213. https://doi.org/10.3390/s150924191
Sun W, Zhang X, Peeta S, He X, Li Y, Zhu S. A Self-Adaptive Dynamic Recognition Model for Fatigue Driving Based on Multi-Source Information and Two Levels of Fusion. Sensors. 2015; 15(9):24191-24213. https://doi.org/10.3390/s150924191
Chicago/Turabian StyleSun, Wei, Xiaorui Zhang, Srinivas Peeta, Xiaozheng He, Yongfu Li, and Senlai Zhu. 2015. "A Self-Adaptive Dynamic Recognition Model for Fatigue Driving Based on Multi-Source Information and Two Levels of Fusion" Sensors 15, no. 9: 24191-24213. https://doi.org/10.3390/s150924191
APA StyleSun, W., Zhang, X., Peeta, S., He, X., Li, Y., & Zhu, S. (2015). A Self-Adaptive Dynamic Recognition Model for Fatigue Driving Based on Multi-Source Information and Two Levels of Fusion. Sensors, 15(9), 24191-24213. https://doi.org/10.3390/s150924191