Integrated High Resolution Digital Color Light Sensor in 130 nm CMOS Technology
Abstract
:1. Introduction
2. Principles of Operation
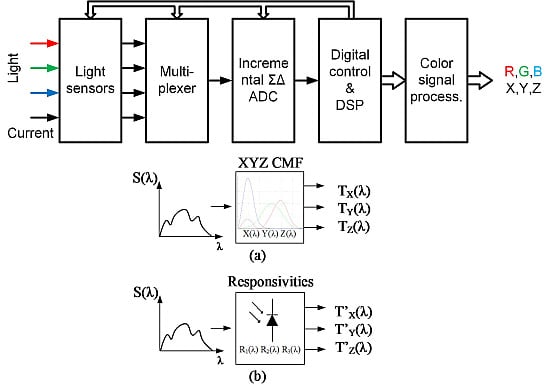
3. Color Sensor Design and Measurements
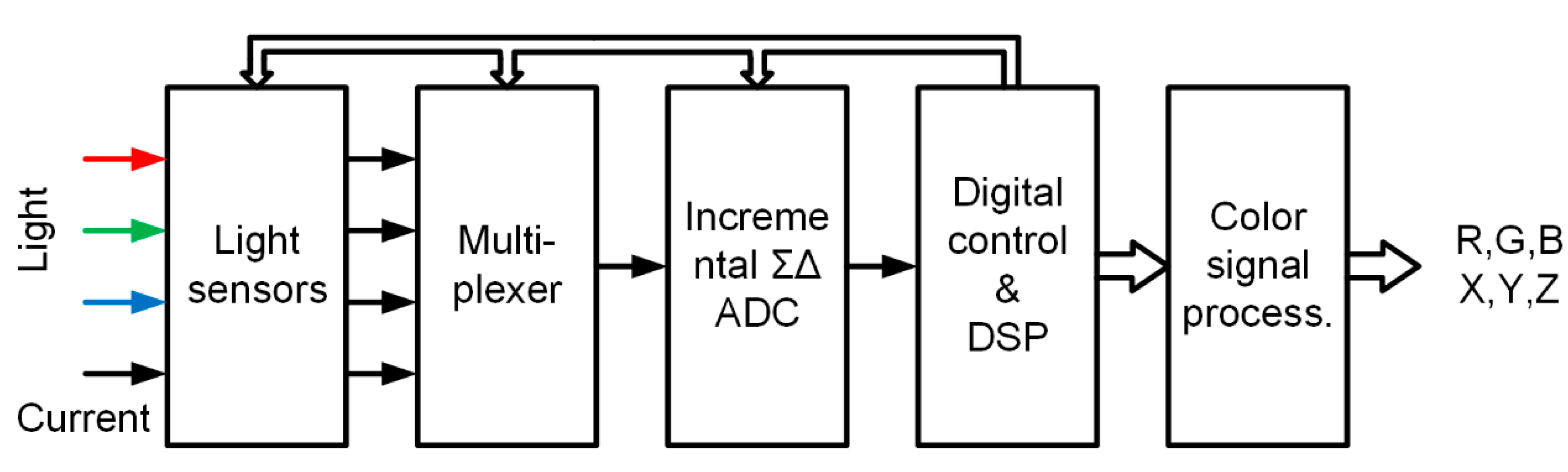
3.1. Proposed Photo Sensor Principles
3.1.1. “Red” Spectral Response Sensor
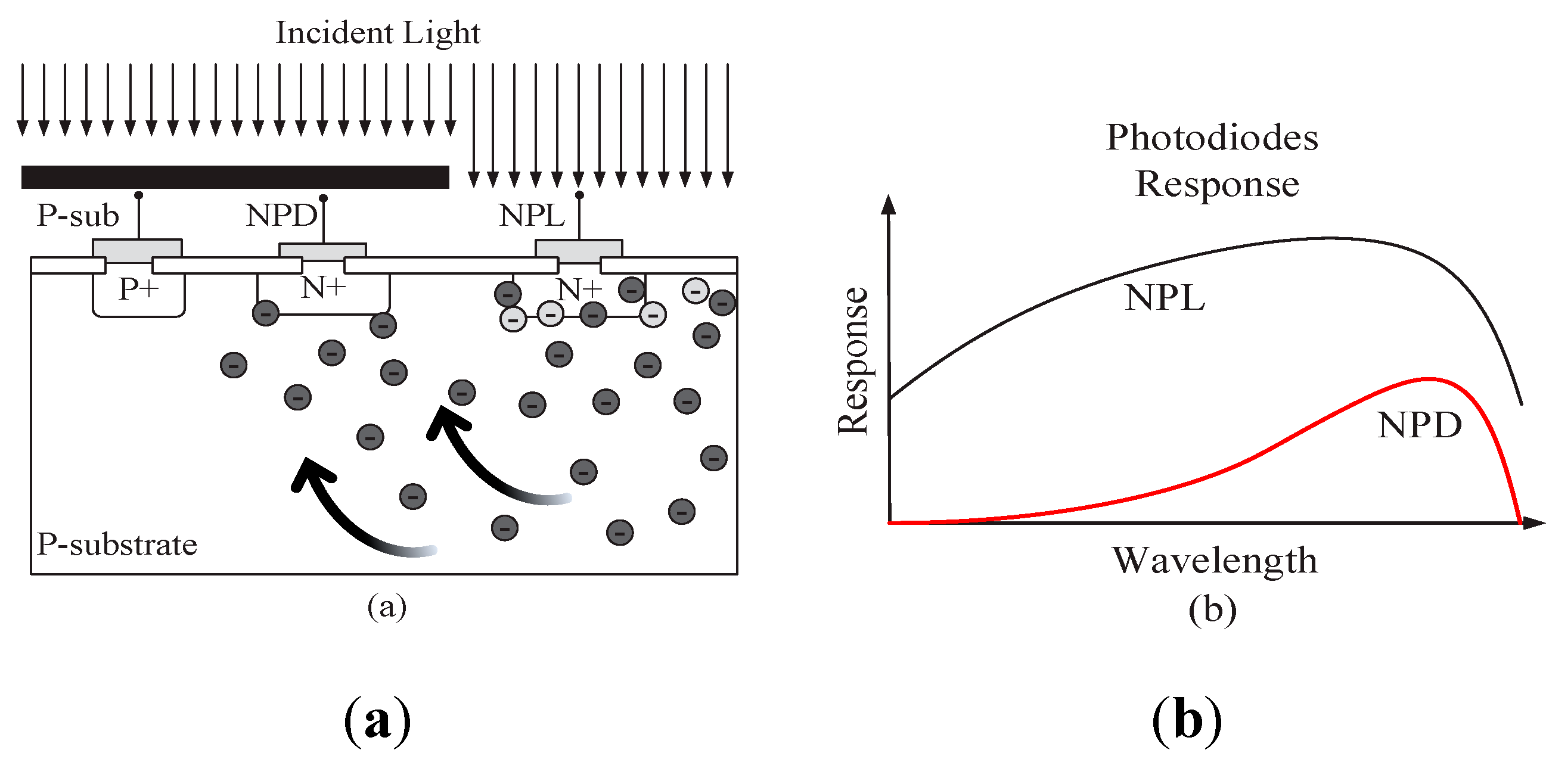
3.1.2. “Blue” Spectral Response Sensor
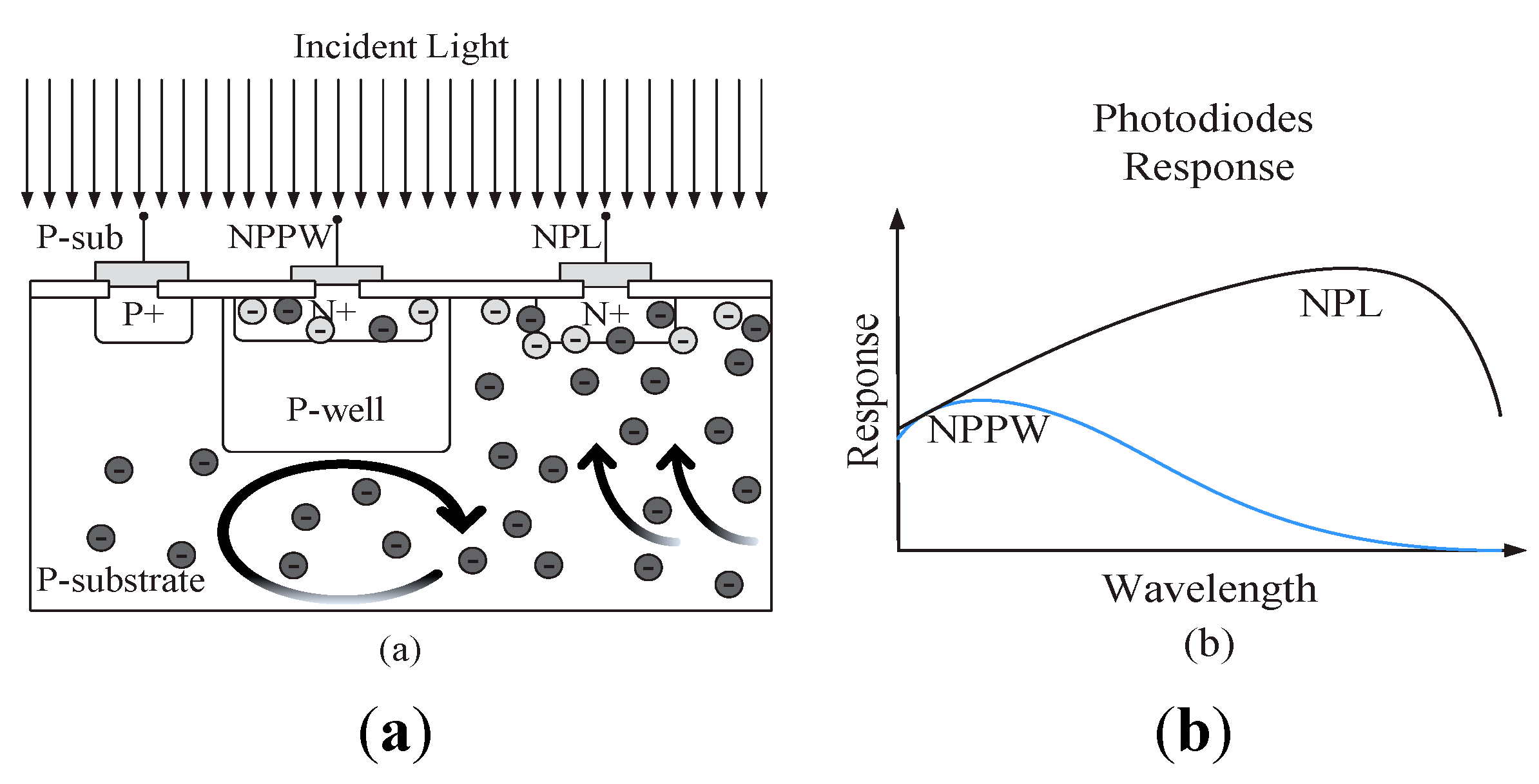
3.2. Proposed Color Sensor Implementation
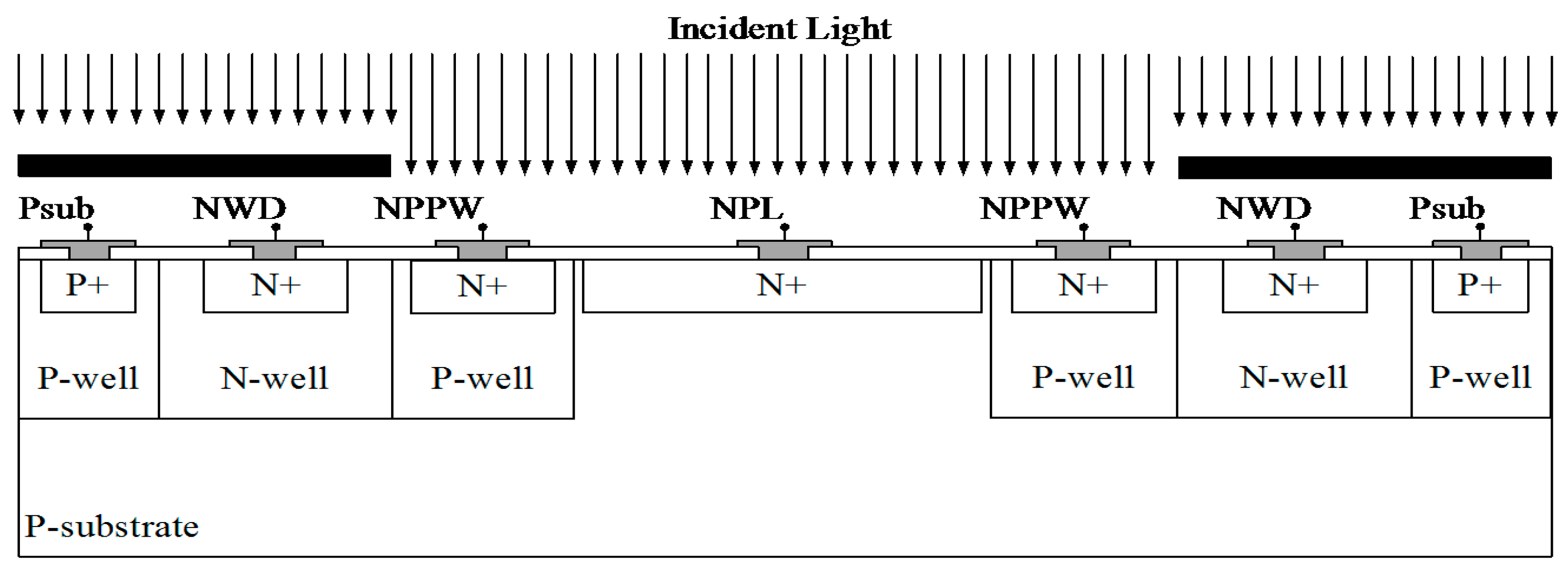
3.2.1. Color Sensor Simulations
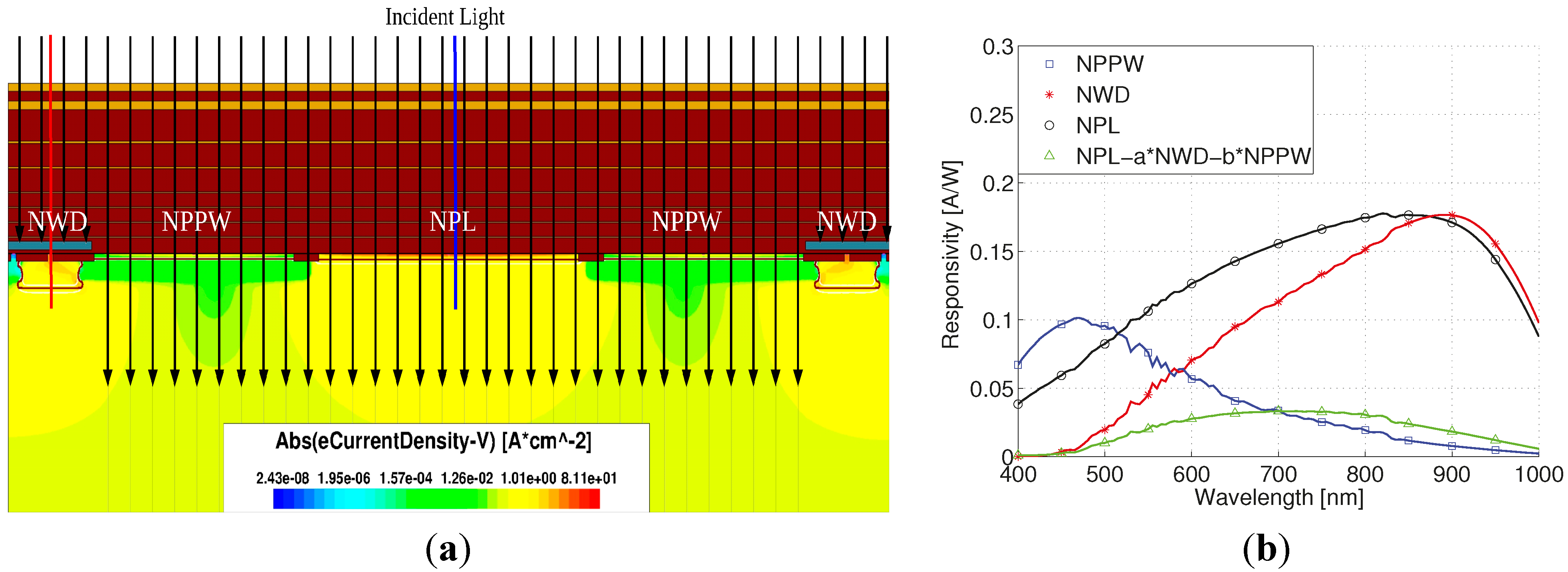
4. High Resolution Light to Digital Conversion
4.1. Photocurrent to Digital Converter
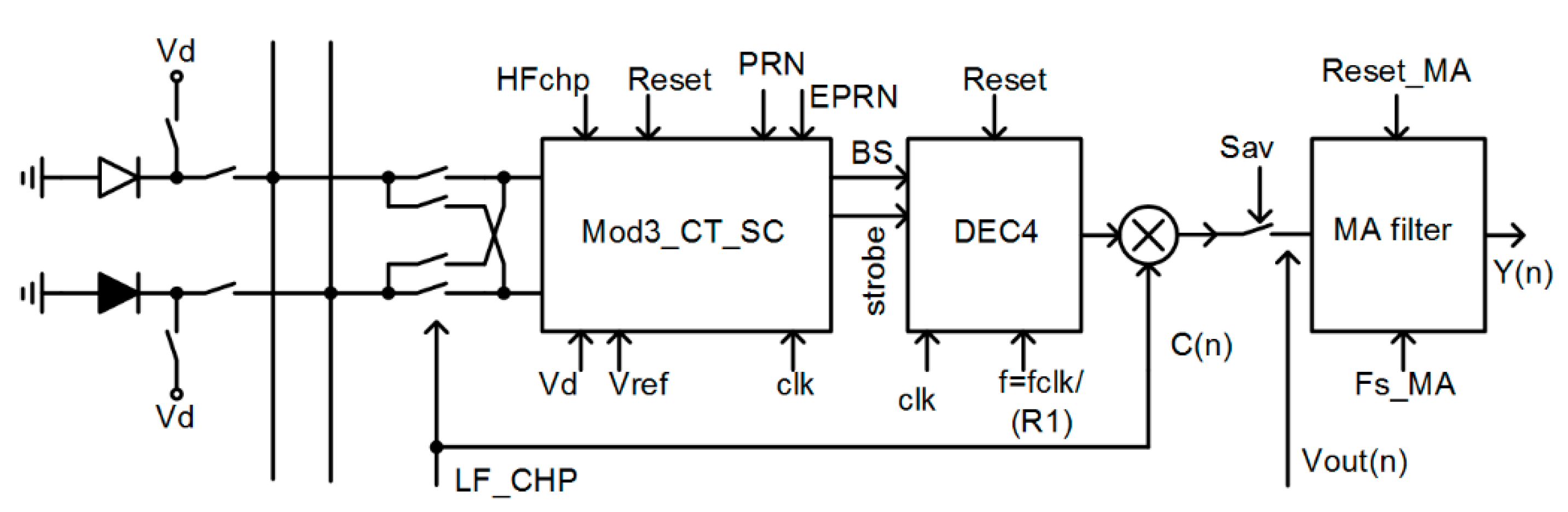
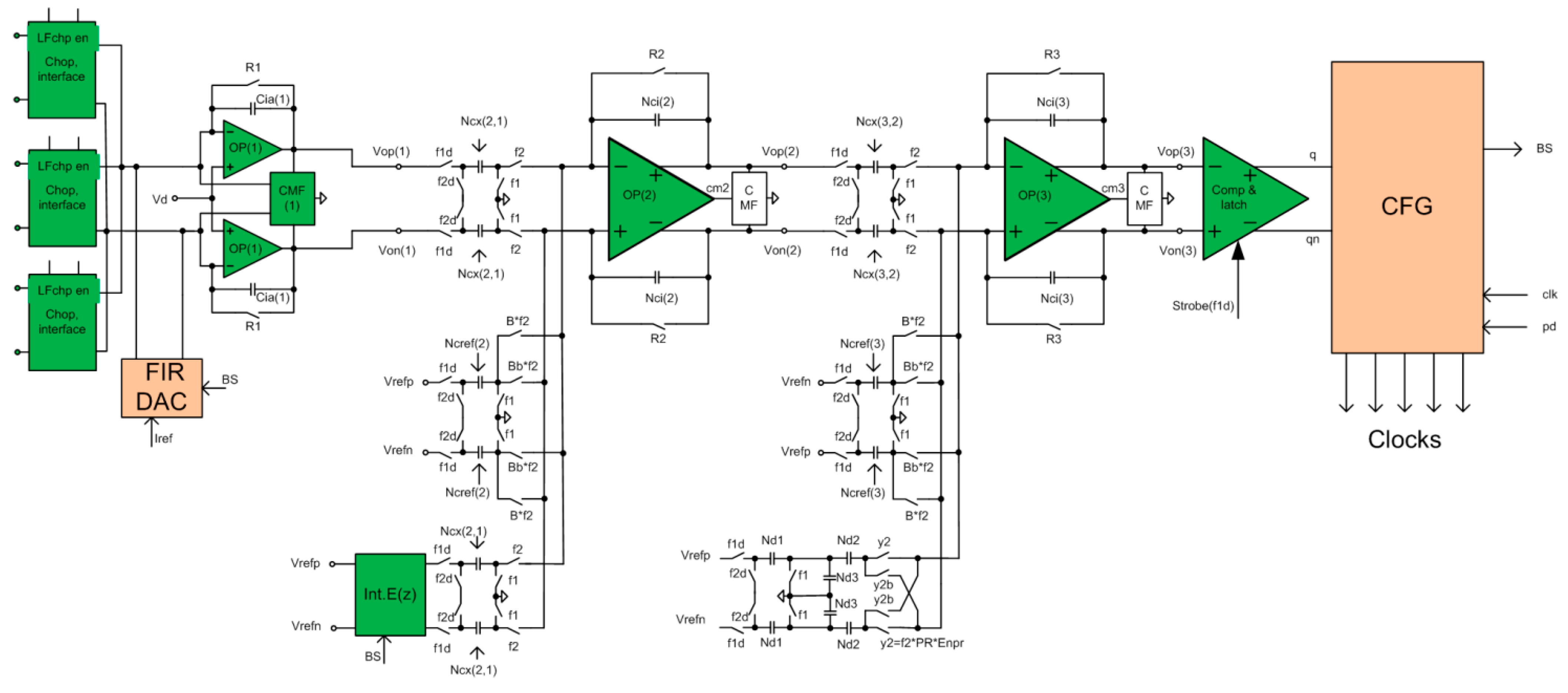
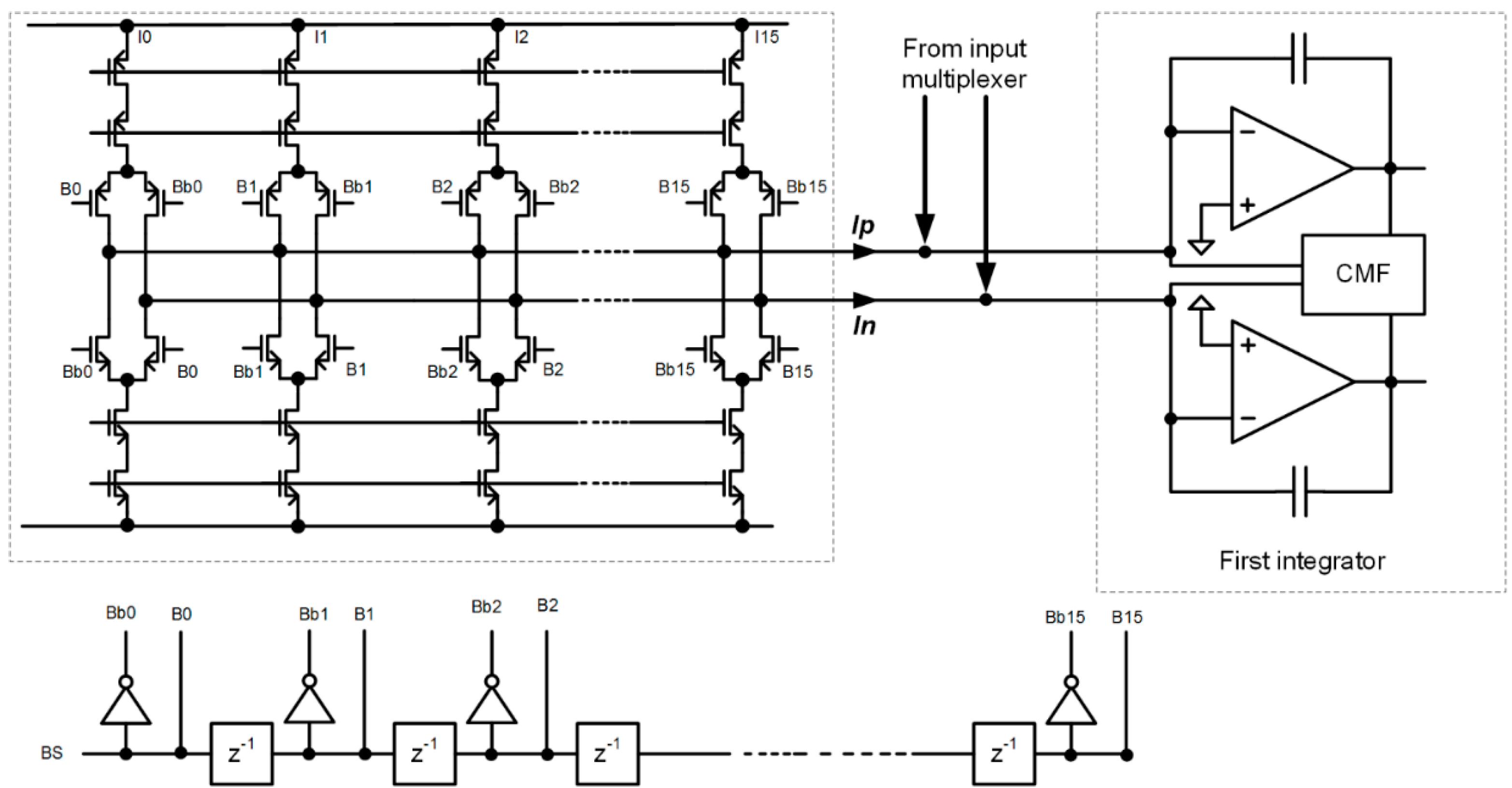
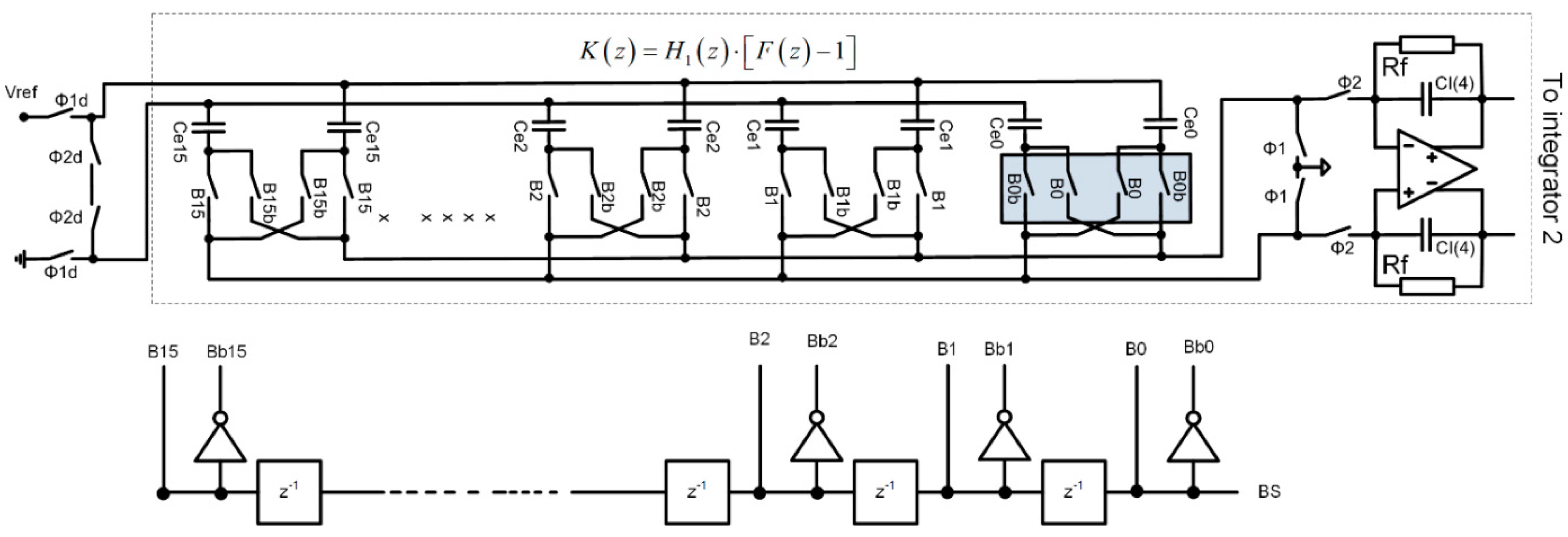
4.2. Modelling and Simulations
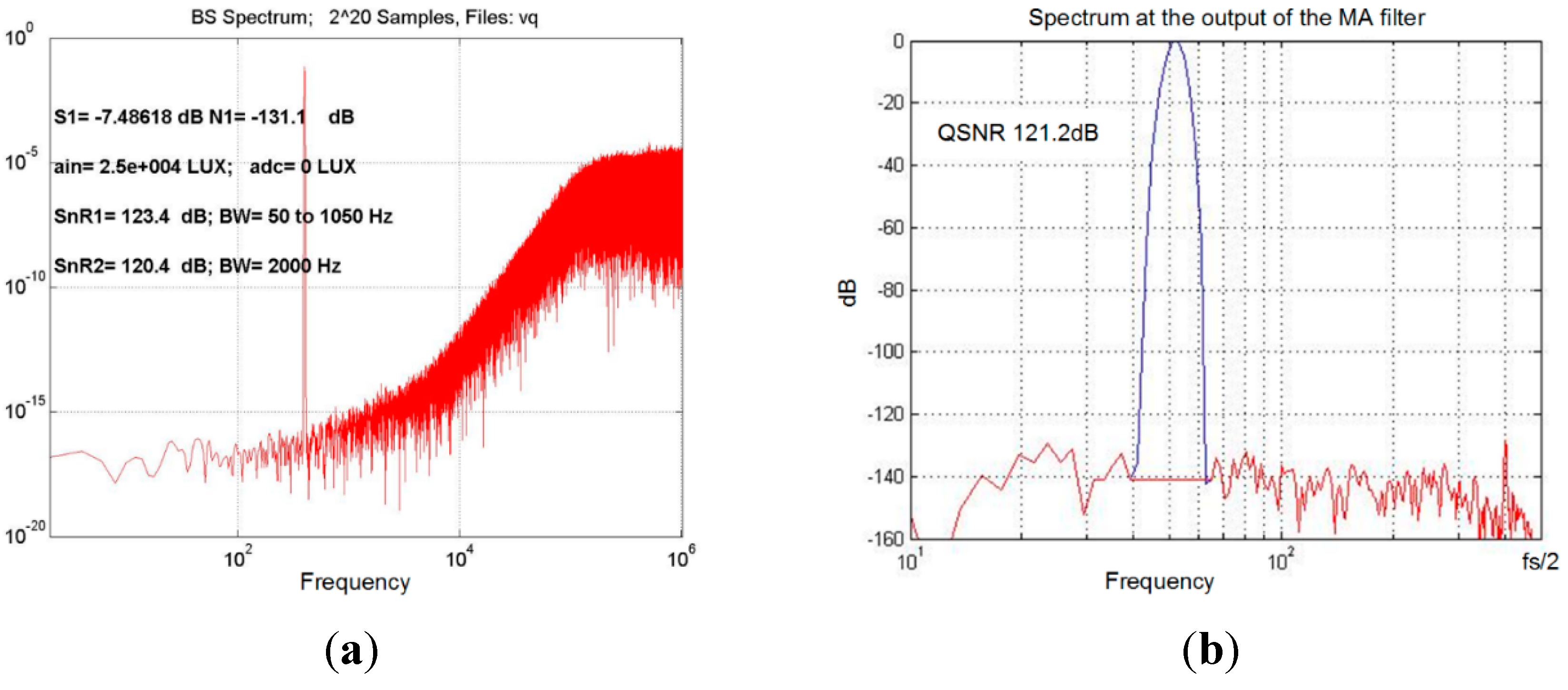
4.3. Circuit Design
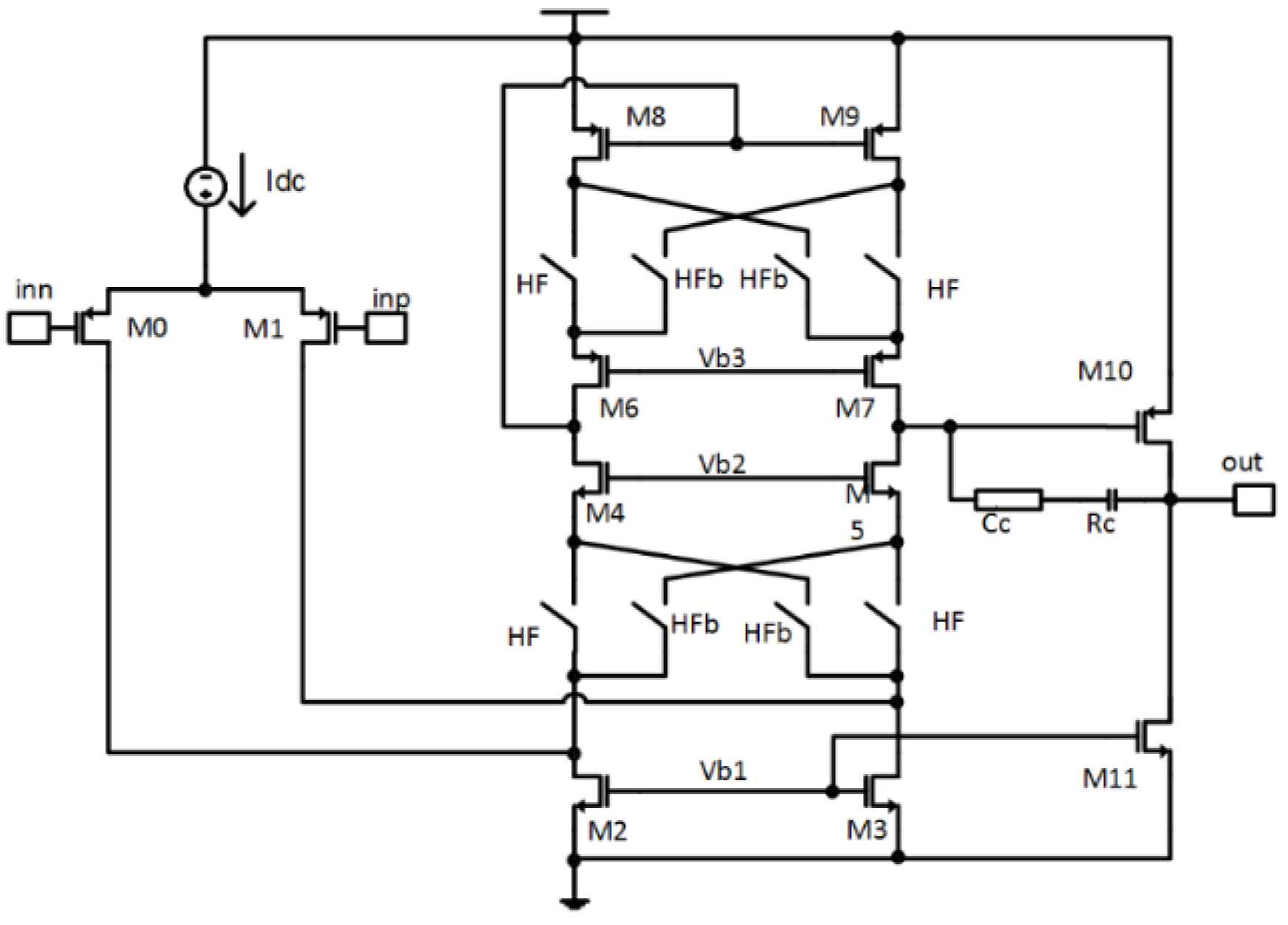
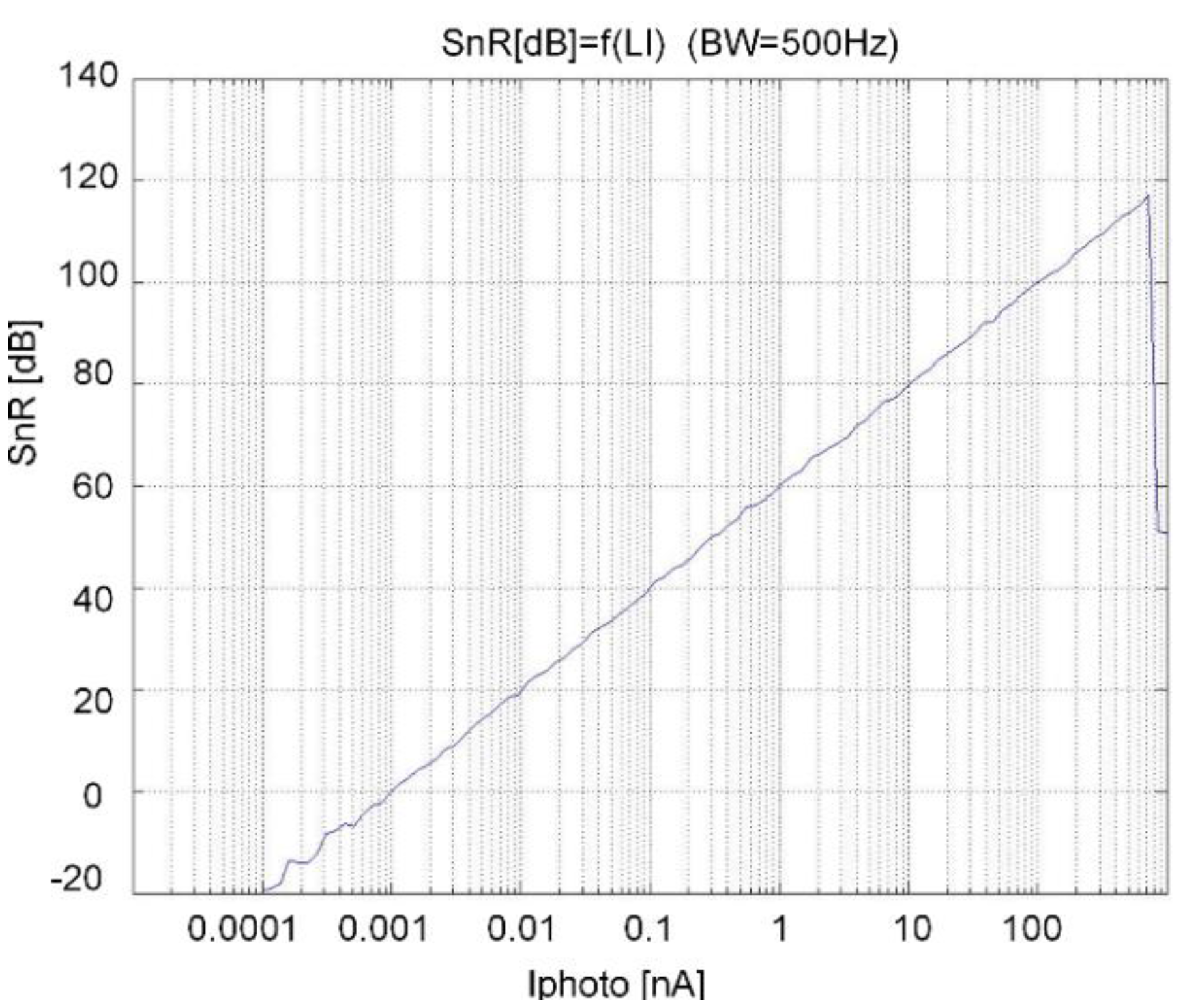
4.4. System and Circuit Simulation Results
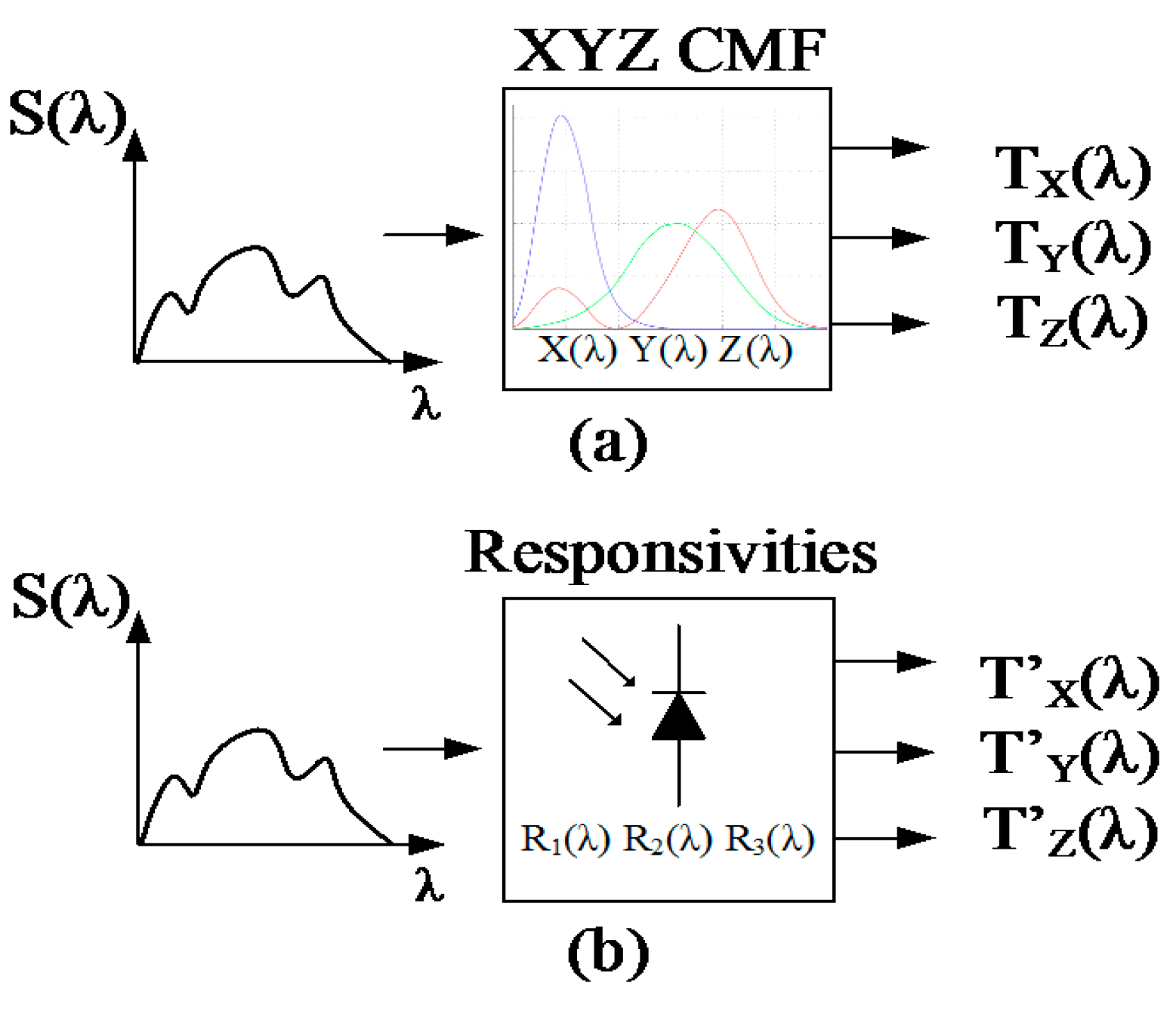
5. Color Signal Processing
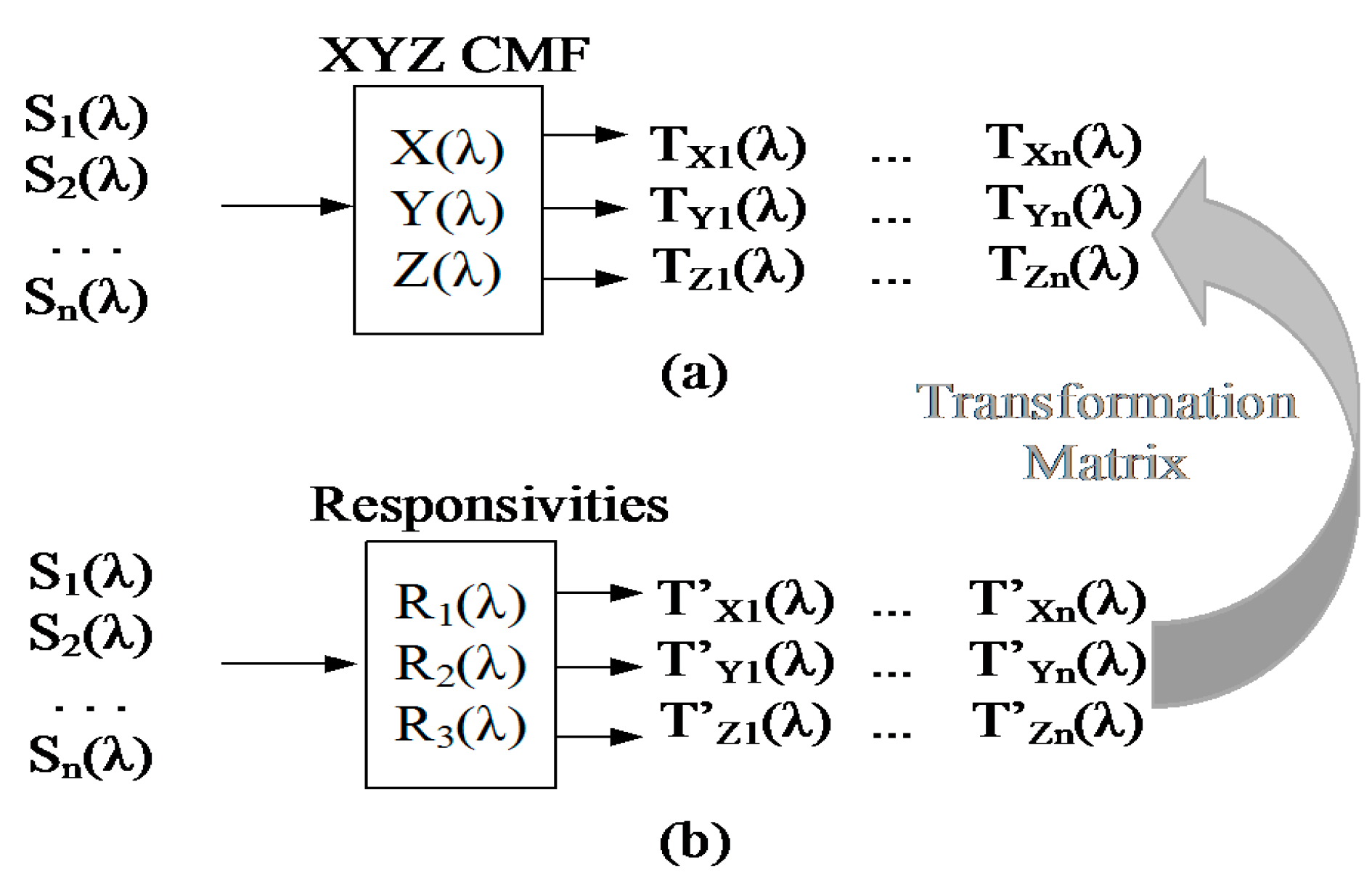
6. Experiments, Measurement Results, and Discussion
6.1. Color Sensor Measurements

| Pn-Junction | Bias Voltage | ||
|---|---|---|---|
| 2 V | 1.5 V | 0 V | |
| P-substrate/N+ lighted | 3.9 pF | 4.2 pF | 6 pF |
| P-substrate/N-well dark | 5.5 pF | 6 pF | 8 pF |
| P-well/N+ | 18 pF | 19.2 pF | 28 pF |
6.2. X,Y,Z Color Transformation
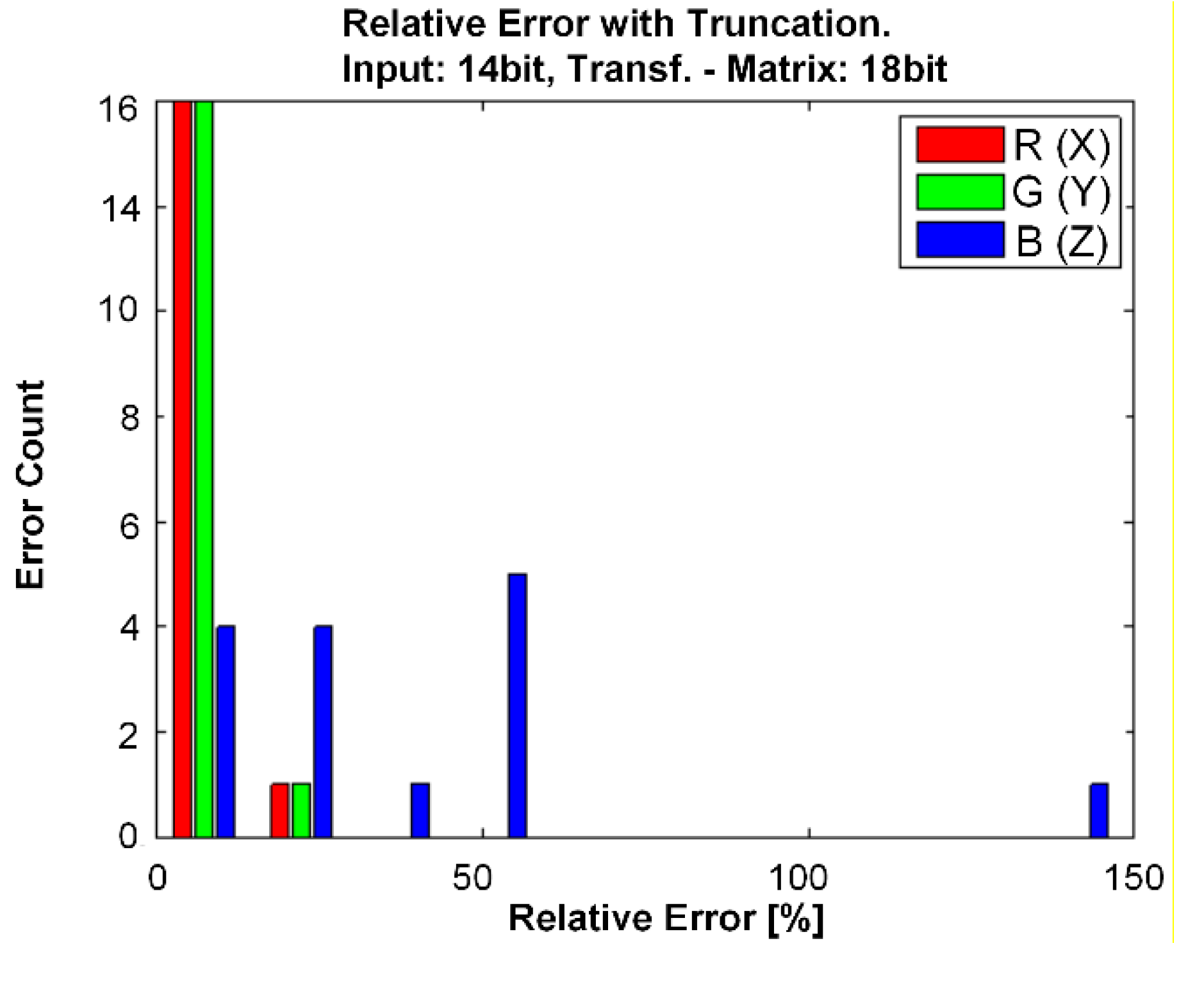
6.3. Measurements of the Photocurrent-to-Digital Converter
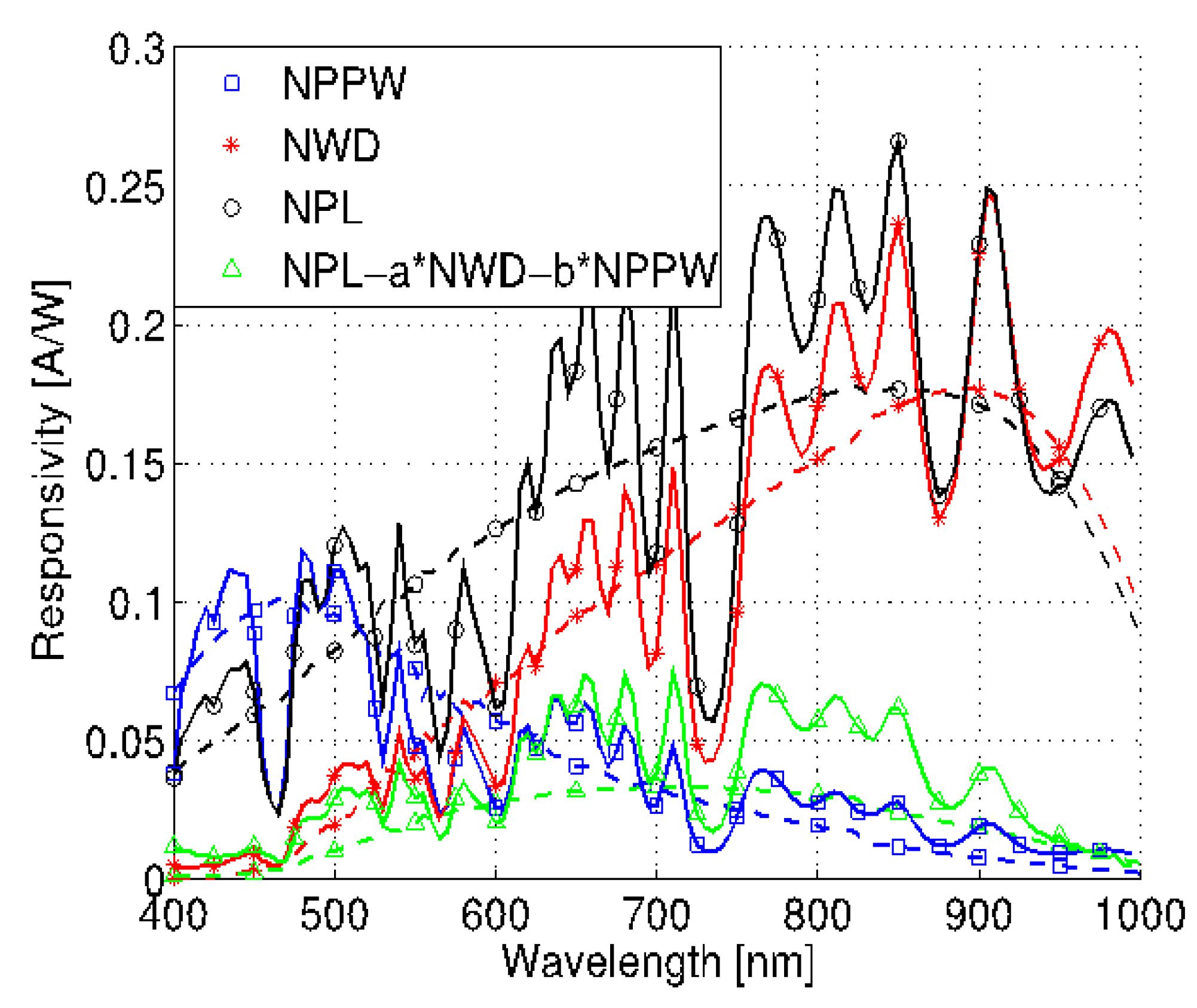
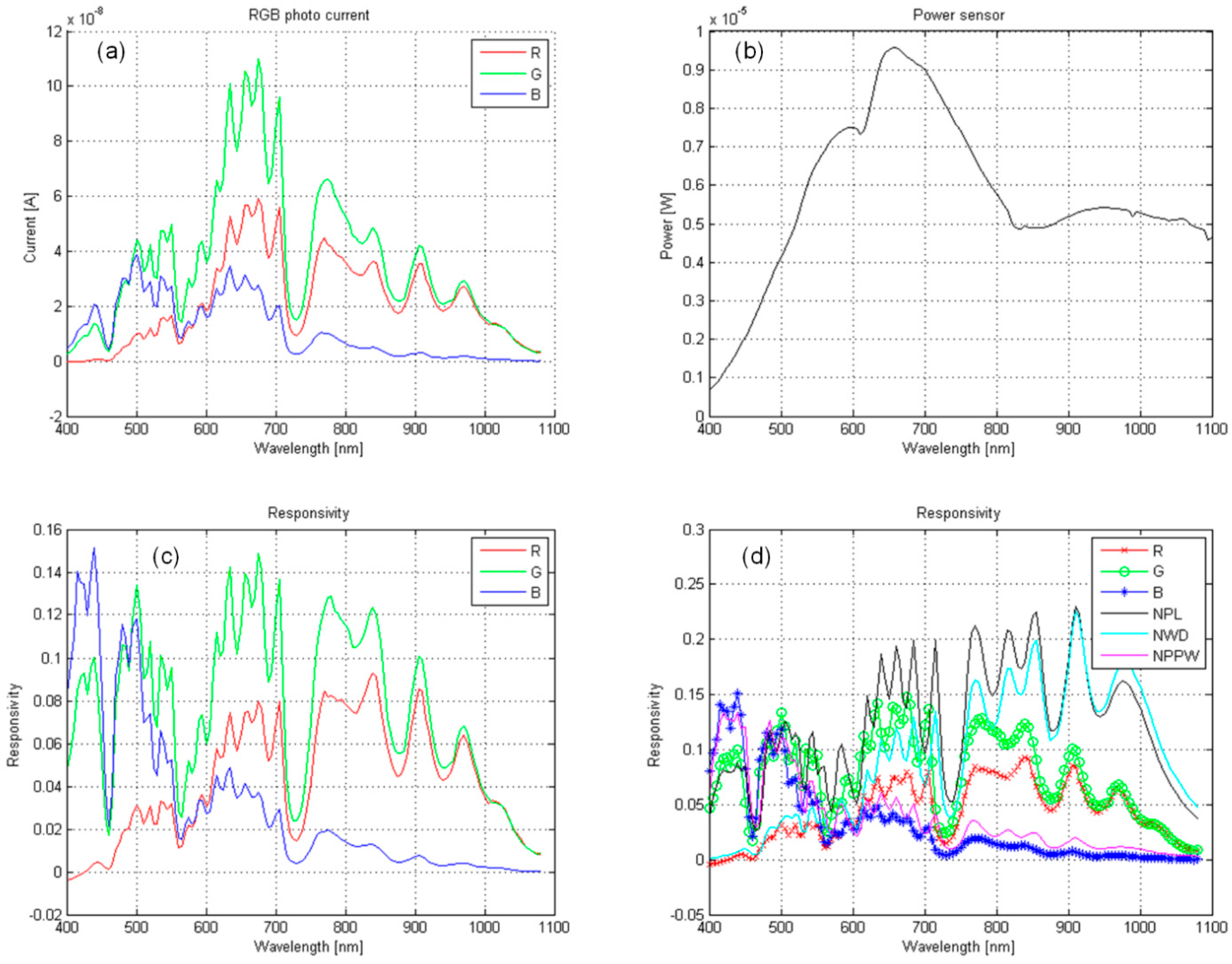
6.4. Integrated Digital Color Sensor Measurements

- (a)
- The photo currents of differently sensitive photo-diodes as a function of the wavelength of the incident light. This is the result of a measurement with the integrated detection system.
- (b)
- Power of the incident light as a function of the wavelength (see Figure 19b).
- (c)
- Responsivity calculated with (P is the incident light power).
- (d)
- The comparison of responsivity: integrated light detection system (lines with symbols) and the optical lab measurement setup, explained in Section 3.2.2.
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- CIE. Commision Internationale de l’E´clairage Proceedings 1924. Cambridge University Press: Cambridge, UK, 1926. [Google Scholar]
- Bayer, B.E. Color Imaging Array. U.S. Patent 3,971,065, 20 July 1976. [Google Scholar]
- Merrill, R.B. Color Separation in an Active Pixel Cell Imaging Array Using a Triple-Well-Structure. U.S. Patent 5,965,875, 12 October 1999. [Google Scholar]
- Sturm, J.; Hainz, S.; Langguth, G.; Zimmermann, H. Integrated photodiodes in standard BiCMOS technology. Proc. SPIE 2003, 4969, 109–110. [Google Scholar]
- Polzer, A.; Gaberl, W.; Zimmermann, H. Filter-less Vertical Integrated RGB Color Sensor for Light Monitoring. In Proceedings of the 34th International Convention IEEE, Opatija, Croatia, 23 May 2011; pp. 55–59.
- Wolffenbuttel, R.F. A simple integrated color indicator. IEEE J. Solid-State Circuits 1987, 22, 350–356. [Google Scholar] [CrossRef]
- Wolffenbuttel, R.F. Integrated all-silicon color filtering element with an enhanced wavelength tunability. IEEE Electron. Dev. Lett. 1988, 9, 337–339. [Google Scholar] [CrossRef]
- Wolffenbuttel, R.F.; de Graaf, G. Performance of an integrated silicon colour sensor with a digital output in terms of response to colours in the colour triangle. Sens. Actuators A Phys. 1990, 22, 574–580. [Google Scholar] [CrossRef]
- Pauchard, A.; Besse, P.A.; Popovic, R.S. A Silicon Blue/UV Selective Stripe-Shaped Photodiode. Sens. Actuators A Phys. 1999, 76, 172–177. [Google Scholar] [CrossRef]
- Langfelder, G. Design of a fully cmos compatible 3-lm size color pixel. Microelectron. Rel. 2010, 50, 169–173. [Google Scholar] [CrossRef]
- Wachowiak, A.; Slesazeck, S.; Jordan, P.; Holz, J.; Mikolajick, T. New color sensor concept based on single spectral tunable photodiode. In Proceedings of the 43rd European Solid-State Device Res. Conference, Bucharest, Rumania, 16–20 September 2013; pp. 127–130.
- Bonfini, G.; Brogna, A.S.; Garbossa, C.; Colombini, L.; Bacci, M.; Chicca, S.; Bigongiari, F.; Guerrini, N.C.; Ferri, G. An ultralow-power switched opamp-based 10-b integrated adc for implantable biomedical applications. IEEE CAS I 2004, 51, 174–178. [Google Scholar] [CrossRef]
- Luschas, S.; Lee, H.S. High-Speed ∑Δ Modulators with Reduced Timing Jitter Sensitivity. IEEE CAS I 2002, 49, 712–720. [Google Scholar] [CrossRef]
- Garcia, J.; Rodriguez, S.; Rusu, A. A low-power CT incremental 3rd order ADC for biosensor applications. IEEE CAS I 2013, 60, 25–36. [Google Scholar]
- Batistell, G.; Sturm, J. Filter-less Color Sensor in Standard CMOS Technology. In Proceedings of the 43rd European Solid-State Device Res. Conference, Bucharest, Rumania, 16–20 September 2013; pp. 123–126.
- Batistell, G.; Sturm, J.; Fant, A.; Strle, D. Color Sensor for Ambient Light Measurements in 130 nm CMOS Technology. In Proceedings of 50th Conference on Microelectronics, Devices and Materials (MIDEM), Ljubljana, Slovenia, 8 October 2014; pp. 104–107.
- Batistell, G.; Zhang, V.C.; Sturm, J. Color recognition sensor in standard cmos technology. Solid-State Electron. 2014, 102, 59–68. [Google Scholar] [CrossRef]
- Findlater, K.M.; Renshaw, D.; Hurwitz, J.E.D.; Henderson, R.K.; Purcell, M.D.; Smith, S.G.; Bailey, T.E.R. A CMOS image sensor with a double-junction active pixel. IEEE Trans. Electron. Devices 2003, 50, 32–42. [Google Scholar] [CrossRef]
- De Graaf, G.; Wolffenbuttel, R.F. Illumination source identification using a cmos optical microsystem. IEEE Trans. Instrum. Meas. 2004, 53, 239–242. [Google Scholar]
- Polzer, A.; Gaberl, W.; Zimmermann, H. Integrated filter-less bicmos sensor for RGB-led color determination. In Proceedings of the IEEE Sensors, Limerick, Ireland, 28 October 2011; pp. 1937–1940.
- Eltoukhy, H.; Salama, K.; El Gamal, A. A 0.18 um CMOS bioluminescence detection lab-on-chip. IEEE JSCC 2006, 41, 651–662. [Google Scholar]
- Schreier, R.; Temes, G.C. Understanding Delta-Sigma Data Converters, 1st ed.John Wiley & Sons: Somerset, NJ, USA, 2005; pp. 86–89. [Google Scholar]
- Delta Sigma Toolbox. Available online: http://www.mathworks.com/matlabcentral/fileexchange/19-delta-sigma-toolbox?s_tid=srchtitle (accessed on 12 April 2010).
- Reddy, K.; Pavan, S. Fundamental limitations of continuous-time delta–sigma modulators due to clock jitter. IEEE CAS I 2007, 54, 2184–2194. [Google Scholar] [CrossRef]
- Strle, D. Mixed-signal Circuits Modelling and Simulations using Matlab. In Engineering Education and Research Using MATLAB; In-Tech: Rijeka, Croatia, 2011; pp. 113–148. [Google Scholar]
- Strle, D.; Raič, D. Advanced Decimator Modeling with a HDL Conversion in Mind. In MATLAB Applications for the Practical Engineer; In-Tech: Rijeka, Croatia, 2014; pp. 397–418. [Google Scholar]
- Sturm, J.; Batistell, G.; Faller, L.M.; Zhang, V.C. Integrated cmos optical sensor for light spectral analysis. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 1–8. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strle, D.; Nahtigal, U.; Batistell, G.; Zhang, V.C.; Ofner, E.; Fant, A.; Sturm, J. Integrated High Resolution Digital Color Light Sensor in 130 nm CMOS Technology. Sensors 2015, 15, 17786-17807. https://doi.org/10.3390/s150717786
Strle D, Nahtigal U, Batistell G, Zhang VC, Ofner E, Fant A, Sturm J. Integrated High Resolution Digital Color Light Sensor in 130 nm CMOS Technology. Sensors. 2015; 15(7):17786-17807. https://doi.org/10.3390/s150717786
Chicago/Turabian StyleStrle, Drago, Uroš Nahtigal, Graciele Batistell, Vincent Chi Zhang, Erwin Ofner, Andrea Fant, and Johannes Sturm. 2015. "Integrated High Resolution Digital Color Light Sensor in 130 nm CMOS Technology" Sensors 15, no. 7: 17786-17807. https://doi.org/10.3390/s150717786
APA StyleStrle, D., Nahtigal, U., Batistell, G., Zhang, V. C., Ofner, E., Fant, A., & Sturm, J. (2015). Integrated High Resolution Digital Color Light Sensor in 130 nm CMOS Technology. Sensors, 15(7), 17786-17807. https://doi.org/10.3390/s150717786