GPS/GLONASS Combined Precise Point Positioning with Receiver Clock Modeling
Abstract
:1. Introduction
2. Mathematical Models
2.1. Functional Model
2.2. Stochastic Model
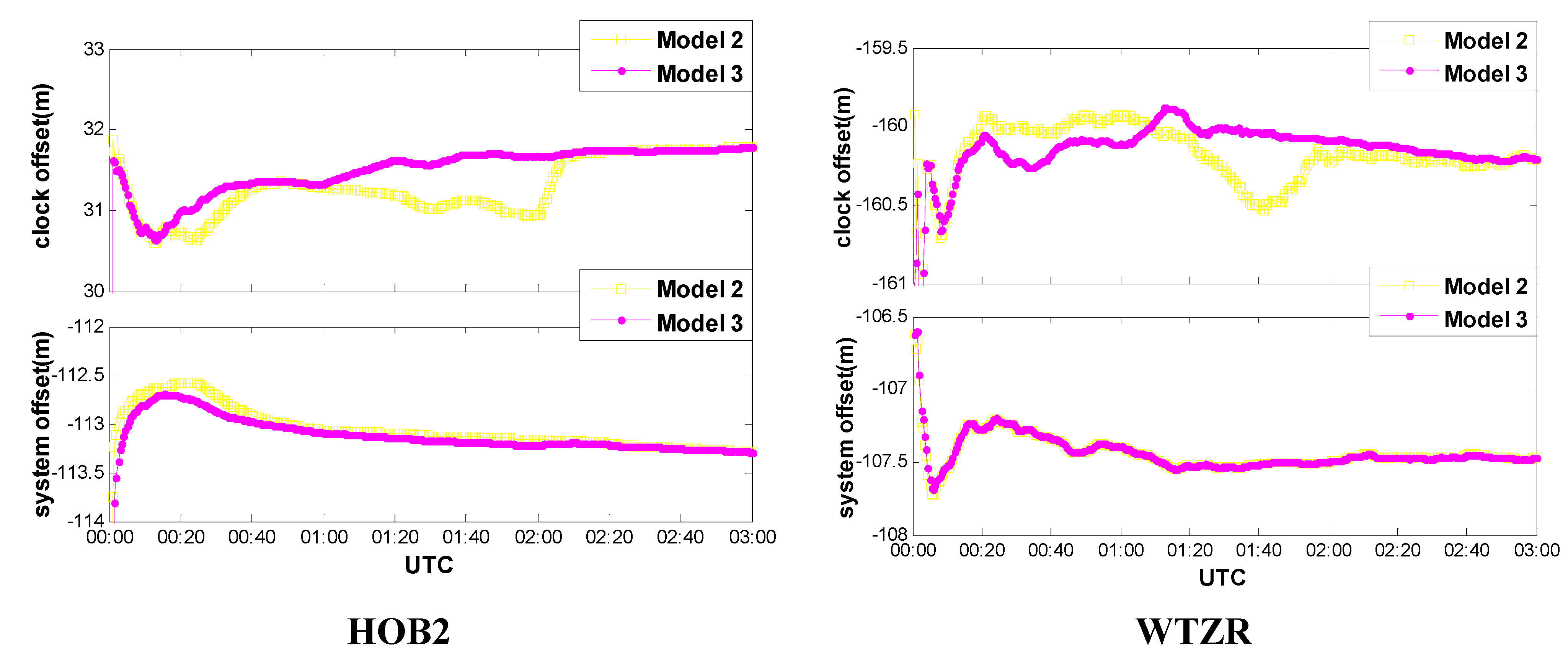
2.3. Receiver Clock Model
3. Performance Evaluations
- Model 1: GPS-only PPP with receiver clock modeling;
- Model 2: GPS/GLONASS PPP without receiver clock modeling;
- Model 3: GPS/GLONASS PPP with receiver clock modeling.
3.1. Accuracy and Reliability Analysis
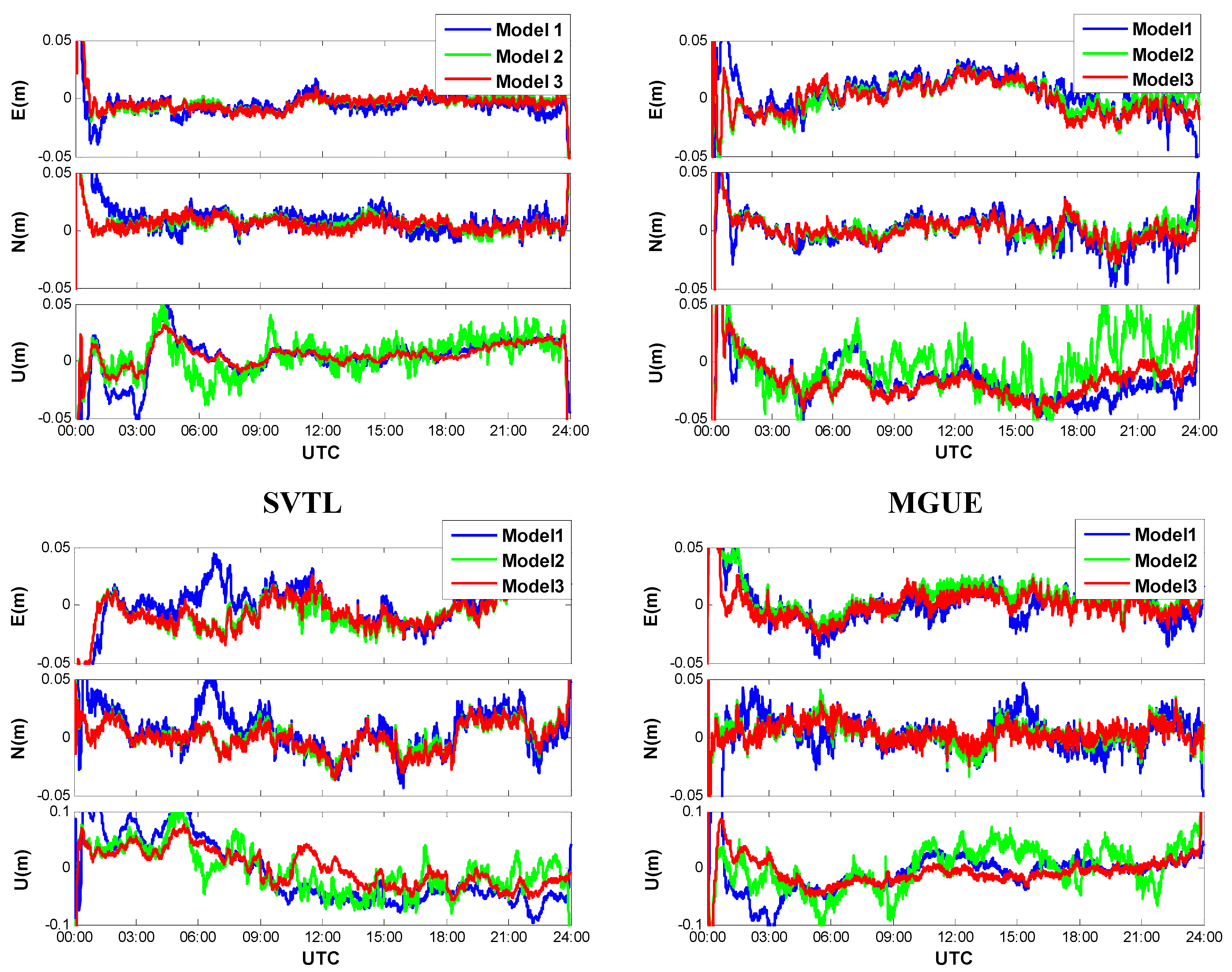
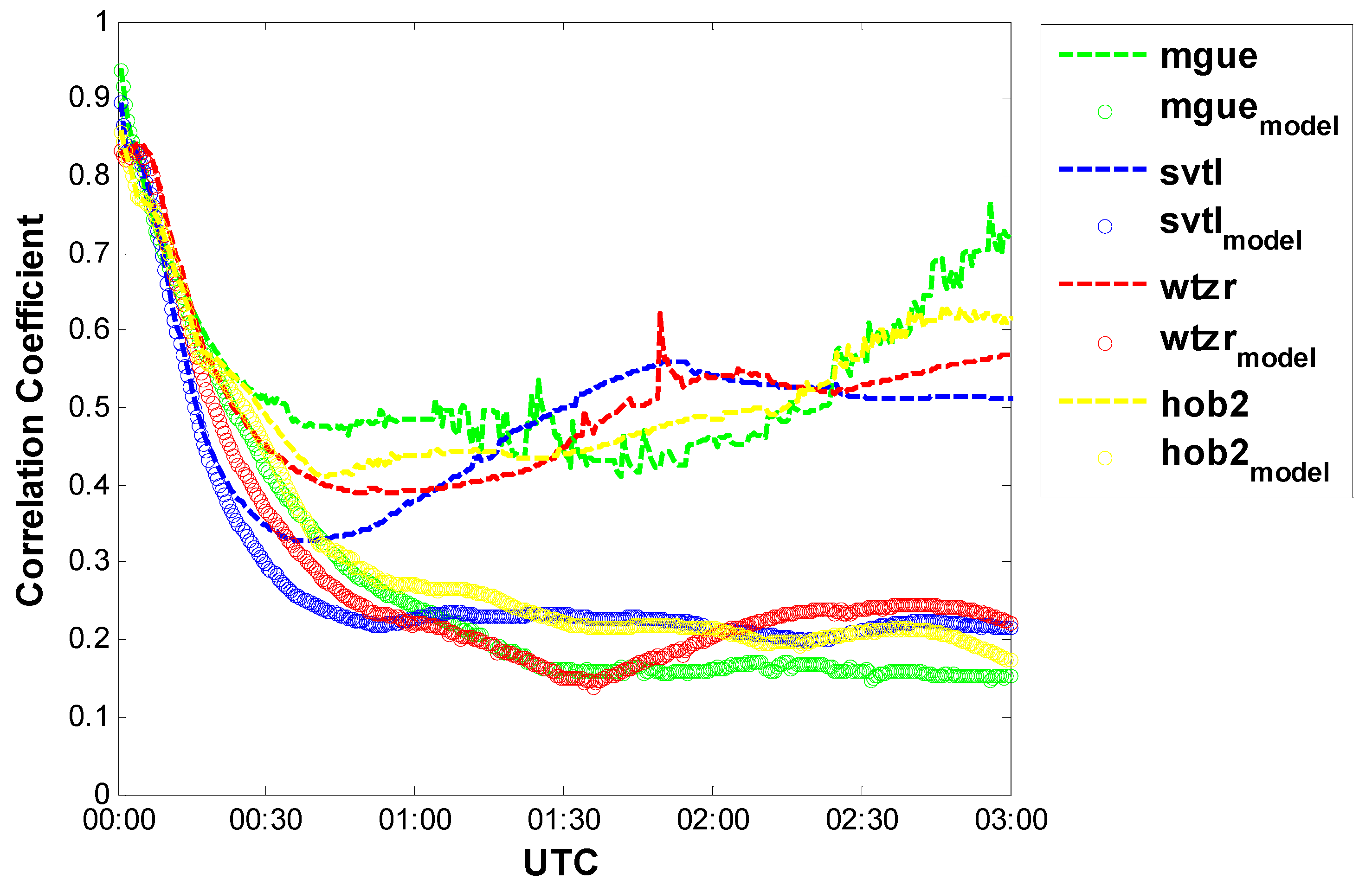
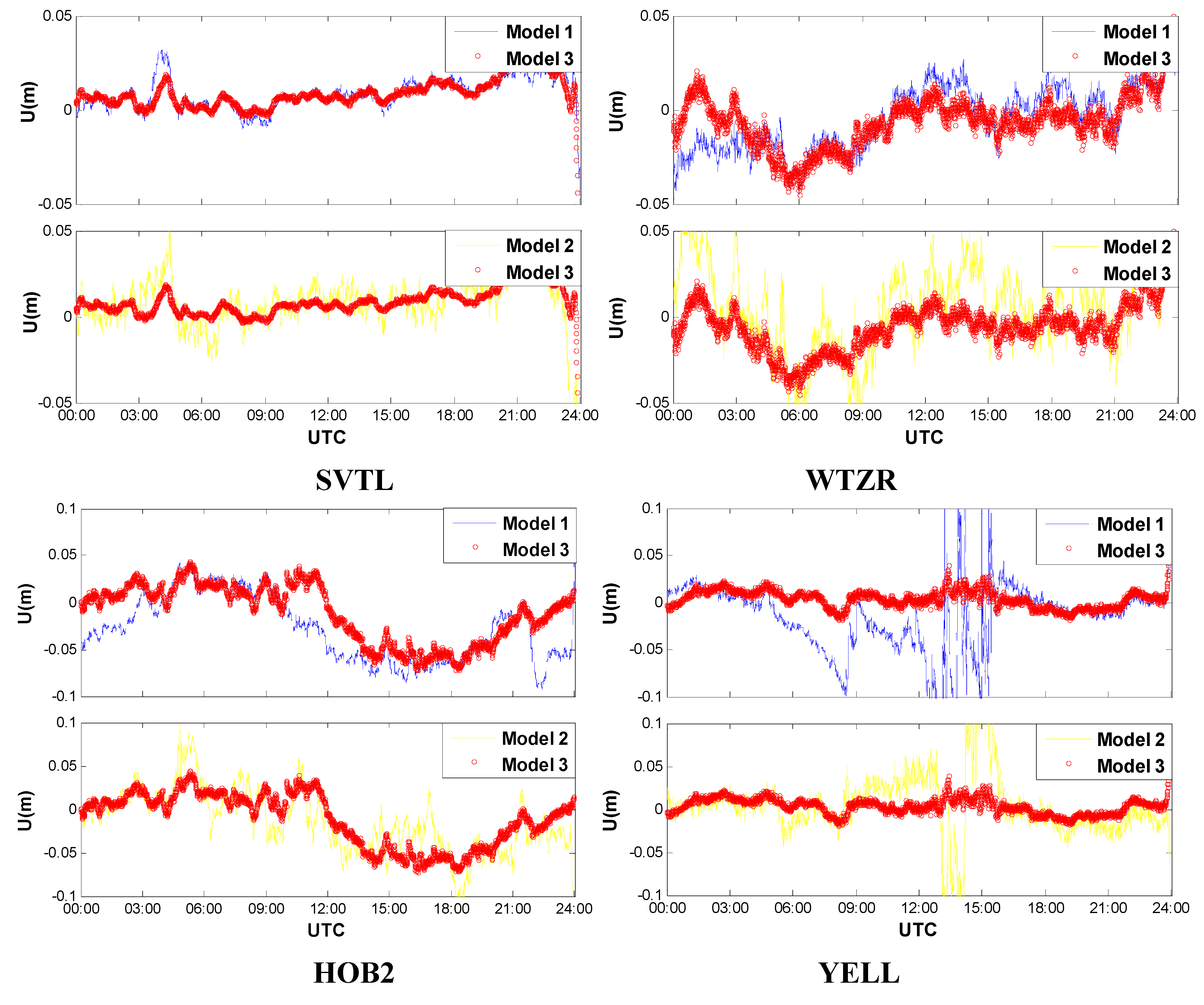
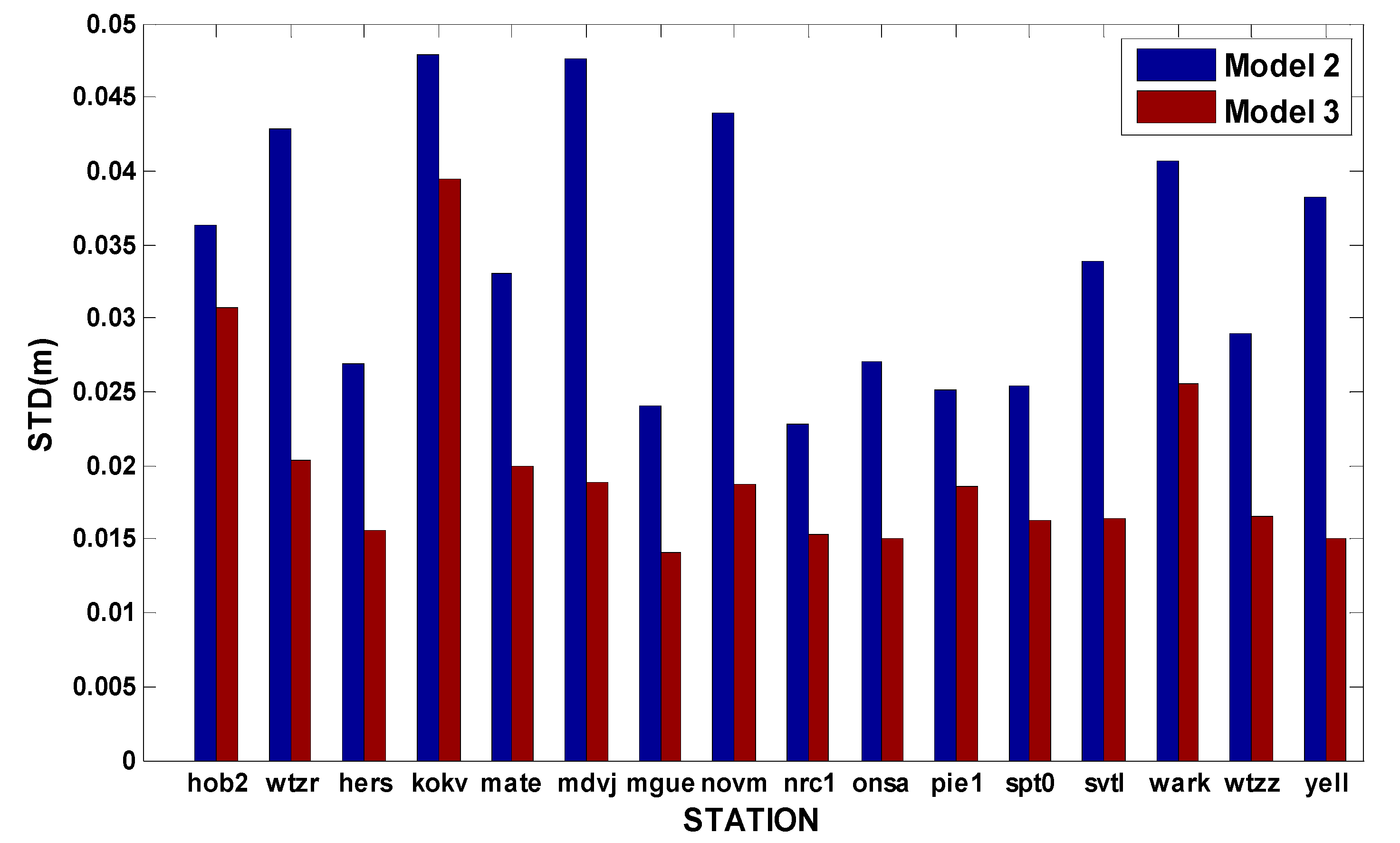
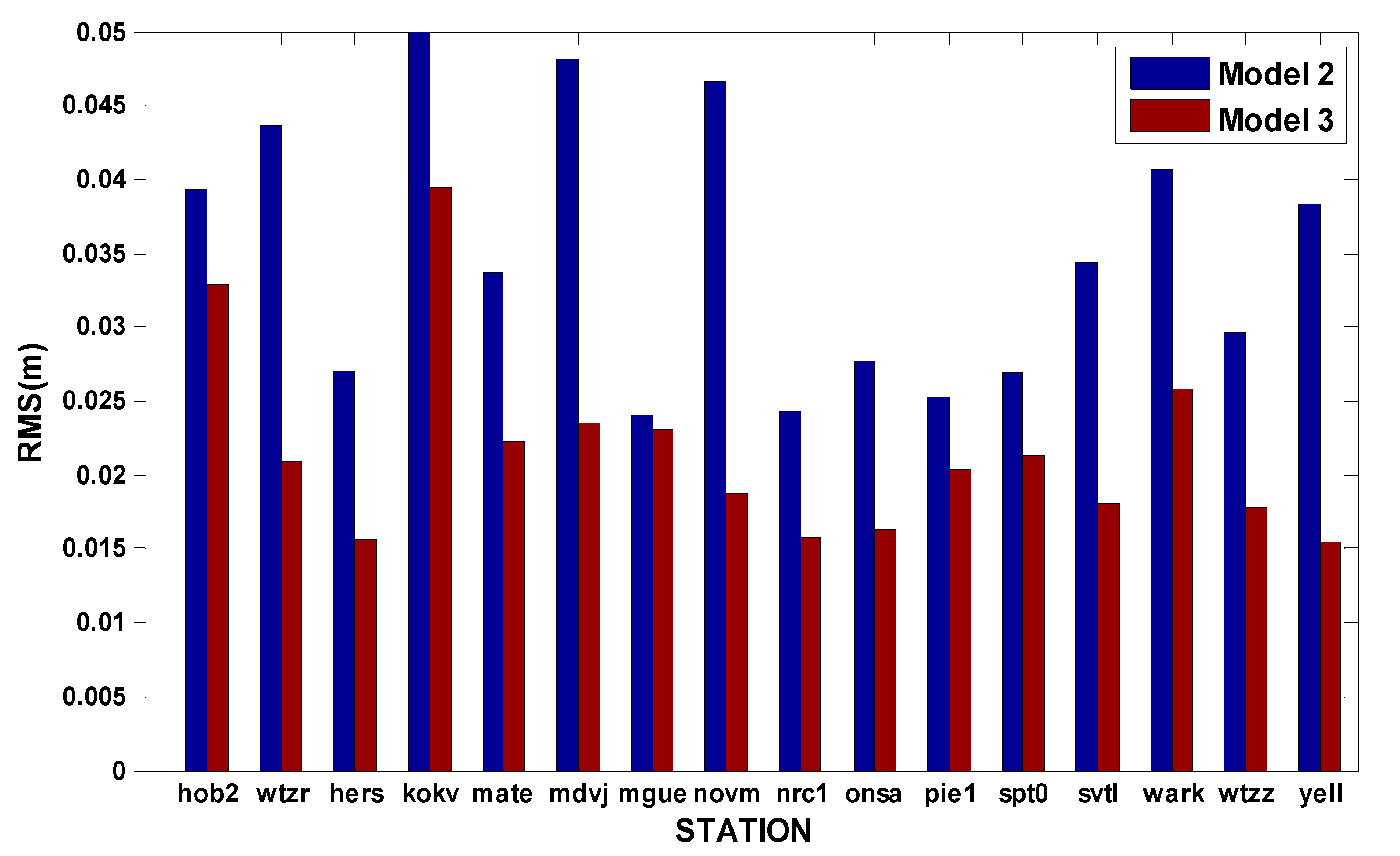
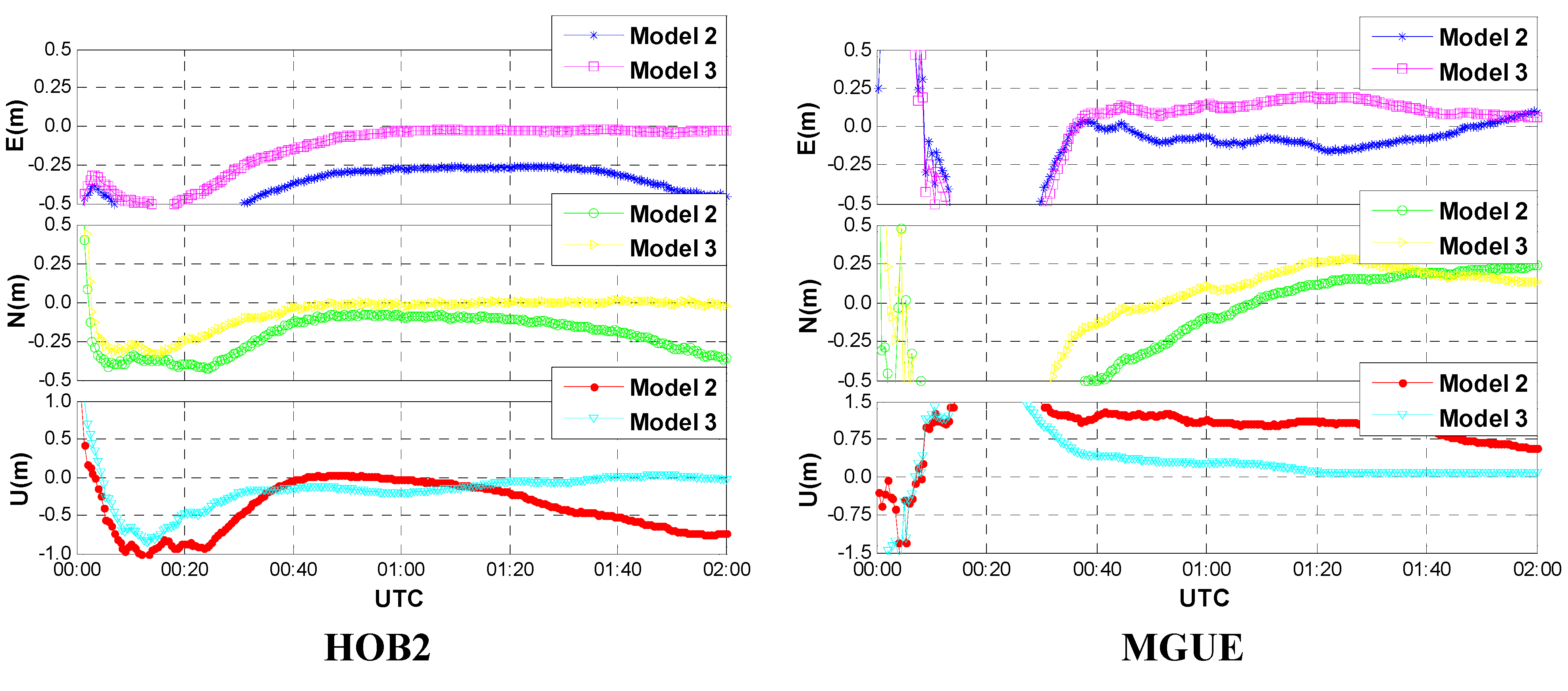
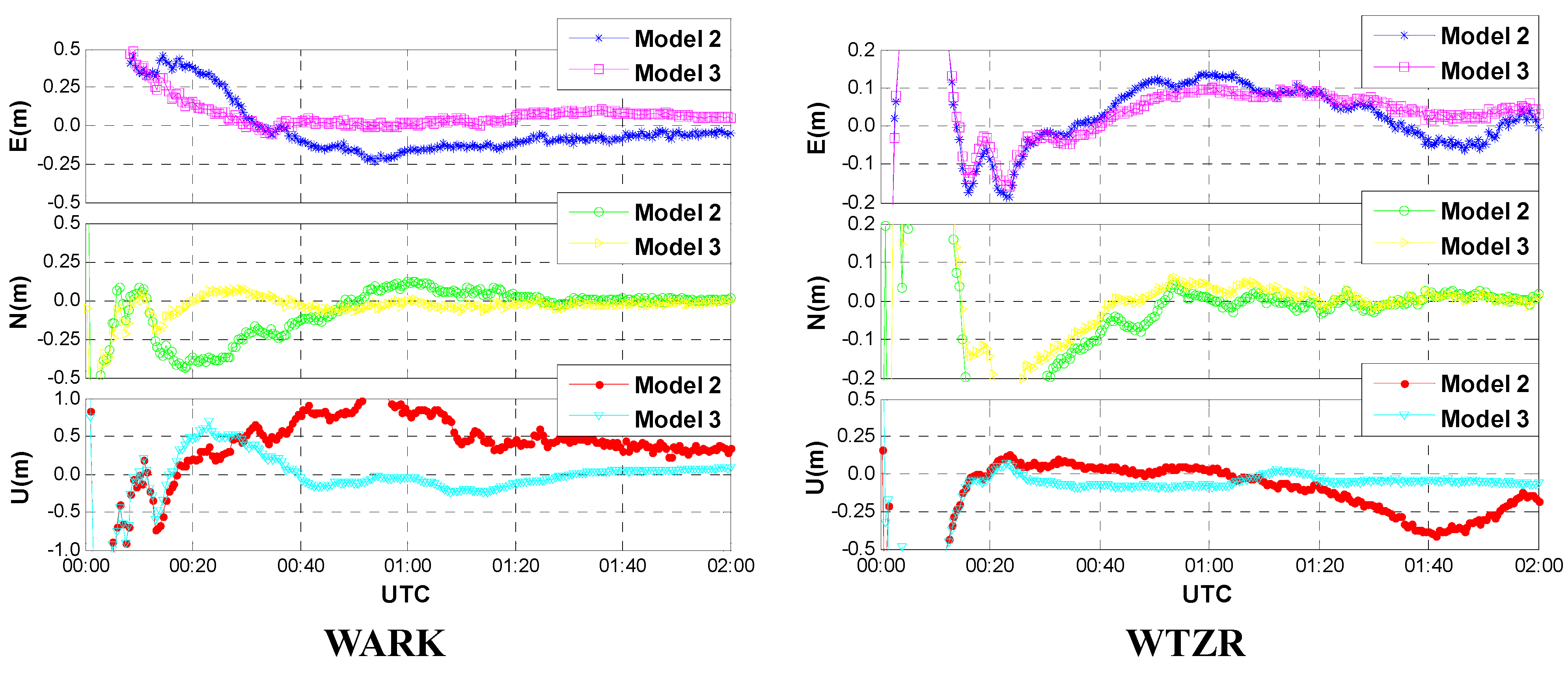
3.2. Convergence Analysis
3.3. Impacts of Different Inter-System Bias Models
- Scheme 1: GPS/GLONASS PPP, the ISB is modeled as constant daily;
- Scheme 2: GPS/GLONASS PPP, the ISB is modeled as white noise process;
- Scheme 3: GPS/GLONASS PPP, the ISB is modeled as random walk process.
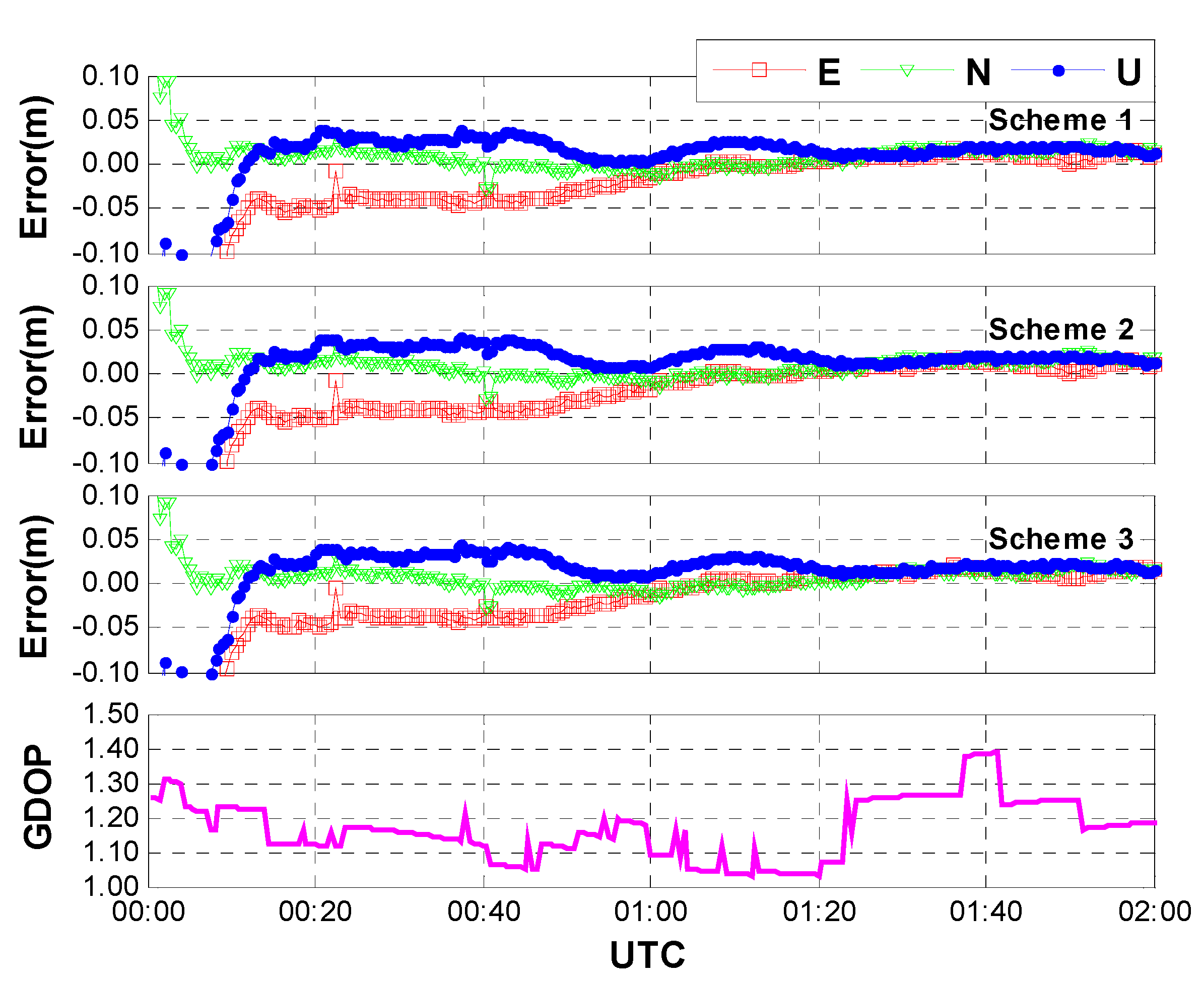
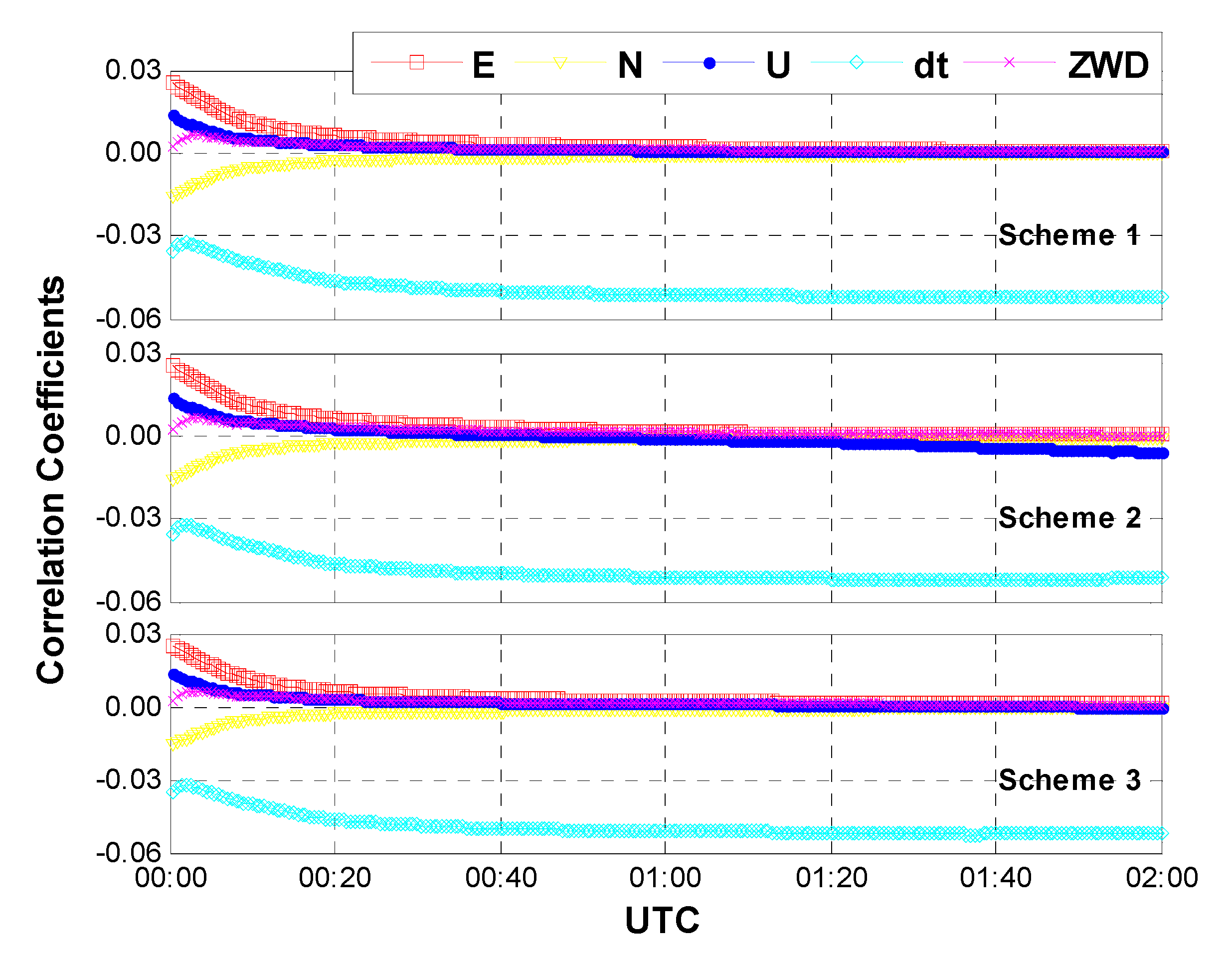
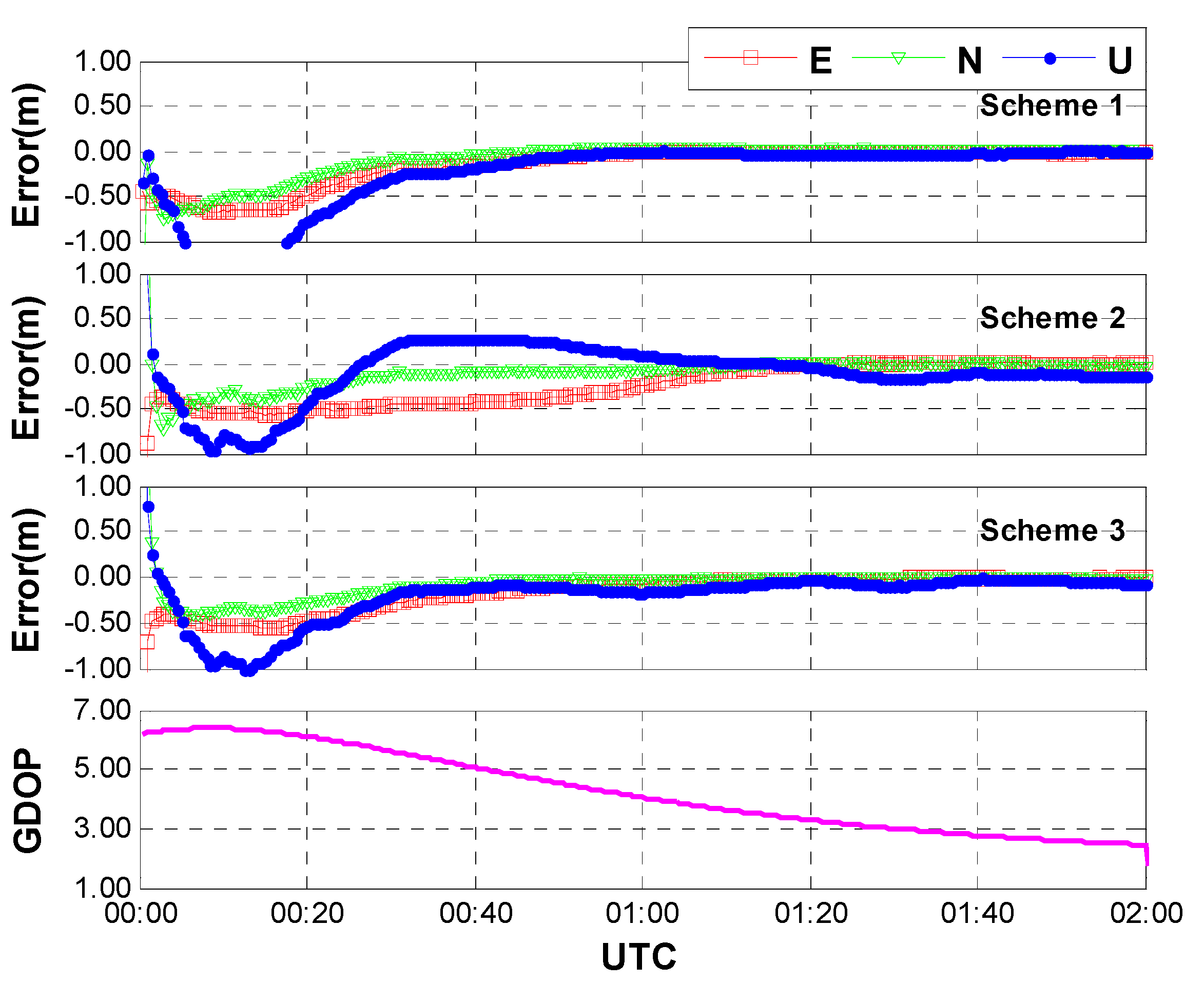
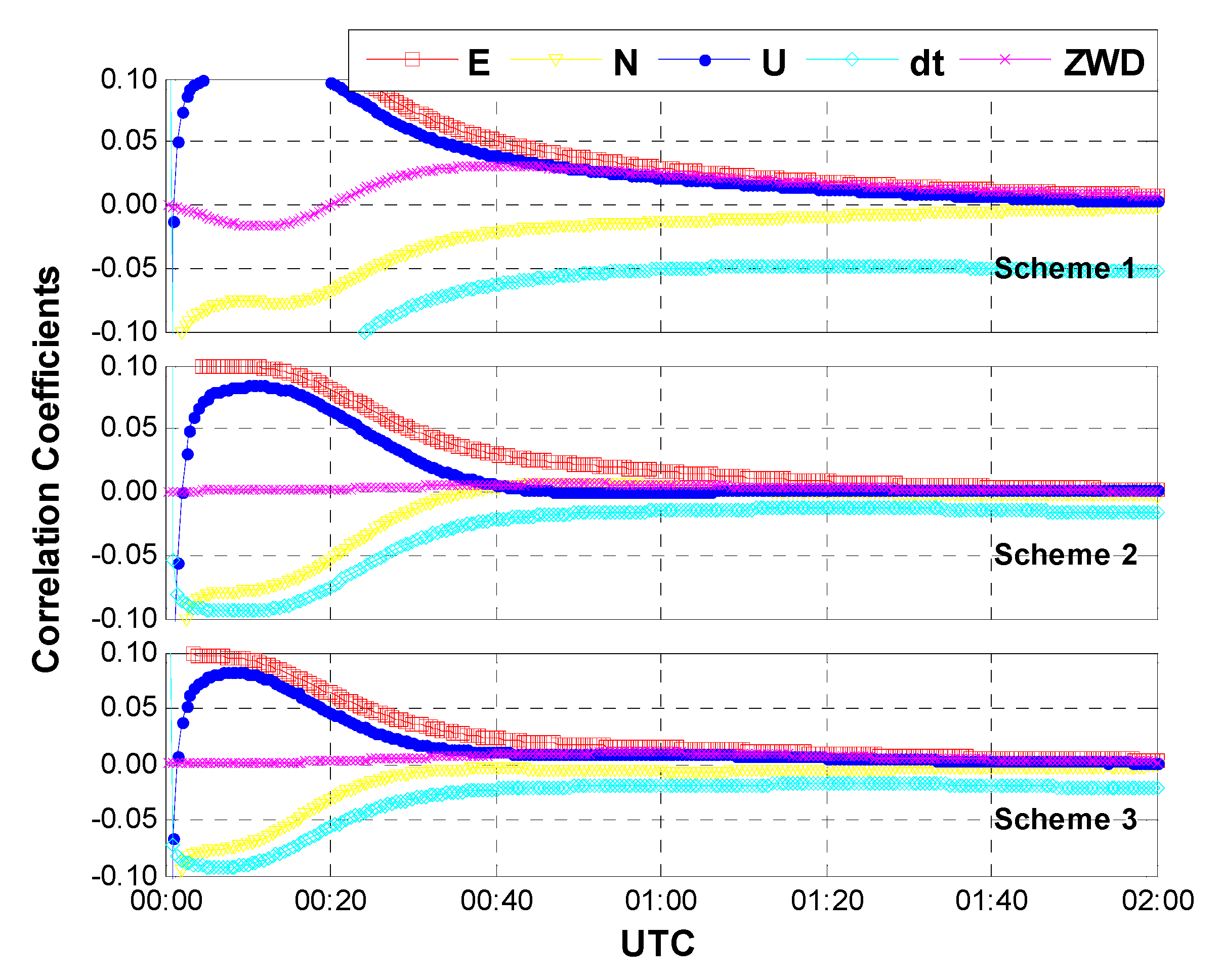
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, X.; Andersen, O.B. Surface ice flow velocity and tide retrieval of the amery ice shelf using precise point positioning. J. Geod. 2006, 80, 171–176. [Google Scholar] [CrossRef]
- Geng, J.; Teferle, F.N.; Meng, X.; Dodson, A.H. Kinematic precise point positioning at remote marine platforms. GPS Solut. 2010, 14, 343–350. [Google Scholar] [CrossRef]
- Xu, P.; Shi, C.; Fang, R.; Liu, J.; Niu, X.; Zhang, Q.; Yanagidani, T. High-rate precise point positioning (PPP) to measure seismic wave motions: An experimental comparison of GPS PPP with inertial measurement units. J. Geod. 2012, 87, 361–372. [Google Scholar] [CrossRef]
- Li, X.; Ge, M.; Zhang, H.; Wickert, J. A method for improving uncalibrated phase delay estimation and ambiguity-fixing in real-time precise point positioning. J. Geod. 2013, 87, 405–416. [Google Scholar] [CrossRef]
- Rabbou, M.A.; El-Rabbany, A. PPP Accuracy Enhancement Using GPS/GLONASS Observations in Kinematic Mode. Positioning 2015, 6, 1. [Google Scholar] [CrossRef]
- Farah, A. Accuracy Assessment Study for Kinematic GPS–PPP Using Single-and Dual-Frequency Observations with Various Software Packages. Arab. J. Sci. Eng. 2015, 1–7. [Google Scholar] [CrossRef]
- Li, X. Precise positioning with current multi-constellation Global Navigation Satellite Systems: GPS, GLONASS, Galileo and BeiDou. Sci. Rep. 2015, 5, 8328. [Google Scholar] [CrossRef] [PubMed]
- Dabove, P.; Ambrogio, M.M. GPS & GLONASS Mass-Market Receivers: Positioning Performances and Peculiarities. Sensors 2014, 14, 22159–22179. [Google Scholar]
- Kouba, J.; Héroux, P. Precise point positioning using IGS orbit and clock products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Weinbach, U.; Schőn, S. Improved GRACE kinematic orbit determination using GPS receiver clock modeling. GPS Solut. 2013, 17, 511–520. [Google Scholar] [CrossRef]
- Lichten, S.M.; Border, J.S. Strategies for high-precision global positioning system orbit determination. J. Geophys. Res. Solid Earth 1987, 92, 12751–12762. [Google Scholar] [CrossRef]
- Orliac, E.; Dach, R.; Voithenleitner, D.; Hugentobler, U.; Wang, K.; Rothacher, M.; Svehla, D. Clock modeling for GNSS applications. In Proceedings of the AGU Fall Meeting, San Francisco, CA, USA, 5–9 December 2011.
- Orliac, E.; Dach, R.; Wang, K.; Rothacher, M.; Hugentobler, U.; Voithenleitner, D.; Heinze, M.; Svehla, D. Impact of code and phase biases and clock modeling on ambiguity resolution. In Proceedings of the AGU Fall Meeting, San Francisco, CA, USA, 5–9 December 2012.
- Yang, Y.; Yue, X.K.; Yuan, J.P.; Rizos, C. Enhancing the kinematic precise orbit determination of low earth orbiters using GPS receiver clock modeling. Adv. Space Res. 2014, 54, 1901–1912. [Google Scholar] [CrossRef]
- Weinbach, U.; Schőn, S. GNSS receiver clock modeling when using high-precision oscillators and its impact on PPP. Adv. Space Res. 2011, 47, 229–238. [Google Scholar] [CrossRef]
- Wang, K.; Rothacher, M. Stochastic modeling of high-stability ground clocks in GPS analysis. J. Geod. 2013, 87, 427–437. [Google Scholar] [CrossRef]
- Hefty, J.; Gerhatova, L. Experience from combination of GPS and GLONASS observations in the Precise Point Positioning algorithms. In Proceedings of the EGU General Assembly, Vienna, Austria, 2–7 May 2010.
- Azab, M.; El-Rabbany, A.; Shoukry, M.N.; Khalil, R. Precise point positioning using combined GPS/GLONASS measurements. In Proceedings of the International Federation of Surveyors, Copenhagen, Denmark, 18–22 May 2011.
- Dai, L.; Hatch, R. Integrated StarFire GPS with GLONASS for real-time precise navigation and positioning. In Proceedings of the ION GNSS, Portland, OR, USA, 19–23 September 2011.
- Pei, X.; Chen, J.; Wang, J.; Zhang, Y.; Li, H. Application of inter-system hardware delay bias in GPS/GLONASS PPP. In Proceedings of the CSNC 2012 Proceedings Lecture Notes in Electrical Engineering Volume 160, Guangzhou, China, 15–19 May 2012.
- Anquela, A.B.; Martίn, A.; Berné, J.L.; Padίn, J. GPS and GLONASS static and kinematic PPP results. J. Surv. 2013, 139, 47–58. [Google Scholar] [CrossRef]
- Cai, C.; Gao, Y. Modeling and assessment of combined GPS/GLONASS precise point positioning. GPS Solut. 2013, 17, 223–236. [Google Scholar] [CrossRef]
- Héroux, P.; Kouba, J. GPS Precise Point Positioning using IGS orbit products. Phys. Chem. Earth Part A Solid Earth Geol. 2001, 26, 573–578. [Google Scholar] [CrossRef]
- Abdel-Salam, M.A. Precise Point Positioning Using Un-Differenced Code and Carrier Phase Observations. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2005. [Google Scholar]
- Allan, D.W. Time and frequency (time-domain) characterization, estimation and prediction of precision clocks and oscillators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1987, 34, 647–654. [Google Scholar] [CrossRef] [PubMed]
- Brown, R.G.; Hwang, P.Y.C. Introduction to Random Signals and Applied Kalman Filtering, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2005; pp. 430–431. [Google Scholar]
- Herring, T.A.; Davis, J.L.; Shapiro, I.I. Geodesy by radio interferometry: The application of Kalman filtering to the analysis of very long baseline interferometry data. J. Geophys. Res. 1990, 95, 12561–12581. [Google Scholar] [CrossRef]
- Weinbach, U. Feasibility and Impact of Receiver Clock Modeling in Precise GPS Data Analysis. Ph.D. Thesis, Gottfried Wilhelm Leibniz Universität Hannover, Hannover, Germany, 2013. [Google Scholar]
- Dow, J.M.; Neilan, R.E.; Rizos, C. The International GNSS Service in a changing landscape of Global Navigation Satellite Systems. J. Geod. 2009, 83, 191–198. [Google Scholar] [CrossRef]
- Angrisano, A.; Gaglione, S.; Gioia, C. Performance assessment of GPS/GLONASS single point positioning in an urban environment. Acta Geod. Geophys. 2013, 48, 149–161. [Google Scholar] [CrossRef]
- Cai, C.; Gao, Y. A combined GPS/GLONASS navigation algorithm for use with limited satellite visibility. J. Navig. 2009, 62, 671–685. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Chen, X.; Guo, F. GPS/GLONASS Combined Precise Point Positioning with Receiver Clock Modeling. Sensors 2015, 15, 15478-15493. https://doi.org/10.3390/s150715478
Wang F, Chen X, Guo F. GPS/GLONASS Combined Precise Point Positioning with Receiver Clock Modeling. Sensors. 2015; 15(7):15478-15493. https://doi.org/10.3390/s150715478
Chicago/Turabian StyleWang, Fuhong, Xinghan Chen, and Fei Guo. 2015. "GPS/GLONASS Combined Precise Point Positioning with Receiver Clock Modeling" Sensors 15, no. 7: 15478-15493. https://doi.org/10.3390/s150715478
APA StyleWang, F., Chen, X., & Guo, F. (2015). GPS/GLONASS Combined Precise Point Positioning with Receiver Clock Modeling. Sensors, 15(7), 15478-15493. https://doi.org/10.3390/s150715478




