A Rapid Method to Achieve Aero-Engine Blade Form Detection
Abstract
:1. Introduction
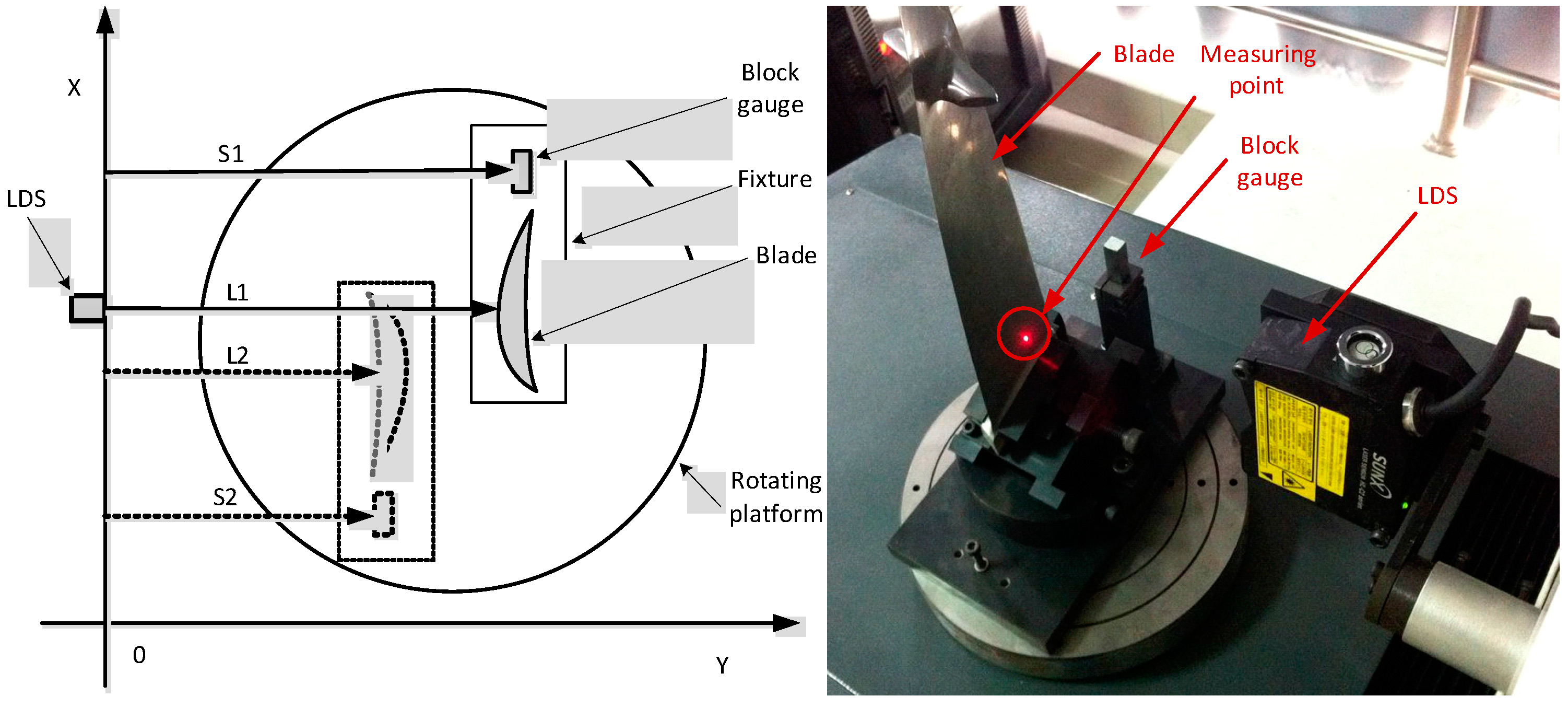
2. The Blade Measurement System
2.1. Laser Displacement Sensor

| Names | Specifications |
|---|---|
| Model No. | HL-C211BE |
| Installation Mode | Diffuse Reflection |
| Measurement center distance | 110 mm |
| Measuring range | ±15 mm |
| Linearity | ±0.03% F.S. |
| Beam diameter | 80 μm |
| Repeatability | 0.1 μm |
| Resolution | 0.25 um |
| Temperature characteristics | 0.01% F.S./°C |
2.2. Measurement Mechanism Features and Parameters

| Name | X | Y | Z | Rotary Table (W) |
|---|---|---|---|---|
| Measuring range | 220 mm | 180 mm | 360 mm | 360° |
| Velocity | 8~15 mm/s | 8~15 mm/s | 8~15 mm/s | 3~15 Rev/min |
| Straightness | 0.6 μm | 0.4 μm | 0.6 μm | Rotation 0.3 μm |
| Axis Misalignment | 6"/200 mm | 7"/200 mm | 6"/200 mm | Runout ≤ 0.5 μm |
| Perpendicularity | 1.6 μm | 1 μm | 1.8 μm | 0.5 μm |
| Overall accuracy | ≤2 μm | |||
| Carrying | ≥50 Kg | |||

2.3. Control System Principles

3. Laser Triangulation Principle and Inclination Error Compensation Model
3.1. Laser Triangulation Principle
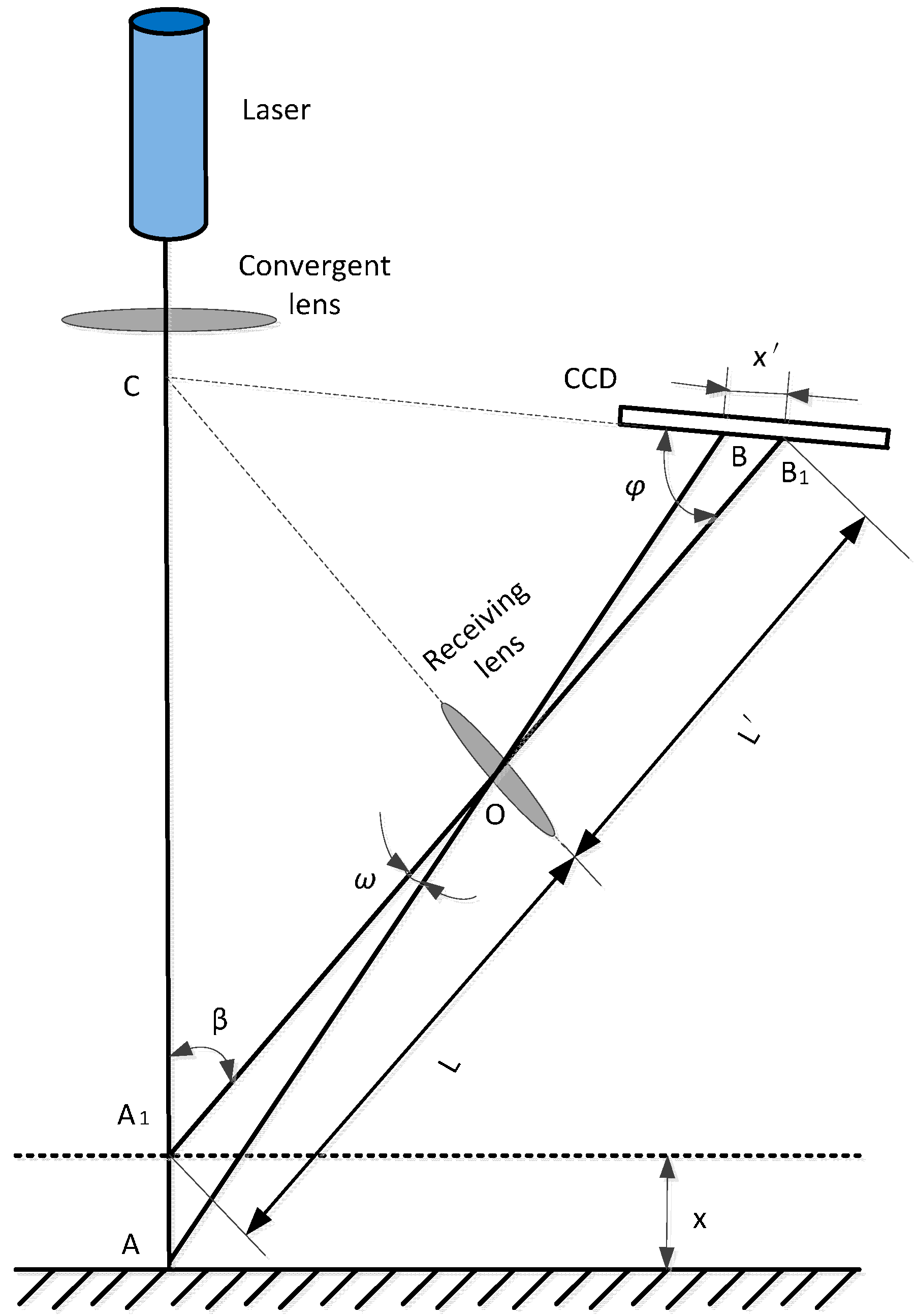
3.2. Inclination Error Model
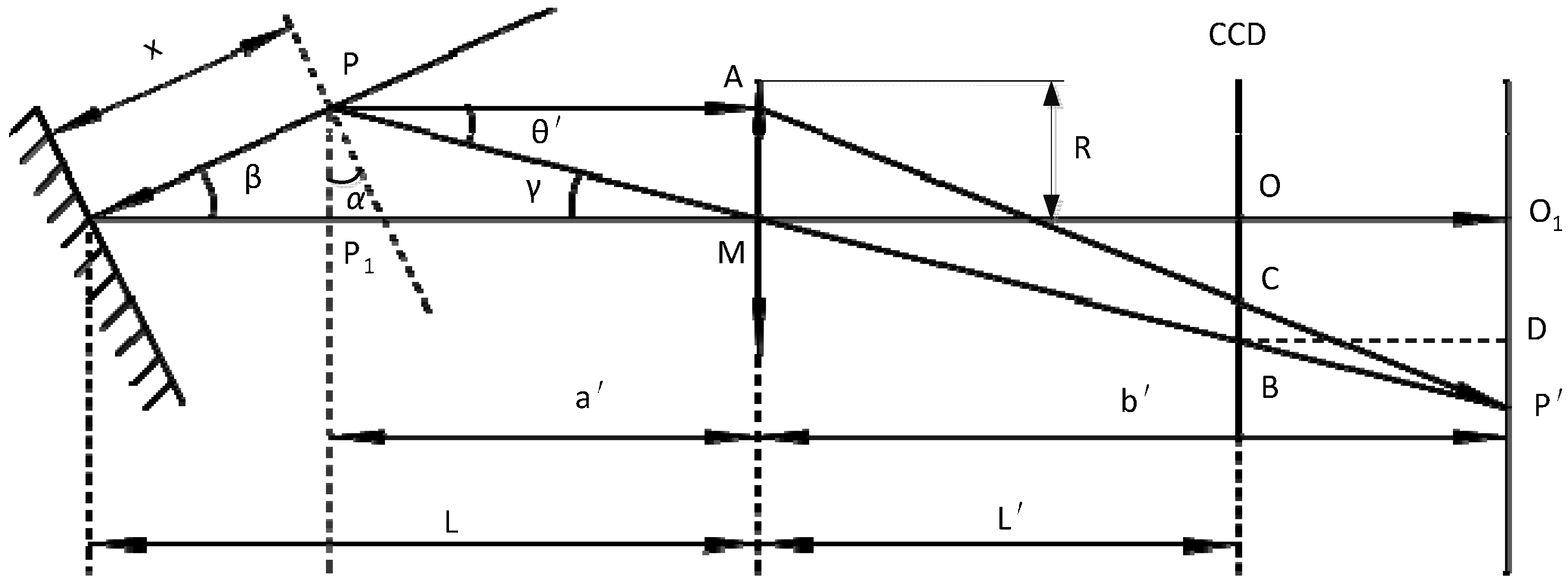
- When the object surface inclination α is constant, the measurement error Eα increases with increasing depth of field measurements;
- When the displacement x of the object is constant, the measurement error Eα increases with increasing body surface angle increases;
- When , direction of the error is the same with the direction of displacement; When , direction of the error is the same displacement in the opposite direction;
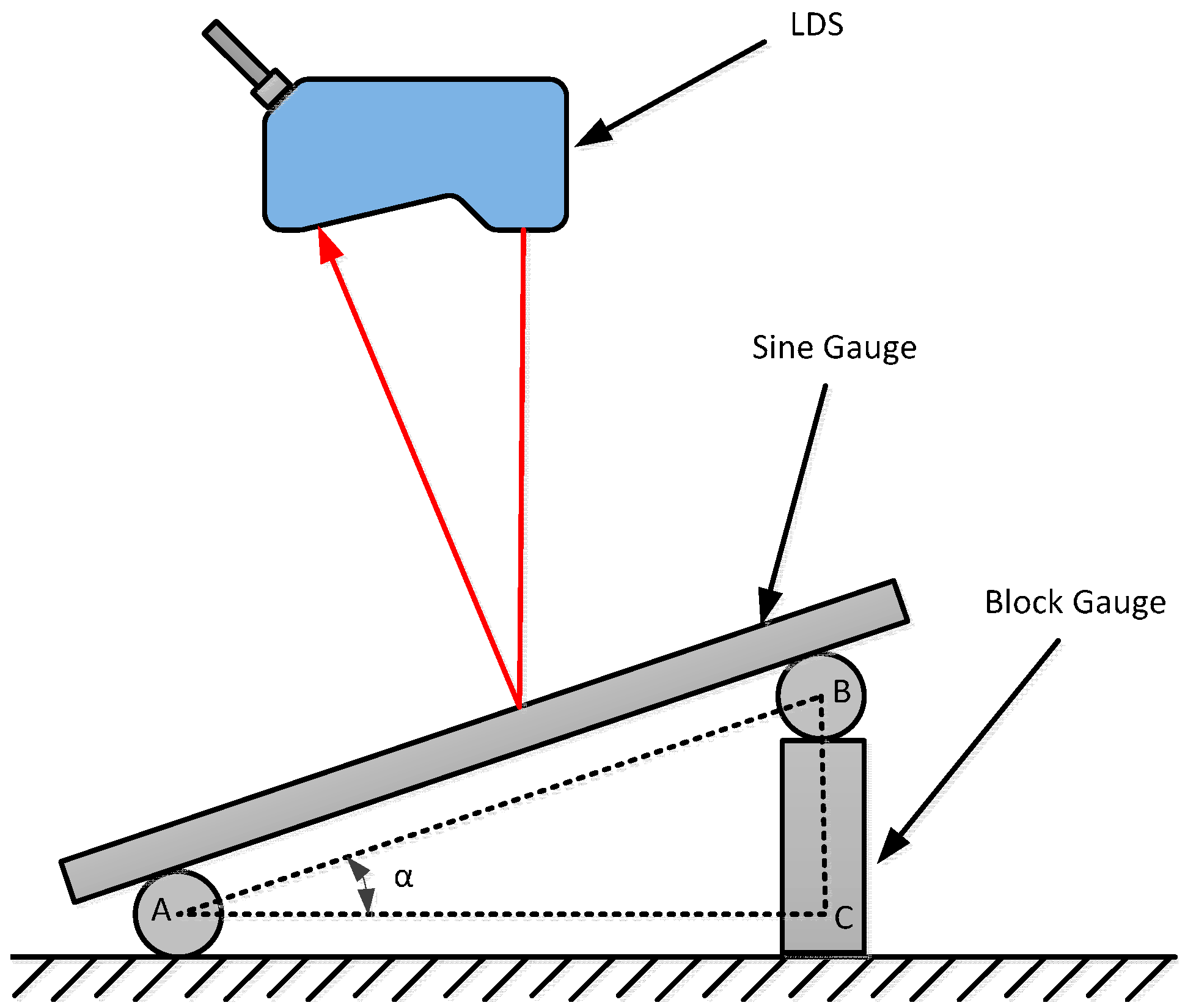
3.3. Inclination Error Compensation Experiment


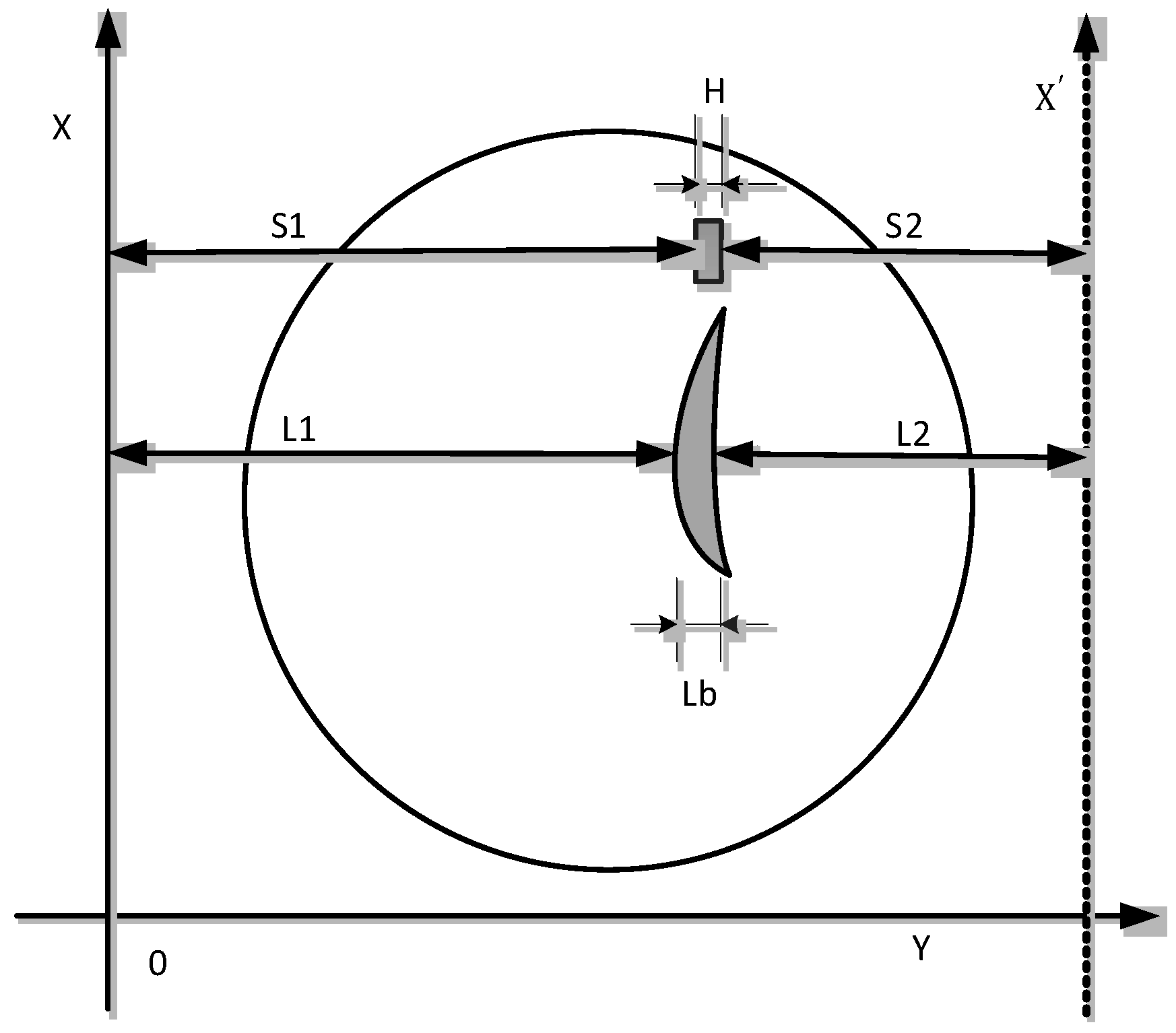
4. The Blade Surface Measurement Path Planning
4.1. Measurement Path Constraint Condition
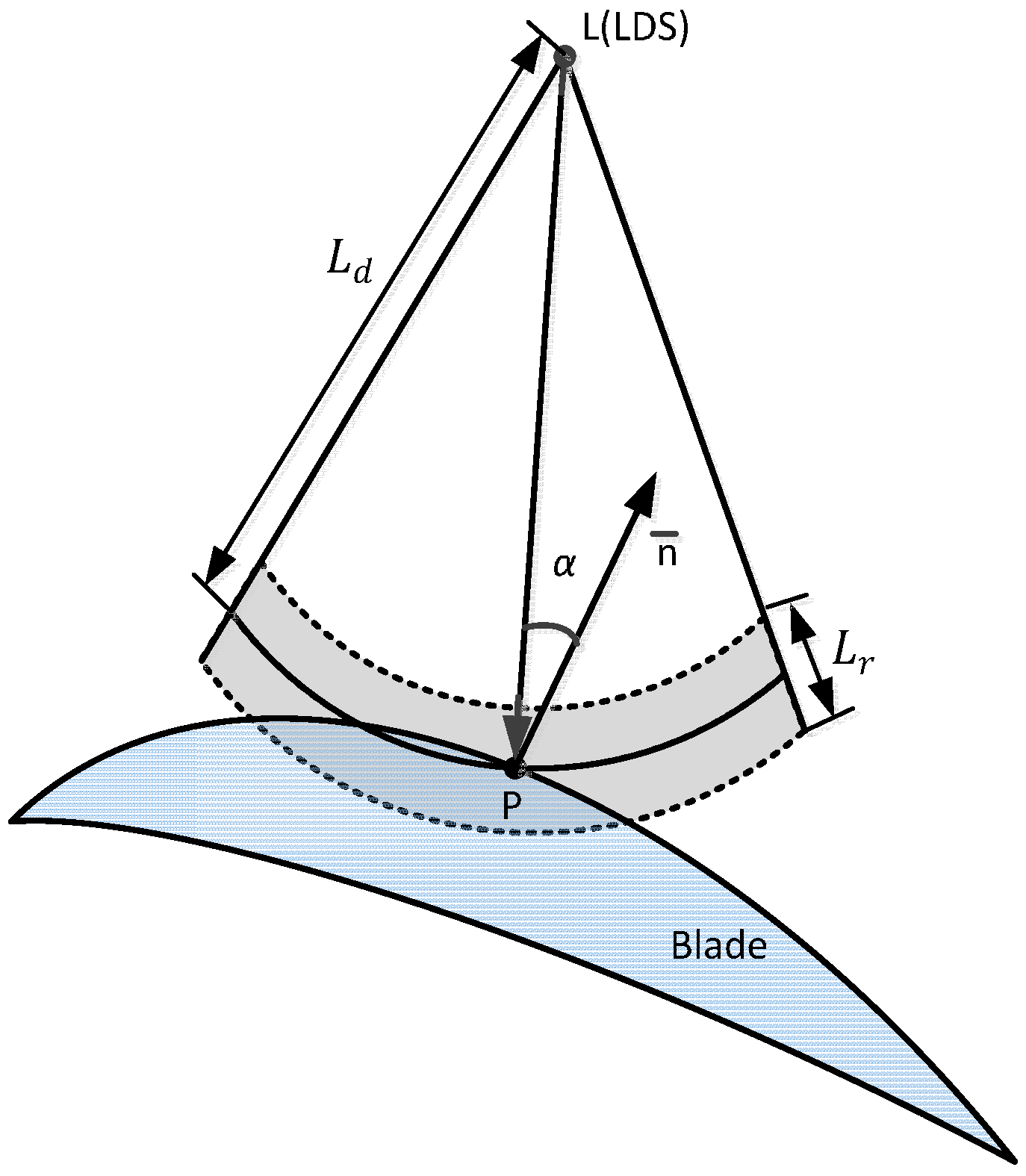
4.2. The LDS Scanning Path Planning
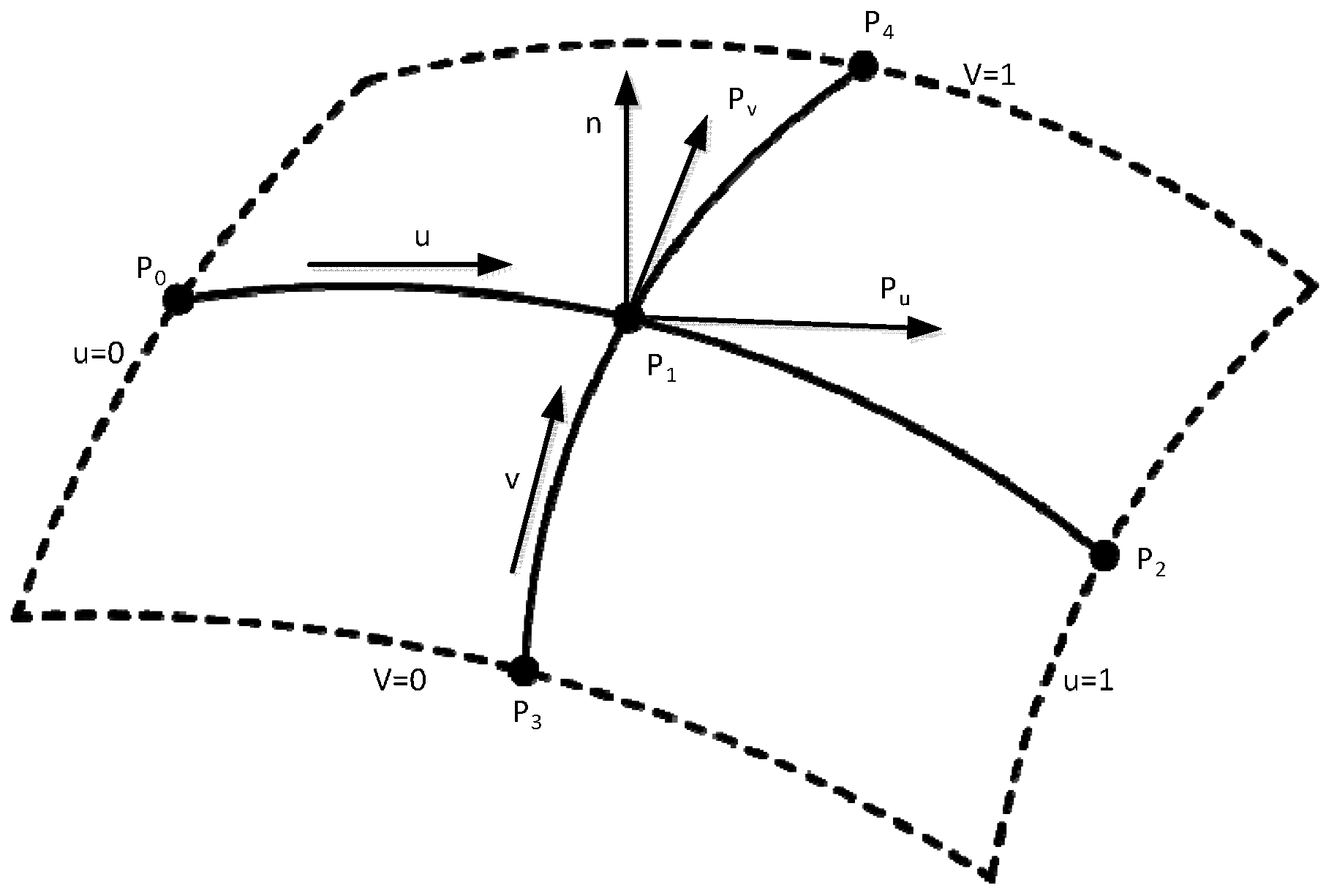
4.3. The Calculation Method of the Blade Surface Inclination Angle
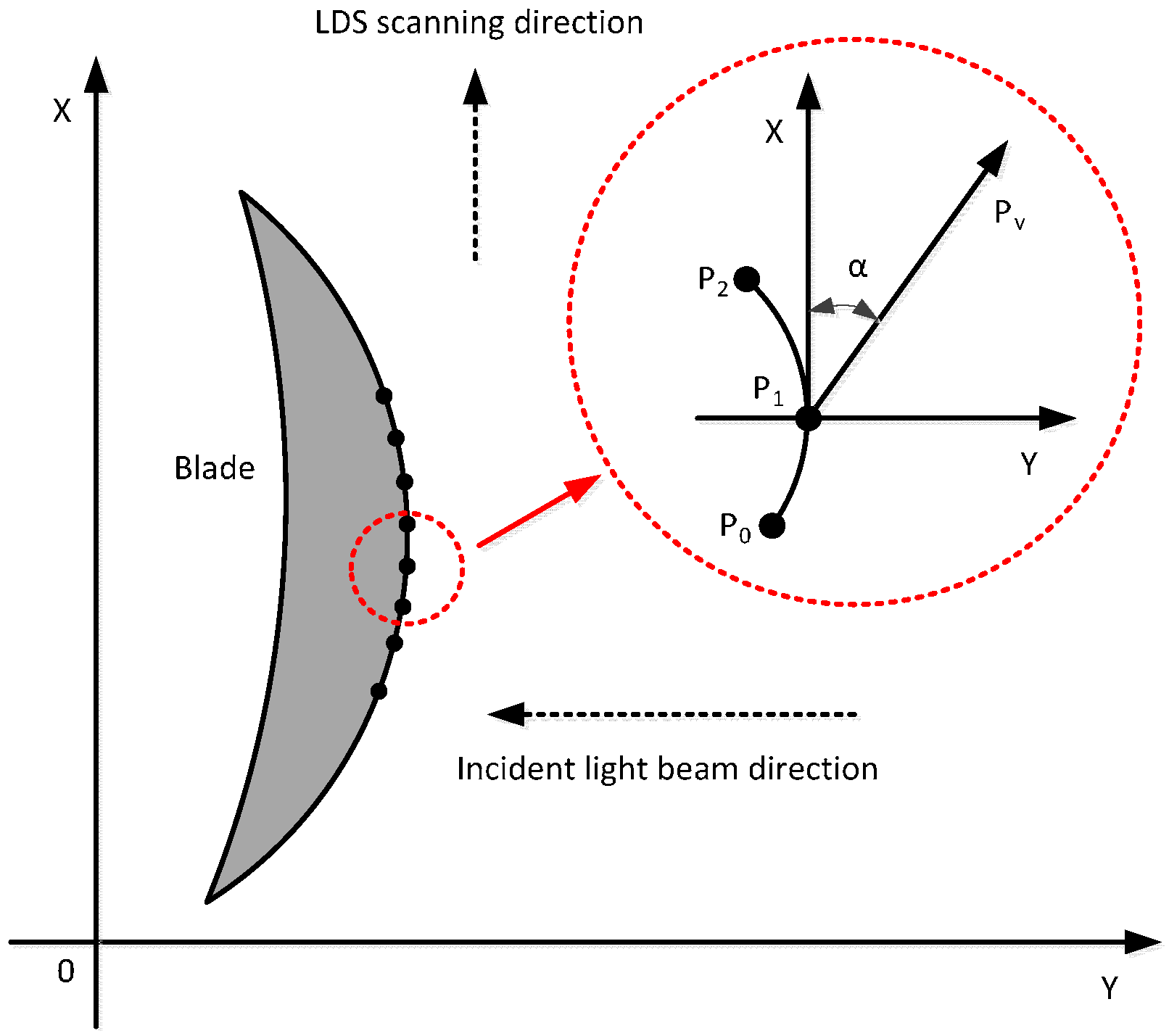
5. The Experimental Data Analysis
| No. | X-Axis | RawL2 | Angle | Error | Exact |
|---|---|---|---|---|---|
| … | … | … | … | … | … |
| 220 | 88.7216 | 1.3578 | 12.1418 | 0.0025 | 1.3553 |
| 221 | 89.7509 | 1.4703 | 13.4518 | 0.0027 | 1.4676 |
| 222 | 90.5905 | 1.6135 | 14.1069 | 0.0030 | 1.6105 |
| 223 | 91.4285 | 1.7280 | 14.1837 | 0.0032 | 1.7248 |
| 224 | 92.4542 | 1.8773 | 14.3970 | 0.0034 | 1.8739 |
| 225 | 93.2782 | 2.0230 | 15.0744 | 0.0037 | 2.0193 |
| 226 | 94.1166 | 2.1383 | 16.3334 | 0.0039 | 2.1344 |
| 227 | 94.9440 | 2.2918 | 15.9000 | 0.0042 | 2.2876 |
| 228 | 95.9858 | 2.4555 | 16.1109 | 0.0046 | 2.4509 |
| 229 | 96.8228 | 2.6163 | 16.5751 | 0.0049 | 2.6114 |
| 230 | 97.6458 | 2.7550 | 17.0762 | 0.0051 | 2.7499 |
| 231 | 98.4832 | 2.9133 | 17.9380 | 0.0054 | 2.9079 |
| 232 | 99.5132 | 3.1010 | 17.8846 | 0.0058 | 3.0952 |
| 233 | 100.3537 | 3.2683 | 17.6309 | 0.0061 | 3.2622 |
| 234 | 101.1788 | 3.4335 | 18.4268 | 0.0065 | 3.4270 |
| 235 | 102.0151 | 3.5970 | 18.5351 | 0.0068 | 3.5902 |
| 236 | 103.0547 | 3.7943 | 19.1727 | 0.0072 | 3.7871 |
| 237 | 103.8791 | 3.9696 | 19.5836 | 0.0075 | 3.9621 |
| 238 | 104.7187 | 4.1545 | 19.7252 | 0.0079 | 4.1466 |
| 239 | 105.7483 | 4.3723 | 19.6610 | 0.0083 | 4.3640 |
| 240 | 106.5852 | 4.5598 | 19.7357 | 0.0087 | 4.5511 |
| 241 | 107.4090 | 4.7570 | 20.1276 | 0.0091 | 4.7479 |
| 242 | 108.2464 | 4.9363 | 19.6711 | 0.0095 | 4.9268 |
| 243 | 109.2880 | 5.1550 | 20.9436 | 0.0099 | 5.1451 |
| 244 | 110.1149 | 5.3635 | 21.2326 | 0.0104 | 5.3531 |
| … | … | … | … | … | … |

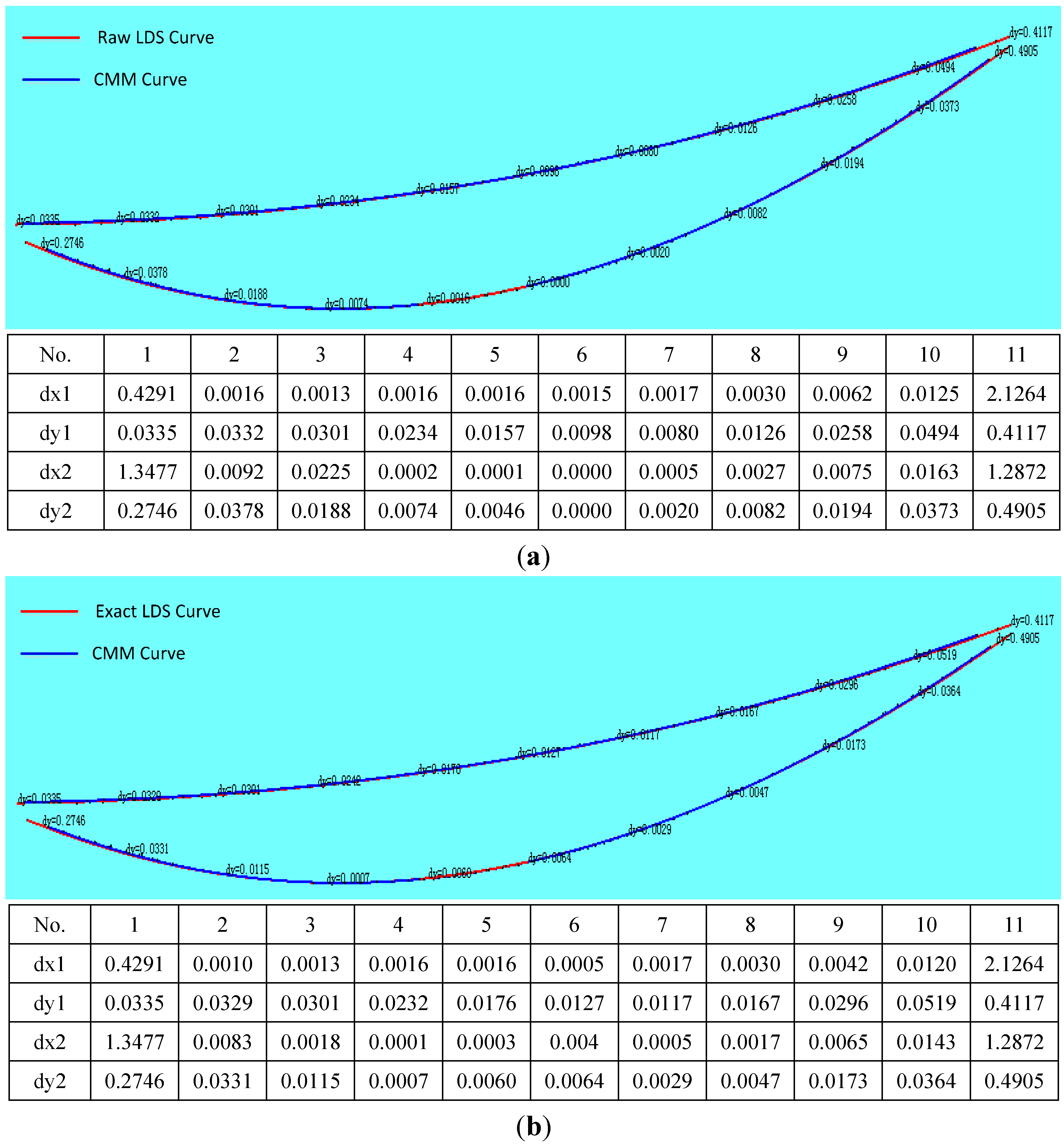
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lin, X.; Guo, Y.; Wu, G. CMM measuring data processing algorithms for blades about the contour measurement. Chin. J. Sci. Instrum. 2013, 34, 2442–2450. [Google Scholar]
- Fu, Y.; Wan, M. The three-dimensional measurement research of aero-engine blade based on structured light. In Proceedings of International Symposium on Photoelectronic Detection and Imaging 2011: Advances in Imaging Detectors and Applications, Beijing, China, 24 May 2011.
- Li, H.-W.; Shen, Z.-C.; Qin, Y.-H.; Bao, H.; Zhou, Y.-Z. Application of phase-measurementprofilometry in blade measurement. J. Aerosp. Power 2012, 27, 275–281. [Google Scholar]
- Mansour, G. A developed algorithm for simulation of blades to reduce the measurement points and time on coordinate measuring machine (CMM). Measurement 2014, 54, 51–57. [Google Scholar] [CrossRef]
- Harizanova, J.; Sainov, V. Three-dimensional profilometry by symmetrical fringes projection technique. Opt. Lasers Eng. 2006, 44, 1270–1282. [Google Scholar] [CrossRef]
- Hu, Y.; Xi, J.; Li, E.; Chicharo, J.; Yang, Z. Three-dimensional profilometry based on shift estimation of projected fringe patterns. Appl. Opt. 2006, 45, 678–687. [Google Scholar] [CrossRef] [PubMed]
- Guan, C.; Hassebrook, L.G.; Lau, D.L. Composite structured light pattern for threedimensional video. Opt. Exp. 2003, 11, 406–417. [Google Scholar] [CrossRef]
- Fan, K.-C.; Tsai, T.-H. Optimal shape error analysis of the matching image for a free-form surface. Robot. Comput. Integr. Manuf. 2001, 17, 215–222. [Google Scholar] [CrossRef]
- Kouyi, G.L.; Vazquez, J.; Poulet, J.B. 3D free surface measurement and numerical modelling of flows in storm overflows. Flow Meas. Instrum. 2003, 14, 79–87. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, G.; Wei, Z.; Zhou, F. Large 3D free surface measurement using a mobile coded light-based stereo vision system. Sens. Actuators A 2006, 132, 460–471. [Google Scholar] [CrossRef]
- Nishikawaa, S.; Ohnoa, K.; Mori, M.; Fujishima, M. Non-Contact Type On-Machine Measurement System for Turbine Blade. Procedia CIRP 2014, 24, 1–6. [Google Scholar] [CrossRef]
- Zhang, S.G.; Ajmal, A.; Wootton, J.; Chisholm, A. A feature-based inspection process planning system for co-ordinate measuring machine (CMM). J. Mater. Process. Technol. 2000, 107, 111–118. [Google Scholar] [CrossRef]
- Hsu, T.-H.; Lai, J.-Y.; Ueng, W.-D. On the development of airfoil section inspection and analysis technique. Int. J. Adv. Manuf. Technol. 2006, 30, 129–140. [Google Scholar] [CrossRef]
- Lin, A.C.; Lin, S.-Y.; Fang, T.-H. Automated sequence arrangement of 3D point data for surface fitting in reverse engineering. Comput. Ind. 1998, 35, 149–173. [Google Scholar] [CrossRef]
- Jin, H.Y. Based on Laser Trigonometry Measuring Technology Research. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2006. [Google Scholar]
- Sun, J.; Zhang, J.; Liu, Z.; Zhang, G. A vision measurement model of laser displacement sensor and its calibration method. Opt. Lasers Eng. 2013, 51, 1344–1352. [Google Scholar] [CrossRef]
- Li, B.; Li, F.; Liu, H.; Cai, H.; Mao, X.; Peng, F. A measurement strategy and an error-compensation model for the on-machine laser measurement of large-scale free-form surfaces. Meas. Sci. Technol. 2014, 25. [Google Scholar] [CrossRef]
- Lee, K.H.; Park, H.; Son, S.A. framework for laser scan planning of freeform surfaces. Int. J. Adv. Manuf. Technol. 2001, 17, 171–180. [Google Scholar] [CrossRef]
- Funtowicz, F.; Zussman, E.; Meltser, M. Optimal scanning of freeform surfaces using a laser-stripe. In Proceedings of Israel-Korea Geometric Modeling Conference, Tel Aviv, Israel, February 1998; pp. 47–50.
- Son, S.; Kim, S.; Lee, K.H. Path planning of multi-patched freeform surfaces for laser scanning. Int. J. Adv. Manuf. Technol. 2003, 22, 424–435. [Google Scholar] [CrossRef]
- Lee, R.T.; Shiou, F.J. Multi-beam laser probe for measuring position and orientation of freeform surface. Measurement 2011, 44, 1–10. [Google Scholar] [CrossRef]
- Lee, R.T.; Shiou, F.J. Calculation of the unit normal vector using the cross-curve moving mask method for probe radius compensation of a freeform surface measurement. Measurement 2010, 43, 469–478. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, B.; Li, B. A Rapid Method to Achieve Aero-Engine Blade Form Detection. Sensors 2015, 15, 12782-12801. https://doi.org/10.3390/s150612782
Sun B, Li B. A Rapid Method to Achieve Aero-Engine Blade Form Detection. Sensors. 2015; 15(6):12782-12801. https://doi.org/10.3390/s150612782
Chicago/Turabian StyleSun, Bin, and Bing Li. 2015. "A Rapid Method to Achieve Aero-Engine Blade Form Detection" Sensors 15, no. 6: 12782-12801. https://doi.org/10.3390/s150612782
APA StyleSun, B., & Li, B. (2015). A Rapid Method to Achieve Aero-Engine Blade Form Detection. Sensors, 15(6), 12782-12801. https://doi.org/10.3390/s150612782





